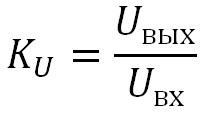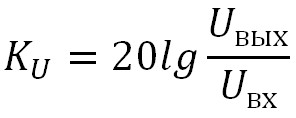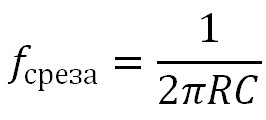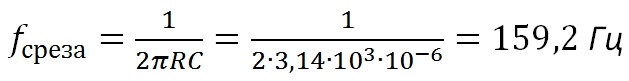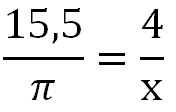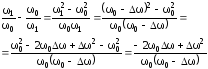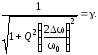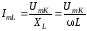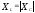Полоса пропуская как найти

Амплитудно-частотная характеристика

Аббревиатура АЧХ расшифровывается как амплитудно-частотная характеристика. На английском этот термин звучит как «frequency response», что в дословном переводе означает «частотный отклик». Амплитудно-частотная характеристика цепи показывает зависимость уровня сигнала на выходе данного устройства от частоты передаваемого сигнала при постоянной амплитуде синусоидального сигнала на входе этого устройства. АЧХ может быть определена аналитически через формулы, либо экспериментально. Любое устройство предназначено для передачи (или усиления) электрических сигналов.  АЧХ устройства определяется по зависимости  коэффициента передачи (или коэффициента усиления) от частоты.

Коэффициент передачи

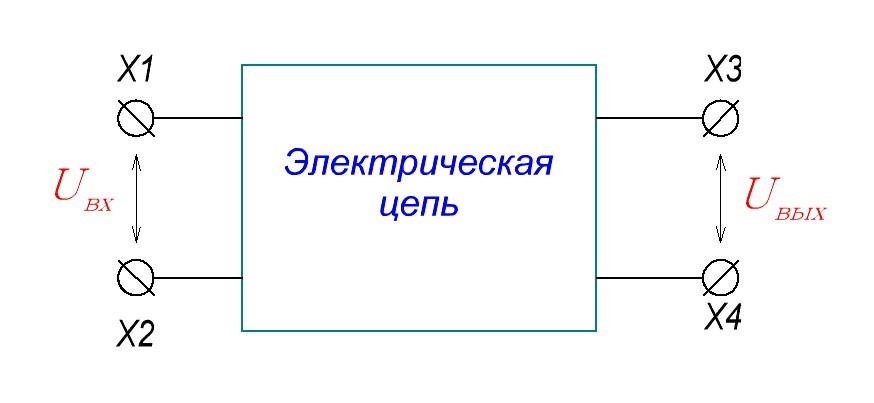
Что такое коэффициент передачи? Коэффициент передачи — это отношение напряжения на выходе цепи к напряжению на ее входе. Или формулой:

где

U_вых   — напряжение на выходе цепи

U_вх  — напряжение на входе цепи

В усилительных устройствах коэффициент передачи больше единицы. Если устройство вносит ослабление передаваемого сигнала, то коэффициент передачи меньше единицы.

Коэффициент передачи может быть выражен через децибелы:

Строим АЧХ RC-цепи в программе Proteus

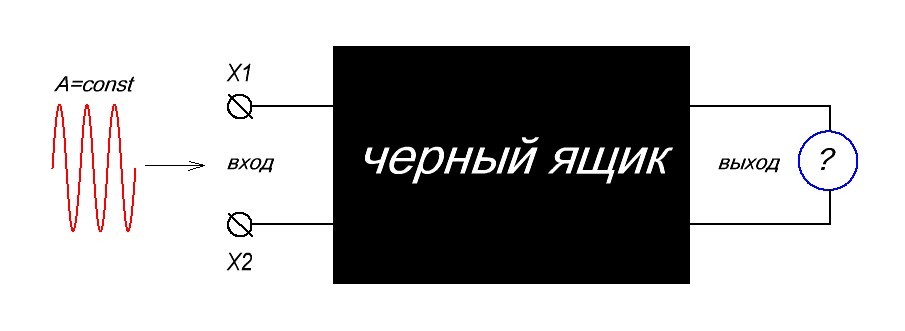
Для того, чтобы досконально разобраться, что такое АЧХ, давайте рассмотрим рисунок ниже.

Итак, имеем «черный ящик», на вход которого мы будем подавать синусоидальный сигнал, а на выходе черного ящика мы будем снимать сигнал. Должно соблюдаться условие: нужно менять частоту входного синусоидального сигнала, но его амплитуда должна быть постоянной.

Что нам  делать дальше? Надо измерить амплитуду сигнала на выходе после черного ящика при интересующих нас значениях частоты входного сигнала. То есть мы должны изменять частоту входного сигнала от 0 Герц (постоянный ток) и до какого-либо конечного значения, которое будет удовлетворять нашим целям, и смотреть, какая амплитуда сигнала будет на выходе при соответствующих значениях на входе.

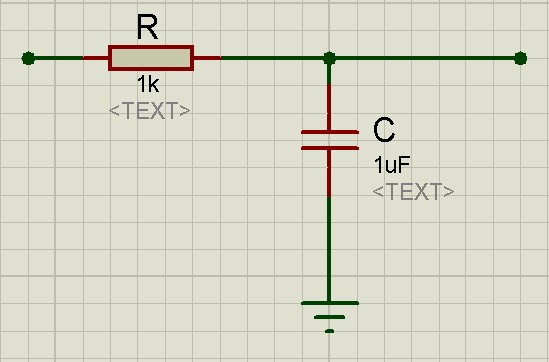
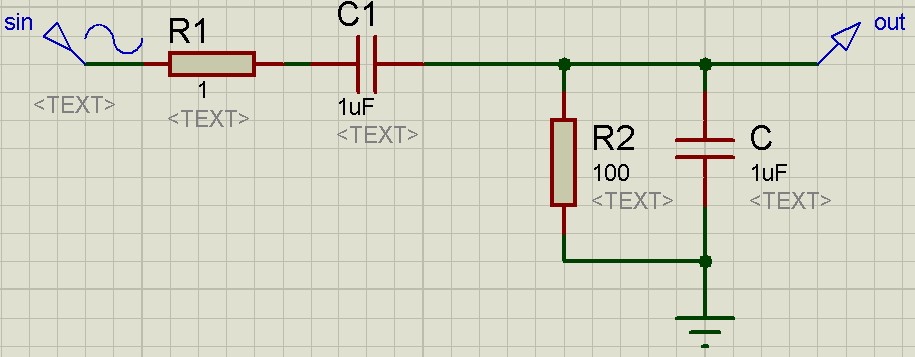
Давайте разберем все это дело на примере. Пусть в черном ящике у нас будет самая простая RC-цепь с уже известными номиналами радиоэлементов.

Как я уже говорил, АЧХ может быть построено экспериментально, а также с помощью программ-симуляторов. На мой взгляд, самый простой и мощный симулятор для новичков — это Proteus. С него и начнем.

Собираем данную схему в рабочем поле программы Proteus

Для того, чтобы подать на вход схемы синусоидальный сигнал, мы кликаем на кнопочку «Генераторы», выбираем SINE, а потом соединяем его со входом нашей схемы.

Для измерения выходного сигнала достаточно кликнуть на значок  с буквой «V»  и соединить выплывающий значок с выходом нашей схемы:

Для эстетики, я уже поменял название входа и выхода на sin и out. Должно получиться как-то вот так:

Ну вот, пол дела уже сделано.

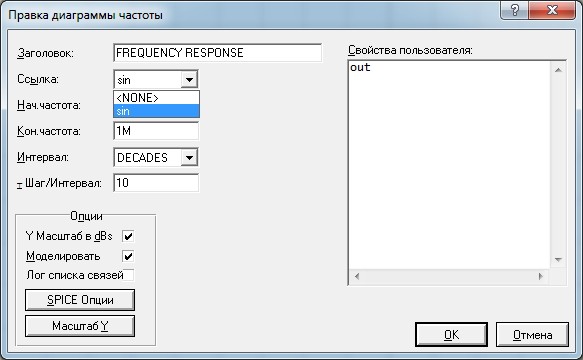
Теперь осталось добавить важный инструмент. Он называется «frequency response», как я уже говорил, в дословном переводе с английского — «частотный отклик». Для этого нажимаем кнопочку «Диаграмма» и в списке выбираем «frequency»

На экране появится что-то типа этого:

Кликаем ЛКМ два раза и открывается вот такое окошко, где в качестве входного сигнала мы выбираем наш генератор синуса (sin), который у нас сейчас задает частоту на входе.

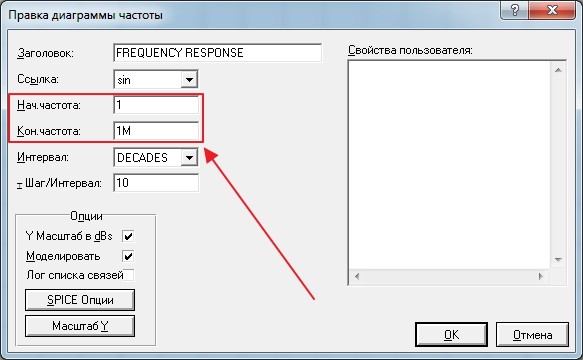
Здесь же выбираем диапазон частоты, который будем «загонять» на вход нашей цепи. В данном случае это диапазон от 1 Гц и до 1 МГц. При установке начальной частоты в 0 Герц Proteus выдает ошибку. Поэтому, ставьте начальную частоту близкую к нулю.

Нажимаем ОК.

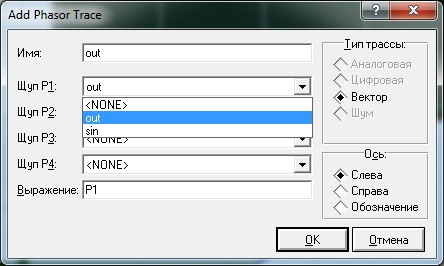
Далее нажимаем ПКМ на самой табличке Frequency Response и видим вот такой выплывающий список, в котором нажимаем «Добавить трассы»

Долго не думая, выбираем в первом же окошке наш выход out

и в результате должно появится окошко с нашим выходом

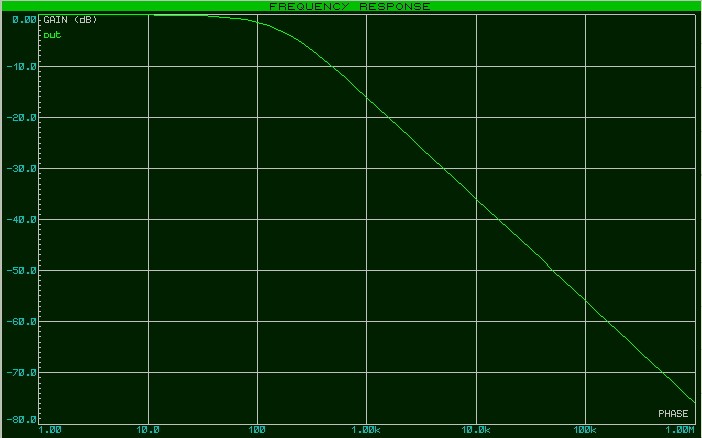
Нажимаем пробел и радуемся результату

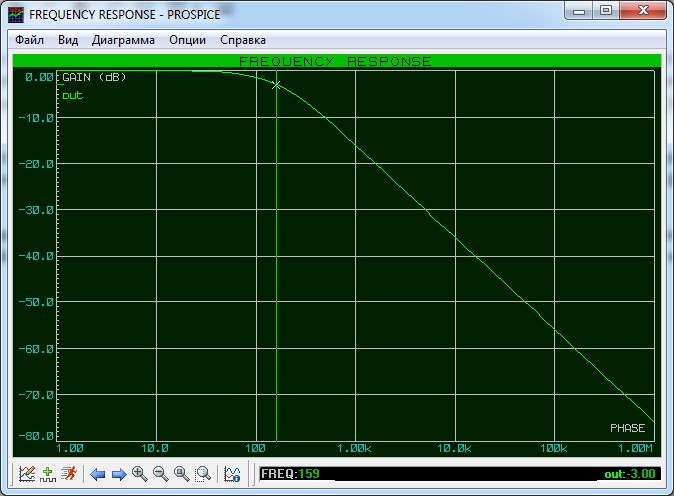
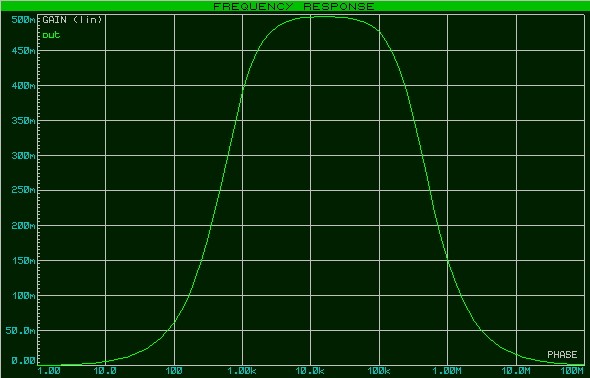
Итак, что интересного можно обнаружить, если взглянуть на нашу АЧХ? Как вы могли заметить, амплитуда на выходе цепи падает с увеличением частоты. Это означает, что наша RC-цепь является своеобразным частотным фильтром. Такой фильтр пропускает низкие частоты, в нашем случае до 100 Герц, а потом с ростом частоты начинает их «давить». И чем больше частота, тем больше он ослабляет амплитуду выходного сигнала. Поэтому, в данном случае, наша  RC-цепь является самым простейшим фильтром низкой частоты (ФНЧ).

Полоса пропускания

В среде радиолюбителей и не только встречается также такой термин, как полоса пропускания. Полоса пропускания — это диапазон частот, в пределах которого АЧХ радиотехнической цепи или устройства достаточно равномерна, чтобы обеспечить передачу сигнала без существенного искажения его формы.

Как же определить полосу пропускания? Это сделать довольно легко. Достаточно на графике АЧХ найти уровень в -3 дБ от максимального значения АЧХ и найти точку пересечения прямой с графиком. В нашем случае это можно сделать легче пареной репы. Достаточно развернуть нашу диаграмму на весь экран и с помощью встроенного маркера посмотреть частоту на уровне в -3 дБ в точке пересечения с нашим графиком АЧХ. Как мы видим, она равняется 159 Герц.

Частота, которая получается на уровне в -3 дБ, называется частотой среза. Для RC-цепи ее можно найти по формуле:

Для нашего случая расчетная частота получилась 159,2 Гц, что подтверждает и Proteus.

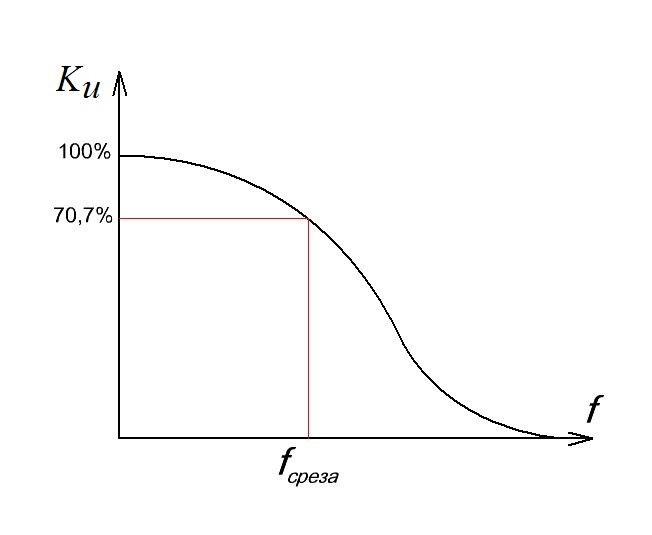
Кто не желает связываться  с децибелами, то можно провести линию на уровне 0,707 от максимальной амплитуды  выходного сигнала и смотреть пересечение с графиком. В данном примере, для наглядности, я взял максимальную амплитуду за уровень в  100%.

Как построить АЧХ на практике?

Как построить АЧХ на практике, имея в своем арсенале генератор частоты и осциллограф?

Итак, поехали. Собираем нашу цепь в реале:

Ну а теперь цепляем ко входу схемы генератор частоты, а с помощью осциллографа следим за амплитудой выходного сигнала, а также будем следить за амплитудой входного сигнала, чтобы мы были точно уверены, что на вход RC-цепи подается синус с постоянной амплитудой.

Для экспериментального изучения АЧХ  нам потребуется собрать простенькую схемку:

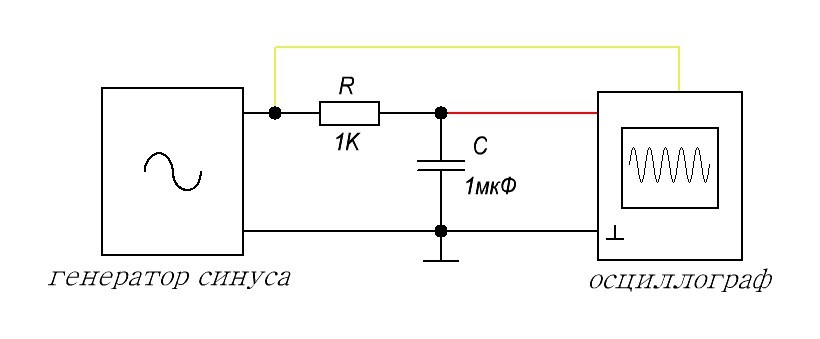
Наша задача состоит в том, чтобы менять частоту генератора и уже наблюдать, что покажет осциллограф на выходе цепи. Мы будем прогонять нашу цепь по частотам, начиная от самой малой. Как я уже сказал, желтый канал предназначен для визуального контроля, что мы честно проводим опыт.

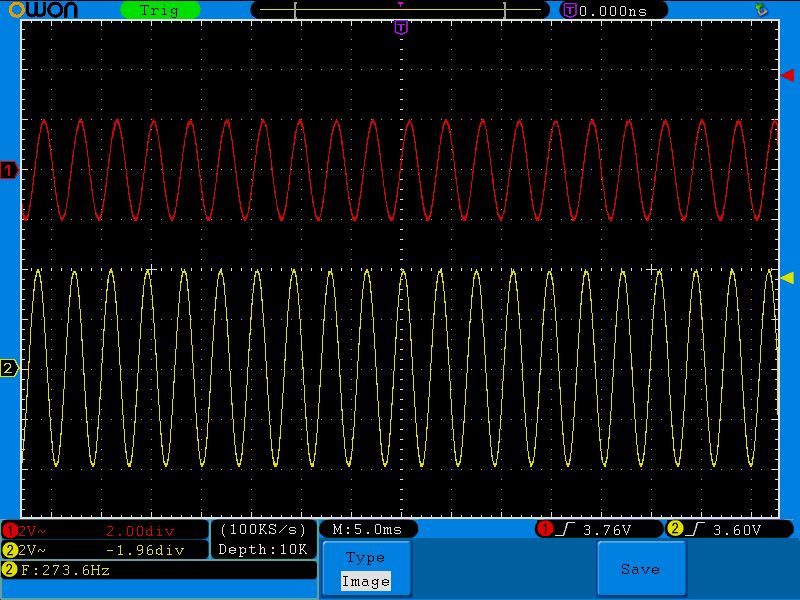
Постоянный ток, проходящий через эту цепь,  на выходе будет давать амплитудное значение входного сигнала, поэтому первая точка будет иметь координаты (0;4), так как амплитуда нашего входного сигнала 4 Вольта.

Следующее значение смотрим на осциллограмме:

Частота 15 Герц, амплитуда на выходе 4 Вольта. Итак, вторая точка (15;4)

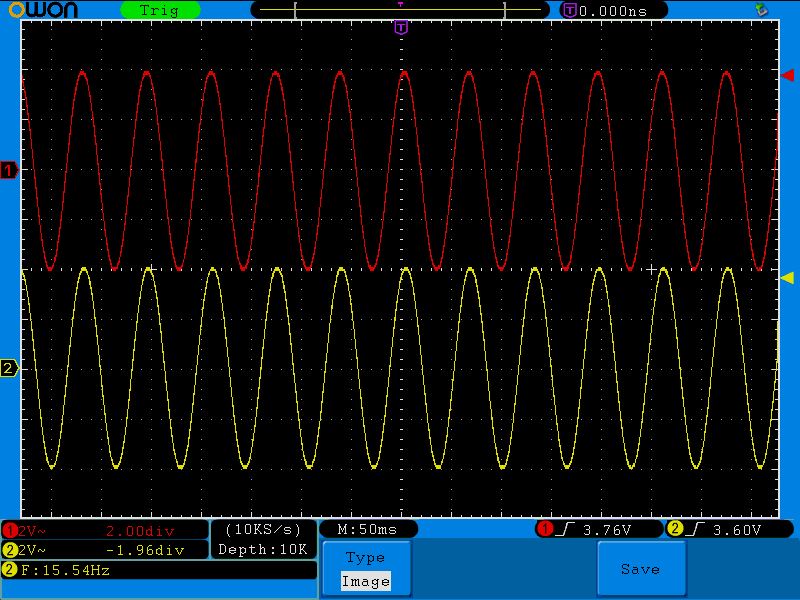
Третья точка (72;3.6). Обратите внимание на амплитуду выходного красного сигнала. Она начинает проседать.

Четвертая точка (109;3.2)

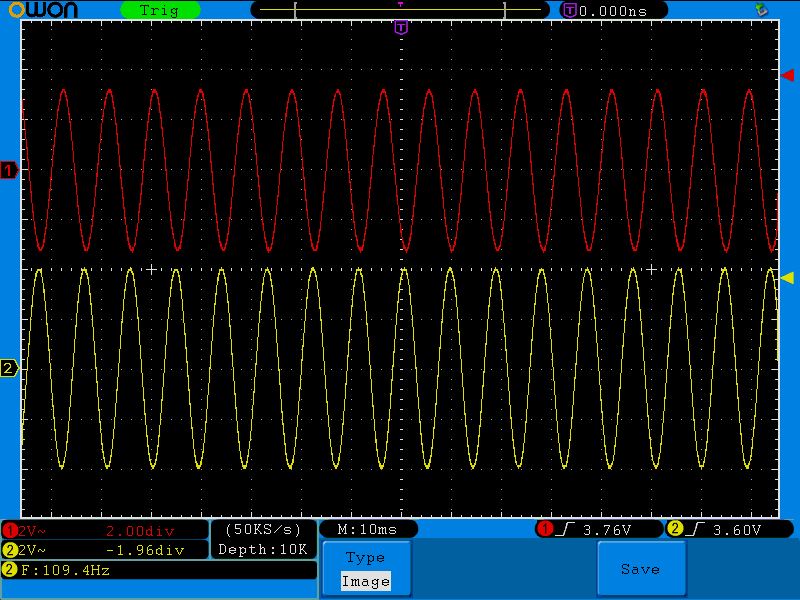
Пятая точка (159;2.8)

Шестая точка (201;2.4)

Седьмая точка (273;2)

Восьмая точка (361;1.6)

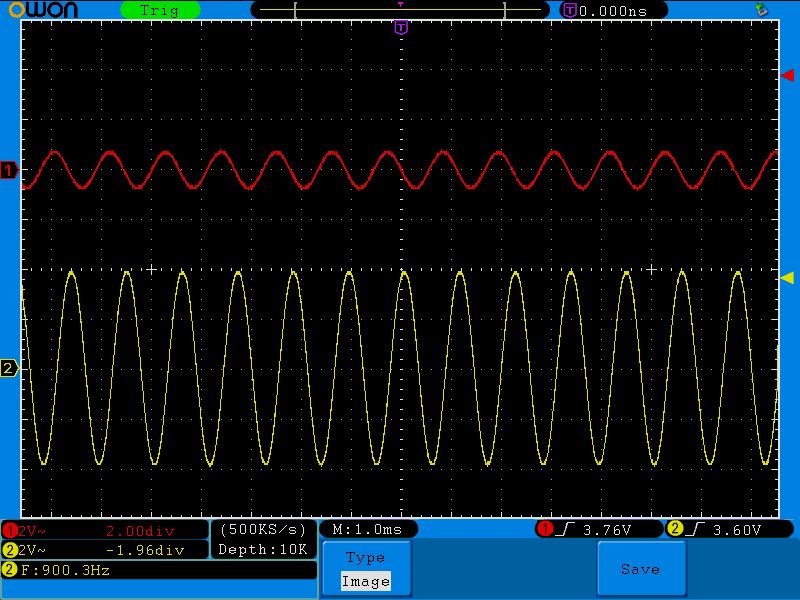
Девятая точка (542;1.2)

Десятая точка (900;0.8)

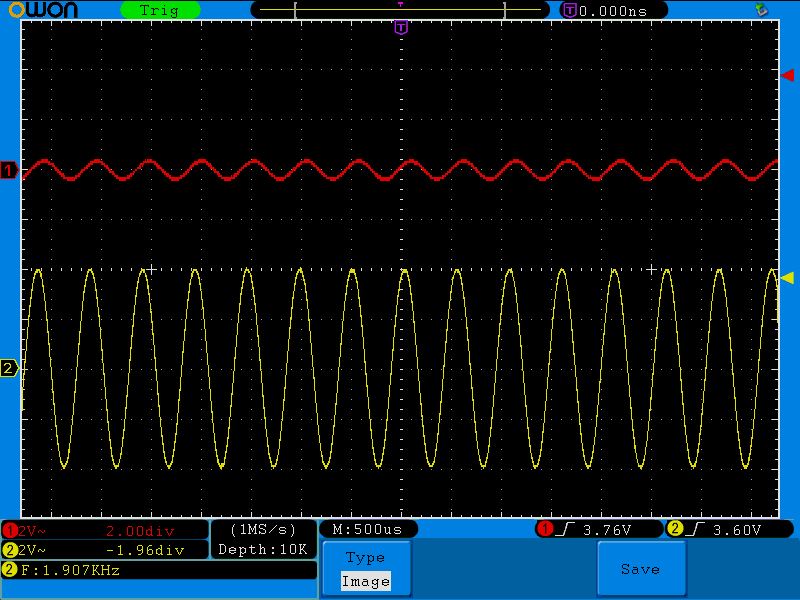
Ну и последняя одиннадцатая точка (1907;0.4)

В результате измерений у нас получилась табличка:

Строим график по полученным значениям и получаем нашу экспериментальную АЧХ 

Получилось не так, как в технической литературе. Оно и понятно, так как по Х берут логарифмический масштаб, а не линейный, как у меня на графике. Как вы видите, амплитуда выходного сигнала будет и дальше понижаться с увеличением частоты. Для того, чтобы еще более точно построить нашу АЧХ, требуется взять как можно больше точек.

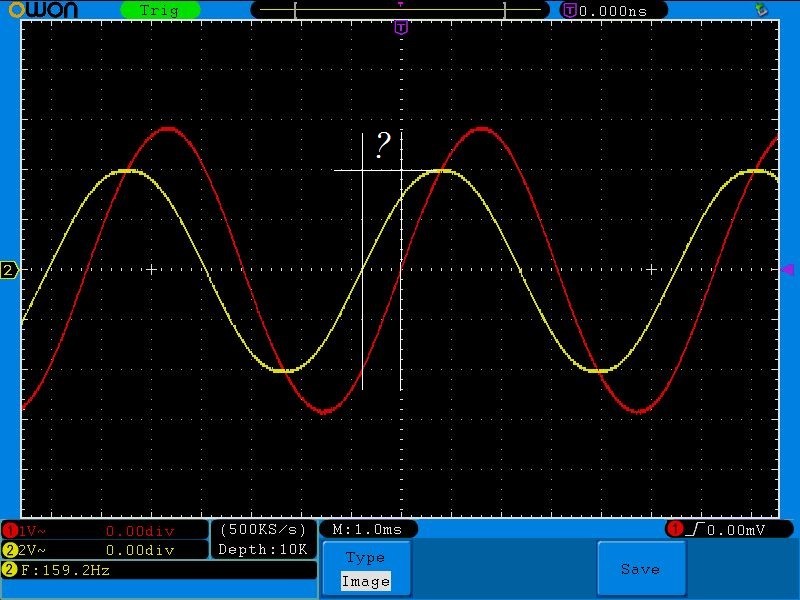
Давайте вернемся к этой осциллограмме:

Здесь на частоте среза амплитуда выходного сигнала получилась ровно 2,8 Вольт, которые как раз и находятся на уровне в 0,707. В нашем случае 100% это 4 Вольта. 4х0,707=2,82 Вольта.

АЧХ полосового фильтра

Существуют также схемы, АЧХ которых имеет вид холма или ямы. Давайте рассмотрим один из примеров. Мы будем рассматривать так называемый полосовой фильтр, АЧХ которого имеет вид холма.

Собственно сама схема:

А вот ее АЧХ:

Особенность таких фильтров, что они имеют две частоты среза. Определяются они также на уровне в -3дБ  или на уровне в  0,707 от максимального значения коэффициента передачи, а еще точнее K_{u max}/√2.

Так как в дБ смотреть график неудобно, поэтому я переведу его в линейный режим по оси Y, убирая маркер

В результате перестроения получилась такая АЧХ:

Максимальное значение на выходе составило 498 мВ при амплитуде входного сигнала в 10 Вольт. Мдя, неплохой «усилитель») Итак, находим значение частот на уровне в 0,707х498=352мВ. В результате получились две частоты среза — это частота в 786 Гц и в 320 КГц. Следовательно, полоса пропускания данного фильтра от 786Гц и до 320 КГц.

На практике для получения АЧХ используются приборы, называемые характериографами для исследования АЧХ. Вот так выглядит один из образцов Советского Союза

Фазо-частотная характеристика

ФЧХ расшифровывается как фазо-частотная характеристика, phase response — фазовый отклик. Фазо-частотная характеристика — это зависимость сдвига по фазе между синусоидальными сигналами на входе и выходе устройства от частоты входного колебания.

Разность фаз

Думаю, вы не раз слышали такое выражение, как » у него произошел сдвиг по фазе». Это выражение не так давно пришло в наш лексикон и обозначает оно то, что человек слегка двинулся умом. То есть было все нормально, а потом раз! И все :-). И в электронике такое тоже часто бывает)  Разницу между фазами сигналов в электронике называют разностью фаз. Вроде бы «загоняем» на вход  какой-либо сигнал, а выходной сигнал ни с того ни с сего взял и сдвинулся по времени, относительно входного сигнала.

Для того, чтобы определить разность фаз, должно выполняться условие: частоты сигналов должны быть равны. Пусть даже один сигнал будет с амплитудой в Киловольт, а другой в милливольт. Неважно! Лишь бы соблюдалось равенство частот. Если бы  условие равенства не соблюдалось, то сдвиг фаз между сигналами все время бы изменялся.

Для определения сдвига фаз используют двухканальный осциллограф. Разность фаз чаще всего обозначается буквой φ и на осциллограмме это выглядит примерно так:

Строим ФЧХ RC-цепи в Proteus

Для нашей исследуемой цепи

Для того, чтобы отобразить ее в Proteus мы снова открываем функцию «frequency response»

Все  также выбираем наш генератор

Не забываем проставлять испытуемый диапазон частот:

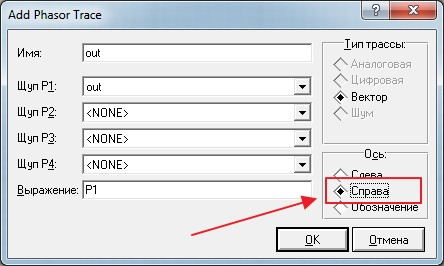
Далее нажимаем ПКМ на самой табличке Frequency Response и видим вот такой выплывающий список, в котором нажимаем «Добавить трассы»

Долго не думая, выбираем в первом же окошке наш выход out

И теперь главное отличие: в колонке «Ось» ставим маркер на «Справа»

Нажимаем пробел и вуаля!

Можно его развернуть на весь экран

При большом желании эти две характеристики можно объединить на одном графике

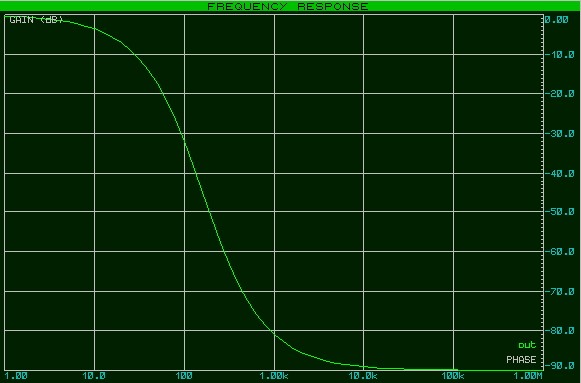
Обратите внимание, что на частоте среза сдвиг фаз между входным и выходным сигналом составляет 45 градусов или в радианах п/4 (кликните для увеличения)

В данном опыте при частоте более 100 КГц разность фаз достигает значения в 90 градусов (в радианах π/2) и уже не меняется.

Строим ФЧХ на практике

ФЧХ на практике можно измерить также, как и АЧХ, просто наблюдая разность фаз и записывая показания в табличку. В этом опыте мы просто убедимся, что на частоте среза у нас действительно разность фаз между входным и выходным сигналом будет 45 градусов или  π/4 в радианах.

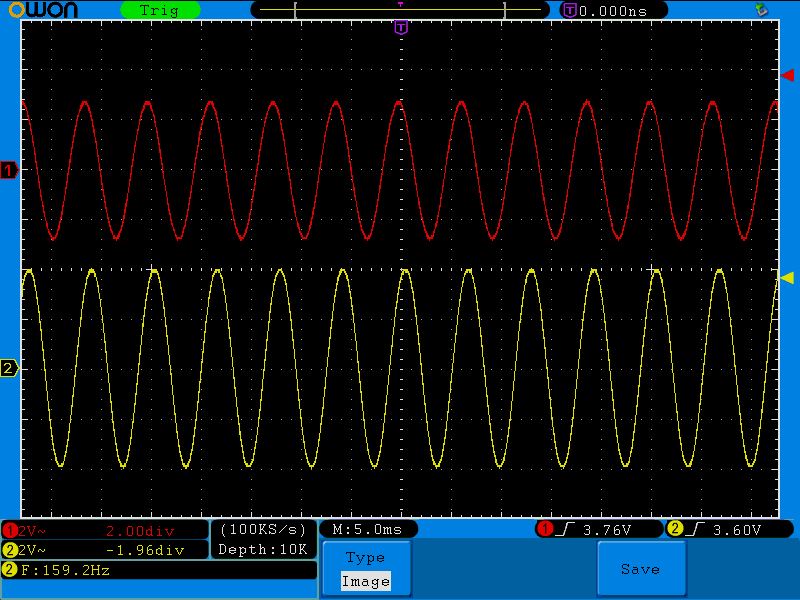
Итак, у меня получилась вот такая осциллограмма на частоте среза в 159,2 Гц

Нам надо узнать разность фаз между этими двумя сигналами

Весь период — это 2п, значит половина периода — это π. На полупериод у нас приходится где-то 15,5 делений. Между двумя сигналами разность в 4 деления. Составляем пропорцию:

Отсюда х=0,258п или можно сказать почти что 1/4п. Следовательно, разница фаз между двумя этими сигналами равняется п/4, что почти в точности совпало с расчетными значениями в Proteus.

Если Вы лучше воспринимаете информацию через видео, то к Вашему вниманию:

Резюме

Амплитудно-частотная характеристика цепи показывает зависимость уровня сигнала на выходе данного устройства от частоты передаваемого сигнала при постоянной амплитуде синусоидального сигнала на входе этого устройства.

И еще интересная статья — последовательное и параллельное соединение проводников.

Фазо-частотная характеристика — это зависимость сдвига по фазе между синусоидальными сигналами на входе и выходе устройства от частоты входного колебания.

Коэффициент передачи — это отношение напряжения на выходе цепи к напряжению на ее входе. Если коэффициент передачи больше единицы, то электрическая цепь усиливает входной ссигнал, если же меньше единицы, то ослабляет.

Полоса пропускания — это диапазон частот, в пределах которого АЧХ радиотехнической цепи или устройства достаточно равномерна, чтобы обеспечить передачу сигнала без существенного искажения его формы. Определяется по уровню 0,707 от максимального значения АЧХ.

Полоса пропускания

Полоса пропускания (прозрачности) — диапазон частот, в пределах которого амплитудно-частотная характеристика (АЧХ) акустического, радиотехнического, оптического или механического устройства достаточно равномерна для того, чтобы обеспечить передачу сигнала без существенного искажения его формы. Иногда, вместо термина «полоса пропускания», используют термин «эффективно передаваемая полоса частот (ЭППЧ)». В ЭППЧ сосредоточена основная энергия сигнала (не менее 90%). Этот диапазон частот устанавливается для каждого сигнала экспериментально в соответствии с требованиями качества.

Содержание

Основные параметры полосы пропускания

Основные параметры, которые характеризуют полосу пропускания частот — это ширина полосы пропускания и неравномерность АЧХ в пределах полосы.

Ширина полосы

Ширина полосы пропускания — полоса частот, в пределах которой неравномерность частотной характеристики не превышает заданной.

Ширина полосы обычно определяется как разность верхней и нижней граничных частот участка АЧХ, на котором амплитуда колебаний

Например, контур, настроенный на частоту fо = 2000 кГц и обладающий затуханием ? = 0,01, имеет полосу пропускания Ппр =0,01 * 2000 = 20 кГц.

Как видно, для получения узкой полосы пропускания необходимо применять контур с высокой добротностью, а для широкой полосы добротность, либо работать на весьма высокой резонансной частоте.

Из приведенной формулы следует, что fo = Q * Ппp. Так как у контура среднего качества Q не менее 20, то рабочая частота должна не менее, чем в 20 раз, превышать полосу пропускания. Например, телевизионную передачу, для которой Ппр составляет несколько мегагерц, нужно вести на частотах не ниже нескольких десятков мегагерц, т.е. на ультракоротких волнах.

Желательно, чтобы контур имел полосу пропускания соответствующую полосе частот, которая характерна для данного вида передачи. Если полоса пропускания меньше, то получатся искажения за счет плохого пропускания некоторых колебаний. Более широкая полоса нежелательна, так как могут быть помехи от сигналов радиостанций, работающих на соседних частотах.

Если необходима широкая полоса пропускания, то приходится часто применять контуры с низкой добротностью. Добротность контура снижается, а полоса пропускания увеличивается, если параллельно контуру присоединяют активное сопротивление R, называемое шунтирующим (рис.2). Действительно, переменное напряжение U, имеющееся на контуре, приложено к сопротивлению R и создает в нем ток. Следовательно, в этом сопротивлении будет расходоваться мощность. Чем меньше сопротивление R, тем больше в нем потери мощности и тем больше затухание контура. Если сопротивление R будет очень малым, то оно замкнет накоротко один из элементов контура (конденсатор на (рис.2 а) или весь контур (рис.2 б). Тогда контур вообще не сможет работать как колебательная система и проявлять свои резонансные свойства.

Шунтирование контура активным сопротивлением делают иногда специально с целью расширения полосы пропускания. Кроме того, подобное шунтирование существует вследствие того, что контур соединен с другими деталями и цепями. За счет этого происходит нежелательное ухудшение качества контура.

Внутреннее сопротивление генератора, питающего параллельный контур, также влияет на добротность контура и его полосу пропускания. Это можно легко объяснить следующим образом.

Пусть генератор в какой-то момент прекратил свое действие. Тогда колебания в контуре станут затухать, а внутреннее сопротивление генератора, присоединенного к контуру, будет играть роль шунтирующего сопротивления, увеличивающего затухание.

Чем больше Ri генератора, тем слабее его влияние, а значит, кривая резонанса контура острее и его полоса пропускания меньше, т.е. резонансные свойства контура выражены резче. При малом Ri генератора добротность контура настолько снижается и полоса пропускания становится такой широкой, что резонансные свойства у контура практически отсутствуют.

К подобному выводу о влиянии Ri генератора мы пришли уже ранее при рассмотрении работы параллельного контура.

Назначение и классификация электронных усилителей , страница 2

если K_{U (дБ)}=1, то K_U =1,12.

Динамический диапазон усиления — диапазон амплитудной характеристики, на котором увеличение входного сигнала вызывает пропорциональное увеличение сигнала на выходе (рис. 3, зона II)

Полоса пропускания усилителя – это диапазон частот, в пределах которого изменение коэффициента усиления не превышает заданной величины (рис. 6).

Полосу пропускания Df определяют на амплитудно-частотной характеристике, построенной как зависимость коэффициента усиления от частоты К=F(f). Допустимым уровнем уменьшения коэффициента усиления для усилителей низкой частоты принято считать на нижней f_H и верхней f_В частотах полосы пропускания K_Н=K_B =0,707К_О (по допустимым коэффициентам частотных искажений М_Н=М_В=). Здесь K_Н, K_B, К_О — коэффициенты усиления на нижней, верхней и средней частотах полосы пропускания.

Рис. 6. Определение полосы пропускания усилителя низкой частоты.

Полосу пропускания находят как разность между f_Ви f_Н

Df=f_В— f_Н.

К параметрам усилителей относят и различные искажения сигнала. Искажения бывают частотные, фазовые, нелинейные.

Частотные искажения определяют коэффициентами частотных искажений на верхней и нижней частотах М_В и М_Н

где w_В и w_Н – верхняя и нижняя круговые частоты;

t_В и t_Н – постоянные времени, зависящие от элементов схемы усилителя, влияющих на частотные искажения на верхних или нижних частотах.

Определим постоянные времени t_В и t_Н для однокаскадного усилителя с общим эмиттером (рис. 7)

t_В=t_b +t_К,

где t_b – постоянная времени, зависящая от граничной частоты усиления транзистора f_b,

t_K – постоянная времени, зависящая от емкости С_К коллекторного перехода транзистора;

где r_K – дифференциальное сопротивление закрытого коллекторного перехода,

R_K – коллекторная нагрузка,

R_Н– нагрузка усилителя.

Рис. 7. Однокаскадный усилитель с общим эмиттером.

Таким образом, на частотные искажения на верхних частотах М_В влияют усилительный прибор – транзистор своими параметрами f_b, C_K и r_K и элементы схемы R_K и R_H.

На нижней частоте w_Н на частотные искажения М_Н будут влиять конденсаторы С_Р, С_Э и С_С, так как реактивное сопротивление конденсатора х_С=1/wС и с уменьшением рабочей частоты х_С будет увеличиваться и конденсаторы будут оказывать все большее влияние:

t_Н=t_{Н Ср}+t_{Н Сэ}+t_{Н Сс},

где t_НСр – постоянная времени, зависящая от емкости конденсатора С_Р, величины сопротивления источника входного сигнала R_Г и сопротивления , — входное сопротивление транзистора; r_Б – удельное сопротивление базы, r_Э — дифференциальное сопротивление открытого эмиттерного перехода; b— коэффициент усиления транзистора;

t_{Н Сэ}– постоянная времени, зависящая от емкости конденсатора С_Э, величины сопротивления R_Э и сопротивления r_Э;

t_{Н Сс} – постоянная времени, зависящая от емкости конденсатора С_С и величины r_К, R_Ки R_Н.

Зная М_Н и М_В, можно рассчитать коэффициенты усиления и .

Определив частотные искажения М_В и М_Н для однокаскадного усилителя, можно найти М_В и М_Н для многокаскадного усилителя:

Таким образом, создавая многокаскадный усилитель и добиваясь как можно большего К_ОБЩ., не нужно забывать что частотные искажения будут увеличиваться по такой же зависимости.

Фазовые искаженияразличны на верхней и нижней частотах:

Нелинейные искажения возникают при работе усилительного прибора на нелинейных участках вольт-амперной характеристики. Оценивают нелинейные искажения коэффициентом нелинейных искажений g или клирфактором

где U₂, U₃. U_n — амплитуды высших гармонических составляющих в выходном напряжении U_ВЫХ, появление которых вызвано отличием его формы от синусоидальной;

U₁ — амплитуда первой (основной) гармоники сигнала.

Коэффициент полезного действия усилителя

где P_ВЫХ — мощность, выделяемая в нагрузке усилителя;

P₀— мощность, потребляемая от источника питания.

Амплитудно-частотная
характеристика последовательного
контура характеризуется тем, что на
резонансной частоте она имеет максимальное
значение. На частотах, отстоящих
значительно от резонансной частоты,
значения амплитудно-частотной
характеристики близки к нулю. Если к
контуру прикладывать сигналы одинаковой
амплитуды, но с разными частотами, то
сигналы с частотой, равной резонансной
частоте, будут создавать большой ток в
контуре и большие напряжения на реактивных
элементах. В этом случае говорят, что
контур пропускает этот сигнал. Если
частота сигнала значительно отличается
от ₀,
то в контуре практически отсутствуют
электрические колебания. В этом случае
говорят, что контур такой сигнал
подавляет. Для оценки этих свойств
контура вводится понятие его полосы
пропускания.

Полосой
пропускания
называется интервал частот, включающий
резонансную частоту контура, на границах
которого значение тока контура меньше
значения тока на резонансной частоте
в заданное число раз.

Как
правило, за исключением особой аппаратуры,
требуется, чтобы на границе полосы
пропускания ток контура был меньше тока
на резонансной частоте враз.

На
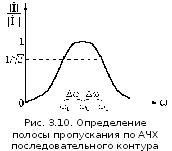
рис.3.10 показано определение полосы
пропускания с помощью АЧХ. В соответствии
с заданным уровнем подавления на границе
полосы пропускания должно выполняться
условие:

. (3.31)

Значит
на границах полосы пропускания АЧХ
должна иметь значение:

. (3.32)
Исходя из этого, на рис.3.10 найдена полоса
пропускания, границы которой обозначаются
частотами ₁
и ₂.
Полоса пропускания обозначается как 
и измеряется в единицах измерения
частоты. Тогда полоса пропускания будет
равна:

. (3.33)

В
зоне полосы пропускания АЧХ практически
симметрична относительно резонансной
частоты. Поэтому интервалы между
резонансной частотой и границами полосы
пропускания обозначим как ∆.

, .

С
учетом этого выражение для полосы
пропускания (3.33) принимает вид:

. (3.34)

Рассмотренный
способ определения полосы пропускания
возможен только при наличии графика
АЧХ. Это не всегда удобно.

Найдем
аналитическое выражение для определения
полосы пропускания. Для этого воспользуемся
формулой (3.29) определения АЧХ.

. (3.35)

Найдем,
какой имеет вид (3.35) для границ полосы
пропускания. Для этого предварительно
найдем выражение в круглых скобках
формулы (3.35) для ₁
и ₂.

Для
=₁
получаем:

В
контурах радиоаппаратуры полоса
пропускания узкая и составляет единицы
килогерц, а резонансная частота высокая
и составляет сотни килогерц. Это позволяет
пренебречь величиной ∆
в числителе и знаменателе. Тогда
рассматриваемое соотношение принимает
вид:

Для
=₂,
с учетом сказанного получаем:

Из
приведенного анализа видно, что
рассматриваемая часть формулы (3.35) на
граничных частотах ₁
и ₂
имеет
одинаковые выражения, отличающиеся
только знаком. Но так как рассмотренное
соотношение в формуле (3.35) находится в
квадрате, то эта формула для обеих границ
полосы пропускания имеет один и тот же
вид:

(3.36)

При
решении задачи о полосе пропускания в
общем виде вводится понятие коэффициента
неравномерности .
Он показывает, какую часть от резонансного
тока принимает ток контура на границах
полосы пропускания и имеет разные
значения в зависимости от вида аппаратуры
(0.707; 0.1; 0.01 и т. д.) Тогда, в соответствии
с понятием полосы пропускания, приравняем
(3.36) к коэффициенту неравномерности:

Решаем
это уравнение относительно 2∆
и с учетом (3.34) находим:

.

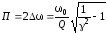
При
коэффициенте неравномерности

полоса пропускания одиночного
последовательного контура определяется
формулой:

(3.37)

На
границах полосы пропускания последовательный
одиночный колебательный контур обладает
рядом свойств, которые полезно знать
при расчете схем с его применением.

1.
Мощность, потребляемая контуром на
границах полосы пропускания, в 2 раза
меньше мощности, потребляемой контуром
на резонансной частоте.

Действительно,
на резонансной частоте мощность,
потребляемая контуром, выражается через
действующее значение тока контура
известным соотношением:

Обозначим
действующее значение тока на границе
полосы пропускания через I. Тогда, с
учетом (3.31), мощность, потребляемая
контуром на каждой из границ полосы
пропускания, равна:

2.
На границах полосы пропускания
сопротивление резистора контура R равно
модулю суммы его реактивных элементов:

На
резонансной частоте ток в контуре равен:

На
границах полосы пропускания ток контура
в общем виде (для =₁
и =₂)
определяется формулой:

С
учетом (3.31) приравняем эти токи:

После
несложных преобразований находим:

(3.38)

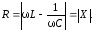
3.
На границах полосы пропускания фаза
тока контура относительно входного
сигнала равна 45.

Комплексное
значение тока контура равно:

.

Фаза
тока равна:

. (3.39)

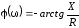
Исходя
из (3.38), модуль аргумента (3.39) на границах
полосы пропускания равен 1. Исходя из
свойств ФЧХ, на частотах <₀
контур имеет емкостные свойства (Х<0)
и, следовательно:

.

На
частотах >₀
контур имеет индуктивные свойства (Х >
0), следовательно:

4.
На границах полосы пропускания обобщенная
расстройка
.

Из
(3.36) видно, что обобщенная расстройка,
с учетом ранее выполненного анализа
для ₁
и
₂
имеет вид:

,

где
«плюс» имеет место для ₂,
а «минус» — для ₁.

Тогда,
учитывая (3.34) и (3.37), получаем:

.

5.
На границе полосы пропускания модуль
полного сопротивления контура равен:

.

Это
легко проверить, учитывая второе из
рассмотренных свойств (3.38). Из выражения
модуля полного сопротивления контура
находим:

.

1. Параллельный
   контур
   без
   диссипаций
   в
   реактивных
   ветвях
   –
   полное
   сопротивление,
   резонанс
   в
   контуре,
   напряжение
   на
   контуре
   и
   токи
   в
   ветвях,
   векторная
   диаграмма.

Параллельные
колебательные контура

Параллельные
одиночные колебательные контура
характеризуются тем, что основные
элементы их — конденсатор и индуктивность
соединены между собой параллельно.
Резисторы могут быть включены как
параллельно с реактивными элементами,
так и последовательно. В первом случае
диссипация энергии в параллельных
ветвях, содержащих реактивные элементы,
отсутствует. Во втором случае в этих
ветвях имеют место диссипативные
процессы. Рассмотрим каждый из названных
видов параллельных контуров.

3.3.1.
Параллельный колебательный контур без
диссипации в реактивных ветвях

Общие
соотношения.
В параллельном колебательном контуре
без диссипации в реактивных ветвях
резистор включен параллельно с
конденсатором и индуктивностью, которые
здесь считаются идеальными (рис.3.18). Их
диссипации могут быть учтены в резисторе
по параллельной схеме замещения
(рис.1.4).

Сопротивление
контура.
Для рассмотрения свойств контура
определим его полное сопротивление
_K
(рис.3.18,в). Представим контур в виде
параллельно соединенных реактивных и
резистивного сопротивлений (рис.3.18,б).

Воспользуемся
проводимостями этих элементов:

; ; ; .

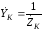
Как
известно, эквивалентная проводимость
параллельно соединенных элементов
равна сумме проводимостей этих элементов.
Тогда эквивалентная проводимость
контура имеет вид:

.

Отсюда
находим величину эквивалентного
сопротивления контура, выделяя в нем
вещественную и мнимую составляющие:

(3.50)

Представим
сопротивление контура в показательной
форме:

, (3.51)

где ;.

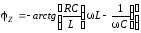
Напряжение
на контуре.
В отличие от последовательного контура,
в параллельном контуре входным параметром
является ток контура i_К(t),
а выходным — напряжение на контуре u_К(t).
Это связано с особенностью функционирования
параллельных контуров в радиотехнических
устройствах, таких как резонансные
усилители, резонансные фильтры и др. В
связи с этим задаем ток с определенной
амплитудой и нулевой фазой, который в
гармонической форме записи и в комплексной
форме имеет виды:

; .

Напряжение
на контуре определяется в соответствии
с законом Ома:

, (3.52)

где , .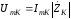

Токи
в контуре.
Определим токи во всех ветвях контура.
Напряжение на контуре, а, значит,
напряжение, приложенное к каждой из
ветвей, имеет вид:

. (3.53)

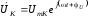
Токи
в ветвях определяются по закону Ома:

,где.

, где
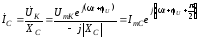
(3.54)

,где

Резонанс
в контуре.
Условие резонанса и резонансная частота.
Как отмечалось, признаком резонанса
являются максимальные значения тока и
напряжения в схеме при определенной
частоте сигнала. При этом в полном
сопротивлении цепи мнимая составляющая
равна нулю. Это мы видели в последовательном
одиночном колебательном контуре.
Воспользуемся этим условием. Тогда из
выражения (3.50) видно, что условием
резонанса в контуре является выполнение
следующего равенства:

. (3.55)

Это
значит, что при резонансе сопротивления
конденсатора и катушки индуктивности
равны:

.

Решая
(3.55) относительно частоты, находим
выражение для резонансной частоты
контура:

. (3.56)

Определим
сопротивление контура, напряжение на
контуре и токи в ветвях на резонансной
частоте.

Сопротивление
контура на резонансной частоте можно
определить из (3.51). С учётом условия
резонанса (3.55) видно, что на резонансной
частоте модуль и фаза сопротивления
контура принимают значения:

, .

Напряжение
на контуре при резонансе определяется
из (3.53) с учётом равенства нулю фазы
сопротивления контура на резонансной
частоте

где

,
(3.57)

.

Токи
в ветвях контура при резонансе определяются
из (3.54) с учётом (3.55) и (3.57):

,
где ;

,
где
;
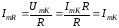
(3.58)

,
где.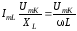

В
силу равенства

видно, что токи в ветвях с индуктивностью
и конденсатором равны по величине, а по
фазе отличаются друг от друга на 180.
Это хорошо видно на векторной диаграмме
(рис.3.19). Совершенно очевидно,

что
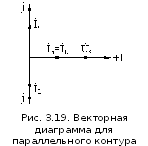
в соответствии с первым законом Кирхгофа
контурный ток равен сумме токов ветвей
контура:

.

Однако,
как видно из векторной диаграммы, токи

и

при суммировании уничтожают друг друга
и контурный ток определяется током,
протекающим через резистор:

. (3.59)

В
силу рассмотренных свойств параллельного
контура, резонанс в параллельном контуре
еще называют резонансом токов.

Мощности
в контуре.
Мгновенная мощность контура определяется
как произведение мгновенного тока
контура на мгновенное напряжение:

На
резонансной частоте ,
тогда

.

Средняя
мощность, потребляемая контуром, равна:

.

С
учетом (3.58) выражение для средней мощности
контура принимает вид:

.

В
полученном выражении мгновенной мощности
контура на резонансной частоте отсутствует
реактивная составляющая мощности.
Однако под действием контурного
напряжения через конденсатор и
индуктивность протекают токи. Определим
мгновенные мощности на этих элементах
так, как это делали при анализе идеальных
емкостного и индуктивного двухполюсников.

Для
емкостной ветви и индуктивной ветви
получим:

,

. (3.60)

При
резонансе
.
Из (3.60) следует, что мгновенные мощности
на конденсаторе и индуктивности равны
по величине и противоположны по фазе.

Добротность
контура.
Добротность контура, как и прежде, найдем
из отношения амплитуды реактивной
мощности контура к средней мощности.
Для этого воспользуемся амплитудными
значениями мощностей на конденсаторе
и индуктивности (3.60). После очевидных
преобразований имеем:

. (3.61)

Из
(3.61) видно, что добротность контура без
диссипации в параллельных ветвях
(рис.3.18) тем выше, чем больше величина
R, и тем меньше затухают колебания в
контуре.

С
учетом полученного выражения для
добротности полное сопротивление
контура (3.50) примет вид:

(3.62)

Последнее
выражение для сопротивления контура
позволяет рассмотреть зависимость от
частоты его модуля и фазы:

,. (3.63)

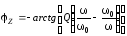
На
рис.3.20 представлены эти зависимости.
Модуль сопротивления контура имеет
наибольшее значение на резонансной
частоте. Если R имеет конечное значение
(присутствует в контуре), то Z_К0=R
(график 1). Если R стремится к бесконечности
(резистор отсутствует), то Z_К0
также стремится к бесконечности (график
2).

Фазовая
характеристика сопротивления контура
позволяет установить его свойства на
различных частотах. Если воспользоваться
треугольником сопротивления, то видно,
что на низких частотах (слева от
резонансной частоты) контур должен
иметь свойства реального индуктивного
двухполюсника, а на высоких частотах
(справа от резонансной частоты) контур
должен иметь свойства реального
емкостного двухполюсника.

Сравним
амплитуды токов I_L
и I_C
с
амплитудой тока I_R.
Используя соотношения (3.58), находим:

; .

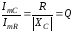
Амплитудно-частотной
характеристикой (АЧХ)
параллельного контура называется
зависимость от частоты модуля напряжения
на контуре.

Как
и для последовательного контура, удобно
АЧХ для параллельного контура рассматривать
в приведенном виде. Для этого необходимо
найти модуль отношения напряжения на
контуре в комплексной форме при
произвольной частоте к напряжению на
контуре при резонансной частоте.

Напряжение
на контуре при произвольной частот и
на резонансной частоте находятся по
закону Ома:

; .

Для
удобства рассмотрения АЧХ здесь
напряжение на контуре и сопротивление
контура на резонансной частоте обозначены,
соответственно как
и.

Берем
отношение этих напряжений и, с учетом
(3.58) и что,
получаем:

. (3.64)

Модуль
полученного выражения (3.60) является
амплитудно-частотной характеристикой
параллельного контура.

. (3.65)

На
рис.3.21 представлены графики АЧХ
параллельного контура для двух значений
добротности. Увеличение добротности
делает график АЧХ более крутым.

Фазо-частотной
характеристикой
параллельного контура называется
зависимость от частоты фазы напряжения
на контуре.

Как
видно из (3.52), фаза напряжения на контуре
равна фазе комплексного сопротивления
контура. Учитывая (3.63), фазо-частотная
характеристика параллельного контура
принимает вид:

. (3.66)

На
рис.3.22 представлен график ФЧХ параллельного
контура. Так как фаза контурного тока
равна нулю, то ФЧХ контура показывает,
в каком фазовом соотношении (опережает,
совпадает, отстает) находится напряжение
по отношению к току. Эта информация
позволяет судить о свойствах контура.
Так, на резонансной частоте фаза
контурного напряжения равна нулю. Значит
на резонансной частоте напряжение
контура и ток совпадают по фазе. Исходя
из теории двухполюсников, этим свойством
обладает резистивный двухполюсник.
Следовательно, на резонансной частоте
контур может быть заменен резистором.
Об этом свойстве контура уже говорилось.

На
низких частотах (слева от резонансной
частоты) фаза контурного напряжения
положительная. Значит, в этом интервале
частот напряжение опережает ток контура.
Из теории двухполюсников известно, что
этим свойством обладает реальный
индуктивный двухполюсник. Следовательно,
на низких частотах параллельный контур
может быть заменен последовательно
соединенными резистором и индуктивностью.
На высоких частотах (справа от резонансной
частоты) фаза контурного напряжения
отрицательная. Значит, в этом интервале
частот контурное напряжение отстает
от контурного тока. Следовательно, на
этом интервале частот контур обладает
свойствами реального емкостного
двухполюсника, и может быть заменен
последовательно соединенными резистором
и конденсатором. Необходимо отметить,
что величины индуктивности и емкости
в схемах замещения контура индуктивным
и емкостным двухполюсниками не равны
значениям индуктивности и ёмкости
контура и на различных частотах будут
иметь различные значения.

Полоса
пропускания.
Физический смысл полосы пропускания
резонансных контуров рассматривался
для последовательного одиночного
колебательного контура. Для параллельного
контура физический смысл полосы
пропускания совершенно аналогичен.
Отличительная особенность параллельного
контура состоит в том, что выходным
сигналом является контурное напряжение,
и АЧХ отображает его зависимость от
частоты.

Полосой
пропускания параллельного одиночного
колебательного контура называется
интервал частот, включающий резонансную
частоту контура, на границах которого
значение напряжения контура меньше
значения напряжения на резонансной
частоте в

раз.

Это
требование для значения напряжения на
границе полосы пропускания можно
выразить так:

; .

Последнее
соотношение позволяет определить
границы полосы пропускания и ее величину
по АЧХ контура (рис.3.23):

.

Пользуясь
полученными соотношениями для
последовательного колебательного
контура, АЧХ для параллельного контура
на границах полосы пропускания примет
вид, аналогичный (3.36):

.
(3.67)

Приравнивая
(3.67) к коэффициенту неравномерности 
и решая полученное уравнение относительно
2∆ω, находим:

; .

Как
отмечалось, для широкого круга
приемно-передающих устройств коэффициент
неравномерности берется равным:

.

С
учетом этого находим выражение для
полосы пропускания одиночного
параллельного резонансного контура:

. (3.68)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Как определить полосу пропускания

Полосой пропускания называется диапазон частот, пропускаемых пьезофильтром или фильтром сосредоточенной селекции. От полосы пропускания фильтра промежуточной частоты, установленного в радиоприемнике, зависит избирательность последнего по соседнему каналу.

Инструкция

Обесточьте радиоприемник и разрядите накопительные конденсаторы его блока питания.

Отключите вход и выход пьезофильтра или фильтра сосредоточенной селекции от других узлов приемника. К входу подключите генератор стандартных сигналов (параллельно ему желательно присоединить частотомер), а к выходу — милливольтметр с детекторной головкой. На генераторе предварительно установите амплитуду выходного сигнала порядка 0,5 В.

Узнайте значение промежуточной частоты приемника из документации к нему или из обозначений на самих фильтрах. В современных аппаратах промежуточная частота тракта АМ обычно равна 450, 455, 460 или 465 кГц, а тракта ЧМ — 10,7 МГц. В старых конструкциях встречаются значения промежуточной частоты тракта ЧМ, составляющие 8,4 или 6,5 МГц.

Установите на генераторе частоту примерно на 20 процентов ниже номинального значения промежуточной частоты приемника. Плавно вращайте ручку в сторону увеличения частоты. Заметьте момент, когда показания милливольтметра резко возрастут. Запишите, на какую частоту при этом настроен генератор. Узнайте ее по шкале генератора либо, при наличии частотомера — по его показаниям (они точнее). Это — нижняя граница полосы пропускания.

Продолжайте увеличивать частоту генератора. Заметьте момент, когда показания милливольтметра резко упадут. Аналогичным образом определите верхнюю границу полосы пропускания.

При необходимости вычислите ширину полосы, вычтя нижнюю ее границу из верхней.

Значительную помощь в определении полосы пропускания может оказать прибор, состоящий из генератора качающейся частоты, генератора меток и осциллографа. Зная, чему равна разность частот между соседними метками на экране, составьте пропорцию и вычислите ширину показанной на том же экране полосы пропускания фильтра. Данный прибор позволяет также наблюдать форму границ полосы (являются ли спады плавными или резкими).

После окончания эксперимента отключите питание всех приборов, отсоедините их, а фильтр присоедините обратно к остальным элементам приемника.

Обратите внимание

Не работайте под напряжением.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Требования к полосе пропускания варьируются для разных сетей. Понимание того, как правильно рассчитать полосу пропускания, имеет важное значение для построения и обслуживания сети.

Полоса пропускания является одним из наиболее важных факторов при проектировании и обслуживании LAN, WAN или беспроводной сети, где требуются многие функции. В отличие от сервера, который можно настраивать и переконфигурировать на протяжении всего срока службы, полоса пропускания сети — это элемент дизайна сети, который обычно выбирается с самого начала, и в дальнейшем его можно модифицировать только перестройкой сети.

Что такое полоса пропускания сети?

Термин «полоса пропускания» (bandwidth) определяет скорость передачи данных, внутри сети. Это объём данных, которые могут быть переданы между двумя точками за заданный период времени. Данные, поступающие в сеть, называются входящим трафиком (ingress), а данные, покидающие сеть, называются исходящим трафиком (egress). Полоса пропускания обычно выражается в битах в секунду или, иногда, в байтах в секунду.

Важно понимать разницу между теоретической пропускной способностью (throughput) сети и реальными результатами при вычислении полосы пропускания сети. Например, сеть 1000BASE-T с неэкранированной витой парой — сеть Gigabit Ethernet (GbE) теоретически может поддерживать 1000 Мбит/с, но этот уровень никогда не может быть достигнут на практике из-за накладных расходов на аппаратное и системное программное обеспечение.

Полоса пропускания и пропускная способность

Полосу пропускания (bandwidth) не следует путать с пропускной способностью (throughput), которая относится к скорости. Хотя сети с высокой пропускной способностью часто бывают быстрыми, это не всегда так.

Полосу пропускания можно уподобить автостраде. Сеть с широкой полосой пропускания похожа на многорядное шоссе, которое в любой момент может вместить сотни автомобилей.

Сеть с низкой полосой пропускания похожа на однополосную дорогу, по которой машины едут одна за другой.

Хотя по широкому шоссе, скорее всего, автомобили будут двигаться быстрее, движение в час пик может легко привести к остановке легковых и грузовых автомобилей. Или, возможно, автомобили не могут быстро выехать на шоссе, потому что оно забито большими грузовиками для доставки, которые занимают много места на дороге. Точно так же даже сеть с высокой пропускной способностью может работать медленно перед лицом таких проблем, как перегрузка и приложения, требующие широкой полосы пропускания.

Что произойдёт, если неправильно рассчитать требования к полосе пропускания? При этом, будет почти гарантировано сеть будет работать медленно. Тем не менее, значительное слишком широкая полоса пропускания может оказаться непозволительно дорогостоящим для большинства предприятий.

Как рассчитать полосу пропускания

Итак, как определить правильную формулу, которая будет соответствовать вашим требованиям к полосе пропускания? Сначала нужно получить ответ на вопросы: какие приложения запускают пользователи и каково соглашение об уровне обслуживания (SLA) и производительности для этих приложений? Некоторых сетевых администраторов интересует только количество пользователей в виртуальной локальной сети. Но чтобы определить фактическое использование полосы пропускания, вам нужно знать, что пользователи будут делать в сети.

Возможно, что 200 пользователей вызовут меньше проблем, чем группа из трех пользователей, которые перегружают сеть необычным «жручим» клиент-серверным приложением, например, видеоконференцсвязью с высоким разрешением изображения.

Вывод формулы

Выводим формулу для расчёта полосы пропускания

Расчёт требований полосы пропускания состоит из двух основных этапов:

• Определение доступной полосы пропускания сети.
• Определите средний коэффициент использования (utilization), необходимый для каждого приложения.

Обе эти цифры должны быть выражены в байтах в секунду. Рассмотрим следующую формулу: Сеть 1 GbE имеет доступную пропускную способность 125 миллионов Байт/с. Это вычисляется, если количество битов в секунду — в сети 1 GbE это будет 1 миллиард — разделить на восемь, чтобы определить байты:

1000000000 бит/с / 8 = 125000000 Байт/с

После определения полосы пропускания сети нужно оценить, какую часть полосы пропускания использует каждое приложение. Можно использовать сетевой анализатор, чтобы определить количество байтов, которые приложение по отправляет по сети в секунду.

Для этого:

• В анализаторе сети включите опцию накопленных байтов.
• Используйте захват трафика между тестовой рабочей станцией, на которой запущено приложение.
• В итоговом окне декодирования будет показано количество пакетов в начале передачи файла.
• Следите за отметкой времени до одной секунды позже, а затем посмотрите на поле накопленных байтов.

Как интерпретировать результаты расчётов

Если вы определили, что ваше приложение передаёт данные со скоростью 200 000 байт/с, тогда нужно вычислить: 125 000 000 байт/с / 200 000 байт/с = 625 пользователей, которые могут одновременно использовать это приложение. В этом случае сеть будет в порядке даже с несколькими сотнями одновременных пользователей.

Однако посмотрим, что произошло бы в случае с сетью со скоростью 100 Мбит/с: 13 102 000 байт/с / 200 000 байт/с = 65,51 одновременных пользователей. Это будет сеть, которая не сможет поддерживать более 65 пользователей, одновременно запускающих приложение. Знание формулы для расчёта пропускной способности чрезвычайно важно для сетевых администраторов.