Полярная система координат как найти угол - Исправление недочетов и поиск решений вместе с Examum.ru

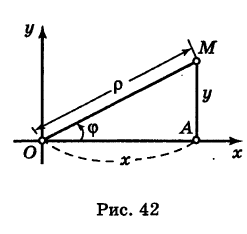
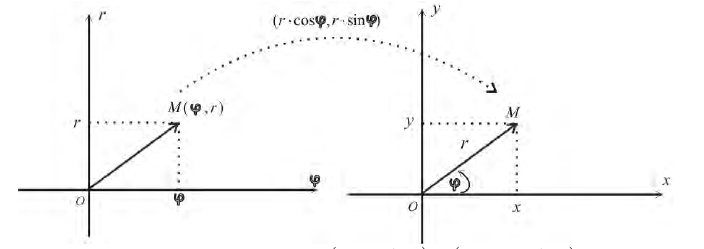
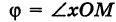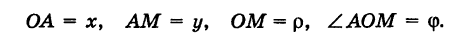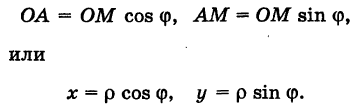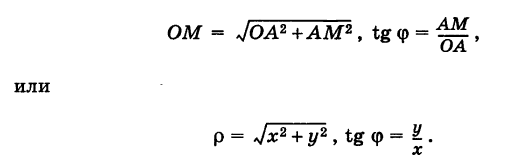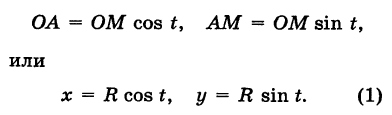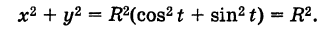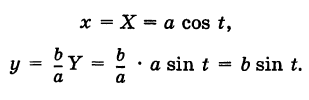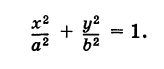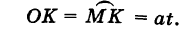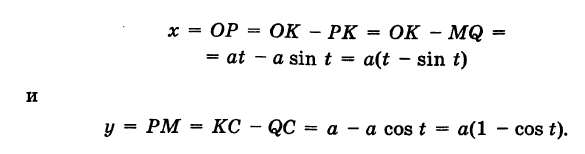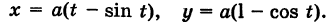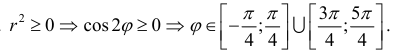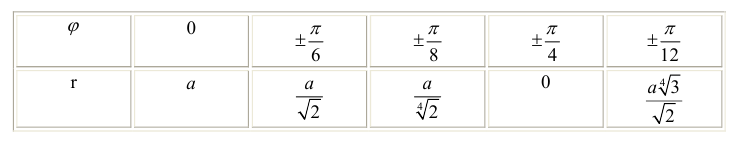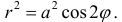Полярные координаты — определение и вычисление с примерами решения

Полярные координаты. параметрические уравнения линии

Полярные координаты

Основная идея метода координат состоит в том, что положение точки на плоскости однозначно определяется с помощью двух чисел. Конкретный геометрический смысл этих чисел дает ту или иную систему координат. Наиболее важной после прямоугольной системы, исключительно употреблявшейся нами до сих пор, является полярная система координат, к рассмотрению которой мы и переходим.

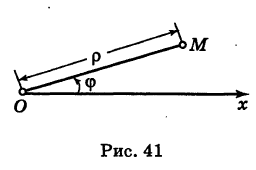
Возьмем на плоскости точку О, которую назовем полюсом. Проведем из полюса О направленную полупрямую Ох, называемую полярной осью (рис. 41).

Пусть М — произвольная точка плоскости. Соединим точку М с полюсом О отрезком ОМ. Длина отрезка ОМ = р называется полярным радиусом точки М, а угол

Точка М с полярными координатами риф записывается следующим образом: М (р, ф), причем на первом месте ставится полярный радиус р, а на втором — полярный угол ф.

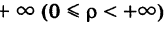
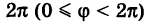
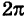
Что касается значений, принимаемых полярными координатами, то достаточно, очевидно, рассматривать значения р от 0 до и значения ф от 0 до , при этом, как мы условились, угол ф отсчитывается от полярной оси против хода часовой стрелки. Однако в некоторых вопросах приходится рассматривать углы, большие , а также отрицательные углы, т. е. углы, отсчитываемые от полярной оси по направлению движения часовой стрелки.

Связь между прямоугольными и полярными координатами

Рассмотрим переход от полярных координат к прямоугольным и обратно.

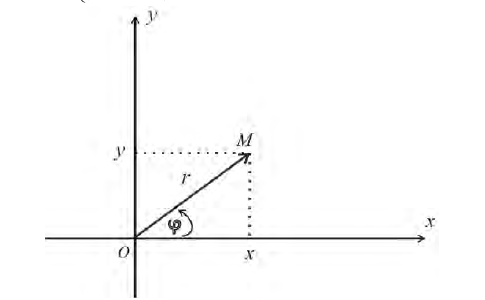
Предположим, что полюс полярной системы совпадает с началом прямоугольной системы координат Оху, а полярная ось является положительной полуосью Ох (рис. 42).

Тогда для произвольной точки М имеем

Считая угол ф острым, из прямоугольного треугольника АОМ находим

Полученные формулы справедливы для любого угла ф. Так выражаются прямоугольные координаты точки М через ее полярные координаты. Далее, из этого же прямоугольного треугольника АОМ получаем

Так выражаются полярные координаты точки через ее прямоугольные координаты.

Заметим, что при определении полярного угла ф по tg ф нужно учитывать знаки координат х и у.

Ранее мы видели, что линии могут быть заданы с помощью уравнений, связывающих их текущие прямоугольные координаты. Покажем теперь на простейшем примере, что линии могут определяться и уравнениями относительно полярных координат.

Пример:

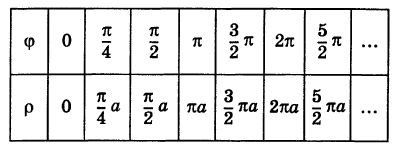
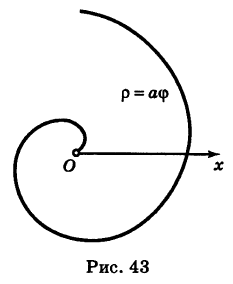
Рассмотрим кривую 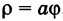, где а — некоторое положительное число. Эта кривая называется спиралью Архимеда. Для ее построения составляем таблицу соответственных значений ф и р:

По этой таблице наносим точки и соединяем их линией, уточняя, если в этом есть необходимость, положение промежуточных точек (рис. 43).

Параметрические уравнения линии

Иногда бывает удобнее вместо уравнения линии, связывающего прямоугольные координаты 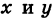, рассматривать так называемые параметрические уравнения линии, дающие выражения текущих координат х и у в виде функций от некоторой переменной величины t (параметра). Параметрические уравнения играют важную роль, например, в механике, где координаты х и у движущейся точки М (х, у) рассматриваются как функции времени (уравнения движения).

Пример:

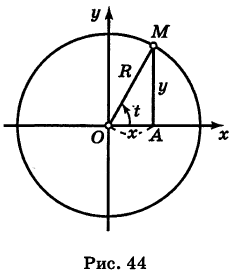
Выведем параметрические уравнения окружности.

Пусть М — произвольная точка окружности радиуса R с центром в начале координат (рис. 44). В определяемом ею прямоугольном треугольнике АОМ обозначим угол хОМ через t. Тогда, очевидно, будут иметь место равенства

Это и есть параметрические уравнения окружности.

Чтобы получить обычное уравнение окружности, нужно исключить параметр t. Для этого возводим уравнения (1) в квадрат и складываем их:

Пример:

Выведем параметрические уравнения эллипса.

Эллипс с полуосями а и b можно рассматривать как равномерно сжатую вдоль вертикального диаметра окружность радиуса а, где коэффициент сжатия k = b/a. Пусть М (х, у) — точка эллипса, N (X, У) — соответствующая точка окружности (рис. 45), где

За параметр t примем угол, образованный радиусом ON окружности с положительным направлением оси Ох: . Используя формулы (2), имеем

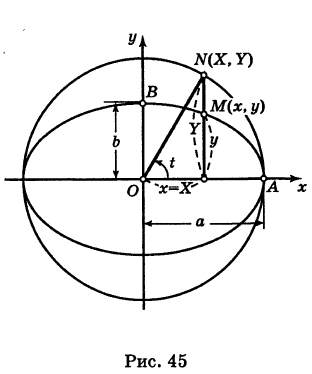
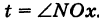
Таким образом, параметрические уравнения эллипса с полуосями а и b есть

Исключив из уравнений (3) параметр получим каноническое уравнение эллипса

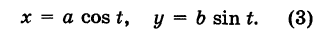
Имея параметрические уравнения линии, можно по точкам построить ее.

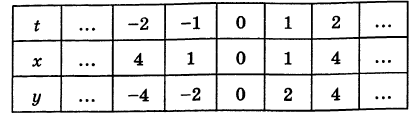
Пример:

Решение:

Составляем таблицу значений:

Нанося точки с соответствующими координатами (х, у) на плоскость Оху и соединяя их линией, получим искомую кривую (рис. 46).

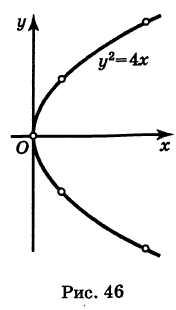
Эта кривая— парабола. В самом деле, исключив параметр t из уравнений (4), получим 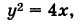т. е. каноническое уравнение параболы.

Параметрические уравнения циклоиды

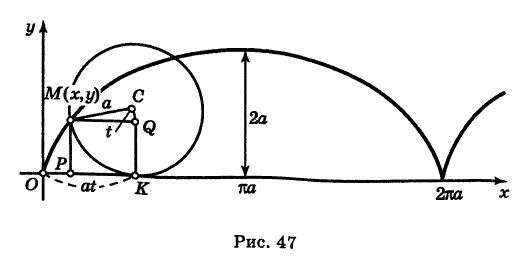
Определение: Циклоидой называется кривая, описываемая точкой окружности, катящейся без скольжения по прямой линии (рис. 47).

Выведем параметрические уравнения циклоиды, приняв прямую за ось Ох, предполагая, что радиус катящейся окружности равен айв начальном положении движущаяся точка М совпадает с началом координат. За параметр t примем угол поворота (в радианах) подвижного радиуса МС окружности относительно вертикального радиуса КС, где К — точка касания окружности с осью Ох (рис. 47). Так как качение окружности происходит без скольжения, то, очевидно, имеем

Отсюда на основании рис. 47 для координат текущей точки М циклоиды получаем следующие выражения:

Таким образом, параметрические уравнения циклоиды есть

Полярная система координат

Определение 1. Рассмотрим плоскость с прямоугольной декартовой системой координат Оху . Пусть М(х, у) – точка на плоскости, M ≠ 0. Полярными координатами точки М называются числа r − длина ее радиус-вектора (полярный
радиус) и ϕ − угол, образованный радиус-вектором с положительным направлением оси Ох (полярный угол), 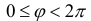. Точка О при этом называется
полюсом, а полуось Ох – полярной осью.
Замечание. Зависимость между прямоугольными (х, у) и полярными ( , ) r ϕ
координатами точки М задается в виде: 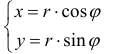(1)

Рис.1. Полярные координаты точки.
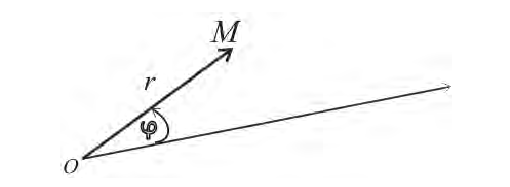
Полярный полюс О и полярную ось можно выбрать на плоскости и не вводя
прямоугольную систему координат:

Пример 1.

Построим на плоскости линию, заданную уравнением: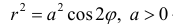
− лемниската.
Решение.

Вычислим значения r при различных значениях ϕ :

Проводим лучи из начала координат под углами ϕ к оси Ох и на них откладываем
отрезки длины r , получим :

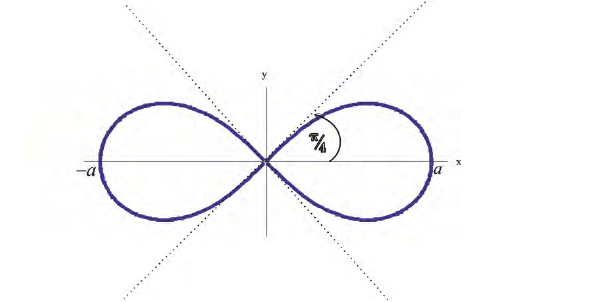
Рис.3. Лемниската

Пример 2.

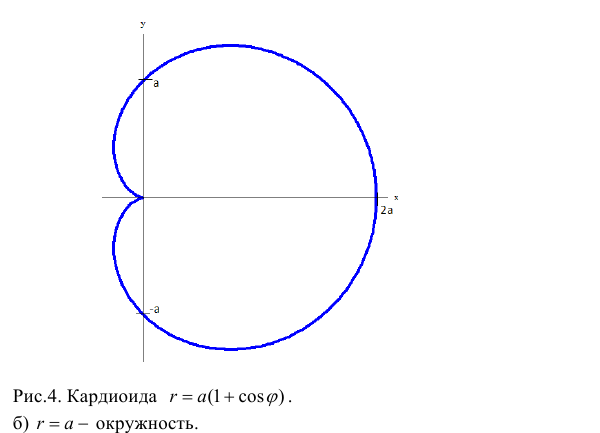
а) Построим кривую 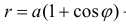− кардиоида. Рассуждая, как в примере 1 получим:

Замечание. Если в определении 1 отбросить требование 0 ≤ ϕ 0, то формулы (1) будут задавать непрерывное отображение точек плоскости (O, r, ϕ) на точки плоскости (x, O, y).

При этом, если r > 0, то векторы 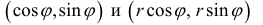сонаправлены, если r

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Полярная система координат

Полярные координаты точки на плоскости — это два числа, которые определяют положение этой точки относительно некоторой фиксированной точки (полюса) и некоторого фиксированного луча (полярной оси). Первая координата точки —полярный радиус — определяет расстояние точки от полюса: ; вторая координата — полярный угол — угол, на который надо повернуть ось в положительном или отрицательном направлении до совпадения с лучом (рис. 11).

Полярный угол

Полярный угол считается положительным при отсчете от полярной оси против часовой стрелки и отрицательным — при отсчете в противоположную сторону.

Если в полярной системе координат условимся длину полярного радиуса считать неотрицательной и полярный угол брать в интервале , то этим устанавливается взаимно однозначное соответствие между точками плоскости и полярными координатами , за исключением полюса, который конкретного полярного угла не имеет.

Это соответствие удобно иметь в виду при решении задач на построение отдельных точек на плоскости, определение расстояния между двумя точками, деление отрезка в заданном отношении и др.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

При исследовании функций и построении их графиков часто полярный радиус принимает отрицательные значения, а полярный угол принимает значения, большие или отрицательные. Например, в функции при полярный радиус в функции угол может принимать произвольные значения.

Отрицательные значения откладывают от полярной оси по часовой стрелке, а отрицательные значения — на продолжении луча с другой стороны от полюса. Тогда значения между 0 и или между и называют главными.

В этом случае произвольная пара координат определяет на плоскости только одну точку, а одной точке плоскости соответствует множество пар чисел. Действительно, при изменении от до луч может бесконечное число раз занимать одно и то же положение, например луч при где — целое положительное или отрицательное число, занимает одно и то же положение (рис. 12). Точка на луче с полярным радиусом может быть определена одной из пар координат

Это следует иметь в виду и при построении графиков функций, заданных в полярной системе координат.

Возможно вам будут полезны данные страницы:

Переход от декартовых координат к полярным и наоборот выполняется по формулам

где , — декартовы координаты произвольной точки а , — ее полярные координаты. Здесь декартова система координат выбрана так, что ее начало совпадает с полюсом полярной системы, а ось абсцисс — с полярной осью.

Кроме прямоугольной системы координат на плоскости часто используют полярную систему координат, которая полностью определяется упорядоченной парой точек и . Первую из них — точку — называют полюсом полярной системы координат. Из полюса в направлении второй точки проводят луч , называемый полярной осью (рис. 3.4).

Расстояние между точками и выбирают в качестве единицы масштаба. Ясно, что полюс полярной системы координат , ее полярная ось и установленная единица масштаба однозначно определяют на плоскости положение точки . Поэтому выбор этой тройки геометрических объектов часто рассматривают как выбор конкретной полярной системы координат.

Положение точки в полярной системе координат фиксируется расстоянием между точкой и полюсом , называемым полярным радиусом, и углом между полярной осью и вектором полярным углом. Полярный радиус и полярный угол составляют полярные координаты точки на плоскости, которые записывают так: .

Полярный угол измеряют в радианах и отсчитывают от полярной оси. Если значение угла положительно, то его отсчитывают против хода часовой стрелки, в противном случае — по ходу часовой стрелки (см. рис. 3.4). Для полюса , а угол не определен. Для остальных точек плоскости , а полярный угол определен с точностью до . Поэтому для полярного угла иногда фиксируют промежуток его изменения, например или .

Координаты точки на плоскости часто записывают как в полярной, так и в прямоугольной системах координат и используют преобразования этих координат друг в друга.

Если нет специальных указаний, то при этом подразумевают следующее взаимное расположение прямоугольной и полярной систем координат (рис. 3.5): полюс полярной системы координат совмещен с началом прямоугольной системы координат; полярная ось совпадает с положительной частью оси абсцисс, а масштаб в полярной системе для вычисления расстояний берется равным единице длины в прямоугольной системе координат. В этом случае прямоугольные координаты точки на плоскости выражаются через ее полярные координаты с помощью соотношений (см. рис. 3.5)

С учетом ограничения на полярный угол полярные координаты точки определяются через ее прямоугольные координаты следующим образом:

Пример с решением

Найдем полярные координаты точек и .

Для точки имеем: а для точки

Координаты. Полярная система координат.

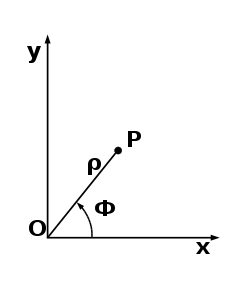
Полярная система координат — двухмерная система координат, согласно ей всякая точка на плоскости характеризуется параметрами полярного угла и полярного радиуса. К такой системе координат целесообразно обращаться тогда, когда соотношения между точками удобнее представить в виде радиусов и углов. В более широко известной, декартовой или прямоугольной системе координат, соотношения сходного рода получиться указать, лишь применив тригонометрические уравнения.

Полярная система координат формируется точкой О — полюсом, лучом Ор — полярной осью, и единичным вектором e одной направленности с лучом Ор.

Представим на плоскости точку М, не совмещающуюся с О. Местоположение точки М характеризуется параметрами: ее расстоянием r от полюса О и углом φ, сформированным отрезком ОМ с полярной осью (отсчет углов берем против часов стрелки).

Параметры r и φ — полярные координаты точки М, указывают М(r; φ), при этом r — полярный радиус, φ — полярный угол. При этом полярный угол учитывается в радианах.

При указании совокупности точек плоскости стоить только полярный угол φ локализовать на интервале (—π; π] (либо 0< φ < 2πr), а полярный радиус — [0;∞). При этих условиях у всякой точки плоскости (исключая О) будет уникальная пара координат r и φ.

Существует взаимосвязь между прямоугольными и полярными координатами. Для доказательства этого соединим полюс 0 с началом координат системы x0y, а полярную ось — с положительной полуосью 0х. Допустим, x и у — прямоугольные координаты точки М, а r и φ — ее полярные координаты.

Прямоугольные координаты точки М устанавливаются посредством полярных координат такими соотношениями:

Полярные же координаты точки М устанавливаются посредством ее декартовых координат (тот же рисунок) такими соотношениями:

Вычисляя параметры φ, требуется определить (по знакам x и у) четверть, в которой располагается требуемый угол, и брать во внимание, что -π < φ< π.

Источник

Содержание:

Полярный угол
Пример с решением

Полярный угол

Полярный угол считается положительным при отсчете от полярной оси против часовой стрелки и отрицательным — при отсчете в противоположную сторону.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Это следует иметь в виду и при построении графиков функций, заданных в полярной системе координат.

Возможно вам будут полезны данные страницы:

Переход от декартовых координат к полярным и наоборот выполняется по формулам

Пример с решением

Найдем полярные координаты точек и .

Для точки имеем: а для точки

Лекции:

Сходимость функционального ряда
Производная второго порядка
Метод Жордана Гаусса
Некоторые простые неявные функции
Рациональные числа
Алгебраические выражения
Каноническое уравнение гиперболы
Метод интервалов
Обратная матрица примеры решения
Дифференцирование функций, заданных неявно и параметрически

Источник

Полярная система координат (полярные координаты)

Полярная система координат на плоскости — это совокупность точки , называемой полюсом, и полупрямой , называемой полярной осью. Кроме того, задается масштабный отрезок для измерения расстояний от точек плоскости до полюса. Как правило, на полярной оси выбирается вектор vec{i} , приложенный к точке , длина которого принимается за величину масштабного отрезка, а направление вектора задает положительное направление на полярной оси (рис.2.28,а).

Положение точки в полярной системе координат, полярные радиус и угол

Положение точки в полярной системе координат определяется расстоянием (полярным радиусом) от точки до полюса (т.е. r=vertoverrightarrow{OM}vert ) и углом varphi (полярным углом) между полярной осью и вектором . Полярный радиус и полярный угол составляют полярные координаты точки , что записывается в виде M(r,varphi) . Полярный угол измеряется в радианах и отсчитывается от полярной оси:

— в положительном направлении (против направления движения часовой стрелки), если значение угла положительное;

— в отрицательном направлении (по направлению движения часовой стрелки), если значение угла отрицательное.

Полярный радиус определен для любой точки плоскости и принимает неотрицательные значения rgeqslant0 . Полярный угол varphi определен для любой точки плоскости, за исключением полюса , и принимает значения -pi<varphileqslantpi , называемыми главными значениями полярного угла. В некоторых случаях целесообразно считать, что полярный угол определен с точностью до слагаемых 2pi n , где ninmathbb{Z} . В этом случае значениям varphi+2pi n полярного угла для всех соответствует одно и то же направление радиус-вектора.

С полярной системой координат Orvarphi можно связать прямоугольную систему координат Ovec{i}vec{j} , начало которой совпадает с полюсом, а ось абсцисс (точнее положительная полуось абсцисс) — с полярной осью. Ось ординат достраивается перпендикулярно оси абсцисс так, чтобы получилась правая прямоугольная система координат (рис.2.28,б). Длины базисных векторов определяются масштабным отрезком на полярной оси.

Наоборот, если на плоскости задана правая прямоугольная система координат, то, приняв положительную полуось абсцисс за полярную ось, получим полярную систему координат {связанную с данной прямоугольной).

Выведем формулы, связывающие между собой прямоугольные координаты x,y точки , отличной от точки , и ее полярные координаты r,varphi . По рис.2.28,б получаем

$begin{cases}x=rcdotcosvarphi,\[2pt]y=rcdotsinvarphi.end{cases}$

(2.17)

Эти формулы позволяют найти прямоугольные координаты по известным полярным координатам. Обратный переход выполняется по формулам:

$left{begin{aligned}r&= sqrt{x^2+y^2},\ cosvarphi&= frac{x}{r}=frac{x}{sqrt{x^2+y^2}},\ sinvarphi&= frac{y}{r}=frac{y}{sqrt{x^2+y^2}}.end{aligned}right.$

(2.18)

Последние два равенства определяют полярный угол с точностью до слагаемых 2pi n , где ninmathbb{Z} . При xne0 из них следует, что $operatorname{tg}frac{y}{x}$ . Главное значение полярного угла varphi~(-pi<varphileqslantpi) находится по формулам (рис.2.29):

Главное значение полярного угла

$varphi=left{begin{aligned}operatorname{arctg}frac{y}{x},quad&x>0,\pi+operatorname{arctg}frac{y}{x},quad&x<0,,ygeqslant0,\-pi+operatorname{arctg}frac{y}{x},quad&x<0,,y<0,\frac{pi}{2},quad&x=0,,y>0,\-frac{pi}{2},quad&x=0,,y<0.end{aligned}right.$

Пример 2.9. В полярной системе координат Orvarphi :

а) изобразить координатные линии $r=1,~r=2,~r=3,~varphi=frac{pi}{4},~varphi=frac{pi}{2}$ ;

б) изобразить точки M_1,~M_2 с полярными координатами $r_1=3,~varphi_1=frac{9pi}{4},~r_2=3,~varphi=-frac{7pi}{4}$ . Найти главные значения полярных углов этих точек;

в) найти прямоугольные координаты точек M_1,~M_2 .

Решение. а) Координатные линии r=1,~r=2,~r=3 представляют собой окружности соответствующих радиусов, а линии $varphi=frac{pi}{4},$ $varphi=frac{pi}{2}$ и $varphi=frac{3pi}{4}$ — полупрямые (рис.2.30,а).

б) Построим точки $M_1!left(3,frac{9pi}{4}right)$ и $M_2!left(3,-frac{7pi}{4}right)$ (рис.2.30,б,в). Их координаты отличаются полярным углом, однако, имеют одно и то же главное значение $varphi=frac{pi}{4}$ . Следовательно, это одна и та же точка, которая совпадает с точкой $M!left(3,frac{pi}{4}right)$ , изображенной на рис.2.30,а.

в) Учитывая пункт «б», найдем прямоугольные координаты точки . По формулам (2.17) получаем:

$x=rcdotcosvarphi=3cdotcosfrac{pi}{4}=frac{3sqrt{2}}{2};~y=rcdotsinfrac{pi}{4}=frac{3sqrt{2}}{2},$ то есть $M!left(frac{3sqrt{2}}{2},frac{3sqrt{2}}{2}right).$

Построение линии в полярной системе координат

Замечания 2.8

1. Главное значение полярного угла можно выбрать иначе, например, 0leqslantvarphi<2pi .

2. Расстояние между двумя точками M_1(r_1,varphi_1) и M_2(r_2,varphi_2) (длина отрезка M_1M_2 ) вычисляется по формуле

Ориентированная площадь параллелограмма, построенного на радиус-векторах

$M_1M_2=sqrt{r_1^2+r_2^2-2cdot r_1cdot r_2cdotcos(varphi_2-varphi_1)},$

что следует из теоремы косинусов (рис.2.31).

3. Ориентированная площадь $S_{ast}^{land}$ параллелограмма (рис.2.31), построенного на радиус-векторах $overrightarrow{OM_1}$ и $overrightarrow{OM_2}$ , находится по формуле

$S_{astoverrightarrow{OM_1},overrightarrow{OM_2}}^{land}=overrightarrow{OM_1}landoverrightarrow{OM_2}=r_1cdot r_2cdotsin(varphi_2-varphi_1).$

Она положительна, если varphi_1<varphi_2 (при этом ориентация пары радиус- векторов $overrightarrow{OM_1}$ и $overrightarrow{OM_2}$ правая), и отрицательна, если varphi_1>varphi_2 (ориентация пары радиус-векторов $overrightarrow{OM_1}$ и $overrightarrow{OM_2}$ левая).

Пример 2.10. Даны полярные координаты $varphi_A=frac{pi}{3},~r_A=4$ и $varphi_B=frac{2pi}{3},~r_B=2$ точек и (рис.2.32). Требуется найти:

Чертёж точек в полярных координатах

а) скалярное произведение bigllangleoverrightarrow{OA},overrightarrow{OB}biglrangle ;

б) длину отрезка ;

в) внешнее произведение overrightarrow{OA}landoverrightarrow{OB} ;

г) площадь $S_{OAB}$ треугольника OAB ;

д) координаты середины отрезка в прямоугольной системе координат, связанной с данной полярной.

Решение. а) По определению скалярного произведения находим

$leftlangleoverrightarrow{OA},overrightarrow{OB}rightrangle=left|overrightarrow{OA}right|{cdot}left|overrightarrow{OB}right|!cdotcospsi=r_Acdot r_Bcdotcos(varphi_B-varphi_A)=4cdot2cdotcosfrac{pi}{3}=4.$

б) Находим длину отрезка (см. пункт 2 замечаний 2.8):

$AB=sqrt{r_A^2+r_B^2-2cdot r_Acdot r_Bcdotcos(varphi_B-varphi_A)}=sqrt{4^2+2^2-2cdot4cdot2cdotfrac{1}{2}}=2sqrt{3}.$

в) Внешнее произведение находим как ориентированную площадь параллелограмма, построенного на векторах overrightarrow{OA} и overrightarrow{OB} :

$overrightarrow{OA}landoverrightarrow{OB}=r_Acdot r_Bcdotsin(varphi_B-varphi_A)=2cdot4cdotsinfrac{pi}{3}=4sqrt{3}.$

Площадь положительная, так как векторы overrightarrow{OA} и overrightarrow{OB} образуют правую пару (varphi_A<varphi_B) .

г) Площадь треугольника OAB находим как половину площади параллелограмма, построенного на радиус-векторах overrightarrow{OA} и overrightarrow{OB} .

Так как $S_{astoverrightarrow{OA},overrightarrow{OB}}=left|overrightarrow{OA}landoverrightarrow{OB}right|=4sqrt{3}$ (см. пункт «в»), то $S_{OAB}=frac{1}{2}cdot4sqrt{3}=2sqrt{3}$ .

д) По формулам (2.17) находим прямоугольные координаты точек и :

$begin{gathered}x_A=r_Acdotcosvarphi_A=4cdotfrac{1}{2}=2,quad y_A=r_Acdotsinvarphi_A=4cdotfrac{sqrt{3}}{2}=2sqrt{3};\[3pt] x_B=r_Bcdotcosvarphi_B=2cdotfrac{-1}{2}=-1,quad y_B=r_Bcdotsinvarphi_B=2cdotfrac{sqrt{3}}{2}=sqrt{3}.end{gathered}$

а затем координаты середины отрезка (см. пункт 3 замечаний 2.1):

$x_C=frac{x_A+x_b}{2}=frac{2+(-1)}{2}=frac{1}{2};quad y_C=frac{y_A+y_B}{2}=frac{2sqrt{3}+sqrt{3}}{2}=frac{3sqrt{3}}{2}.$

Пример 2.11. На координатной плоскости Oxy отмечена точка A(4,-3) . Найти:

Полярные координаты точки и её образа, поворот радиус-вектора на угол вокруг начала координат

а) полярные координаты точки , образа точки при повороте радиус-вектора overrightarrow{OA} на угол $frac{pi}{3}$ вокруг начала координат (рис.2.33);

б) полярные координаты точки A_1 , образа точки при инверсии плоскости относительно окружности единичного радиуса с центром в начале координат (см. пример б преобразований плоскости в разд. 2.2.4).

Решение. а) Найдем полярные координаты точки . По формулам (2.17), учитывая рис.2.29, получаем:

$r_A=sqrt{x_A^2+y_A^2}=sqrt{4^2+(-3)^2}=5;quadvarphi_A=operatorname{arctg}frac{y_A}{x_A}=operatorname{arctg}frac{-3}{4}=-operatorname{arctg}frac{3}{4},$

так как точка лежит в text{IV} четверти.

При повороте радиус-вектора overrightarrow{OA} вокруг полюса на угол $frac{pi}{3}$ полярный радиус не изменяется, а полярный угол увеличивается. Следовательно, полярные координаты точки : $r_{A'}=r_{A}=5$ , $varphi_{A'}=varphi_{A}+frac{pi}{3}=frac{pi}{3}-operatorname{arctg}frac{3}{4}$ , причем $varphi_{A'}$ — главное значение полярного угла $(-pi<varphi_{A'}leqslantpi)$ .

б) При инверсии относительно окружности радиуса полярные координаты r',varphi' образа выражаются через полярные координаты r,varphi прообраза следующими формулами:

$r'=frac{R^2}{r},quadvarphi'=varphi.$

Поэтому, учитывая пункт «а», находим (для R=1 ):

$r_{A_1}=frac{1}{r_A}=frac{1}{5},quadvarphi_{A_1}=varphi_{A}=-operatorname{arctg}frac{3}{4}.$

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

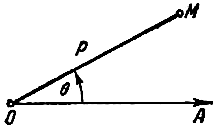
Символ
М(
;

)
обозначает, что точка М имеет полярные
координаты

Полярный
угол

имеет
бесконечно много возможных значений
(отличающихся друг от друга на величину
вида

,
где n
—
целое положительное число). Значение
полярного угла, удовлетворяющее
неравенствам

,
называется главным.

В
случаях одновременного рассмотрения
декартовой и полярной систем координат
условимся: 1). Пользоваться одним и тем
же масштабом, 2). При определении полярных
углов считать положительным повороты
в том направлении, в каком следует
вращать положительную ось абсцисс,
чтобы кратчайшим путем совместить ее
с положительной осью ординат (таким
образом, если оси декартовой системы
находятся в обычном расположении, то
есть ось Ох направлена вправо, а ось Оу
— вверх, то и отсчет полярных углов должен
быть обычным, то есть положительными
следует считать те углы, которые
отсчитываются против часовой стрелки).

При
этом условии, если полюс полярной системы
координат совпадает с началом декартовых
прямоугольных координат, а полярная
ось совпадает с положительной полуосью
абсцисс, то переход от полярных координат
произвольной точки х к декартовым
координатам той же точки осуществляется
по формулам

В
этом же случае формулы

являются
формулами перехода от декартовых
координат к полярным.

При
одновременно рассмотрении в дальнейшем
двух полярных систем координат условимся
считать направление положительных
поворотов и масштаб для обеих систем
одинаковыми.

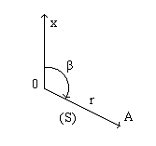
Полярная система координат

П
олярная
система координат
– система плоских координат образованная
направленным прямым лучом OX, называющимся
полярной осью. Чаще всего за полярную
ось принимают ось северного направления
какого-либо меридиана. Начало координат
— точка O — называется полюсом системы.

Положение
любой точки в полярной системе определяется
двумя координатами: радиусом-вектором
r
(или полярным расстоянием S) – расстоянием
от полюса до точки, и полярным углом 
при точке O, образованным осью OX и радиусом
вектором точки и отсчитываемым от оси
OX по ходу часовой стрелки.

Под
полярным углом 
в геодезии часто принимают дирекционный
угол
направления, с помощью которого определяют
координаты точек и расстояния между
ними.

П
ереход
от прямоугольных
координат
к полярным и обратно для случая, когда
начала обеих систем находятся в одной
точке и оси OX у них совпадают, выполняется
по формулам прямой
геодезической задачи:

tg
= Y/X, 
= arctg(Y/X)

Полярная
система координат
— двумерная система координат, в которой
каждая точка на плоскости определяется
двумя числами — полярным углом и полярным
радиусом. Полярная система координат
особенно полезна в случаях, когда
отношения между точками проще изобразить
в виде радиусов и углов; в более
распространённой, декартовой
или прямоугольной системе координат,
такие отношения можно установить только
путём применения тригонометрических
уравнений.

Полярная
система координат задаётся лучом,
который называют нулевым или полярной
осью. Точка, из которой выходит этот луч
называется началом координат или
полюсом. Любая точка на плоскости
определяется двумя полярными координатами:
радиальной и угловой. Радиальная
координата (обычно обозначается r)
соответствует расстоянию от точки до
начала координат. Угловая координата,
также называется полярным углом или
азимутом
и обозначается

,
равна углу, на который нужно повернуть
против часовой стрелки полярную ось
для того, чтобы попасть в эту точку.^[1]

Определённая
таким образом радиальная координата
может принимать значения от нуля
до бесконечности,
а угловая координата изменяется в
пределах от 0° до 360°. Однако, для удобства
область значений полярной координаты
можно расширить за пределы полного
угла, а также разрешить ей принимать
отрицательные значения, что отвечает
повороту полярной оси по часовой стрелке.

Графическое представление

Точка
в полярной системе координат.

Каждая
точка в полярной системе координат
может быть определена двумя полярными
координатами, что обычно называются r
(радиальная координата) и

(угловая
координата, полярный угол, азимут, иногда
пишут θ или t).
Координата r
соответствует расстоянию до полюса, а
координата

равна
углу в направлении против часовой
стрелки от луча через 0° (иногда называется
полярной осью)^[1].

Например,
точка с координатами

будет
выглядеть на графике как точка на луче,
который лежит под углом 60° к полярной
оси, на расстоянии 3 единиц от полюса.
Точка с координатами

будет
нарисована на том же месте, поскольку
отрицательное расстояние изображается
в положительную в противоположном
направлении (на 180°).

Одной
из важных особенностей полярной системы
координат является то, что одна и та же
точка может быть представлена бесконечным
количеством способов. Это происходит
потому, что для определения азимута
точки нужно повернуть полярную ось так,
чтобы он указывал на точку. Но направление
на точку не изменится, если осуществить
произвольное число дополнительных
полных оборотов. В общем случае точка

может
быть представлена в виде

или

,
где n
— произвольное целое
число^[10].

Для
обозначения полюса используют координаты

.
Независимо от координаты

точка
с нулевым расстоянием от полюса всегда
находится на нём^[11].
Для получения однозначных координат
точки, обычно следует ограничить значение
расстояния до неотрицательных значений

,
а угол

к
интервалу

или

(в
радианах

или

)^[12].

Углы
в полярных координатах задаются либо
в градусах, либо в радианах, при этом

.
Выбор, как правило, зависит от области
применения. В навигации
традиционно используют градусы, в то
время как в некоторых разделах физики,
и почти во всех разделах математики
используют радианы^[13].

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Полярная система координат (полярные координаты)

Полярная система координат на плоскости — это совокупность точки , называемой полюсом , и полупрямой , называемой полярной осью . Кроме того, задается масштабный отрезок для измерения расстояний от точек плоскости до полюса. Как правило, на полярной оси выбирается вектор , приложенный к точке , длина которого принимается за величину масштабного отрезка, а направление вектора задает положительное направление на полярной оси (рис.2.28,а).

Положение точки в полярной системе координат определяется расстоянием ( полярным радиусом ) от точки до полюса (т.е. ) и углом ( полярным углом ) между полярной осью и вектором . Полярный радиус и полярный угол составляют полярные координаты точки , что записывается в виде . Полярный угол измеряется в радианах и отсчитывается от полярной оси:

— в отрицательном направлении (по направлению движения часовой стрелки), если значение угла отрицательное.

Полярный радиус определен для любой точки плоскости и принимает неотрицательные значения . Полярный угол определен для любой точки плоскости, за исключением полюса , и принимает значения , называемыми главными значениями полярного угла . В некоторых случаях целесообразно считать, что полярный угол определен с точностью до слагаемых , где . В этом случае значениям полярного угла для всех соответствует одно и то же направление радиус-вектора.

С полярной системой координат можно связать прямоугольную систему координат , начало которой совпадает с полюсом, а ось абсцисс (точнее положительная полуось абсцисс) — с полярной осью. Ось ординат достраивается перпендикулярно оси абсцисс так, чтобы получилась правая прямоугольная система координат (рис.2.28,б). Длины базисных векторов определяются масштабным отрезком на полярной оси.

Наоборот, если на плоскости задана правая прямоугольная система координат, то, приняв положительную полуось абсцисс за полярную ось, получим полярную систему координат <связанную с данной прямоугольной).

Выведем формулы, связывающие между собой прямоугольные координаты точки , отличной от точки , и ее полярные координаты . По рис.2.28,б получаем

Последние два равенства определяют полярный угол с точностью до слагаемых , где . При из них следует, что . Главное значение полярного угла находится по формулам (рис.2.29):

Пример 2.9. В полярной системе координат :

а) изобразить координатные линии ;

б) изобразить точки с полярными координатами . Найти главные значения полярных углов этих точек;

в) найти прямоугольные координаты точек .

Решение. а) Координатные линии представляют собой окружности соответствующих радиусов, а линии и — полупрямые (рис.2.30,а).

б) Построим точки и (рис.2.30,б,в). Их координаты отличаются полярным углом, однако, имеют одно и то же главное значение . Следовательно, это одна и та же точка, которая совпадает с точкой , изображенной на рис.2.30,а.

в) Учитывая пункт «б», найдем прямоугольные координаты точки . По формулам (2.17) получаем:

1. Главное значение полярного угла можно выбрать иначе, например, .

2. Расстояние между двумя точками и (длина отрезка ) вычисляется по формуле

что следует из теоремы косинусов (рис.2.31).

3. Ориентированная площадь параллелограмма (рис.2.31), построенного на радиус-векторах и , находится по формуле

Она положительна, если (при этом ориентация пары радиус- векторов и правая), и отрицательна, если varphi_2″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAEcAAAASBAMAAAD73d5oAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMAwPxBoV0BgTEhELHR4JFxAbyQhgAAASJJREFUKM9jYCAdsEYRoyqmCqvwUgYGa1E4jy3mJczQCQzLRRZAOY8ZWBUPTUCoCvSEMGYzcJ0VcoCwOQUY1jZwFyAZbegBppwZ+Bw41CBC/AFALjuyIgZrCZCJxxgmMjBAFTFO4NrAwGLAwIlQNAWkiNkB6BCgNcYgZzE2sAYw9CSYX0cYJJwAVsQmwMAdsO7LDSCHbxt3A8dlhpniMIdDncSlwbGB7SHDbwZHEOdskalTAAMDTFEM1HMMnxyda6UYPjEUgThLlJRAeqGK4MHEwHpJ6T6I9gHzvNsY4IpYkQK8yQrkNg4NMEefAaEIGXwCqWFY2ADWrIxD0UGw+yVYQRS7Gg5FYBv4gq3B8QKONzvdSnRFBmA7lRQJJx22NKDLACxqN6Lf3w5xAAAAAElFTkSuQmCC» style=»vertical-align: middle;» /> (ориентация пары радиус-векторов и левая).

Пример 2.10. Даны полярные координаты и точек и (рис.2.32). Требуется найти:

а) скалярное произведение ;

б) длину отрезка ;

в) внешнее произведение ;

г) площадь треугольника ;

д) координаты середины отрезка в прямоугольной системе координат, связанной с данной полярной.

Решение. а) По определению скалярного произведения находим

б) Находим длину отрезка (см. пункт 2 замечаний 2.8):

в) Внешнее произведение находим как ориентированную площадь параллелограмма, построенного на векторах и :

Площадь положительная, так как векторы и образуют правую пару .

г) Площадь треугольника находим как половину площади параллелограмма, построенного на радиус-векторах и .

д) По формулам (2.17) находим прямоугольные координаты точек и :

а затем координаты середины отрезка (см. пункт 3 замечаний 2.1):

Пример 2.11. На координатной плоскости отмечена точка . Найти:

а) полярные координаты точки , образа точки при повороте радиус-вектора на угол вокруг начала координат (рис.2.33);

б) полярные координаты точки , образа точки при инверсии плоскости относительно окружности единичного радиуса с центром в начале координат (см. пример б преобразований плоскости в разд. 2.2.4).

Решение. а) Найдем полярные координаты точки . По формулам (2.17), учитывая рис.2.29, получаем:

так как точка лежит в четверти.

При повороте радиус-вектора вокруг полюса на угол полярный радиус не изменяется, а полярный угол увеличивается. Следовательно, полярные координаты точки : , , причем — главное значение полярного угла .

б) При инверсии относительно окружности радиуса полярные координаты образа выражаются через полярные координаты прообраза следующими формулами:

Поэтому, учитывая пункт «а», находим (для ):

Полярный угол между векторами

Угол между векторами.

Формула вычисления угла между векторами

cos α =	a · b
\| a \|·\| b \|

Примеры задач на вычисление угла между векторами

Примеры вычисления угла между векторами для плоских задачи

Решение: Найдем скалярное произведение векторов:

a · b = 3 · 4 + 4 · 3 = 12 + 12 = 24.

Найдем модули векторов:

| a | = √ 3 2 + 4 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 3 2 = √ 16 + 9 = √ 25 = 5

Найдем угол между векторами:

cos α =	a · b	=	24	=	24	= 0.96
\| a \| · \| b \|	5 · 5	25

Решение: Найдем скалярное произведение векторов:

a · b = 5 · 7 + 1 · 5 = 35 + 5 = 40.

Найдем модули векторов:

| a | = √ 7 2 + 1 2 = √ 49 + 1 = √ 50 = 5√ 2
| b | = √ 5 2 + 5 2 = √ 25 + 25 = √ 50 = 5√ 2

Найдем угол между векторами:

cos α =	a · b	=	40	=	40	=	4	= 0.8
\| a \| · \| b \|	5√ 2 · 5√ 2	50	5

Примеры вычисления угла между векторами для пространственных задач

Решение: Найдем скалярное произведение векторов:

a · b = 3 · 4 + 4 · 4 + 0 · 2 = 12 + 16 + 0 = 28.

Найдем модули векторов:

| a | = √ 3 2 + 4 2 + 0 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 4 2 + 2 2 = √ 16 + 16 + 4 = √ 36 = 6

Найдем угол между векторами:

cos α =	a · b	=	28	=	14
\| a \| · \| b \|	5 · 6	15

Решение: Найдем скалярное произведение векторов:

a · b = 1 · 5 + 0 · 5 + 3 · 0 = 5.

Найдем модули векторов:

| a | = √ 1 2 + 0 2 + 3 2 = √ 1 + 9 = √ 10
| b | = √ 5 2 + 5 2 + 0 2 = √ 25 + 25 = √ 50 = 5√ 2

Найдем угол между векторами:

cos α = a · b | a | · | b | = 5 √ 10 · 5√ 2 = 1 2√ 5 = √ 5 10 = 0.1√ 5

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Нахождение угла между векторами

Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.

Для рассмотрения понятия угла между векторами обратимся к графической иллюстрации: зададим на плоскости или в трехмерном пространстве два вектора a → и b → , являющиеся ненулевыми. Зададим также произвольную точку O и отложим от нее векторы O A → = b → и O B → = b →

Углом между векторами a → и b → называется угол между лучами О А и О В .

Полученный угол будем обозначать следующим образом: a → , b → ^

Очевидно, что угол имеет возможность принимать значения от 0 до π или от 0 до 180 градусов.

a → , b → ^ = 0 , когда векторы являются сонаправленными и a → , b → ^ = π , когда векторы противоположнонаправлены.

Векторы называются перпендикулярными, если угол между ними равен 90 градусов или π 2 радиан.

Если хотя бы один из векторов является нулевым, то угол a → , b → ^ не определен.

Нахождение угла между векторами

Косинус угла между двумя векторами, а значит и собственно угол, обычно может быть определен или при помощи скалярного произведения векторов, или посредством теоремы косинусов для треугольника, построенного на основе двух данных векторов.

Согласно определению скалярное произведение есть a → , b → = a → · b → · cos a → , b → ^ .

Если заданные векторы a → и b → ненулевые, то можем разделить правую и левую части равенства на произведение длин этих векторов, получая, таким образом, формулу для нахождения косинуса угла между ненулевыми векторами:

cos a → , b → ^ = a → , b → a → · b →

Данная формула используется, когда в числе исходных данных есть длины векторов и их скалярное произведение.

Исходные данные: векторы a → и b → . Длины их равны 3 и 6 соответственно, а их скалярное произведение равно — 9 . Необходимо вычислить косинус угла между векторами и найти сам угол.

Решение

Исходных данных достаточно, чтобы применить полученную выше формулу, тогда cos a → , b → ^ = — 9 3 · 6 = — 1 2 ,

Теперь определим угол между векторами: a → , b → ^ = a r c cos ( — 1 2 ) = 3 π 4

Ответ: cos a → , b → ^ = — 1 2 , a → , b → ^ = 3 π 4

Чаще встречаются задачи, где векторы задаются координатами в прямоугольной системе координат. Для таких случаев необходимо вывести ту же формулу, но в координатной форме.

Длина вектора определяется как корень квадратный из суммы квадратов его координат, а скалярное произведение векторов равно сумме произведений соответствующих координат. Тогда формула для нахождения косинуса угла между векторами на плоскости a → = ( a x , a y ) , b → = ( b x , b y ) выглядит так:

cos a → , b → ^ = a x · b x + a y · b y a x 2 + a y 2 · b x 2 + b y 2

А формула для нахождения косинуса угла между векторами в трехмерном пространстве a → = ( a x , a y , a z ) , b → = ( b x , b y , b z ) будет иметь вид: cos a → , b → ^ = a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2

Исходные данные: векторы a → = ( 2 , 0 , — 1 ) , b → = ( 1 , 2 , 3 ) в прямоугольной системе координат. Необходимо определить угол между ними.

Решение

Для решения задачи можем сразу применить формулу:

cos a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 2 2 + 0 2 + ( — 1 ) 2 · 1 2 + 2 2 + 3 2 = — 1 70 ⇒ a → , b → ^ = a r c cos ( — 1 70 ) = — a r c cos 1 70

Также можно определить угол по формуле:

cos a → , b → ^ = ( a → , b → ) a → · b → ,

но предварительно рассчитать длины векторов и скалярное произведение по координатам: a → = 2 2 + 0 2 + ( — 1 ) 2 = 5 b → = 1 2 + 2 2 + 3 2 = 14 a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 = — 1 cos a → , b → ^ = a → , b → ^ a → · b → = — 1 5 · 14 = — 1 70 ⇒ a → , b → ^ = — a r c cos 1 70

Ответ: a → , b → ^ = — a r c cos 1 70

Также распространены задачи, когда заданы координаты трех точек в прямоугольной системе координат и необходимо определить какой-нибудь угол. И тогда, для того, чтобы определить угол между векторами с заданными координатами точек, необходимо вычислить координаты векторов в виде разности соответствующих точек начала и конца вектора.

Исходные данные: на плоскости в прямоугольной системе координат заданы точки A ( 2 , — 1 ) , B ( 3 , 2 ) , C ( 7 , — 2 ) . Необходимо определить косинус угла между векторами A C → и B C → .

Решение

Найдем координаты векторов по координатам заданных точек A C → = ( 7 — 2 , — 2 — ( — 1 ) ) = ( 5 , — 1 ) B C → = ( 7 — 3 , — 2 — 2 ) = ( 4 , — 4 )

Теперь используем формулу для определения косинуса угла между векторами на плоскости в координатах: cos A C → , B C → ^ = ( A C → , B C → ) A C → · B C → = 5 · 4 + ( — 1 ) · ( — 4 ) 5 2 + ( — 1 ) 2 · 4 2 + ( — 4 ) 2 = 24 26 · 32 = 3 13

Ответ: cos A C → , B C → ^ = 3 13

Угол между векторами можно определить по теореме косинусов. Отложим от точки O векторы O A → = a → и O B → = b → , тогда, согласно теореме косинусов в треугольнике О А В , будет верным равенство:

A B 2 = O A 2 + O B 2 — 2 · O A · O B · cos ( ∠ A O B ) ,

b → — a → 2 = a → + b → — 2 · a → · b → · cos ( a → , b → ) ^

и отсюда выведем формулу косинуса угла:

cos ( a → , b → ) ^ = 1 2 · a → 2 + b → 2 — b → — a → 2 a → · b →

Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.

Хотя указанный способ имеет место быть, все же чаще применяют формулу:

Полярная система координат (полярные координаты)

Полярная система координат на плоскости — это совокупность точки , называемой полюсом , и полупрямой , называемой полярной осью . Кроме того, задается масштабный отрезок для измерения расстояний от точек плоскости до полюса. Как правило, на полярной оси выбирается вектор , приложенный к точке , длина которого принимается за величину масштабного отрезка, а направление вектора задает положительное направление на полярной оси (рис.2.28,а).

— в отрицательном направлении (по направлению движения часовой стрелки), если значение угла отрицательное.

Наоборот, если на плоскости задана правая прямоугольная система координат, то, приняв положительную полуось абсцисс за полярную ось, получим полярную систему координат (ориентация пары радиус-векторов и левая).

Пример 2.10. Даны полярные координаты и точек и (рис.2.32). Требуется найти:

а) скалярное произведение ;

б) длину отрезка ;

в) внешнее произведение ;

г) площадь треугольника ;

д) координаты середины отрезка в прямоугольной системе координат, связанной с данной полярной.

Решение. а) По определению скалярного произведения находим

б) Находим длину отрезка (см. пункт 2 замечаний 2.8):

в) Внешнее произведение находим как ориентированную площадь параллелограмма, построенного на векторах и :

Площадь положительная, так как векторы и образуют правую пару .

г) Площадь треугольника находим как половину площади параллелограмма, построенного на радиус-векторах и .

д) По формулам (2.17) находим прямоугольные координаты точек и :

а затем координаты середины отрезка (см. пункт 3 замечаний 2.1):

Пример 2.11. На координатной плоскости отмечена точка . Найти:

Решение. а) Найдем полярные координаты точки . По формулам (2.17), учитывая рис.2.29, получаем:

так как точка лежит в четверти.

Поэтому, учитывая пункт «а», находим (для ):

Координаты. Полярная система координат.

источники:

http://b4.cooksy.ru/articles/polyarnyy-ugol-mezhdu-vektorami

http://www.calc.ru/Koordinaty-Polyarnaya-Sistema-Koordinat.html

Источник