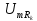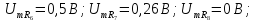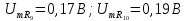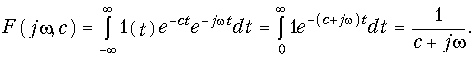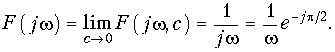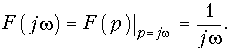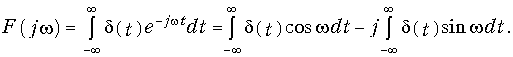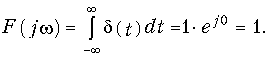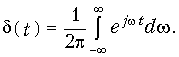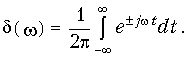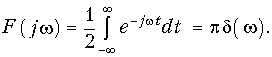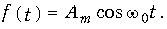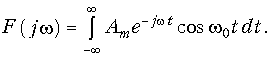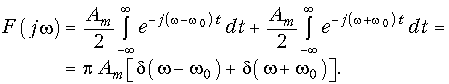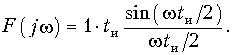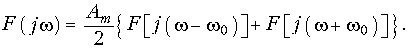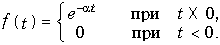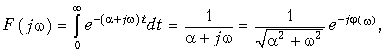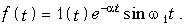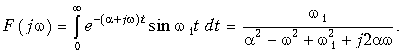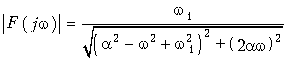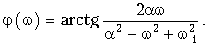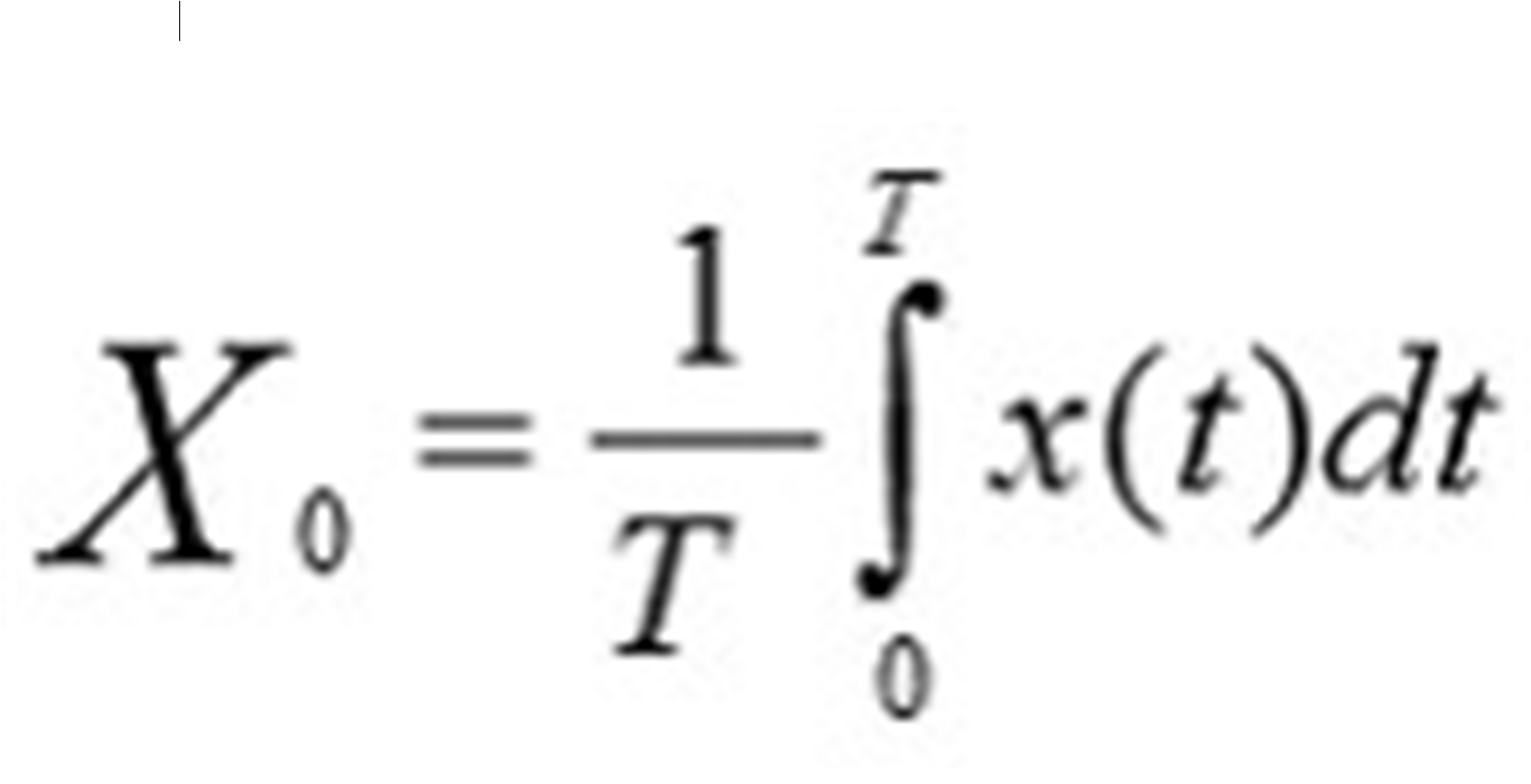МИНИСТЕРСТВО
ОБРАЗОВАНИЯ НАУКИ
РОССИЙСКОЙ
ФЕДЕРАЦИИ
ФЕДЕРАЛЬНО
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ
ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
МОСКОВСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПРИБОРОСТРОЕНИЯ
И ИНФОРМАТИКИ
В.
В. Филинов
Электроника
и схемотехника.
Расчёт
спектров электрических сигналов.
Учебно-методическое
пособие
Москва
— 2014
УДК
621.38
ББК
32.85
Рекомендовано
к изданию в качестве учебно-методического
пособия редакционно-издательским
советом МГУПИ
Рецензент:
д.т.н.
профессор Шкатов П. Н. (МГУПИ)
Филинов
В.В.
Электроника
и схемотехника. Расчет спектров
электрических сигналов.
Учебно-методическое пособие. М.: МГУПИ,
2014
Учебно-методическое
пособие предназначено для студентов
(бакалавров и специалистов) специальностей
по радиоэлектронике и информационной
безопасности, изучающих курс лекций
“Электроника и схемотехника”,
предназначено при подготовке к выполнению
практических и расчетно-графических
работ (РГР) по теме “Расчет спектров
электрических сигналов”. Приведены
примеры расчета спектров периодических
и непериодических сигналов, а также
задания для выполнения РГР. Полезно для
магистров и аспирантов технических
направлений МГУПИ.
Утверждено
и рекомендовано решением УМС факультета
«Приборостроения и радиоэлектроники»
МГУПИ в качестве учебно-методического
пособия.
©
Московский Государственный Университет
Приборостроения и Информатики, 2014
©
Филинов В.В., 2014
Оглавление
Стр.
Введение.
Необходимые формулы
………………………………………4
-
Спектры
амплитуд и фаз периодических сигналов
..…………6
Пример
1 ……………………………………………………………………6
Пример
2 …………………………………………………………………..10
Пример
3 …………………………………………………………………..11
Пример
4 …………………………………………………………………..12
Пример
5 …………………………………………………………………..13
Пример
6 …………………………………………………………………..14
Пример
7 …………………………………………………………………..16
Пример
8 …………………………………………………………………..17
Пример
9 …………………………………………………………………..18
Пример
10 …………………………………………………………………23
Пример
11 …………………………………………………………………24
-
Спектральная
плотность амплитуд и фаз периодических
сигналов
……..….…………..………………………..…….………………27
Пример
12 …………………………..……………………….……………27
Пример
13 …………………………..……………………….……………29
Пример
14 …………………………..……………………….……………31
Пример
15 …………………………..……………………….……………31
Пример
16 …………………………..……………………….……………33
Пример
17 …………………………..……………………….……………34
Пример
18 …………………………..……………………….……………36
Пример
19 …………………………..……………………….……………37
-
Литература
……………………………………………………………….39 -
Задания
для расчетно-географических
работ…………..………39
Необходимые
формулы.
Применительно
к периодическому гармоническому
напряжению
можно использовать разложение в ряд
Фурье:
(1)
Простейшим
периодическим сигналом является
гармоническое колебание вида
Разложение
последовательности прямоугольных
импульсов рис. 1.1 имеет вид:
(2)
Разложение
последовательности пилообразных
импульсов рис. 1.2 имеет вид:
(3)
Две
равнозначные записи ряда Фурье:
Ряд Фурье в
комплексной форме:
Выражение
для комплексного спектра сигнала:
Ряд
Фурье периодической последовательности
прямоугольных импульсов амплитудой U
(рис. 1.5а)
имеет вид:
Напряжение
на участках цепи находят, используя
принцип суперпозиции, например напряжение
на резисторах:
Расчет
цепи от отдельных постоянной и
гармонических составляющих напряжения
проводится в символической форме. При
этом нужно иметь в виду, что на k-й
гармонике сопротивление индуктивности

а сопротивление емкости
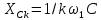
Интеграл
Фурье:
Уравнения
(10) и (11) являются основными в теории
спектров непериодических сигналов,
причем (10) называется прямым,
а (11) –
обратным
преобразованием Фурье (интегралом
Фурье).
Комплексная
придаточная функция по напряжению:
Из
выражений:
следует,
что спектральная плотность амплитуд
реакции цепи равна произведению
спектральной плотности амплитуд
воздействия АЧХ
цепи, а спектральная плотность фаз
реакции цепи равна сумме спектральной
плотности фаз
воздействия и ФЧХ
цепи.
-
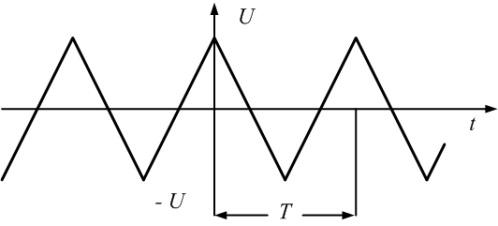
Спектры амплитуд и фаз периодических сигналов.
Пример
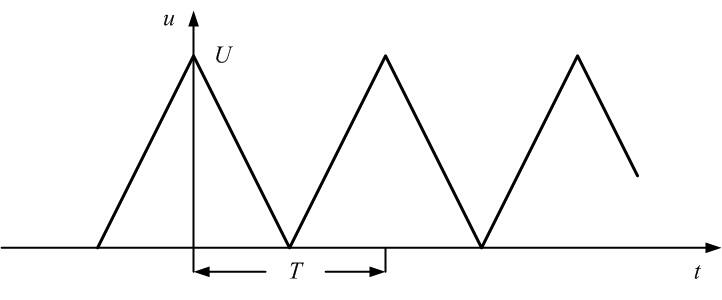
1.
Определим параметры синусоид, формирующих
последовательности прямоугольных (рис.
1.1, а) и пилообразных (рис. 1.2, а) импульсов,
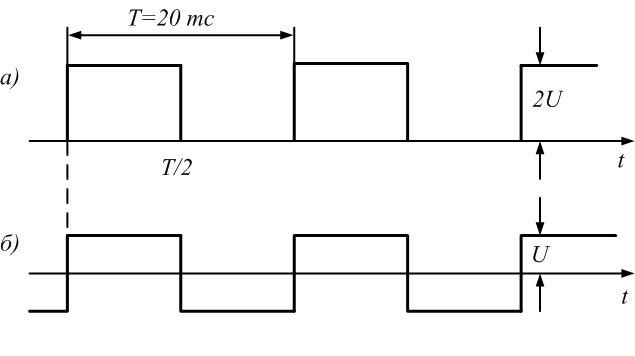
имеющих амплитуду U = 10 В
и период Т = 20 мс.
а)
Для формирования периодической
последовательности прямоугольных
импульсов амплитуда основной синусоиды
должна быть
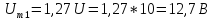
Частота
колебаний этой синусоиды обратно
пропорциональна периоду:
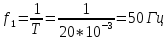
Круговая
частота

Таким образом, основная синусоида
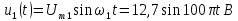
Все
последующие синусоиды в соответствии
с (2) должны иметь амплитуды в нечетное
количество раз меньшие, а частоты — в
это же нечетное количество раз большие,
чем у основной синусоиды:

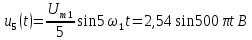
и
т.д.
Последовательность
прямоугольных импульсов, изображенных
на рис. 1.1, а,
—
это сумма синусоид:
.
Сигнал
изображен
на рис. 1.1, д.
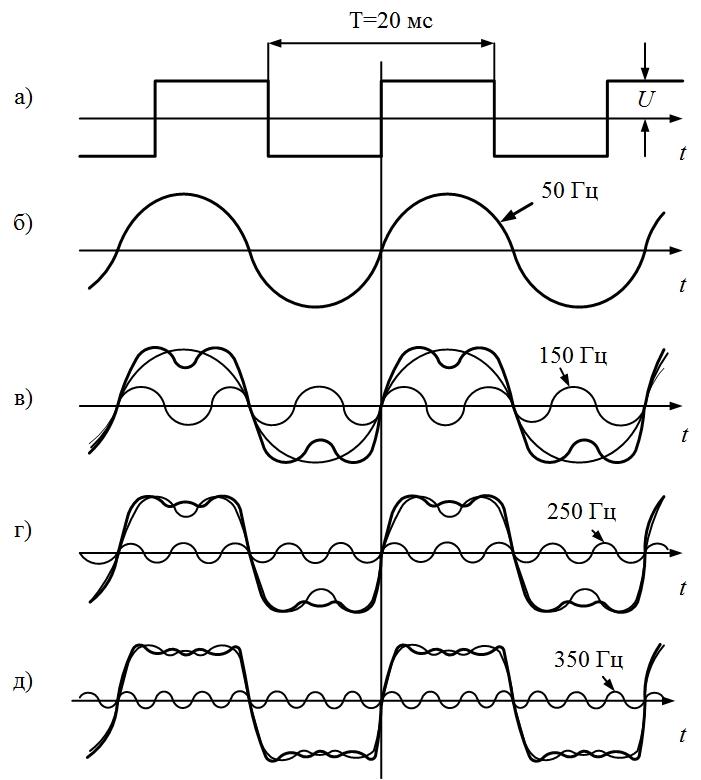
6)
Для формирования последовательности
пилообразных импульсов необходимо,
чтобы амплитуда основной синусоиды
была, как мы уже знаем [1, 3], равна
Частота
основной синусоиды

Таким
образом,
Рис.
1.1. Последовательность прямоугольных
импульсов и образующие ее синусоиды
Рис.
1.2. Последовательность пилообразных
импульсов и образующие ее синусоиды
Таблица
1.1. Ряды Фурье наиболее часто встречающихся
сигналов
|
Сигнал |
Ряд |
|
|
|
|
|
|
|
|
|
|
|
k-четные; |
|
|
k-четные; |
|
|
|
Последующие
синусоиды в соответствии с (3) будут
иметь вид
и
т.д.
Последовательность
пилообразных импульсов — это сумма
синусоид:
.
Чем
больше синусоид используется при
формировании сигнала, тем ближе его
форма к пилообразной (рис. 1.е).
Пример
2.
Определим гармонический состав
последовательности треугольных
импульсов, изображенных на рис. 1.3,
имеющих амплитуду, U
= 10 B
и период Т = 10 мс.
Периодический
сигнал на рис. 1.3 отличается от сигнала
во второй строке табл. 1.1 на величину
постоянной составляющей
Частота
основной составляющей сигнала
или
Амплитуда
основной составляющей сигнала
рассчитывается по формуле, приведенной
в табл. 1.1, или по одной из формул (1):
Четная
функция (рис. 1.3) содержит только
косинусоиды, амплитуды и частоты
которых определяются по формулам,
приведенным во второй строке табл. 1.1.
Амплитуда
и частота третьей гармоники:
Рис.
1.3. Последовательность треугольных
импульсов
Амплитуда
и частота пятой гармоники:
Амплитуда
и частота седьмой гармоники:
и
т.д.
Гармонический
состав последовательности треугольных
импульсов (рис.1.3) имеет вид:
Пример
3.
Представим переменное напряжение,
выпрямленное двухполупериодным
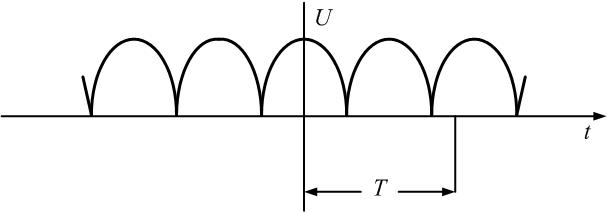
выпрямителем (пятая строка табл. 1.1),
рядом Фурье в тригонометрической форме
(5).
Из
табл. 1.1 следует, что переменное напряжение
u(t) представлено рядом Фурье:
k
– четные.
Постоянная
составляющая напряжения u(
t)
рассчитывается по формуле

0,635U.
Нечетные
гармоники отсутствуют в ряде Фурье,
поскольку функция u(
t)—
четная.
Для
расчета амплитуд четных гармоник
нео6ходимо определить

1,27U.
Тогда амплитуда второй гармоники
Начальная
фаза второй гармоники равна нулю:
Амплитуда
четвертной гармоники
Фаза
четвертой гармоники
, так как в ряде Фурье перед слагаемым
стоит знак «минус».
Амплитуда
шестой гармоники
а
ее фаза, а также фазы десятой, четырнадцатой
и т.д. гармоник равны нулю.
Амплитуда
восьмой гармоники
а
ее начальная фаза, так же как и фазы
гармоник с номерами 12, 16, 20 и т.д., равна
180˚.
Тригонометрическая
форма ряда Фурье рассматриваемого
напряжения имеет вид:
.
Пример
4.
Представим ряд Фурье, полученный в
примере 3, в комплексной форме, ограничив
его восьмой гармоникой.
В
соответствии с (6) значения постоянной
составляющей и амплитуд гармоник
уменьшаются в 2 раза по сравнению со
значениями, которые 6ыли рассчитаны в
примере 3. Поэтому ряд Фурье в комплексной
форме имеет вид
Пример
5.
Построим спектр амплитуд и фаз
выпрямленного напряжения
(строка
5 табл, 1.1), имеющего амплитуду U
= 10 В и период Т = 10 мс.
При
решении примера 3 была получена
тригонометрическая форма ряда Фурье,
соответствующая выпрямленному напряжению:
.
Частота
основной составляющей сигнала
определяется
периодом колебаний:
В
спектре сигнала отсутствуют нечетные
гармоники, так как само колебание
является четной функцией. Частоты высших
гармоник с четными номерами кратны этим
номерам: частота второй гармоники равна
2
= 200 Гц, четвертой, шестой, восьмой гармоник
— 400, 600, 800 Гц соответственно и т.д.
Постоянная
составляющая
Амплитуды
четных гармоник спектра в соответствии
с выражениями, полученными для ряда
Фурье, имеют следующие значения:
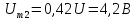

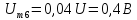
и
т.д.
Фазы
гармоник поочередно принимают значения
0 и 180˚.
Рис.
1.4. Спектры амплитуд и фаз выпрямленного
напряжения
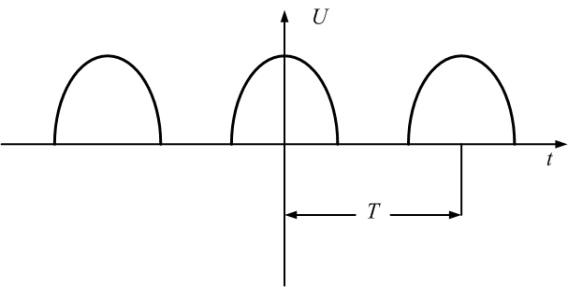
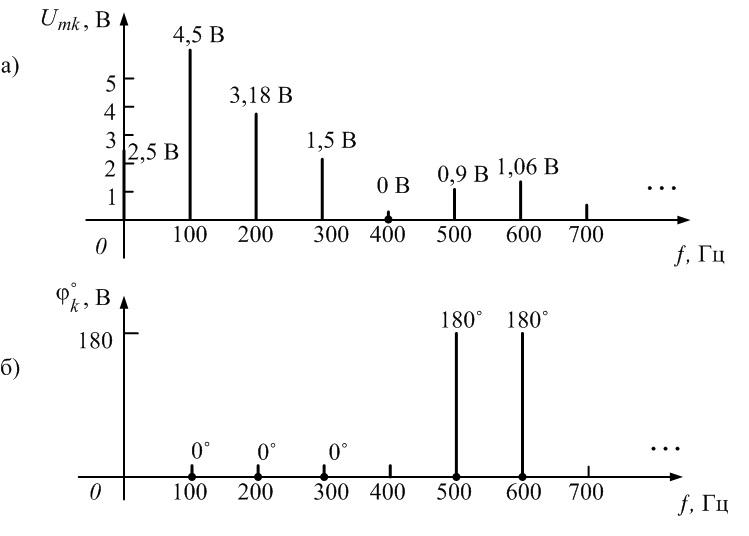
Пример
6.
Рассмотрим периодическую последовательность
прямоугольных импульсов, показанную
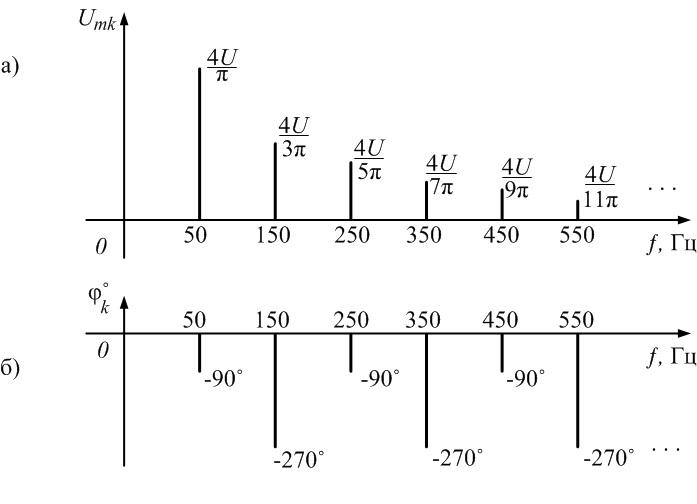
на рис. 1.5, а:
Рис.
1.5. Последовательности прямоугольных
импульсов
Она
имеет постоянную составляющую, равную
в соответствии с (1)
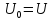
Коэффициенты
вычисляются
по формуле (1):
Здесь
6ыло учтено, что

1/Т.
Коэффициенты
вычисляются по формуле (1):
Выражение
удовлетворяет соотношению
Поэтому
Форма
ряда Фурье будет содержать только
синусоиды с нечетными гармоническими
частотами:
что,
естественно, с точностью до постоянной
составляющей U
совпадает с полученным ранее выражением
(2).
Переход
к форме ряда Фурье (5) дает
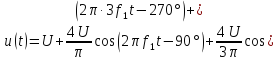
Спектр
такого сигнала без постоянной составляющей
показан на рис. 1.6:
Рис.
1.6. Спектры амплитуд и фаз сигнала рис.
1.5а
Пример
7.
Представим спектр сигнала
из примера 6 в комплексной форме.
Комплексный
спектр периодической последовательности
прямоугольных импульсов рассчитывается
по формуле (7):
Функция
имеет значения
Это
значит, что комплексный спектр
существует только для нечетных гармоник:
Заметим,
что в спектре
нет постоянной составляющей

которая рассчитывается по формуле (1) и
равна U.
Полученный
комплексный спектр
соответствует спектрам амплитуд и фаз,
изображенным на рис. 1.6.
Пример
8.
Найдем спектр последовательности
прямоугольных импульсов, изображенных
на рис. 1.7.
Сигнал,
изображенный на рис. 1.7, имеет следующие
параметры: амплитуда U
= 10 В, длительность импульса τ= 10 мс,
период повторения импульсов Т
= 40 мс, скважность q
= Т/τ = 4. Спектр этого сигнала в форме
(Табл. 1.1, строка 6) имеет вид
Постоянная
составляющая
Частота
первой гармоники
Частоты
высших гармоник кратны 100 Гц. Амплитуды
первых шести гармоник, рассчитываемые
по формуле (3.28)
имеют
следующие значения:
Фазы
первой, второй, третьей гармоник равны
0˚, фазы пятой и шестой гармоник равны
180˚, так как при расчете
и
получены отрицательные значения.
Амплитуды и фазы последующих гармоник
рассчитывают аналогичным образом.
Причем, амплитуды гармоник, кратных
скважности q, т.е. четвертой, восьмой,
двенадцатой, шестнадцатой гармоник и
т.д., равны нулю. Спектры амплитуд и фаз
сигнала, изображенного на рис. 1.7,
приведены на рис. 1.8.
Рис.
1.7. Последовательность прямоугольных
импульсов со скважностью q = 4
Рис.
1.8. Спектр последовательности прямоугольных
импульсов со скважностью q = 4
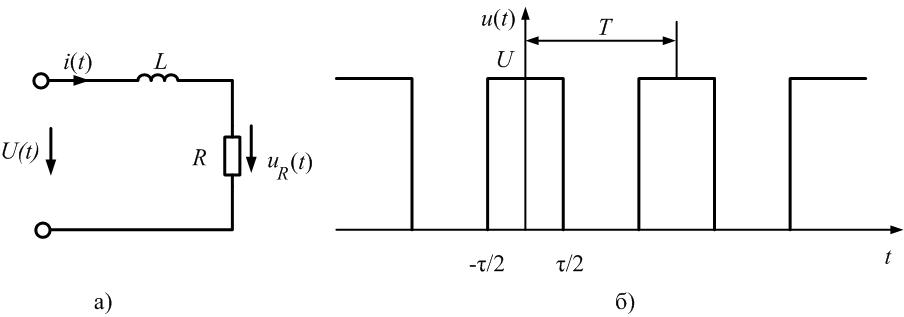
Пример
9.
Определим напряжение на резисторе
в
последовательном колебательном контуре,
на который подается последовательность
прямоугольных импульсов (рис. 1.10).
Параметры элементов контура и сигнала
заданы: R = 2 Ом; L = 0,704 мГн; С = 4 мкФ; U = 5
В; Т = 1 мс; τ = 0,5 мс.
Найдем
параметры постоянной и гармонических
составляющих сигнала (рис. 1.10),
представленного рядом Фурье (8). Частота
первой гармоники
или
Частоты
третьей, пятой и т.д. гармоник равны
соответственно: 3
= 18,84 рад/с; 3
= 3 кГц; 5
= 31,4 рад/с; 5
= 5 кГц; … .
Амплитуды
четных гармоник равны нулю. Амплитуды
нечетных гармоник рассчитываются по
формуле (1):
.
Ряд
Фурье сигнала имеет вид:
Рис.
1.9. Последовательный колебательный
контур с источником периодического
сигнала
Рис.
1. 10. Последовательность прямоугольных
импульсов
Определим
резонансную частоту
и
контура
(рис. 1.9):
Резонанс
в контуре наступает на частоте третьей
гармоники входного напряжения.
Добротность
контура
Определим
гармонические составляющие тока в цепи
и напряжения на резисторе в каждой из
составляющих ряда Фурье схем, изображенных
на рис. 1.9.
Схема
последовательного колебательного
контура с источником постоянного
напряжения

= 2,5 В приведена на рис. 1.11. В этой цепи
сопротивление индуктивности равно
нулю, а сопротивление конденсатора
равно бесконечности, поэтому
= 0;
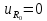
В
цепи, изображенной на рис. 1.12, в контур
включен источник напряжения, соответствующий
напряжению первой гармоники. Синусоидальное
напряжение
заменено
на комплексное

На частоте
= 1 кГц (
)
сопротивление индуктивности
а
сопротивление емкости
Рис.
1.11. Контур с источником постоянного
напряжения
Рис.
1.12. Контур с источником напряжения
первой гармоники
Комплексное
сопротивление цепи
Определим
комплексные значения тока
и напряжение
:
Это
соответствует составляющей синусоидального
напряжения (9) в исходной цепи:
На
третьей гармонике синусоидальный
источник заменяется источником
комплексного напряжения
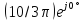
В результате имеем цепь, изображенную
на рис. 1.13.
На
частоте
= 3 кГц (
)
в цепи наступает резонанс напряжений.
Сопротивления индуктивности и емкости
равны по величине и противоположны по
знаку:
Комплексное
сопротивление цепи
= R = 2 Ом. Ток
Рис.
1.13. Контур с источником третьей гармоники
Рис.
1.14. Контур с источником напряжения
пятой гармоники
Напряжение
на резисторе
равно входному напряжению:

пятой гармонике синусоидальный источник
заменяется
источником комплексного напряжения
(рис. 1.14). На частоте
= 5 кГц (
)
сопротивления индуктивности и емкости
равны соответственно
и
Комплексное
сопротивление цепи
рассчитаем
по формуле:
Напряжение
на резисторе
Таким
образом, ряд Фурье напряжения на резисторе
имеет вид,
Рис.
1.15. Спектры амплитуд и фаз входного
напряжения и напряжения на резисторе
в колебательном контуре
Спектры
амплитуд и фаз этого напряжения изображены
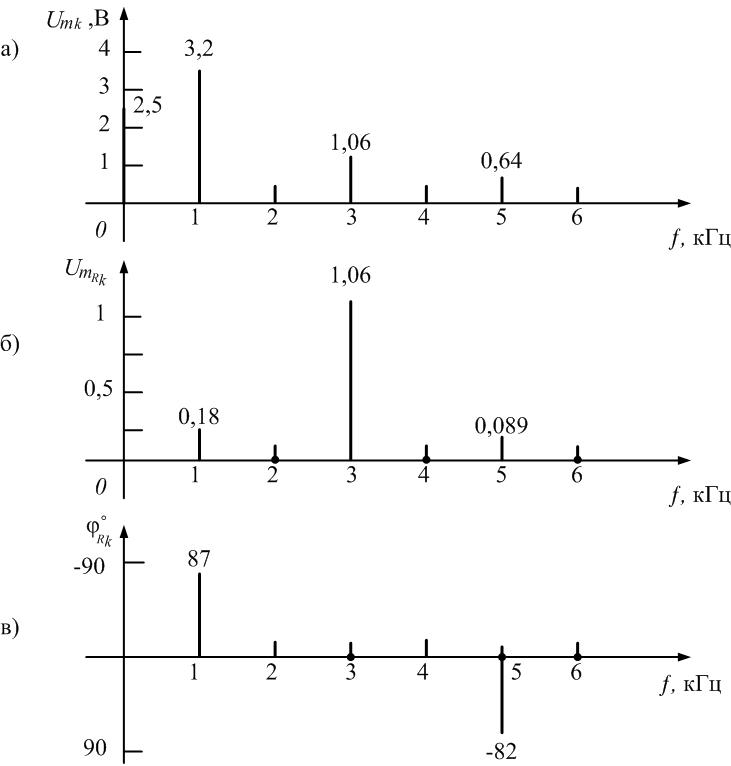
на рис. 1.15
( 6, в).
Анализ спектра
показывает, что колебательный контур
выделил третью гармонику из входной
последовательности и подавил остальные
гармоники, т.е. явление резонанса можно
использовать для, выделения отдельных
гармоник из периодического несинусоидального
сигнала.
Пример
10.
Сравним спектры амплитуд (рис. 1.15) входной
последовательности прямоугольных
импульсов
и напряжения
на резисторе колебательного контура
из примера 9, чтобы определить коэффициенты
передачи по напряжению цепи на частотах
гармоник.
В
соответствии с формулой и рис. 1.15 (а),
постоянная составляющая
в спектре напряжения
равна 2,5 В. Амплитуды первой, третьей и
пятой гармоник имеют значения:
Постоянная
составляющая в спектре напряжения
на резисторе (рис. 3.15, б)
равна нулю, а амплитуды нечетных гармоник
равны соответственно
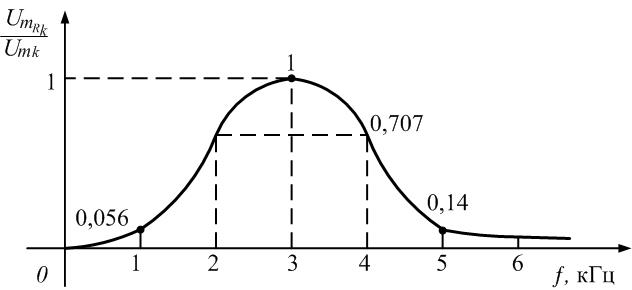
Коэффициенты
передачи по напряжению
на частотах гармоник рассчитаем по
формуле
На
частоте f
= 0 кГц получаем
= 0/2,5 = 0. На частоте f
= 1 кГц (частота основной составляющей)
= 0,18/3,2 = 0,056.
Рис.
1.16. Коэффициенты передачи по напряжению
на резисторе R на частотах гармоник
На
частоте
f=3
кГц (третья гармоника)
= 1,06/1,06 = 1.
На
частоте f=
5 кГц (пятая гармоника)
= 0,089/0,64= 0,14.
На
рис. 1.16 приведен график зависимости
коэффициента передачи контура от частоты
гармоник. На частоте резонанса коэффициент
передачи максимален и равен 1. На частотах
первой и пятой гармоник коэффициент
передачи резко уменьшается.
Пример
11.
Определим спектр амплитуд напряжения
на резисторе в цепи, изображенной на
рис. 1.17, а,
на вход которой поступает периодическая
последовательность прямоугольных
импульсов (рис. 1.17, б),
если заданы R
= 50 Ом, L
= 10 мГн, U
= 10 В, τ = 1 мс, Т = 4 мс.
Рис.
1.17. RL-цепь
и сигнал на ее входе
Найдем
комплексный спектр входного сигнала
u(t),
воспользовавшись (7):
Применив
формулу Эйлера, получим
Вычислим
амплитуды спектральных составляющих
Амплитуда
постоянной составляющей
Частота
основной составляющей
а
ее амплитуда
Аналогичным
образом определяются частоты и амплитуды
высших гармоник:
|
При |
k=2 |
2 |
|
|
k=3 |
3 |
|
|
|
k=4 |
4 |
|
|
|
k=5 |
5 |
|
|
|
k=6 |
6 |
|
|
|
k=7 |
7 |
|
|
|
k=8 |
8 |
|
|
|
k=9 |
9 |
|
|
|
k=10 |
10 |
|
Спектр
амплитуд
входного сигнала изображен на рис.
1.18, а.
Огибающая спектра амплитуд прямоугольных
импульсов изменяется по закону

нули спектра расположены на частотах,
кратных
=1 кГц (четвертая, восьмая, двенадцатая
и т.д. гармоники). Комплексная передаточная
функция цепи (рис. 1.17, а) определяется
по формуле
|
При |
k=0 |
|
|
k=1 |
|
|
|
k=2 |
|
|
|
k=3 |
|
|
|
k=4 |
|
|
|
k=5 |
|
|
|
k=6 |
|
|
|
k=7 |
|
|
|
k=8 |
|
|
|
k=9 |
|
|
|
k=10 |
|
Рис.
1.18. Спектры амплитуд последовательности
прямоугольных импульсов и напряжения
на резисторе в RL-цепи
и коэффициенты передачи цепи
График
зависимости коэффициента передачи
RL-цепи
от частоты изображен на рис. 3.18 (б).
Спектр
амплитуд
напряжения на резисторе, рассчитываем
в виде:
принимает
значения:
и
приведен на рис. 1.18 (в).
Определим спектры наиболее распространенных типов электрических сигналов.
Единичная функция задается уравнением (7.19) (см. рис. 7.2, а). Строго говоря, функция (7.19) не удовлетворяет условию абсолютной интегрируемости, поэтому воспользуемся следующим приемом: умножим 1(t) на «гасящий» множитель е–ct(с = const). При этом можно использовать прямое преобразование Фурье (9.6):
Преобразование F(jw, c) носит название обобщенного преобразования Фурье. Для получения спектра единичной функции перейдем к пределу:
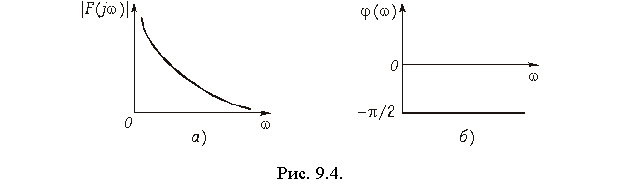
Из уравнения (9.38) получаем амплитудный |F(jw)| = 1/w (рис. 9.4, а) и фазовый спектр функции j(w) (рис. 9.4, б): j(w) = = —p/2, т. е. амплитудный спектр при w = 0 обращается в бесконечность, что свидетельствует о наличии в исходной функции 1(t) скачка при t = 0 (см. рис. 7.2, а). Для образования этого скачка в соответствии с (9.38) при t = 0 осуществляется суммирование бесконечно большого числа синусоидальных составляющих. Спектр (9.38) может быть получен и с помощью изображения единичной функции (7.20):
Единичная импульсная функция. Функция d(t) задается аналитически условиями (7.21). Для нахождения спектра d-функции воспользуемся прямым преобразованием Фурье (9.6), которое с учетом (9.8)—(9.10) можно записать в виде
Так как второе слагаемое равно нулю, а первое — единице вследствие свойств (7.21)—(7.23), то окончательно получим
Таким образом, d-функция имеет равномерный амплитудный и нулевой фазовый спектры. Равенство нулю на всех частотах фазового спектра означает, что все гармонические составляющие d-функции, суммируясь с нулевыми начальными фазами, образуют при t = 0 пик бесконечно большого значения.
Следует отметить, что сдвиг d-функции на время t приводит согласно свойствам преобразования Фурье к спектру 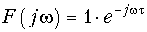
Из равенства (9.39) согласно обратному преобразованию Фурье (9.7) следует, что
Учитывая условие взаимозаменяемости параметров t и w, последнее выражение можно переписать в следующем виде:
Уравнения (9.40) и (9.41) широко используются в теории сигналов и цепей.
Спектр постоянной составляющей функции a0/2 = 1/2 с учетом (9.41) определяется уравнением
Таким образом, спектр постоянной составляющей равен нулю на всех частотах, кроме w = 0, где F(jw) обращается в бесконечность, то есть имеем на частоте w = 0 дискретную составляющую частоты в форме d-функции.
Спектр гармонического колебания. Проиллюстрируем методику использования прямого преобразования Фурье при определении спектра гармонического колебания
Преобразование (9.6) для функции (9.43) имеет вид
Формально функция (9.43) не удовлетворяет условию абсолютной интегрируемости, так как имеет показатель роста с = 0. По этому для вычисления интеграла (9.44) воспользуемся формулой Эйлера (3.18) и уравнением (9.41):
т. е. гармоническое колебание имеет дискретный спектр, состоящий из двух спектральных линий на частотах ±w0.
Спектр одиночного прямоугольного импульса (см. рис. 9.2) можно найти как непосредственно из прямого преобразования Фурье (9.6), так и путем предельного перехода при q ® ¥ (T® ¥) в разложении (5.27). В результате получим
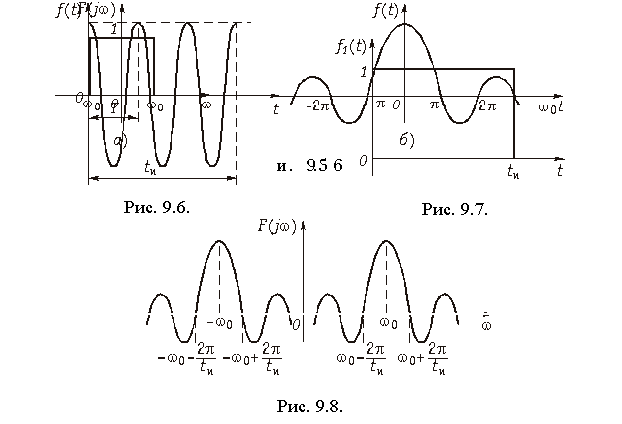
На рис. 9.3 изображен спектр одиночного импульса. Сравнение рис. 9.3 и рис. 9.4 показывает, что по своей форме спектр одиночного импульса совпадает с огибающей дискретного спектра последовательности периодических импульсов, однако спектр одиночного импульса является сплошным.
Из условия взаимосвязи между частотными и временными характеристиками сигнала следует, что сигнал с ограниченным по частоте ±w0 спектром прямоугольной формы (рис. 9.5, а) имеет бесконечную протяженность и форму, аналогичную спектру прямоугольного импульса (рис. 9.5, б).
Спектр радиоимпульса (рис. 9.6) можно найти как произведение видеоимпульса прямоугольной формы (рис. 9.7) и гармонического колебания (9.43). Тогда, воспользовавшись теоремой свертки (9.30), получим:
На рис. 9.8 показан вид спектра радиоимпульса.
Аналогичным образом можно найти спектр сигналов и более сложной формы.
Пример. Найти спектр экспоненциального импульса
В соответствии с прямым преобразованием (9.6) получаем
где 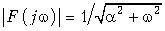
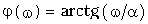
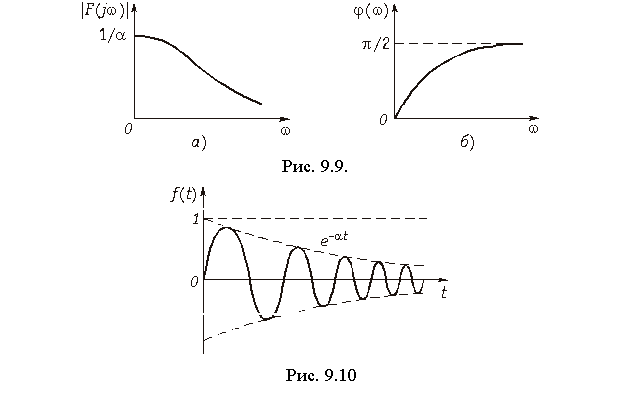
Пример 2. Определить спектр затухающего колебания (рис. 9.10)
Согласно (9.6) находим
Отсюда находим спектры:
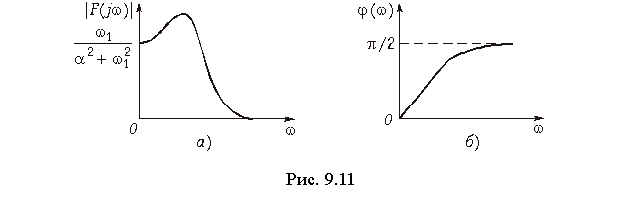
амплитудный (рис. 9.11, а)
и фазовый (рис. 9.11, б)
В таблице 9.1 приведены спектры некоторых наиболее распространенных сигналов.
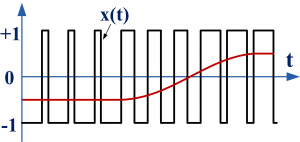
Значение постоянной составляющей сигнала – это среднее значение этого сигнала на рассматриваемом промежутке времени. Теоретически постоянная составляющая сигнала вычисляется интегральным выражением
где интервал времени T стремится к бесконечности. При практической интерпретации этого понятия в задачах обработки сигнала интеграл берётся на скользящем интервале времени заданного размера (т.е. по выборке изучаемого участка сигнала). Постоянная составляющая сигнала, исходя из геометрического смысла интеграла, хорошо видна на графике сигнала во времени как величина, равная площади между осью нулевого значения сигнала и графиком (учитывая, что под осью площадь отрицательна, а над осью – положительна). На графике показано красной кривой значение постоянной составляющей X0 для скользящего окна интегрирования с размером, сравнимым с периодом сигнала.
Для цифрового сигнала оценка постоянной составляющей – это среднее арифметическое выборки из N отсчетов.
В спектральном представлении сигнала информацию о постоянной составляющей сигнала несёт нулевая гармоника спектра этого сигнала.
Размер выборки для вычисления постоянной составляющей зависит от условий задачи. Например, если сигнал имеет выраженные гармонические составляющие с известной частотой, то целесообразно, чтобы выборка включала целое число периодов этих составляющих (иначе на выходе будут пульсации). Если спектр сигнала не известен заранее, можно применить оконную функцию – например, окно Ханна:
Это позволяет уменьшить влияние нецелых периодов на концах выборки. Примеры оконных функций можно найти, например, здесь.
На практике, когда сигналы представлены напряжением или током, для обозначения режима измерения постоянного напряжения или тока, который по сути является режимами измерения постоянной составляющей этих сигналов, широко применяется термин DC (direct current).
Не во всех сигналах постоянная составляющая информационна. Для удаления постоянной составляющей из сигнала применяют фильтры высокой частоты.
Некоторые среды передачи сигнала не позволяют передавать постоянную составляющую сигнала (например, среды, имеющие емкостную или индуктивую гальваническую развязку), Для передачи постоянной составляющей сигнала через такие среды используют различные технические принципы, связанные со специальными способами модуляции и кодирования сигнала.
Постоянная составляющая может быть и не связана с сигналом, а порождаться самим прибором или преобразователем (из-за неидельности его характеристик) в виде смещения нуля.
Любой сигнал можно разложить на составляющие. Такое разложение сигнала называется спектральным. При этом сигнал можно представить в виде графика зависимости параметров сигнала от частоты, такая диаграмма называется спектральной или спектром сигнала.
Спектр сигнала — это совокупность простых составляющих сигнала с определенными амплитудами, частотами и начальными фазами.
Между спектром сигнала и его формой существует жесткая взаимосвязь: изменение формы сигнала приводит к изменению его спектра и наоборот, любое изменение спектра сигнала приводит к изменению его формы. Это важно запомнить, поскольку при передаче сигналов в системе передачи, они подвергаются преобразованиям, а значит, происходит преобразование их спектров.
Различают два вида спектральных диаграмм:
— спектральная диаграмма амплитуд;
— спектральная диаграмма фаз.
В спектральной диаграмме амплитуд — отображаются все составляющие со своими амплитудами и частотами.
В спектральной диаграмме фаз — отображаются все составляющие со своими начальными фазами и частотами.
Любой сигнал имеет одну спектральную диаграмму амплитуд и одну спектральную диаграмму фаз, в составе которых может содержаться множество составляющих.
Не зависимо от того, какой спектр (амплитуд или фаз), он изображается в виде множества линий — составляющих. В спектре амплитуд высота спектральной линии равна амплитуде составляющей сигнала, а в спектре фаз — начальной фазе составляющей. Причем: в спектре амплитуд все составляющие имеют положительные значения, а в спектре фаз как положительные, так и отрицательные. Если амплитуда спектральной составляющей имеет отрицательный знак, то в спектре амплитуд она берется по модулю, а в спектре фаз знак составляющей изменяется на противоположный.
Классификация спектров сигналов.
1. По виду спектры бывают дискретными (линейчатыми) или сплошными.
Дискретным является спектр, у которого можно выделить отдельные составляющие.
Сплошным является спектр, у которого нельзя выделить отдельные составляющие, так как они расположены настолько близко, что сливаются друг с другом.
2. По диапазону частот различают спектры ограниченные и неограниченные.
Ограниченным является спектр, у которого вся энергия сигнала (все спектральные составляющие) находятся в ограниченном диапазоне частот (fmax ? ?).
Неограниченным является спектр, у которого вся энергия сигнала находится в неограниченном диапазоне частот (fmax ? ?). На практике такие спектры ограничивают.
Спектральное представление периодических сигналов
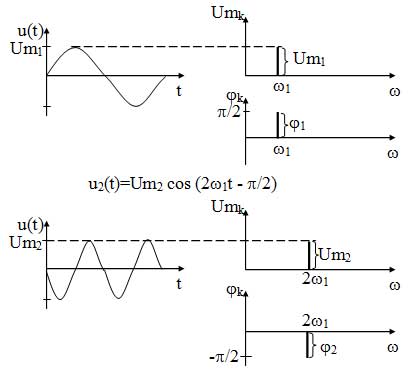
1. Гармоническое колебание.
Математическая модель гармонического колебания имеет вид:
u(t)=Ums sin (?st+?s) (11)
Как видно из математической модели, в спектре данного колебания присутствует одна гармоническая составляющая, которая находится на частоте ?s. Высота составляющей в спектре амплитуд равна амплитуде колебания Ums, а в спектре фаз — начальной фазе колебания ?s. Причем при построении спектра необходимо учитывать связь между временной диаграммой сигнала и спектром амплитуд. Амплитуда составляющей спектра должна по высоте соответствовать амплитуде колебания на временной диаграмме.
Необходимо отметить, что при увеличении частоты сигнала, его составляющая будет удаляться по оси частот от нуля (рисунок 13).
Рисунок 13 — Спектральное представление гармонических колебаний
Как видно из рисунков, спектр гармонического колебания является дискретным и ограниченным.
2. Периодические, негармонические сигналы.
Основной особенностью спектрального представления таких сигналов является наличие в их спектре множества спектральных составляющих. Такие сигналы могут быть описаны рядом Фурье, согласно которому:
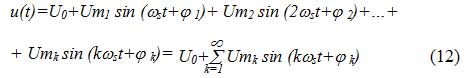
Преобразуем данный ряд, используя тригонометрическое свойство
sin(x+y) = sin x cos y + cos x sin y (13)
Полагая что x=?k и y=k?ct получим:

Umk sin ? k = ak; Umk cos ?k = bk (15)
Тогда ряд примет вид:
Параметры ряда можно определить через коэффициенты ak и bk:
где k=1, 2, 3 …
Амплитуда постоянной составляющей и коэффициенты могут быть определены через значение сигнала u(t):

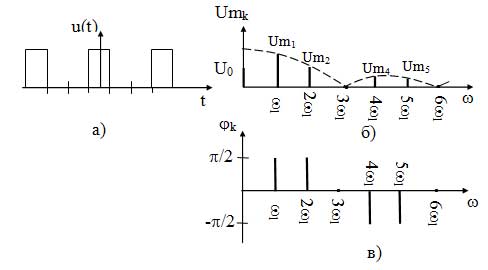
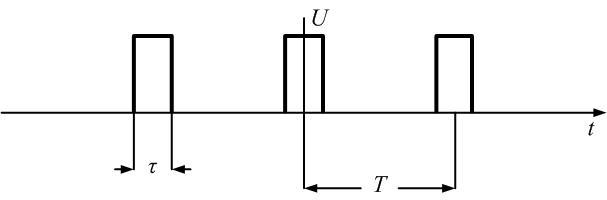
Рассмотрим спектральное представление периодических, негармонических сигналов на примере периодической последовательности прямоугольных импульсов (ПППИ).
При построении спектра необходимо рассчитать следующие параметры:
а) скважность сигнала:
q = T/?и (21)
б) значение постоянной составляющей:
U0=Ums/q (22)
I0=Ims/q
в) частоту первой гармоники спектра, которая равна частоте сигнала:
f1=fs=1/T (23)
г) амплитуды гармонических составляющих спектра:
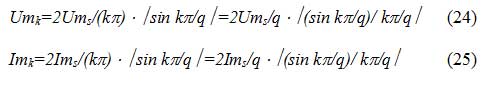
1. Все гармонические составляющие находятся на частотах, кратных частоте первой гармоники (2?1, 3?1, 4?1 и т. д.);
2. Для спектра амплитуд:
а) спектр ПППИ имеет лепестковый характер, т. е. в спектре можно выделить множество «лепестков»;
б) количество гармонических составляющих в лепестке зависит от скважности и равно q — 1;
в) амплитуды гармонических составляющих, находящихся на частотах, кратных скважности, равны нулю;
г) форма спектра обозначается огибающей — пунктирной линией, плавно соединяющей вершины гармонических составляющих;
д) точка, из которой исходит огибающая, равна 2U0 или 2I0.
3. Для спектра фаз:
а) все гармонические составляющие, на частотах, не кратных скважности, имеют одинаковую высоту, равную ?/2 (90°);
б) все гармонические составляющие в одном лепестке имеют одинаковый знак, а в соседних противоположный.
в) составляющие на частотах кратных скважности имеют начальную фазу равную нулю.
Спектры ПППИ при скважности q=3 представлены на рисунке 14.
Как видно из диаграмм спектр ПППИ является дискретным и неограниченным. Поэтому за ширину спектра принимают диапазон частот, в пределах которого находится два первых лепестка, т. к. в них содержится около 95% энергии сигнала:
?fs = 2/?и. (26)
Рисунок 14 — Спектральное представление ПППИ: а) временная диаграмма; б) спектральная диаграмма амплитуд; в) спектральная диаграмма фаз
Как видно из формулы ширина спектра ПППИ зависит только от длительности импульса и не зависит от его периода.
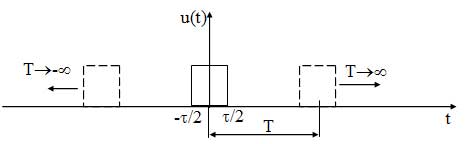
3. Непериодические сигналы.
Поскольку в непериодических сигналах нельзя выделить период, т. к. Т??, то рассчитать и построить спектр тем же методом, что и для периодических сигналов нельзя. Однако знать спектр таких сигналов необходимо, т. к. все информационные сигналы являются непериодическими. Для построения спектра непериодического сигнала производят следующую процедуру: сигнал мысленно представляют как периодический с произвольным периодом, ддля которого строят спектр. Затем осуществляют предельный переход устремляя период к бесконечности (Т??) (рисунок 15). При этом частота первой гармоники и, соответственно, расстояние между гармоническими составляющими стремится к нулю (f1=1/Т), поэтому все составляющие сливаются друг с другом и образуют сплошной спектр.
Рисунок 15 — Импульсный сигнал u(t) и его представление периодическим сигналом
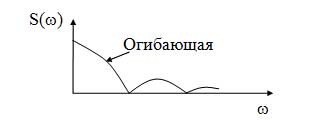
Форма спектра непериодических сигналов обозначается огибающей (сплошной линией) (рисунок 16).
Рисунок 16 — Спектральная диаграмма непериодического сигнала
Ряд Фурье, для таких сигналов, также нельзя записать, т. к. в этом случае амплитуда постоянной составляющей и коэффициенты ak и bk равны нулю. В этом случае значение сигнала в любой момент времени также равно нулю, что является не верным. Поэтому для таких сигналов используют преобразования Фурье:
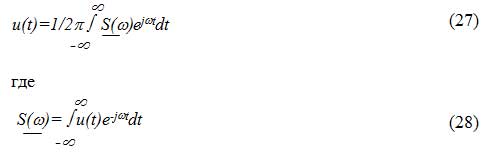
Величина S(?) является комплексной спектральной плотностью непериодического сигнала u(t). Она равна:
S(?) = S(?)e ^(-j?(?)) (29)
где S(?) спектральная плотность амплитуд или амплитудный спектр непериодического сигнала, а ?(?) — фазовый спектр непериодического сигнала.
Спектральная плотность амплитуд непериодического сигнала на любой частоте ? равна суммарной амплитуде составляющих находящихся в малой полосе ?? в окрестностях частоты ? пересчитанных на 1 Герц.
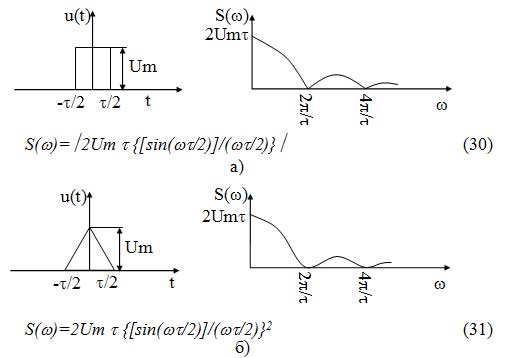
Временные диаграммы и спектральные плотности амплитуд для прямоугольного и треугольного импульсов представлены на рисунке 18:
Рисунок 18 — Спектральное представление непериодических сигналов: а) прямоугольный импульс; б) треугольный импульс
Содержание
- РЕЛЕ ЭЛЕКТРИЧЕСКИЕ
- ГОСТ 27916—88 (МЭК 255—11)
- напряжения*
- Питание **
- Статическое измерительное реле
Значение постоянной составляющей сигнала – это среднее значение этого сигнала на рассматриваемом промежутке времени. Теоретически постоянная составляющая сигнала вычисляется интегральным выражением
где интервал времени T стремится к бесконечности. При практической интерпретации этого понятия в задачах обработки сигнала интеграл берётся на скользящем интервале времени заданного размера (т.е. по выборке изучаемого участка сигнала). Постоянная составляющая сигнала, исходя из геометрического смысла интеграла, хорошо видна на графике сигнала во времени как величина, равная площади между осью нулевого значения сигнала и графиком (учитывая, что под осью площадь отрицательна, а над осью – положительна). На графике показано красной кривой значение постоянной составляющей X0 для скользящего окна интегрирования с размером, сравнимым с периодом сигнала.
Для цифрового сигнала оценка постоянной составляющей – это среднее арифметическое выборки из N отсчетов.
В спектральном представлении сигнала информацию о постоянной составляющей сигнала несёт нулевая гармоника спектра этого сигнала.
Размер выборки для вычисления постоянной составляющей зависит от условий задачи. Например, если сигнал имеет выраженные гармонические составляющие с известной частотой, то целесообразно, чтобы выборка включала целое число периодов этих составляющих (иначе на выходе будут пульсации). Если спектр сигнала не известен заранее, можно применить оконную функцию – например, окно Ханна:
Это позволяет уменьшить влияние нецелых периодов на концах выборки. Примеры оконных функций можно найти, например, .
На практике, когда сигналы представлены напряжением или током, для обозначения режима измерения постоянного напряжения или тока, который по сути является режимами измерения постоянной составляющей этих сигналов, широко применяется термин DC (direct current).
Не во всех сигналах постоянная составляющая информационна. Для удаления постоянной составляющей из сигнала применяют фильтры высокой частоты.
Некоторые среды передачи сигнала не позволяют передавать постоянную составляющую сигнала (например, среды, имеющие емкостную или индуктивую гальваническую развязку), Для передачи постоянной составляющей сигнала через такие среды используют различные технические принципы, связанные со специальными способами модуляции и кодирования сигнала.
Постоянная составляющая может быть и не связана с сигналом, а порождаться самим прибором или преобразователем (из-за неидельности его характеристик) в виде смещения нуля.
БЗ 11-88/795
ГОСУДАРСТВЕННЫЙ СТАНДАРТ
СОЮЗА ССР
РЕЛЕ ЭЛЕКТРИЧЕСКИЕ
ОТКЛЮЧЕНИЕ И ПЕРЕМЕННАЯ СОСТАВЛЯЮЩАЯ ВСПОМОГАТЕЛЬНЫХ ВОЗДЕЙСТВУЮЩИХ ВЕЛИЧИН ПОСТОЯННОГО ТОКА ИЗМЕРИТЕЛЬНЫХ РЕЛЕ
ГОСТ 27916—88 (МЭК 255—11)
Издание официальное
ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР ПО СТАНДАРТАМ
Москва
УДК 621.318.5-83:006.354 Группа Е71
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
РЕЛЕ ЭЛЕКТРИЧЕСКИЕ
Отключение и переменная составляющая вспомогательных воздействующих величин постоянного тока измерительных реле
ГОСТ
27916—88
(МЭК 255—11)
ОКП 34 2500
Срок действия с 01.01.91 до 01.01.96
Несоблюдение стандарта преследуется по закону
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Область распространения
Настоящий стандарт устанавливает дополнительные требования, которые должны обеспечиваться, и дополнительные параметры, значения которых должны уточняться изготовителем, относящиеся к отключениям и переменным составляющим, влияющим на вспомогательные воздействующие величины постоянного тока статических измерительных реле.
Требования, содержащиеся в стандарте, также распространяются на некоторые электромеханические реле с одной вспомогательной воздействующей величиной постоянного тока.
2. ТРЕБОВАНИЯ, ОТНОСЯЩИЕСЯ К ОТКЛЮЧЕНИЯМ ВСПОМОГАТЕЛЬНОЙ ВОЗДЕЙСТВУЮЩЕЙ ВЕЛИЧИНЫ
ПОСТОЯННОГО ТОКА
Этот раздел касается отключений вспомогательной воздействующей величины постоянного тока, рассматриваемой как влияющая величина, имеющая основное стандартное значение, но не имеющая номинального диапазона.
2.1. Отключение
Под отключением понимают как прерывание возбуждения, так и короткое замыкание вспомогательной воздействующей вели-
Издание официальное
Перепечатка воспрещена © Издательство стандартов, 1989
чины*. Рассматривают только одиночные отключения. Отдельные испытания могут быть необходимы для определения результатов отключения или короткого замыкания в цепи возбуждения. Условия испытаний должны оговариваться.
2.2. Стандартные нормальные значения влияющих величин или факторов и допуски при испытаниях
|
Таблица 1 |
|||
|
Влияющая величина или фактор |
Принимаемое условие |
Допуски при* испытаниях |
|
|
Вспомогательные воздействующие величины |
Отключение |
0 мс |
Отсутст вуют |
2.3. Стандартные значения пределов ном и
|
нальных диапазонов влияющих торов |
величин и фак-Таблица 2 |
|
|
Влияющая величина или фактор |
Номинальный диапазон |
|
|
Вспомогательные воздей |
Отключение |
Не оговаривается |
|
ствующие величины |
2.4. Влияние отключения вспомогательной воздействующей величины постоянного тока
Влияние должно быть определено при отключении, продолжительность которого должна оговариваться изготовителем и выбираться из следующих значений: 2—5—10—20—50—100—200 мс.
Отключение должно быть внезапным, т. е. вспомогательная воздействующая величина должна изменяться от 0 до номинального значения или наоборот. Изготовитель должен точно определить условия испытания.
Примечание, В особых случаях могут потребоваться дополнительные сведения, чтобы показать влияние скорости изменения вспомогательного напряжения, например, влияние на преобразователь Постоянного тока одного напряжения в постоянный ток другого напряжения.
Если необходимо, то изготовитель оговаривает влияние отключений на:
точность;
* Для исключения короткого замыкания в цепь питания можно включить последовательно полное сопротивление; влияние полного сопротивления из срабатывание реле должно оговариваться изготовителем, если необходимо.
время срабатывания;
характеристику возврата;
другие характеристики, если это имеет значение.
Реле не должно ложно изменять своего выходного состояния, когда происходит включение или отключение вспомогательной воздействующей величины (см. приложение 1).
3. ТРЕБОВАНИЯ, ОТНОСЯЩИЕСЯ К ПЕРЕМЕННОЙ СОСТАВЛЯЮЩЕЙ ВСПОМОГАТЕЛЬНОЙ ВОЗДЕЙСТВУЮЩЕЙ ВЕЛИЧИНЫ В УСТАНОВИВШЕМСЯ РЕЖИМЕ
Раздел касается переменной составляющей вспомогательной воздействующей величины постоянного тока, рассматриваемой в качестве влияющей величины, имеющей основное стандартное значение и пределы номинального диапазона.
3*1. Определение переменной составляющей
В настоящем стандарте переменную составляющую постоянного тока определяют по формуле
Ртт—Цв .10р Uo
где Umm — максимальное мгновенное значение напряжения;
UB — минимальное мгновенное значение напряжения;
Uo — постоянная составляющая.
3.2. Условия определения влияния переменной составляющей вспомогательной воздействующей величины
Для статических реле очень важно, чтобы влияния переменной составляющей напряжения были проверены при максимальных и минимальных значениях напряжения постоянного тока (110 и 80% номинального значения).
Форма волны должна быть синусоидальной (или волна выпрямлена двухполупериодно) и ее частота должны быть двойной по отношению к частоте сети, если не оговорено особо изготовите-
|
л ем (см. приложение 1). 3.3. Стандартные значения нального диапазона |
пределов номи* Таблица 3 |
|
|
Влияющая: величина или фактор |
Номинальный диапазон |
|
|
Вспомогательные воздействующие величины |
Переменная составляющая постоянного тока |
От 0 до 12% номинального значения напряжения постоянного тока |
ПРИЛОЖЕНИЕ
Рекомендуемое
ПОЯСНЕНИЯ, КАСАЮЩИЕСЯ ВСПОМОГАТЕЛЬНЫХ ИСТОЧНИКОВ СТАТИЧЕСКИХ ИЗМЕРИТЕЛЬНЫХ РЕЛЕ
Особые требования, относящиеся к двум влияющим факторам: отключениям и переменной составляющей постоянного тока, которые распространяются на вспомогательные источники, указаны в табл, 1—3 настоящего стандарта, Несмотря на то, что они касаются измерительных реле, требующих одного вспомогательного источника, в этом приложении содержится информация, помогающая определить точку приложения влияющих величин, когда требуется определить их влияние на рабочие характеристики реле. Для объяснения критериев выбора условий испытаний даны дополнительные сведения.
Хотя в некоторых случаях статические измерительные реле автономны в части питания, т. е. они имеют свой внутренний источник постоянного тока от входной воздействующей величины (выходных величин трансформатора тока или напряжения), для правильного срабатывания большая часть статических реле требует отдельного внешнего источника напряжения при переменном или постоянном токе, Почти всегда неотъемлемой частью измерительного реле является вспомогательный источник питания реле, который может быть простым регулятором (стабилизатором), преобразователем переменного тока в-постоянный или преобразователем постоянного тока одного напряжения в постоянный ток другого напряжения, Этот источник питания выполняет в основном три функции:
а) понижает уровень напряжения внешнего источника до уровня напряжения, соответствующего для статических цепей;
б) уменьшает изменения напряжения внешнего источника, подавая внутреннее стабилизированное напряжение (собственное напряжение);
в) обеспечивает изоляционный и фильтровый барьер между собственным и общим источниками таким образом, чтобы напряжение помех, возникающее в последнем, не передавалось на чувствительные статические цепи,
В случае необходимости источники питания для статических измерительных реле получают от внешнего источника напряжения переменного или постоянного тока, Этот внешний источник, если только он не предусмотрен для особой группы устройств защиты, расположен в центральном здании или подстанции и не зависит от изготовителя устройства защиты, Этот источник питания, как правило, подвержен влиянию помех, напряжений высокой частоты, колебаний и т. д. Примером такого источника является общеподстанционная батарея, которая питает включающие катушки, реле защиты и т д. Считается, что на практике могут выполняться многочисленные отключения, и полное результирующее сопротивление источника до входных зажимов измерительного реле может также изменяться от нуля до бесконечности. Однако фактически условия испытаний, оговоренные в настоящем стандарте, ограничены единичными отключениями в виде короткого замыкания или размыкания цепи на зажимах измерительного реле, Значения продолжительности этого отключения, охватывающего промежуток от 0 до 200 мс, были оговорены. Это предусмотрено в основном для учета повреждений в вспомогательных цепях питания и соответствующего времени срабатывания автоматических выключателей.
На черт, 1 и 2 представлены схемы соединений статических реле со своим источником питания, На черт, 1 внешний источник соединен непосредственно с входными зажимами измерительного реле. Вспомогательный источник реле или «входной интерфейс» расположен в корпусе, и его выходное напряжение подают на статические цепи реле в пределах корпуса.
Для некоторых исполнений устройств защиты из-за мощности, требующейся для питания, и результирующей мощности рассеяния во вспомогательном источнике, необходимо, чтобы последний размещался в отдельном корпусе* В этом случае источник поставляется либо непосредственно изготовителем реле, либо соответствует спецификациям реле, применяющегося с определенным устройством защиты, Сочетание вспомогательного источника и измерительного реле рассматривают как сложное устройство ввиду того, что источник является дополнительным элементом, который необходим для работы измерительного реле и испытывается вместе с ним На черт, 2 показан пример, когда источник расшь ложен в отдельном корпусе. Внешний источник соединен с его входными зажимами, и вспомогательный источник реле представляет собой интерфейс между общим источником и питанием собственным напряжением. В основном его применяют для соединения выходных зажимов вспомогательного источника с входными зажимами реле, используя экранированные штепсельные разъемы с особыми типами вилок и розеток, Это обусловливает защиту от высокочастотных помех, препятствует применению по недосмотру других источников, предотвращает ошибочное соединение автономного питания реле с устройством, для которого оно не предусмотрено,
В обоих рассмотренных выше случаях влияния отключения и колебаний внешнего источника должны быть рассмотрены на зажимах устройства, к которым этот источник непосредственно подсоединен, т. е, к точкам А (черт. 1 и 2), Даже когда вспомогательный источник реле помещен в корпус, отделенный от корпуса измерительного реле, эти влияющие факторы относятся к входным зажимам вспомогательного источника реле, если только последний составляет неотъемлемую часть измерительного реле, поставлен и испытан как составная часть оборудования реле, Следует учесть, что если плавкие предохранители помещены между источником питания и реле (см. черт, 2), это условие должно рассматриваться как выполненное в соответствии со схемой черт, 1, даже если вспомогательный источник в действительности располагается вне корпуса реле.
Внутренний вспомогательный источник
О
*
напряжения*
О
т
Питание **
|
—О |
|||
|
ч |
ч |
||
|
—О О» |
—О |
||
|
Автономное питание |
Статическое измерительное реле
i — вспомогательный источник реле (входной интерфейс); 2 — статические цепи
* Внешний отдаленный (общий источник, см. примечание 1),
** Других аппаратов, например, отключающих катушек, других реле и т, д(
Черт. 1
Внешний вспомогательный источник
1 — вспомогательный источник реле (входной интерфейс); 2 — статическое измерительное реле; 3 — статические измерительные реле (см.
примечание 3)
* Внешний отдаленный (общий источник, см, примечание 1),
** Других устройств.
*** См. примечание 2,
Черт, 2
Примечания:
1. Этот источник напряжения может быть переменного или постоянного тока.
2. Экранированные провода и специальные штепсельные разъемы применялись в основном для этих соединений,
3. Внешний вспомогательный источник может питать несколько реле.
ИНФОРМАЦИОННЫЕ ДАННЫЕ
1. РАЗРАБОТАН И ВНЕСЕН Министерством электротехнической промышленности СССР
ИСПОЛНИТЕЛИ
Г. С. Нудельман (руководитель разработки), Т. Т. Кан
2. УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Государственного комитета СССР по стандартам от 29.11.88 № 3868
3. Срок первой проверки — 1993 г.; периодичность проверки —
5 лет
4. В стандарт введен международный стандарт МЭК 255—11 (1979 г.)
5. ВВЕДЕН ВПЕРВЫЕ
1. Общие положения
1.1, Область распространения …… I
2, Требования, относящиеся к отключениям вспомогательной воздействующей величины постоянного тока . .•…»»•.> 1
2.1. Отключение , , . 1
2.2, Стандартные нормальные значения влияющих величин или факторов и допуски при испытаниях * г 2
2.3, Стандартные значения пределов номинальных диапазонов влияющих величин и факторов » …2
2.4, Влияние отключения вспомогательной воздействующей величины
постоянного тока , . t ж . ( 2
3. Требования, относящиеся к переменной составляющей вспомогательной
воздействующей величины в установившемся режиме ….
3J, Определение переменной составляющей ,
3.2, Условия определения влияния переменной составляющей вспомога тельной воздействующей величины ,
3.3. Стандартные значения пределов номинального диапазона .
Приложение. Пояснения, касающиеся вспомогательных источников стати
ческих измерительных реле , ,
Информационные данные . . , , ……. «


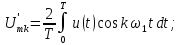

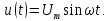
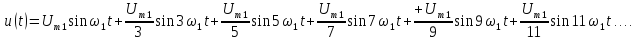
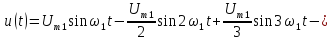
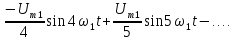


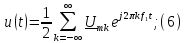

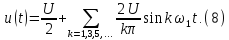

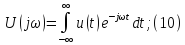
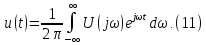
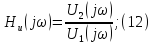
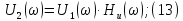
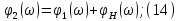


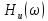
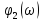

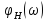

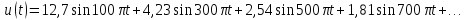

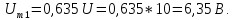



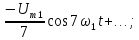
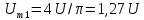
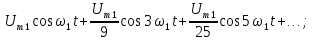


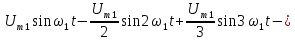

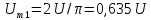
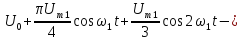
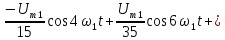


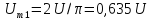
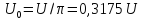
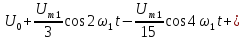

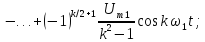
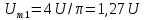

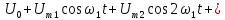
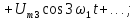
 ;
; ;
;
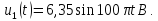

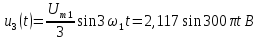
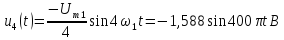
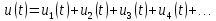

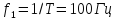
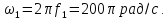
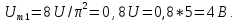



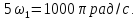
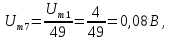


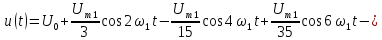
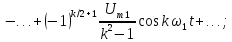
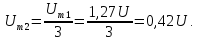

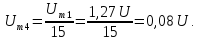
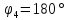
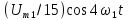


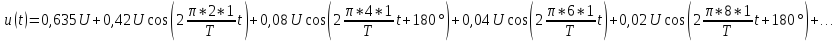
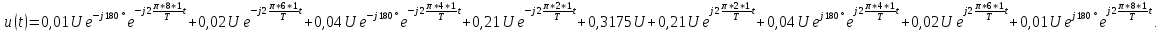
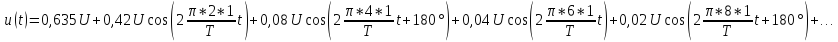
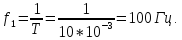
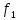
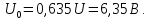





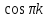
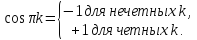
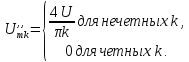
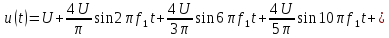








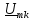
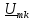
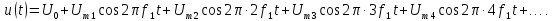
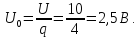

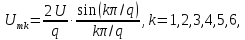

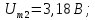

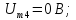
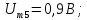
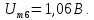
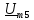


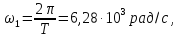

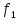



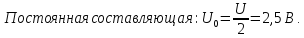
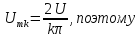
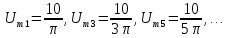

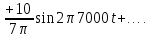

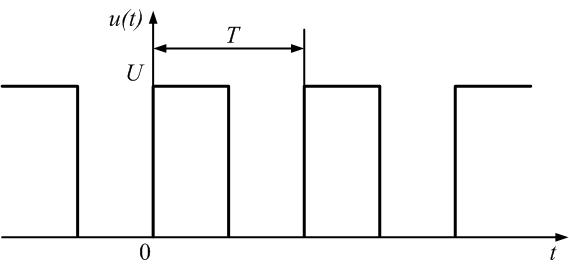
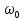
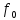
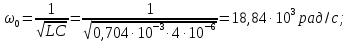



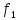
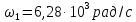
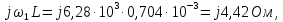
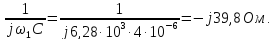


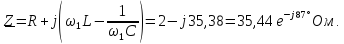






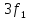
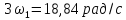



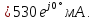




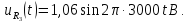
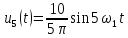





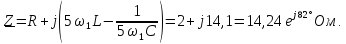
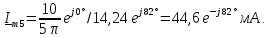
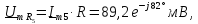
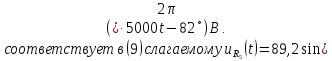

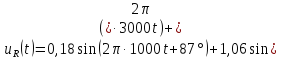

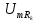
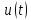


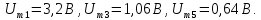
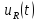
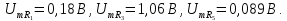

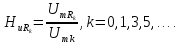

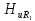
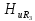
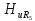

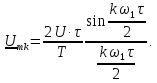
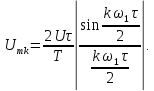
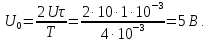

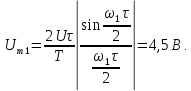
 =0,5
=0,5 =3,28
=3,28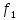 =0,75
=0,75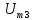 =1,5
=1,5 =1
=1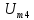 =0
=0 =1,25
=1,25 =0,9
=0,9 =1,5
=1,5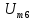 =1,06
=1,06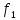 =1,75
=1,75 =0,64
=0,64 =2,0
=2,0 =0
=0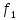 =2,25
=2,25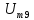 =0,5
=0,5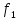 =2,5
=2,5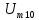 =0,64
=0,64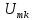

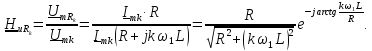
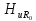 =1;
=1; =0,95;
=0,95;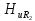 =0,85;
=0,85;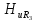 =0,73;
=0,73; =0,62;
=0,62; =0,54;
=0,54;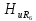 =0,47;
=0,47;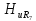 =0,41;
=0,41;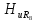 =0,37;
=0,37;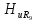 =0,33;
=0,33; =0,3.
=0,3.