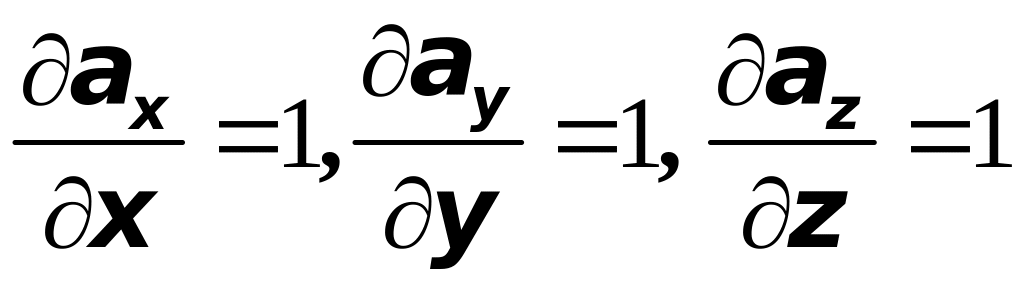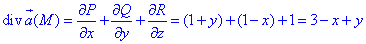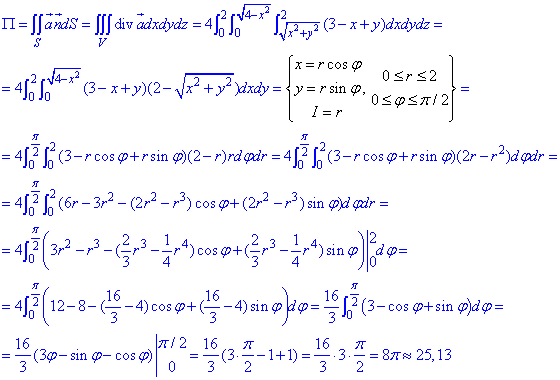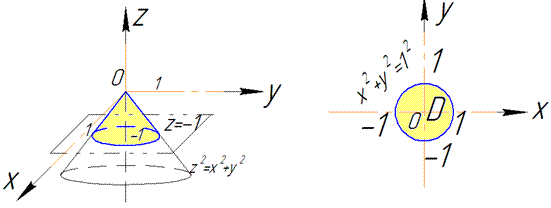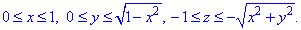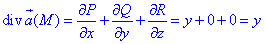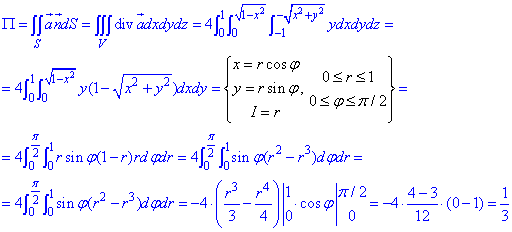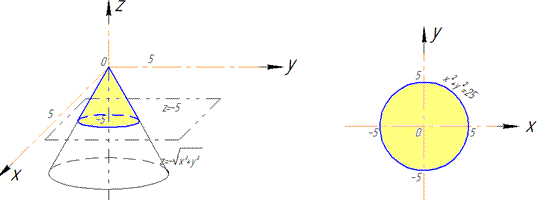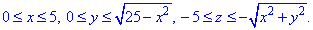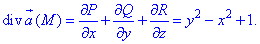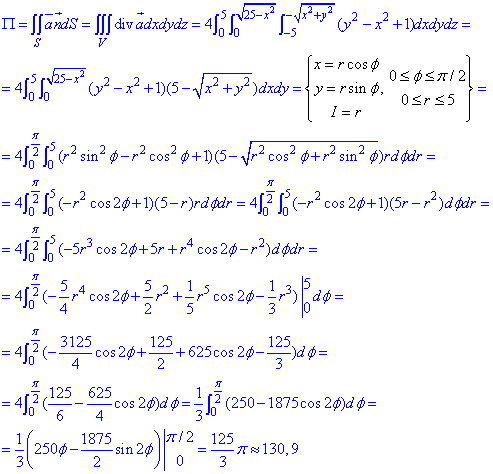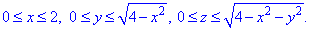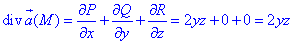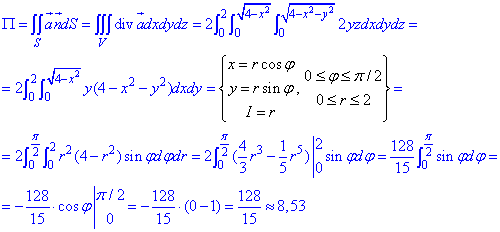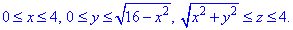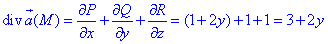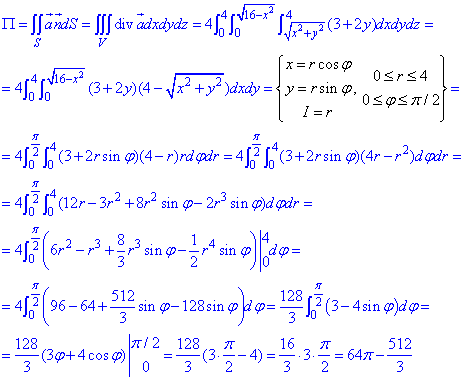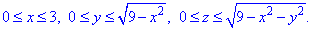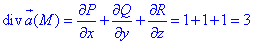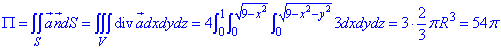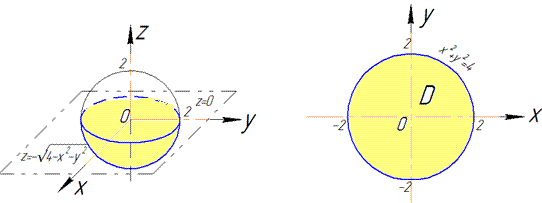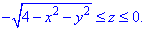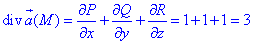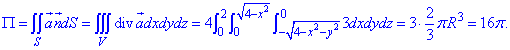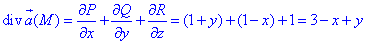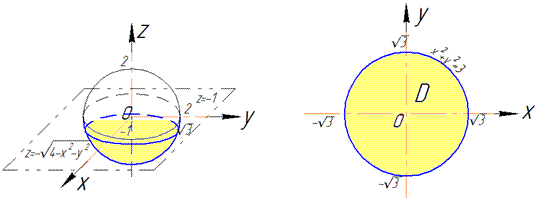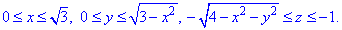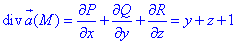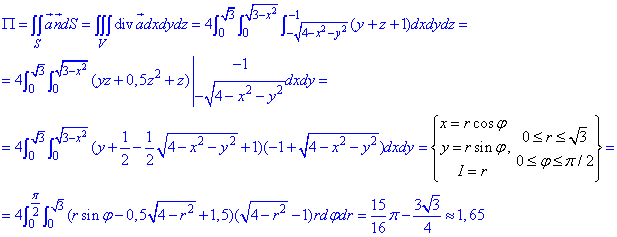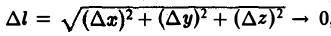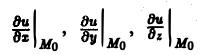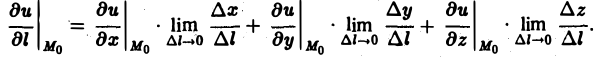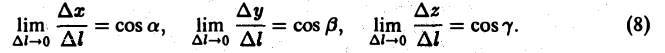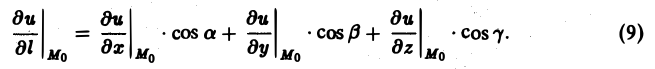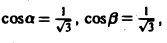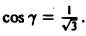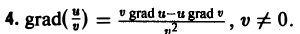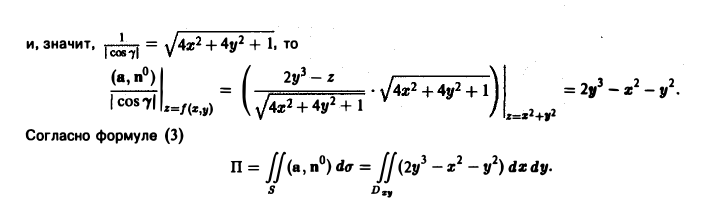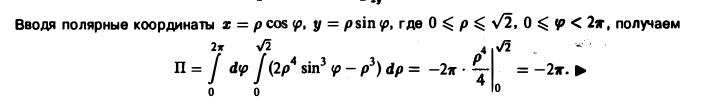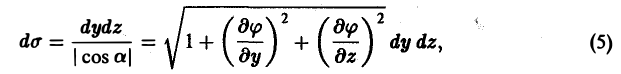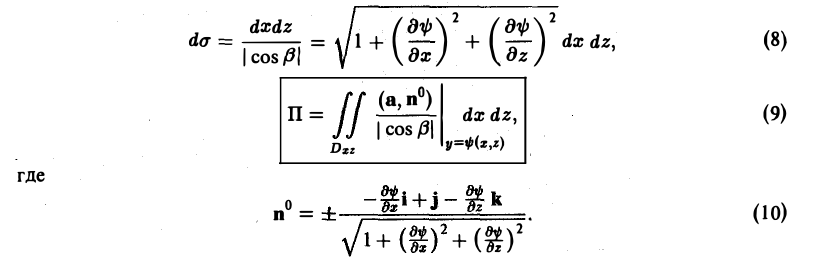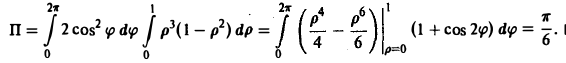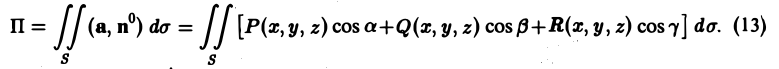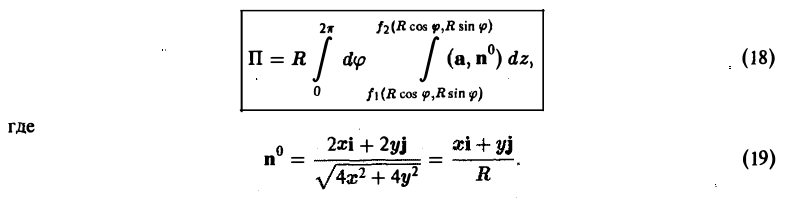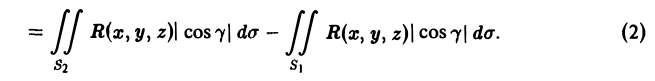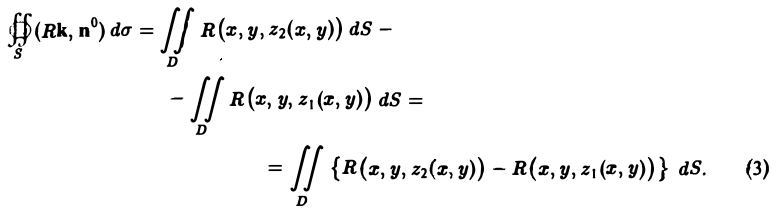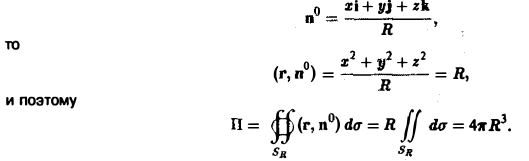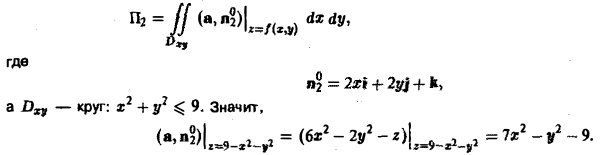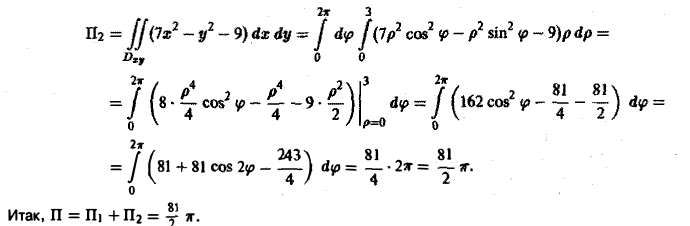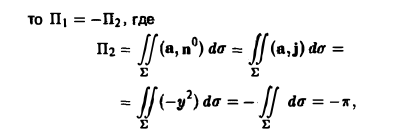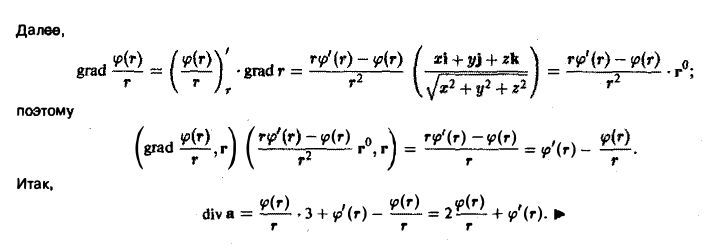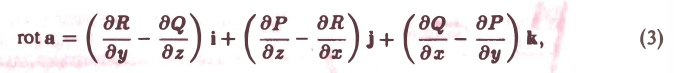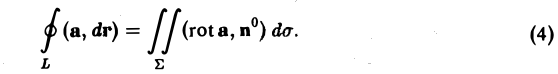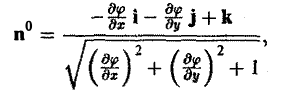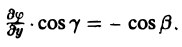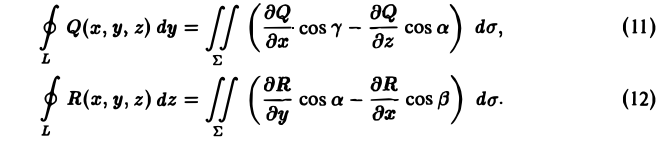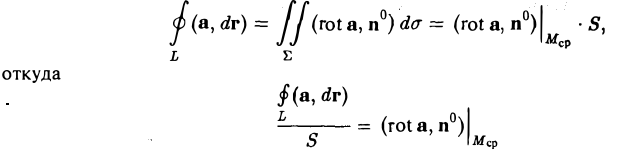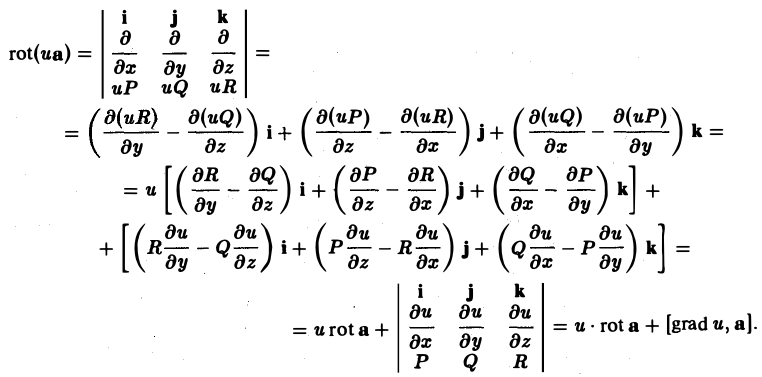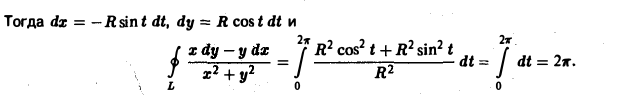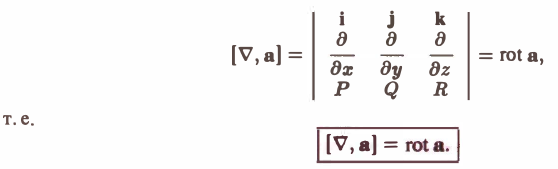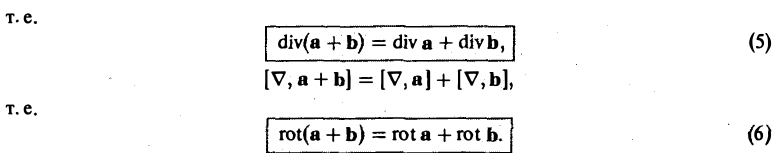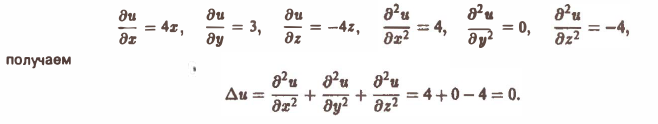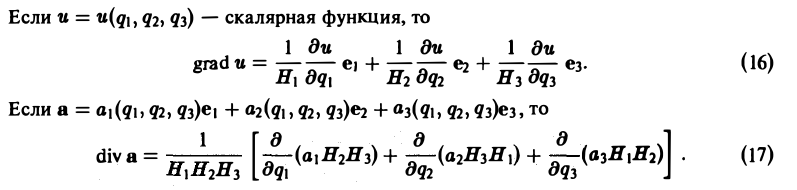Разделяя переменные, получим
.
Откуда следует общий интеграл уравнения
.
Учитывая, что интегральная кривая
проходит через точку
,
имеем
.
Итак, векторная линия, проходящая через
точку
,
представляет собой окружность
.
П
рис. 5
усть в поле вектора
находится двухсторонняя поверхность
.
Выберем на ней элементарную площадку,
площадь которой равна
.
Выберем на ней определённую сторону и
пусть нормаль, соответствующая выбранной
стороне поверхности, есть
.
Будем считать, что в пределах выбранной
площадки вектор
постоянен, обозначим через
проекцию вектора
на направление нормали
(рис. 5).
Определение.
Элементарным потоком векторного
поля
через площадку
в выбранную сторону называется
.
Разбивая поверхность
на ячейки и суммируя элементарные потоки
вектора
по всем частичным ячейкам при условии,
что ранг дробления стремится к нулю,
получим
;
называется потоком векторного поля
через поверхность
в выбранную сторону.
Выясним теперь механический смысл
потока векторного поля (рис. 5).
Допустим, что указанная выше поверхность
лежит в векторном поле
скоростей текущей жидкости. Тогда за
время
,
исходя из данного момента времени
,
частицы жидкости продвинутся через
элементарную площадку и заполнят
наклонный цилиндр, основанием которого
является элементарная площадка, а высота
,
если векторы
и
лежат в одном полупространстве. Масса
частиц жидкости, заполнявших этот
цилиндр,
,
где
— плотность текущей жидкости. Выполняя
суммирование всех этих масс по всей
поверхности
,
получим
.
Правая часть этого соотношения даёт
нам количество жидкости, протекающей
через поверхность
за время
,
тогда очевидно, что выражение
даёт нам количество жидкости, протекающей
через поверхность
в выбранную сторону за единицу времени.
В этом и заключается механический смысл
потока векторного поля.
§ 3. Теорема Остроградского (векторная форма). Дивергенция векторного поля и её механический смысл
Рассмотрим
поле вектора
.
Определение.
Дивергенцией векторного поля
называется выражение
.
Очевидно,
что с помощью оператора Гамильтона
дивергенцию можно записать так:
.
Теорема
Остроградского (векторная форма).
Поток
векторного поля
через замкнутую поверхность
наружу равен тройному интегралу от
дивергенции векторного поля
по телу
,
ограниченному поверхностью
,
т.е. короче:
.
Доказательство.
Мы будем предполагать, что выполняются
условия, при которых существуют интегралы,
о которых речь пойдёт ниже.
Рассмотрим
поток векторного поля
через поверхность
наружу:
,
где
— есть внешняя нормаль к поверхности
,
ограничивающей тело
,
— проекция вектора
на эту нормаль.
Пусть
нормаль
образует углы
,
,
с координатными осями
,
и
соответственно, тогда
,
где
— есть орт, соответствующий вектору
и при этом
.
Тогда поток
можно выразить так:
.
Воспользуемся
теперь формулой, устанавливающей связь
между поверхностными интегралами
первого и второго рода, тогда выражение
для потока
можно записать так:
.
Вспоминая,
что под знаком тройного интеграла в
правой части стоит дивергенция векторного
поля
,
тогда окончательно можно написать
.
Выясним
теперь механический смысл дивергенции
векторного поля.
Допустим,
что векторное поле есть поле скоростей
текущей жидкости
и пусть плотность этой жидкости
.
Возьмём в поле вектора
замкнутую поверхность
,
ограничивающую малый объём. По теореме
Остроградского
.
Применяя
теорему о среднем, получим
,
где
-некоторая «средняя точка», лежащая
в теле
.
Отсюда
.
Сжимая
тело в точку, в пределе проучим
.
Вывод:
дивергенция векторного поля
даёт нам расход жидкости из точечного
источника в единицу времени, т.е. удельную
силу источника. Заметим, что если
в данной точке положительна, то это
значит, что в этой точке происходит
втекание жидкости (т.е. в этой точке
сток).
Принимая
во внимание это рассуждение, можно дать
механическое истолкование теоремы
Остроградского:
расход жидкости из
тела
,
ограниченного поверхностью
,
в единицу времени
равен сумме попарных произведений сит
источников.
Заметим,
что попутно мы доказали независимость
дивергенции векторного поля от выбора
системы координат. Действительно, с
одной стороны
,
а с другой — это удельная
сила источника, а независимость последней
от системы координат очевидна.
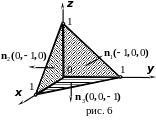
П
ример.
Найти поток векторного поля
из тела, ограниченного координатными
плоскостями
,
,
и плоскостью
наружу по теореме Остроградского и
непосредственно (рис. 6).
Решение.
1-й метод решения. Вычислим поток
векторного поля по теореме Остроградского.
Найдём
.
Имеем:
,
,
.
Значит,
,
Следовательно,
.
Поток
векторного поля
.
2-й
метод решения. Вычислим поток
векторного поля с помощью интеграла
первого рода.
Имеем:
,
где
полная поверхность тела
,
состоящая из четырёх частей:
;
здесь
,
и
— направляющие косинусы внешней нормали
к поверхности;
,
,
.
Поток
можно представить в виде суммы четырёх
потоков:
.
Вычислим каждый из потоков:
1.
,
,
т.е.
,
,
,
.
Следовательно,
,
т.к. на поверхности
.
2.
,
,
т.е.
,
,
.
Таким образом:
.
Здесь
,
причём
на
,
следовательно,
.
3.
,
,
т.е.
,
,
,
,
т.к. на поверхности
.
4.
.
Поверхность
имеет уравнение
,
следовательно,
,
тогда
.
Поверхностный интеграл здесь вычисляется
по верхней стороне поверхности
,
значит направляющие косинусы нормали
будут равны:
.
Тогда получим

.
Окончательно:
.
3-й
метод решения. Вычислим тот же
самый поток с помощью поверхностного
интеграла второго рода
.
В нашем
случае
,
как и в предыдущем случае, поток
представим в виде суммы четырёх потоков
соответственно, через поверхности
,
,
,
:
1. На
,
,
а значит
.
2. На
,
,
а сторона поверхности, по которой
вычисляется интеграл, нижняя, значит

3. На
,
,
сторона поверхности нижняя значит
.
4.
.
На
.
Следовательно,

.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Формула Остроградського-Гаусса имеет широкое приложение в математике, физике, химии.
Дальше будут приведенные ответы к примерам по интегрированию, которые предусматривают нахождение потока векторного поля через дивергенцию.
В большинстве заданий вычисления двойных интегралов предусматривает замену переменных, а точнее — переход к полярной системе координат. Это упрощает подынтегральные выражения, однако ведет к пересчету пределов интегрирование.
На словах это легко понять, однако на практике необходимо анализировать приведенные примеры на формулу Остроградського-Гаусса и много решать самостоятельно, чтобы разобраться в теме.
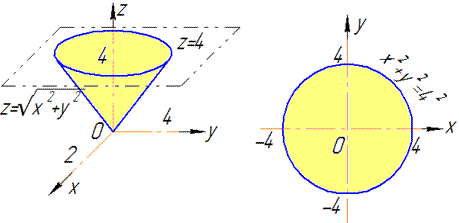
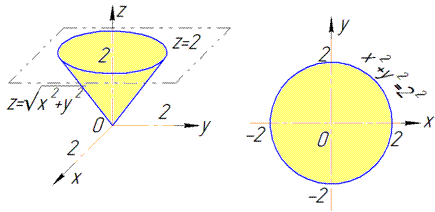
Пример 7.1 Найти поток векторного поля 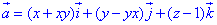
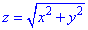
z=2 (нормаль внешня к замкнутой поверхности, образованной данными поверхностями).
Решение: Уравнение 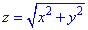
z=2 — плоскость параллельная к плоскости Oxy. (шапка).
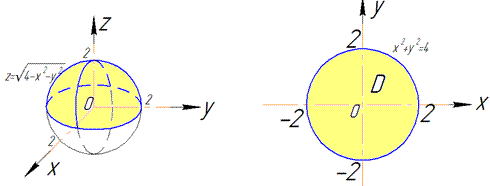
Приведены поверхность и плоскость изобразим в пространстве
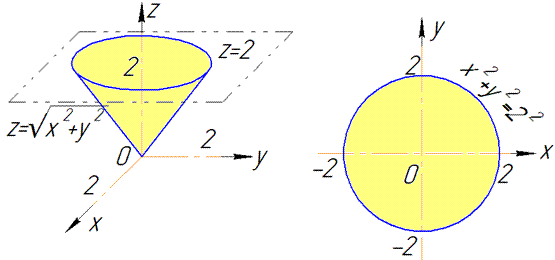
В сечении с конусом получим круг радиуса R=2.
Как видим из рисунка, четверть области V задается следующими пределами:
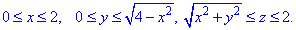
Здесь учли четность всех функций, поєтому результат интегрирования умножим на 4.
Вычислим дивергенцию векторного поля 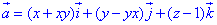
где P=P(x;y;z)=x+xy, Q=Q(x;y;z)=y-yx, R=R(x;y;z)=z-1.
Последние функции берем из a.
Найдем поток векторного поля 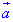
Пример 7.3 Найти поток векторного поля 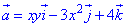
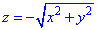
z=-1 (нормаль внешня к замкнутой поверхности, образованной данным сечением).
Решение: 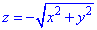
z=-1 — плоскость параллельная к Oxy.
В сечении с конусом получим круг радиуса R=1.
Как видим из рисунка четверть области V задается следующими пределами:
Здесь учли четность всех функций, поэтому результат интегрирования будем умножать на 4.
Находим дивергенцию векторного поля 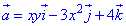
где P=P(x;y;z)=xy, Q=Q(x;y;z)=-3x2, R=R(x;y;z)=4.
За формулой Остроградського-Гаусса вычисляем тройной интеграл:
Переход к полярной системе координат значительно упрощает нахождения двойного интегралу.
Пример 7.4 Вычислить поток векторного поля 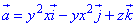
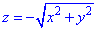
z=-5 (нормаль внешня к замкнутой поверхности, образованной данными поверхностями).
Решение: Уравнение 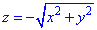
z=-5 — плоскость параллельная к плоскости Oxy.
В сечении с конусом получим круг радиуса R=1.
Из рисунка следует что четверть области V задается следующими пределами:
Здесь учитываем четность функций, поэтому результат будем множить на 4.
Находим дивергенцию векторного поля 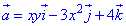
где P=P(x;y;z)=xy, Q=Q(x;y;z)=-3x2, R=R(x;y;z)=4.
За формулой Остроградського-Гаусса вычисляем поток поля 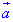
Переход к полярной системе координат значительно упрощает нахождения двойного интегралу.
Пример 7.5 Вычислить поток векторного поля 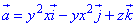
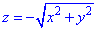
z=-5 (нормаль внешня к замкнутой поверхности, образованной данными поверхностями).
Решение: Уравнение 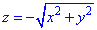
z=-5 — плоскость, какая параллельная к плоскости Oxy.
В сечении с конусом получим круг радиуса R=5.
Как видим из рисунка четверть области V задается следующими пределами:
Принимая во внимание четность всех функций, можем сузить область интегрирования, а результат умножить на 4.
Дивергенция векторного поля 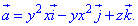
где P=P(x;y;z)=y2x, Q=Q(x;y;z)=-yx2, R=R(x;y;z)=z.
Поток поля 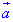
Опять имеем замену переменных под интегралом. Этот прием является незаменимым при нахождении интегралов по поверхностям вращения — подынтегральные функции и пределы упрощаются, отпадает потребность бороться с корнями и выискивать экзотические формулы интегралов из справочников.
Пример 7.7 Найти поток векторного поля 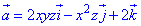
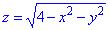
z=0 (нормаль внешня к замкнутой поверхности, образованной данными поверхностями).
Решение: Сведем поверхность 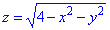
z=0 — плоскость параллельная к плоскости Oxy.
В сечении со сферой получим круг с центром в (0;0;0) и радиусом R=2.
Из рисунку видим четверть области V задается следующими пределами:
Здесь учли четность всех функций поэтому результат будем множить на 2.
Вычисляем дивергенцию 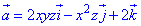
где P=P(x;y;z)=2xyz, Q=Q(x;y;z)=-x2z, R=R(x;y;z)=2.
Поток векторного поля 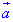
Пример 7.8 Найти поток векторного поля 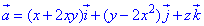
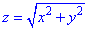
z=4 (нормаль внешня к замкнутой поверхности, образованной данными поверхностями).
Решение: Уравнение 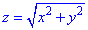
Сечение z=4 — плоскость параллельная к плоскости Oxy.
В сечении с конусом получим круг радиуса R=4.
Как видим из рисунка, четверть области V задается следующими пределами:
Четность всех функций позволяет искать интеграл на меньшей поверхности, затем результат нужно будет умножить на 4.
Дивергенцию векторного поля 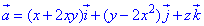
где P=P(x;y;z)=x+2xy, Q=Q(x;y;z)=y-2x2, R=R(x;y;z)=z.
Интегрированием вычисли поток векторного поля 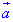
Пример 7.14 Определить поток векторного поля 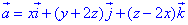
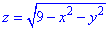
z=0 (нормаль внешня к замкнутой поверхности, образованной данными поверхностями).
Решение: Уравнение 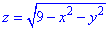
В сечении с плоскостью z=0 получим круг радиуса R=3.
Четверть области V задается следующими пределами:
Принятие во внимание четности функций позволяет записать пределы лишь в четверти области, потому поток необходимо умножить на 4.
Посчитаем дивергенцию поля 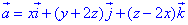
где P=P(x;y;z)=x, Q=Q(x;y;z)=y+2z, R=R(x;y;z)=z-2x.
Применяем формулу Остроградського-Гаусса для определения потока векторного поля 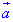
Пример 7.15 Найти поток векторного поля 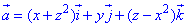
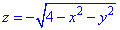
z=0 (нормаль внешня к замкнутой поверхности, образованной данными поверхностями).
Решение: Поверхность 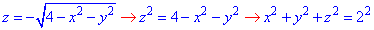
В сечении плоскости z=0 со сферой получим круг радиуса R=2.
Четверть области V задается следующими пределами:
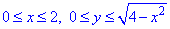
Результат интегрирования необходимо умножить на 4, поскольку учитываем четность функций.
Вычислим дивергенцию векторного поля 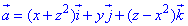
где функции P=P(x;y;z)=x+z2, Q=Q(x;y;z)=-y, R=R(x;y;z)=z-x2.
Интегрированием находим поток векторного поля 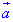
Он равен P=16pi.
Пример 7.16 Найти поток векторного поля 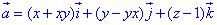
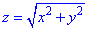
z=2 (нормаль внешня к замкнутой поверхности, образованной данными поверхностями).
Решение: Корневая зависимость 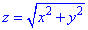
z=2 — плоскость параллельная к плоскости Oxy.
В сечении с конусом получим круг радиусом R=2.
Четверть области V задается следующими пределами: 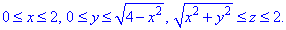
Четность функций учтена, поэтому результирующий интеграл нужно умножить на четверку.
Вычислим дивергенцию векторного поля 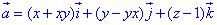
где P=P(x;y;z)=x+xy, Q=Q(x;y;z)=y-yx, R=R(x;y;z)=z-1.
За формулой Остроградського-Гаусса вычисляем поток векторного поля 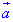
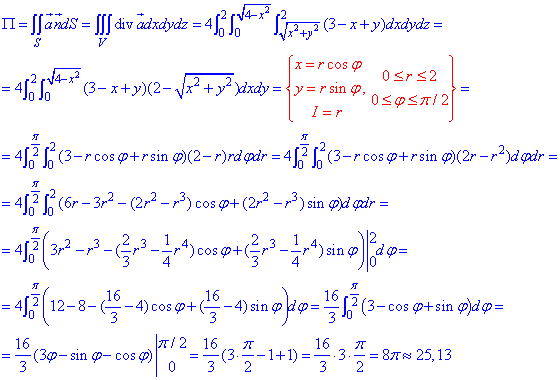
Переход к полярной системе координат при интегрировании Вы должны хорошо знать, такой прием позволяет упростить широкий класс интегралов, а дальнейшие вычисления свести к простым интегралам от показательных и тригонометрических функций. В отдельных случаях Вам придется применять формулы понижение степеней для перехода от квадратов синусов и косинусов к их первым степеням.
Пример 7.24 Вычислить поток векторного поля 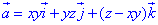
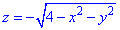
z=-1 (нормаль внешня к замкнутой поверхности, образованной данными поверхностями).
Решение: Превращаем уравнение поверхности 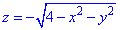
z^2=4-x^2-y^2, x^2+y^2+z^2=2^2 — сфера (нижняя часть) с центром в начале координат (0;0;0) и радиусом R=2.
z=-1 — плоскость параллельная к плоскости Oxy.
В сечении со сферой получим круг радиусом корень из трех
Четверть области V задается следующими пределами:
В силу четности функций, выписываем пределы лишь на 1/4 поверхности сферы.
Дивергенция векторного поля 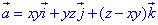
где функции P=P(x;y;z)=xy, Q=Q(x;y;z)=yz, R=R(x;y;z)=z-xy.
Поток векторного поля 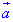
На этом ознакомление с примерами на вычисление потока векторного поля не завершается, больше готовых ответов Вы найдете на соседних страницах.
Векторный анализ — раздел математики, распространяющий методы математического анализа на векторы, как правило в двух- или трёхмерном пространстве. Объектами приложения векторного анализа являются: Векторные поля — отображения одного векторного пространства в другое.
Скалярное поле. Поверхности и линии уровня. Производная по направлению
Если в каждой точке пространства или части пространства определено значение некоторой величины, то говорят, что задано иоде данной величины. Поле называется скалярным, если рассматриваемая величина скалярна, т.е. вполне характеризуется своим числовым значением. Например, поле температур.
Скалярное поле задается скалярной функцией точки и = f(М). Если в пространстве введена декартова система координат, то и есть функция трех переменных х, у, z — координат точки М:
u = f(x,y,z). (1)
Определение:
Поверхностью уровня скалярного поля называется множество точек, в которых функция f(М) принимает одно и то же значение. Уравнение поверхности уровня
f(x, y, z) = с = const. (2)
Пример:
Найти поверхности уровня скалярного поля
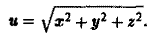
Согласно определению уравнением поверхности уровня будет
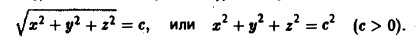
Это уравнение сферы (с ≠ 0) с центром в начале координат.
Скалярное поле называется плоским, если во всех плоскостях, параллельных некоторой плоскости, поле одно и то же. Если указанную плоскость принять за плоскость хОу, го функция поля не будет зависеть от координаты г, т. е. будетфункцией только аргументов х и у,
u=f(x, y). (3)
Плоское поле можно характеризовать с помощью линий уровня — множества точек плоскости, в которых функция f(x, у) имеет одно и то же значение. Уравнение линии уровня —
f(х, у) = с = const. (4)
Пример:
Найти линии уровня скалярного поля
Линии уровня задаются уравнениями
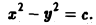
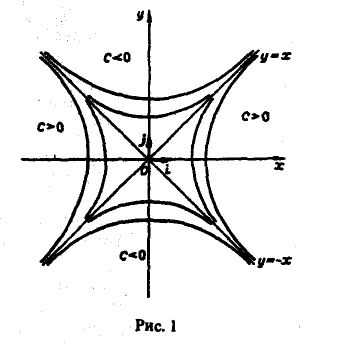
При с = О получаем пару прямых у = х, у = -х. При с ≠ 0 получаем семейство гипербол (рис. 1).
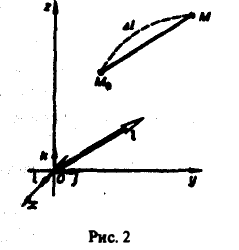
Производная по направлению
Пусть имеется скалярное поле, определяемое скалярной функцией и = f(M). Возьмем точку М0 и выберем направление, определяемое вектором I. Возьмем другую точку М так, чтобы вектор М0М был параллелен вектору 1 (рис.2). Обозначим длину вектора МоМ через ∆l, а приращение функции f(М) — f(Mo), соответствующее перемещению ∆l, через ∆и. Отношение
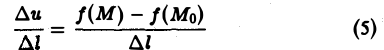
определяет среднюю скорость изменения скалярного поля на единицу длины поданному направлению I.
Пусть теперь ∆l стремится к нулю так, чтобы вектор М0М все время оставался параллельным вектору I.
Определение:
Если при ∆l —> 0 существует конечный предел отношения (5), то его называют производной функции и = f(M) в данной точке М0 по данному направлению I и обозначают символом
Так что, по определению,
(6)
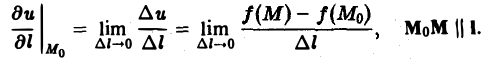
Это определение не связано с выбором системы координат, т. е. Hocит вариантный характер.
Найдем выражение для производной по направлению в декартовой системе координат. Пусть функция f(М) = f(х, у, z) дифференцируема в точке Мо(хо, yо, zо). Рассмотрим значение f(M) в точке М(х0 + ∆х,у0 + ∆y, zo + ∆z). Тогда полное приращение функции можно записать в следующем виде:
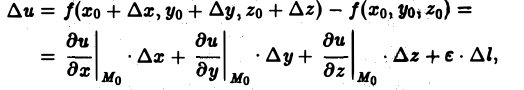
где ε = 0 при
а символы
означают, что частные производные вычислены в точке Мо. Отсюда (7)
Здесь величины 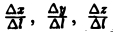
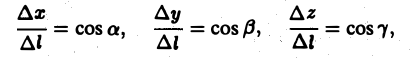
где
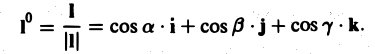
Так как M —» Mo, оставаясь все время на прямой, параллельной вектору I, то углы а, β, γ постоянны, а потому
Окончательно из равенств (7) и (8) получаем
Замечание:
Частные производные 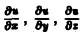
Пример:
Найти производную функции
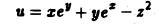
в точке Mo(3,0,2) по направлению к точке M1(4,1, 3).
Имеем
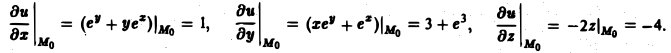
Вектор МoМ = {1, 1, 1} имеет длину |МоМ| = /3. Его направляющие косинусы:
По формуле (9) будем иметь
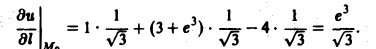
Тот факт, что 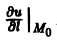
Для плоского поля U = f(x, у) производная по направлению 1 в точке Мо(х0, у0) вычисляется по формуле (10)
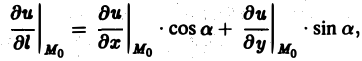
где а — угол, образованный вектором I с осью Ох.
Замечание:
Формула (9) для вычисления производной по направлению I в данной точке М0 остается в силе и тогда, когда точка М стремится к точке Мо по кривой, для которой вектор I является касательным в точке Мо.
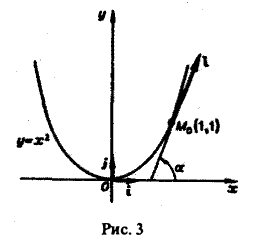
Пример:
Вычислить производную скалярного поля
и = arctg(xy)
в точке Mo(1, 1), принадлежащей параболе у = х2, по направлению этой кривой (в направлении возрастания абсциссы).
Направлением I параболы у = х2 в точке Mo{1, 1) считается направление касательной к параболе в этой точке (рис.3).
Пусть касательная к параболе в точке Мо образует с осью Ох угол a. Тогда tga =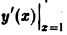
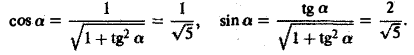
Вычислим значения 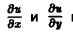
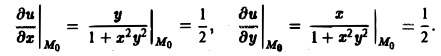
Теперь по формуле (10) получаем
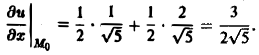
Пример:
Найти производную скалярного поля и = In(xy + yz + zx) в точке Mo(0, 1, 1) по направлению окружности
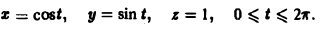
Векторное уравнение окружности имеет вид
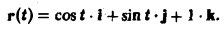
Находим единичный вектор т касательной к окружности
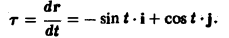
Точке Mo(0,1, 1) соответствует значение параметра t= π/2 Значение т в точке Мо будет равно
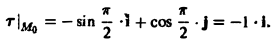
Отсюда получаем направляющие косинусы касательной к окружности в точке Mо: cos a = — 1, cos β = 0, cos γ = 0.
Вычислим значения частных производных данного скалярного поля в точке Mo(0, 1, 1)
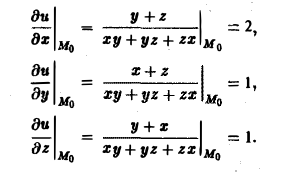
Значит, искомая производная
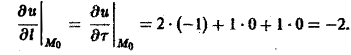
Градиент скалярного поля
Пусть скалярное поле определяется скалярной функцией
u = f(x, y. z),
которая предполагается дифференцируемой.
Определение:
Градиентом скалярного поля u в данной точке М называется вектор, обозначаемый символом grad и и определяемый равенством
(1)
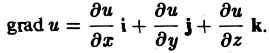
Ясно, что этот вектор зависит от функции f, так и от точки М, в которой вычисляется ее производная.
Пусть I° — единичный вектор в направлении I, т. е.
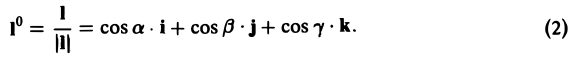
Тогда формулу для производной по направлению можно записать в следующем виде:
(3)
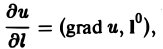
тем самым производная от функции и по направлению I равна скалярному произведению градиента функции u(M) на орт I° направления I.
Основные свойства градиента
Теорема:
Градиент скалярного поля перпендикулярен к поверхности уровня (или к линии уровня, если поле плоское).
Проведем через произвольную точку М поверхность уровня и = const и выберем на этой поверхности гладкую кривую L, проходящую через точку М (рис. 4). Пусть 1 — вектор, касательный к кривой L в точке М.
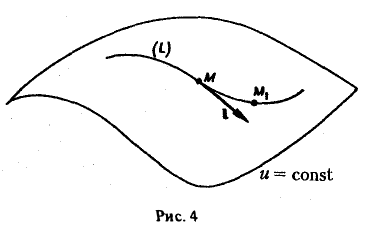
Так как на поверхности уровня и(М) = и(М1) для любой точки М1 ∈ L, то
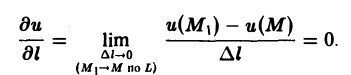
С другой стороны, 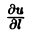
Итак, вектор grad и ортогонален к любой касательной к поверхности уровня в точке М. Тем самым он ортогонален к самой поверхности уровня в точке М.
Теорема:
Градиент направлен в сторону возрастания функции поля.
Ранее мы доказали, что градиент скалярного поля направлен по нормали к поверхности уровня, которая может быть ориентирована либо в сторону возрастания функции и(М), либо в сторону ее убывания.
Обозначим через п нормаль к поверхности уровня, ориентированную в сторону возрастания функции и(М), и найдем производную функции и в направлении этой нормали (рис. 5). Имеем
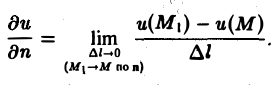
Так как по условию и(М1) > и(М), то и(М1) — и(М) > 0, и поэтому
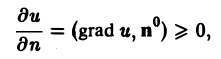
т.е. (grad и, п°) ≥ 0.
Отсюда следует, что grad и направлен в ту же сторону, что и выбранная нами нормаль п, т.е. в сторону возрастания функции и(М).
Теорема:
Длина градиента равна наибольшей производной по направлению в данной точке поля,
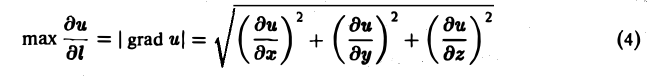
(здесь mах 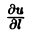
Имеем
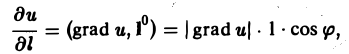
где φ — угол между векторами I и grad n. Так как наибольшее значение cos φ равно 1, то наибольшим значением производной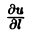
Пример:
Найти направление наибольшего изменения скалярного поля
и = ху + yz + zx
в точке Mо(1, 1, 1), а также величину этого наибольшего изменения в указанной точке.
Направление наибольшего изменения скалярного поля указывается вектором grad u(M). Имеем grad u(М) = (у + z)i + (х + г)j + (у + х)к, так что
grad и{Мo) = 2i + 2j + 2k.
Этот вектор определяет направление наибольшего возрастания поля в точке Мо(1,1,1). Величина наибольшего изменения поля в этой точке равна
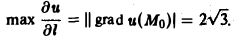
Инвариантное определение градиента
Величины, характеризующие свойства изучаемого объекта и не зависящие от выбора системы координат, называются инвариантами данного объекта. Например, длина кривой — инвариант этой кривой, а угол касательной к кривой с осью Ох — не инвариант.
Основываясь на доказанных выше трех свойствах градиента скалярного поля, можно дать следующее инвариантное определение градиента.
Определение:
Градиент скалярного поля есть вектор, направленный по нормали к поверхности уровня в сторону возрастания функции поля и имеющий длину, равную наибольшей производной по направлению (в данной точке).
Пусть п° — единичный вектор нормали, направленный в сторону возрастания поля. Тогда

Пример:
Найти градиент расстояния
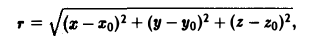
где Мo(хo,уo,zo) — некоторая фиксированная точка, а М(х,у,z) — текущая.
Имеем
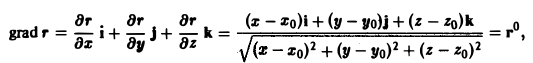
где r° — единичный вектор направления MoM.
Правила вычисления градиента
- grad си(М) = с grad и{М), где с — постоянное число.
- grad(u + v) = grad и + grad v.
Приведенные формулы получаются непосредственно из определения градиента и свойств производных.
3. grad(u v) = v grad и+ и grad v.
По правилу дифференцирования произведения
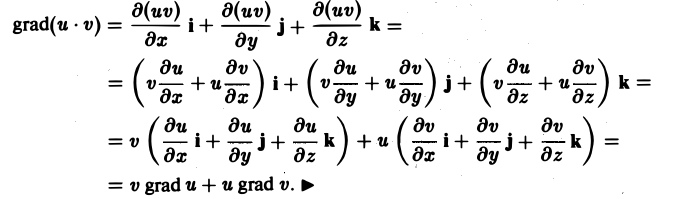
Доказательство аналогично доказательству свойства 3.
Пусть F(u) — дифференцируемая скалярная функция. Тогда
grad F(u) = F'(u) grad и.
По определению градиента имеем
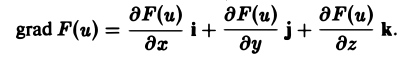
Применим ко всем слагаемым правой части правило дифференцирования сложной функции. Получим
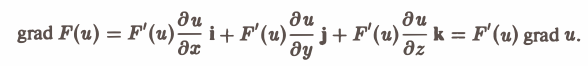
В частности,
grad F(r) = F'(r) • p°. (6)
Формула (6) следует из формулы grad r = r°.
Пример:
Найти производную по направлению радиус-вектора r от функции u = sin r, где r = |r|. По формуле (3)

а по формуле (6) grad sin r = cos r • r° . В результате получим, что
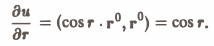
Пример:
Пусть дано плоское скалярное поле

где r1, r2 — расстояния от некоторой точки Р(х,у) плоскости до двух фиксированных точек F1 и F2 этой плоскости, F1 ≠ F2.
Рассмотрим произвольный эллипс с фокусами F1 и F2 и докажем, что всякий луч света, вышедший из одного фокуса эллипса, после отражения от эллипса попадает в другой его фокус.
Линии уровня функции (7) суть
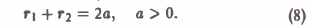
Уравнения (8) описывают семейство эллипсов с фокусами в точках F1 и F2.
Согласно результату примера 2 имеем
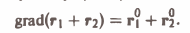
Тем самым градиент заданного поля равен вектору PQ диагонали ромба, построенного на ортах 
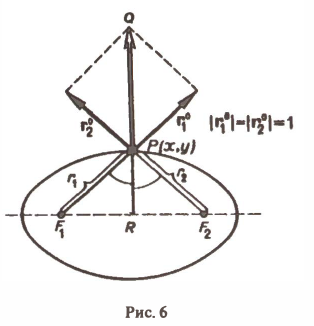
По теореме 1 градиент PQ перпендикулярен к эллипсу (8) в точке Р(х,у). Следовательно, нормаль к эллипсу (8) в любой его точке делит пополам угол между радиус-векторами, проведенными в эту точку. Отсюда и из того, что угол падения равен углу отражения, получаем: луч света, вышедший из одного фокуса эллипса, отразившись от него, непременно попадает в другой фокус этого эллипса.
Векторное поле. Векторные линии и их дифференциальные уравнения
Определение:
Если в каждой точке M(x,y,z) пространства или части пространства определена векторная величина
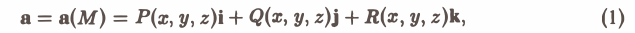
то говорят, что там задано векторное поле а.
Задание векторного поля равносильно заданию трех скалярных функций от трех переменных Р(х, у, z), Q(x, у, z), R(x, у, z).
Примерами векторных полей могут служить: силовое поле — поле некоторой силы F, поле скоростей v течения некоторой жидкости и др.
Для геометрической характеристики векторного поля служат векторные линии. Векторной линией векторного поля а называется кривая, касательная к которой в любой точке М имеет то же направление, что и вектор поля а в этой точке (рис. 7).
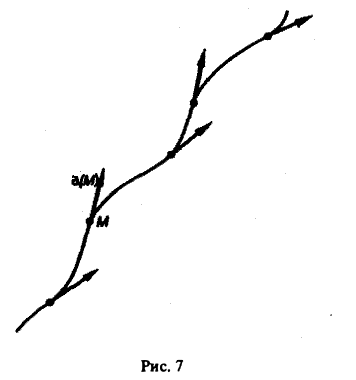
В силовом поле векторные линии называются силовыми линиями‘, в поле скоростей движения жидкости векторные линии называются линиями тока.
Дифференциальные уравнения векторных линий
Пусть векторное поле определяется вектор-функцией
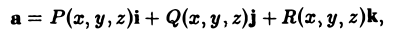
где P(x,y,z), Q(x, у, z), R(x,y,z) — непрерывные функции переменных х, у, z, имеющие ограниченные частные производные первого порядка. Пусть
r(t) = x(t)i + y(t)j + z(t)k
— есть радиус-вектор текущей точки векторной линии векторного поля a (t — параметр). Из определения векторной линии следует, что вектор
а = Р(х, у, z)i + Q{x, у, z)j + R(x, у, z)k
и вектор касательной к этой кривой
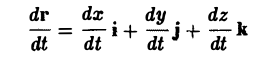
должны быть коллинеарны в каждой точке векторной линии. Условием коллинеарности векторов является пропорциональность их координат:
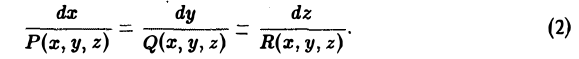
Таким образом, мы получили для векторных линий систему дифференциальных уравнений в симметричной форме.
Допустим, что нам удалось найти два независимых интеграла системы (2): (3)
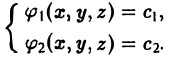
Система уравнений (3) определяет векторную линию как линию пересечения двух поверхностей. Произвольно меняя параметры c1 и c2 мы получаем семейство векторных линий как семейство с двумя степенями свободы.
Пример:
Hайти векторные линии векторного поля
а = хi + уj + 2zk.
Выписываем дифференциальные уравнения векторных линий, dx dy dz
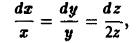
или
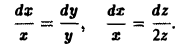
Интегрируя эту систему, получим два уравнения
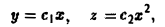
где c1, c2 — произвольные постоянные. Пересечение плоскостей у = c1х с параболическими цилиндрами z = c2x2 дает двухпараметрическое семейство векторных линий поля (рис. 8).
Определение:
Векторное поле называется плоским, если все векторы а параллельны одной и той же плоскости и в каждой плоскости, параллельной указанной, векторное поле одно и то же.
Посмотрим, как плоское векторное поле описывается в координатах. Если указанную в определении плоскость (или любую ей параллельную) принять за плоскость хОу, то векторы плоского поля не будут содержать компоненты по оси Oz и координаты векторов не будут зависеть от z:
Дифференциальные уравнения векторныхлиний плоского поля можно записать в следующем виде
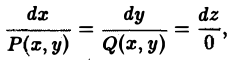
или
(5)
Отсюда видно, что векторные линии плоского поля являются плоскими кривыми, лежащими в плоскостях, параллельных плоскости хОу.
Пример:
Найти векторные линии магнитного поля бесконечно длинного прямого провода.
Предположим, что проводник направлен вдоль оси Oz и по нему течет ток силы J, т. е. вектор тока
J = J • k.
Тогда вектор напряженности Н магнитного поля определяется по формуле

где
р = xi + yj + zk
— радиус-вектор точки М, р — расстояние от оси провода до точки М. Раскрывая векторное произведение (6), получим
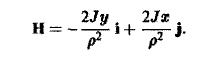
Дифференциальные уравнения векторных линий:
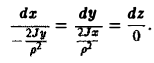
Отсюда x = const, 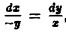
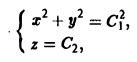
т.е. векторные линии являются окружностями с центрами на оси Oz (рис.9).
Пример:
Найти векторные линии поля сил тяготения, образованного притягивающей материальной точкой массы т, расположенной в начале координат.
В данном случае сила F определяется так:
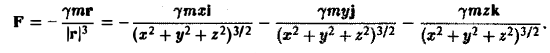
Дифференциальные уравнения векторных линий:
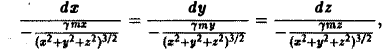
откуда, умножая каждую из дробей на 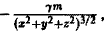
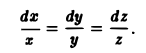
Чтобы получить уравнения векторных линий в параметрической форме, приравняем каждую из дробей величине 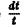
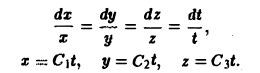
Это — полупрямые, выходящие из начала координат.
Чтобы из семейства векторных линий выделить одну, надо задать точку М0(хо, yo, zо). через которую эта векторная линия должна проходить, и по координатам заданной точки определить величины С1, C2, C3.
Пусть, например, точка Мо имеет координаты хо = 3, yо = 5, zо = 7. Уравнение векторной линии, проходящей через точку Mo(3, 5, 7), можно записать так:
x = 3t, у — 5t, z = 7t.
Сама точка Мо получается при значении параметра t = 1.
Поток вектора через поверхность и его свойства
Рассмотрим сначала частный случай поля скоростей v течения жидкости. Выделим в поле некоторую поверхность Σ. Потоком жидкости через поверхность Σ называется количество жидкости, протекающее через поверхность Σ за единицу времени.
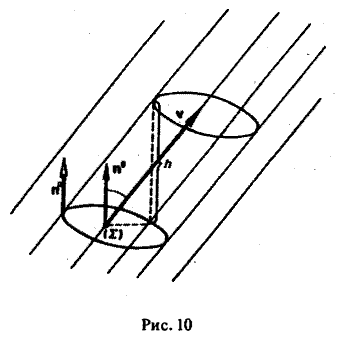
Этот поток легко вычислить, если скорость течения постоянна (v = const), а поверхность Σ —плоская. В этом случае поток жидкости равен объему цилиндрического тела с параллельными основаниями и образующими длины |v|, так как за единицу времени каждая частица перемещается на величину v (рис. 10),
П =Sh,
где S — площадь основания, h = npnv = (v, n°) — высота цилиндра и n — нормаль к его основанию, |п°| = 1.
Итак, при постоянной скорости v поток жидкости через плоскую поверхность Σ равен
(1)
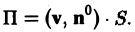
Если скорость v изменяется непрерывно, а поверхность Σ — гладкая, то можно разбить поверхность Σ на столь малые части Σk (k = 1, 2,…, п), чтобы каждую часть Σk можно было приближенно считать плоской и вектор v на ней постоянным.
Так как поток жидкости через поверхность Σ равен сумме потоков жидкости через все ее части Σk, то мы получаем для вычисления потока приближенную формулу (2)
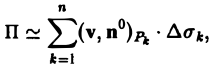
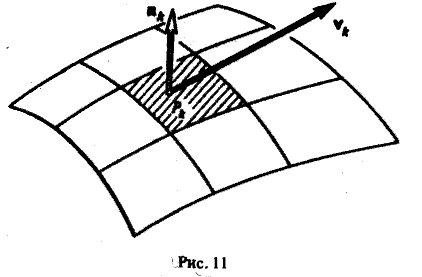
где п — общее число частей Σk, на которые разбита поверхность Σ, Рк — точка, лежащая на k-ой части, ∆σk — площадь части Σk поверхности, ( v, n°)pk означает скалярное произведение векторов v и п° в точке Pk ∈ Σk (рис. 11).
Назовем потоком жидкости через поверхность Σ предел суммы (2) при стремлении к нулю наибольшего из диаметров площадок Σk,
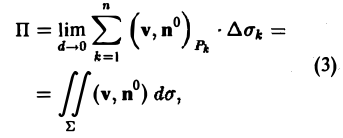
где d — наибольший из диаметров частей Σk (k= 1,2,…,п). Интеграл (3), определяющий поток жидкости, берется от скалярной функции (v, п°) по площади поверхности Σ.
Понятие потока произвольного вектора а через поверхность Σ вводится п о аналогии с введенным выше понятием потока жидкости через поверхность.
Определение:
Потоком вектора (векторного поля) а через поверхность Σ называется интеграл по поверхности Σ от проекции вектора а на нормаль к поверхности

Ясно, что интеграл (4) существует, если вектор а = Pi+Qj+Rk непрерывен, т. е. непрерывны его координаты Р(x, у, z), Q(x, у, z), R(x, y,z), и поверхность Σ — гладкая, т. е. имеет непрерывно меняющуюся касательную плоскость
Пример:
Поле создается точечным зарядом (электричесkое поле) или точечной маcсой (поле тяготения), помещенными в начале координат. Тогда вектор напряженности поля в любой точке Р будет равен
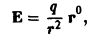
где q — величина заряда (массы), r = ОР — радиус-вектор точки Р. Требуется найти поток вектора напряженности Е через SR — сферу радиуса R с центром в начале координат.
Так как направление нормали к сфере совпадает с направлением радиус-вектора r, то п° = r° и поэтому
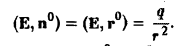
На сфере SR радиуса R имеем r = R, так что (Е, n°) = 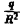
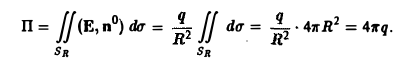
Свойства потока вектора через поверхность
1. Линейность.
(5)
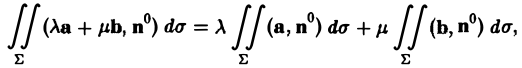
где λ и μ — постоянные числа.
2. Аддитивность. Если поверхность Σ разбита кусочно-гладкой кривой на две части Σ1 и Σ2, то поток через поверхность Σ равен сумме потоков через поверхности Σ1 и Σ2,
(6)
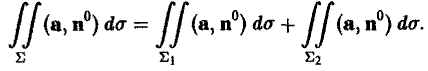
Это свойство позволяет распространить понятие потока на кусочно-гладкие поверхности Σ.
Понятие ориентации поверхности
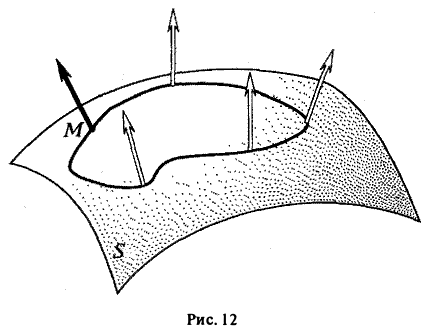
Взяв, к примеру, цилиндрическую поверхность, замечаем, что если в некоторой ее точке М выбрать определенный (один из двух) единичный вектор нормали и непрерывно перемещаться затем по поверхности вместе с соответствующим вектором нормали по любому пути, не переходящему через край повержюсти, то при возвращении в точку М единичный вектор нормали совпадает с исходным (рис. 12).
Вместе с тем, существуют поверхности, для которых это не так. Примером такой поверхности может служить лист Мёбиуса (рис. 13). Существует путь (отмеченная на рисунке пунктиром средняя линия листа), перемещаясь по которому, мы возвратимся в начальную точку с единичным вектором нормали, противоположным исходному.
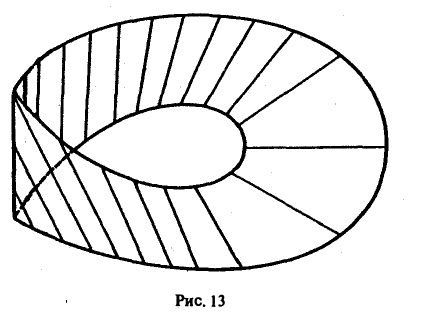
Описанное свойство разбивает все поверхности на два класса — двусторонние, или ориентируемые (плоскость, сфера, поверхность куба и т.п.), и односторонние, или неориентируемые (лист Мёбиуса).
3. Зависимость потока от ориентации поверхности (от ориентации вектора нормали к поверхности). Понятие потока вводится только для двусторонних поверхностей. Будем считать, что если в одной точке такой поверхности направление вектора нормали уже выбрано, то в любой другой ее точке берется тот вектор нормали, который получается из выбранного при непрерывном перемещении точки по поверхности (без перехода через границу). В частности, на замкнутой поверхности во всех точках берется либо внешняя нормаль, либо внутренняя (внутренняя нормаль направлена внутрь тела, ограниченного замкнутой поверхностью).
Обозначим через Σ+ ту сторону поверхности Σ, на которой выбран вектор нормали п+ = п, а через Σ- — сторону поверхности Σ, на которой берется вектор нормали (п_ = -п). Тогда получим
(7)
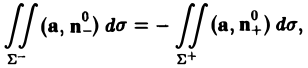
где п°_ = -п°+. Таким образом, при изменении ориентации поверхности (при изменении направления вектора нормали п° к поверхности Σ) поток вектора меняет знак на противоположный.
Пример:
Вычислить поток радиус-вектора r = хi + yj + zk через поверхность прямого кругового цилиндра высоты Н с радиусом основания R и осью Oz.
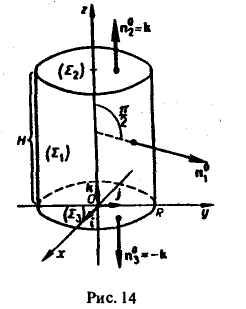
Поверхность Σ состоит из трех частей: боковой поверхности Σ1, верхнего основания Σ2 и нижнего основания Σ3 цилиндра. Искомый поток П в силу свойства аддитивности равен
П = П1 +П2 + П3,
где П1, П2, П3 — потоки данного поля через Σ1, Σ2 и Σ3 соответственно.
На боковой поверхности цилиндра вектор внешней нормали п°1 параллелен плоскости хОу, и поэтому
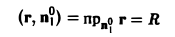
(см. рис. 14). Следовательно,
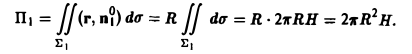
На верхнем основании Σ2 вектор нормали п°2 параллелен оси Оz, и поэтому можно положить п°2 = k. Тогда имеем
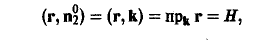
так что
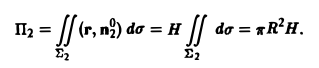
На нижнем основании Σ3 вектор г перпендикулярен к вектору нормали п°3 = -k. Поэтому (r, п°3) = (r, -k) = 0 и
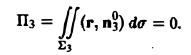
Значит, искомый поток
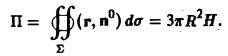
Здесь символ 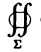
Поток вектора через незамкнутую поверхность
Укажем некоторые способы вычисления потока вектора через незамкнутые поверхности.
Метод проектирования на одну из координатных плоскостей
Пусть поверхность S однозначно проектируется на область Dxy плоскости хОу. В этом случае поверхность S можно задать уравнением вида
z = f(x, у).
Орт п° нормали к поверхности S находится по формуле
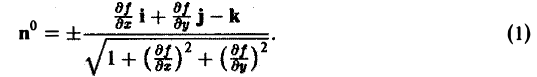
Если в формуле (1) берется знак « -», то угол γ между осью Oz и нормалью п° —острый; если же знак «+», то угол γ — тупой.
Так как элемент площади dσ этой поверхности равен
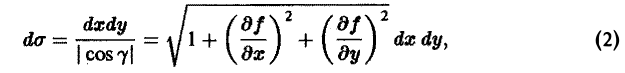
то вычисление потока П через выбранную сторону поверхности S сводится к вычислению двойного интеграла по формуле
(3)
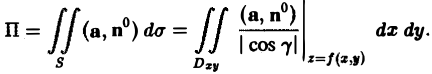
Символ
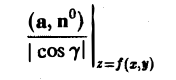
означает, что при вычислении в подынтегральной функции надо вместо z всюду поставить f(i, у).
Пример:
Найти поток вектора
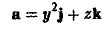
через часть поверхности параболоида
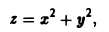
отсеченной плоскостью z = 2. По отношению к области, ограниченной параболоидом, берется внешняя нормаль (рис. 15).
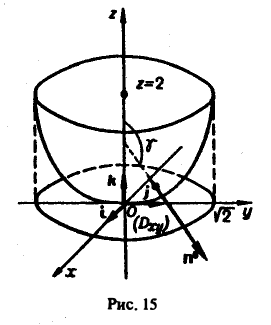
Данная поверхность проектируется на круг Dxy плоскости хОу с центром в начале координат радиуса R =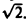
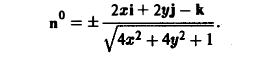
Согласно условию задачи вектор п° образует с осью Oz тупой угол γ, поэтому перед дробью следует взять знак минус. Таким образом,
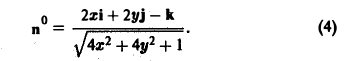
Находим скалярное произведение
Если поверхность S проектируется однозначно на область Dyz плоскости yOz, то ее можно задать уравнением х = φ{у, z). В этом случае имеем
(6)
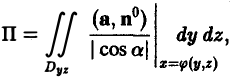
где
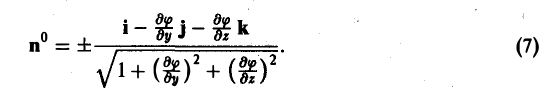
Знак «+» в последней формуле соответствует тому, что угол а между осью Ох и вектором нормали п° острый, и знак «-», если указанный угол тупой.
Наконец, если поверхность S проектируется однозначно на область Dxz плоскости xOz, то ее можно задать уравнением у = ψ(x, z) и тогда
Знак «+» перед дробью в формуле (10) означает, что угол β между осью Оу и вектором нормали п° — острый, а знак «—», что угол β — тупой.
Замечание:
Для нахождения потока вектора
а = Р(х, у, z)i + Q(z, у, z)j + R(х, у, k)
к через поверхность S, заданную уравнением z = f(x, у), методом проектирования на координатную плоскость хОу, не обязательно находить орт п° нормали, а можно брать вектор
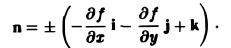
Тогда формула (2) для вычисления потока П примет вид:
(11)
Аналогичные формулы получаются для потоков через поверхности, заданные уравнениями х = φ(у, z) или у = ψ(х, z).
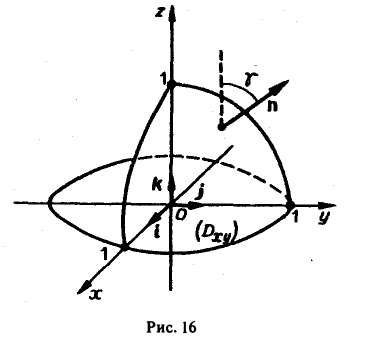
Пример:
Вычислить поток вектора
а = хzi
через внешнюю сторону параболоида
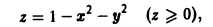
ограниченного плоскостью z = 0 (рис. 16).
Имеем
n = ±(2ri + 2yj+k).
Так как угол γ — острый, следует выбрать знак «+». Отсюда
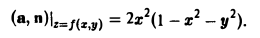
Искомый поток вычисляется так:
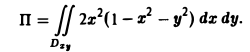
Переходя к полярным координатам х = р cos φ, y = p sin φ, 0 ≤ р ≤ 1. 0 ≤ φ < 2π, получим
Метод проектирования на все координатные плоскости
Пусть поверхность S однозначно проектируется на все три координатные плоскости. Обозначим через Dxy, Dxz, Dyz проекции S на плоскости хОу, xOz, yOz соответственно. В этом случае уравнение F(x, y, z) = 0 поверхности S однозначно разрешимо относительно каждого из аргументов, т. е.
x = x(y,z), y = y(x,z), z = z(x,y). (12)
Тогда поток вектора
а = Р(х, у, z)i + Q(x, у, z)j + R(x, у, z)k
через поверхность S, единичный вектор нормали к которой равен
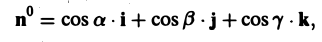
можно записать так:
Известно, что
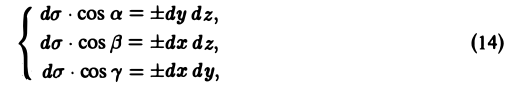
причем знак в каждой из формул (14) выбирается таким, каков знак cos a, cos β, cos γ на поверхности S. Подставляя соотношения (12) и (14) в формулу (13), получаем, что (15)
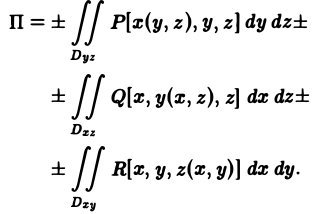
Пример:
Вычислить поток векторного поля
а = yi + zj + zk
через треугольник, ограниченный плоскостями z + y+ z = l (l>0), x=0, у — 0, z = 0 (угол γ — острый) (рис. 17).
Имеем
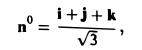
так что
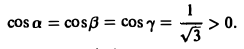
Значит, перед всеми интегралами в формуле (15) следует взять знак « + ». Полагая Р = у, Q = z, R = х, получим
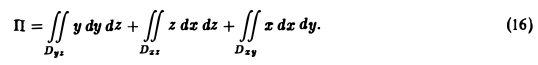
Вычислим первый интеграл в правой части формулы (16). Область Dyz — треугольник ВОС в плоскости yOz, уравнение стороны ВС: y+z = l, 0 ≤ у ≤ I. Имеем
Аналогично получим
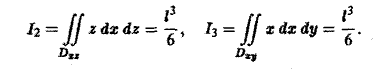
Значит, искомый лоток равен
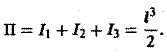
Метод введения криволинейных координат на поверхности
Если поверхность S является частью кругового цилиндра или сферы, при вычислении потока удобно, не применяя проектирования на координатные плоскости, ввести на поверхности криволинейные координаты.
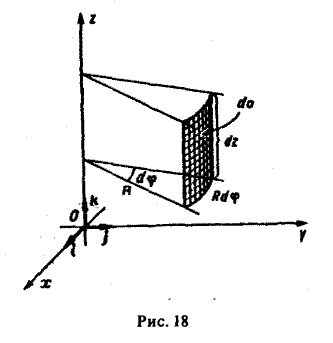
А. Поверхность S является частью кругового цилиндра
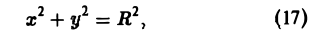
ограниченного поверхностями z = f1(x,y) и z = f2(х. у), где f1(x. y) ≤ f2(x, y) (рис. 18). Полагая х = R cos φ, у = R sin φ, z = z, будем иметь
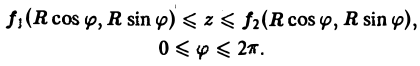
Элемент площади поверхности выражается так:
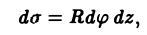
и поток вектора а через внешнюю сторону поверхности S вычисляется по формуле:
Пример:
Найти поток вектора
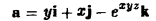
через внешнюю сторону поверхности цилиндра
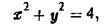
ограниченной плоскостями
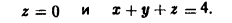
Имеем
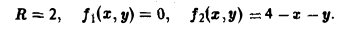
Так как
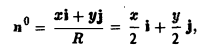
то скалярное произведение (а, п°) на цилиндре (х = 2 cos φ, у = 2 sin φ, z = z) равно:
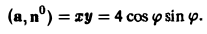
Тогда по формуле (18) получим
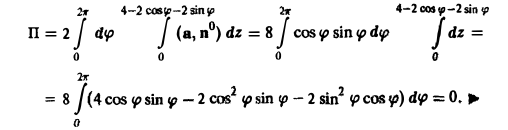
В. Поверхность S является частью сферы

ограниченной коническими поверхностями, уравнения которых в сферических координатах имеют вид 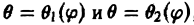
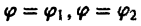
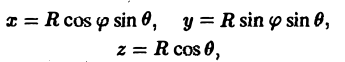
где 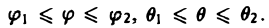
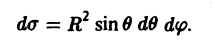
В этом случае поток векторного поля а через внешнюю часть поверхности S вычисляется по формуле
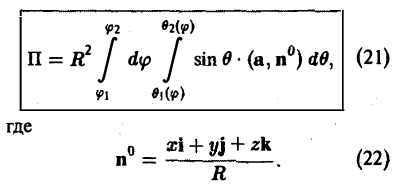
Пример:
Найти поток вектора
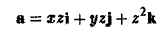
через внешнюю часть сферы
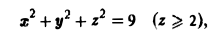
отсеченную плоcкостью z = 2 (рис. 20).
В данном случае имеем
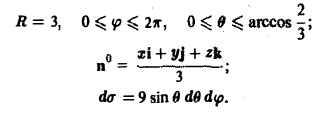
Положим
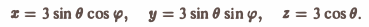
Тогда скалярное произведение (а, п°) выразится так:
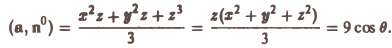
По формуле (21) получим
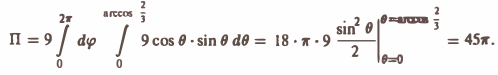
Замечание:
Здесь мы воспользовались формулой
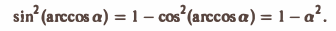
Поток вектора через замкнутую поверхность. Теорема Гаусса—Остроградского
Теорема:
Если в некоторой области G пространства R3 координаты вектора
а = Р(х, у, z)i + Q(x, у, z)j + R(x, у, z)k
непрерывны и имеют непрерывные частные производные 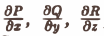
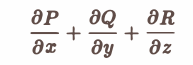
по области V, ограниченной поверхностью S:
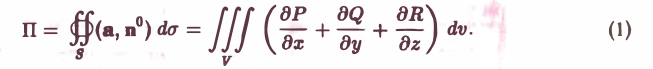
Здесь п0 — орт внешней нормали к поверхности, а символ 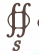
Рассмотрим сначала вектор а, имеющий только одну компоненту а = R(x, у, z)k, и предположим, что гладкая поверхность S пересекается каждой прямой, параллельной оси Oz, не более чем в двух точках. Тогда поверхность S разбивается на две части S1 и S2, однозначно проектирующиеся на некоторую область D плоскости хОу (рис.21).
Внешняя нормаль к поверхности S2 образует острый угол γ с осью Oz, а внешняя нормаль к поверхности S1 образует тупой угол с осью Oz. Поэтому cos γ = (п°, к) > 0 на S2 и cos γ < 0 на S1, так что на S2 имеем cos γ = |cos γ|, а на S1 cos γ = —| cos γ|. В силу аддитивности потока имеем
Пусть dσ — элемент площади на поверхности S. Тогда
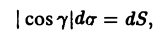
где dS — элемент площади области D. Сведем интегралы по поверхности к двойным интеграл ам по области D плоскости хОу, на которую проектируются поверхности S1 и S2. Пусть S2 описывается уравнением z = z2(x, у), а S, — уравнением z = z1(x, у). Тогда
Так как приращение непрерывно дифференцируемой функции можно представить как интеграл от ее производной
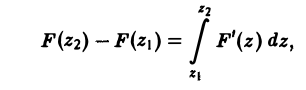
то для функции R(x, у, z) будем иметь
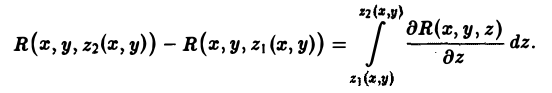
Пользуясь этим, получаем из формулы (3)
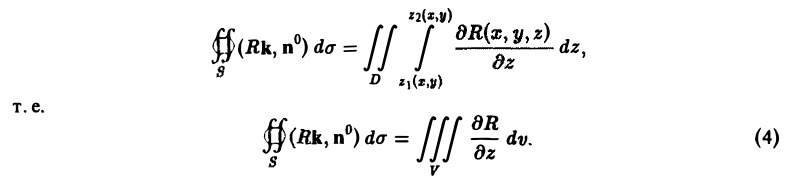
Если поверхность S содержит часть цилиндрической поверхности с образующими, параллельными оси Oz (рис. 22), то на этой части поверхности (Rk, п°) = 0 и интеграл ∫∫ (Rk, n°) dσ по ней равен нулю. Поэтому формула (4) остается справедливой и для поверхностей, содержащих указанные цилиндрические части.
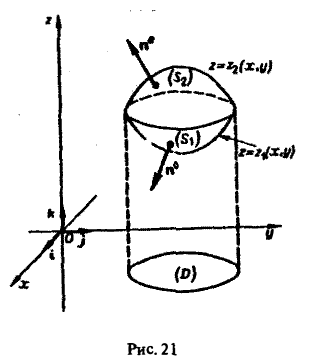
Формула (4) переносится и на случай, когда поверхность 5 пересекается вертикальной прямой более, чем в двух точках (рис. 23).
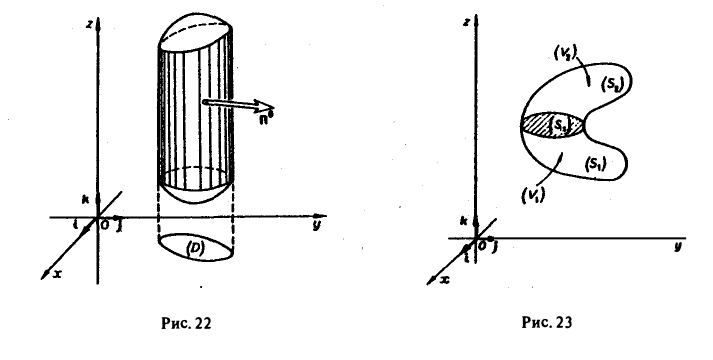
Разрежем область V на части, поверхность каждой из которых пересекается вертикальной прямой не более чем в двух точках, и обозначим через Sp поверхность разреза. Пусть S1 и S2 — те части поверхности S, на которые она разбивается разрезом Sp,a V1 и V2 — соответствующие части области V, ограниченные поверхностями
Здесь Sp+ означает, что вектор нормали к разрезу Sp направлен вверх (образует с осью Oz острый угол), a Sp— — что этот вектор нормали направлен вниз (образует с осью Oz тупой угол). Имеем:
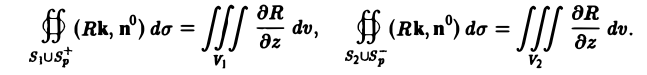
Складывая полученные равенства и пользуясь аддитивностью потока и тройного интеграла, получим
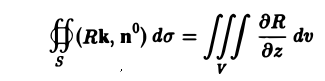
(интегралы по разрезу Sp взаимно уничтожаются). Рассмотрим, наконец, вектор
а = Р{х, у, z)i + Q(x, у, z)j + R(x, у, z)k.
Для каждой компоненты Pi, Qj, Rк мы можем написать формулу, аналогичную формуле (4) (все компоненты равноправны). Получим
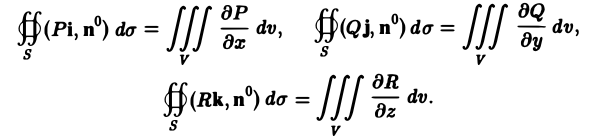
Складывая эти равенства и пользуясь линейностью потока и тройного интеграла, получаем формулу Гаусса—Остроградского
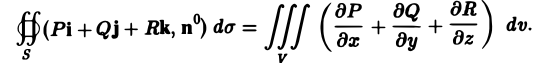
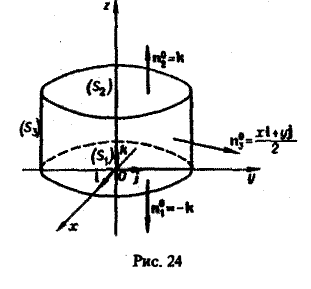
Пример:
Вычислить поток вектора
а = 2xi — (z — 1)k
через замкнутую поверхность
1) по определению, 2) по формуле Остроградского.
1) Поток вектора а равен сумме
(рис. 24), где
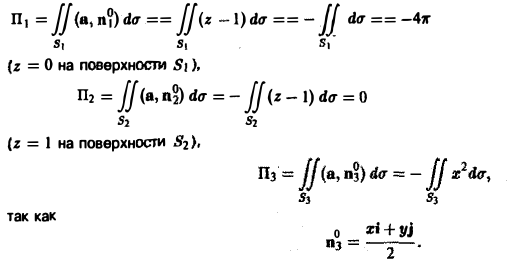
Перейдем на цилиндре к криволинейным координатам
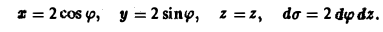
Тогда
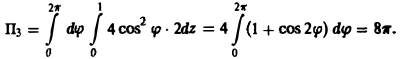
Следовательно, П = -4π + 0 + 8π = 4π.
2) По формуле Гаусса—Остроградского имеем
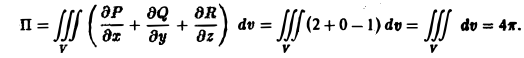
Пример:
Вычислить поток радиус-вектора
r = xi + yj + zk
через сферу радиуса R с центром в начале координат:
1) по определению; 2) по формуле Остроградского.
1) Так как для сферы
2) Сначала находим
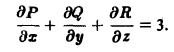
Отсюда
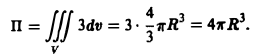
Пример:
Вычислить поток вектора
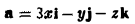
через замкнутую поверхность S, заданную условиями:

1) по определению; 2) по формуле Остроградстого (рис.25).
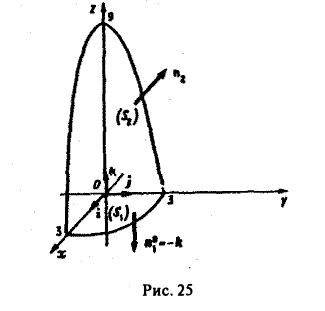
1} Имеем
где
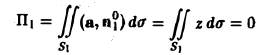
(на S1 имеем z = 0),
Поэтому
Имеем
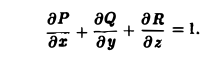
Поэтому
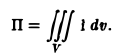
Переходя к цилиндрическим координатам
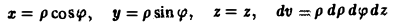
и замечая, что z = 9 — р на поверхности S, имеем
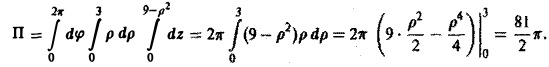
Замечание:
При вычислении потока через незамкнутую поверхность часто бывает удобно подходящим образом дополнить ее до замкнутой и воспользоваться формулой Гаусса—Оcтроградского.
Пример:
Вычислить поток вектора
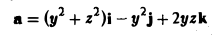
через поверхность S:
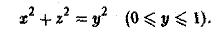
Заданная поверхность S есть конус с осью Оу (рис. 26).
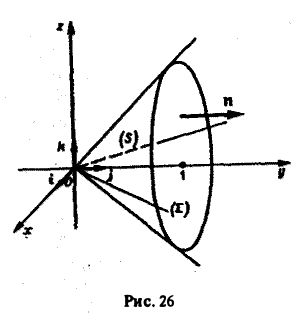
Замкнем этот конус куском Σ плоскости у = I. Тогда, обозначая через П1 искомый поток, а через П2 поток по поверхности Σ, будем иметь
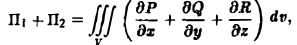
где V — объем конуса, ограниченного поверхностями S и Σ.
Так как
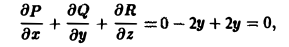
т.к. на поверхности Σ выполняется равенство у = 1. Следовательно, П1 = π.
Дивергенция векторного поля. Соленоидальные (трубчатые) поля
Пусть S — замкнутая поверхность. Рассмотрим поле скоростей v течения жидкости и вычислим поток жидкости через поверхность 5. Если он положителен, то это означает, что из той части пространства, которая ограничена поверхностью S, вытекает больше жидкости, чем втекает в нее. В этом случае говорят, что внутри S имеются источники (выделяющие жидкость). Напротив, если поток отрицателен, то внутрь S втекает больше жидкости, чем вытекает из нее. В этом случае говорят, что внутри S имеются стоки (поглощающие жидкость).
Тем самым, величина
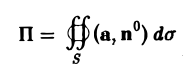
позволяет судить о природе части векторного поля, заключенного внутри поверхности S, а именно, о наличии источников или стоков внутри нее и их производительности (мощности).
Понятие о потоке вектора через замкнутую поверхность приводит к понятию дивергенции, или расходимости поля, которое дает некоторую количественную характеристику поля в каждой его точке.
Пусть М — изучаемая точка поля. Окружим ее поверхностью S произвольной формы, например, сферой достаточно малого радиуса. Область, ограниченную поверхностью 5, обозначим через (V), а ее объем через V.
Вычислим поток вектора а через поверхность S. Имеем
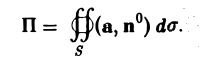
Составим отношение этого потока П к величине объема V,

Так как числитель представляет собой производительность источников (стоков) внутри области (V), то отношение (1) дает среднюю производительность единицы объема.
Определение:
Если отношение (1) имеет конечный предел, когда область (V) стягивается в точку М, то этот предел называют дивергенцией векторного поля (дивергенцией вектора а) в точке М и обозначают div а(М). То есть по определению
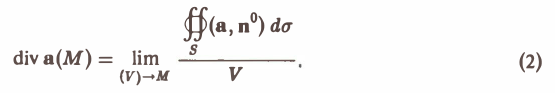
Дивергенция векторного поля есть скалярная величина (числитель и знаменатель дроби (2) суть скалярные величины).
Если diva(M) > 0, то в точке М расположен источник, если diva(M) < 0, то в точке М — сток.
Формула (2) позволяет сделать следующее заключение: дивергенция поля а в точке М есть объемная плотность потока вектора а в этой точке. Эта формула дает инвариантное определение дивергенции, не связанное с выбором систем координат — все величины, входящие в формулу (2), определяются непосредственно самим полем и от координатной системы не зависят.
Покажем, как вычисляется дивергенция в декартовых координатах при условии, что координаты вектора
а = Р(х, у, z)i + Q(x, у, z)j + R(x, y, z)k
непрерывны и имеют непрерывные частные производные 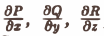
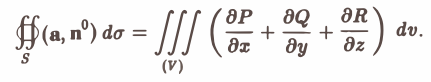
Пользуясь теоремой о среднем для тройного интеграла, получим
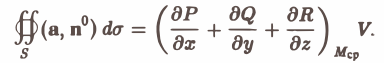
Подставляя это выражение в формулу (2), определяющую дивергенцию, найдем
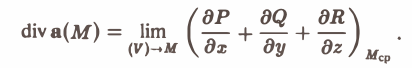
Когда область (V) стягивается в точку М, то и точка Мcp стремится к точке М и, в силу предположенной непрерывности частных производных, получаем
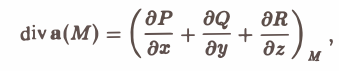
или, короче,
(3)
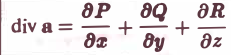
(все величины в формуле (3) вычисляются водной и той же точке).
Формула (3) дает выражение дивергенции в декартовых координатах. Попутно доказано само существование дивергенции вектора а при условии, что производные 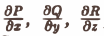
Используя формулу (3) для дивергенции, запишем формулу Гаусса—Остроградского в векторной форме. Имеем
(4)
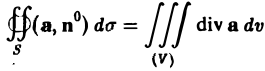
— поток вектора а через замкнутую поверхность S равен тройному интегралу от дивергенции вектора а по области (V), ограниченной поверхностью S.
Правила вычисления дивергенции
1, Дивергенция обладает свойством линейности
(5)
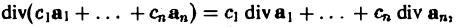
где С1,…, Сп — постоянные числа.
Пусть
а = Р(х, у, z)i + Q(x, у, z)j + R(x, у, z)k
и С — постоянное число. Тогда
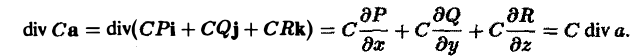
Если
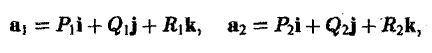
то
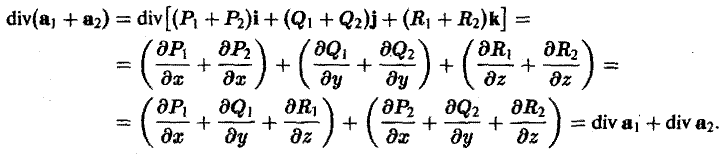
2. Дивергенция постоянного вектора с равна нулю
div e = 0. (6)
3. Дивергенция произведения скалярной функции и(М) на вектор а(М) вычисляется по формуле
div(ua) = u diva + (gprad u,a). (7)
В самом деле,
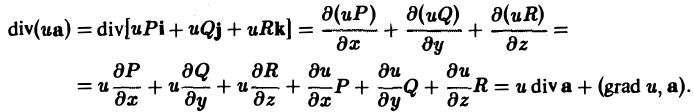
Пример:
Найти дивергенцию вектора
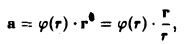
где r = |r| — расстояние от начала координат до переменной точки М(х,у,z),
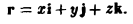
По формуле (7) имеем
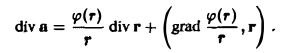
Так как r = xi + уj + zk. то
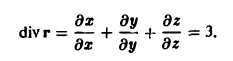
Трубчатое (соленоидальное) поле
Если во всех точках некоторой области G дивергенция векторного поля, заданного в этой области, равна нулю
div а ≡ 0, (8)
то говорят, что в этой области поле соленоидальное (или трубчатое).
Из формулы Гаусса—Остроградского вытекает, что в трубчатом поле поток вектора через любую замкнутую поверхность S, лежащую в этом поле, равен нулю
(9)
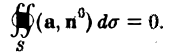
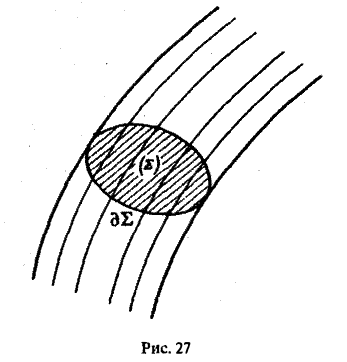
Свойства трубчатого поля
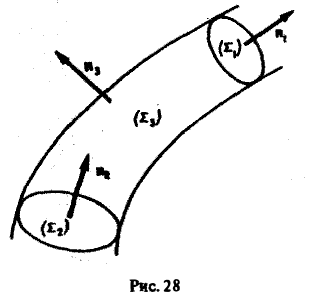
Рассмотрим в области, где задано поле вектора а, какую-нибудь площадку Σ (рис.27). Назовем векторной трубкой совокупность векторных линий, проходящих через границу γ = θΣ этой площадки. Пусть Σ1 — некоторое сечение векторной трубки. Выберем вектор нормали щ к сечению Σ1 так, чтобы он был направлен в ту же сторону, что и вектор а поля.
Теорема:
В трубчатом поле поток вектора а через любое сечение векторной трубки один и тот же.
Пусть Σ1 и Σ2 —непересекающиеся сечения одной и той же векторной трубки. Надо доказать, что
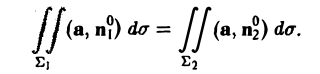
Обозначим через Σ3 часть поверхности векторной трубки, заключенную между сечениями Σ1 и Σ2. Поверхности Σ1, Σ2, Σ3 вместе образуют замкнутую поверхность Σ (рис.28).
Так как по условию поле вектора а — трубчатое, то
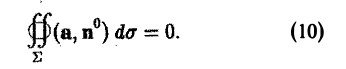
В силу аддитивности потока соотношение (10) можно переписать так:
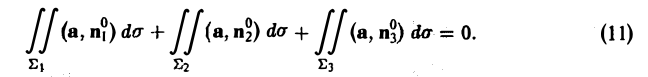
В точках поверхности Σ3, составленной из векторных линий, имеем 
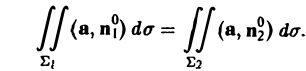
Пусть поверхность Σ имеет ориентированный замкнутый контур L своей границей. Будем говорить, что поверхность Σ натянута на контур L. Вектор нормали п к поверхности Σ будем ориентировать так, чтобы из конца нормали обход контура L был виден против часовой стрелки (рис. 29).
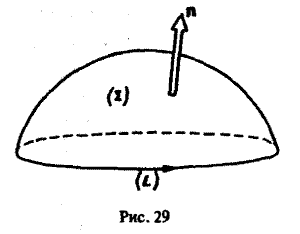
Теорема:
В трубчатом поле поток вектора а через любую поверхность, натянутую на данный контур, один и тот же:
Замечание:
В трубчатом поле векторные линии могут быть либо замкнутыми кривыми, либо иметь концы на границе области, где поле задано.
Пример:
Рассмотрим силовое поле, создаваемое точечным зарядом q, помешенным в начале координат. Вычислим дивергенцию вектора Е напряженности

Имеем
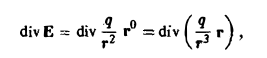
где
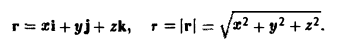
Пользуясь формулой (7), получим
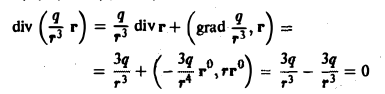
для r ≠ 0. Таким образом, поле вектора Σ, заданного формулой (13), будет трубчатым в любой области G, не содержащей точки O(0,0,0).
Вычислим поток вектора Σ через сферу Sr радиуса R с центром в начале координат O(0,0,0) (рис.30).
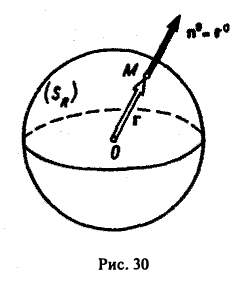
Имеем
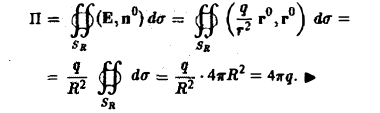
Замечание:
Можно показать, что поток вектора (13) через любую замкнутую поверхность Σ, охватывающую точку O(0,0,0), всегда равен 4 πg.
Циркуляция векторного поля. Ротор вектора. Теорема Стокса
Пусть в некоторой области G задано непрерывное векторное поле
а(М) = Р(х, у, х)i + Q(x, у, z)j + R(х, у, z)k
и замкнутый ориентированный контур L.
Определение:
Циркуляцией вектора а по замкнутому контуру L называется криволинейный интеграл 2-го рода от вектора а по контуру L
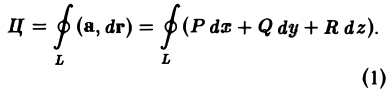
Здесь dr — вектор, длина которого равна дифференциалу дуги L, а направление совпадаете направлением касательной к L, определяемым ориентацией контура (рис. 31) символ 
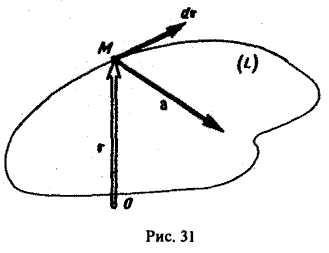
Пример:
Вычислить циркуляцию векторного поля
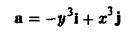
вдоль эллипса L:
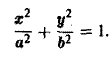
По определению циркуляции имеем
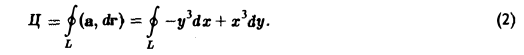
Параметрические уравнения данного эллипса имеют вид:
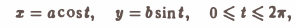
и, значит, dx = -a sin tdt, dy = b cos tdt. Подставляя эти выражения в формулу (2), найдем
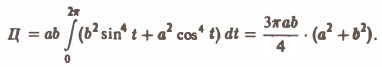
Ротор (вихрь) векторного поля
Рассмотрим поле вектора
а(М) = Р(х, у, z)i + Q(x, у, z)j + R(х, у, z)k,
Р, Q, R которого непрерывны и имеют непрерывные частные производные первого порядка по всем своим аргументам.
Определение:
Ротором вектора а(M) называется вектор, обозначаемый символом rot а и определяемый равенством
или, в символической, удобной для запоминания форме,
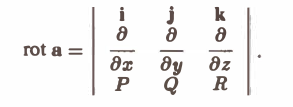
Этот определитель раскрывают по элементам первой строки, при этом операции умножения элементов второй строки на элементы третьей строки понимаются как операции дифференцирования, например,
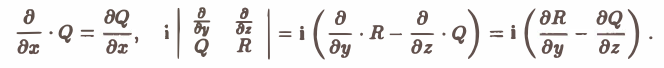
Определение:
Если в некоторой области G имеем rot а = 0, то поле вектора а в области G называется безвихревым.
Пример:
Найти ротор вектора
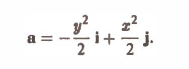
Согласно формуле (3) имеем
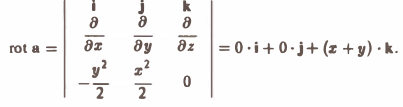
Так как rot а — вектор, то мы можем рассматривать векторное поле — поле ротора вектора а. Предполагая, что координаты вектора а имеют непрерывные частные производные второго порядка, вычислим дивергенцию вектора rot а. Получим
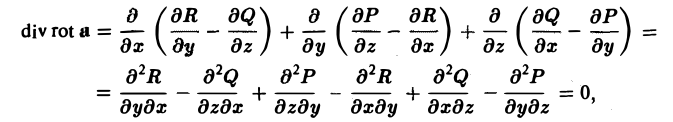
т. е.
div rot a = 0. (3′)
Таким образом, поле вектора rot а соленоидально.
Теорема Стокса:
Циркуляция вектора а вдоль ориентированного замкнутого контура L равна потоку ротора этого вектора через любую поверхность Е, натянутую на контур L,
При этом предполагается, что координаты вектора а имеют непрерывные частные производные в некоторой области G пространства, содержащей поверхность Σ, и что ориентация орта нормали п° к поверхности Σ С G согласована с ориентацией контура L так, что из конца нормали обход контура в заданном направлении виден совершающимся против часовой стрелки.
Учитывая, что а = Pi + Qj + Rk, n° = cos ai + cos βj + cos γk, и пользуясь определением ротора (3), перепишем формулу (4) в следующем виде:
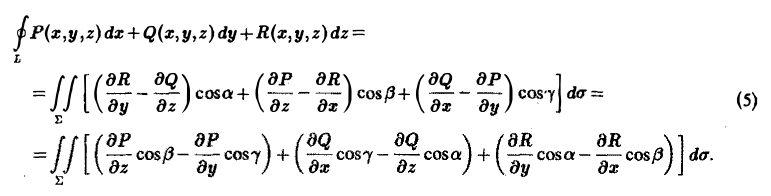
Рассмотрим сначала случай, когда гладкая поверхность Σ и ее контур L однозначно проектируются на область D плоскости хОу и ее границу — контур λ соответственно (рис. 32). Ориентация контура L порождает определенную ориентацию контура λ. Для определенности будем считать, что контур L ориентирован так, что поверхность Σ остается слева, так что веkтор нормали п к поверхности Σ составляет с осью Oz острый угол γ (cos γ > 0).
Пусть z = φ{х,у) — уравнение поверхности Σ и функция ф(х,у) непрерывна и имеет непрерывные частные производные 
Линия L лежит на поверхности Σ. Поэтому, пользуясь уравнением этой поверхности z = φ(х, у),мы можем заменить z под знаком интеграла на φ(x, у). Координаты (х, у)
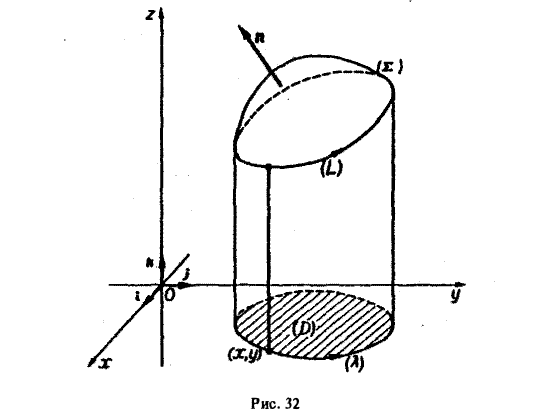
переменной точки кривой λ равны координатам соответствующей точки на кривой L, а потому интегрирование по L можно заменить интегрированием по λ,
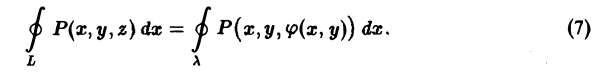
Применим к интегралу, стоящему справа, формулу Грина. Имеем
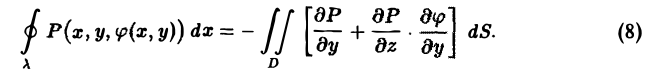
Перейдем теперь от интеграла по области D к интегралу по поверхности Σ. Так как dS = cos γ • dσ,то из формулы (8) получим, что
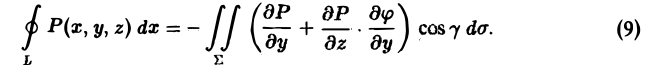
Вектор нормали n° к поверхности Σ определяется выражением
или n° = cos a • i + cos β • j + cos γ • k. Отсюда видно, что
Поэтому равенство (9) можно переписать так:
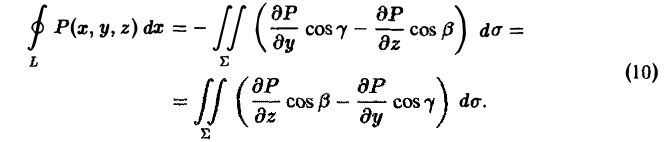
Считая Σ гладкой поверхностью, однозначно проектирующейся на все три координатные плоскости, аналогично убеждаемся в справедливости формул
Складывая равенства (10), (11) и (12) почленно, получим формулу Стокса (5), или, короче,
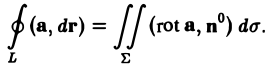
Замечание:
Мы показали, что поле вектора rota — соленоидальное, и потому поток вектора rota не зависит от вида поверхности Σ, натянутой на контур L.
Замечание:
Формула (4) выведена в предположении, что поверхность Σ однозначно проектируется на все три координатные плоскости. Ecли это условие не выполнено, то разбиваем Σ на части так, чтобы каждая часть указан ному условию удовлетворяла, а затем пользуемся аддитивностью интегралов.
Пример:
Вычислить циркуляцию вектора
а = yi — xj + k
по линии L:
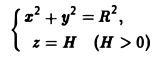
1) пользуясь определением; 2) по теореме Стокса.
1) Зададим линию L параметрически:
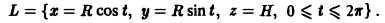
Тогда dx = -R sin t dt, dy = R cos t dt, H dz = 0, так что
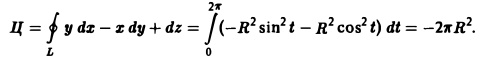
2) Найдем rot a:
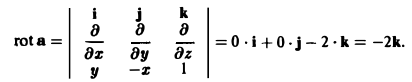
Натянем на контур L кусок плоскости z = H, так что п° = k. Тогда
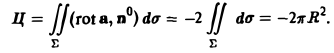
Инвариантное определение ротора поля
Из теоремы Стокса можно получить инвариантное определение ротора поля, не связанное с выбором системы координат.
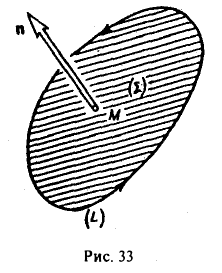
Теорема:
Проекция ротора а на любое направление не зависит от выбора системы координат и равна поверхностной плотности циркуляции вектора а по контуру площадки, перпендикулярной этому направлению,
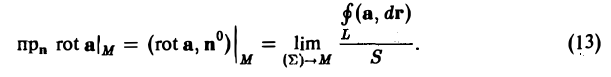
Здесь ( Σ ) — плоская площадка, перпендикулярная вектору п; S — площадь этой площадки; L — контур площадки, ориентированный так, чтобы обход контура был виден из конца вектора п против хода часовой стрелки; ( Σ ) → М означает, что площадка ( Σ ) стягиваетcя к точке М, в которой рассматривается вектор rot а, причем вектор нормали п к этой площадке остается все время одним и тем же (рис. 33).
Применим сначала к циркуляции
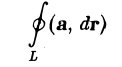
вектора а теорему Стокса, а затем к полученному двойному интегралу — теорему о среднем значении:
(скалярное произведение (rot a, n°) берется в некоторой средней точке Mср площадки ( Σ )).
При стягивании площадки ( Σ ) к точке М средняя точка Мср тоже стремится к точке М и, в силу предполагаемой непрерывности частных производных от координат вектора а (а значит, и непрерывности rot а), мы получаем
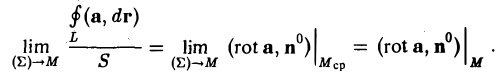
Поскольку проекция вектора rot а на произвольное направление не зависит от выбора системы координат, то сам вектор rota инвариантен относительно этого выбора. Отсюда получаем следующее инвариантное определение ротора поля: ротор поля есть вектор, длина которого равна наибольшей поверхностной плотности циркуляции в данной точке, направленный перпендикулярно той площадке, на которой эта наибольшая плотность циркуляции достигается; при этом ориентация вектора rot a согласуется с ориентацией контура, при которой циркуляция положительна, по правилу правого винта.
Физический смысл ротора поля
Пусть твердое тело вращается вокруг неподвижной оси l с угловой скоростью w. Не нарушая общности, можно считать, что ось l совпадает с осью Oz (рис. 34). Пусть М(г) — изучаемая точка тела, где
r = xi + уj + zk.
Вектор угловой скорости в нашем случае равен w ≡ wk, вычислим вектор v линейной скорости точки М,
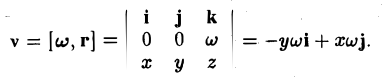
Отсюда
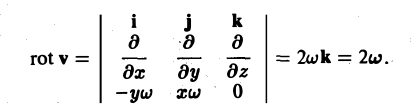
Итак, вихрь поля скоростей вращающегося твердого тела одинаков во всех точках поля, параллелен оси вращения и равен удвоенной угловой скорости вращения.
Правила вычисления ротора
1, Ротор постоянного вектора с равен нулевому вектору,
rot e = 0.
2. Ротор обладает свойством линейности
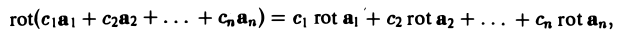
где c1, c2,…, cn — постоянные числа.
3. Ротор произведения скалярной функции и(М) на векторную а(М) вычисляется по формуле
rot(wa) = и rot а + [grad и, а].
В самом деле,
Независимость криволинейного интеграла от пути интегрирования
Определение:
Область G трехмерного пространства называется поверхностно односвязной, если на любой замкнутый контур, лежащий в этой области, можно натянуть поверхность, целиком лежащую в области G.
Например, внутренность сферы или все трехмерное пространство являются поверхностно односвязными областями; внутренность тора или трехмерное пространство, из которого исключена прямая, поверхностно односвязными областями не являются.
Пусть в поверхностно односвязной области G задано непрерывное векторное поле
а (М) = Р(М)i + Q(M)j + R(M) k.
Тогда имеет место следующая теорема.
Теорема:
Для того чтобы криволинейный интеграл
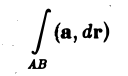
в поле вектора а не зависел от пути интегрирования, а зависел только от начальной и конечной точек пути (А и В), необходимо и достаточно, чтобы циркуляция вектора a вдаль любого замкнутого контура L, расположенного в области G, была равна нулю.
Необходимость. Пусть интеграл
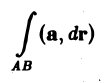
не зависит от пути интегрирования. Покажем, что тогда
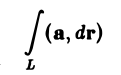
по любому замкнутому контуру L равен нулю.
Рассмотрим произвольный замкнутый контур L в поле вектора а и возьмем на нем произвольно точки A и В (рис.35).
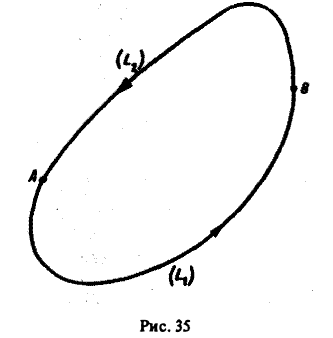
По условию имеем
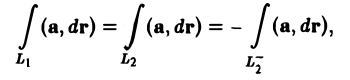
где L1 и L2 — различные пути, соединяющие точки А и В; откуда

Но L1 U L2 как раз и есть выбранный замкнутый контур L. Достаточность. Пусть
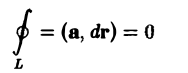
для любого замкнутого контура L. Покажем, что в этом случае интеграл
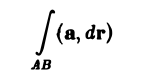
не зависит от пути интегрирования.
Возьмем в поле вектора а две точки А и В, соединим их произвольными линиями L1 и L2 к покажем, что

Для простоты ограничимся случаем, когда линии L1 и L2 не пересекаются. В этом случае объединение L1 ∪ L2 образует простой замкнутый контур L (рис. 36).
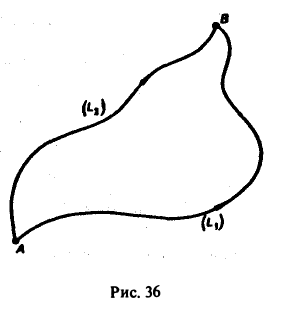
По условию
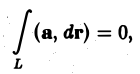
а по свойству аддитивности
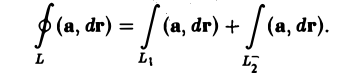
Следовательно,
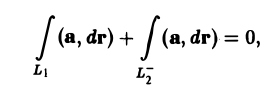
откуда справедливость равенства (2) и вытекает.
Теорема 9 выражает необходимое и достаточное условия независимости криволинейного интеграла от формы пути, однако эти условия трудно проверяемы. Приведем более эффективный критерий.
Теорема:
Для того, чтобы криволинейный интеграл
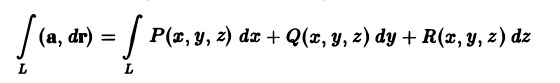
не зависел от пути интегрирования L, необходимо и достаточно, чтобы векторное поле а(М) = Р(X, у, z)i + Q(x, у, z)j + R(x, у, z)k было безвихревым,
rot a(M) = 0. (3)
Здесь предполагается, что координаты Р(х, у, z), Q(x, у, z), R(x, у, z) вектора а(М) имеют непрерывные частные производные первого порядка и область определения вектора а(М) поверхностно односвязна.
Замечание:
В силу теоремы 9 независимость криволинейного интеграла от пути интегрирования равносильна равенству нулю циркуляции вектора а вдоль любого замкнутого контура. Это обстоятельство мы используем при доказательстве теоремы.
Необходимость. Пусть криволинейный интеграл не зависит от формы пути, или, что то же, циркуляция вектора а по любому замкнутому контуру L равна нулю. Тогда
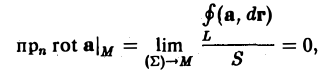
т. е. в каждой точке поля проекция вектора rot а на любое направление равна нулю. Это означает, что сам вектор rot а равен нулю во всех точках поля,
rot а ≡ 0.
Достаточность. Достаточность условия (3) вытекает из формулы Стокса, так как если rot а ≡ 0, то и циркуляция вектора по любому замкнутому контуру L равна нулю:
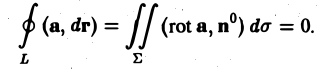
Ротор плоского поля a = P(x, y)i + Q(x, y)j равен
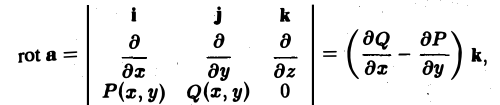
что позволяет сформулировать для плоского поля следующую теорему.
Теорема:
Для того, чтобы криволинейный интеграл
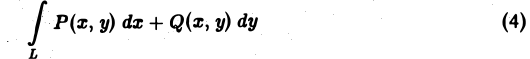
в односвязном плоском поле не зависел от формы линии L, необходимо и достаточно, чтобы соотношение

выполнялось тождественно во всей рассматриваемой области.
Если область неодносвязна, то выполнение условия
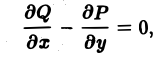
вообще говоря, не обеспечивает независимости криволинейного интеграла от формы линии.
Пример:
Пусть
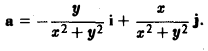
Рассмотрим интеграл
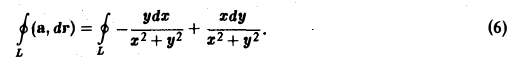
Ясно, что подынтегральное выражение не имеет смысла в точке 0(0,0). Поэтому исключим эту точку. В остальной части плоскости (это будет уже не сщносвязная область!) координаты вектора а непрерывны, имеют непрерывные частные производные и
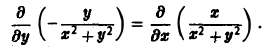
Рассмотрим интеграл (6) вдоль замкнутой кривой L — окружности радиуса R с центром в начале координат
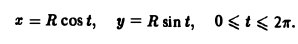
Отличие циркуляции от нуля показывает, что интеграл (6) зависит от формы пути интегрирования.
Потенциальное поле
Определение:
Поле вектора а(М) называется потенциальным, если существует скалярная функция и{М) такая, что
grad и = a. (1)
При этом функция и{М) называется потенциалом поля ее поверхности уровня называются эквипотенциальными поверхностями.
Пусть
а = Р(х, у, z)i + Q(x, у, z)j + R(x, у, z)k.
Так как
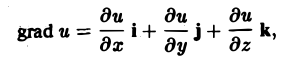
то соотношение (1) равносильно следующим трем скалярным равенствам:
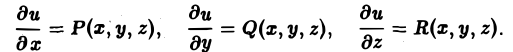
Заметим, что потенциал поля определяется с точностью до постоянного слагаемого: если grad и = а и grad v = а, то
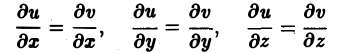
и, следовательно, и = v + с, где с — постоянное число.
Пример:
Поле радиус-вектора г является потенциальным, так как
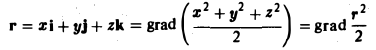
(напомним, что 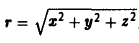
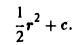
Пример:
Поле вектора
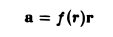
является потенциальным.
Пусть функция φ(r) такая, что
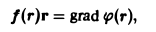
найдена. Тогда
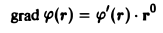
и
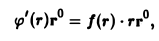
откуда
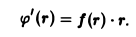
Значит,
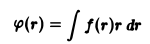
— потенциал поля.
Теорема:
Для того чтобы поле вектора а было потенциальным, необходимо и достаточно, чтобы оно было безвихревым,
rot а ≡ 0, (2)
т. е. чтобы его ротор равнялся нулю во всех точках поля. При этом предполагается непрерывность всех частных производных от координат вектора а и поверхностная односвязность области, в которой задан вектор а.
Необходимость. Необходимость условия (2) устанавливается непосредственным подсчетом: если поле потенциально, т. е. а = grad и, то
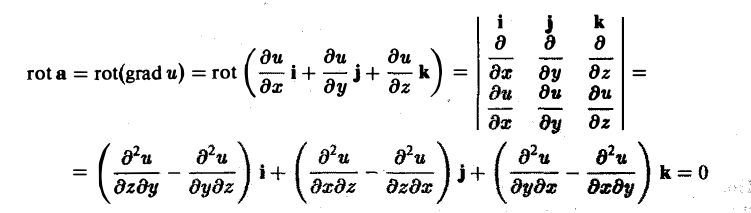
в силу независимости смешанных производных от порядка дифференцирования.
Достаточность. Пусть поле вектора безвихревое (2). Для того чтобы доказать потенциальность этого поля, построим его потенциал и(М). Из условия (2) следует, что криволинейный интеграл

не зависит от формы линии L, а зависит только от ее начальной и конечной точек. Зафиксируем начальную точку Мо(xo, yо, zo), а конечную точку М(х, y, z) будем менять. Тогда интеграл (3) будет функцией точки М(х, у, z). Обозначим эту функцию через и(М) и докажем, что
grad u = а.
В дальнейшем будем записывать интеграл (3), указывая лишь начальную и конечную точку пути интегрирования,
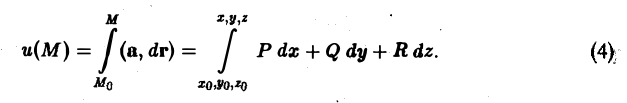
Равенство grad и = а равносильно трем скалярны м равенства м
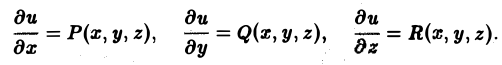
Докажем первое из них,
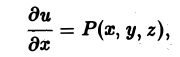
второе и третье равенства доказываются аналогично.
По определению частной производной имеем
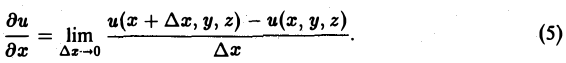
Рассмотрим точку М1(х + ∆х, у, z), близкую к точке M(x,y,z). Так как функция и(М) определяется соотношением (4), в котором криволинейный интеграл не зависит от пути интегрирования, то выберем путь интегрирования так, как указано на рис.37.
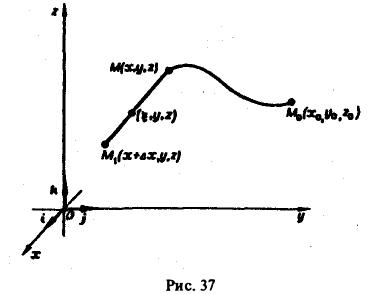
Тогда
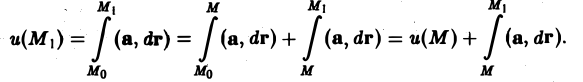
Отсюда
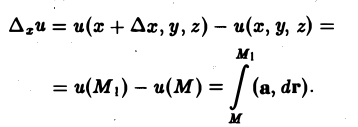
Последний интеграл берется вдоль отрезка прямой ММ1, параллельной оси Ох. На этом отрезке в качестве параметра можно принять координату х:
x = х, у = const, z = const.
Тогда dx = dx,dy = 0, dz = 0, так что
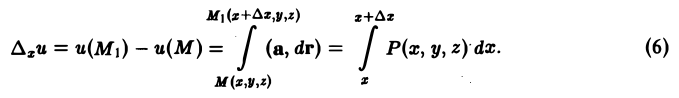
Применяя к интегралу в правой части (6) теорему о среднем, получаем

где величина ξ заключена между х и х + ∆х. Из формулы (7) вытекает, что
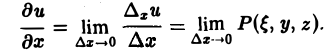
Так как ξ —► x при ∆x —» 0, то в силу непрерывности функции Р(х, у, z) получаем
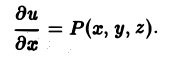
Аналогично доказывается, что
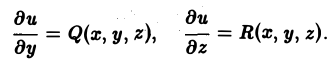
Следствие:
Векторное поле является потенциальным тогда и только тогда, когда криволинейный интеграл в нем не зависит от пути.
Вычисление криволинейного интеграла в потенциальном поле
Теорема:
Интеграл 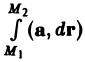
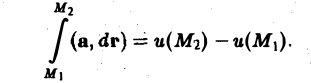
Ранее былодоказано, что функция

является потенциалом поля.
В потенциальном поле криволинейный интеграл
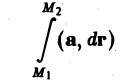
не зависит от пути интегрирования. Поэтому, выбирая путь отточки М1 к точке М2 так, чтобы он прошел через точку Mo (рис. 38), получаем
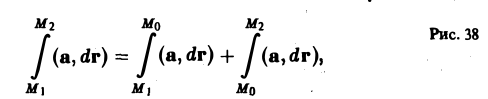
или, меняя ориентацию пути в первом интеграле справа,
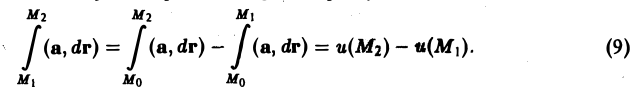
Так как потенциал поля определяется с точностью до постоянного слагаемого, то любой потенциал рассматриваемого поля можетбыть записан в виде
v(M) = u(M) + c, (10)
где с — постоянная.
Делая в формуле (10) замену u(M2) = v(M2) — с, и(М1) = v(M1) — с, получим для произвольного потенциала v(M) требуемую формулу
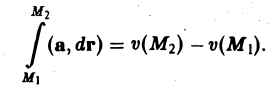
Пример:
В примере 1 было показано, что потенциалом поля радиус-вектора г является функция
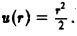
Поэтому
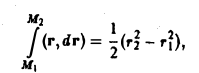
где ri (i = 1,2) — расстояние от точки Mi(i = 1,2) до начала координат.
Вычисление потенциала в декартовых координатах
Пусть задано потенциальное поле
а(М) = Р(х, у, г)i + Q(x, у, z)j + R(x, у, z)k.
Ранее было показано, что потенциальная функция и(М) может быть найдена по формуле
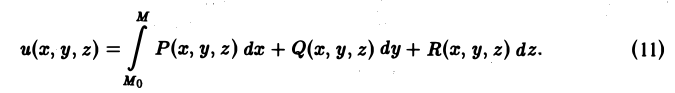
Интеграл (11) удобнее всего вычислять так: зафиксируем начальную точку Мо(хо, yо, zо) и соединим ее с достаточно близкой текущей точкой M(x,y,z) ломаной М0М1М2М, звенья которой параллельны координатным осям, М0М1,||Ох, M1М2||Оу, М2М|| Oz (рис.39).
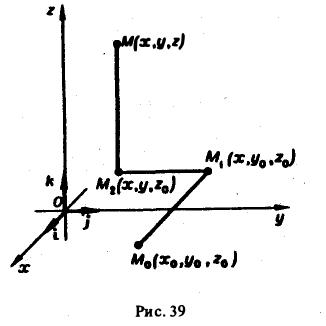
При этом на каждом звене ломаной изменяется только одна координата, что позволяет существенно упростить вычисления. В самом деле, на отрезке М0М1 имеем:
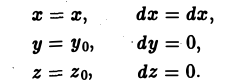
На отрезке М1М2:
х = const, dx = 0, у = у, dy = dy, z = z0 и dz = 0.
На отрезке M1M:
x = const, dx = 0, у = const, dy = 0, z = z и dz = dz.
Следовательно, потенциал u(M) равен
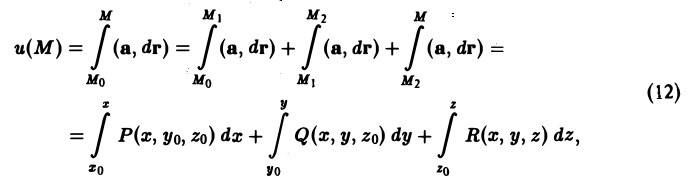
где x, у, z — координаты текущей точки на звеньях ломаной, вдоль которых ведется интегрирование.
Пример:
Доказать, что векторное поле
а = {у + z)i + (х + z)j + (х + y)k
является потенциальным, и найти его потенциал.
Проверим, будет ли поле вектора а(М) потенциально. С этой целью вычислим ротор поля. Имеем
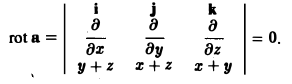
Поле является потенциальным. Потенциал этого поля найдем с помощью формулы (12). Возьмем за начальную точку Mо начало координат О (так обычно поступают, если поле а(М) определено в начале координат). Тогда получим
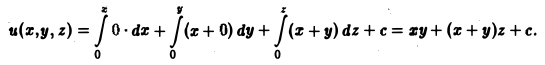
Итак,
u(z, у, z) = ху + xz + yz + с,
где с — произвольная постоянная.
Потенциал этого поля можно найти и по-иному. По определению потенциал и(х, у, г) есть скалярная функция, для которой grad и = а. Это векторное равенство равносильно трем скалярным равенствам:

Интегрируя (13) по х, получим
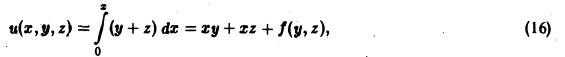
где f(y,z) — произвольная дифференцируемая функция от у и z. Продифференцируем (16) по у:
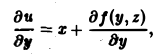
откуда, учитывая (14), будем иметь
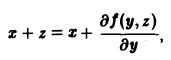
или

Проинтегрировав (17) по у, найдем
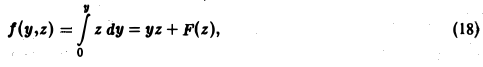
где F(z) — некоторая функция х. Подставив (18) в (16), получим
и(х, у, z) = ху + xz + у z + F(z).
Дифференцируя последнее равенство по z и учитывая соотношение (15), получим уравнение для F(z),
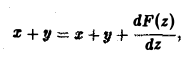
откуда 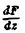
u(x,y,z) = ху +yz + zx +с.
Оператор Гамильтона
Мы рассмотрели три основные операции векторного анализа: вычисление grad и для скалярного поля и = и(х, у, z) и div а и rot а для векторного поля а = а(x, у, z). Эти операции могут быть записаны в более простом виде с помощью символического оператора ∇ («набла»): (1)
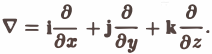
Оператор ∇ (оператор Гамильтона) обладает как дифференциальными, так и векторными свойствами. Формальное умножение, например, умножение 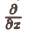
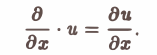
В рамках векторной алгебры формальные операции над оператором ∇ будем проводить так, как если бы он был вектором. Используя этот формализм, получим следующие основные формулы:
1, Если и = и(х, у, z) — скалярная дифференцируемая функция, то по правилу умножения вектора на скаляр получим
2. Если
a = P(x, y, z)i + Q(x, y, z)j + (x, y, z)k,
где P, Q, R — дифференцируемые функции, то по формуле для нахождения скалярного произведения получим
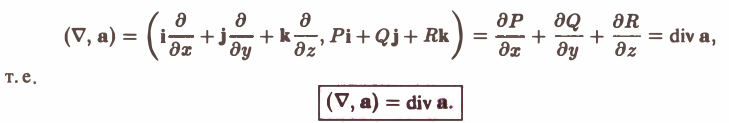
3. Вычисляя векторное произведение [ ∇, а], получим
Для постоянной функции и = с получим
∇c = 0,
а для постоянного вектора с будем иметь
( ∇, с) = 0 и [ ∇, с] = 0.
Из распределительного свойства для скалярного и векторного произведений получаем
( ∇, a + b) = ( ∇, а) + ( ∇, b),
Замечание:
Формулы (5) и (6) можно трактовать так же как проявление дифференциальных свойств оператора «набла»( ∇ — линейный дифференциальный оператор). Условились считать, что оператор ∇ действует на все величины, написанные за ним. В этом смысле, например,
( ∇, а) ≠ (а, ∇ ),
ибо ( ∇, а) = div а есть функция 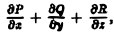
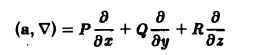
— скалярный дифференциальный оператор.
Применяя оператор ∇ к произведению каких-либо величин, надо иметь в виду обычное правило дифференцирования произведения.
Пример:
Доказать, что
grad(u v) = v Brad и + u grad v. (7)
По формуле (2) с учетом замечания 1 получаем
∇(uv) = v∇u + u ∇v,
или
grad(uv) = v grad u + u grad v.
Чтобы отметить тот факт, что «набла» не действует на какую-либо величину, входящую в состав сложной формулы, эту величину отмечают индексом с («const»), который в окончательном результате опускается.
Пример:
Пусть и(x,y,z) — скалярная дифференцируемая функция, a(x,y,z) — векторная дифференцируемая функция. Доказать, что
div(ua) =u diva + (a, grad u). (8)
Перепишем левую часть (8) в символическом виде
div(ua) = ( ∇, ua).
Учитывая дифференциальный характер оператора ∇, получаем
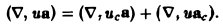
Так как ис — постоянный скаляр, то его можно вынести за знак скалярного произведения, так что
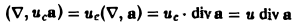
(на последнем шаге мы опустили индекс с).
В выражении ( ∇, иас) оператор ∇ действует только на скалярную функцию и, поэтому
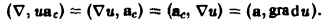
В итоге получаем
div(ua) = u div а + (a, grad и).
Замечание:
Используя формализм действий с оператором ∇ как с вектором, надо помнить, что ∇ не является обычным вектором — он не имеет ни длины, ни направления, так что, например, вектор ( ∇, а} не будет, вообще говоря, перпендикулярным вектору а (впрочем, для плоского поля а = Р(х, y)i + Q(x, y)j вектор
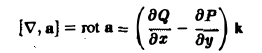
перпендикулярен плоскости хОу, а значит, и вектору а).
Не имеет смысла и понятие коллинеарности по отношению к символическому вектору ∇. Например, выражение [∇ φ, ∇ ψ] где φ и ψ — скалярные функции, формально напоминает векторное произведение двух кoллинеарных векторов, которое всегда равно нулю. Однако в общем случае это не имеет места. В самом деле, вектор ∇ φ = grad φ направлен по нормали к поверхности уровня φ = const, а вектор ∇ ψ = grad ψ определяет нормаль к поверхности уровня ψ = const. В общем случае эти нормали не обязаны быть коллинеарными (рис. 40). С другой стороны, в любом дифференцируемом скалярном поле φ (х, у, z) имеем [∇ φ, ∇ ψ] = 0.
Эта примеры показывают, что с оператором «набла» нужно обращаться с большой осторожностью и при отсутствии уверенности в полученном результате его следует проверить аналитическими методами.
Дифференциальные операции второго порядка. Оператор Лапласа
Дифференциальные операции второго порядка получаются в результате двукратного применения оператора ∇.
1, Пусть имеем скалярное поле и = и(x,y,z). В этом поле оператор ∇ порождает векторное поле
∇u = grad и.
В векторном поле grad и можно определить две операции:
( ∇, ∇u) = div grad u, (1)
что приводит к скалярному полю, и
[ ∇, ∇m] = rot grad u, (2)
что приводит к векторному полю.
2. Пусть задано векторное поле а = Pi + Qj + Rk. Тогда оператор (2) порождает в нем скалярное поле
(∇, а) = div a.
В скалярном поле div а оператор ∇ порождает векторное поле
∇ (∇,a) = grad div а. (3)
3. В векторном поле а = Pi + Qj + Rк оператор ∇ порождает также векторное поле
[∇, а] = rot a.
Применяя к этому полю снова оператор ∇, получим:
а) скалярное поле
(∇, [∇, а]) = div rot а, (4).
б) векторное поле
(∇, [∇, а]) = rot rot а. (5)
Формулы (1)-(5) определяют так называемые дифференциальные операции второго порядка.
Выберем в пространстве прямоугольную декартову систему координат Oxyz и рассмотрим каждую из формул (1)-(5) более подробно.
1, Предполагая, что функция и(х, у, z) имеет непрерывные вторые частные производные по х, у и z, получим
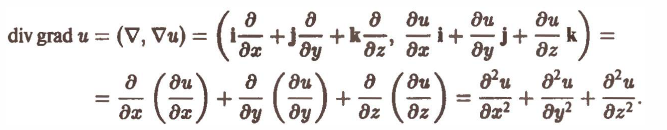
Символ
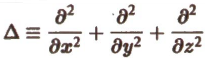
называется оператором Лапласа, или лапласианом. Его можно представить как скалярное произведение оператора Гамильтона ∇ на самого себя, т.е.
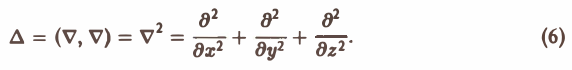
Оператор ∆ (дельта) играет важную роль в математической физике. Уравнение (6)
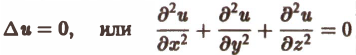
называется уравнением Лапласа. С его помощью описывается, например, стационарное распределение тепла.
Скалярное поле и(х, у, z), удовлетворяющее условию ∆и = 0, называется лапла-совым или гармоническим полем.
Например, скалярное поле и = 2х2 + Зу — 2x2 является гармоническим во всем трехмерном пространстве: из того, что
2. Пусть функция u(z, у, z) имеет непрерывные частные производные второго порядка включительно. Тогда
rot grad u ≡ 0. (7)
В самом деле, действуя формально, получим
rot grad и = [∇, ∇u] = [ ∇, ∇ ] u = 0,
ибо [∇, ∇] = 0 как векторное произведение двух одинаковых «векторов».
Тот же результат можно получить, используя выражения градиента и ротора в декартовых координатах
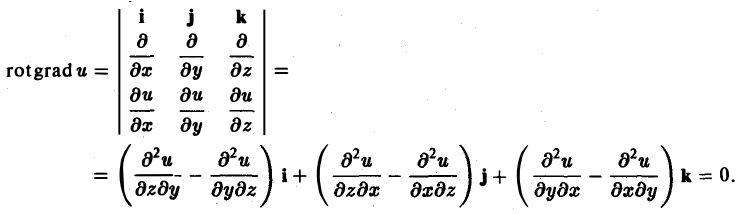
3. Пусть задано векторное поле
а = Р(х, у, z)i + Q(x, у, z)j + R(x, у, z)k,
координаты которого P, Q, R имеют непрерывные частные производные второго порядка. Тогда получим
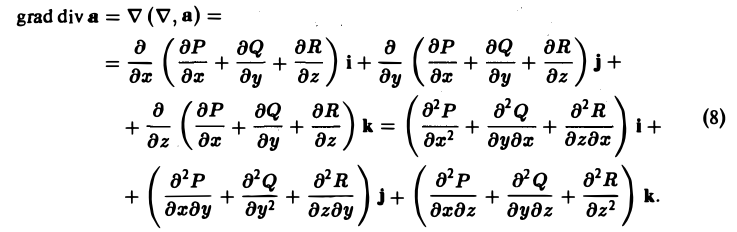
4. При тех же условиях, что и в пункте 3, имеем (9)
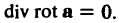
Это соотношение уже было доказано ранее путем непосредственных вычислений. Здесь мы приведем его формальное доказательство, используя известную формулу из векторной алгебры
(А, [В, С]) = (С,[А,В])= (В, [С, А]).
Имеем
div rot а = (∇, [∇, а]) = (а, [∇, ∇]) = О,
так как [∇, ∇] = 0 как векторное произведение двух одинаковых «векторов».
5. Покажем, наконец, что при тех же условиях, что и ранее,
rot rot а = grad div а — ∆а. (10)
Так как
rot rot а = [ ∇, [∇,a]),
то, полагая в формуле для двойного векторного произведения [А, [В, С]] = В(А, С) — (А, В)С,
А = ∇, B = ∇, С = а,
получим
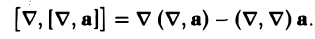
Но ( ∇, а) = div а и ( ∇, ∇) = ∆. Поэтому окончательно будем иметь
rot rot а = grad div а — ∆а,
где grad div а выражается по формуле (8), а ∆а для вектора а = Pi + Qj + Rk надо понимать так:
∆а = ∆Р • i + ∆Q • j + ∆R • k.
В заключение приведем таблицу дифференциальных операций второго порядка.
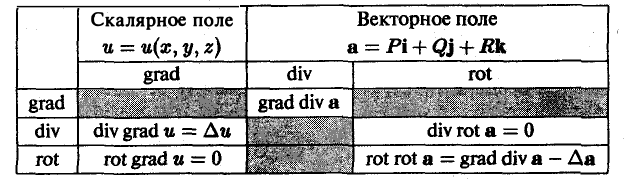
Заштрихованные прямоугольники означают, что соответствующая операция не имеет смысла (например, градиент от rot а).
Понятие о криволинейных координатах
Во многих задачах бывает удобно определять положение точки простр анства не декартовыми координатами (х, у, z), а тремя другими числами (q1, q2, q3), более естественно связанными с рассматриваемой частной задачей.
Если задано правило, согласно которому каждой точке М пространства отвечает определенная тройка чисел (q1, q2, q3) и, обратно, каждой такой тройке чисел отвечает единственная точка М, то говорят, что в пространстве задана криволинейная координатная система. В этом случае величины q1, q2, q3 называют криволинейными координатами точки М.
Координатными поверхностями в системе криволинейных координат q1, q2, q3 называются поверхности
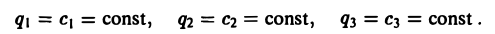
На координатных поверхностях одна из координат сохраняет постоянное значение. Линии пересечения двух координатных поверхностей называются координатными линиями.
В качестве примеров криволинейных координат рассмотрим цилиндрические и сферические координаты.
Цилиндрические координаты
В цилиндрических координатах положение точки М в пространстве определяется тремя координатами:
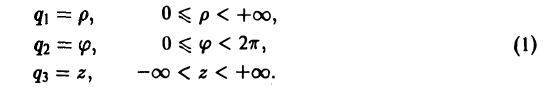
Координатные поверхности:
р = const — круговые цилиндры с осью Оz;
φ = const — полуплоскости, примыкающие к оси Oz;
z = const — плоскости, перпендикулярные оси Oz (рис. 41).
Координатные линии:
1) линии (р) — лучи, перпендикулярные оси Oz и имеющие начало на этой оси, т. е. линии пересечения координатных поверхностей φ = const, z = const;
2) линии (φ) — окружности с центрами на оси Oz, лежащие в плоскостях, перпендикулярных оси Oz;
3) линии (z) — прямые, параллельные оси Oz.
Связь декартовых координат точки (х, у, z) с цилиндрическими координатами (р, φ, z) задается формулами
x = p cos φ, y = p sin φ, z = z. (2)
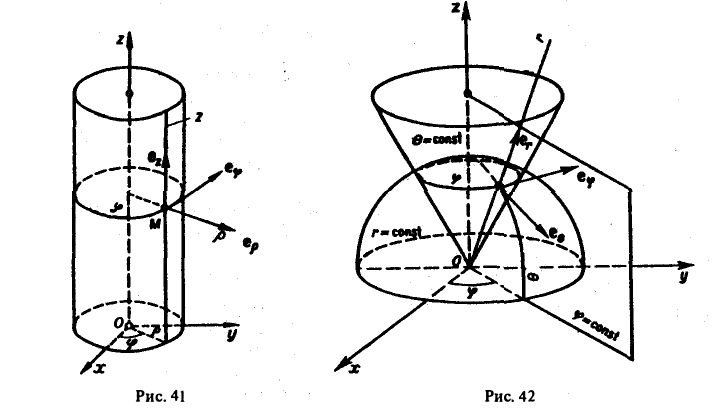
Сферические координаты
В сферических координатах положение точки М в пространстве определяется следующими координатами:
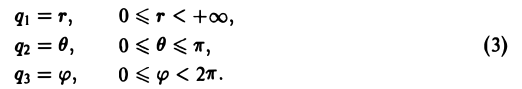
Координатные поверхности (рис. 42):
r = const — сферы с центром в точке О;
θ = const — круговые полуконусы с осью Oz;
φ = const — полуплоскости, примыкающие к оси Oz.
Координатные линии:
1) линии (г) — лучи, выходящие из точки О;
2) линии (θ) — меридианы на сфере;
3) линии (φ) — параллели на сфере.
Связь декартовых координат (х, у, z) точки М с ее сферическими координатами (r, θ, φ) задается формулами
х = r cos φ sin θ,
у = r sin φ sin θ, (4)
z = r cos θ.
Введем единичные векторы e1, е2, е3 (орты), направленные по касательным к координатным линиям(q1),(q2),(q3)в тoчке М в сторону возрастания переменных q1,q2,q3 соответственно.
Определение:
Система криволинейных координат называется ортогональной, если в каждой точке М орты e1, е2, е3 попарно ортогональны.
В такой системе ортогональны и координатные линии, и координатные поверхности.
Примерами ортогональных криволинейных координат служат системы цилиндрических и сферических координат. Мы ограничимся рассмотрением только ортогональных систем координат.
Пусть r = r(q1, q2, q3) — радиус-вектор точки М. Тогда можно показать, что
(5)
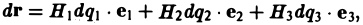
где
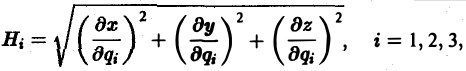
— коэффициенты Ламэ данной криволинейной системы координат. Вычислим коэффициенты Ламэ для цилиндрических координат
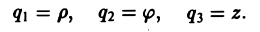
Так как х = р cos φ, у = р sin φ, z = z, то
(6)
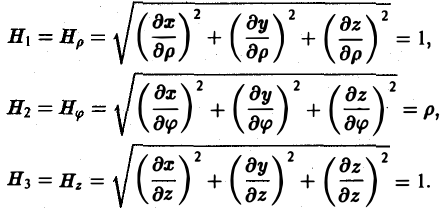
Аналогично для сферических координат имеем
(7)
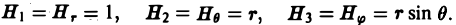
Величины
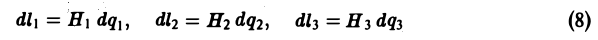
являются дифференциалами длин дуг соответствующих координатных линий.
Основные операции векторного анализа в криволинейных координатах
Дифференциальные уравнения векторных линий
Рассмотрим поле вектора
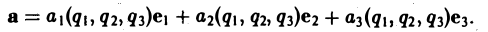
Уравнения векторных линий в криволинейных координатах q1,q2, q3 имеют вид
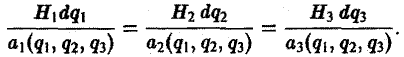
В цилиндрических координатах (q1 = р, q2= φ, q3 = z)
(1)
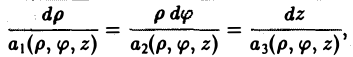
в сферических координатах (q1 = r, q2 = θ, q3 = φ)
(2)
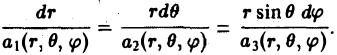
Градиент в ортогональных координатах
Пусть и = u(q1, q2, q3) — скалярное пoле. Тогда

В цилиндрических координатах (q1 = р, q2 = φ, q3 = z)
(3)
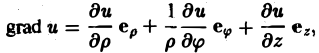
в сферических координатах (q1 = r, q2 = θ, q3 = φ) (4)
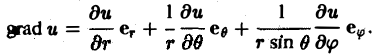
Ротор в ортогональных координатах
Рассмотрим векторное поле
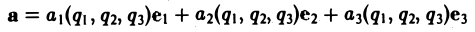
и вычислим rot а. Имеем
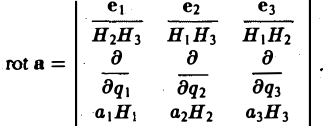
В цилиндрических координатах
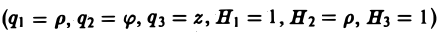
(5)
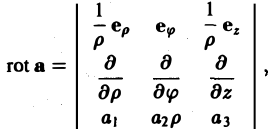
в сферических координатах
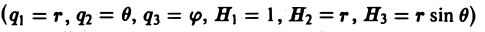
(6)
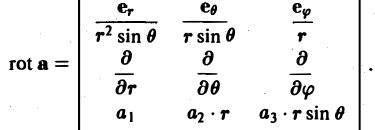
Дивергенция в ортогональных координатах
Дивергенция div а векторного поля
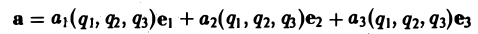
вычисляется по формуле
(7)
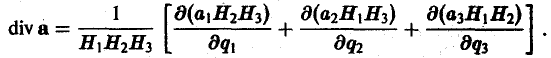
В цилиндрических координатах
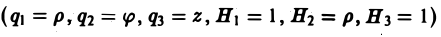
в цилиндрических координатах
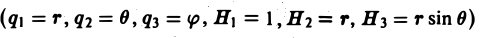
в сферических координатах
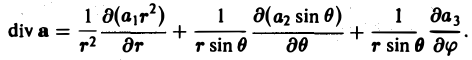
Применяя формулу (7) к единичным векторам е1, е2, е3, получим
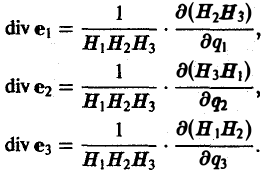
Вычисление потока в криволинейных координатах
Пусть S — часть координатной поверхности q1 = с = const, ограниченная координатными линиями
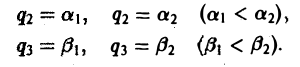
Тогда поток вектора
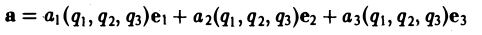
через поверхность S в направлении вектора e1 вычисляется по формуле
(8)
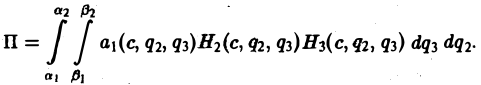
Аналогично вычисляется поток через часть поверхности q2 = с, а также через часть поверхности д3 = с, где с = const.
Пример:
Найти поток П векторного поля
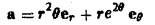
через внешнюю сторону верхней полусферы S радиуса R с центром в начале координат.
Полусфера S есть часть координатной поверхности r = const, а именно r = R. На полусфере S имеем
Учитывая, что в сферических координатах
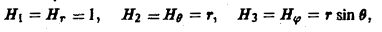
по формуле (8) найдем
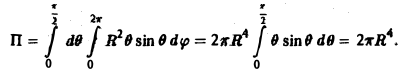
Вычисление потенциала в криволинейных координатах
Пусть в некоторой области Ω задано потенциальное векторное поле
т. e. rot а = 0 в области Ω.
Для нахождения потенциала и = и(q1, q2, q3) этого векторного поля запишем равенство а(М) = grad u(M) в следующем виде:
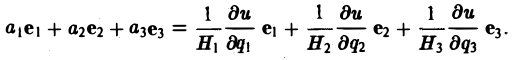
Отсюда следует, что
(9)
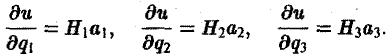
Интегрируя систему дифференциальных уравнений с частными производными (9), найдем искомый потенциал
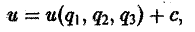
где с — произвольная постоянная.
В цилиндрических координатах
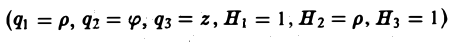
система (9) принимает вид
В сферических координатах
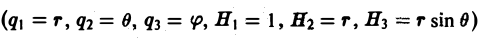
система (9) имеет вид
Пример:
Найти потенциал векторного поля, заданного в цилиндрических координатаx
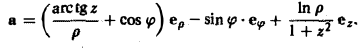
Убедимся, что rot a = 0. По формуле (S) получим
т.е. данное поле потенциально.
Искомый потенциал u = и(р, φ, z) является решением следующей системы дифференциальных уравнений с частными производными (см. формулу (10)):
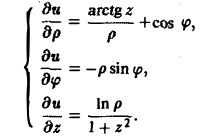
Интегрированием по р из первого уравнения находим
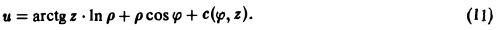
Дифференцируя соотношение (11) no φ и используя второе уравнение, получим
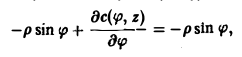
или 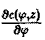
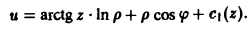
Дифференцируя это соотношение по z и используя третье уравнение, получим
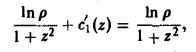
или c1`(z) =0, откуда c1(z) = с. Итак, потенциал данного поля
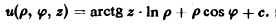
Линейный интеграл и циркуляция в ортогональных криволинейных координатах
Пусть векторное поле
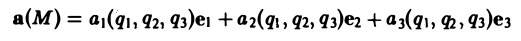
определено и непрерывно в области Ω изменения ортогональных криволинейных координат q1, q2, q3. Так как дифференциал радиус-вектора r любой точки M(q1, q2, q3) ∈ Ω выражается формулой
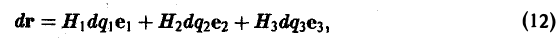
то криволинейный интеграл вектора а(М) по ориентированной гладкой или кусочно-гладкой кривой L ⊂ Ω будет равен
(13)
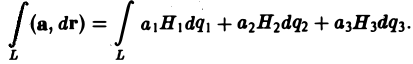
В частности, для цилиндрических координат (q1 = р, q2 = φ, q3 = z, Н1 = 1, Н2 = р, Н3=1) будем иметь
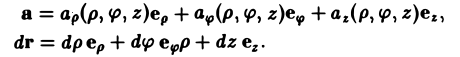
Отсюда по формуле (13) получим
(14)
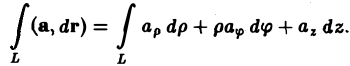
Аналогично для сферических координат (q1 = r, q2 = θ, q3 = φ, Н1 = 1, Н2 = r, H3 = r sin θ будем иметь
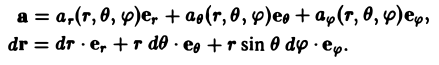
Отсюда по формуле (13) получим
(15)
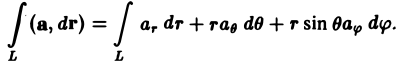
Если кривая L замкнута (начальная и конечная точки кривой L совпадают), то циркуляция Ц векторного поля а (М) в криволинейных координатах q1, q2, q3 вычисляется по формуле (13), а в случае цилиндрических или сферических координат — по формулам (14) или (15) соответственно.
Пример:
Вычислить циркуляцию векторного поля, заданного в цилиндрических координатах
по замкнутой кривой L,
Координаты данного вектора равны соответственно
Контур L представляет собой замкнутую кривую, расположенную в плоскости z = 0 (рис. 43).
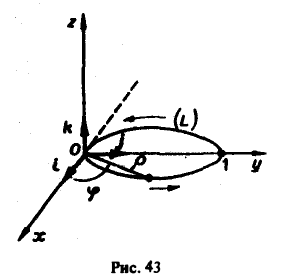
Подставляя координаты данного вектора в формулу .(14), получим
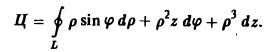
На кривой L имеем
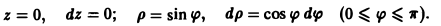
Искомая циркуляция будет равна
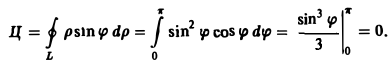
Оператор Лапласа в ортогональных координатах
Используя формулы (16) и (17), для оператора Лапласа ∆ получим следующее выражение:
В цилиндрических координатах
1) получим
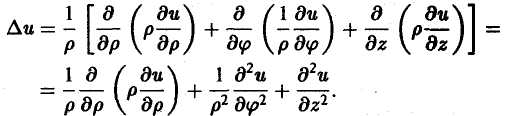
В сферических координатах
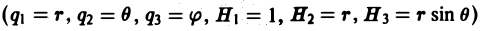
будем иметь
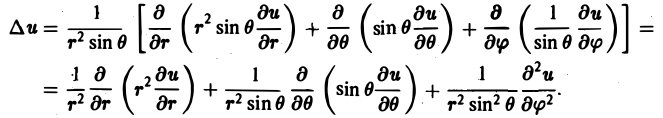
Пример:
Найти все решения уравнения Лапласа ∆и = 0, зависящие только от расстояния r.
Так как искомое решение и должно зависеть только от расстояния точки М от начала координат г, т. е. и = и (r), то уравнение Лапласа ∆и = 0 в сферических координатах будет иметь вид
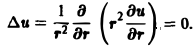
Отсюда 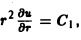
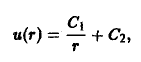
где С1 и С2 — постоянные.
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат