Правильный пятиугольник как найти угол - Исправление недочетов и поиск решений вместе с Examum.ru

Правильный пятиугольник

Правильный пятиугольник — это такой пятиугольник у которого все пять сторон равны и его пять углов равны.

Правильный пятиугольник

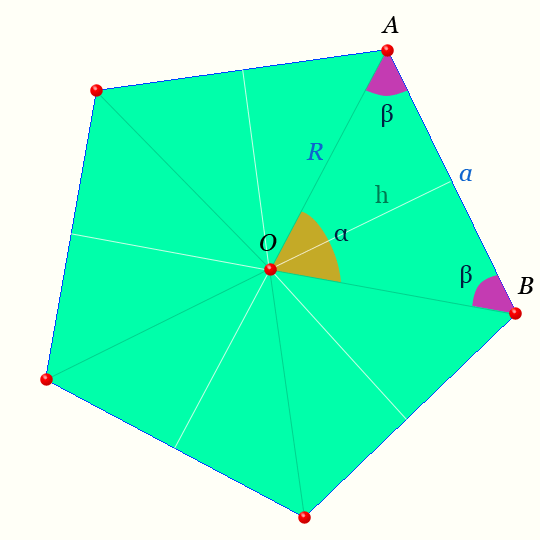
Центр правильного пятиугольника — на рисунке точка O равноудалена от вершин.

Светлая линия обозначающая высоту треугольника AOB : h называется — апофемой.

Отрезки OA, OB — радиусы правильного пятиугольника.

Обозначения на рисунке для правильного пятиугольника

n=5	число сторон и вершин правильного пятиугольника,	шт
α	центральный угол правильного пятиугольника,	радианы, °
β	половина внутреннего угла правильного пятиугольника,	радианы, °
γ	внутренний угол правильного пятиугольника,	радианы, °
a	сторона правильного пятиугольника,	м
R	радиусы правильного пятиугольника,	м
p	полупериметр правильного пятиугольника,	м
L	периметр правильного пятиугольника,	м
h	апофемы правильного пятиугольника,	м

Основные формулы для правильного пятиугольника

Периметр правильного пятиугольника

[ L = 5a ]

Полупериметр правильного пятиугольника

[ p = frac{5}{2}a ]

Центральный угол правильного пятиугольника в радианах

[ α = frac{2}{5}π ]

Центральный угол правильного пятиугольника в градусах

[ α = frac{360°}{5} = 72° ]

Половина внутреннего угла правильного пятиугольника в радианах

[ β = frac{3}{10}π ]

Половина внутреннего угла правильного пятиугольника в градусах

[ β = frac{3}{10}180° = 54° ]

Внутренний угол правильного пятиугольника в радианах

[ γ = 2β = frac{3}{5}π ]

Внутренний угол правильного пятиугольника в градусах

[ γ = frac{3}{5}180° = 108° ]

Площадь правильного пятиугольника

[ S = ph = frac{5}{2}ha ]

Или учитывая формулу Площади правильного пятиугольника получим

[ S = frac{5}{2} a sqrt{Big(frac{a}{2 sin(π/5)}Big)^2-frac{a^2}{4}} ]

Отсюда получим апофему правильного пятиугольника

[ h = sqrt{Big(frac{a}{2 sin(π/5)}Big)^2-frac{a^2}{4}} ]

Правильный пятиугольник	стр. 269

Источник

По теореме о сумме углов выпуклого многоугольника, сумма углов правильного пятиугольника равна 180º(5-2)=540º.

Так как все углы правильного n-угольника равны между собой, каждый внутренний угол правильного пятиугольника равен 540º:5=108º (в частности, ∠A₂A₁A₅=108º).

Сумма внешних углов многоугольника, взятых по одному при каждой вершине, равна 360º. Поскольку все внешние углы правильного пятиугольника равны между собой, градусная мера каждого, например, угла 1, равна

∠1=360º:5=72º (можно было внешний угол искать как смежный с внутренним).

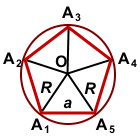
Каждый центральный угол правильного пятиугольника, например, угол A₁O A₂, равен

∠A₁O A₂=360º:5=72º.

Как и любой другой правильный многоугольник, правильный пятиугольник вписан в окружность и описан около окружности.

Соединив центр правильного многоугольника с его вершинами, получим пять равных равнобедренных треугольников.

Основанием каждого такого треугольника равно стороне 5-угольника, боковые стороны равны радиусу описанной окружности, угол при вершине — центральному углу 5-угольника.

В треугольнике A₁OA₅

$[{A_1}{A_5} = a,]$

$[{A_1}O = {A_5}O = R,]$

$[angle {A_1}O{A_5} = {72^o}.]$

Проведём из вершины высоту OF.

По свойству равнобедренного треугольника, OF является также медианой и биссектрисой треугольника A₁OA₅, то есть

$[{A_1}F = frac{1}{2}{A_1}{A_5} = frac{a}{2},]$

$[angle {A_1}OF = frac{1}{2}angle {A_1}O{A_2} = {36^o}.]$

OF — радиус вписанной в A₁A₂A₃A₄A₅окружности: OF=r.

Рассмотрим прямоугольный треугольник A₁OF.

По определению синуса,

$[sin angle {A_1}OF = frac{{{A_1}F}}{{{A_1}O}},]$

откуда

$[{A_1}O = frac{{{A_1}F}}{{sin angle {A_1}OF}},]$

$[R = frac{{frac{a}{2}}}{{sin {{36}^o}}} = frac{a}{{2sin {{36}^o}}}.]$

Так как

$[sin {36^o} = sqrt {frac{{5 - sqrt 5 }}{8}} ,]$

то

$[R = frac{a}{{2sqrt {frac{{5 - sqrt 5 }}{8}} }} = frac{{asqrt 8 }}{{2sqrt {5 - sqrt 5 } }} = frac{{a cdot 2sqrt 2 }}{{2sqrt {5 - sqrt 5 } }} = ]$

$[ = frac{{asqrt 2 }}{{sqrt {5 - sqrt 5 } }} = frac{{asqrt 2 cdot sqrt {5 + sqrt 5 } }}{{sqrt {5 - sqrt 5 } cdot sqrt {5 + sqrt 5 } }} = frac{{asqrt 2 cdot sqrt {5 + sqrt 5 } }}{{sqrt {{5^2} - {{(sqrt 5 )}^2}} }} = ]$

$[ = frac{{asqrt 2 cdot sqrt {5 + sqrt 5 } }}{{sqrt {20} }} = frac{{asqrt 2 cdot sqrt {5 + sqrt 5 } }}{{2sqrt 5 }} = ]$

$[ = frac{{asqrt 2 cdotsqrt {5 + sqrt 5 } cdotsqrt 5 }}{{2sqrt 5 cdotsqrt 5 }} = frac{{asqrt {50 + 10sqrt 5 } }}{{10}}.]$

Таким образом, формула радиуса описанной около правильного пятиугольника окружности —

$[R = frac{{asqrt {50 + 10sqrt 5 } }}{{10}}.]$

По определению котангенса,

$[ctgangle {A_1}OF = frac{{OF}}{{{A_1}F}},]$

$[OF = {A_1}F cdot {rm{ctg}}angle {A_1}OF = frac{a}{2} cdot {rm{ctg}}{36^o}.]$

Подставив значение котангенса 36°, получаем:

$[OF = frac{a}{2}cdotfrac{{sqrt {25 + 10sqrt 5 } }}{5}.]$

Итак, формула радиуса вписанной в правильный пятиугольник окружности

$[r = frac{{asqrt {25 + 10sqrt 5 } }}{{10}}.]$

Применив формулу

можно найти площадь правильного пятиугольника. Здесь

$[p = frac{{5a}}{2},r = frac{{asqrt {25 + 10sqrt 5 } }}{{10}},]$

следовательно, формула для нахождения площади A₁A₂A₃A₄A₅

$[S = frac{{5a}}{2}cdotfrac{{asqrt {25 + 10sqrt 5 } }}{{10}} = frac{{{a^2}sqrt {25 + 10sqrt 5 } }}{4}.]$

Все диагонали правильного пятиугольника равны.

Длина диагонали равна

$[d = frac{{a(sqrt 5 + 1)}}{2}.]$

Источник

Где найти формулы для правильного пятиугольника?

Правильный пятиугольник или пентагон (англ. regular pentagon) — это пятиугольник, все стороны и все углы которого равны между собой.

Формулы для правильного пятиугольника:

Величина α внутренних углов правильного пятиугольника (n=5) составляет:
α = (n – 2)/n · 180° = (3/5) · 180° = 108°.
Площадь правильного пятиугольника со стороной a рассчитывается по формуле:
S = (5/4) a² ctg(π/5) = (1/4) √5 √(5 + 2√5) a² ≈ 1,720 a².
Площадь правильного пятиугольника, вписанного в окружность радиуса R рассчитывается по формуле:
S = (5/2) R² sin(2π/5) = (5√2/8) √(5 + √5) R² ≈ 2,378 R².
Площадь правильного пятиугольника, описанного вокруг окружности радиуса r рассчитывается по формуле:
S = 5 r² tg(π/5) = 5 √(5 – 2√5) r² ≈ 3,633 r².
Высота правильного пятиугольника со стороной a составляет:
h = (1/2) a tg 72° = (1/2) √(5 + 2√5) a² = 1,539 a.
Отношение диагонали d правильного пятиугольника к его стороне a равно золотому сечению:
d/a = (1 + √5) / 2 ≈ 1,618.
Радиус r окружности, вписанной в правильный пятиугольник со стороной a составляет:
r = (1/10) √5 √(5 + 2√5) a ≈ 0,688 a.
Радиус R окружности, описанной вокруг правильного пятиугольника со стороной a составляет:
R = (1/10) √10 √(5 + √5) a ≈ 0,851 a.
Радиус R окружности, описанной вокруг правильного пятиугольника, можно найти по радиусу r вписанной в него окружности по формуле:
R = (√5 – 1) r ≈ 1,236 r.

Факты о правильном пятиугольнике:

Правильный пятиугольник может быть построен с помощью циркуля и линейки, или вписыванием его в заданную окружность, или построением на основе заданной стороны. Впервые это построение описал Евклид в своих «Началах» около 300 года до н.э.
Все диагонали правильного пятиугольника равны между собой. Вместе они образуют пятиконечную звезду, называемую также пентаграммой. Отношение длины диагонали к длине стороны правильного пятиугольника равно золотому сечению.
Правильными пятиугольниками нельзя замостить плоскость без промежутков и наложений. Это наименьший по числу сторон правильный многоугольник, который обладает таким свойством.
Додекаэдр — единственный правильный многогранник, грани которого представляют собой правильные пятиугольники. Правильный пятиугольник — наибольший по числу сторон правильный многоугольник, из которых можно собрать правильный многогранник.
В природе не существует кристаллов с гранями в форме правильного пятиугольника. Однако, при формировании водяного льда на ровной поверхности меди при температурах 100—140 K на поверхности сначала возникают цепочки молекул шириной около 1 нм пентагональной структуры.
Правильный пятиугольник можно получить, завязав узлом полоску бумаги, а затем сплющив узел.
Пентагоном называют министерство обороны США, поскольку оно размещается в здании, имеющем в плане форму правильного пятиугольника (пентагона).

Источники:

ru.wikipedia.org — Википедия: Правильный пятиугольник
wolframalpha.com — Wolfram|Alpha: regular pentagon (англ. яз.)

Дополнительно на Геноне:

Какой величины углы у правильного треугольника?
Что такое пентаграмма?
Сколько диагоналей у пятиугольника?
Кто такой Евклид?
Почему у здания Пентагона пять углов?

Последнее редактирование ответа: 20.10.2011

Оставить отзыв

Оставить отзыв

Вы можете написать свои замечания к ответу, предложения об улучшении или просто поблагодарить автора. Комментарий, после проверки, увидят автор и редактор ответа. Будьте, пожалуйста, вежливыми. Спасибо!

Если Вы хотите получить уведомление об
исправлении ответа укажите свой e-mail:

Неправильный формат адреса электронной почты

Похожие вопросы

Сколько существует правильных многогранников?
Каково определение правильного многогранника?
Как использовать уровни коррекции Фибоначчи?
Где найти развертки правильных многогранников?
Что такое правильный многогранник?
Под каким углом пересекаются диагонали октаэдра?
Что такое диагональ?
Какой угол между диагоналями куба?
Сколько диагоналей у 12-угольника, 24-угольника?
Сколько диагоналей у многоугольника?

В соответствии с пользовательским соглашением администрация не несет ответственности за содержание материалов, которые размещают пользователи. Для урегулирования спорных вопросов и претензий Вы можете связаться с администрацией сайта genon.ru.
Размещенные на сайте материалы могут содержать информацию, предназначенную для пользователей старше 18 лет, согласно Федерального закона №436-ФЗ от 29.12.2010 года «О защите детей от информации, причиняющей вред их здоровью и развитию». Обращение к пользователям 18+.

Источник

Обучайтесь и развивайтесь всесторонне вместе с нами, делитесь знаниями и накопленным опытом, расширяйте границы знаний и ваших умений.

поделиться знаниями или
запомнить страничку

Все категории
экономические
43,662
гуманитарные
33,654
юридические
17,917
школьный раздел
611,978
разное
16,905

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Источник

Если ты в девятом классе, то формула нахождения угла правильного n-угольника = (180°(n-2)):n ; где а — угол правильного n-угольника, n — количество сторон.

Тоесть, подставив в формулу известные нам значения, получаем :

а = (180°(5-2)):5

а = 108°.

Если ты в восьмом классе, то формула почти такая же. Сумму всех углов делишь на количество сторон. Тоже самое. Ответ один и тот же получится.

Ответ: 108°.

Источник