Правила нахождения
числа по доле и доли по числу.
·
Чтобы
найти число по доле, нужно одну его долю умножить на количество
долей.
1/3 часть=8
Число — ?
Решение: 8·3=24
·
Чтобы
найти долю числа, нужно число разделить на количество равных
долей.
Число-20
1/4 — ?
Решение: 20:4=5
·
Чтобы
найти дробь(часть) от числа, нужно число разделить на знаменатель
и
умножить на числитель дроби.
5/7 — (5- числитель
7-знаменатель)
Число-49
Найти — 5/7
Решение: 49:7·5=35
Ответ: 5/7=35.
Правила
нахождения числа по доле и доли по числу.
·
Чтобы
найти число по доле, нужно одну его долю умножить на количество
долей.
1/3 часть=8
Число — ?
Решение: 8·3=24
·
Чтобы
найти долю числа, нужно число разделить на количество равных
долей.
Число-20
1/4 — ?
Решение: 20:4=5
·
Чтобы
найти дробь(часть) от числа, нужно число разделить на знаменатель
и
умножить на числитель дроби.
5/7 — (5- числитель
7-знаменатель)
Число-49
Найти — 5/7
Решение: 49:7·5=35
Ответ: 5/7=35.
- Главная
- Справочники
- Справочник по математике для начальной школы
- Доли
В этой теме мы познакомимся с образованием долей, научимся их записывать, читать и сравнивать.
Доли появляются, если нам нужно разделить ЦЕЛОЕ на равные части, например, яблоко:

На доли можно разделить окружность:
или прямоугольник:
Доля – это каждая из равных частей целого.
Название доли зависит от того, на сколько частей разделили целое.
Половина
Половина — это самая известная доля.
Например, яблоко разделили на две части, получилась половина яблока.

Любую долю можно записать как деление двух чисел. Мы разделили целое на две доли, каждую из долей мы можем записать в виде дроби, в которой черта обозначает знак деления.
Прочитать такую долю можно как ОДНА ВТОРАЯ.
Треть
Если целое разделили на три части, то получили ТРЕТЬ, третью часть.
Прочитать такую долю можно как ОДНА ТРЕТЬЯ.
Четверть
Если целое разделили на четыре части, получили ЧЕТВЕРТЬ, четвёртую часть.
Прочитать такую долю можно как ОДНА ЧЕТВЁРТАЯ.
Запись и чтение долей



Сравнение долей
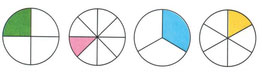
Для примера сравним две доли: одну шестую и одну третью.
Какая доля больше? Рассмотри рисунок:
Красным закрашены названные доли. Посмотри, какая доля больше? Одна третья.
Значит, одна третья часть БОЛЬШЕ, чем одна шестая часть.
Сравним ещё две доли: одну восьмую и одну четвёртую.
Какая доля больше? Рассмотри рисунок:
Красным закрашены названные доли. Посмотри, какая доля больше? Одна четвёртая.
Значит, одна четвёртая часть БОЛЬШЕ, чем одна восьмая часть.
Вывод: Чем долей больше, тем одна её часть МЕНЬШЕ.
Правило встречается в следующих упражнениях:
3 класс
Страница 94,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 106,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 66,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 68,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 38. ПР 5. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 45. Тест 2. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 27,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 78,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 82,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 46. Урок 17,
Петерсон, Учебник, часть 1
4 класс
Страница 65,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 82,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 88,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 52. Тест 2. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 84. Тест 3. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 59,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 62,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 34,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 51,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 76,
Моро, Волкова, Рабочая тетрадь, часть 2
5 класс
Задание 216,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 82,
Мерзляк, Полонский, Якир, Учебник
Номер 83,
Мерзляк, Полонский, Якир, Учебник
Номер 2,
Мерзляк, Полонский, Якир, Учебник
Математика, 3 класс
Урок №34. Задачи на нахождение доли числа и числа по его доле.
Перечень вопросов, рассматриваемых в теме:
— как решать задачи на нахождение доли числа и числа по его доли?
— какие наиболее эффективные способы используются для нахождения доли величины и величины по ее доле?
— каким образом сравнивать разные доли одной и той же величины?
Глоссарий по теме:
Задача – это текст, содержащий численные компоненты
Доля – это каждая из равных частей единицы.
Условие – это часть задачи, в которой рассказывается о том, что неизвестно, содержит числовые данные.
Вопрос – это часть задачи, в которой сообщается о том, что нужно узнать.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 97.
2. Волкова С. И. Проверочные работы 3 класс. Издательство «Просвещение» 2017, с. 38-39.
3. Волкова С. И. Тесты 3 класс. Издательство «Просвещение»2017, с. 20-27.
4.Рудницкая В. Н. Тесты по математике 3 класс. М.: Издательство «Экзамен», 2016 с. 44-47.
Теоретический материал для самостоятельного изучения
Появление долей связывается с практическими потребностями: задачи, где нужно производить деление на части, были очень распространены. Кроме того, в жизни человеку приходилось не только считать предметы, но и измерять величины. Люди встретились с измерениями длин, площадей земельных участков, объемов, массы тел. При этом случалось, что единица измерения не укладывалась целое число раз в измеряемой величине. Например, измеряя длину участка шагами, человек встречался с таким явлением: в длине укладывалось десять шагов, и оставался остаток меньше одного шага.
Таким образом, во всех цивилизациях понятие доли возникло из процесса дробления целого на равные части. Русский термин «дробь», как и его аналоги в других языках, происходит от лат. fractura, который, в свою очередь, является переводом арабского термина с тем же значением: ломать, раздроблять.
Доля это каждая из равных частей единицы. Название доли зависит от того, на сколько равных частей разделили единицу. Разделили на две части название доли «половина», на три — «треть», на четыре — «четверть».
Использование знаний о долях применяется для решения задач.
Рассмотрим рисунок.
12 см
1) Полоску длиной 12 см разделили на 2 части. Одна часть, или ее называют одна вторая, составляет 6 см. Составим выражение:
12 : 2 = 6 см
2) Полоску этой же длины разделим на 3 части. Одна третья составляет 4 см.
12 см
12 : 3 = 4 см
3) Найдем одну шестую полоски. Одна шестая составляет 2 см.
12 см
12 : 6 = 2 см
Вывод: чтобы найти долю от числа, надо число разделить на количество частей (долей).
Рассмотрим рисунок.
1) Длина второй части отрезка составляет 8 см. Чему равна длина всего отрезка?
? см
8 ∙ 2 = 16 см
По 8 см возьмем 2 раза получим 16 см.
2) Длина четвертой части отрезка составляет 4 см. Найдем длину всего отрезка.
? см
4 ∙ 4 = 16 см
4 умножим на 4, получим 16 см.
3) Найдем длину отрезка, если восьмая часть составляет 2 см.
? см
2 ∙ 8 = 16 см
Вывод: чтобы найти число по его доле, надо долю этого числа умножить на число долей.
Решим задачу.
6 листов составляют половину тетради. Сколько всего листов в тетради? Половин в тетради может быть только две. Если в каждой по 6 листов, то вся тетрадь содержит: 6 ∙ 2 = 12 (листов).
Вывод: чтобы найти число по его доле, надо долю этого числа умножить на число долей.
Решим задачу.
Чему равна треть суток?
В сутках 24 часа. Чтобы найти треть суток, нужно 24:4=8 (часов).
Вывод: чтобы найти долю от числа, надо число разделить на количество частей (долей)
Задания тренировочного модуля:
1. Выберите верный ответ.
В мотке 24 м кружев. Отрезали восьмую часть мотка. Сколько кружев отрезали?
16 м
32 м
3 м
4м
Правильный ответ:
3м
2. Соотнесите ответы.
Длина коридора 12 м. Мальчик прошел по коридору 4 м. Какую часть коридора он прошёл?
Правильный ответ:
План урока:
Понятие доли
Окружность. Круг
Диаметр круга
Единицы времени
Здравствуйте, ребята. Меня зовут Игрек, я самый умный фиксик.
Рад я встрече с вами снова.
Вы к открытиям готовы?
Урок математики начнем,
Доли разберем.
На уроке вы узнаете новые математические понятия.
Приготовьте тетрадь, ручку, простой карандаш, линейку, циркуль.
Понятие доли
Вы когда-нибудь заглядывали в тетради к старшеклассникам? Смотрите, какой у меня пример.
Видите сложение, вычитание, умножение? Знаки этих действий известны: плюс, минус, точка. Деление же в примере обозначено горизонтальной чертой.На рисунке она выделена красным цветом. Я расскажу, когда в математике используют черту.
Мы умеем делить несколько предметов, но часто деление нужно, чтобы раздробить одно число на равные части — доли от целой величины.
Один разделить на два — это одна вторая. Что же это такое?
В жизни вы часто так делали. Например, один апельсин делили с другом: брали нож и разрезали его пополам.
Каждый из вас получал половину или одну долю.
На лесной полянке собралось девять друзей, апельсин делили на всех. Рассмотрите рисунок. Как называется каждая часть фрукта?
Совершенно верно, это долька. Апельсин поделили на 9 одинаковых долек.Каждая 1 долька апельсина — это одна из девяти равных долей целого фрукта.
Вы теперь поняли, ребята, что в жизни человеку приходится не только пересчитывать предметы, но и делить (дробить) целое на части, вот так появилось в математике понятие доли и дроби.
Знак доли (дроби) обозначают дробной горизонтальной или наклонной чертой. Например, так — 1/9 (одна девятая). Запись придумали арабы в 16 веке.
Доли называют по количеству частей раздробленного одного предмета:
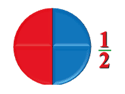
- Разделите, например, яблоко на две равные части, у вас получится название доли «половина» или 1/2 (одна вторая)
- Разрежьте яблоко на три части. Один кусок — это «треть» — 1/3 (одна третья)
- Разломите на четыре доли — «четверть» — 1/4 (одна четвертая)
Знание о долях помогает решить задачи.
Запомните правило по математике нахождения доли.Чтобы найти долю от числа надо число разделить на эту долю. В дроби число, на которое делят, записано под чертой и называется знаменателем. То число, которое надо разделить, пишут над чертой. Это числитель.
Задание 1
Найдите пятую долю от числа 25. Это значит, что надо выполнить действие деления.
Привычный пример 25 : 5 можно записать вот таким образом:
Или так — 25/5. 25 – это числитель, а 5 — знаменатель.
25: 5 = 5
Ответ: одна пятая доля от числа 25 равна пяти.
Задание 2
Чему равна 1/4 доля от полоски длинной 16 см?
Полоску согните пополам, ещё раз пополам. Разверните. На сколько долей линией сгиба разделили полоску? Правильно, на 4.
Закрасьте одну такую долю.
Какую долю вы закрасили? (одну четвёртую)
16 : 4 = 4(см)
Ответ: длина одной четвертой доли полоски составляет 4 см.
Задание 3
Решите задачи на понятие доли. Рассмотрите рисунки. Какая доля каждой фигуры закрашена серым цветом?
Рассуждаем так.
На рисунке 1 отрезок разделили на 7 частей.Значит, закрашена одна седьмая (1/7) доля фигуры.
Проверьте:
На следующих рисунках заштрихована 1/16 доля квадрата, 1/6 доля шестиугольника, 1/5 доля круга.
Чтобы разобрать понятие массовой доли, представьте себе килограмм яблок (1000 г), который мама купила своим трем детям.
Из этого килограмма самому младшему ребенку досталась половина всех яблок (несправедливо, конечно!). Старшему — лишь 200 г, а среднему — 300 г.
Значит, массовая доля яблок у младшего ребенка составит половину, или одну вторую (1/2) массовую долю.
У старшего ребенка будет:
1000 : 200 = 5 — одна пятая (1/5) массовая доля
Далее рассуждаем так:
Младшему ребенку дали половину яблок.
1000 : 2 = 500(г)
Яблоки разделили между детьми по 500г, 200г и 300г. Вы знаете, что 500 — это 5 сотен, 200 — 2 сотни, 300 — 3 сотни.
На сколько сотен разделили все яблоки?
5 сотен + 2 сотни + 3 сотни = 10 сотен.
Сколько граммов будет в одной десятой доле?
1000 : 10 = 100 (г) в одной десятой доле
У среднего ребенка 300 г. Во сколько раз больше, чем 100 г?
300 : 100 = 3
В три раза. Значит, у среднего ребенка будет не одна, а три десятых массовых долей 3/10.
Ребята, вы молодцы. Верное решение.
Окружность. Круг
А сейчас познакомимся с самой совершенной фигурой, как считал древнегреческий математик Пифагор. Ответьте на вопрос: «Какие известные вам геометрические плоские фигуры не содержат углов?»
Правильно, круги, а еще окружности.
Совершенная форма этой геометрической фигуры привлекает внимание художников, дизайнеров, архитекторов. Они используют её в своих изделиях для украшения.
Ограда на набережной реки Невы в Санкт-Петербурге
Назовите предметы из обычной жизни, которые по форме похожи на эти фигуры.Правильно, круглые очки. Вы очень внимательные ребята.
Посмотрите на рисунок. Назовите окружности и круги.
Проверьте себя:
Но как начертить такие ровные окружности? Приглашаю на помощь лучшего друга.
Эх, циркач, удалой.
Чертит круг одной ногой,
А иглой — проткнет бумагу,
Он воткнется — и ни шагу.
Знакомьтесь, ребята, к нам пришел новый житель страны Геометрии – чертежный инструмент. Он поможет разобраться, как изобразить круг.
Привет, я циркуль. Мое имя произошло от старинного латинского слова «циркулюс», что означает круг.
Давайте потренируемся чертить циркулем:
- В тетради или альбоме поставьте точку карандашом. Это центр окружности.
- Аккуратно раздвиньте «ножки» циркуля, например, на 30 мм. Измерьте расстояние между грифелем и иголкой по линейке.
- Крепко воткните иголку циркуля в центр, а другой «ножкой», вращая головку циркуля большим, указательным и средним пальцем, начертите грифелем замкнутую линию.
Источник
Линию, нарисованную грифелем циркуля, называют окружностью.
Точки на окружности А и В расположены от центра на равном расстоянии. Их соединяет отрезки ОА и ОВ – называются радиусами окружности.
Продлите по линейке отрезок ВО поперек всей окружности. Вы начертили диаметр окружности— отрезок ВС. Он прошел через центр и соединил 2 точки на окружности В и С.
Как вы думаете, сколько диаметров можно провести в одной окружности?
Совершенно верно — сколько угодно, как говорят математики — бесконечное число.
Посмотрите на колесо от велосипеда.
Втулка — это центр, а спицы напоминают радиусы и диаметры.
Если величину диаметра умножить на 3, мы получим примерную длину окружности. Точную формулу вычисления вы узнаете в 7 классе на уроках геометрии, а также, что такое вписанная и описанная окружности.
А сейчас возьмите альбомный лист, начертите окружность и по этой границе аккуратно вырежьте фигуру. Её можно закрасить любым цветом, например, синим, как на рисунке. Это круг — часть плоскости, ограниченная окружностью.
У круга есть площадь. Окружность вырезать невозможно, потому что это просто замкнутая кривая линия вокруг круга — его граница.
Решите задачу
На клетчатой бумаге нарисован круг, площадь которого равна 40. Найдите площадь закрашенной части фигуры.
Рассуждайте так: на рисунке закрашена четвертая доля фигуры. Значит надо выполнить деление.
40 : 4 = 10
Ответ: площадь равна 10
Диаметр круга
Нарисуйте две окружности с радиусом 3 см. Фигуру справа закрасьте желтым карандашом. Получится круг.В обеих фигурах проведите диаметры и радиусы.
Измерьте диаметр окружности и диаметр круга. Сколько у вас получилось?
Правильно, 6 см. Радиус круга равен 3 см. Он два раза помещается в диаметре, значит это половина или одна вторая доля от целого.
6 : 3 = 2
Радиус круга равен половине или 1/2 диаметра.
Путем несложных математических вычислений можно понять, что диаметр в 2 раза больше радиуса.
АВ = АО + ОВ
Решите задачу
Третьеклассник вырезал круг радиусом 50 мм. Сколько сантиметров в его диаметре?
Решение:
50 ∙ 2 = 100 (мм)
100 мм = 10 см
Ответ: диаметр круга равен 10 см.
Вы хорошо справились.
Нам пора провести зарядку для глаз, чтобы сберечь зрение.
Физкультминутка
- Зажмурьтесь, потом откройте глаза шире. Лоб остается гладким без морщин. Повторите упражнение три раза.
- Теперь подойдите к окну, посмотрите вдаль. Внимательно вглядитесь, потом попытайтесь увидеть кончик носа. Получилось? Тогда повторяйте упражнение четыре раза. Не спешите.
- Медленно делайте круговые движения снизу вверх, направо, вниз, влево глазами, как будто вращаете большое колесо, 2 раза в одну сторону. Теперь обратно. Не двигайте головой, следите только глазами.
- Найдите взглядом верхний правый угол комнаты, хлопните в ладоши, опустите взор на кончик носа.Смотрите вверхний левый угол, далее на кончик носа. Повторите пять раз.
- Прикройте глаза, 10 секунд постойте спокойно, ровно неглубоко подышите.
Ребята, я тоже люблю укреплять здоровье. Вчера пошел на хоккейную площадку. Но вместо игры попросили начертить круги больших диаметров, чтобы обновить разметку поля.
Задача 1
Как начертить без циркуля круг для вбрасывания шайбы диаметром 300 мм?
Решение:
300 мм = 30 см
Радиус круга равен половине диаметра.
30 : 2 = 15 (см)
Возьмите гвоздь, карандаш, нитку длиной 15 см. Начертите окружность как показано на рисунке.
Задача 2
Из центра поля нужно нарисовать круг синей краской диаметром 9 метров.
Рассуждаем: диаметр круга 9 м, значит радиус — половина.
9 м = 900 см
900 : 2 = 450 (см) = 4 м 50 см.
На центральную точку встает друг Гвоздик, крепко держит конец веревки, а к другому концу нужно закрепить кисть с краской. Фиксик Игрек на коньках едет вокруг Гвоздика, рисует линию окружности. Главное — туго натягивать веревку, чтобы радиус в 450 см не уменьшался. Вот такая разметка получается в центре хоккейной площадки:
После работы пора поиграть в хоккей.
Похожим способом можно начертить 7 окружностей больших диаметров на картоне для новогодней елки. Посмотрите на рисунок, какая красавица получается.
Поделку делайте вместе с родителями. Для больших кругов возьмите карандаш, гвоздик и нитку. Маленькие — нарисуйте циркулем. Понадобится начертить всего 11 окружностей для десяти обручей елки.
Задача 3
Диаметр первого нижнего круга елки равен 80 см, а каждого следующего уменьшается на 8 см. Найдите, чему равны диаметры следующих кругов.
Какой диаметр маленького круга наверху у елки?
Для решения задачи вспомните таблицу умножения на 8.
Обратный отсчет диаметров круга по таблице 80, 72, 64, 56, 48, 40, 32, 24, 16, 8.
Диаметр маленького круга 8 см.
Вы отлично выполнили вычисления.
Теперь отгадайте новую загадку. Что идет, не двигаясь с места? (Правильно, это время.)
Единицы времени
Каждый человек хочет понять время. Оно нам нужно, потому что мы живем по режиму, а магазины, библиотеки, вокзалы — по расписанию. Определенное количество дел намечаем сделать в единицу времени.
Давайте познакомимся с единицами измерения времени.
Земля обращается вокруг Солнца за 365 суток. Это год. Один раз в 4 года он увеличивается на сутки, и называется високосным.
С глубокой древности круг считается символом годовых сезонных циклов: зимы, весны, лета и осени. Рассмотрите рисунок годового круга: он поделен на 4 доли — четыре времени года.
Источник
Единица величины каждого времени года делится на 3 месяца.
В году 3 ∙ 4 = 12 месяцев. Месяц — единица времени, за которую Луна обходит планету Земля вокруг.
В каждом месяце 30 или 31, а в феврале 28 или 29 суток.
Исторически основной единицей для времени были сутки (часто говорят «день»). За одни сутки Земля поворачивается вокруг своей оси.
В результате деления суток на меньшие временные интервалы возникли часы, минуты и секунды. Сутки – единица времени, равная 24 часам. Один час — это 60 минут. Минута состоит из 60 секунд.
Выполните задания
1. Выразите время в указанных единицах измерения
|
8 ч 25 мин. = … мин. |
95 мин. = … ч … мин. |
|
2 мин. 14 сек. = … сек. |
187 сек. = … мин. … сек. |
Решение:
1 час = 60 мин. Значит, в восьми часах будет в 8 раз больше. Нужно выполнить умножение.
60 ∙ 8 = 480 (мин.)
В 8 часах — 480 минут да еще 25 мин. Действие сложения.
480 + 25 = 505 (мин.)
Ответ: 8 ч 25 мин. = 505 мин.
Дальше решайте аналогично:
2 мин. 14 сек. = 60 ∙ 2 + 14 = 134 сек.
95 мин. = 1 ч 35 мин.
187 сек. = 3 ч. 7 сек.
2. Выберите единицы времени, которые расположены в порядке возрастания
а) час, минута, секунда
б) секунда, минута, час
в) минута, час, секунда
Проверьте себя.
Правильный ответ — б.
3. Автомобиль до Москвы едет 2 суток, а обратно 48 часов. Почему такая разница?
Проверьте себя.
2 сут. = 48 ч. Разницы нет.
Наш урок подходит к концу. Я надеюсь, что вы будете ценить свое время, не будете терять его зря.
Я с вами прощаюсь, а вы проверьте свои знания.
В материалах урока использованы кадры из м/с «Фиксики», 2010
Содержание:
- § 1 Нахождение числа по его доле
- § 2 Нахождение числа по его части
- § 3 Решение задачи по теме урока
- § 4 Краткие итоги урока
§ 1 Нахождение числа по его доле
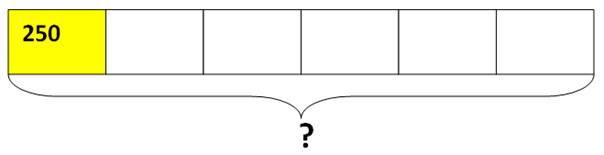
Рассмотрим такую задачу. Конфеты разложили в 6 пакетов. Каждый пакет весит 250 грамм. Сколько грамм весят все конфеты?
Из условия задачи известно, что целое разделили на 6 равных долей. Одна доля 1/6 весит 250 грамм. Чтобы найти вес всех конфет, необходимо вес 250 одной доли умножить на количество долей 6:
250 · 6 = 1500 грамм весят все конфеты.
Можем сделать вывод:
Чтобы найти неизвестное число А, можно его долю B =1/n умножить на n:A = B · n.
§ 2 Нахождение числа по его части
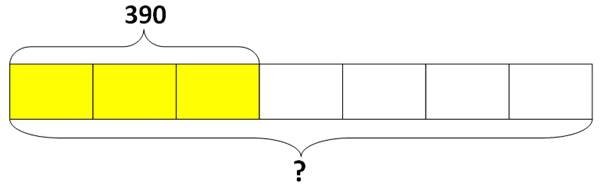
Рассмотрим еще одну задачу. Конфеты разложили в 7 пакетов. 3/7 всех конфет весят 390 грамм. Сколько грамм весят все конфеты?
Из условия задачи известно, что целое разделили на 7 равных долей. 3 доли весят 390 грамм. 3/7 = 390. Для того чтобы найти вес всех конфет, необходимо в первую очередь найти вес одной доли 390 : 3, а затем умножить вес одной доли на количество всех долей 390 : 3 · 7. Или 390 разделить на 3 числитель дроби 3/7 и умножить на ее знаменатель 7,
390 : 3 · 7 = 910 грамм весят все конфеты.
Можно сделать вывод:
Чтобы найти число А по его части B =m/n, можно эту часть В разделить на числитель m и умножить на знаменатель n:A = B : m · n.
§ 3 Решение задачи по теме урока
Опираясь на полученные знания, решим задачу.
Задача:
Масса яблок составляет 25% от массы яблочного пирога и равна 225 грамм. Чему равна масса всего пирога?
Решение:
25% = 25/100 = 225 грамм,
100% (весь пирог) = неизвестное число = ? грамм.
Значит, по правилу A = B : m · n масса всего пирога равна
225 : 25 · 100 = 900 грамм.
§ 4 Краткие итоги урока
Подведем итоги нашего урока:
— Для того чтобы найти неизвестное число А, можно его долю B =1/n умножить на n:A = B · n.
— Для того чтобы найти число А по его части B = m/n, можно эту часть В разделить на числитель m и умножить на знаменатель n:A = B : m · n.
Список использованной литературы:
- Петерсон Л.Г. Математика. 4 класс. Часть 1. / Л.Г. Петерсон. – М.: Ювента, 2014. – 96 с.: ил.
- Математика. 4 класс. Методические рекомендации к учебнику математики «Учусь учиться» для 4 класса. / Л.Г. Петерсон . – М.: Ювента, 2014. – 280 с.: ил.
- Зак С.М. Все задания к учебнику математики для 4 класса Л.Г. Петерсон и комплекту самостоятельных и контрольных работ. ФГОС. – М.: ЮНВЕС, 2014.
- CD-ROM. Математика. 4 класс. Сценарии уроков к учебнику к 1 части Петерсон Л.Г. – М.: Ювент, 2013.