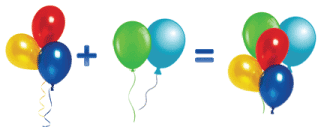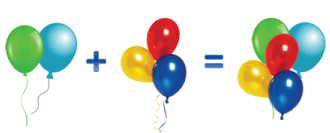1. Как
найти неизвестное слагаемое?
— Чтобы
найти первое слагаемое, надо из суммы вычесть второе слагаемое.
— Чтобы
найти второе слагаемое, надо из суммы вычесть первое слагаемое.
2. Как
найти неизвестное уменьшаемое?
Чтобы
найти уменьшаемое, надо к разности прибавить вычитаемое.
3. Как
найти неизвестное вычитаемое?
Чтобы
найти вычитаемое, надо из уменьшаемого вычесть разность.
1. Как
найти неизвестное слагаемое?
— Чтобы
найти первое слагаемое, надо из суммы вычесть второе слагаемое.
— Чтобы
найти второе слагаемое, надо из суммы вычесть первое слагаемое.
2. Как
найти неизвестное уменьшаемое?
Чтобы
найти уменьшаемое, надо к разности прибавить вычитаемое.
3. Как
найти неизвестное вычитаемое?
Чтобы
найти вычитаемое, надо из уменьшаемого вычесть разность.
1. Как
найти неизвестное слагаемое?
— Чтобы
найти первое слагаемое, надо из суммы вычесть второе слагаемое.
— Чтобы
найти второе слагаемое, надо из суммы вычесть первое слагаемое.
2. Как
найти неизвестное уменьшаемое?
Чтобы
найти уменьшаемое, надо к разности прибавить вычитаемое.
3. Как
найти неизвестное вычитаемое?
Чтобы
найти вычитаемое, надо из уменьшаемого вычесть разность.
1. Как
найти неизвестное слагаемое?
— Чтобы
найти первое слагаемое, надо из суммы вычесть второе слагаемое.
— Чтобы
найти второе слагаемое, надо из суммы вычесть первое слагаемое.
2. Как
найти неизвестное уменьшаемое?
Чтобы
найти уменьшаемое, надо к разности прибавить вычитаемое.
3. Как
найти неизвестное вычитаемое?
Чтобы
найти вычитаемое, надо из уменьшаемого вычесть разность.
1. Как
найти неизвестное слагаемое?
— Чтобы
найти первое слагаемое, надо из суммы вычесть второе слагаемое.
— Чтобы
найти второе слагаемое, надо из суммы вычесть первое слагаемое.
2. Как
найти неизвестное уменьшаемое?
Чтобы
найти уменьшаемое, надо к разности прибавить вычитаемое.
3. Как
найти неизвестное вычитаемое?
Чтобы
найти вычитаемое, надо из уменьшаемого вычесть разность.
1. Как
найти неизвестное слагаемое?
— Чтобы
найти первое слагаемое, надо из суммы вычесть второе слагаемое.
— Чтобы
найти второе слагаемое, надо из суммы вычесть первое слагаемое.
2. Как
найти неизвестное уменьшаемое?
Чтобы
найти уменьшаемое, надо к разности прибавить вычитаемое.
3. Как
найти неизвестное вычитаемое?
Чтобы
найти вычитаемое, надо из уменьшаемого вычесть разность.
1. Как
найти неизвестное слагаемое?
— Чтобы
найти первое слагаемое, надо из суммы вычесть второе слагаемое.
— Чтобы
найти второе слагаемое, надо из суммы вычесть первое слагаемое.
2. Как
найти неизвестное уменьшаемое?
Чтобы найти
уменьшаемое, надо к разности прибавить вычитаемое.
3. Как
найти неизвестное вычитаемое?
Чтобы
найти вычитаемое, надо из уменьшаемого вычесть разность.
1. Как
найти неизвестное слагаемое?
— Чтобы
найти первое слагаемое, надо из суммы вычесть второе слагаемое.
— Чтобы
найти второе слагаемое, надо из суммы вычесть первое слагаемое.
2. Как
найти неизвестное уменьшаемое?
Чтобы
найти уменьшаемое, надо к разности прибавить вычитаемое.
3. Как
найти неизвестное вычитаемое?
Чтобы
найти вычитаемое, надо из уменьшаемого вычесть разность.
- Главная
- Справочники
- Справочник по математике для начальной школы
- Сложение
Познакомимся со сложением.
Рассмотрим числовой ряд.
Числа идут слева направо, по порядку, как при счёте.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Посмотри на числовой ряд, по которому идёт заяц.
Какое действие выполняет заяц?
Прибавляет число 2.
К какому числу он прибавляет число 2?
К числу 4.
Наш зайчик стоит на числе 4 и думает, в какую сторону ему идти.
Подскажи ему.
В какую сторону пойдёт зайчик?
Вправо, потому что у него на табличке знак +.
Сколько шагов вправо сделает заяц?
2, потому что ему нужно прибавить 2.
На каком делении остановится заяц?
На числе 6.
Когда прибавляем, становится больше.
Чем правее, тем числа больше.
4 + 2 = 6
Рассмотрим еще один пример.
Какое действие выполняет заяц?
Прибавляет число 5.
К какому числу он прибавляет число 5?
К числу 3. Мы поставили зайчика на число 3.
В какую сторону он пойдёт?
Вправо, потому что у него на табличке знак +.
Сколько шагов вправо сделает зайчик? 5.
На каком делении он остановится? На числе 8.
3 + 5 = 8
Как называются числа при сложении?
Первое слагаемое и второе слагаемое.
Результат называется суммой.
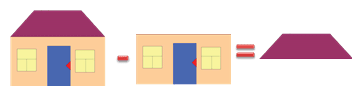
Рассмотрите рисунок.
Представь части домика как слагаемые и сумму.
Как найти неизвестное слагаемое
Второе слагаемое неизвестно.
Рассмотри рисунок и догадайся, как его можно найти.
Нужно из суммы вычесть первое слагаемое.
Рассмотри рисунок.
Неизвестно первое слагаемое.
Как его можно найти?
Нужно из суммы вычесть второе слагаемое.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Проверка сложения
Если из суммы двух слагаемых, вычесть одно из слагаемых, то получится второе слагаемое.
8 + 4 = 12
12 — 4 = 8
12 — 8 = 4
Именно эта связь между суммой и слагаемыми используют для проверки вычислений.
Например, 35 + 7 = 42.
Правильно ли произведено вычисление? Можно проверить так:
42 — 7 = 35, мы из суммы вычли одно из слагаемых и получили ВТОРОЕ слагаемое. Значит, вычисление произведено верно и пример решен правильно.
Перестановка слагаемых
Сделаем запись к рисунку.
3 + 2 = 5
Сделаем запись к этому рисунку.
2 + 3 = 5
Теперь рассмотрим обе записи к рисункам:
3 + 2 = 5
3 — первое слагаемое
2 — второе слагаемое
5 сумма
2 + 3 = 5
2 — первое слагаемое
3 — второе слагаемое
5 — сумма
Мы заметили, что сумма в обеих записях одинаковая, хотя слагаемые мы записывали по-разному.
Это переместительный закон сложения, который гласит:
От перестановки мест слагаемых сумма не меняется.
Сочетательный закон сложения
Рассмотрим пример: (37 + 29) + 1 = …. (читаем: к сумме чисел 37 и 29 прибавить
1) Какие числа удобно сложить сначала, чтобы получился удобный способ? Числа 29 и 1.
Сумму чисел 29 и 1 возьмем в скобки.
37 + (29 + 1) = … (читаем: к 37 прибавить сумму чисел 29 и 1)
Решаем. Сначала выполним действие в скобках.
29 + 1 = 30
37 + 30 = 67, значит,
(37 + 29) + 1 = 67
Вывод: два соседних слагаемых можно заменить их суммой.
Советуем посмотреть:
Табличное сложение
Письменное сложение в столбик
Правило встречается в следующих упражнениях:
1 класс
Страница 57. Тест 2. Вариант 2,
Волкова, Проверочные работы
Страница 25,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 50,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 57,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 82,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 19,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 16. Урок 9,
Петерсон, Учебник, часть 2
Страница 57. Урок 29,
Петерсон, Учебник, часть 2
Страница 60. Урок 31,
Петерсон, Учебник, часть 3
Страница 84. Урок 43,
Петерсон, Учебник, часть 3
2 класс
Страница 4,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 81,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 84,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 69. Тест 1. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 77,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 7,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 40,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 3. Урок 1,
Петерсон, Учебник, часть 1
Страница 80. Дополнительные задачи,
Петерсон, Учебник, часть 1
Страница 32. Урок 12,
Петерсон, Учебник, часть 2
3 класс
Страница 8,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 79,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 41,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 11,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 43,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 48,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 49,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 31. Урок 14,
Петерсон, Учебник, часть 3
Страница 32. Урок 15,
Петерсон, Учебник, часть 3
Страница 69. Повторение,
Петерсон, Учебник, часть 3
4 класс
Страница 62,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 95,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 13. Тест 1. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 15. Тест 2. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 41. Тест 1. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 42. Тест 2. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 85. Тест 3. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 64,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 84,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 99,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
5 класс
Задание 219,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Способ найти 1 слагаемое
Разберём в качестве примера решение одного элементарного уравнения. Из чего оно состоит? Как правило, это сумма и два слагаемых, одно из которых известно, другое — нет. Преимущественно неизвестное слагаемое обозначается буквой «икс», прописью x.
Например, уравнение выглядит следующим образом: 3+x=8. Как его решить? Воспользуемся законами элементарной логики. У нас есть сумма двух чисел. Одно из них известно, а второе — нет. То есть для того, чтобы узнать неизвестное, необходимо из суммы вычесть известное слагаемое. Получаем результат: 8−3=5.
Конечно, взрослому человеку с рациональным и логическим мышлением это кажется простым и понятным. А как быть, если необходимо научить ребёнка нахождению слагаемого? Можно объяснить на простых и понятных примерах. Например, задать вопрос: У Димы было 3 рубля, и после того как Петя дал ему денег, у Димы стало 8 рублей. Сколько рублей ему дал Петя?
Самый простой пример — счёты на пальцах. Сначала можно показать ребёнку 3 пальца, а потом 8. После чего попросить его посчитать, сколько пальцев вы добавили. Главное — не пытаться всё объяснить сложными словами. Предложенные примеры буду более эффективными. Однако повторить правило нахождения неизвестного слагаемого не будет лишним. Оно формулируется следующим образом: чтобы найти неизвестное слагаемое, надо известное слагаемое вычесть из суммы.
После того как вы решили уравнение, рекомендуется сделать проверку, чтобы убедиться, что всё сделано правильно. Сложите получившийся результат неизвестного слагаемого с известным слагаемым. Если сумма совпадает с суммой, то решение правильное. В нашем случае проверка: 3+5=8.
Другие методы
Правило, которое позволяет быстро найти неизвестное слагаемое, довольно простое. Однако для того, чтобы облегчить его понимание, из него можно вывести правила, связанные с вычитанием.
Так, в примерах со сложением мы имеем два слагаемых и сумму: 3+5=8. Здесь 3 и 5 — слагаемые, а 8 — сумма. А в примерах с вычитанием мы имеем:
- Уменьшаемое.
- Вычитаемое.
- Разность.
Например, 7 — 4=3. В этом случае уменьшаемое — 7, вычитаемое — 3, а разность — 4. Уменьшаемое и вычитаемое также могут быть неизвестными. И крайне важно знать, как их вычислять.
Правила нахождения уменьшаемого
При поиске уменьшаемого уравнение может выглядеть следующим образом: x-2=4. Мы имеем разность — результат вычитания и число, которое вычитаем. Необходимо найти уменьшаемое — самое большое число в примере. Формулировка правила: чтобы найти неизвестное уменьшаемое, необходимо к разности прибавить вычитаемое.
Так, если мы вычитаем из неизвестного числа другое число и получаем результат, известный нам, то для поиска уменьшаемого необходимо сложить разность и вычитаемое. Простейший пример: дома были конфеты. Их количество мы не знаем. После того как Дима съел 2 конфеты, их осталось 4. Вопрос: сколько их всего было изначально? Для того чтобы узнать, прибавим 2 к 4 и получим результат — было 6 конфет. Для проверки вычтем 2 из 6. Получим результат 4 — решение верное.
Поиск вычитаемого
Нахождение вычитаемого — это такой же простой процесс, как и поиск уменьшаемого. Уравнение может иметь следующий вид: 7-x=3. Мы имеем разность — результат вычитания, и уменьшаемое число. Формулировка правила: чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
Так, если мы вычитаем из одного числа неизвестное число и получаем определённый результат (разность), значит, для поиска неизвестного вычитаемого вычтем из известного числа разность. В нашем примере x=7−3, результат равен 4. Для проверки вычтем 4 из 7, и получим 3 — решение верное. Ещё один вариант проверки — сложить 3 и 4. Так как сумма равна 7, решение правильное.
Общие правила
Для того чтобы гораздо быстрее решать элементарные уравнения, необходимо знать некоторые правила математики и логики. Здесь даже навыки арифметики не имеют такого решающего значения, как понимание того, что именно необходимо находить.
В случае с неизвестным слагаемым оно находится очень просто. От перестановки слагаемых сумма не меняется. То есть совершенно неважно, какой вид имеет уравнение x+2=6, или 2+x=6. В любом случае компонент x будет равен 4.
Дело в том, что уравнения с одним неизвестным предусмотрены школьной программой третьего класса. А ученики могут путаться и испытывать трудности в их решении, не зная этого правила.
Первое, с чего стоит начинать развитие навыка решения — это многократное повторение. Достаточно решать 5—10 уравнений в день с одним неизвестным компонентом, и уже через несколько дней ученик будет справляться с подобными заданиями гораздо быстрее. И только потом можно переходить к более сложным заданиям.
А также для улучшения понимания необходимо решать обратные уравнения. Что это значит? Вычитание — процесс, обратный сложению. То есть при сложении 3 и 4 сумма равна 7. А при вычитании 4 из 7 разность равна 3. В первом уравнении можно искать неизвестные слагаемые. При этом решать его с теми же числами, но на поиск уменьшаемого или вычитаемого.
Решение подобных уравнений точно не навредит ученику, это лишь ускорит процесс формирования навыка. При проверке и решении обратных уравнений в голове откладывается взаимосвязь между всеми компонентами примеров, а их решение практически доводит до автоматизма. Главное — постоянно тренировать этот навык.
Уравнения с умножением и делением
После освоения уравнений на сложение и вычитание можно будет переходить к следующему уровню сложности. Это уравнения с умножением и делением.
Компоненты уравнения с умножением:
- Два множителя.
- Произведение.
Например, 3*x=6. Здесь 3 и x — множители, а 6 — произведение. Так, умножая одно число на другое, в результате получается произведение. То есть, если одно из этих чисел неизвестно, необходимо разделить произведение на известный множитель. В этом случае действует такое же правило, как и при сложении. При перестановке мест множителей произведение не меняется.
Компоненты уравнения с делением:
- Делимое.
- Делитель.
- Частное.
Возьмём простейший пример 8: x=4. Здесь делимое 8, делитель x, а частное — 4. Для поиска неизвестного делителя необходимо разделить делимое на частное. Для упрощения понимания можно представить это уравнение в виде элементарной задачи. В классе 8 учеников, которые разделились на группы по 4 человека. Вопрос: сколько получилось групп?
Есть ещё один вариант — с поиском делимого. Например, уравнение x:2=5. Для поиска делимого необходимо частное умножить на делитель. Пример задачи: 2 мальчика заработали по 5 долларов каждый, какова общая сумма их заработка?
Между делением и умножением похожая взаимосвязь, как между сложением и вычитанием. То есть для того, чтобы лучше решать уравнения с умножением, необходимо также решать их с делением и наоборот. Этот подход в тренировке навыка решения уравнений ускоряет мыслительный процесс.
Поиск неизвестных компонентов уравнения не такой уж и сложный. Главное — начинать с простого и регулярно решать уравнения с одним неизвестным. И тогда для вас будут открыты более сложные задачи — с двумя и более неизвестными.
Памятка по нахождению неизвестных компонентов действий.
Скачать:
Предварительный просмотр:
Выучи названия компонентов действий и правила нахождения неизвестных компонентов:
- Сложение: слагаемое, слагаемое, сумма. Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
- Вычитание: уменьшаемое, вычитаемое, разность. Чтобы найти уменьшаемое, нужно к вычитаемому прибавить разность. Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.
- Умножение: множитель, множитель, произведение. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
- Деление: делимое, делитель, частное. Чтобы найти делимое, нужно делитель умножить на частное. Чтобы найти делитель, нужно делимое разделить на частное.
Выучи названия компонентов действий и правила нахождения неизвестных компонентов:
- Сложение: слагаемое, слагаемое, сумма. Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
- Вычитание: уменьшаемое, вычитаемое, разность. Чтобы найти уменьшаемое, нужно к вычитаемому прибавить разность. Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.
- Умножение: множитель, множитель, произведение. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
- Деление: делимое, делитель, частное. Чтобы найти делимое, нужно делитель умножить на частное. Чтобы найти делитель, нужно делимое разделить на частное.
По теме: методические разработки, презентации и конспекты
- Мне нравится
Как найти слагаемое при решении уравнения? Это можно сделать одним из двух способов.
1) Воспользоваться правилом:
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
2) Если забыли правило, можно придумать простой пример на сложение.
Например, 2+5=7. Как найти первое слагаемое — 2? Надо из 7 вычесть 5. Отсюда выводим правило: чтобы найти неизвестное первое слагаемое, надо из суммы вычесть второе слагаемое.
Как найти второе слагаемое — 5? Нужно из 7 вычесть 2. Отсюда получаем: чтобы найти второе слагаемое, надо из суммы вычесть первое слагаемое.
А так как от перестановки мест слагаемых сумма не меняется, можно не уточнять, какое по счету слагаемое мы ищем.
Рассмотрим, как найти неизвестное слагаемое, на конкретных примерах.
1)
| x | + | 27 | = | 92 |
| сл. | сл. | сум. |
Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое:
x=92-27
x=65
Ответ: 65.
2)
| 43 | + | y | = | 70 |
| сл. | сл. | сум. |
Чтобы найти неизвестное слагаемое, из суммы вычитаем известное слагаемое:
y=70-43
y=27
Ответ: 27.
Решение более сложных уравнений, содержащих несколько действий, обсудим позднее.