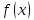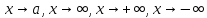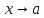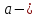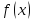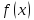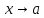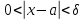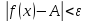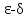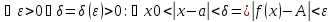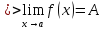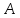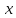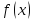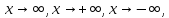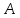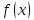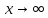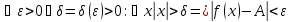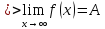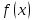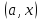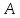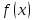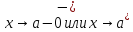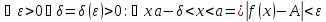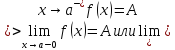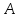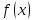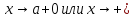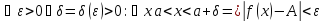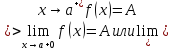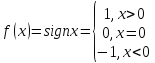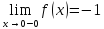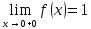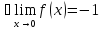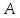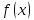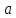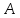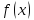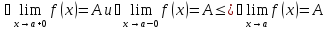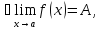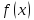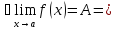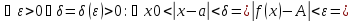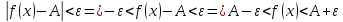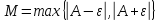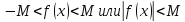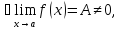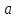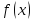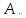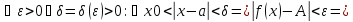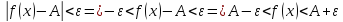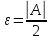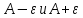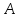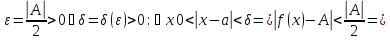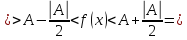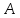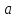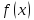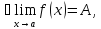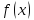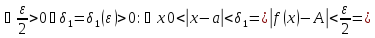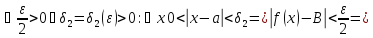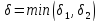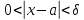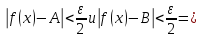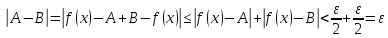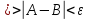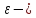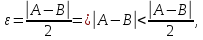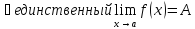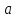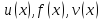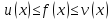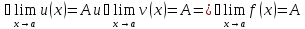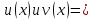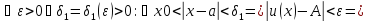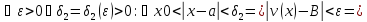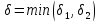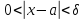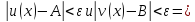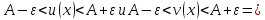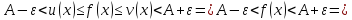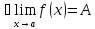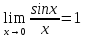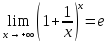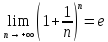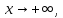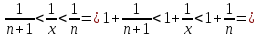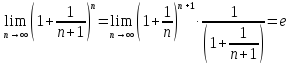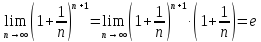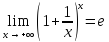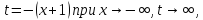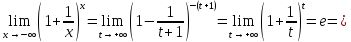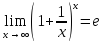Предел функции как найти дельта - Исправление недочетов и поиск решений вместе с Examum.ru

	немогу понять как найти дельта от эпсилон 24.10.2010, 13:13
30/11/07 384

ewert

Re: немогу понять как найти дельта от эпсилон

24.10.2010, 13:18

Заслуженный участник

11/05/08
32162

Решить неравенство. Но сначала, конечно, сократить дробь.

Eiktyrnir	Re: немогу понять как найти дельта от эпсилон 24.10.2010, 13:39
30/11/07 384	Решить неравенство. Но сначала, конечно, сократить дробь. Извините 1000 раз. Я вот понял, что это система неравенств. Т.е. получил вот что $left\| x-3 right\| < frac{epsilon}{4}$ тогда получается, что $0 <frac{epsilon}{4} < delta$ и следовательно $delta(epsilon)>frac{epsilon}{4}$ так?

ewert

Re: немогу понять как найти дельта от эпсилон

24.10.2010, 13:41

Заслуженный участник

11/05/08
32162

ShMaxG

Re: немогу понять как найти дельта от эпсилон

24.10.2010, 14:37

Заслуженный участник

11/04/08
2701
Физтех

ewert

Re: немогу понять как найти дельта от эпсилон

24.10.2010, 15:06

Заслуженный участник

11/05/08
32162

А не наоборот ли?

Да, наоборот. Я, как обычно, не обратил внимания на направление неравенства.

Eiktyrnir	Re: немогу понять как найти дельта от эпсилон 30.10.2010, 17:15
30/11/07 384	To ShMaxG ewert — спасибо огромное. Вывели из умственного «ступора».

Eiktyrnir	Re: немогу понять как найти дельта от эпсилон 05.11.2010, 14:04
30/11/07 384

Sasha2	Re: немогу понять как найти дельта от эпсилон 05.11.2010, 14:11
21/06/06 1721	А какой вообще смысл в этой задаче поиска дельты для епсилон, коли предел уже найден?

ShMaxG

Re: немогу понять как найти дельта от эпсилон

05.11.2010, 14:13

Заслуженный участник

11/04/08
2701
Физтех

maxmatem	Re: немогу понять как найти дельта от эпсилон 05.11.2010, 14:16
15/08/09 1458 МГУ	Sasha2 Цитата: А какой вообще смысл в этой задаче поиска дельты для епсилон, коли предел уже найден? Вполне возможно, что тс.,решил проверить верно ли он вычислил предел, вот и воспользовался определение предела, чз епсилон-дельту.Но это мне так показалось

Eiktyrnir	Re: немогу понять как найти дельта от эпсилон 05.11.2010, 14:25
30/11/07 384	Значит, еще раз. … Ну понятно, что если выбирать $[0 < delta left( varepsilon right) le frac{varepsilon }{4}]$ , то $[0 < left\| {x - 3} right\| < delta left( varepsilon right) le frac{varepsilon }{4} Rightarrow left\| {x - 3} right\| < frac{varepsilon }{4}]$ , что и нужно. Вот теперь я кажется вас начинаю понимать… Нашел еще типовой пример здесь и успокоился… Cпасибо огромное еще раз! Низкий вам поклон.

Модераторы: Модераторы Математики, Супермодераторы

Источник

Лекция 2

Предел
функции

Зададим
некоторую функцию

и рассмотрим поведение этой функции
при изменении
,
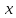
в частности, при

и т.д.

Когда

и

число, то будем предполагать, что функция

определена в окрестности точки
,
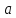
за исключением, быть может, самой точки
.

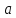
Определение
1.
Число

называется пределом функции

при

,
если

для
любого сколь угодно малого эпсилон
больше нуля найдется дельта, функция
от эпсилон , больше нуля, такое что из
условия,

следует условие для функции

или
запишем определение на языке

или,
используя, определение окрестности
точки, получим:

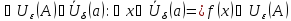
Геометрическая
интерпретация :

Для
любой эпсилон окрестности предела

найдется дельта окрестность предельной
точки
,
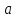
такая что как только

попадает в дельта окрестность предельной
точки
,
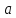
так функция

попадает в эпсилон
окрестность предела
.

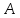
Аналогично
можно дать определение предела при

предположив, что функция

определена при достаточно больших
значениях аргумента

Определение
2.
Число

называется пределом функции

при

,
если

Геометрическая
интерпретация :

Односторонние
пределы функции

Введем
понятие одностороннего предела функции

,
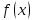
предположив при этом , что функция

определена слева ( или справа) от точки
,
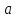
то есть в интервале

( или в интервале

)

Определение
3.
Число

называется левосторонним пределом
функции

при

,
если

Определение
4.
Число

называется правосторонним пределом
функции

при

,
если

Пример1:Найти
левосторонний
и правосторонний
пределы функции

Данная
функция имеет левосторонний
при

и правосторонний
при
пределы,
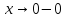
но не имеет предела при

Теорема
: Если
функция

имеет в точке

оба односторонних предела( справа и
слева) и эти пределы равны числу

, то функция

в точке

имеет предел, равный

.

Отметим,
что справедливо и обратное утверждение:

Из
существования у функции

предела в точке
,
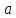
равного числу

, следует существование в этой точке
обоих односторонних пределов , также
равных числу

.

Свойства
функции, имеющих предел

Теорема
1(
об ограниченности функции, имеющей
предел): Если

то
функция

ограничена в окрестности точки
.

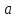
Доказательство:

Обозначим
через

, тогда

то
есть функция

ограничена в окрестности точки
.

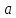
Теорема
2(
о сохранении знака предела): Если

то
в некоторой окрестности предельной
точки
функция

сохраняет знак предела, т.е. знак числа

Доказательство:

Возьмём

, тогда

имеют знак совпадающий со знаком числа

Для
этого

функция

одного знака с числом

в
некоторой окрестности предельной точки
.

Теорема
3(
о единстве предела): Если
у функции

то
этот предел единственный.

Доказательство(
методом от противного):
Предположим, что у функции

существует два предела

при
различных
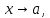
между собой, т.е.

В
силу определения пределов это означает,
что

Обозначим
через

тогда при

будут выполняться оба неравенства:

где

любое число, например возьмем

получили
противоречие, значит наше предположение
было не верно, а

Теорема
4(
о пределе промежуточной функции): Если
в окрестности точки

определены
три функции

, причем выполняется соотношение

и

Доказательство:
из
существования пределов у функций

Обозначим
через

тогда при

будут выполняться оба неравенства:

Замечательные
пределы

Первый
замечательный предел:

Второй
замечательный предел:

Доказательство:
нам
известно

Пусть

,
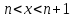
где целое положительное число

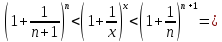
Найдем
пределы последовательностей, стоящих
по краям неравенства.

Тогда
по теореме о пределе промежуточной
функции

Пусть
теперь
,
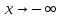
введем переменную

Соседние файлы в папке Лекции

Источник

Понятие предела.

Начать изучение
Два определения предела функции и их эквивалентность.

Начать изучение
Определение предела по Коши.

Начать изучение
Определение предела по Гейне.

Начать изучение
Эквивалентность двух определений предела.

Начать изучение
Различные типы пределов.

Начать изучение
Односторонние конечные пределы.

Начать изучение
Бесконечные пределы в конечной точке.

Начать изучение
Предел в бесконечности.

Начать изучение
Свойства пределов функций.

Начать изучение
Локальные свойства функции, имеющей предел.

Начать изучение
Свойства пределов, связанные с неравенствами.

Начать изучение
Бесконечно малые функции.

Начать изучение
Свойства пределов, связанные с арифметическими операциями.

Начать изучение
Пределы монотонных функций.

Начать изучение
Критерий Коши существования предела функции.

Начать изучение

Понятие предела.

Важную роль в курсе математического анализа играет понятие предела, связанное с поведением функции в окрестности данной точки. Напомним, что (delta) — окрестностью точки (a) называется интервал длины (2delta) с центром в точке (a), то есть множество
$$
U_{delta}(a)={x:|x-a| < delta}={x:a-delta < x < a+delta}.nonumber
$$

Если из этого интервала удалить точку (a), то получим множество, которое называют проколотой (delta)-окрестностью точки (a) и обозначают (dot{U}_{delta}(a)), то есть
$$
dot{U}_{delta}(a)={x:|x-a|<delta, xneq a}={x:0<|x-a|<delta}.nonumber
$$

Предваряя определение предела функции, рассмотрим два примера.

Пример 1

Исследуем функцию (f(x)=displaystyle frac{x^2-1}{x-1}) в окрестности точки (x=1).

Решение

(triangle) Функция (f) определена при всех (xinmathbb{R}), кроме (x=1), причем (f(x)=x+1) при (xneq 1). График этой функции изображен на рис. 10.1.

Рис. 10.1

Из этого рисунка видно, что значения функции близки к 2, если значения (x) близки к 1 ((xneq 1)). Придадим этому утверждению точный смысл.

Пусть задано любое число (varepsilon>0) и требуется найти число (delta>0) такое, что для всех (x) из проколотой (delta)-окрестности точки (x=1) значения функции (f(x)) отличаются от числа 2 по абсолютной величине меньше, чем на (varepsilon).

Иначе говоря, нужно найти число (delta>0) такое, чтобы для всех (xindot{U}_{delta}(a)) соответствующие точки графика функции (y=f(x)) лежали в горизонтальной полосе, ограниченной прямыми (y=2-varepsilon) и (y=2+varepsilon) (см. рис. 10.1), то есть чтобы выполнялось условие (f(x)in U_{varepsilon}(2)). В данном примере можно взять (delta=varepsilon).

В этом случае говорят, что функция (f(x)) стремится к двум при (x), стремящемся к единице, а число 2 называют пределом функции (f(x)) при (xrightarrow 1) и пишут (displaystyle lim{xrightarrow 1}f(x)=2) или (f(x)rightarrow 2) при (xrightarrow 1.quadblacktriangle)

Пример 2

Исследуем функцию
$$
f(x)=left{begin{array}{ll}
1-x, mbox{если} x < 0,\
0, mbox{если} x=0,\
1-x^{2}, mbox{если} x>0,
end{array}right.nonumber
$$
в окрестности точки (x=0.)

Решение

Рис. 10.2

(triangle) Из графика этой функции (рис. 10.2) видно, что для любого (varepsilon>0) можно найти (delta>0) такое, что для всех (xindot{U}_{delta}(0)) выполняется условие (f(x)in U_{varepsilon}(1)). В самом деле, прямые (y=1+varepsilon) и (y=1-varepsilon) пересекают график функции (y=f(x)) в точках, абсциссы которых равны (x_{1}=-varepsilon, x_2=sqrt{varepsilon}). Пусть (delta) — наименьшее из чисел (|x_{1}|) и (x_2), т.e. (displaystyle delta=min(varepsilon,sqrt{varepsilon})). Тогда если (|x|<delta) и (xneq 0), то (|f(x)-1|<varepsilon), то есть для всех (xindot{U}_{delta}(0)) выполняется условие (f(x)in U_{varepsilon}(1)). В этом случае говорят, что функция (f(x)) стремится к единице при (x), стремящемся к нулю и пишут,
$$
displaystyle lim_{xrightarrow 0}{f(x)}=1.quadblacktrianglenonumber
$$

В первом примере функция не определена в точке (x=1), а во втором функция определена в точке (x=0), но значение функции в точке (x=0) не совпадает с ее пределом при (xrightarrow 0).

Два определения предела функции и их эквивалентность.

Определение предела по Коши.

Определение.

Число (A) называется пределом функции (f(x)) в точке (a), если эта функция определена в некоторой окрестности точки (a), за исключением, быть может, самой точки (a), и для каждого (varepsilon>0) найдется число (delta>0) такое, что для всех (x), удовлетворяющих условию (|x-a|<delta, xneq a), выполняется неравенство (|f(x)-A|<delta). В этом случае пишут (displaystyle lim_{xrightarrow a}{f(x)}=A) или (f(x)rightarrow A) при (xrightarrow a).

С помощью логических символов это определение можно записать так:
$$
displaystyle left{lim_{xrightarrow a}f(x)=Aright}Leftrightarrowforallvarepsilon>0 existsdelta>0: forall x:0 <|x-a| <deltarightarrow|f(x)-A|<varepsilon,nonumber
$$

или, используя понятие окрестности, в виде
$$
displaystyle left{lim_{xrightarrow a}f(x)=Aright}Leftrightarrowforallepsilon>0 existsdelta>0: forall xindot{U}_{delta}(a)rightarrow f(x)in U_{varepsilon}(A).nonumber
$$

Таким образом, число (A) есть предел функции (f(x)) в точке (a), если для любой (varepsilon)-окрестности числа (A) можно найти такую проколотую (delta)-окрестность точки (a), что для всех (x), принадлежащих этой (delta)-окрестности, соответствующие значения функции содержатся в (varepsilon)-окрестности числа (A).

Замечание.

В определении предела функции в точке (a) предполагается, что (xneq a). Это требование связано с тем, что точка (a) может не принадлежать области определения функции. Отсутствие этого требования сделало бы невозможным использование предела для определения производной, так как производная функции (f(x)) в точке (a) — это предел функции
$$
F(x) = frac{f(x)-f(a)}{x-a},nonumber
$$
которая не определена в точке (a).

Отметим еще, что число (delta), фигурирующее в определении предела, зависит, вообще говоря, от (varepsilon), то есть (delta=delta(varepsilon)).

Определение предела по Гейне.

Определение.

Число (A) называется пределом функции (f(x)) в точке (a), если эта функция определена в некоторой проколотой окрестности точки (alpha), то есть (existsdelta_{0}>0: dot{U}_{delta_{0}}(a)subset D(f)), и для любой последовательности ({x_{n}}), сходящейся к (a) и такой, что (x_{n}in U_{delta_0}(a)) для всех (ninmathbb{N}), соответствующая последовательность значений функции ({f(x_{n})}) сходится к числу (A).

Пример 3

Пользуясь определением предела по Гейне, доказать, что функция

$$
f(x)=sinfrac{1}{x}nonumber
$$
не имеет предела в точке (x=0).

Решение

(triangle) Достаточно показать, что существуют последовательности ({x_{n}}) и ({widetilde{x}_{n}}) с отличными от нуля членами, сходящиеся к нулю и такие, что (displaystyle lim_{nrightarrowinfty}f(x_{n})neqlim_{nrightarrowinfty} f(widetilde{x}_n)).

Возьмем
$$
x_{n} = left(frac{pi}{2}+2pi nright)^{-1},quad widetilde{x}_{n}=(pi n)^{-1}.nonumber
$$

Тогда (displaystyle lim_{nrightarrowinfty}x_{n}=lim_{nrightarrowinfty}widetilde{x}_{n}=0, f(x_{n})=1) и (f(widetilde{x}_{n})=0) для всех (ninmathbb{N}) и поэтому (displaystyle lim_{nrightarrowinfty}f(x_{n})=1), a (displaystyle lim_{nrightarrowinfty}f(widetilde{x}_{n})=0). Следовательно, функция (displaystyle sinfrac{1}{x}) не имеет предела в точке (x=0.quad blacktriangle)

Замечание.

Если функция (f) определена в проколотой (delta_{0})-окрестности точки (a) и существуют число (A) и последовательность ({x_n}) такие, что (x_n in dot{U}_{delta_{0}}(a)) при всех (n inmathbb{N}, displaystyle lim_{nrightarrowinfty}x_{n}=a) и (displaystyle lim_{nrightarrowinfty}f(x_{n})=A), то число (A) называют частичным пределом функции (f) в точке (a).

Так, например, для функции (f(х)=displaystyle sinfrac{1}{x}) каждое число (A in [-1, 1]) является ее частичным пределом. В самом деле, последовательность ({x_{n}}), где (x_{n}=displaystyle (arcsin A+2pi n)^{-1}), образованная из корней уравнения (displaystyle sinfrac{1}{x}=A) (рис. 10.3), такова, что (x_nneq 0) для всех (ninmathbb{N}, displaystyle lim_{nrightarrowinfty}x_n=0) и (displaystyle lim_{nrightarrowinfty}f(x_{n})=A).

Рис. 10.3

Эквивалентность двух определений предела.

Теорема 1

Определения предела функции по Коши и по Гейне эквиваленты.

Доказательство

(circ) В определениях предела функции (f(x)) по Коши и по Гейне предполагается, что функция (f) определена в некоторой проколотой окрестности точки (a), то есть существует число (delta_0>0) такое, что (dot{U}_{delta_{0}}in D(f)).

Пусть число (A) есть предел функции (f) в точке (a) по Коши; тогда (existsdelta_{0}>0: dot{U}_{delta_{0}}subset D(f)) и
$$
forallvarepsilon>0quadexistsdeltain(0,delta_{0}]:quadforall xindot{U}_{delta}(a)rightarrow f(x)in U_{varepsilon}(A).label{ref1}
$$
Рассмотрим произвольную последовательность ({x_{n}}), сходящуюся к числу (a) и такую, что (x_{n}indot{U}_{delta_{0}}(a)) для всех (ninmathbb{N}). Согласно определению предела последовательности для найденного в eqref{ref1} числа (delta=delta (varepsilon)>0) можно указать номер (n_delta) такой, что (forall ngeq n_{delta}rightarrow x_{n}indot{U}_{delta}(a)), откуда в силу условия eqref{ref1} следует, что (f(x_{n})in U_{varepsilon}(A)). Таким образом,
$$
forall varepsilon>0quadexists N_{varepsilon}: forall ngeq N_{varepsilon}rightarrow f(x_{n})in U_{varepsilon}(A),label{ref2}
$$
где (N_{varepsilon}=n_{delta(varepsilon)}), причем условие eqref{ref2} выполняется для любой последовательности ({x_{n}}) такой, что (displaystyle lim_{nrightarrowinfty}x_{n}=a) и (x_{n}indot{U}_{delta_{0}}(a)subset D(f)). Следовательно, (displaystyle lim_{nrightarrowinfty} f(x_{n})=A), то есть число (A) — предел функции (f(x)) в точке (a) по Гейне.
Докажем, что если число (A) есть предел функции (f(x)) в точке (a) по Гейне, то это же число является пределом функции (f) по Коши, то есть выполняется условие eqref{ref1}. Допустим, что это неверно. Тогда
$$
existsvarepsilon_{0}>0:quadforalldeltain(0,delta_{0}]quadexists x(delta)indot{U}_{delta}(a): |f(x(delta))-A|geqvarepsilon_{0}.label{ref3}
$$
Согласно eqref{ref3} в качестве (delta) можно взять любое число из полуинтервала ((0,delta_{0}]). Возьмем (delta=delta_{0}/n), где (ninmathbb{N}), и обозначим (x_n=x(delta_{0}/n)). Тогда в силу eqref{ref3} для любого (ninmathbb{N}) выполняются неравенства
$$
begin{gather} 0 < |x_{n}-a| < delta_{0}/n,label{ref4}\ |f(x_{n})-A|geqvarepsilon_{0}.label{ref5} end{gather}
$$Из eqref{ref4} следует, что (displaystyle lim_{xrightarrowinfty}x_{n}=a) и (x_{n}indot{U}_{delta_{0}}(а)) при всех (ninmathbb{N}), а из eqref{ref5} заключаем, что число (A) не может быть пределом последовательности ({f(x_{n})}). Следовательно, число (A) не является пределом функции (f) в точке (a) по Гейне. Полученное противоречие доказывает, что должно выполняться утверждение eqref{ref1}. (bullet)

Замечание.

Пусть (а) — предельная точка числового множества (E), то есть такая точка, в любой окрестности которой содержится по крайней мере одна точка множества (E), отличная от (a). Тогда число (A) называют пределом по Коши функции (f(x)) в точке (a) по множеству (E) и обозначают (displaystyle lim_{xrightarrow a, xin E}f(x)=A), если
$$
forallvarepsilon>0quad existsdelta>0:quadforall xin dot{U}_{delta}(a)cap Erightarrow|f(x)-A|<varepsilon.nonumber
$$

Различные типы пределов.

Односторонние конечные пределы.

Число (A) называют пределом слева функции (f(x)) в точке a и обозначают (displaystyle lim_{xrightarrow {a-0}}f(x)) или (f(a-0)), если
$$
forallvarepsilon>0quadexistsdelta>0:quadforall xin(a-delta,a)rightarrow|f(x)-A_{1}| < varepsilon.nonumber
$$

Аналогично число (A_2) называют пределом справа функции (f(x)) в точке (a) и обозначают (displaystyle lim_{xrightarrow a+0}f(х)) или (f(a+0)), если
$$
forallvarepsilon>0quadexistsdelta>0: forall xin (a,a+delta)rightarrow|f(x)-A_2| < varepsilon.
$$

Числа (A_1) и (A_2) характеризуют поведение функции (f) соответственно в левой и правой полуокрестности точки (a), поэтому пределы слева и справа называют односторонними пределами. Если (a=0), то предел слева функции (f(x)) обозначают (displaystyle lim_{xrightarrow -0}f(x)) или (f(-0)), а предел справа обозначают (displaystyle lim_{xrightarrow +0}f(x)) или (f(+0)).

Например, для функции (f(x)=operatorname{sign} x), где
$$
operatorname{sign} x=left{begin{array}{ll}
-1, если x <0,\
0, если x=0,\
1, если x>0,
end{array}right.nonumber
$$
график которой изображен на рис. 10.4 (displaystyle lim_{xrightarrow-0}f(x)=f(-0)=-1, displaystyle lim_{xrightarrow+0}f(x)=f(+0)=1).

Рис. 10.4

Отметим еще, что если
$$
forallvarepsilon>0 existsdelta>0:forall xindot{U}_{delta}(a)rightarrow f(x)in[A,A+varepsilon),
$$
то есть значения функции лежат в правой (varepsilon)-полуокрестности числа (A), то пишут (displaystyle lim_{xrightarrow A}f(x)=A+0). В частности, если (A=0), то пишут (displaystyle lim_{xrightarrow a}f(x)=+0).

Аналогично
$$
displaystyle {lim_{xrightarrow a}f(x)=A-0}Leftrightarrowforallvarepsilon>0 existsdelta>0: forall xindot{U}_{delta}(a)rightarrow f(x)in (A-varepsilon,Arbrack.nonumber
$$
Например, для функции
$$
varphi (x)=left{begin{array}{ll}
1-x, если x <0,\
2, если x=0,\
1+sqrt{x}, если x>0,
end{array}right.nonumber
$$
график которой изображен на рис. 10.5, (displaystyle lim_{xrightarrow 0}f(x)=1+0).

Рис. 10.5

Аналогичный смысл имеют записи вида
$$
lim_{xrightarrow a-0}f(x)=A+0,quad lim_{xrightarrow a+0}f(x)=A-0nonumber
$$

Например,
$$
displaystyle {lim_{xrightarrow a-0}f(x)=A+0}Leftrightarrowforallvarepsilon>0existsdelta>0:forall xin(a-delta,a)rightarrow f(x)in[A,A+varepsilon).
$$

Бесконечные пределы в конечной точке.

Говорят, что функция (f(x)), определенная в некоторой проколотой окрестности точки (a), имеет в этой точке бесконечный предел, и пишут (lim_{xrightarrow a}f(x)=infty), если
$$
forallvarepsilon>0quadexistsdelta>0: forall xindot{U}_{delta}(a)rightarrow|f(x)|>varepsilon.label{ref6}
$$

В этом случае функцию (f(x)) называют бесконечно большой при (xrightarrow a).

Согласно условию eqref{ref6} график функции (y=f(x)) для всех (xin dot{U}_{delta}(a)) лежит вне горизонтальной полосы (|y| <varepsilon). Обозначим
$$
U_{varepsilon}(infty)={y:|y|>varepsilon}=(-infty, -varepsilon)cup(varepsilon,+infty)
$$
и назовем это множество (varepsilon)-окрестностью бесконечности. Тогда запись (displaystyle lim_{xrightarrow a}f(x)=infty) означает, что для любой (varepsilon)-окрестности бесконечности (U_{varepsilon}(infty)) найдется такая проколотая (delta)-окрестность точки (a), что для всех (xin dot{U}_{delta}(a)) выполняется условие (f(x)in U_{varepsilon}(infty)).

Рис. 10.6

Например, если (f(x)=1/x), то (displaystyle lim_{xrightarrow 0}f(x)=infty), так как условие eqref{ref6} выполняется при (delta=1/varepsilon) (рис.10.6).

Аналогично говорят, что функция (f(x)), определенная в некоторой проколотой окрестности точки (a), имеет в этой точке предел, равный (+infty), и пишут (displaystyle lim_{xrightarrow a}f(x)=+infty), если (forallvarepsilon>0quadexistsdelta>0: forall xindot{U}_{delta}(a)rightarrow f(x)>varepsilon), то есть (f(x)in U_{varepsilon}(+infty)), где множество (U_varepsilon (+infty )) называют (varepsilon)-окрестностью символа (+infty).

Если
$$
forallvarepsilon>0quadexistsdelta>0:forall xindot{U}_{delta}(a)rightarrow f(x) <-varepsilon,nonumber
$$
то есть (f(x)in U_{varepsilon}(-infty)), где (U_{varepsilon}(-infty)=(-infty, -varepsilon)), то говорят, что функция (f) имеет в точке (а) предел, равный (-infty), и пишут
(displaystyle lim_{xrightarrow a}{f(x)}=-infty), а множество (Uvarepsilon (-infty )) называют (varepsilon) — окрестностью символа (-infty ).

Рис. 10.7

Рис. 10.8

Например, если (f(x)=lg x^2) (рис. 10.7), то (displaystyle lim_{xrightarrow 0}f(x)=-infty), а если (f(x)=frac{1}{x^{2}}) (рис. 10.8), то (displaystyle lim_{x rightarrow 0} f(x)=+infty).

Предел в бесконечности.

Если

$$
forallvarepsilon>0existsdelta>0:forall xin U_{delta}(+infty)rightarrow f(x)in U_{varepsilon}(A),nonumber
$$

то говорят, что число (A) есть предел функции (f(x)) при x, стремящемся к плюс бесконечности, и пишут (displaystyle lim_{x rightarrow+infty} f(x)=A.)

Например, если (f(x)=displaystylefrac{3-2x}{x+1}), то (displaystyle lim_{xrightarrow infty} f(x)=-2). В самом деле (f(x)=-2+frac{5}{x+1}), и если (x>0), то (x+1>x>0.) Поэтому (displaystylefrac{5}{x+1}<frac{5}{x}), откуда следует, что неравенство(displaystyle|f(х)+2|<frac{5}{x}<varepsilon) для любого (varepsilon >0) выполняется при любом (x >delta), где (delta=displaystylefrac{5}{varepsilon}), то есть при любом (xin U_{delta}(+infty)).

Если (forallvarepsilon>0 existsdelta>0:forall xin U_{delta}(-infty)rightarrow f(x)in U_{varepsilon}(A)), то есть неравенство (|f(x)-A|<varepsilon) выполняется для всех (xin(-infty, -delta)) , то говорят, что число (A) есть предел функции (f(x))} при x, стремящемся к минус бесконечности, и пишут (displaystyle lim_{xrightarrow-infty}f(x)=A). Например, (displaystylelim_{xrightarrow-infty}frac{3-2x}{x+1}=-2).

Аналогично, если
$$
forall varepsilon>0 existsdelta>0:forall xin U_{delta}(infty)rightarrow f(x)in U_{varepsilon}(A),nonumber
$$
то говорят, что число A есть предел функции f(x) при x, стремящемся к бесконечности, и пишут (displaystyle lim_{xrightarrowinfty}=A). Например, если (f(x)=frac{3-2x}{x+1}), то (displaystyle lim_{xrightarrowinfty}f(x)=-2.)

Точно так же вводится понятие бесконечного предела в бесконечности. Например,запись (displaystyle lim_{xrightarrow+infty} f(x)=-infty) означает, что
$$
forallvarepsilon>0 existsdelta>0:forall xin U_{delta}(+infty)rightarrow f(x)in U_{varepsilon}(-infty).nonumber
$$
Аналогично определяются бесконечные пределы при (xrightarrowinfty) и (xrightarrow-infty.)

Свойства пределов функций.

В рассматриваемых ниже свойствах речь идет о конечном пределе функции в заданной точке. Под точкой понимается либо число (a), либо один из символов ( a-0, a+0, -infty, +infty, infty). Предполагается, что функция определена в некоторой окрестности или полуокрестности точки (a), не содержащей саму точку (a). Для определенности будем формулировать и доказывать свойства пределов, предполагая, что (a) — число, а функция определена в проколотой окрестности точки (a).

Локальные свойства функции, имеющей предел.

Покажем, что функция, имеющая конечный предел в заданной точке, обладает некоторыми локальными свойствами, то есть свойствами, которые справедливы в окрестности этой точки.

Свойство 1

Если функция (f(x)) имеет предел в точке (a), то существует такая проколотая окрестность точки (a), в которой эта функция ограничена.

Доказательство

(circ) Пусть (displaystyle lim_{xrightarrow a}f(x)=A). В силу определения предела по заданному числу (varepsilon=1) можно найти число (delta>0) такое, что для всех (xindot{U}_{delta}(a)) выполняется неравенство (|f(x)-A| <1) или (A-1 <f(x) <A+1.) Это означает, что функция (f) ограничена на множестве (dot{U}_{delta}(a). bullet)

Свойство 2

Свойство сохранения знака предела.

Если (displaystyle lim_{xrightarrow a}f(x)=A), причем (Aneq 0,) то найдется такая проколотая окрестность точки (a), в которой значения функции (f) имеют тот же знак, что и число (A).

Доказательство

(circ) Согласно определению предела по заданному числу (varepsilon = frac{|A|}{2}>0) можно найти такое число (delta>0), что для всех (xindot{U}_{delta}(a)) выполняется неравенство (displaystyle |f(x)-A|<frac{|A|}{2}), или
$$ A-frac{|A|}{2} <f(x) <A+frac{|A|}{2}.label{ref7}
$$ Если (A>0), то из левого неравенства eqref{ref7} следует, что
$$
f(x)>frac{A}{2}>0 для xindot{U}_{delta}(a).nonumber
$$
Если (A<0), то из правого неравенства eqref{ref7} следует, что
$$
f(x) <frac{A}{2} <; 0 для xindot{U}_{delta}(a). bulletnonumber
$$

Свойство 3

Если (displaystyle lim_{xrightarrow a}g(x)=B), причем ( Bneq0), то существует число (delta>0) такое, что функция (displaystylefrac{1}{g(x)}) ограничена на множестве (dot{U}_{delta}(a).)

Доказательство

(circ) В силу определения предела по заданному числу (varepsilon=frac{|B|}{2}) можно найти число (delta>0), такое, что для всех (xindot{U}_delta(a)) выполняется неравенство
$$
|g(x)-B| < frac{|B|}{2}.label{ref8}
$$

Из неравенства eqref{ref8} и известного неравенства
$$
|B|-|g(x)|leq|g(x)-B|nonumber
$$
следует, что (displaystyle |B|-|g(x)|<frac{|B|}{2}), откуда (|g(x)|>frac{|B|}{2}),и поэтому (displaystyle frac{1}{|g(x)|} < frac{2}{|B|}) для (xindot{U}_{delta}(a),) то есть функция (displaystyle frac{1}{g(x)}) ограничена на множестве (dot{U}_{delta}(a). bullet)

Свойства пределов, связанные с неравенствами.

Свойство 1

Если существует число (delta>0) такое, что для всех (dot{U}_{delta}(a)) выполняются неравенства
$$
g(x)leq f(x)leq h(x),label{ref9}
$$
и если
$$
lim_{xrightarrow a}g(x)=lim_{xrightarrow a}h(x)=A,label{ref10}
$$
то существует (displaystyle lim_{xrightarrow a}f(x)=A.)

Доказательство

(circ) Воспользуемся определением предела функции по Гейне. Пусть ({x_{n}}) — произвольная последовательность такая, что (x_nindot{U}_{delta}(a)) для (ninmathbb{N}) и (displaystyle lim_{nrightarrow infty}f(x)=a). Тогда в силу условия eqref{ref10} (displaystyle lim_{nrightarrowinfty}g(x_{n})=lim_{nrightarrowinfty}h(x_{n})=A.)

Так как, согласно условию eqref{ref9}, для всех (ninmathbb{N}) выполняется неравенство
$$
g(x_{n})leq f(x_{n})leq h(x_{n}),nonumber
$$
то в силу свойств пределов последовательностей (displaystyle lim_{nrightarrowinfty}f(x_{n})=A). Следовательно, (displaystyle lim_{nrightarrow a}f(x)=A. bullet)

Свойство 2

Если существует число (delta>0) такое, что для всех (xin dot{U}_{delta}(a)) справедливо неравенство (f(x)leq g(x)) , и если (displaystyle lim_{xrightarrow a}f(x)=A, lim_{xrightarrow a}g(x)=B), то ( Aleq B).

Доказательство

(circ) Для доказательства этого свойства достаточно воспользоваться определением предела функции по Гейне и соответствующими свойствами пределов последовательностей. (bullet)

Замечание.

Если исходное неравенство является строгим, то есть (f(x)<g(x)), то в случае существования пределов функций (f) и (g) в точке a можно утверждать только, что
$$
lim_{xrightarrow a}f(x)leqlim_{xrightarrow a}g(x),nonumber
$$
то есть знак строгого неравенства между функциями при переходе к пределу, вообще говоря, не сохраняется.

Бесконечно малые функции.

Если (displaystyle lim_{xrightarrow a}alpha(x)>0) , то функцию (alpha(x)) называют бесконечно малой при (xrightarrow a).

Бесконечно малые функции обладают следующими свойствами:

сумма конечного числа бесконечно малых при (xrightarrow a) функций есть бесконечно малая функция при (xrightarrow a);
произведение бесконечно малой при (xrightarrow a) функции на ограниченную в некоторой проколотой окрестности точки a функцию есть бесконечно малая при (xrightarrow a) функция.

Эти свойства легко доказать, используя определения бесконечно малой и ограниченной функции, либо с помощью определения предела функции по Гейне и свойств бесконечно малых последовательностей. Из свойства 2) следует, что произведение конечного числа бесконечно малых при (xrightarrow a) функций есть бесконечно малая при (xrightarrow a) функция.

Замечание.

Из определения предела функции и определения бесконечно малой функции следует, что число (A) является пределом функции (f(x)) в точке (a) тогда и только тогда, когда эта функция представляется в виде
$$
f(x)=A+a(x),nonumber
$$ где (a(x)) — бесконечно малая при (xrightarrow a) функция.

Свойства пределов, связанные с арифметическими операциями.

Свойство

Если функции (f(x)) и (g(x)) имеют конечные пределы в точке (а), причем (displaystyle lim_{xrightarrow a}f(x)=A, lim_{xrightarrow a}g(x)=B), то:

$$
lim_{xrightarrow a}(f(x)+g(x))=A+B;nonumber
$$
$$
lim_{xrightarrow a}(f(x)g(x))=AB;label{ref11}
$$
$$
lim_{xrightarrow a}frac{f(x)}{g(x)}=frac{A}{B} — при условии, что Bneq 0.nonumber
$$

(circ) Для доказательства этих свойств достаточно воспользоваться определением предела функции по Гейне и свойствами пределов последовательностей. (bullet)

Отметим частный случай утверждения eqref{ref11}:
$$
lim_{xrightarrow a}(C f(x))=Clim_{xrightarrow a}f(x),nonumber
$$
то есть постоянный множитель можно вынести за знак предела.

Пределы монотонных функций.

Ранее мы уже ввели понятие монотонной функции. Докажем теорему о существовании односторонних пределов у монотонной функции.

Теорема 2

Если функция (f) определена и является монотонной на отрезке ([a,b]), то в каждой точке (x_{0}in(a,b)) эта функция имеет конечные пределы слева и справа, a в точках (а) и (b) — соответственно правый и левый пределы.

Доказательство

(circ) Пусть, например, функция (f) является возрастающей на отрезке ([a,b]). Зафиксируем точку (х_0in)(а, (b)]. Тогда
$$
forall xin[a,x_{0})rightarrow f(x)leq f(x_{0}).label{ref12}
$$

В силу условия eqref{ref12} множество значений, которые функция (f) принимает на промежутке ([a,x_{0})), ограничено сверху, и по теореме о точной верхней грани существует
$$
sup_{aleq x <x_{0}}f(x)=M, где Mleq f(x_0).nonumber
$$
Согласно определению точной верхней границы (см. здесь) выполняются условия:
$$
forall xin[a, x_{0})rightarrow f(x)leq M;label{ref13}
$$
$$
forallvarepsilon>0 exists x_{varepsilon}in[a, x_{0}):M-varepsilon <f(x_{varepsilon}).label{ref14}
$$
Обозначим (delta=x_{0}-x_{varepsilon}), тогда (delta>0), так как (x_varepsilon <x_{0}.) Если (xin (x_varepsilon,x_0)), то есть (xin (x_0-delta,x_0)), то
$$
f(x_{varepsilon})leq f(x),label{ref15}
$$
так как (f) — возрастающая функция. Из условий eqref{ref13}—eqref{ref15} следует, что
$$
forallvarepsilon>0 existsdelta>0:forall xin(x_{0}-delta,x_{0})rightarrow f(x)in(M-varepsilon,M].nonumber
$$
Согласно определению предела слева это означает, что существует
$$
lim_{xrightarrow x_{0}-0} f(x)=f(x_{0}-0)=M.nonumber
$$
Итак,
$$
f(x_{0}-0)=sup_{aleq x <x_{0}}f(x).nonumber
$$

Аналогично можно доказать, что функция а имеет в точке (x_0in [a, b)) предел справа, причем
$$
f(x_{0}+0)=displaystyle inf_{x_{0} <xleq b}f(x). bullet
$$

Следствие.

Если функция (f) определена и возрастает на отрезке ([a,b], x_{0}in(a,b),) то
$$
f(x_{0}-0) < f(x_{0})leq f(x_0+0)label{ref16}
$$

Замечание.

Теорема о пределе монотонной функции справедлива для любого конечного или бесконечного промежутка. При этом, если (f) — возрастающая функция, не ограниченная сверху на ((a,b)), то (displaystyle lim_{xrightarrow b-0}f(x)= +infty) (в случае, когда (b =+infty) пишут (displaystyle lim_{xrightarrow +infty}f(x)= +infty)), а если (f) — возрастающая и не ограниченная снизу на промежутке ((a,b)) функция, то (displaystyle lim_{xrightarrow a+0}f(x)=-inftyquad (lim_{xrightarrow-infty}f(x)=-infty)).

Критерий Коши существования предела функции.

Будем говорить, что функция (f(x)) удовлетворяет в точке (x=a) условию Коши, если она определена в некоторой проколотой окрестности точки (a) и
$$
forallvarepsilon>0quad existsdelta=delta(varepsilon)>0: forall x’,x″in dot{U}_{delta}(a)rightarrow|f(x’)-f(x″)| < varepsilon.label{ref17}
$$

Лемма

Пусть существует число (delta >0) такое, что функция (f(x)) определена в проколотой (delta) — окрестности точки (a), и пусть для каждой последовательности {(x_n)}, удовлетворяющей условию (x_nindot{U}_{delta}(a)) при всех (ninmathbb{N}) и сходящейся к (a), соответствующая последовательность значений функции ({f(x_n)}) имеет конечный предел. Тогда этот предел не зависит от выбора последовательности ({x_n}), то есть если
$$
lim_{nrightarrowinfty}f(x_{n})=A,nonumber
$$
и
$$
lim_{nrightarrowinfty}f(widetilde{x_{n}})=widetilde{A},nonumber
$$
где (widetilde{x}_n =dot{U}_{delta}(a)) при всех (n inmathbb{N}) и ( widetilde{x}_{n}rightarrow a ) при (nrightarrowinfty) то (widetilde{A}=A.)

Доказательство

(circ) Образуем последовательность
$$
x_{1},widetilde{x}_{1}, x_{2},widetilde{x}_{2},ldots, x_{n},widetilde{x}_{n},ldotsnonumber
$$
и обозначим k-й член этой последовательности через (y_{k}). Так как (displaystyle lim_{krightarrowinfty}y_k=a) (см. пример 3 здесь) и (y_kin dot{U}_{delta}(a)) при любом (kinmathbb{N}), то по условию леммы существует конечный (displaystyle lim_{krightarrowinfty}f(y_{k})=A’) Заметим, что ({f(x_{n})}) и ({f(widetilde{x}_{n})}) являются подпоследовательностями сходящейся последовательности ({f(y_k)}). Поэтому (A=A’,widetilde{A}=A’) откуда получаем, что (A=widetilde{A}. bullet)

Теорема 3

Для того чтобы существовал конечный предел функции (f(x)) в точке (x = a) необходимо и достаточно, чтобы эта функция удовлетворяла в точке a условию Коши eqref{ref17}.

Доказательство

(circ) Необходимость. Пусть (displaystyle lim_{xrightarrow a}f(x)=A); тогда
$$
forallvarepsilon>0 existsdelta>0:forall xindot{U}_{delta}(a)rightarrow|f(x)-A|<frac{varepsilon}{2}.label{ref18}
$$

Если (х’,x″) любые точки из множества (dot{U}_{delta}(a)), то из eqref{ref18} следует, что
$$
|f(x’)-f(x″)|=|(f(x’)-A)-(f(x″)-A)|leq|f(x’)-A|+|f(x″)-A| <frac{varepsilon}{2}+frac{varepsilon}{2}=varepsilon,nonumber
$$
то есть выполняется условие Коши eqref{ref17}.

Достаточность. Докажем, что если (existsdelta_{0}:dot{U}_{delta}(a)subset D(f)) и выполняется условие eqref{ref17}, то существует предел функции (f) в точке (a). Воспользуемся определением предела функции по Гейне. Пусть ({x_{n}}) — произвольная последовательность такая, что (x_nindot{U}_{delta}(a)) и (displaystylelim_{xrightarrowinfty}x_n=a.) Докажем, что соответствующая последовательность значений функции ({f(x_{n})}) имеет конечный предел, не зависящий от выбора последовательности ({x_{n}})

Если выполняется условие eqref{ref17}, то для каждого (varepsilon>0) можно найти число (delta=delta_varepsilon>0) такое, что
$$
forall x’,x″in dot{U}_{delta}(a)rightarrow|f(x’)-f(x″)| <varepsilon.label{ref19}
$$

Так как (displaystyle lim_{xrightarrowinfty}x_{n}=a), то, задав число (delta=delta(varepsilon)>0,) указанное в условии eqref{ref19}, найдем в силу определения предела последовательности номер (n_{delta}=N_{varepsilon}) такой, что
$$
forall n>N_{varepsilon}rightarrow 0<|x_{n}-a| <delta.nonumber
$$
Это означает, что для любого (ngeq N_{varepsilon}) и для любого (mgeq N_{varepsilon}) выполняются условия (x_{n}in dot{U}_{delta}(a), x_{m}in dot{U}_{delta}(a)) и в силу eqref{ref19} (|f(x_n)-f(x_m)| <varepsilon). Таким образом, последовательность ({f(x_{n})}) является фундаментальной и согласно критерию Коши для последовательности имеет конечный предел. В силу леммы этот предел не зависит от выбора последовательности ({x_{n}}) сходящейся к точке (a). Следовательно, функция (f(x)) имеет конечный предел в точке (a). (bullet)

Замечание.

Теорема 3 остается в силе, если точку (a) заменить одним из символов (a-0, a+0,-infty, +infty); при этом условие eqref{ref17} должно выполняться в окрестности этого символа.

Источник

Infinitesimal approach is kinda out-dated in today’s mathematics. The reason is that it’s not rigorous enough, also, the advantage of the epsilon-delta definition is that it can be generalized to more general spaces. You know, before the progress of topology, mathematicians extensively used the idea behind the distance (Euclidean distance) between two points, which is called the metric function. I mean, when they wanted to think about closeness of two points in a space, they thought about the distance between those two points. The notion of ‘closeness'(being close) is now a bit more generalized in today’s mathematics and it has been replaced by open sets and neighborhoods. Later they realized that many properties of the real line and many concepts in mathematical analysis could be independently studied in a more general approach which doesn’t necessarily use the idea of a metric function for determining how close two things are. The epsilon-delta definition of continuity has the advantage that it could be seen as an intermediate step in generalizing the concept of a continuous map to more general spaces where you can’t define a metric function.

The epsilon-delta definition of limit says that if you want f(x) to be arbitrary close to a value L as x approaches a, i.e $displaystyle lim_{x to a} f(x)= L$, all you need to do as that you find a delta such that the distance between x and a is smaller than delta. We can write this in math symbols as:

$displaystyle forall epsilon, exists delta$ s.t. $0<|x-a|<delta$ $implies$ $|f(x)-L|<epsilon$

For continuity, you allow the case x=a, so the definition becomes

$displaystyle forall epsilon, exists delta$ s.t. $|x-a|<delta$ $implies$ $|f(x)-f(a)|<epsilon$

Notice that you can talk about $f(a)$ instead of $L$ since f is continuous.

This intuitively means that you can make f(x) arbitrarily close as you want to L (or f(x)) provided that you take x close enough to a. What does close enough to a mean in this case? It means that the distance between x and a shouldn’t exceed delta. This is what it means. If you take x close enough to a, then f(x) will be close enough to L (or f(a)). And here, close enough means that the distance between f(x) and L (or f(a)) is less than your desired epsilon.

I hope that it’s clear now.

Источник

Я учусь решать задачи с пределами функции через эпсилон-дельта определение. В данном решение у меня не совпал ответ с ответом из задачника (дельта <= 4/51). Подскажите, где у меня ошибка в решении, а также скажите, верны ли в общем ход решения и его оформление?

Задача: Определить, при каких положительных значениях $$delta$$ из неравенства $$0 < mid x — x_{0} mid < delta$$ следует неравенство $$mid f(x) — a mid < varepsilon$$, если:
$$f(x) = frac{x^2-4x+3}{x^2-2x-3}, x_{0} = 3, a = frac{1}{2}, varepsilon = 0,01$$

Решение: $$lim_{x rightarrow infty }f(x) = frac{x^2-4x+3}{x^2-2x-3} = frac{1}{2}$$

Требуется найти такие значения $$delta > 0$$ для $$varepsilon =0,01$$, что из неравенства $$0< mid x — 3 mid < delta$$ следует неравенство $$mid frac{x^2-4x+3}{x^2-2x-3} mid < 0,01$$

Преобразуем последнее неравенство:

$$mid frac{x^2-4x+3}{x^2-2x-3} mid < frac{1}{100}$$

$$mid frac{(x-1)(x-3)}{(x+1)(x-3)} — frac{1}{2} mid < frac{1}{100}$$

$$mid frac{x-1}{x+1} — frac{1}{2} mid <frac{1}{100}$$

$$mid frac{x-3}{2x+2} mid <frac{1}{100}$$

$$mid x-3 mid < frac{2x + 2}{100}$$

Вывод:Из неравенства $$0< mid x — 3 mid < delta$$ следует неравенство $$mid x-3 mid < frac{2x + 2}{100}$$, значит искомое значение $$delta < frac{2x + 2}{100} = 0, 8$$

Источник