Производная больше нуля как найти

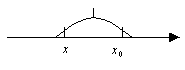
Монотонность.

Функция называется
возрастающей если большему значению
аргумента соответствует большее значение
функции, а меньшему соответствует
меньше.

Функция называется
убывающей если большему значению
аргумента соответствует меньшее значение
функции, а меньшему соответствует
большее.

Теорема.
У возрастающей функции производная
больше 0 ().

Доказательство:

x		-1
y		min
	–	0	+

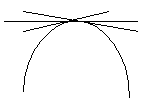
Экстремумы
функции.

Т
очка
-называется
точкой max,
если существует некоторая окрестность
точки, что для любой точки x
из этой
окрестности
.

Точка
-называется
точкой min,
если существует некоторая окрестность
точки, что для любой точки x
из этой
окрестности
.

Необходимый признак
экстремума, если

-точка экстремума.

Если

и
,
то это точка экстремума.

Если

— точка экстремума и существует
,
то производная
=0.

Точка, в которой
производная, равна нулю, называется
критической точкой.

,
теорема Логранжа.

Первый достаточный
признак экстремума.

Если при переходе
через критическую точку производная
меняет знак с ”+”
на “-“,то
в этой точке максимум.

Если при переходе
через критическую точку производная
меняет знак с ”-”
на “+“,то
в этой точке минимум.

Второй достаточный
признак экстремума.

Если в критической точке 2-ая производная больше нуля, то это точка минимума, а если в критической точке 2-ая производная меньше нуля, то это точка максимума.

Пример:

x		1		3
y		Max		Min
	+	0	—	0	+

Выпуклость и
вогнутость.

Если
в окрестности точки, график функции
ниже касательной, то в окрестности этой
точки график функции выпуклый.

Если
в окрестности точки, график функции
выше касательной, то в окрестности этой
точки график функции вогнутый.

Теорема.
В точке
выпуклости 2-ая производная меньше 0. В
точке вогнутости вторая производная
больше 0.

Доказательство:

Если
прямая проходит через точку

Применим
теорему Логранжа:

Поставим
“-“
в
,
учитывая, что
>0

тогда
должна
быть <0.

Второй
раз применим теорему Логранжа:

Для вогнутости
поставим “+”

должно
быть >0.

Точка, в которой
вторая производная равна нулю, называется
точкой перегиба.

y		п		п
	+	0	—	0	+

Асимптоты.

Асимптотой к кривой
называется прямая, к которой график
функции неограниченно приближается.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Производная функции. Геометрический смысл производной



Производная функции — одна из сложных тем в школьной программе. Не каждый выпускник ответит на вопрос, что такое производная.

В этой статье просто и понятно рассказано о том, что такое производная и для чего она нужна. Мы не будем сейчас стремиться к математической строгости изложения. Самое главное — понять смысл.

Запомним определение:

Производная — это скорость изменения функции.

На рисунке — графики трех функций. Как вы думаете, какая из них быстрее растет?

Ответ очевиден — третья. У нее самая большая скорость изменения, то есть самая большая производная.

Вот другой пример.

Костя, Гриша и Матвей одновременно устроились на работу. Посмотрим, как менялся их доход в течение года:

На графике сразу все видно, не правда ли? Доход Кости за полгода вырос больше чем в два раза. И у Гриши доход тоже вырос, но совсем чуть-чуть. А доход Матвея уменьшился до нуля. Стартовые условия одинаковые, а скорость изменения функции, то есть производная, — разная. Что касается Матвея — у его дохода производная вообще отрицательна.

Определение.

Производная – это скорость изменения функции.

Интуитивно мы без труда оцениваем скорость изменения функции. Но как же это делаем?

На самом деле мы смотрим, насколько круто идет вверх (или вниз) график функции. Другими словами — насколько быстро меняется у с изменением х. Очевидно, что одна и та же функция в разных точках может иметь разное значение производной — то есть может меняться быстрее или медленнее.

Производная функции обозначается .

Покажем, как найти с помощью графика.

Нарисован график некоторой функции . Возьмем на нем точку А с абсциссой . Проведём в этой точке касательную к графику функции. Мы хотим оценить, насколько круто вверх идет график функции. Удобная величина для этого — тангенс угла наклона касательной.

Производная функции в точке  равна тангенсу угла наклона касательной, проведённой к графику функции в этой точке.

Обратите внимание — в качестве угла наклона касательной мы берем угол между касательной и положительным направлением оси ОХ.

Иногда учащиеся спрашивают, что такое касательная к графику функции. Это прямая, имеющая на данном участке единственную общую точку с графиком, причем так, как показано на нашем рисунке. Похоже на касательную к окружности.

Найдем . Мы помним, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. Из треугольника

Мы нашли производную с помощью графика, даже не зная формулу функции. Такие задачи часто встречаются в ЕГЭ по математике.

Есть и другое важное соотношение. Вспомним, что прямая задается уравнением

.

Величина k в этом уравнении называется угловым коэффициентом прямой. Она равна тангенсу угла наклона прямой к оси X.

.

Мы получаем, что

Запомним эту формулу. Она выражает геометрический смысл производной.

Производная функции в точке  равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.

Другими словами, производная равна тангенсу угла наклона касательной.

Мы уже сказали, что у одной и той же функции в разных точках может быть разная производная. Посмотрим, как же связана производная с поведением функции.

Нарисуем график некоторой функции . Пусть на одних участках эта функция возрастает, на других — убывает, причем с разной скоростью. И пусть у этой функции будут точки максимума и минимума.

В точке A функция возрастает. Касательная к графику, проведенная в точке A, образует острый угол  с положительным направлением оси X. Значит, в точке A производная положительна.

В точке B наша функция убывает. Касательная в этой точке образует тупой угол  с положительным направлением оси X. Поскольку тангенс тупого угла отрицателен, в точке B производная отрицательна.

Вот что получается:

Если функция возрастает, ее производная положительна.

Если убывает, ее производная отрицательна.

А что же будет в точках максимума и минимума? Мы видим, что в точках C (точка максимума) и D (точка минимума) касательная горизонтальна. Следовательно, тангенс угла наклона касательной в этих точках равен нулю, и производная тоже равна нулю.

Точка С — точка максимума. В этой точке возрастание функции сменяется убыванием. Следовательно, знак производной меняется в точке С с «плюса» на «минус».

В точке D — точке минимума — производная тоже равна нулю, но ее знак меняется с «минуса» на «плюс».

Вывод: с помощью производной можно узнать о поведении функции всё, что нас интересует.

Если производная положительна, то функция возрастает.

Если производная отрицательная, то функция убывает.

В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».

В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».

Запишем эти выводы в виде таблицы:

Сделаем два небольших уточнения. Одно из них понадобится вам при решении задач ЕГЭ. Другое — на первом курсе, при более серьезном изучении функций и производных.

1. Возможен случай, когда производная функции в какой-либо точке равна нулю, но ни максимума, ни минимума у функции в этой точке нет. Это так называемая точка перегиба:

В точке E касательная к графику горизонтальна, и производная равна нулю. Однако до точки E функция возрастала — и после точки E продолжает возрастать. Знак производной не меняется — она как была положительной, так и осталась.

2. Бывает и так, что в точке максимума или минимума производная не существует. На графике это соответствует резкому излому, когда касательную в данной точке провести невозможно.

А как найти производную, если функция задана не графиком, а формулой? В этом случае применяется таблица производных. В ней вы найдете производные всех элементарных функций и правила взятия производных, то есть дифференцирования.

Геометрический смысл производной, задачи

Покажем, что такое геометрический смысл производной, на примере нескольких задач из Банка заданий ФИПИ.

Задача 1. На рисунке изображен график функции ). Найдите количество решений уравнения )=0 на отрезке [-2,5; 9,5].

Решение:

Производная функции равна нулю в точках максимума и минимума функции Таких точек на графике 5.

Ответ: 5.

Задача 2. На рисунке изображен график функции y= ) — производной функции ). Сколько точек максимума имеет функция ) на отрезке ? В ответе запишите это число.

Решение:

Обратите внимание, что на этом рисунке изображен не график функции, а график ее производной.

В вариантах ЕГЭ по математике таких задач много. Пользуясь графиком производной, надо ответить на вопрос о поведении функции.

В точке максимума функции производная равна нулю и меняет знак с «плюса» на «минус». Такая точка на отрезке на графике одна.

Ответ: 1.

Задача 3. На рисунке изображены график функции и касательная к нему в точке с абсциссой Найдите значение производной функции в точке

Решение:

Вспомним определение.

Производная функции в точке равна тангенсу угла наклона касательной, проведенной к графику функции в этой точке (то есть угловому коэффициенту касательной).

Это геометрический смысл производной.

В точке функция y = f(x) убывает. Касательная, проведенная к ее графику в этой точке, образует тупой угол с положительным направлением оси Х. Найдем тангенс острого угла смежного с углом

Ответ: -0,5.

Задача 4. На рисунке изображен график производной функции определенной на отрезке В какой точке отрезка принимает наименьшее значение?

Решение:

На рисунке изображен график производной. Если функция возрастает — ее производная положительна. Если функция убывает — ее производная отрицательна. В точке минимума производная равна нулю и меняет знак с «минуса» на «плюс».

На рисунке есть такая точка, и это x = 1,5.

Слева от этой точки, на отрезке [1; 1,5] производная отрицательна, и функция убывает. Справа от этой точки, на интервале [1,5; 5), производная положительна, и функция возрастает.

Значит, — точка минимума функции

Поэтому и свое наименьшее значение функция принимает в точке 1,5.

Ответ: 1,5.

Задача 5. На рисунке изображен график — производной функции В какой точке отрезка функция принимает наименьшее значение?

Решение:

На рисунке изображен график производной. Если функция возрастает — ее производная положительна. Если функция убывает — ее производная отрицательна. В точке минимума производная равна нулю и меняет знак с «минуса» на «плюс».

На рисунке есть такая точка, и это x = 3.

Слева от этой точки производная отрицательна, и функция убывает. Справа от точки x = 3 производная положительна, и функция возрастает.

Значит, — точка минимума функции

Кстати, вид графика функции определить нетрудно. Это квадратичная парабола с ветвями вверх.

Ответ: 3.

Задача 6. На рисунке изображен график производной непрерывной функции В какой точке отрезка функция принимает наибольшее значение?

Решение:

На отрезке расположена точка в которой производная равна нулю и меняет знак с «+» на «-».

Это значит, что — точка максимума функции на отрезке и наибольшее значение функция принимает именно в этой точке.

Ответ: — 2,5.

Задача 7. На рисунке изображен график производной функции определенной на интервале (-3;7). В какой точке отрезка [-2; 4] функция принимает наименьшее значение?

Решение:

Точка минимума функции f(x) — это x = 0. В этой точке производная равна 0 и меняет знак с «минуса» на «плюс».

Слева от точки 0 производная отрицательна, функция убывает. Справа от этой точки производная положительна, функция возрастает.

Наименьшее значение на отрезке достигается при x = 0.

Ответ: 0.

Задача 8. На рисунке изображены график функции и касательная к нему в точке с абсциссой Найдите значение производной функции в точке

Решение:

Производная функции в точке равна тангенсу угла наклона касательной, проведенной к графику функции в этой точке.

— касательная к

В точке производная отрицательная, т.к. функция — убывает в этой точке.

— угол, который образует касательная с положительным направлением оси Х.

Угол — тупой, а смежный с ним угол — острый.

Ответ: -0,375.

Задача 9. На рисунке изображен график непрерывной функции f(x) и касательные CD и MN, проведенные к ее графику в точках А и В. Найдите отношение значений производной функции f(x) в точках А и В.

Решение:

Найдём значения производных в точках А и В с помощью графика.

где — угол наклона касательной к графику функции в точке с абсциссой

Для точки А:

Для точки В:

Отношение производных:

Ответ: 0,15.

Условия касания

Пусть прямая касается графика функции в точке Тогда для точки выполняются условия касания:

Первое уравнение показывает, что значения функций и в точке равны друг другу. Это верно, поскольку эта точка лежит и на одном, и на другом графике.

Второе условие показывает, что производная функции в точке равна угловому коэффициенту касательной, то есть k.

Задача 10. Прямая касается графика функции причем абсцисса точки касания положительна. Найдите b.

Решение:

Запишем условие касания:

Начнем со второго уравнения:

Т.к. то

Найдем подставив в первое уравнение:

отсюда

Ответ: -7.

Условия касания встречаются нам не только в заданиях 1 части ЕГЭ по математике, но и в задачах с параметрами. Более того, это один из приемов решения уравнений и неравенств с параметрами.

Физический смысл производной

Мы узнали, что такое геометрический смысл производной. Научились находить производную с помощью графика функции и решать задачи ЕГЭ. Производная помогает нам исследовать функции, находить их точки максимума и минимума, строить графики функций.

И оказывается, что с производной вы познакомились намного раньше — в школьном курсе физики. Вы уже пользовались этим математическим понятием, но не называли его словом «производная».

Вспомним тему «Кинематика» в физике. Это раздел физики, описывающий механическое движение. Величины, которыми описывается движение какого-либо тела, — это скорость v, время t, координата х, если тело движется вдоль прямой. Или координаты x и y, если оно движется по плоскости.

Вспомним формулу для равномерного прямолинейного движения: где x — координата.

Пусть 3 материальных точки — например, три автомобиля — одновременно выезжают с постоянными скоростями из точки А и едут по прямолинейному шоссе. На графике показано, как меняется их координата x с течением времени. У какого из автомобилей скорость больше?

Очевидно, у третьего. Считая, что x = vt, для первого автомобиля найдем = 20 км/ч. Возможно, это машина, которая поливает или чистит дорогу, и поэтому так медленно едет. Для второго автомобиля = 40 км/ч, для третьего = 75 км/ч.

Но если пройденный путь, то есть изменение координаты тела, мы разделим на время, то найдем тангенс угла наклона для каждой из этих прямых. Так и есть.

Скорость тела — это производная от его координаты по времени.

А теперь пусть тело, например, автомобиль, движется вдоль оси x, причем его скорость не является постоянной. Зависимость его координаты от времени x(t) показана на графике.

Возьмем на графике точку, соответствующую моменту времени и проведем в этой точке касательную к графику функции.

Тангенс угла наклона этой касательной численно равен мгновенной скорости тела в момент

Мы получили, что мгновенная скорость — это производная от координаты по времени.

Это физический смысл производной.

Но не только скорость в физике является производной от другой физической величины, координаты.

Ускорение — это производная от скорости по времени. Сила тока — производная от заряда по времени.

Изучая курс физики в школе и в вузе, вы увидите множество уравнений, связывающих одни физические величины с производными других физических величин. Такие уравнения называются дифференциальными. А само действие взятия производной называется дифференцированием.

Вот задача из вариантов ЕГЭ по математике, где используется физический смысл производной.

Задача 11. Материальная точка M начинает движение из точки A и движется по прямой на протяжении 12 секунд. График показывает, как менялось расстояние от точки A до точки M со временем. На оси абсцисс откладывается время t в секундах, на оси ординат — расстояние s.

Определите, сколько раз за время движения скорость точки M обращалась в ноль (начало и конец движения не учитывайте).

Решение:

Производная — это скорость изменения функции. Мгновенная скорость движущегося тела (материальной точки) является производной от его координаты по времени. Это физический смысл производной.

Найдем на графике s(t) точки, в которых производная функции s(t) равна нулю. Таких точек 6. Это точки максимума и минимума функции s(t).

Ответ: 6.

Изучая высшую математику в вузе, вы узнаете еще одно определение производной.

Производной функции f(x) в точке называется предел отношения приращения функции к приращению аргумента при приращении аргумента, стремящемся к нулю.

Это определение есть в вашем школьном учебнике алгебры. Но намного важнее не механически его запомнить, а понять его смысл. Первые шаги к этому мы сделали, определив производную как скорость изменения функции. Мы также узнали, что такое геометрический смысл производной и физический смысл производной.