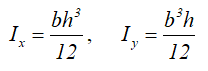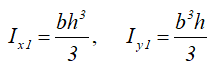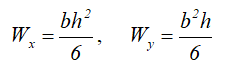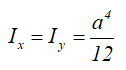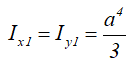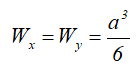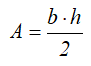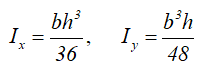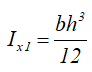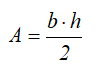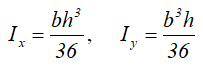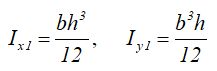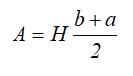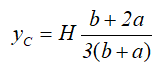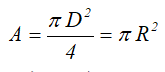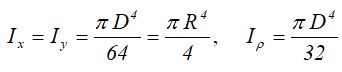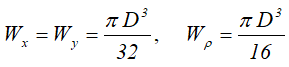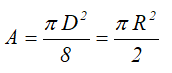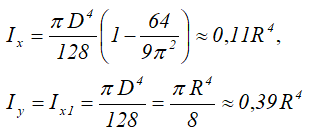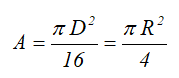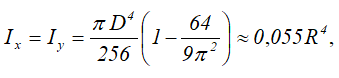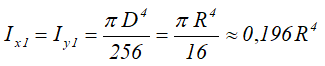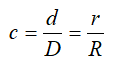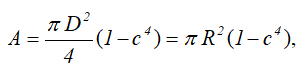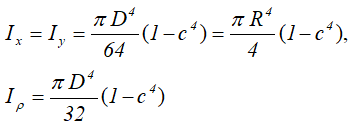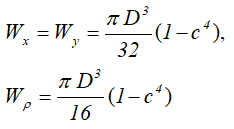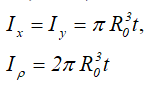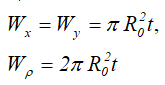Центр треугольника
Треугольник — наиболее распространенная форма деталей в сферах машиностроения и строительства. Точка пересечения 3-х медиан считается центром треугольника. На эту точку приходится также центр тяжести и центр симметрии предметов треугольной формы. При разработке дизайнерских, инженерных проектов очень важно точно рассчитать центр тяжести элементов металлической или бетонной конструкции.
Существует несколько понятий центра для треугольника.
Инцентр — точка пересечения его биссектрис. Это — центр описанной около треугольника окружности.
Ортоцентр — точка пересечения его высот.
Центр тяжести,центр масс или центроид (обозн. М) — точка пересечения медиан треугольника.
Рассмотрим треугольник. Определим середины его сторон и соединим их с противолежащими углами. Точка пересечения медиан и будет центром тяжести тр-ка. Медиана делится этой точкой в пропорции 2:1 , (считая от вершины тр-ка).
Как найти центр треугольника
Если известны координаты его вершин, найдем сумму трех значений координат «х» и трех значений координат «у». Поделим каждую сумму на 3, получим среднее значение сумм координат «х» и «у», что и будет координатами центра тяжести.
Центром равностороннего треугольника является точка пересечения высот, биссектрис и медиан.
Центр равностороннего треугольника является также центром вписанной и описанной окружности.
Центроид расположен на отрезке, соединяющем ортоцентр и центр описанной окружности. Центроид делит отрезок 2:1.
Быстро найти центр треугольника G можно с помощью онлайн калькулятора. Для этого:
- ввести в поле калькулятора координаты вершин треугольника;
- нажать кнопку Вычислить. Калькулятор вычислит значение центра треугольника G.
Центр тяжести треугольника
Этот онлайн калькулятор находит центроид, или барицентр (центр тяжести) треугольника по координатам его вершин
Центр тяжести (центр масс, барицентр) треугольника для треугольника с равномерно распределённой массой (или в вершинах которого находятся равные массы) находится в центроиде треугольника. Центроидом называется точка пересечения медиан треугольника. Центроид относится к так называемым замечательным точкам треугольника. Например, помимо того, что он является центром тяжести, он также делит каждую медиану в отношении 2:1, считая от вершины, а три отрезка прямых, соединяющих вершины треугольника с центроидом, разбивают данный треугольник на три равновеликих треугольника.
Чтобы вычислить положение центра тяжести по координатам вершин треугольника, достаточно вычислить среднее арифметическое координат вершин по оси x и по оси y, что и делает калькулятор ниже.
Прямоугольный треугольник
Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).
Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.
Стороны, прилежащие к прямому углу, называются катетами .
Признаки равенства прямоугольных треугольников
Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ).
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ).
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и острому углу ).
Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ).
Свойства прямоугольного треугольника
1. Сумма острых углов прямоугольного треугольника равна 90˚.
2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.
И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.
3. Теорема Пифагора:
, где – катеты, – гипотенуза. Видеодоказательство
4. Площадь прямоугольного треугольника с катетами :
5. Высота прямоугольного треугольника, проведенная к гипотенузе выражается через катеты и гипотенузу следующим образом:
6. Центр описанной окружности – есть середина гипотенузы.
7. Радиус описанной окружности есть половина гипотенузы :
8. Медиана, проведенная к гипотенузе, равна ее половине
9. Радиус вписанной окружности выражается через катеты и гипотенузу следующим образом:
Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.
http://planetcalc.ru/9363/
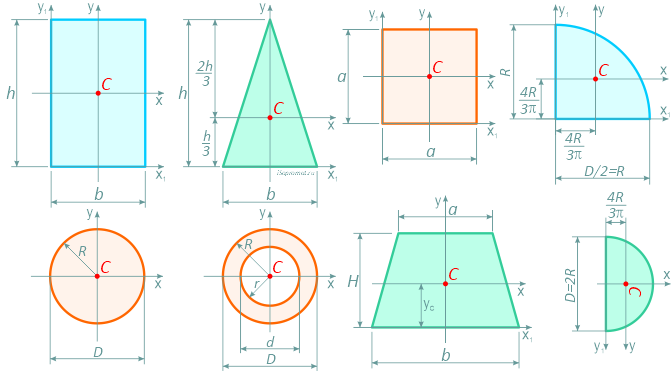
Формулы площадей, центров тяжести, осевых и полярных моментов инерции, моментов сопротивления и других геометрических характеристик основных простых фигур: прямоугольника, квадрата, равнобедренного и прямоугольного треугольника, круга, полукруга, четверти круга, кольцевого и тонкостенного сечений.
Обозначения в формулах:
C — положение центра тяжести фигуры;
A — площадь сечения;
Ix , Iy — осевые моменты инерции сечения относительно главных осей;
Ix1 , Iy1 — осевые моменты инерции относительно вспомогательных (смещённых) осей;
Iρ — полярный момент инерции сечения;
Wx , Wy — осевые моменты сопротивления;
Wρ — полярный момент сопротивления
Прямоугольник
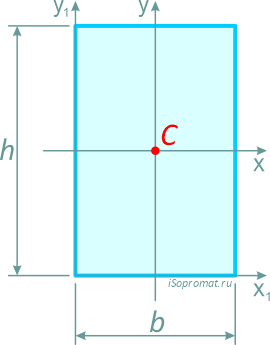
Прямоугольник высотой h и шириной b.
Центр тяжести прямоугольника в точке пересечения его диагоналей, на расстоянии половины высоты (h/2) по вертикали и половины ширины (b/2) по горизонтали.
Площадь
Центральные осевые моменты инерции прямоугольника
Моменты инерции относительно смещенных осей, проходящих через нижнюю левую точку
Осевые моменты сопротивления прямоугольного сечения
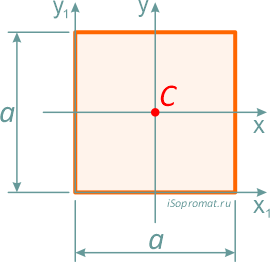
Квадрат
Квадрат — это частный случай прямоугольника, у которого высота равна ширине, т.е. h=b=a.
Центр тяжести квадрата находится так же на пересечении диагоналей — на расстоянии половины стороны (a/2) по высоте и ширине.
Площадь
Центральные осевые моменты инерции квадрата
Моменты инерции относительно смещенных осей, проходящих через нижнюю левую точку
Осевой момент сопротивления квадратного сечения
Треугольник равнобедренный
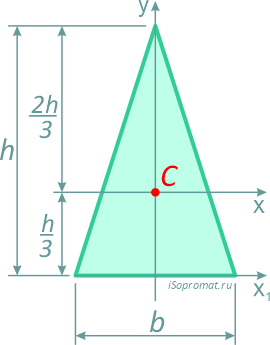
Равнобедренный треугольник высотой h и шириной основания b.
Центр тяжести треугольника располагается в точке пересечения его медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от его вершин.
Площадь
Центральные осевые моменты инерции треугольника
Момент инерции относительно смещенной оси x1, проходящей через его основание
Прямоугольный треугольник
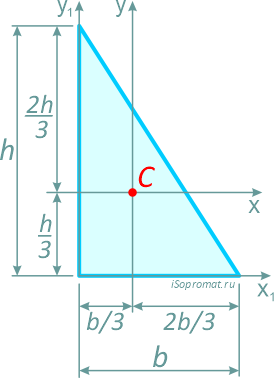
Прямоугольный треугольник высотой h и шириной основания b.
Центр тяжести прямоугольного треугольника располагается аналогично, на пересечении медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от вершины.
Площадь
Центральные осевые моменты инерции прямоугольного треугольника
Моменты инерции относительно смещенных осей x1 и y1, проходящих через точку, соединяющую его катеты
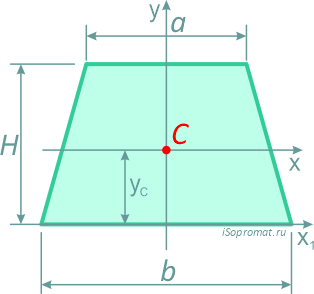
Трапеция
Равнобокая трапеция высотой H и шириной оснований: малого a и большого b.
Площадь трапеции
Центр тяжести на линии, соединяющей середины оснований трапеции, на высоте, определяемой по формуле:
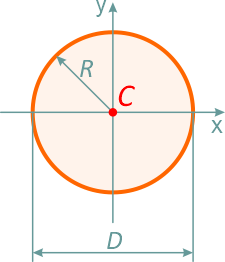
Круг
Круг диаметром D (d) или радиусом R (r)
Площадь круга через его диаметр и радиус
Центральные осевые и полярный моменты инерции круга
Осевые и полярный моменты сопротивления
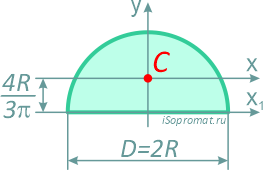
Полукруг
Половина круга диаметром D (d) или радиусом R (r)
Площадь
Осевые моменты инерции полукруга
Четверть круга
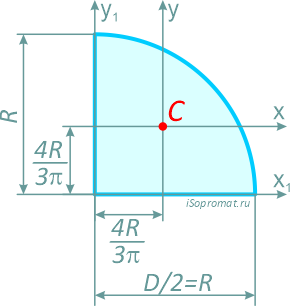
Четверть круга диаметром D (d) или радиусом R (r)
Площадь
Центральные осевые моменты инерции четверти круга
Моменты инерции относительно смещенных осей x1 и y1
Кольцо
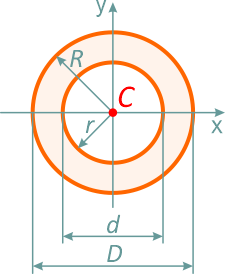
Кольцо с внешним диаметром D и внутренним d, (радиусами: внешним R и внутренним r)
Отношение внутреннего диаметра (радиуса) к внешнему обозначается буквой c.
Площадь
Центральные осевые и полярный моменты инерции кольца
Осевые и полярный моменты сопротивления
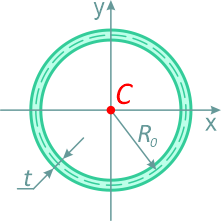
Тонкостенное сечение (труба)
Тонкостенный профиль (сечение трубы) средним радиусом R0 и толщиной стенки трубы t при R0>>t
Площадь
Центральные осевые и полярный моменты инерции трубного сечения
Осевые и полярный моменты сопротивления
Пример определения координат центра тяжести сложной фигуры:
Другие видео
Смотрите также:
Определение координат центра тяжести сложных фигур
Геометрические характеристики сечений
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Центр треугольника
Треугольник — наиболее распространенная форма деталей в сферах машиностроения и строительства. Точка пересечения 3-х медиан считается центром треугольника. На эту точку приходится также центр тяжести и центр симметрии предметов треугольной формы. При разработке дизайнерских, инженерных проектов очень важно точно рассчитать центр тяжести элементов металлической или бетонной конструкции.
Существует несколько понятий центра для треугольника.
Инцентр — точка пересечения его биссектрис. Это — центр описанной около треугольника окружности.
Ортоцентр — точка пересечения его высот.
Центр тяжести,центр масс или центроид (обозн. М) — точка пересечения медиан треугольника.
Рассмотрим треугольник. Определим середины его сторон и соединим их с противолежащими углами. Точка пересечения медиан и будет центром тяжести тр-ка. Медиана делится этой точкой в пропорции 2:1 , (считая от вершины тр-ка).
Как найти центр треугольника
Если известны координаты его вершин, найдем сумму трех значений координат «х» и трех значений координат «у». Поделим каждую сумму на 3, получим среднее значение сумм координат «х» и «у», что и будет координатами центра тяжести.
Центром равностороннего треугольника является точка пересечения высот, биссектрис и медиан.
Центр равностороннего треугольника является также центром вписанной и описанной окружности.
Центроид расположен на отрезке, соединяющем ортоцентр и центр описанной окружности. Центроид делит отрезок 2:1.
Быстро найти центр треугольника G можно с помощью онлайн калькулятора. Для этого:
- ввести в поле калькулятора координаты вершин треугольника;
- нажать кнопку Вычислить. Калькулятор вычислит значение центра треугольника G.
Центр тяжести треугольника
Этот онлайн калькулятор находит центроид, или барицентр (центр тяжести) треугольника по координатам его вершин
Центр тяжести (центр масс, барицентр) треугольника для треугольника с равномерно распределённой массой (или в вершинах которого находятся равные массы) находится в центроиде треугольника. Центроидом называется точка пересечения медиан треугольника. Центроид относится к так называемым замечательным точкам треугольника. Например, помимо того, что он является центром тяжести, он также делит каждую медиану в отношении 2:1, считая от вершины, а три отрезка прямых, соединяющих вершины треугольника с центроидом, разбивают данный треугольник на три равновеликих треугольника.
Чтобы вычислить положение центра тяжести по координатам вершин треугольника, достаточно вычислить среднее арифметическое координат вершин по оси x и по оси y, что и делает калькулятор ниже.
Прямоугольный треугольник
Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).
Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.
Стороны, прилежащие к прямому углу, называются катетами .
Признаки равенства прямоугольных треугольников
Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ).
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ).

Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ).
Свойства прямоугольного треугольника
1. Сумма острых углов прямоугольного треугольника равна 90˚.
2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.
И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.
3. Теорема Пифагора:
, где
– катеты,
– гипотенуза. Видеодоказательство
4. Площадь прямоугольного треугольника с катетами
:
5. Высота прямоугольного треугольника, проведенная к гипотенузе выражается через катеты
и гипотенузу
следующим образом:
6. Центр описанной окружности – есть середина гипотенузы.
7. Радиус описанной окружности есть половина гипотенузы
:
8. Медиана, проведенная к гипотенузе, равна ее половине
9. Радиус вписанной окружности выражается через катеты
и гипотенузу
следующим образом:
Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.
источники:
http://planetcalc.ru/9363/
http://egemaximum.ru/pryamougolnyj-treugolnik/
Загрузить PDF
Загрузить PDF
Центр тяжести треугольника (центроид) – это точка центра масс. Представьте себе треугольную линейку, положенную на кончик карандаша. Линейка будет балансировать, если кончик карандаша будет находиться в ее центре тяжести. Расположение центроида, которое легко находится с помощью геометрии, необходимо знать при работе над дизайнерским или инженерным проектом.
-
1
Найдите середину одной стороны треугольника. Для этого измерьте сторону и разделите ее длину пополам. Середину отметьте точкой A.
- Например, если сторона треугольника равна 10 см, то середина находится на расстоянии 5 см (
) от вершины треугольника.
- Например, если сторона треугольника равна 10 см, то середина находится на расстоянии 5 см (
-
2
Найдите середину второй стороны треугольника. Для этого измерьте сторону и разделите ее длину пополам. Середину отметьте точкой В.
- Например, если вторая сторона треугольника равна 12 см, то середина находится на расстоянии 6 см (
) от вершины треугольника.
- Например, если вторая сторона треугольника равна 12 см, то середина находится на расстоянии 6 см (
-
3
Соедините середины сторон с противолежащими вершинами. Вы получите две медианы.[1]
- Вершина – это точка, в которой сходятся две стороны треугольника.
-
4
Отметьте точку пересечения двух медиан. Эта точка является центром тяжести треугольника.[2]
[3]
- Центр тяжести находится на пересечении трех медиан, но так как медианы всегда пересекаются в одной точке, можно работать только с двумя медианами.
Реклама
-
1
Проведите медиану. Медиана – это отрезок, который соединяет вершину треугольника с серединой противолежащей стороны. Можно работать с любой медианой.
-
2
Измерьте длину медианы. Сделайте это аккуратно и точно.
- Например, медиана равна 3,6 см.
-
3
Найдите третью часть (треть) медианы. Для этого разделите длину медианы на три. Сделайте это аккуратно и точно. Округлив полученное значение, вы не найдете центроид.
- В нашем примере медиана равна 3,6 см. Поэтому разделите 3,6 на 3:
. Таким образом, треть медианы равна 1,2 см.
- В нашем примере медиана равна 3,6 см. Поэтому разделите 3,6 на 3:
-
4
Треть медианы отметьте точкой. Эта точка является центроидом, потому что он всегда делит медиану треугольника в отношении 2:1. То есть центр тяжести находится на расстоянии, которое равно ⅓ длины медианы, от середины стороны, или на расстоянии, которое равно ⅔ длины медианы, от вершины треугольника.[4]
- Например, если медиана равна 3,6 см, то центроид находится на расстоянии 1,2 см от середины стороны.
Реклама
-
1
Определите координаты трех вершин треугольника. Координаты могут быть даны; в противном случае будет дан треугольник, построенный на координатной плоскости. Координаты представляются в виде
.
- Например, дан треугольник PQR, вершины которого имеют следующие координаты: P (3,5), Q (4,1), R (1,0).
-
2
Сложите значения координат «х». Не забудьте сложить все три значения. Вы не найдете центр тяжести, если будете работать только с двумя значениями.
- Например, если координаты «х» равны 3, 4 и 1, сложите эти значения:
.
- Например, если координаты «х» равны 3, 4 и 1, сложите эти значения:
-
3
Сложите значения координат «у». Не забудьте сложить все три значения.
- Например, если координаты «у» равны 5, 1 и 0, сложите эти значения:
.
- Например, если координаты «у» равны 5, 1 и 0, сложите эти значения:
-
4
Найдите средние значения сумм координат «х» и «у». Полученные значения будут соответствовать центру тяжести треугольника.[5]
Чтобы найти среднее значение, разделите каждую сумму на 3. -
5
Нанесите точку центра тяжести на треугольник. Центр тяжести находится в точке, координаты которой равны средним значениям сумм координат «х» и «у».
- В нашем примере центр тяжести – это точка с координатами
.
Реклама
- В нашем примере центр тяжести – это точка с координатами
Советы
- Не имеет значения, с какой стороной треугольника вы работаете – центр тяжести будет находится в одной и той же точке. Если построить медианы для всех трех сторон, они пересекутся в одной точке.
Реклама
Похожие статьи
Об этой статье
Эту страницу просматривали 145 472 раза.
Была ли эта статья полезной?
Download Article
Download Article
The center of gravity, or centroid, is the point at which a triangle’s mass will balance. To help visualize this, imagine you have a triangular tile suspended over the tip of a pencil. The tile will balance if the pencil tip is placed at its center of gravity. Finding the centroid might be necessary in various design and engineering applications, and can be found by using simple geometry.
-
1
Find the midpoint of one side of the triangle. To find the midpoint, measure the side, and divide the length in half. Label the midpoint A.
- For example, if one side of the triangle is 10 cm long, the midpoint will be at 5 cm, since
.
- For example, if one side of the triangle is 10 cm long, the midpoint will be at 5 cm, since
-
2
Find the midpoint of a second side of the triangle. Measure the length of the side, and divide the length in half. Label the midpoint B.[1]
- For example, if the side of the triangle is 12 cm long, the midpoint will be at 6 cm, since
.
Advertisement
- For example, if the side of the triangle is 12 cm long, the midpoint will be at 6 cm, since
-
3
Draw a line from the midpoint of each side to its opposite vertex. These two lines are the median of each side.[2]
- A vertex is the point at which two sides of a triangle meet.
-
4
Draw a point where the two medians intersect. This point is the triangle’s center of gravity, also called the centroid, or center of mass.[3]
- The center of gravity is where the three medians intersect, but since the medians only intersect in one point, you can use a shortcut and find the center of gravity by only finding the intersection of two medians.
Advertisement
-
1
Draw a median of your triangle. Remember, the median is a line drawn from the midpoint of a side to the opposite vertex. You can use any median in the triangle.
-
2
Measure the length of the median. Make sure the measurement is exact.
- For example, you might have a median that is 3.6 cm long.
-
3
Divide the length of the median into thirds. To do this, divide the length by three. Again, make an exact calculation. If you round, you will not find the center of gravity.
- For example, if your median is 3.6 cm long, you would divide 3.6 by 3:
, so ⅓ of the median is 1.2 cm.
- For example, if your median is 3.6 cm long, you would divide 3.6 by 3:
-
4
Mark a point on the median ⅓ from the midpoint. This point is the triangle’s centroid, which will always divide a median into a 2:1 ratio; that is, the centroid is ⅓ the median’s distance from the midpoint, and ⅔ the median’s distance from the vertex.[4]
- For example, on a median that is 3.6 cm long, the centroid will be 1.2 cm up from the midpoint.
Advertisement
-
1
Determine the coordinates of the three vertices of the triangle. This method only works if you are working with a coordinate plane. The coordinates may already be given, or you may have a triangle drawn on a graph without the coordinates labeled. Remember that coordinates should be listed
.[5]
- For example, you might be given triangle PQR, and you need to find and label point P (3, 5), point Q (4, 1), and R (1, 0).
-
2
Add the value of the x-coordinates. Remember to add all three coordinates. You will not calculate the correct center of gravity if you only use two coordinates.[6]
- For example, if your three x-coordinates are 3, 4, and 1, add these three values together:
.
- For example, if your three x-coordinates are 3, 4, and 1, add these three values together:
-
3
Add the value of the y-coordinates. Remember to add all three coordinates.[7]
- For example, if your three y-coordinates are 5, 1, and 0, add these three values together:
.
- For example, if your three y-coordinates are 5, 1, and 0, add these three values together:
-
4
Find the average of the x- and y-coordinates. These coordinates will correspond to the triangle’s center of gravity, also known as the centroid or center of mass.[8]
To find the average, divide the sum of the coordinates by 3. -
5
Plot the center of gravity on the triangle. The center of gravity, or centroid, is the average of the x- and y-coordinates.[9]
- In the example problem, the center of gravity is the point
.
- In the example problem, the center of gravity is the point
Advertisement
Add New Question
-
Question
The length of a rectangle is x units and the width is x-5. How do I find an equation for the perimeter and area of the rectangle?
For the perimeter, add the four sides together and simplify. For the area, multiply the length by the width.
-
Question
Is the center of gravity of triangular cardboard outside or on the body?
The center of gravity is always inside the triangle.
-
Question
How can I determine the center of gravity of an Isoceles triangle without knowing the mass?
The horizontal coordinate will be half of the base, and the vertical will be one third of the height.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
It does not matter which side you select, the center of gravity will be at the same point. If you perform this process on all three sides, the lines will cross at a single point.
Thanks for submitting a tip for review!
Advertisement
References
About This Article
Article SummaryX
To calculate the center of gravity of a triangle, start by drawing a line from the midpoint of any 1 of the sides to the opposite vertex to create a median. Next, measure the median and divide it into thirds. For example, if the median is 3.6 cm long, mark the spots that are 1.2 cm and 2.4 cm along the median, starting from the midpoint. The spot that’s 1.2 inches from the midpoint is the centroid, or the center of gravity of the triangle. To learn more, like how to find the center of gravity of a triangle using intersecting medians, scroll down.
Did this summary help you?
Thanks to all authors for creating a page that has been read 274,568 times.