Прямые измерения как найти их результат

Прямые и косвенные измерения

По
способу получения результата измерения
делятся на прямые и косвенные. Если
значение физической величины находят
непосредственным отсчетом по шкале
прибора, то такие измерения называются
прямыми
(измерения давления барометром,
температуры – термометром, времени –
секундомером, длины – штангенциркулем
или линейкой, силы тока – амперметром
и т.п.). Эти измерения могут быть
однократными и многократными. Многократное
измерение – повторение экспериментельной
операции, в результате которой получается
одно из значений измеряемой величины

,
называемыхрезультатами
наблюдений.
Совокупность результатов наблюдений
подлежит совместной обработке для
получения результата измерения.

Часто
прямое измерение физической величины
оказывается невозможным или слишком
трудоемким. При косвенных
измерениях результат определяется по
формулам на основе результатов прямых
измерений других величин (например,
определение электрического cопротивления
образца по измеренным силе тока и
напряжению). Одну и ту же величину часто
можно найти путем как прямых, так и
косвенных измерений. Например, скорость
автомобиля может быть определена по
спидометру (прямое измерение) или найдена
делением пройденного пути на время
движения (косвенное измерение).

При косвенных
измерениях погрешность искомой физической
величины накапливается из погрешностей
прямых измерений величин, входящих в
расчетную формулу.

Погрешности многократных прямых измерений (случайные погрешности)

Пусть
изучается физическая величина
и многократными измерениями получены
результатов наблюдений

,

причем все измерения
выполнены одним и тем же методом и с
одинаковой степенью тщательности. Этот
ряд значений величины называется
выборкой.Предположим, что на
результат измерений оказывают действие
только случайные (неконтролируемые)
факторы, а промахи и систематические
ошибки отсутствуют.

Задача экспериментатора
состоит в том, чтобы найти наилучшую
оценку и доверительную погрешность
результата измерений для заданного
значения доверительной вероятности.
(При обработке экспериментальных
результатов можно поступать и по–другому:
произвольно задавать значение
доверительной погрешности и вычислять
соответствующее ей значение вероятности).
Указанная задача строго решается с
помощью теории вероятностей и
математической статистики.

В большинстве
случаев случайные ошибки подчиняются
установленному Гауссом нормальному
закону распределения, вид которого
может быть получен на основании следующих
предположений:

1) величина случайной
погрешности может иметь любое значение;

2) вероятность появления
погрешности снижается с ростом ее
величины – большие погрешности
маловероятны;

3) погрешности, равные
по величине, но разные по знаку, встречаются
одинаково часто – равные по модулю
погрешности равновероятны.

Выведенный на основе
указанных предположений закон нормального
распределения случайных величин
(распределение Гаусса) выражается
формулой

,
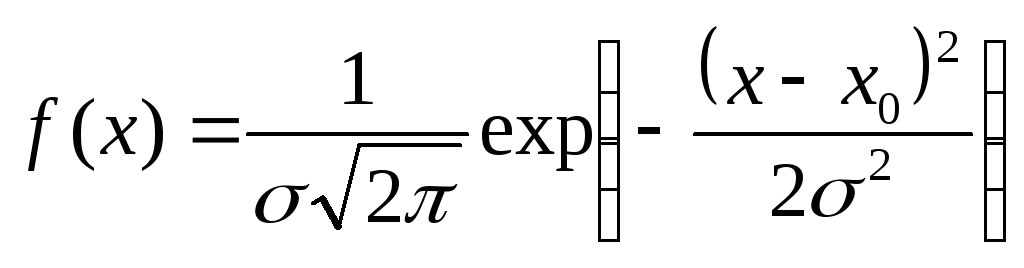
(3)

где
– числовое значение определяемой
величины,и– параметры распределения;– плотность вероятности (вероятность
того, что значениепринадлежит некоторому единичному
интервалу значений), так что функцияопределяет вероятность попадания
значенияв интервал отдо.

Параметр
,
соответствующий максимуму плотности
вероятности,
называетсяматематическим ожиданиемслучайной величины.
Параметрназываетсясредним квадратическим
отклонением величиныот ее математического ожиданияи характеризует меру ее разброса
относительно.
Очевидно, что

т.е. вероятность того,
что случайная величина
вообще имеет какое–то значение, равна
единице.

Поскольку максимальное значение
плотность вероятностипринимает при,
то величинучасто считают приблизительно равной
истинному значению измеряемой величины.
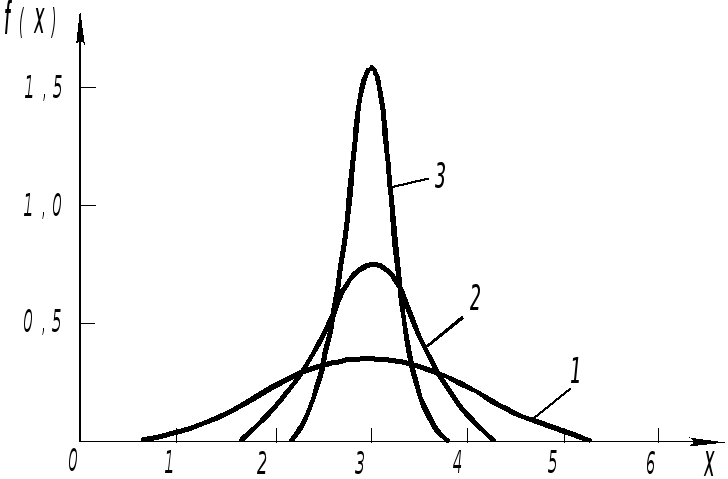
На рис.представлен график этой функции. Из
вышесказанного ясно, что площадь
заштрихованной фигуры численно равна
вероятности, с которой любой отсчет
попадает в интервал отдо.

Рис.1. Нормальное
(гауссово) распределение

(1–,2–/2,3–/4)
.

Из теории следует,
что наилучшей оценкой истинного значения
измеряемой случайной величиныявляется среднее арифметическое
(выборочное среднее) значение

.
(4)

Заметим также, что
с увеличением значения
увеличивается разброс отсчетов, т.е.
точность измерений понижается. В условиях
реального эксперимента точное значение,
как правило, неизвестно. По многократным
измерениямможно получить приближенную оценку
этого параметра в виде среднеквадратичной
погрешности отдельного результатаизмерения

,
(5)

которая характеризует
ошибку каждого отдельного измерения и
при неограниченном увеличении числа
наблюдений ()
стремится к истинной среднеквадратичной
ошибке.

Если произвести
несколько серий многократных измерений,
т.е. получить несколько выборок и для
каждой вычислить выборочное среднее,
то получим выборку для новой случайной
величины
,
которая также распределена нормально
с математическим ожиданием.
Однако параметрменьше, чем:

.

Это означает, что
выборочное среднее
имеет приблизительно вменьший разброс, чем единичное измерение.
Поэтому для оценкилучше использовать выборочное среднееи среднеквадратичную погрешность среднего арифметического результатаизмерения, которая вычисляется по
формуле

,
(6)

В выражениях (5) и
(6) обозначение среднеквадратичной
ошибки
заменено на обозначение,
чтобы подчеркнуть, что величиныивычисляются на основе ограниченного
числа наблюдений, т.е. являются
эмпирическими оценками теоретических
параметрови.

При проведении
реальных технических измерений число
отдельных измерений, как правило,
невелико и лежит в пределах от
до.
В такой ситуации рассмотренный метод
приводит к существенному искажению
результатов. В теории погрешностей при
малом числе измерений применяют
специальный метод вычисления доверительного
интервала, основанный на распределении
Стьюдента. В 1908 г. английский математик
У. Госсет (псевдоним ’’Стьюдент’’)
доказал, что указанными соотношениями
можно пользоваться и при небольшом
числе наблюдений

(),
следует только на конечной стадии ввести
в расчет специальный коэффициент,
величина которого зависит от числа
наблюденийи требуемого значения доверительной
вероятности,
– так называемый коэффициент Стьюдента.

Таблица 1

Коэффициенты Стьюдента
.

Выполнение
и обработку результатов прямых
многократных измерений рекомендуется
производить в следующем порядке.

1.
Прямыми измерениями получить ряд
значений
измеряемой величины.

2.
Вычислить среднеарифметическое значение
результата измерений

.

3. Вычислить отклонения
отдельных результатов наблюдений от
среднего

4.
Вычислить значения
и сумму.

5.
Для данных значений числа измерений
и доверительной вероятностинайти по таблице коэффициент Стьюдентаи вычислить случайную погрешность

.
(7)

6. Округлив
погрешность и предварительный результат,
записать окончательный результат
измерений в виде

Пример.
Обработка результатов прямых многократных
измерений диметра

некоторого вала штангенциркулем.

Получены
6 значений
,
которые внесены во 2–й столбец таблицы
2.

Таблица 2

Соседние файлы в предмете Физика

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Погрешности измерений, представление результатов эксперимента

1. Шкала измерительного прибора
2. Цена деления
3. Виды измерений
4. Погрешность измерений, абсолютная и относительная погрешность
5. Абсолютная погрешность серии измерений
6. Представление результатов эксперимента
7. Задачи

п.1. Шкала измерительного прибора

Шкала – это показывающая часть измерительного прибора, состоящая из упорядоченного ряда отметок со связанной с ними нумерацией. Шкала может располагаться по окружности, дуге или прямой линии.

Примеры шкал различных приборов:

п.2. Цена деления

Цена деления измерительного прибора равна числу единиц измеряемой величины между двумя ближайшими делениями шкалы. Как правило, цена деления указана на маркировке прибора.

Алгоритм определения цены деления
Шаг 1. Найти два ближайшие пронумерованные крупные деления шкалы. Пусть первое значение равно a, второе равно b, b > a.
Шаг 2. Посчитать количество мелких делений шкалы между ними. Пусть это количество равно n.
Шаг 3. Разделить разницу значений крупных делений шкалы на количество отрезков, которые образуются мелкими делениями: $$ triangle=frac{b-a}{n+1} $$ Найденное значение (triangle) и есть цена деления данного прибора.

Пример определения цены деления:

Определим цену деления основной шкалы секундомера. Два ближайших пронумерованных деления на основной шкале:a = 5 c b = 10 cМежду ними находится 4 средних деления, а между каждыми средними делениями еще 4 мелких. Итого: 4+4·5=24 деления. Цена деления: begin{gather*} triangle=frac{b-a}{n+1}\ triangle=frac{10-5}{24+1}=frac15=0,2 c end{gather*}

п.3. Виды измерений

Вид измерений

Определение

Пример

Прямое измерение

Физическую величину измеряют с помощью прибора

Измерение длины бруска линейкой

Косвенное измерение

Физическую величину рассчитывают по формуле, куда подставляют значения величин, полученных с помощью прямых измерений

Определение площади столешницы при измеренной длине и ширине

п.4. Погрешность измерений, абсолютная и относительная погрешность

Погрешность измерений – это отклонение измеренного значения величины от её истинного значения.

Составляющие погрешности измерений

Причины

Инструментальная погрешность

Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)

Погрешность метода

Определяется несовершенством методов и допущениями в методике.

Погрешность теории (модели)

Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.

Погрешность оператора

Определяется субъективным фактором, ошибками экспериментатора.

Инструментальная погрешность измерений принимается равной половине цены деления прибора: $$ d=frac{triangle}{2} $$

Если величина (a_0) — это истинное значение, а (triangle a) — погрешность измерения, результат измерений физической величины записывают в виде (a=a_0pmtriangle a).

Абсолютная погрешность измерения – это модуль разности между измеренным и истинным значением измеряемой величины: $$ triangle a=|a-a_0| $$

Отношение абсолютной погрешности измерения к истинному значению, выраженное в процентах, называют относительной погрешностью измерения: $$ delta=frac{triangle a}{a_0}cdot 100text{%} $$

Относительная погрешность является мерой точности измерения: чем меньше относительная погрешность, тем измерение точнее. По абсолютной погрешности о точности измерения судить нельзя.
На практике абсолютную и относительную погрешности округляют до двух значащих цифр с избытком, т.е. всегда в сторону увеличения.

Значащие цифры – это все верные цифры числа, кроме нулей слева. Результаты измерений записывают только значащими цифрами.

Примеры значащих цифр:
0,403 – три значащих цифры, величина определена с точностью до тысячных.
40,3 – три значащих цифры, величина определена с точностью до десятых.
40,300 – пять значащих цифр, величина определена с точностью до тысячных.

В простейших измерениях инструментальная погрешность прибора является основной.
В таких случаях физическую величину измеряют один раз, полученное значение берут в качестве истинного, а абсолютную погрешность считают равной инструментальной погрешности прибора.
Примеры измерений с абсолютной погрешностью равной инструментальной:

• определение длины с помощью линейки или мерной ленты;
• определение объема с помощью мензурки.

Пример получения результатов прямых измерений с помощью линейки:

Измерим длину бруска линейкой, у которой пронумерованы сантиметры и есть только одно деление между пронумерованными делениями. Цена деления такой линейки: begin{gather*} triangle=frac{b-a}{n+1}= frac{1 text{см}}{1+1}=0,5 text{см} end{gather*} Инструментальная погрешность: begin{gather*} d=frac{triangle}{2}=frac{0,5}{2}=0,25 text{см} end{gather*} Истинное значение: (L_0=4 text{см}) Результат измерений: $$ L=L_0pm d=(4,00pm 0,25) text{см} $$ Относительная погрешность: $$ delta=frac{0,25}{4,00}cdot 100text{%}=6,25text{%}approx 6,3text{%} $$

Теперь возьмем линейку с n=9 мелкими делениями между пронумерованными делениями. Цена деления такой линейки: begin{gather*} triangle=frac{b-a}{n+1}= frac{1 text{см}}{9+1}=0,1 text{см} end{gather*} Инструментальная погрешность: begin{gather*} d=frac{triangle}{2}=frac{0,1}{2}=0,05 text{см} end{gather*} Истинное значение: (L_0=4,15 text{см}) Результат измерений: $$ L=L_0pm d=(4,15pm 0,05) text{см} $$ Относительная погрешность: $$ delta=frac{0,05}{4,15}cdot 100text{%}approx 1,2text{%} $$

Второе измерение точнее, т.к. его относительная погрешность меньше.

п.5. Абсолютная погрешность серии измерений

Измерение длины с помощью линейки (или объема с помощью мензурки) являются теми редкими случаями, когда для определения истинного значения достаточно одного измерения, а абсолютная погрешность сразу берется равной инструментальной погрешности, т.е. половине цены деления линейки (или мензурки).

Гораздо чаще погрешность метода или погрешность оператора оказываются заметно больше инструментальной погрешности. В таких случаях значение измеренной физической величины каждый раз немного меняется, и для оценки истинного значения и абсолютной погрешности нужна серия измерений и вычисление средних значений.

Алгоритм определения истинного значения и абсолютной погрешности в серии измерений
Шаг 1. Проводим серию из (N) измерений, в каждом из которых получаем значение величины (x_1,x_2,…,x_N)
Шаг 2. Истинное значение величины принимаем равным среднему арифметическому всех измерений: $$ x_0=x_{cp}=frac{x_1+x_2+…+x_N}{N} $$ Шаг 3. Находим абсолютные отклонения от истинного значения для каждого измерения: $$ triangle_1=|x_0-x_1|, triangle_2=|x_0-x_2|, …, triangle_N=|x_0-x_N| $$ Шаг 4. Находим среднее арифметическое всех абсолютных отклонений: $$ triangle_{cp}=frac{triangle_1+triangle_2+…+triangle_N}{N} $$ Шаг 5. Сравниваем полученную величину (triangle_{cp}) c инструментальной погрешностью прибора d (половина цены деления). Большую из этих двух величин принимаем за абсолютную погрешность: $$ triangle x=maxleft{triangle_{cp}; dright} $$ Шаг 6. Записываем результат серии измерений: (x=x_0pmtriangle x).

Пример расчета истинного значения и погрешности для серии прямых измерений:
Пусть при измерении массы шарика с помощью рычажных весов мы получили в трех опытах следующие значения: 99,8 г; 101,2 г; 100,3 г.
Инструментальная погрешность весов d = 0,05 г.
Найдем истинное значение массы и абсолютную погрешность.

Составим расчетную таблицу:

№ опыта	1	2	3	Сумма
Масса, г	99,8	101,2	100,3	301,3
Абсолютное отклонение, г	0,6	0,8	0,1	1,5

Сначала находим среднее значение всех измерений: begin{gather*} m_0=frac{99,8+101,2+100,3}{3}=frac{301,3}{3}approx 100,4 text{г} end{gather*} Это среднее значение принимаем за истинное значение массы.
Затем считаем абсолютное отклонение каждого опыта как модуль разности (m_0) и измерения. begin{gather*} triangle_1=|100,4-99,8|=0,6\ triangle_2=|100,4-101,2|=0,8\ triangle_3=|100,4-100,3|=0,1 end{gather*} Находим среднее абсолютное отклонение: begin{gather*} triangle_{cp}=frac{0,6+0,8+0,1}{3}=frac{1,5}{3}=0,5 text{(г)} end{gather*} Мы видим, что полученное значение (triangle_{cp}) больше инструментальной погрешности d.
Поэтому абсолютная погрешность измерения массы: begin{gather*} triangle m=maxleft{triangle_{cp}; dright}=maxleft{0,5; 0,05right} text{(г)} end{gather*} Записываем результат: begin{gather*} m=m_0pmtriangle m\ m=(100,4pm 0,5) text{(г)} end{gather*} Относительная погрешность (с двумя значащими цифрами): begin{gather*} delta_m=frac{0,5}{100,4}cdot 100text{%}approx 0,050text{%} end{gather*}

п.6. Представление результатов эксперимента

Результат измерения представляется в виде $$ a=a_0pmtriangle a $$ где (a_0) – истинное значение, (triangle a) – абсолютная погрешность измерения.

Как найти результат прямого измерения, мы рассмотрели выше.
Результат косвенного измерения зависит от действий, которые производятся при подстановке в формулу величин, полученных с помощью прямых измерений.

Погрешность суммы и разности
Если (a=a_0+triangle a) и (b=b_0+triangle b) – результаты двух прямых измерений, то

• абсолютная погрешность их суммы равна сумме абсолютных погрешностей

$$ triangle (a+b)=triangle a+triangle b $$

• абсолютная погрешность их разности также равна сумме абсолютных погрешностей

$$ triangle (a-b)=triangle a+triangle b $$

Погрешность произведения и частного
Если (a=a_0+triangle a) и (b=b_0+triangle b) – результаты двух прямых измерений, с относительными погрешностями (delta_a=frac{triangle a}{a_0}cdot 100text{%}) и (delta_b=frac{triangle b}{b_0}cdot 100text{%}) соответственно, то:

• относительная погрешность их произведения равна сумме относительных погрешностей

$$ delta_{acdot b}=delta_a+delta_b $$

• относительная погрешность их частного также равна сумме относительных погрешностей

$$ delta_{a/b}=delta_a+delta_b $$

Погрешность степени
Если (a=a_0+triangle a) результат прямого измерения, с относительной погрешностью (delta_a=frac{triangle a}{a_0}cdot 100text{%}), то:

• относительная погрешность квадрата (a^2) равна удвоенной относительной погрешности

$$ delta_{a^2}=2delta_a $$

• относительная погрешность куба (a^3) равна утроенной относительной погрешности

$$ delta_{a^3}=3delta_a $$

• относительная погрешность произвольной натуральной степени (a^n) равна

$$ delta_{a^n}=ndelta_a $$

Вывод этих формул достаточно сложен, но если интересно, его можно найти в Главе 7 справочника по алгебре для 8 класса.

п.7. Задачи

Задача 1. Определите цену деления и объем налитой жидкости для каждой из мензурок. В каком случае измерение наиболее точно; наименее точно?

Составим таблицу для расчета цены деления:

№ мензурки	a, мл	b, мл	n	(triangle=frac{b-a}{n+1}), мл
1	20	40	4	(frac{40-20}{4+1}=4)
2	100	200	4	(frac{200-100}{4+1}=20)
3	15	30	4	(frac{30-15}{4+1}=3)
4	200	400	4	(frac{400-200}{4+1}=40)

Инструментальная точность мензурки равна половине цены деления.
Принимаем инструментальную точность за абсолютную погрешность и измеренное значение объема за истинное.
Составим таблицу для расчета относительной погрешности (оставляем две значащих цифры и округляем с избытком):

№ мензурки	Объем (V_0), мл	Абсолютная погрешность (triangle V=frac{triangle}{2}), мл	Относительная погрешность (delta_V=frac{triangle V}{V_0}cdot 100text{%})
1	68	2	3,0%
2	280	10	3,6%
3	27	1,5	5,6%
4	480	20	4,2%

Наиболее точное измерение в 1-й мензурке, наименее точное – в 3-й мензурке.

Ответ:
Цена деления 4; 20; 3; 40 мл
Объем 68; 280; 27; 480 мл
Самое точное – 1-я мензурка; самое неточное – 3-я мензурка

Задача 2. В двух научных работах указаны два значения измерений одной и той же величины: $$ x_1=(4,0pm 0,1) text{м}, x_2=(4,0pm 0,03) text{м} $$ Какое из этих измерений точней и почему?

Мерой точности является относительная погрешность измерений. Получаем: begin{gather*} delta_1=frac{0,1}{4,0}cdot 100text{%}=2,5text{%}\ delta_2=frac{0,03}{4,0}cdot 100text{%}=0,75text{%} end{gather*} Относительная погрешность второго измерения меньше. Значит, второе измерение точней.
Ответ: (delta_2lt delta_1), второе измерение точней.

Задача 3. Две машины движутся навстречу друг другу со скоростями 54 км/ч и 72 км/ч.
Цена деления спидометра первой машины 10 км/ч, второй машины – 1 км/ч.
Найдите скорость их сближения, абсолютную и относительную погрешность этой величины.

Абсолютная погрешность скорости каждой машины равна инструментальной, т.е. половине деления спидометра: $$ triangle v_1=frac{10}{2}=5 (text{км/ч}), triangle v_2=frac{1}{2}=0,5 (text{км/ч}) $$ Показания каждого из спидометров: $$ v_1=(54pm 5) text{км/ч}, v_2=(72pm 0,5) text{км/ч} $$ Скорость сближения равна сумме скоростей: $$ v_0=v_{10}+v_{20}, v_0=54+72=125 text{км/ч} $$ Для суммы абсолютная погрешность равна сумме абсолютных погрешностей слагаемых. $$ triangle v=triangle v_1+triangle v_2, triangle v=5+0,5=5,5 text{км/ч} $$ Скорость сближения с учетом погрешности равна: $$ v=(126,0pm 5,5) text{км/ч} $$ Относительная погрешность: $$ delta_v=frac{5,5}{126,0}cdot 100text{%}approx 4,4text{%} $$ Ответ: (v=(126,0pm 5,5) text{км/ч}, delta_vapprox 4,4text{%})

Задача 4. Измеренная длина столешницы равна 90,2 см, ширина 60,1 см. Измерения проводились с помощью линейки с ценой деления 0,1 см. Найдите площадь столешницы, абсолютную и относительную погрешность этой величины.

Инструментальная погрешность линейки (d=frac{0,1}{2}=0,05 text{см})
Результаты прямых измерений длины и ширины: $$ a=(90,20pm 0,05) text{см}, b=(60,10pm 0,05) text{см} $$ Относительные погрешности (не забываем про правила округления): begin{gather*} delta_1=frac{0,05}{90,20}cdot 100text{%}approx 0,0554text{%}approx uparrow 0,056text{%}\ delta_2=frac{0,05}{60,10}cdot 100text{%}approx 0,0832text{%}approx uparrow 0,084text{%} end{gather*} Площадь столешницы: $$ S=ab, S=90,2cdot 60,1 = 5421,01 text{см}^2 $$ Для произведения относительная погрешность равна сумме относительных погрешностей слагаемых: $$ delta_S=delta_a+delta_b=0,056text{%}+0,084text{%}=0,140text{%}=0,14text{%} $$ Абсолютная погрешность: begin{gather*} triangle S=Scdot delta_S=5421,01cdot 0,0014=7,59approx 7,6 text{см}^2\ S=(5421,0pm 7,6) text{см}^2 end{gather*} Ответ: (S=(5421,0pm 7,6) text{см}^2, delta_Sapprox 0,14text{%})

Прямое измерение

Полезное