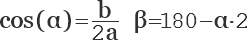Как найти угол при вершине равнобедренного треугольника?
Каким может быть угол при вершине равнобедренного треугольника?
Задача
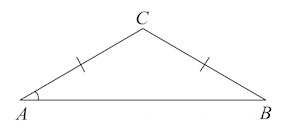
Найти угол при вершине равнобедренного треугольника, если угол при его основании равен α.
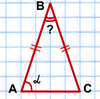
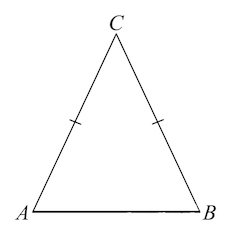
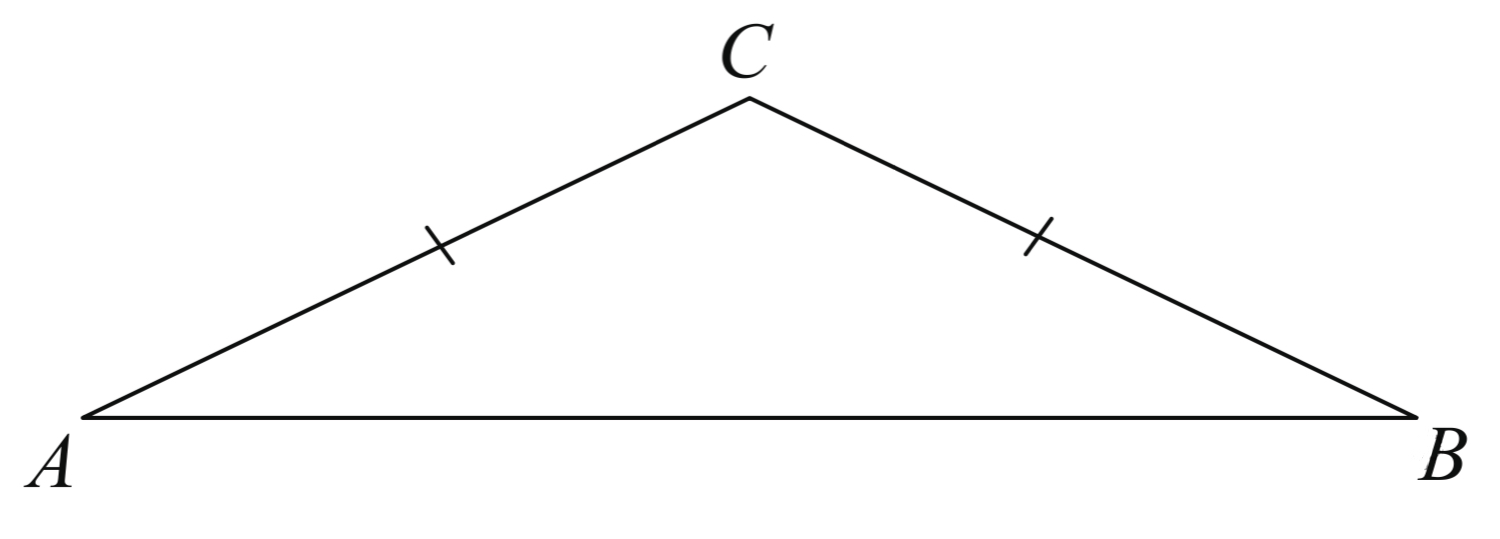
AB=BC,
∠A=α,
Найти: ∠B.
Решение:
Так как сумма углов треугольника равна 180º,
∠A+∠B+∠C=180º.
∠A=∠C (как углы при основании равнобедренного треугольника).
Значит, α+∠B+α=180º, откуда ∠B=180º-2α.
Ответ: 180º-2α.
Выводы:
1) Угол при вершине равнобедренного треугольника равен 180º минус удвоенный угол при его основании.
2) Чем больше угол при основании равнобедренного треугольника, тем меньше угол при его вершине.
3) Если угол при основании α=45º, угол при вершине равнобедренного треугольника — прямой, так как
180º-2∙45º=90º.
Если угол при основании больше 45º, угол при вершине — острый, так как
при α>45º произведение 2α>90º, откуда 180º-2α<90º.
Если угол при основании меньше 45º, угол при вершине равнобедренного треугольника — тупой:
при α<45º произведение 2α<90º, откуда 180º-2α>90º.
Углы равнобедренного треугольника
Угол
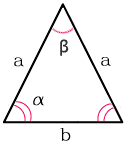
Треугольник с одинаковыми боковыми сторонами называется равнобедренным. В нем равны и углы при основании. Если они известны, то вычислить третий угол не составит труда. Как известно, сумма всех углов треугольника равна 180°. Если из 180° вычесть сумму двух одинаковых углов при основании (а), то найдем третий угол β:
β = 180°-2α
Если известна величина угла b, противолежащего основанию и требуется найти угол (а) при основании, необходимо из 180° вычесть известный угол β. Полученную величину делим на два, т.к. углы при основании равны.
α= (180°-β)/2
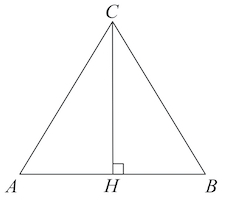
Если известны стороны равнобедренного треугольника, можно рассчитать все его углы. Чтобы найти угол при основании, проведем к основанию высоту, которая делит основание пополам, а треугольник — на два одинаковых прямоугольных треугольника. Гипотенузой вновь образованных треугольников будет боковая сторона равнобедренного треугольника (а), а одним из катетов — половина длины основания (b/2). Используя теорему косинусов определяем косинус угла (а), как отношение прилежащего к искомому углу катета (b/2) к гипотенузе (а) по формуле:
cosα= b/2a
Рассчитать угол при основании равнобедренного треугольника можно также через катеты образованного в нем прямоугольного треугольника (например, abc). Одним из его катетов (b) будет половина длины основания равнобедренного треугольника, другим катетом (а) — высота равнобедренного треугольника. Найти угол α при основании треугольника можно через тангенс угла, как отношение противолежащего ему катета (а) к прилежащему катету (b).
tg (α) = a/b
В таблицк тангенсов находим угол α в градусах. Т.к. Углы при основании равнобедренного треугольника равны, то найти третий угол не составит труда, зная, что сумма всех его углов равна 180°.
Рассчитать углы равнобедренного треугольника зная длину катетов
Равнобедренный треугольник, свойства, признаки и формулы
Равнобедренный треугольник – это треугольник, у которого две стороны равны между собой по длине.
Равнобедренный треугольник (понятие)
Свойства равнобедренного треугольника
Признаки равнобедренного треугольника
Формулы равнобедренного треугольника
Равнобедренный треугольник в природе, технике и культуре
Остроугольный треугольник, прямоугольный треугольник, равнобедренный треугольник, равносторонний треугольник, тупоугольный треугольник
Равнобедренный треугольник (понятие):
Равнобедренный треугольник – это треугольник, у которого две стороны равны между собой по длине.
Две равные стороны равнобедренного треугольника называются боковыми, а третья неравная им сторона – основанием.
Рис. 1. Равнобедренный треугольник
АВ = ВС – боковые стороны, АС – основание,
∠ АВС – вершинный угол, ∠ BАC и ∠ BСA – углы при основании
По определению, каждый правильный (равносторонний) треугольник также является равнобедренным, но не каждый равнобедренный треугольник – правильным (равносторонним).
Угол, образованный боковыми сторонами, называется вершинным углом, а углы, одной из сторон которых является основание, называются углами при основании.
Различают следующие виды равнобедренных треугольников:
– остроугольный – все углы острые;
– прямоугольный – угол при вершине прямой, а при основании углы острые;
– тупоугольный – угол при вершине тупой, а при основании углы острые;
– равносторонний (или правильный) – все стороны равны и все углы равны.
Свойства равнобедренного треугольника:
1. В равнобедренном треугольнике углы при основании равны.
Рис. 2. Равнобедренный треугольник
∠ BАC = ∠ BСA
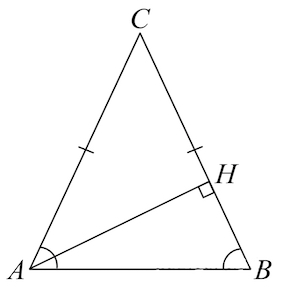
2. Биссектрисы, медианы и высоты, проведённые из этих углов равны между собой.
Рис. 3. Равнобедренный треугольник
АН1 = СН2 – высота, АМ1 = СМ2 – медиана, АL1 = СL2 – биссектриса, проведённые из углов при основании
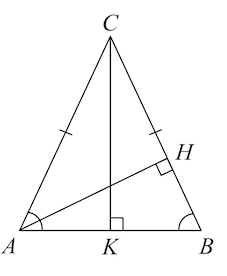
3. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Рис. 4. Равнобедренный треугольник
ВD – биссектриса, высота и медиана, проведенные к основанию – это один и тот же отрезок
4. Центры вписанной и описанной окружностей лежат на медиане (биссектрисе, высоте), проведенной к основанию равнобедренного треугольника.
Рис. 5. Равнобедренный треугольник
R – радиус описанной окружности, r – радиус вписанной окружности
Признаки равнобедренного треугольника:
– если в треугольнике два угла равны, то он равнобедренный;
– если в треугольнике биссектриса является медианой или высотой, то этот треугольник равнобедренный;
– если в треугольнике медиана является биссектрисой или высотой, то этот треугольник равнобедренный;
– если в треугольнике высота является медианой или биссектрисой, то этот треугольник равнобедренный.
Формулы равнобедренного треугольника:
Пусть a – длина двух равных сторон равнобедренного треугольника, b – длина основания, h – высота (биссектриса, медиана) равнобедренного треугольника, проведенная к основанию, α – углы при основании, β – вершинный угол, R – радиус описанной окружности, r – радиус вписанной окружности (см. Рис. 6, 7, 8).
Рис. 6. Равнобедренный треугольник
Формулы длины основания (b):
,
,
.
Формулы длины равных сторон (а):
.
Формулы углов:
Рис. 7. Равнобедренный треугольник
,
,

Формулы периметра (Р) равнобедренного треугольника:
Рис. 8. Равнобедренный треугольник
,
.
Формулы площади (S) равнобедренного треугольника:



Равнобедренный треугольник в природе, технике и культуре:
Например, молекула сероводорода имеет структуру равнобедренного треугольника с атомом серы S в центре.
Рис. 1. Структура молекулы сероводорода
Длина боковой стороны – связи HS = 133,6 пм, а вершинный угол ∠HSH = 92,1°.
Остроугольный треугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Тупоугольный треугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Коэффициент востребованности
9 685
21
Июл 2013
Категория: 01 Геометрия
01. Равнобедренный треугольник. Вычисление углов и длин
2013-07-21
2022-12-02
Задача 1. В треугольнике
Найдите
Решение: + показать
Задача 2. В треугольнике
Найдите
Решение: + показать
Задача 3. В треугольнике
Найдите
Решение: + показать
Задача 4. В треугольнике
Найдите высоту
Решение: + показать
Ответ:
Задача 5. В тупоугольном треугольнике
высота
равна
Найдите

Задача 6. В тупоугольном треугольнике
высота
равна
Найдите косинус угла
.

Задача 7. В тупоугольном треугольнике
высота
равна
Найдите
Решение: + показать
Задача 8. В треугольнике
Найдите высоту
.
Решение: + показать
Задача 9. В равнобедренном треугольнике с основанием
боковая сторона равна
Найдите длину высоты
Решение: + показать
Задача 10. В равнобедренном треугольнике с основанием
боковая сторона равна
Найдите
Решение: + показать
Задача 11. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен Боковая сторона треугольника равна
Найдите площадь этого треугольника.
Решение: + показать
Задача 12. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен Найдите боковую сторону треугольника, если его площадь равна
Решение: + показать
Задача 13. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен Боковая сторона треугольника равна
Найдите площадь этого треугольника.
Решение: + показать
Задача 14. Боковая сторона равнобедренного треугольника равна а основание равно
Найдите площадь этого треугольника.
Решение: + показать
Ответ:
Задача 15. В треугольнике
Найдите высоту
Решение: + показать
Задача 16. В равностороннем треугольнике высота
равна
Найдите стороны этого треугольника.
Задача 17. В треугольнике
угол
равен
Найдите высоту
.
Решение: + показать
Задача 18. В треугольнике
высота
равна
Найдите угол
Ответ дайте в градусах.
Решение: + показать
Задача 19. В треугольнике угол
равен
Найдите угол
Ответ дайте в градусах.
Решение: + показать
Задача 20. Один угол равнобедренного треугольника на больше другого. Найдите меньший угол. Ответ дайте в градусах.
Решение: + показать
Задача 21. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен Боковая сторона треугольника равна
Найдите длину основания этого треугольника.
Решение: + показать
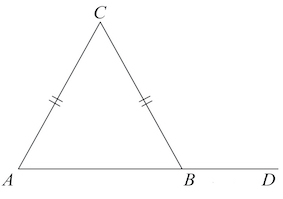
Задача 22. В треугольнике
Внешний угол при вершине
равен
Найдите угол
Ответ дайте в градусах.
Решение: + показать
Вы можете пройти тест по теме «Равнобедренный треугольник. Вычисление углов и длин».
Автор: egeMax |
комментариев 12
Установить Углы равнобедренного треугольника на мобильный
Найти углы равнобедренного треугольника
зная стороны и основание
|
||
| Сторона равнобедренного треугольника a | ||
| Основание равнобедренного треугольника b | ||
|
|
||
| Угол α (градус) | ||
| Угол β (градус) |
Скачать калькулятор
Рейтинг: 3.6 (Голосов 10)
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Сообщить об ошибке
Смотрите также
| Углы | Углы треугольника | Углы прямоугольного | Углы ромба |
| Углы параллелограмма | Многоугольник | Таблица синусов | Таблица косинусов |