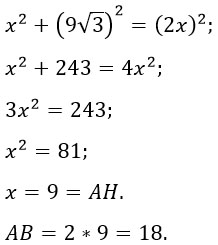Биссектриса равностороннего треугольника найти сторону
Задание 9. Биссектриса равностороннего треугольника равна 12√3. Найдите его сторону.
В равностороннем треугольнике все стороны равны, а биссектриса является также медианой и высотой h (см. рисунок).
Из рисунка видно, что сторону 
равностороннего треугольника можно найти из прямоугольного треугольника, в котором один катет является высотой h, второй – половина основания, равная a/2, к которому проведена высота, а роль гипотенузы будет играть сторона треугольника, равная a. Таким образом, по теореме Пифагора, можно записать равенство:
,
откуда выразим сторону треугольника:
Подставим вместо h=12√3, получим квадрат стороны треугольника:
и сторона равна
.
Задание 10. В треугольнике ABC известно, что AC = 7, BC = 24, угол С равен 90°. Найдите радиус описанной около этого треугольника окружности.
Радиус описанной окружности вокруг прямоугольного треугольника лежит в центре его гипотенузы. В задаче даны катеты прямоугольного треугольника с длинами 7 и 24 соответственно. По теореме Пифагора найдем длину гипотенузы, получим:
.
Таким образом, радиус описанной окружности равен
.
Свойства биссектрисы равностороннего треугольника
В данной публикации мы рассмотрим основные свойства биссектрисы равностороннего треугольника, а также разберем пример решения задачи по данной теме.
Примечание: напомним, что равносторонним называется треугольник, в котором равны как все стороны, так и все углы.
Свойства биссектрисы равностороннего треугольника
Свойство 1
Любая биссектриса равностороннего треугольника одновременно является и медианой, и высотой, и серединным перпендикуляром.
BD – биссектриса угла ABC, которая также является:
- высотой, опущенной на сторону AC;
- медианой, делящей сторону AC на два равных отрезка (AD = DC);
Свойство 2
Все три биссектрисы равностороннего треугольника равны между собой.
Свойство 3
Биссектрисы равностороннего треугольника в точке пересечения делятся в отношении 2:1, считая от вершины.
Свойство 4
Точка пересечения биссектрис равностороннего треугольника является центром описанной и вписанной окружностей.
- r – радиус вписанной окружности;
- R – радиус описанной окружности;
- R = 2r.
Свойство 5
Биссектриса равностороннего треугольника делит его на два равновеликих (равных по площади) прямоугольных треугольника.
Примечание: Три биссектрисы равностороннего треугольника делят его на 6 равновеликих прямоугольных треугольников.
Свойство 6
Любая из внешних биссектрис угла равностороннего треугольника параллельна стороне, лежащей напротив данного угла.
- AD и AE – внешние биссектрисы, параллельные BC;
- BK и BL – внешние биссектрисы, параллельные AC;
- CM и CN – внешние биссектрисы, параллельные AB.
Свойство 7
Длину биссектрисы ( la ) равностороннего треугольника можно выразить через его сторону.
где a – сторона треугольника.
Пример задачи
Радиус вписанной в равносторонний треугольник окружности равен 4 см. Найдите длину его стороны.
Решение
Согласно Свойствам 3 и 4, рассмотренным выше, радиус вписанной окружности составляет 1/3 часть от биссектрисы равностороннего треугольника. Следовательно, вся ее длина равняется 12 см (4 см ⋅ 3).
Теперь мы можем найти сторону треугольника с помощью формулы ниже (получена из Свойства 7):
Решение №2224 Биссектриса равностороннего треугольника равна 17√3. Найдите сторону этого треугольника.
Биссектриса равностороннего треугольника равна 17√3. Найдите сторону этого треугольника.
Источник: ОГЭ Ященко 2022 (50 вариантов)
В равностороннем треугольнике все углы равны 60°, а биссектриса является так же высотой.
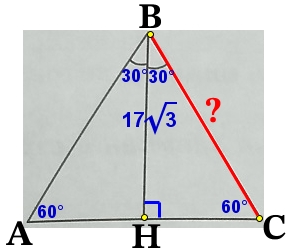
∠АВН = ∠СВН = 60°/2 = 30°
∠ВНС = 90°
В прямоугольном треугольнике ΔНВС, через косинус угла ∠СВН найдём искомую сторону ВС .
Косинус острого угла прямоугольного треугольника – это отношение прилежащего катета к гипотенузе.
|:√3
ВС = 2·17 = 34
Решение:
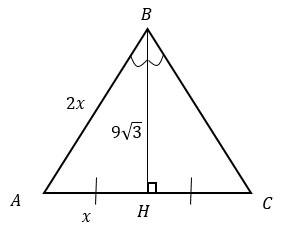
Биссектриса в равностороннем треугольнике является медианой и высотой.
Обозначим половину стороны треугольника за икс. Пусть AH = x, тогда целая сторона АВ = 2x. Т.к. треугольник ABH — прямоугольный, то, используя теорему Пифагора, найдем икс, а затем АВ:
Ответ: 18.
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.
#465
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a, b, c — стороны произвольного треугольника
α, β, γ — противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), (a):
* Внимательно, при подстановке в формулу, для тупого угла (α>90), cosα принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), (a):
Есть следующие формулы для определения катета или гипотенузы
a, b — катеты
c — гипотенуза
α, β — острые углы
Формулы для катета, (a):
Формулы для катета, (b):
Формулы для гипотенузы, (c):
Формулы сторон по теореме Пифагора, (a,b):
Вычислить длину неизвестной стороны через любые стороны и углы
b — сторона (основание)
a — равные стороны
α — углы при основании
β — угол образованный равными сторонами
Формулы длины стороны (основания), (b):
Формулы длины равных сторон , (a):
Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.
H — высота треугольника
a — сторона, основание
b, c — стороны
β, γ — углы при основании
p — полупериметр, p=(a+b+c)/2
R — радиус описанной окружности
S — площадь треугольника
Формула длины высоты через стороны, (H):
Формула длины высоты через сторону и угол, (H):
Формула длины высоты через сторону и площадь, (H):
Формула длины высоты через стороны и радиус, (H):
В прямоугольном треугольнике катеты, являются высотами. Ортоцентр — точка пересечения высот, совпадает с вершиной прямого угла.
H — высота из прямого угла
a, b — катеты
с — гипотенуза
c1 , c2 — отрезки полученные от деления гипотенузы, высотой
α, β — углы при гипотенузе
Формула длины высоты через стороны, (H):
Формула длины высоты через гипотенузу и острые углы, (H):
Формула длины высоты через катет и угол, (H):
Формула длины высоты через составные отрезки гипотенузы , (H):
L— биссектриса, отрезок |OB|, который делит угол ABC пополам
a, b — стороны треугольника
с — сторона на которую опущена биссектриса
d, e — отрезки полученные делением биссектрисы
γ — угол ABC , разделенный биссектрисой пополам
p — полупериметр, p=(a+b+c)/2
Длина биссектрисы через две стороны и угол, (L):
Длина биссектрисы через полупериметр и стороны, (L):
Длина биссектрисы через три стороны, (L):
Длина биссектрисы через стороны и отрезки d, e, (L):
Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.
1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:
L — биссектриса, отрезок ME , исходящий из прямого угла (90 град)
a, b — катеты прямоугольного треугольника
с — гипотенуза
α — угол прилежащий к гипотенузе
Формула длины биссектрисы через катеты, ( L):
Формула длины биссектрисы через гипотенузу и угол, ( L):
2. Найти по формулам длину биссектрисы из острого угла на катет:
L — биссектриса, отрезок ME , исходящий из острого угла
a, b — катеты прямоугольного треугольника
с — гипотенуза
α, β — углы прилежащие к гипотенузе
Формулы длины биссектрисы через катет и угол, (L):
Формула длины биссектрисы через катет и гипотенузу, (L):
L — высота = биссектриса = медиана
a — одинаковые стороны треугольника
b — основание
α — равные углы при основании
β — угол образованный равными сторонами
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):
Формула высоты, биссектрисы и медианы, через стороны, (L):
Формула для вычисления высоты = биссектрисы = медианы.
В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.
L — высота=биссектриса=медиана
a — сторона треугольника
Формула длины высоты, биссектрисы и медианы равностороннего треугольника, (L):
Медиана — отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.
Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.
M — медиана, отрезок |AO|
c — сторона на которую ложится медиана
a, b — стороны треугольника
γ — угол CAB
Формула длины медианы через три стороны, (M):
Формула длины медианы через две стороны и угол между ними, (M):
Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c, пополам.
Медиана в прямоугольном треугольнике (M), равна, радиусу описанной окружности (R).
M — медиана
R — радиус описанной окружности
O — центр описанной окружности
с — гипотенуза
a, b — катеты
α — острый угол CAB
Медиана равна радиусу и половине гипотенузы, (M):
Формула длины через катеты, (M):
Формула длины через катет и острый угол, (M):
Биссектриса равностороннего треугольника равна 17√3. Найдите сторону этого треугольника.
Источник: ОГЭ Ященко 2022 (50 вариантов)
Решение:
В равностороннем треугольнике все углы равны 60°, а биссектриса является так же высотой.
Тогда:
∠АВН = ∠СВН = 60°/2 = 30°
∠ВНС = 90°
В прямоугольном треугольнике ΔНВС, через косинус угла ∠СВН найдём искомую сторону ВС.
Косинус острого угла прямоугольного треугольника – это отношение прилежащего катета к гипотенузе.
cosangle CHB=frac{BH}{BC}\cos:30°=frac{17sqrt{3}}{BC}\frac{sqrt{3}}{2}=frac{17sqrt{3}}{BC}{color{Blue} |:sqrt{3}}\frac{1}{2}=frac{17}{BC}
ВС = 2·17 = 34
Ответ: 34.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 3.9 / 5. Количество оценок: 185
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Равносторонний треугольник – первый из ряда правильных многоугольников, отличается от остальных треугольников тем, что у него все углы и стороны равны, как видно из названия. Здесь, как и в равнобедренном треугольнике, можно найти сторону, зная высоту, из теоремы Пифагора в получившихся прямоугольных треугольниках. Сторона равностороннего треугольника a в квадрате, как гипотенуза, будет равна сумме квадратов высоты и половины основания, которое также является стороной a:
