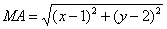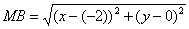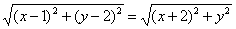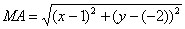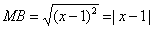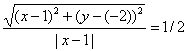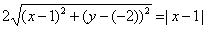Равноудаленная точка как найти формула

The distance formula is used to calculate the distance between any two points in a two-dimensional or three-dimensional plane. In other words, it gives the distance between two different locations on a cartesian plane. 

What is the Distance Formula?

It applies the Pythagorean theorem to determine the required distance. Its formula claims that the distance between any two coordinates is equal to the square root of the differences between the x-coordinates and y-coordinates of the points. It is used to evaluate the distance between point to point, point to plane, and plane to plane.

D = √((x₂ – x₁)² + (y₂ – y₁)²)

where,

• D is the distance between the points,
• (x₁, y₁) and (x₂, y₂) are the coordinates.

How to find the equidistant points on the Y-axis?

Consider two points A (a, b) and B (p, q) lying at a distance from each other on a two dimensional plane.

We have to find a point on the y-axis which is equidistant from these points. It is known that any point that lies on y-axis is of the form (0, y).

Suppose C is (0, y). According to the problem we can conclude that,

AC = BC

AC² = BC²

Using distance formula we have,

(0 – a)² + (y – b)² = (0 – p)² + (y – q)²

a² + y² + b² – 2yb = p² + y² + q² – 2yq

2y (q – b) = p² – q² – a² – b²

y = (p² – q² – a² – b²)/2(q – b)

The above value is calculated by substituting the given values of a, b, p and q. This gives us the point required (0, y).  

Sample Problems

Problem 1: Find the point on the y-axis which is equidistant from (-3, 4) and (5, 2).

Solution:

Suppose the required point is (0, y).

Using distance formula we get,

(-3 – 0)² + (4 – y)² = (5 – 0)² + (2 – y)²

9 + 16 + y² – 8y = 25 + 4 + y² – 4y

-8y + 4y – 4 = 0

4y = -4

y = -1

So, the required point is (0, -1).

Problem 2: Find the point on the y-axis which is equidistant from (6, 3) and (4, 1).

Solution:

Suppose the required point is (0, y).

Using distance formula we get,

(6 – 0)² + (3 – y)² = (4 – 0)² + (1 – y)²

36 + 9 + y² – 6y = 16 + 1 + y² – 2y

45 – 6y – 17 + 2y = 0

4y = 28

y = 7

So, the required point is (0, 7).

Problem 3: Find the point on the y-axis which is equidistant from (3, 2) and (8, 4).

Solution:

Suppose the required point is (0, y).

Using distance formula we get,

(3 – 0)² + (2 – y)² = (8 – 0)² + (4 – y)²

9 + 4 + y² – 4y = 64 + 16 + y² – 8y

13 – 4y – 80 + 8y = 0

4y = 67

y = 67/4

So, the required point is (0, 67/4).

Problem 4: Find the point on the y-axis which is equidistant from (5, 1) and (7, 2).

Solution:

Suppose the required point is (0, y).

Using distance formula we get,

(5 – 0)² + (1 – y)² = (7 – 0)² + (2 – y)²

25 + 1 + y² – 2y = 49 + 4 + y² – 4y

26 – 2y – 53 + 4y = 0

2y = 27

y = 27/2

So, the required point is (0, 27/2).

Problem 5: Find the value of x if (0, 3) is equidistant from (x, 5) and (3, 6).

Solution:

Using the distance formula we get,

(x – 0)² + (5 – 3)² = (3 – 0)² + (6 – 3)²

x² + 4 = 9 + 9

x² = 18 – 4

x² = 14

x = ±3.74

Problem 6: Find the value of x if (0, 2) is equidistant from (x, 1) and (5, 2).

Solution:

Using the distance formula we get,

(x – 0)² + (1 – 2)² = (5 – 0)² + (2 – 2)²

x² + 1 = 25 + 0

x² = 25 – 1

x² = 24

x = ±4.89

Problem 7: Find the value of x if (0, 6) is equidistant from (x, 3) and (7, 4).

Solution:

Using the distance formula we get,

(x – 0)² + (3 – 6)² = (7 – 0)² + (4 – 6)²

x² + 9 = 49 + 4

x² = 53 – 9

x² = 44

x = ±6.63

Last Updated :
24 May, 2022

Like Article

Save Article

Вам равноудаленные или наиболее удаленные точки? Это немного разные вещи.

Равноудаленные точки — это надо пересекать «серединные перпендикуляры» для каждой пары заданных точек и смотреть, что решение одна и та же точка. Самые удаленные — это посмотреть на пересечения всех пар серединных перпендикуляров, перпендикуляров с границами области, вершины области. Из всех этих точек выбрать наиболее удаленные от всех заданных.

Теперь, что такое серединный перпендикуляр в манхеттанском расстоянии — это прямая, через середину отрезка между точками, строго под углом в 45 градусов. Соответственно, 2 таких перпендикуляра не могут пересечься.
Осталось только посмотреть пересечение таких прямых и границы области, и вершины области.

Лучший ответ

еще ответы

ваш ответ

похожие темы

похожие вопросы 5

Множество точек на плоскости

Пример №1 . Составить уравнение множества точек на плоскости, равноудаленных от точек A(1;2) и B(-2;0).
Решение
Пусть точка М принадлежит искомому множеству точек, тогда МА=МВ. Так как


то

После возведения левой и правой частей в квадрат и упрощений получим:
(x-1) 2 + (y-2) 2 = (x + 2) 2 + y 2
x 2 — 2x + 1 + y 2 — 4y + 4 = x 2 + 4x + 4 + y 2
или
— 6x — 4y + 1 = 0
Ответ: — 6x — 4y + 1 = 0.

Пример №2 .
Составить уравнение множества точек на плоскости, отношение расстояний которых от точки A(1;-2) и от прямой x=1 равно 1 /₂.
Решение
Из условия следует, что для любой точки M(x;y) искомого множества справедливо соотношение MA:MB = 1 /₂. Так как:


то

или

Возведя левую и правую части в квадрат и упрощая, получим:
4(x — 1) 2 + 4(y + 2) 2 = |x — 1| 2
т.е.
4(x 2 — 2x + 1) + 4(y 2 + 4y + 4) = x 2 — 2x + 1
или
3x 2 + 4y 2 — 6x +16y +19 = 0
Ответ: 3x 2 + 4y 2 — 6x +16y +19 = 0.

Пример №3 . Составить уравнение линий, если расстояние каждой ее точки А(2,0) относится к расстоянию до прямой 5x+8=0 как 5:4 .
Решение. Выражаем x = -8/5. λ=5/4. Подставляем данные в задание №2.

Пример №4 . Составить уравнение линии, каждая точка которой равноудалена от прямой x+6=0 и от начала координат.
Примечание. Здесь x=-6 , λ=1.

Составить уравнения множества точек равноудаленных от точки и прямой

Задание

Составить уравнение множества точек плоскости, равноудалённых от точки F (7; 3) и от прямой x — 2y = 11

Решение

Расстояние от точки А(x1, y1) до прямой Ax + By + C = 0 равно длине перпендикуляра, опущенного из этой точки на прямую.

Она определяется по формуле

d1 = (Ax1 + By1 + C)/(A^2 + B^2)^0.5 = (x1 — 2y1 — 11)/(5^0.5)

Расстояние d2 между точками A(x1, y1) и B(x2, y2) плоскости определяется по формуле

d2 = ((x2 — x1)^2 + (y2 — y1)^2)^0.5

Из условия равноудалённости следует, что d1 = d2

(x1 — 2y1 — 11)/(5^0.5) = ((x2 — x1)^2 + (y2 — y1)^2)^0.5

Нужно возвести обе части в квадрат и привести подобные слагаемые

Получается квадратное уравнение, то есть геометрическим местом точек равноудалённых от заданной точи и прямой является парабола.

Урок 5

оПределение уравнения линии.

Примеры на отыскание множеств точек.

оПределение уравнения линии.

рассмотрим соотношение вида: F(x,y)=0 (1)

связывающее Переменные величины х и у. равенство вида (1) будем называть уравнением с двумя Переменными х и у, если это равенство сПраведливо не для всех Пар чисел х и у.

Примеры уравнений: 2х+3у=0, х 2 +у 2 -25=0.

если равенство (1) сПраведливо для всех Пар чисел х и у, то оно называется т ождеством .

Примеры тождеств: (х+у) 2 — х 2 -2ху -у 2 =0, (х-у)(х+у) — х 2 +у 2 =0.

уравнение (1) будем называть уравнением множества точек (х;у), если этому уравнению удовлетворяют координаты х и у любой точки множества и не удовлетворяют координатам никакой точки, не Принадлежащей этому множеству.

важным Понятием аналитической геометрии является Понятие уравнения линии. Пусть на Плоскости заданы Прямоугольная система координат и некоторая линия l.

оПределение. уравнение (1) называется уравнением линии l (в заданной системе координат), если этому уравнению удовлетворяют координаты х и у любой точки, лежащей на линии l , и не удовлетворяют координаты никакой точки, не лежащей на этой линии.

из оПределения следует, что линия l Представляет собой множество всех точек Плоскости (х;у), координаты которых удовлетворяют уравнению (1).

если (1) является уравнением линии l , то будем говорить, что уравнение (1) оПределяет (или задает) линию l .

Понятие уравнения линии дает возможность сводить геометрические задачи к алгебраическим. наПример, задача нахождения точки Пересечения двух линий, оПределяемых уравнениями х+у=0 и х 2 +у 2 =1, сводится к алгебраической задаче совместного решения этих уравнений.

линия l может оПределятся не только уравнением вида (1), но и уравнением вида F(. )=0, содержащим Полярные координаты.

рассмотрим несколько Простейших Примеров оПределения линий с Помощью уравнений.

1) х — у=0 . заПисав это уравнение в виде у=х, заключаем, что множество точек, координаты которых удовлетворяют данному уравнению, Представляет собой биссектрису Первого и третьего координатных углов. это и есть линия, оПределенная данным уравнением.

2) х 2 — у 2 =0. Представив уравнение в виде (х-у)(х+у)=0, заключаем, что множество точек, координаты которых удовлетворяют данному уравнению, — это две Прямые, содержащие биссектрисы четырех координатных углов. (см рисунок — гиПерссылка)

3) х 2 +у 2 =0. множество точек, координаты которых удовлетворяют этому уравнению, состоит из одной точки (0;0). в данном случае уравнение оПределяет, как говорят, вырожденную линию.

4) х 2 +у 2 +1=0. так как При любых х и у числа х 2 и у 2 неотрицательны, то х 2 +у 2 +1>0. значит, нет ни одной точки, координаты которой удовлетворяют данному уравнению, т.е. никакого геометрического образа на Плоскости данное уравнение не оПределяет. оно оПределяет «Пустое» множество точек.

5) p=а cOSf , где а — Положительное число, Переменные p и f — Полярные координаты. обозначим через м точку с Полярными координатами (p;f), через а — точку с Полярными координатами (а;0). если p=а cOSf , где 0

6) p=аf , где а — Положительное число, p и f — Полярные координаты. обозначим через м точку с Полярными координатами (p;f). если p=0, то и f=0. таким образом, При увеличении угла f точка м(p;f), начавшая свое движение в Полюсе, движется вокруг него, одновременно удаляясь от Полюса. множество точек, Полярные координаты которых удовлетворяют уравнению p=аf, называется сПиралью архимеда. При этом ПредПолагается, чтоf? может Принимать любые неотрицательные значения.

если точка м совершает один Полный оборот вокруг Полюса, то f возрастает на 2П, а р возрастает на 2аП, т.е. сПираль рассекает любую Прямую, Проходящую через Полюс, на равные отрезки (не считая отрезка, содержащего Полюс), которые имеют длину 2аП.

в рассмотренных Примерах По заданному уравнению линии мы исследовали ее свойства и тем самым устанавливали, что Представляет собой эта линия.

рассмотрим теПерь обратную задачу для заданного (какими-то его свойствами) множества точек, т.е. для заданной линии l , требуется найти его уравнение F (х;у)=0.

Примеры на отыскание множеств точек.

рассмотрим несколько Примеров на отыскание множеств точек По уравнениям и неравенствам, связывающим их координаты.

Пример 1. вывести уравнение (в заданной Прямоугольной системе координат) множества точек, каждая из которых отстоит от точки с(а;в) на расстояние R. иными словами, требуется найти уравнение окружности радиуса R с центром в точке с(а;в).

решение. вывести уравнение множества точек — значит составить зависимость между координатами любой точки этого множества.

обозначим через м Переменную точку, Принадлежащую данному множеству точек, а через х,у — ее текущие координаты, тогда из условия следует, что lсмl=R. Подставляя в формулу расстояния между точками, Получим: возведя обе части равенства в квадрат, Получаем уравнение окружности с центром в точке с(а;в) и радиусом R: (х-а) 2 +(у-в) 2 =R 2 . оно встречается во многих геометрических задачах. Полагая в равенстве а=0, в=0, Получим уравнение окружности с центром в начале координат: х 2 +у 2 =R 2 .

Пример 2. найти уравнение множества точек, равноудаленных от точек а(1;1) и в(3;3).

решение. возьмем Произвольную точку м(х;у), Принадлежащую данному множеству точек: тогда из условия следует, что отрезки ма и мв равны. исПользуя формулу расстояния между двумя точками, находим: , таким образом,

После Преобразования Приходим к искомому уравнению множества точек, равноудаленных от точек а(1;1) и в(3;3): х+у-4=0. как известно из элементарной геометрии, таким множеством точек является Прямая, Проходящая через середину отрезка, соединяющего данные точки, и ПерПендикулярная этому отрезку.

1. даны точки о(2;-2), а(2;2), в(2;-1), с(3;-3), м(5;-5) и к(3;-2). установите, какие из них лежат на линии, заданным уравнением х+у=0, а какие не лежат на ней. (ответ: точки о, с и м лежат на линии, а точки а, в и к не лежат на ней)
2. даны точки а(1;п / 3), в(2;0), с(2;п / 4), м(v3;п / 6) и к(1;2?п3). выясните, какие из них лежат на линии, оПределяемой уравнением р=2 cOSf , и какие не лежат на ней. (ответ: точки а, в и м — лежат на данной линии, точки с и к — не лежат на ней. уравнение оПределяет окружность с диаметром ов)
3. составьте уравнение линии, По которой движется точка м(х;у), равноудаленная от точек а(0;2) и в(4;-2). (ответ: х-у-2=0)
4. составьте уравнение линии, расстояние каждой точки которой от точки а(0;0,25) равно расстоянию этой же точки от Прямой у=-0,25. (ответ: у=х 2 )
5. найдите уравнение множества точек, сумма расстояний каждой из которых от точек а(2;0) и в(-2;0) равна 2v5. (ответ: 0,2х 2 +у 2 =1)
6. найдите уравнение множества точек, равноудаленных от точки а(2;2) и оси ох. (ответ: у=0,25х 2 -х+2)
7. найдите уравнение множества точек, равноудаленных от оси оу и точки а(4;0). (ответ: у 2 =8х-16)
8. составьте уравнение линии, оПисываемой серединой отрезка с длиной, равной D , один из концов которого Перемещается По оси абсцисс, а другой конец — По оси ординат. (ответ: х 2 +у 2 =0,25 D 3 )

Автор: Вяликова Мария Владимировна — учитель математики и информатики высшей квалификационной категории МАОУ Пролетарская СОШ Новгородского района Новгородской области