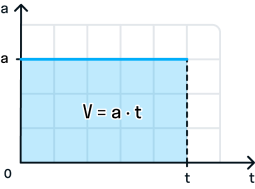
Равноускоренное движение формулы как найти время - Исправление недочетов и поиск решений вместе с Examum.ru

Прямолинейное равноускоренное движение — это прямолинейное движение, при котором скорость тела изменяется (увеличивается или уменьшается) на одну и ту же величину за равные промежутки времени.

Ускорение — физическая величина, характеризующая быстроту изменения скорости тела. То есть, показывает, на какую величину изменяется скорость за единицу времени.

Примеры равноускоренного движения:

разгон самолета перед взлетом;
падающая с крыши сосулька;
торможение лыжника на горном склоне;
разгоняющийся на склоне сноубордист;
свободное падение в результате прыжка с парашютом;
камень брошенный под углом к горизонту;

Равномерное прямолинейное движение является частным случаем равноускоренного движения, при котором ускорение равно нулю.

Равноускоренное движение: формулы

Формула для скорости при равноускоренном движении:

V_к=V_н+at

где: V_к — конечная скорость тела,
V_н — начальная скорость тела,
a=const — ускорение (a>0 при ускорении, a<0 при замедлении)
t — время.

Формула для ускорения при равноускоренном движении:

a=(V_к-V_н)/t

Во время движения тела ускорение остается постоянным.

Задача 1

Кирилл ехал на велосипеде со скоростью 6 м/с, затем начал разгоняться на горке. Чему будет равна его скорость через 10 секунд, если ускорение равно 0,5 м/с?
Решение. Vн=6м/с, ускорение a=0,5м/с, время разгона t=10 секунд.
Получаем: Vн= 6 + 0,5 · 10 = 11 м/с.
Ответ: за 10с Кирилл разгонится до скорости 11 м/с.

Формула расстояния при равноускоренном движении

Если известны время, скорость начальная и скорость конечная

S = t*(V_н+ V_к)/2

Если известны время, скорость начальная и ускорение

S = V_нt + at²/2 **= t*(V_н + at/2)**

где: S — путь, пройденный за время t,
Vн — начальная скорость,
Vк — конечная скорость,
a — ускорение тела,
t — время.

В случае равноускоренного движения с неизвестным временем движения, но с заданными начальной и конечной скоростями пройденный путь можно найти с помощью следующей формулы:

2аS = V_к²−V_н²

где S — путь, пройденный за время t ,
V0 — начальная скорость,
V — скорость в момент времени t,
a — ускорение тела.

Задача 2

Таксист получил заказ и начал движение с ускорением 0,1 м/с2. На каком расстоянии от начала движения его скорость станет равной 15м/с?
Решение. Так как таксист начал движение, начальная скорость равна нулю (Vн=0), Vк=15м/с, ускорение a=0,1м/с2.
Получаем:
S = 15^2 — 0^2 =1125 м.
Ответ: на расстоянии 1 125 м от начала движения скорость такси станет равной 15 м/с.

Перемещение при равноускоренном движении

Важно напомнить разницу между путем и перемещением тела.

Путь — длина траектории. Если тело движется в любом направлении, то его путь увеличивается. Путь — всегда положительное значение.
Перемещение — вектор, соединяющий начальное и конечное положение тела. Проекция перемещения может принимать отрицательное значение.

Например, если путник прошел в одну сторону расстояние S1, а обратно — S2, то: путь тела равен S1 + S2, а перемещение равно S1 − S2. В некоторых задачах путь и перемещение могут совпадать, но не всегда.

Равноускоренное движение: графически

График зависимости ускорения от времени:
Во время движения тела ускорение остается постоянным.

Взаимосвязь скорости, времени и расстояния:
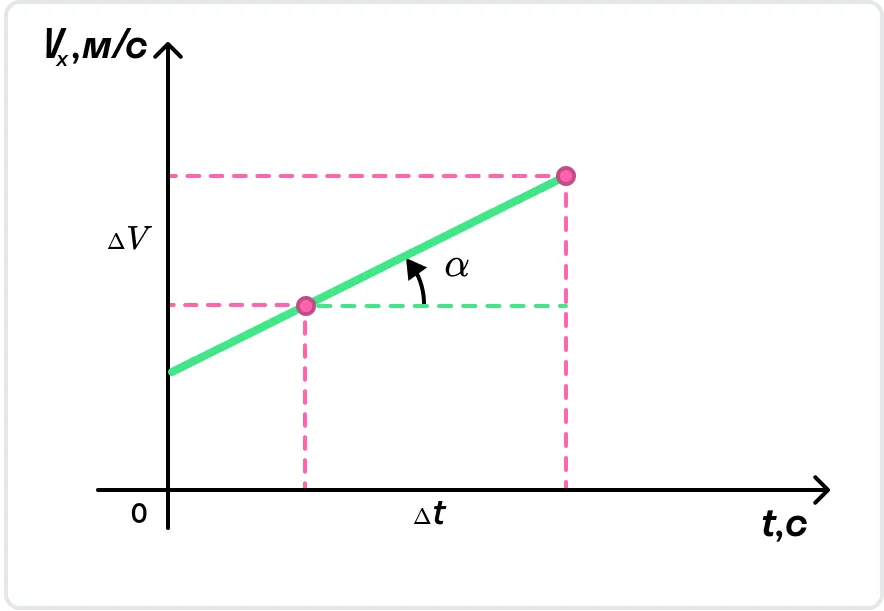
На рисунке показан график, в котором скорость равномерно увеличивается.
С помощью графика скорости можно определить ускорение тела как тангенс угла наклона графика к оси времени.

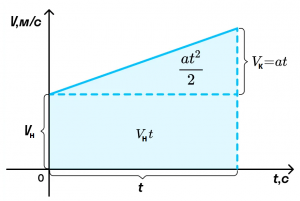
Из графика скорости получим формулу пути при равноускоренном движении тела.

Пройденный телом путь при равноускоренном движении численно равен площади фигуры под графиком зависимости скорости от времени. Вычислим площадь трапеции как сумму площадей прямоугольника V_нt и треугольника at²/2. Получим: S = V_нt + at²/2.

Математически зависимость координаты от времени при равноускоренном движении представляет собой квадратичную функцию, ее график — парабола.

Задача 3

Лыжник подъехал со скоростью 3 м/с к спуску длиной 36 м и съехал с него за несколько секунд, при этом его конечная скорость составила 15 м/с. Определите местонахождение лыжника спустя 2с после начала движения из начала координат.

Дано:
Vн = 3 м/с, начальная координата (t) равна нулю,
Vк = 15м/с,
a — скорость лыжника увеличивается, поэтому ускорение — положительное число,
S = 36м — путь с горы,
t — 2с.

Решение:
Найдем ускорение из формулы пути при равноускоренном движении: 2аS = V_к²−V_н²
Получим: а = (V_к²−V_н² )/2S = (225-9)/(2*36) = 3 м/с2.
Составим уравнение движения лыжника исходя из формулы: S = V_нt + at²/2.
Получаем: x(t) = 3t + 1,5t²
По уравнению определим координату лыжника в момент времени t = 2с:
Получаем: x(2) = 3*2 + 1,5*2² =6+6=12 м.

Ответ: через 2 с после начала движения координата лыжника будет равна 12 м.

Для того, чтобы проверить правильность решения задач на равноускоренное движение, воспользуйтесь калькулятором равноускоренного движения.

Для того, чтобы перевести единицы измерения, воспользуйтесь конвертерами единиц измерения:

Конвертер единиц измерения расстояния (длины)
Конвертер единиц измерения скорости
Конвертер единиц измерения времени

Источник

«Формула времени. Решение задач»

Скорость, время и расстояние — физические величины, взаимосвязаны процессом движения. Виды движений: 1) равномерное (прямолинейное, криволинейное и по окружности), 2) равноускоренное (с постоянным ускорением), 3) гармоническое. Для каждого вида движения своя формула времени.

Время обозначается как t. Единица измерения времени – с (секунды).

Самая простая формула при равномерном прямолинейном движении. Время, необходимое для прохождения пути равняется частному от деления пути на скорость равномерного прямолинейного движения: t = S / v.

При равноускоренном движении время равняется частному от деления разницы конечной и начальной скорости на ускорение: t = (v — v₀) / a или частному от деления пути на разность конечной и начальной скорости: t = S / (v — v₀).

Решение задач через формулу времени

Задача № 1.

Конькобежец может развивать скорость до 13 м/с. За какое время он пробежит дистанцию длиной 2,6 км?

Ответ: 200 с.

Задача № 2.

Двигаясь с ускорением 5 м/с² скорость космической ракеты увеличилась на 100 м/с. За какое время произошло такое изменение скорости?

Ответ: 20 с.

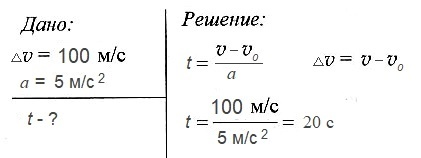
Задача № 3.

Пункты А и В находятся на берегу реки на некотором расстоянии друг от друга. Моторная лодка проходит расстояние АВ вниз по течению реки за время t₁ = 3 ч, а плот то же расстояние – за время t₀ =12 ч. Какое время t₂ затратит моторная лодка на обратный путь?

Решение. Обозначим расстояние между пунктами А и В через L, скорость моторной лодки относительно воды через v_л , а скорость течения через v_т. Тогда t₀ = L / v_т , t₁ = L / (v_л + v_т) , t₂ = L / (v_л — v_т) . Исключая из записанной системы уравнений L, v_л и v_т
находим

Ответ: 6 ч.

Конспект урока «Формула времени. Решение задач».

Следующая тема: «».

Источник

Равноускоренное движение.

Зависимость скорости от времени.
Закон движения.
Прямолинейное равноускоренное движение.
Свободное падение.
Горизонтальный бросок.
Бросок под углом к горизонту.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: виды механического движения, скорость, ускорение, уравнения прямолинейного равноускоренного движения, свободное падение.

Равноускоренное движение — это движение с постоянным вектором ускорения vec a . Таким образом, при равноускоренном движении остаются неизменными направление и абсолютная величина ускорения.

к оглавлению ▴

Зависимость скорости от времени.

При изучении равномерного прямолинейного движения вопрос зависимости скорости от времени не возникал: скорость была постоянна в процессе движения. Однако при равноускоренном движении скорость меняется с течением времени, и эту зависимость нам предстоит выяснить.

Давайте ещё раз потренируемся в элементарном интегрировании. Исходим из того, что производная вектора скорости есть вектор ускорения:

$frac{displaystyle dvec{v}}{displaystyle dt}=vec{a}$ . (1)

В нашем случае имеем . Что надо продифференцировать, чтобы получить постоянный вектор vec a ? Разумеется, функцию vec a t . Но не только: к ней можно добавить ещё произвольный постоянный вектор vec c (ведь производная постоянного вектора равна нулю). Таким образом,

. (2)

Каков смысл константы vec c ? В начальный момент времени t=0 скорость равна своему начальному значению: $vec v=vec v_{0}$ . Поэтому, полагая t=0 в формуле (2), получим:

$vec v_{0}=vec c$ .

Итак, константа vec c — это начальная скорость тела. Теперь соотношение (2) принимает свой окончательный вид:

$vec v=vec v_{0}+vec {a}t$ . (3)

В конкретных задачах мы выбираем систему координат и переходим к проекциям на координатные оси. Часто хватает двух осей и прямоугольной декартовой системы координат, и векторная формула (3) даёт два скалярных равенства:

$v_{displaystyle x}=v{displaystyle 0x}+a_{displaystyle x}t$ , (4)

$v_{displaystyle y}=v{displaystyle 0y}+a_{displaystyle y}t$ . (5)

Формула для третьей компоненты скорости, $v_{displaystyle z}$ если она необходима, выглядит аналогично.)

к оглавлению ▴

Закон движения.

Теперь мы можем найти закон движения, то есть зависимость радиус-вектора от времени. Вспоминаем, что производная радиус-вектора есть скорость тела:

$frac{displaystyle dvec{r}}{displaystyle dt}=vec{v}$

Подставляем сюда выражение для скорости, даваемое формулой (3):

$frac{displaystyle dvec{r}}{displaystyle dt}=vec v_{0}+vec {a}t$ (6)

Сейчас нам предстоит проинтегрировать равенство (6). Это несложно. Чтобы получить $vec v_{0}$ , надо продифференцировать функцию $vec v_{0}t$ . Чтобы получить , нужно продифференцировать $vec {a} t^{2} /2$ . Не забудем добавить и произвольную константу vec c :

$vec r=vec c+vec v_{0} t+frac{displaystyle vec a t^{2}}{displaystyle 2}$ .

Ясно, что vec c — это начальное значение $vec r_{0}$ радиус-вектора vec r в момент времени t=0 . В результате получаем искомый закон равноускоренного движения:

$vec r=vec r_{0}+vec v_{0} t+frac{displaystyle vec a t^{2}}{displaystyle 2}$ . (7)

Переходя к проекциям на координатные оси, вместо одного векторного равенства (7) получаем три скалярных равенства:

$x=x_{0}+ v_{displaystyle 0x} t+frac{displaystyle a_{displaystyle x} t^{2}}{displaystyle 2}$ . (8)

$y=y_{0}+ v_{displaystyle 0y} t+frac{displaystyle a_{displaystyle y} t^{2}}{displaystyle 2}$ . (9)

$z=z_{0}+ v_{displaystyle 0z} t+frac{displaystyle a_{displaystyle z} t^{2}}{displaystyle 2}$ . (10)

Формулы (8) — (10) дают зависимость координат тела от времени и поэтому служат решением основной задачи механики для равноускоренного движения.

Снова вернёмся к закону движения (7). Заметим, что $vec r - vec r_{0}=vec s$ — перемещение тела. Тогда
получаем зависимость перемещения от времени:

$vec s= vec v_{0} t+frac{displaystyle vec a t^{2}}{displaystyle 2}$ .

к оглавлению ▴

Прямолинейное равноускоренное движение.

Если равноускоренное движение является прямолинейным, то удобно выбрать координатную ось вдоль прямой, по которой движется тело. Пусть, например, это будет ось . Тогда для решения задач нам достаточно будет трёх формул:

$v_{displaystyle x}=v_{displaystyle 0x}+a_{displaystyle x}t$ ,

$x=x_{0}+ v_{0 displaystyle x} t+frac{displaystyle a_{displaystyle x} t^{2}}{displaystyle 2}$ ,

$s_{x}= v_{0x} t+frac{displaystyle a_{x} t^{2}}{displaystyle 2}$ ,

где $s_{x}= x-x_{0}$ — проекция перемещения на ось .

Но очень часто помогает ещё одна формула, являющаяся их следствием. Выразим из первой формулы время:

$t=frac{displaystyle v_{displaystyle x}-displaystyle v_{displaystyle 0x}}{displaystyle a_{displaystyle x}}$

и подставим в формулу для перемещения:

$s_{x}= v_{0x} frac{displaystyle v_{displaystyle x}-displaystyle v_{displaystyle 0x}}{displaystyle a_{displaystyle x}}+frac{displaystyle a_{x}}{2} (frac{displaystyle v_{displaystyle x}-displaystyle v_{displaystyle 0x}}{displaystyle a_{displaystyle x}})^{2}$ .

После алгебраических преобразований (проделайте их обязательно!) придём к соотношению:

$s_{x}=frac{displaystyle v_{displaystyle x}^{displaystyle 2}-displaystyle v_{displaystyle 0x}^{displaystyle 2}}{displaystyle 2a_{displaystyle x}}$ .

Эта формула не содержит времени и позволяет быстрее приходить к ответу в тех задачах, где время не фигурирует.

к оглавлению ▴

Свободное падение.

Важным частным случаем равноускоренного движения является свободное падение. Так называется движение тела вблизи поверхности Земли без учёта сопротивления воздуха.

Свободное падение тела, независимо от его массы, происходит с постоянным ускорением свободного падения vec g , направленным вертикально вниз. Почти во всех задачах при расчётах полагают g=10 м/с $^{2}$ .

Давайте разберём несколько задач и посмотрим, как работают выведенные нами формулы для равноускоренного движения.

Задача. Найти скорость приземления дождевой капли, если высота тучи h=2 км.

Решение. Направим ось вертикально вниз, расположив начало отсчёта в точке отрыва капли. Воспользуемся формулой

$s_{y}=frac{displaystyle v_{displaystyle y}^{displaystyle 2}-displaystyle v_{displaystyle 0y}^{displaystyle 2}}{displaystyle 2a_{displaystyle y}}$ .

Имеем: $s_{y}=h, v_{y}=v$ — искомая скорость приземления, $v_{0y}=0, a_{y}=g$ . Получаем: $h^{2}=frac{v^{2}}{2g}$ , откуда . Вычисляем: м/с. Это 720 км/ч, порядка скорости пули.

На самом деле капли дождя падают со скоростью порядка нескольких метров в секунду. Почему такое расхождение? Сопротивление воздуха!

Задача. Тело брошено вертикально вверх со скоростью $v_{0}=30$ м/с. Найти его скорость через t=5 c.

Решение. Направим ось вертикально вверх, поместив начало отсчёта на поверхности Земли. Используем формулу

$v_{displaystyle y}=v_{displaystyle 0y}+a_{displaystyle y}t$ .

Здесь $v_{displaystyle 0y}=v_{0}, a_{y}=-g$ , так что $v_{displaystyle y}=v_{displaystyle 0}-gt$ . Вычисляем: $v_{displaystyle y}=30-10 cdot 5=-20$ м/с. Значит, скорость будет равна 20 м/с. Знак проекции указывает на то, что тело будет лететь вниз.

Задача. С балкона, находящегося на высоте h=15 м, бросили вертикально вверх камень со скоростью $v_{0}=10$ м/с. Через какое время камень упадёт на землю?

Решение. Направим ось вертикально вверх, поместив начало отсчёта на поверхности Земли. Используем формулу

$y=y_{0}+ v_{displaystyle 0y} t+frac{displaystyle a_{displaystyle y} t^{2}}{displaystyle 2}$ .

Имеем: $y=0, y_{0} = h, v_{0y}=v_{0}, a_{y}=-g,$ так что $0=h+v_{0}t-frac{displaystyle g t^{2}}{displaystyle 2}=15+10t-5t^{2}$ , или $t^{2}-2t-3=0$ . Решая квадратное уравнение, получим t=3 c.

к оглавлению ▴

Горизонтальный бросок.

Равноускоренное движение не обязательно является прямолинейным. Рассмотрим движение тела, брошенного горизонтально.

Предположим, что тело брошено горизонтально со скоростью $v_{0}$ с высоты . Найдём время и дальность полёта, а также выясним, по какой траектории происходит движение.

Выберем систему координат OXY так, как показано на рис. 1.

Рис. 1. Горизонтальный бросок

Используем формулы:

$x=x_{0}+ v_{displaystyle 0x} t+frac{displaystyle a_{displaystyle x} t^{2}}{displaystyle 2}$

$y=y_{0}+ v_{displaystyle 0y} t+frac{displaystyle a_{displaystyle y} t^{2}}{displaystyle 2}$

В нашем случае $x_{0} = 0, v_{0x}=v_{0}, a_{x}=0, y_{0} = h, v_{0y}=0, a_{y}=-g$ . Получаем:

$x=v_{0}t, y=h-frac{displaystyle g t^{2}}{displaystyle 2}$ . (11)

Время полёта найдём из условия, что в момент падения координата тела обращается в нуль:

$y(T)=0Rightarrow h-frac{displaystyle gT^{displaystyle 2}}{displaystyle 2}=0Rightarrow T=sqrt{frac{displaystyle 2h}{displaystyle g}}$ .

Дальность полёта — это значение координаты в момент времени :

$L=x(T)=v_{0}T=v_{0} sqrt{frac{displaystyle 2h}{displaystyle g}}$ .

Уравнение траектории получим, исключая время из уравнений (11). Выражаем из первого уравнения и подставляем во второе:

$t=frac{displaystyle x}{displaystyle v_{displaystyle 0}}Rightarrow y=h-frac{displaystyle g}{displaystyle 2}(frac{displaystyle x}{displaystyle v_{displaystyle 0}})^{displaystyle 2}=displaystyle h-frac{displaystyle gx^{displaystyle 2}}{displaystyle 2v^{displaystyle 2}_{displaystyle 0}}$ .

Получили зависимость от , которая является уравнением параболы. Следовательно, тело летит по параболе.

к оглавлению ▴

Бросок под углом к горизонту.

Рассмотрим несколько более сложный случай равноускоренного движения: полёт тела, брошенного под углом к горизонту.

Предположим, что тело брошено с поверхности Земли со скоростью $v_{0}$ , направленной под углом alpha к горизонту. Найдём время и дальность полёта, а также выясним, по какой траектории двигается тело.

Выберем систему координат OXY так, как показано на рис. 2.

Рис. 2. Бросок под углом к горизонту

Начинаем с уравнений:

$x=x_{0}+ v_{displaystyle 0x} t+frac{displaystyle a_{displaystyle x} t^{2}}{displaystyle 2}$ ,

$y=y_{0}+ v_{displaystyle 0y} t+frac{displaystyle a_{displaystyle y} t^{2}}{displaystyle 2}$ .

В нашем случае $x_{0} =y_{0}=0, v_{0x}=v_{0}cos alpha, v_{0y}=v_{0}sin alpha , a_{x}=0, a_{y}=-g$ . Получаем:

$x=(v_{0}cos alpha )t, y=(v_{0}sin alpha)t- frac{displaystyle g t^{2}}{displaystyle 2}$ .

Дальше действуем так же, как и в случае горизонтального броска. В результате приходим к соотношениям:

$T=frac{displaystyle 2v_{displaystyle 0}sinalpha }{displaystyle g}$ ,

$L=frac{displaystyle v_{displaystyle 0}^{displaystyle 2}sin2alpha }{displaystyle g}$ ,

$y=x tgalpha -frac{displaystyle gx^{displaystyle 2}}{displaystyle 2v^{displaystyle 2}_{0}cos^{displaystyle 2}alpha }$ .

(Обязательно проделайте эти вычисления самостоятельно!) Как видим, зависимость от снова является уравнением параболы.Попробуйте также показать, что максимальная высота подъёма определяется формулой:

$H=frac{displaystyle v_{displaystyle 0}^{displaystyle 2}sin^{2} alpha }{displaystyle 2g}$ .

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Равноускоренное движение.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
07.05.2023

Источник

Определение

Равноускоренным движением называется движение при котором скорость за одинаковое время изменяется на одно и то же значение. В физике это самый простой вид движения с ускорением.

К примерам движения тела с постоянным ускорением можно отнести падение камня с обрыва, полёт гранаты, после выстрела из гранатомёта, скатывание санок с горы. Равномерное движение можно считать частным случаем равноускоренного, при котором ускорение всегда остаётся равным нулю.

Давайте подробно рассмотрим движение тела под действием постоянного поля силы тяжести вблизи земли. Пусть оно будет брошено под углом к горизонту. Это одновременно и равномерное и равноускоренное движение. Равномерное – по горизонтали (оси X), равноускоренное – по вертикали (оси Y). Сопротивлением воздуха, влиянием на движение вращения Земли и другими подобными факторами пренебрегаем.

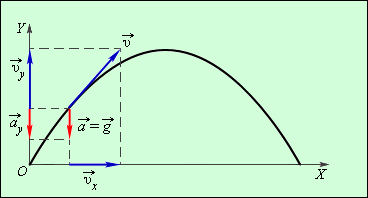
В каждой точке пути на тело действует постоянное ускорение g. Оно не меняется ни по величине, ни по направлению.

Основные формулы равноускоренного движения и график равноускоренного движения

Формула

Скорость при равноускоренном движении тела вычисляется с помощью выражения:

[v=v0+at];

[v0 – text { начальная скорость тела; }]

[a=const – text { —ускорение; }]

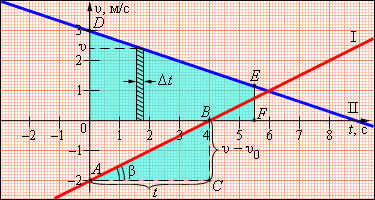
Ускорение здесь определяется, как угол наклона графика скорости. Посмотрите на треугольник ABC.

a=(v-v0)/t=BC/AC.

Чем больше угол β, тем более наклонно выглядит график ускорения по отношению к оси времени. Следовательно, тем большее значение имеет ускорение тела.

Для первого из графиков положим V0=-2м/с. a=0,5м/с².

Для второго графика положим V0=3м/с. a=(-1/3)м/с².

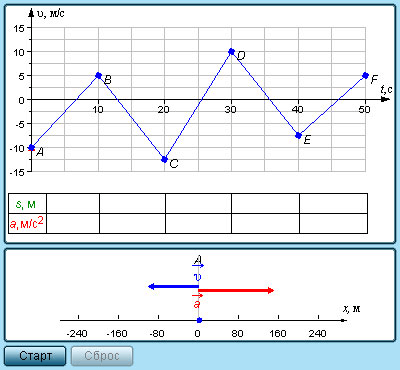
Указанный график позволяет понять многие зависимости равноускоренного движения и вычислить его основные параметры при проецировании на направление движения. Сначала нужно выделить на графике крохотный отрезок времени Δt. Будем считать его настолько коротким, что движение на нём можно принять за равномерное со значением скорости равным скорости в середине указанного временного промежутка. Тогда, перемещение Δs за Δt можно принять равным Δs=vΔt. Заштрихованная область на первом из графиков.

Разделим всё время движения тела на такие бесконечно короткие промежутки Δt. Перемещение s за указанное время t будет равняться площади трапеции обозначаемой ODEF.

S=(|OD|+|EF|/2)*OF|= [(v+v0)/2]*t =[2v0+(v-v0)]*t/2;

Как известно, v-v0=at, исходя из этого окончательная формула равноускоренного движения выглядит следующим образом:

S=v0*t+at²/2

Чтобы узнать, какой будет координата тела в любое время его движения, к начальной координате следует ещё вписать перемещение. Изменение координаты в зависимости от времени есть закон равноускоренного движения по оси Y:

Y=y0+v0*t+at²/2.

Нет времени решать самому?

Наши эксперты помогут!

Закон равноускоренного движения

Формула

[Y=y0+v0*t+at²/2];

Из него видна зависимость равноускоренного движения от начального положения и начальной скорости тела. Если то и другое равно нулю, график равноускоренного движения приобретает вид параболы, пересекающей начало координат и обращённой своими ветвями вниз. Само движение при этом будет происходить по прямой вертикальной линии. Выражение станет законом равноускоренного прямолинейного движения.

S=at²/2

Это самый простой класс равноускоренного движения. Вектор скорости тела в нём всегда направлен по оси Y, меняет только свой знак. С формулами равноускоренного прямолинейного движения работать легче всего, поэтому при решении задач нужно стараться выбрать систему отсчёта именно таким образом.

Подставляя разные начальные значения скорости и координаты, меняя знак ускорения, можно получить самые разные значения. Вы спросите –«Зачем менять знак ускорения? Оно ведь всегда постоянно и направлено точно вниз.» При решении задач, чтобы найти равноускоренное движение, часто бывает удобно изменить направление оси Y, вместе с этим меняется и знак ускорения, оно становится положительным.

Как найти равноускоренное движение тела, если неизвестно время

Часто возникает задача нахождения координаты тела при заданной начальной скорости движения тела, конечной скорости его движения и ускорении, но не заданном времени. Как быть в этой ситуации.

Рассмотрим уравнения:

v=v0+at;

S=v0*t+at²/2

Как систему уравнений. Для её решения, нужно исключить переменную t.

Сначала находим t из первого уравнения

t=(v-v0)/a

Затем подставляем его в выражение для перемещения. В результате получаем уравнение равноускоренного движения, не содержащее время.

s=[v²- (v0)²]/2a

Из данного выражения уже достаточно легко вычислить скорость. Она равна:

V=√(v0)²-2as

При v0=0 s=v²/2a и v=√2as

Источник

Общая характеристика

Скорость, время и расстояние являются физическими показателями, взаимосвязанными между собой процессом движения. На практике и теории известно равномерное и равноускоренное движение тел. Первый случай описывает постоянство времени, а второй — его изменение.

Основные понятия

Однозначное и конкретное определение тяжело сформулировать, но существуют разные концепции современной философской мысли в математике и физике. Течение времени является естественным процессом. Оно уходит, меняется все вокруг, совершаются разные события в мире, поэтому для физической меры характерен контекст событий.

Чтобы измерить время, нужно знать общие повторяющиеся события с одинаковым периодом. Это может быть смена дня, ночи или времени года. Чтобы определить единицу измерения времени (метр, час, секунда), ученые обращались к древнейшим источникам познаний.

Год состоит из двенадцати месяцев или четырех сезонов. Такое количество раз в весенний, летний, зимний и осенний периоды главный спутник Земли меняет свои фазы.

По мере развития прогресса измерение t модифицировалось, появлялись новые солнечные, водные, песчаные, огненные, механические, электронные и молекулярные измерители времени — часы.

Время включено в семь основных физических величин международной системы единиц СИ. Этот показатель используют для остальных составляющих. Четкое понимание t помогает проведению экспериментов и в обычной жизни.

Основной целью навигации и астрономии было измерение t. С 1000 по 1960 год секундное измерение воспринималось как 1/86400 дней. С 1970 г. это понятие видоизменилось, поскольку стала учитываться периодичность земной орбиты.

Самые точные мерила —швейцарские часы FOCS, измеряющие t с погрешностью хода в одну секунду за 30 млн лет.

Физическая величина отражает свойство материальных процессов, имеет определенную продолжительность, следует друг за другом. Взаимосвязан этот показатель с материей, движением, так как является формой его существования.

Длительность физического процесса, происходящего в определенной точке, устанавливают с помощью часов, расположенных в ней. Здесь используется прямое сравнение, уравнивается длительность процессов. Измерение продолжительности сводится к фиксированию начала и окончанию процесса на шкале. Когда говорят о фиксации показаний часов во время начала и завершения процесса, это не относится к фактическому месту их нахождения.

Теория относительности Эйнштейна меняет понимание времени, утверждая, что прогресс его не универсален и зависит от того, кто его изменяет. В такой картине реальности часы тикают с разной скоростью в зависимости от того, кто их носит.

Принимая большое ускорение или располагаясь рядом с сильными силами гравитации (вблизи черной дыры), можно изменить скорость течения времени, остановить его или возвратить. Для человека, находящегося внутри черной дыры, пространство и время кажутся взаимозаменяемыми, поэтому спуск в нее неизбежен, как и течение t вне этой области. Относительность уравнивает время и пространство.

Древняя система исчисления

До существования нашей эры люди привязывали отсчет времени к движению небесных тел или событий, связанных с ними. Древние народы искали основу для построения своей системы исчисления. В Вавилоне это было число 60, благодаря ему окружность содержит 360°, градус равен 60 минутам, а каждая из них состоит из 60 секунд.

Год представлялся окружностью в 360 градусов. Когда-то минимальной мерой исчисления был час. Жители Древнего Вавилона оказались сильны в математике, поэтому производили важные расчеты и решали задачи. Вводилась наименьшая единица времени. 60 минут составляют час, а в минуте столько же секунд.

Объяснение того, что сутки составляют 24 часа, а день делится пополам и равен 12 часам, выявили египтяне. Самой большой единицей измерения является индуистское и буддистское понятие Кальпа. Величина равна 4,32 млрд лет, что совпадает с возрастом планеты. Если перевести век Брахмы в обычные годы, получится 311 трлн и 40 млрд лет.

Первыми старинными часами являются солнечные мерила. Действие их основывается на изменении длины теней предметов по мере движения Солнца по небу. Такие часы внешне представляли собой длинный шест, воткнутый в землю. Затем возникли водяные, песчаные и огненные часы. Работа таких механизмов не привязывалась к движению Солнца, Луны либо звезд.

Первые механические мерила начали производиться мастерами Китая в 725 г. Жители Европы в Средние века устанавливали на башнях соборов часы, которые имели только одну часовую стрелку. Карманные измерители возникли в середине XVII века, а наручные намного позже.

В соответствии с международной системой измерения определение одной секунды привязано к периоду электромагнитного излучения, начинающемуся при переходе между тонкими уровнями основного состояния атома цезия-133. Одна секунда составляет 919 263 770 периодов.

Показатели физики

Не существует определенной концепции или класса времени. Показатель непрерывности процессов можно вычислить по формуле, проанализировать на графике или диаграмме.

Определения и концепции расчета

Термодинамика гласит, что время не вернуть. Его ход зависит от движения системы отсчета и может быть мгновенным.

Существует понятие «релятивистское замедление времени»: если часы находятся в неподвижной системе, то в движущемся теле все процессы замедлены. Этап старения для двух братьев-близнецов может пройти по-разному, если одного отправить в космос, а другого оставить на Земле. Человек в космосе не постареет, поскольку там изменяется масса его тела, а также замедляется гравитационное время. В условиях притяжения меняется ход часов. Чем сильнее поле гравитации, тем больше замедление. Между объектами, имеющими массу, создается взаимодействие.

Периодическая цепь событий рассчитывается неодинаково в зависимости от показателей. Зависимые величины:

время;
скорость;
расстояние.

Секунда — стандартная единица, характеризующая время. Его определение в физике представляется как продолжительный показатель. Время через расстояние и скорость вычисляется по формуле t=S/V. Стандартная расшифровка:

S — расстояние;
V — конечная скорость (километровое значение);
t — время.

Когда скорость измеряется в км/ч, то и время выражается в часах. В любой системе события развиваются одновременно.

Формула времени при равноускоренном движении выглядит как t = (V — V0)/a или t = S/(V — V0), где V0 — начальная скорость, a — ускорение. Таблица показателей:

Вид движения	Скорость (V)	Перемещение (S)	Время (t)
Равномерное	V = знак постоянства (const)	S = Vt	t = S/V
Равноускоренное	V = V0+at	S = V0t+at2/2	t = V-V0/a

Атом изотопа цезия за секунду совершает 9192631770 собственных квантовых переходов. В зависимости от его расположения секунда имеет разные значения.

Решение задач

Понять действие формул времени при равномерном движении или равноускоренном можно, решив задачу. Многие сайты предлагают онлайн-калькулятор для удобного подсчета. В соответствующие графы достаточно ввести основные данные, после чего программа рассчитает все самостоятельно.

Задача 1. Автомобиль ехал со скоростью 200 км/ч и проехал всего 80 км. Требуется определить время движения машины. Условные обозначения:

V — скорость;
S — расстояние;
t — время.

Показатели нужно перевести из километров в метры, из часов в секунды: 1 км = 1 тыс. м, 1 час = 3600 секунд. Получаем S = 80000 м, V= 200000/3600 = 55,55 м/с. Находим скорость по формуле: V= S/t = 80000/55,55 = 1440,14 сек.

t = 1440

14/3600 = 0,4 часа.

Ответ: автомобиль пройдет 0,4 ч.

При неравномерном движении путь, пройденный телом, равен произведению средней скорости на время, в течение которого тело перемещалось.

Задача 2. Движение точки задано уравнением: х = 2t — 0,03t2. Нужно определить, в какой период скорость точки сближения сравняется с нулевой отметкой. Коэффициенты равны 2м/с, 0,03 м/с2.

Условия задачи содержат функцию x (t). Скорость можно вычислить по формуле V = dx/dt = 2 — 0,06t Приравниваем скорость к 0, находим t:

2 — 0,06t = 0

t = 2/0,06 = 33,33 сек.

Необходимо определить зависимость модуля ускорения от времени: A (t)= dv/dt = -0,06.

Задача 3. Самолет для взлета набирает 350 км/ч. Нужно определить время разгона, если скорость достигается в конце взлетной полосы длиной в 2 км. Движение считается равноускоренным.

При равноускоренном движении формула выглядит как S = V0t+at2/2. При этом V= V0+at. Разгон самолета начинается с состояния покоя, то есть V0 = 0.

S = at2/2

V=at.

S = (V/t)*(t2/2) = Vt/2.

S = 2000 м

V=350 км/ч = 97,2 м/с.

t= 2S/V = 2*2000/97,2 = 41,15.

Благодаря вычислению известно, что разгон самолета длится 41,15 сек.

Задача 4. Скорость конькобежца составляет 15 м/с. Нужно вычислить время, за которое он пробежит путь 3 км.

V= 15 м/с.

S = 3 км (3000 м).

t = S/V = 3000/15 = 200

Ответ: за 200 секунд конькобежец пробежит 3 км.

Современная наука распределяет известные представления о времени в разные концепции — относительную и вещественную. По мнению относительной, в природе не существует временных рамок, а понятие времени является отношением между событиями. Время — проявление свойств физических тел и изменений, оно статично, как и пространство.

Источник

Равноускоренное движение: формулы

Формула для скорости при равноускоренном движении:

Vк=Vн+at

Формула для ускорения при равноускоренном движении:

a=(Vк-Vн)/t

Задача 1

Формула расстояния при равноускоренном движении

S = t*(Vн+ Vк)/2

S = Vнt + at2/2 = t*(Vн + at/2)

2аS = Vк2−Vн2

Задача 2

Перемещение при равноускоренном движении

Равноускоренное движение: графически

Задача 3

«Формула времени. Решение задач»

Решение задач через формулу времени

Задача № 1.

Задача № 2.

Задача № 3.

Равноускоренное движение.

Зависимость скорости от времени.

Закон движения.

Прямолинейное равноускоренное движение.

Свободное падение.

Горизонтальный бросок.

Бросок под углом к горизонту.

Основные формулы равноускоренного движения и график равноускоренного движения

Закон равноускоренного движения

Как найти равноускоренное движение тела, если неизвестно время

Общая характеристика

Основные понятия

Древняя система исчисления

Показатели физики

Определения и концепции расчета

Решение задач

V_к=V_н+at

a=(V_к-V_н)/t

S = t*(V_н+ V_к)/2

S = V_нt + at²/2 **= t*(V_н + at/2)**

2аS = V_к²−V_н²