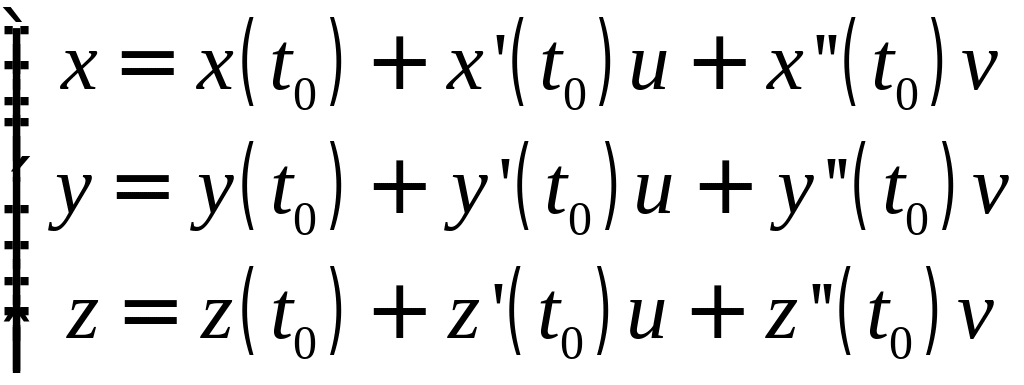Содержание
Касательная, нормальная плоскость, соприкасающаяся плоскость, бинормаль, главная нормаль, репер Френе
Краткие теоретические сведения
Кривая в пространстве
Рассмотрим в пространстве гладкую кривую $gamma$.
-
Векторное уравнение $gamma:, vec{r}=vec{r}(t)$.
-
Параметрическое уравнение $gamma:,, x=x(t),, y=y(t),, z=z(t)$.
Пусть точка $M$ принадлежит данной кривой и отвечает значению параметра $t=t_0$. Тогда радиус-вектор и координаты данной точки равны:
begin{equation*}
vec{r_0}=vec{r}(t_0), quad x_0=x(t_0),, y_0=y(t_0), , z_0=z(t_0).
end{equation*}
Пусть в точке $M$ $ vec{r’}(t_0)neqvec{0}$, то есть $M$ не является особой точкой.
Касательная к кривой
Касательная к кривой, проведенная в точке $M$, имеет направляющий вектор коллинеарный вектору $vec{r’}(t_0)$.
Пусть $vec{R}$ — радиус-вектор произвольной точки касательной, тогда уравнение этой касательной имеет вид
begin{equation*}
vec{R}=vec{r}(t_0)+lambdavec{r’}(t_0).
end{equation*}
Здесь $lambdain(-infty,+infty)$ — параметр, определяющий положение точки на касательной (то есть разным значениям $lambda$ будут соответствовать разные значения $vec{R}$).
Если $vec{R}={X,Y,Z}$, $M = (x(t_0), y(t_0), z(t_0))$, то можно записать уравнение касательной в каноническом виде:
begin{equation*}
frac{X-x(t_0)}{x'(t_0)}=frac{Y-y(t_0)}{y'(t_0)}=frac{Z-z(t_0)}{z'(t_0)}.
end{equation*}
Нормальная плоскость
Плоскость, проходящую через данную точку $M$ кривой $gamma$ перпендикулярно касательной в этой точке, называют нормальной плоскостью.
Пусть $vec{R}$ — радиус-вектор произвольной точки нормальной плоскости, тогда ее уравнение можно записать в векторном виде через скалярное произведение векторов $vec{R}-vec{r}(t_0)$ и $vec{r’}(t_0)$:
begin{equation*}
(vec{R}-vec{r}(t_0))cdotvec{r’}(t_0)=0.
end{equation*}
Если расписать покоординатно, то получим следующее уравнение:
begin{equation*}
x'(t_0)cdot(X-x(t_0))+y'(t_0)cdot(Y-y(t_0))+z'(t_0)cdot(Z-z(t_0))=0.
end{equation*}
Соприкасающаяся плоскость
Плоскость, проходящую через заданную точку $M$ кривой $gamma$ параллельно векторам $vec{r’}(t_0)$, $vec{r»}(t_0)$, когда они неколлинеарны, называют соприкасающейся плоскостью кривой.
Если $vec{R}$ — радиус-вектор произвольной точки соприкасающейся плоскости, то ее уравнение можно записать через смешанной произведение трех компланарных векторов $vec{R}-vec{r}(t_0)$, $vec{r’}(t_0)$, $vec{r»}(t_0)$:
begin{equation*}
(vec{R}-vec{r}(t_0), vec{r’}(t_0), vec{r»}(t_0))=0.
end{equation*}
Зная координаты точки и векторов, определяющих плоскость, запишем смешанное произведение через определитель. Получим следующее уравнение соприкасающейся плоскости:
begin{equation*}
left|
begin{array}{ccc}
X-x(t_0) & Y-y(t_0) & Z-z(t_0) \
x'(t_0) & y'(t_0) & z'(t_0)\
x»(t_0) & y»(t_0) & z»(t_0) \
end{array}
right|=0
end{equation*}
Плоская кривая лежит в своей соприкасающейся плоскости.
Бинормаль и главная нормаль
Прямая, проходящая через точку $M$ кривой $gamma$ перпендикулярно касательной к кривой в этой точке, называется нормалью.
Таких кривых можно провести бесконечно много, все они образуют нормальную плоскость. Мы выделим среди нормалей две — бинормаль и главную нормаль.
Нормаль, перпендикулярную соприкасающейся плоскости, называют бинормалью.
Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью.
Из определения бинормали (перпендикулярна касательной и перпендикулярна соприкасающейся плоскости) следует, что в качестве ее направляющего вектора мы можем взять векторное произведение $ vec{r’}(t_0)timesvec{r»}(t_0)$, тогда ее уравнение можно записать в виде:
begin{equation*}
vec{R}=vec{r}(t_0)+lambda,vec{r’}(t_0)timesvec{r»}(t_0).
end{equation*}
Как и раньше, $vec{R}$ — радиус-вектор произвольной точки бинормали.
Каноническое уравнение прямой:
begin{equation*}
frac{X-x(t_0)}{left|
begin{array}{cc}
y'(t_0) & z'(t_0) \
y»(t_0) & z»(t_0) \
end{array}
right|
}=frac{Y-y(t_0)}{left|
begin{array}{cc}
z'(t_0) & x'(t_0) \
z»(t_0) & x»(t_0) \
end{array}
right|
}=frac{Z-z(t_0)}{left|
begin{array}{cc}
x'(t_0) & y'(t_0) \
x»(t_0) & y»(t_0) \
end{array}
right|
}.
end{equation*}
Из определения главной нормали (перпендикулярна касательной и перпендикулярна бинормали) следует, что в качестве ее направляющего вектора можно взять векторное произведение $vec{r’}(t_0) timesleft[vec{r’}(t_0),vec{r»}(t_0)right]$:
begin{equation*}
vec{R}=vec{r}(t_0)+lambda,vec{r’}(t_0) timesleft[vec{r’}(t_0),vec{r»}(t_0)right].
end{equation*}
Уравнение в каноническом виде распишите самостоятельно.
Спрямляющая плоскость
Плоскость, проходящую через заданную точку $M$ кривой $gamma$ перпендикулярно главной нормали, называют спрямляющей плоскостью.
Другое определение:
Плоскость, определяемую касательной к кривой и бинормалью в той же точке, называют спрямляющей плоскостью.
Второе определение позволяет записать уравнение спрямляющей плоскости через смешанное произведение трех компланарных векторов, определяющих эту плоскость $vec{R}-vec{r}(t_0)$, $vec{r’}(t_0)$, $vec{r’}(t_0)timesvec{r»}(t_0)$:
begin{equation*}
left(vec{R}-vec{r}(t_0),, vec{r’}(t_0),, vec{r’}(t_0)timesvec{r»}(t_0)right)=0.
end{equation*}
Зная координаты соответствующих векторов, можно легко записать это смешанное произведение через определитель, раскрыв который, вы получите общее уравнение спрямляющей плоскости.
Репер Френе
Орт (то есть единичный вектор) касательной обозначим:
$$ vec{tau}=frac{vec{r’}(t_0)}{|vec{r’}(t_0)|}. $$
Орт бинормали:
$$ vec{beta}=frac{vec{r’}(t_0)timesvec{r»}(t_0)}{|vec{r’}(t_0)timesvec{r»}(t_0)|}. $$
Орт главной нормали:
$$ vec{nu}=frac{vec{r’}(t_0) times[vec{r’}(t_0),,vec{r»}(t_0)]}{|vec{r’}(t_0) times [vec{r’}(t_0),,vec{r»}(t_0)]|}. $$
Правая тройка векторов $vec{tau}$, $vec{nu}$, $vec{beta}$ называется репером Френе.
Решение задач
Задача 1
Кривая $gamma$ задана параметрически:
$$
x=t,,, y=t^2,,, z=e^t.
$$
Точка $M$, принадлежащая кривой, соответствует значению параметра $t=0$.
Записать уравнения касательной, бинормали, главной нормали, нормальной плоскости, соприкасающейся плоскости и спрямляющей плоскости, проведенных к данной кривой в точке $M$. Записать векторы репера Френе.
Решение задачи 1
Задачу можно решать разными способами, точнее в разном порядке находить уравнения прямых и плоскостей.
Начнем с производных.
begin{gather*}
gamma: vec{r}(t)=left{ t,, t^2,, e^tright} ,, Rightarrow \
vec{r’}(t)=left{ 1,, 2t,, e^tright},\
vec{r»}(t)=left{ 0,, 2,, e^tright}.
end{gather*}
В точке $M(t_0=0)$:
begin{gather*}
vec{r}(t_0)={ 0,, 0,, 1},\
vec{r’}(t_0)={ 1,, 0,, 1},\
vec{r»}(t_0)={ 0,, 2,, 1}.
end{gather*}
-
Зная координаты точки $M(0,0,1)$ и направляющего вектора $ vec{r’}(t_0)={ 1,0,1 }$, можем записать уравнение касательной:
begin{equation*}
frac{X}{1}=frac{Y}{0}=frac{Z-1}{1}.
end{equation*}
-
Нормальная плоскость проходит через точку $M(0,0,1)$ перпендикулярно вектору $vec{r’}(t_0)={ 1,0,1 }$, поэтому ее общее уравнение имеет вид:
begin{equation*}
1cdot X+0cdot Y+1cdot (Z-1)=0,, Rightarrow ,, X+Z=1.
end{equation*}
-
Запишем теперь уравнение соприкасающейся плоскости, определяемой точкой $M(0,0,1)$ и векторами: $vec{r’}(t_0)={ 1,, 0,, 1}$, $vec{r»}(t_0)={ 0,, 2,, 1}$:
begin{equation*}
left|
begin{array}{ccc}
X-0 & Y-0 & Z-1 \
1 & 0 & 1\
0 & 2 & 1 \
end{array}
right|=0
end{equation*}
Раскрываем определитель, получаем уравнение:
begin{equation*}
-2X-Y+2Z-2=0
end{equation*}
-
Направление бинормали задается вектором $vec{r’}(t_0) times vec{r»}(t_0)$. Координаты этого вектора мы уже нашли, когда вычисляли миноры в определителе, задающем уравнение соприкасающейся плоскости.
$$
{ 1,, 0,, 1} times { 0,, 2,, 1}= left|
begin{array}{ccc}
vec{i} & vec{j} & vec{k} \
1 & 0 & 1\
0 & 2 & 1 \
end{array}
right|= {-2,, -1,, 2}.
$$
Уравнение бинормали:
begin{equation*}
frac{X}{-2}=frac{Y}{-1}=frac{Z-1}{2}.
end{equation*}
-
Направление главной нормали задается вектором $vec{r’}(t_0) times (vec{r’}(t_0)timesvec{r»}(t_0))$.
$$
{ 1,, 0,, 1} times {-2,, -1,, 2}= left|
begin{array}{ccc}
vec{i} & vec{j} & vec{k} \
1 & 0 & 1\
-2 & -1 & 2 \
end{array}
right|= {1,, -4,, -1} ,, Rightarrow ,,
frac{X}{1}=frac{Y}{-4}=frac{Z-1}{-1}.
$$
-
Спрямляющая плоскость перпендикулярна главной нормали, а значит, вектору ${1,, -4,, -1}$, поэтому можем сразу записать ее общее уравнение:
begin{equation*}
1cdot X-4cdot Y-1cdot (Z-1)=0,, Rightarrow ,, X-4Y-Z+1=0.
end{equation*}
Орт касательной: $vec{tau} =frac{1}{sqrt{2}}{1,,0,,1}$,
Орт главной нормали: $vec{nu} =frac{1}{sqrt{18}}{1,,-4,,-1}$,
Орт бинормали: $vec{beta }=frac{1}{3}{-2,,-1,,2}$.
Поскольку направляющий вектор главной нормали у нас был найден как векторное произведение направляющих векторов касательной и бинормали, тройка $vec{tau}$, $vec{nu}$, $vec{beta}$ не будет правой (по определению векторного произведения вектор $vec{tau}timesvec{beta}$ направлен так, что тройка векторов $vec{tau}$, $vec{beta}$, $vec{nu}=vec{tau}timesvec{beta}$ — правая). Изменим направление одного из векторов. Например, пусть
$$ vec{nu} =frac{1}{sqrt{18}}{-1,,4,,1}.$$
Теперь тройка $vec{tau}$, $vec{nu}$, $vec{beta}$ образует репер Френе для кривой $gamma$ в точке $M$.
Задача 2
Написать уравнение соприкасающейся плоскости к кривой
$$
x=t,,, y=frac{t^2}{2},,, z=frac{t^3}{3},
$$
проходящей через точку $N(0,0,9)$.
Решение задачи 2
Нетрудно заметить, что точка $N$ не принадлежит заданной кривой $gamma$. Следовательно соприкасающаяся плоскость проведена в какой-то точке $M(t=t_0)ingamma$, но при этом плоскость проходит через заданную точку $N(0,0,9)$.
Найдем значение параметра $t_0$.
Для этого запишем уравнение соприкасающейся плоскости, проведенной в произвольной точке $M(t=t_0)$. И учтем, что координаты $N$ должны удовлетворять полученному уравнению.
begin{align*}
gamma: vec{r}(t)&=left{ t,, frac{t^2}{2},, frac{t^3}{3}right} ,, Rightarrow \
vec{r’}(t)&=left{ 1,, t,, 3t^2right},\
vec{r»}(t)&=left{ 0,, 1,, 6tright}.
end{align*}
В точке $M(t=t_0)$:
begin{align*}
vec{r}(t_0)&=left{t_0,, frac{t_0^2}{2},, frac{t_0^3}{3}right} \
vec{r’}(t_0)&=left{1,, t_0,, 3t_0^2right},\
vec{r»}(t_0)&=left{0,, 1,, 6t_0right}.
end{align*}
Соприкасающаяся плоскость определяется векторами $vec{r’}(t_0)$, $vec{r»}(t_0)$, поэтому записываем определитель
begin{equation*}
left|
begin{array}{ccc}
X-t_0 & Y-t_0^2/2 & Z-t_0^3/3 \
&&\
1 & t_0 & t^2_0 \
&&\
0 & 1 & 2t_0
end{array}
right|=0 quad Rightarrow
end{equation*}
begin{equation*}
(X-t_0)cdot t_0^2 — (Y-t_0^2/2)cdot 2t_0 + (Z-t_0^3/3)=0.
end{equation*}
Подставляем вместо $X$, $Y$, $Z$ координаты точки $N$: $X=0$, $Y=0$, $Z=9$, упрощаем и получаем уравнение относительно $t_0$:
begin{equation*}
9-t_0^3/3=0 quad Rightarrow quad t_0=3.
end{equation*}
Подставив найденное $t_0$ в записанное ранее уравнение, запишем искомое уравнение соприкасающейся плоскости:
$$ 9X-6Y+Z-9=0. $$
Задача 3
Через точку $Pleft(-frac45,1,2right)$ провести плоскость, являющуюся спрямляющей для кривой:
$$
x=t^2,,, y=1+t,,, z=2t.
$$
Решение задачи 3
Как и в предыдущей задаче нам неизвестны координаты точки, в которой проведена спрямляющая плоскость к заданной кривой. Найдем их.
Спрямляющая плоскость определяется касательной и бинормалью, то есть векторами $vec{r’}(t_0)$ и $vec{r’}(t_0)timesvec{r»}(t_0)$.
В произвольной точке $M(t=t_0)$:
begin{align*}
vec{r}(t_0)&=left{t^2_0,, 1+t_0,, 2t_0right} \
vec{r’}(t_0)&=left{2t_0,, 1,, 2right},\
vec{r»}(t_0)&=left{2,, 0,, 0right}.
end{align*}
begin{equation*}
vec{r’}(t_0)timesvec{r»}(t_0)= left|
begin{array}{ccc}
vec{i} & vec{j} & vec{k} \
2t_0 & 1 & 2\
2 & 0 & 0
end{array}
right|= {0,, 4,, -2}
end{equation*}
Записываем уравнение спрямляющей плоскости:
begin{equation*}
left|
begin{array}{ccc}
X-t_0^2 & Y-1-t_0 & Z-2t_0 \
2t_0 & 1 & 2\
0 & 4 & -2
end{array}
right|= 0
end{equation*}
Раскрываем определитель. Подставляем в уравнение координаты точки $P$: $X=-4/5$, $Y=1$, $Z=2$. Упрощаем и получаем уравнение для нахождения $t_0$:
begin{equation*}
5t_0^2-8t_0-4=0 ,, Rightarrow ,, t_{01}=2,, t_{02}=-frac25.
end{equation*}
Уравнения соприкасающихся плоскостей к заданной кривой, проходящих через $P$, принимают вид:
begin{align*}
& 5X-4Y-8Z+24=0,\
& 25X+4Y+8Z=0.
end{align*}
Репер Френе
- Репер Френе
-
Репер или трёхгранник Френе или Френе — Серре известный также, как естественный, сопровождающий, сопутствующий — ортонормированный репер в трёхмерном пространстве, возникающий при изучении бирегулярных кривых.
Содержание
- 1 Определение
- 2 Формулы Френе
- 3 Скорость и ускорение в осях естественного трёхгранника
- 4 Вариации и обобщения
Определение
Пусть γ(s) — произвольная натурально параметризованная бирегулярная кривая в евклидовом пространстве. Под репером Френе понимают тройку векторов
сопоставленную каждой точке бирегулярной кривой
, где
к кривой в данной точке.
Формулы Френе
Если s — натуральный параметр вдоль кривой, то векторы
связаны соотношениями:
называемыми формулами Френе. Величины
называют, соответственно, кривизной и кручением кривой в данной точке. Уравнения вида
где f(s) всюду положительна называются натуральными уравнениями бирегулярной кривой и полностью её определяют.
Скорость и ускорение в осях естественного трёхгранника
Трёхгранник Френе играет важную роль в кинематике точки при описании её движения в «сопутствующих осях». Пусть материальная точка движется по произвольной бирегулярной кривой. Тогда, очевидно, скорость точки направлена по касательному вектору
. Дифференцируя по времени находим выражение для ускорения:
. Компоненту при векторе
называют тангенциальным ускорением, она характеризует изменение модуля скорости точки. Компоненту при векторе
называют нормальным ускорением. Она показывает, как меняется траектория движения точки.
Вариации и обобщения
При описании плоских кривых часто вводят понятие так называемой ориентированной кривизны.
Пусть γ(s) — произвольная натурально параметризованная плоская регулярная кривая. Рассмотрим семейство единичных нормалей
, таких что двойка
образуют правый базис в каждой точке
. Ориентированной кривизной кривой γ в точке s называют число
. В сделанных предположениях имеет место следующая система уравнений, называемая формулами Френе для ориентированной кривизны
.
По аналогии с трёхмерным случаем, уравнения вида ko = f(s) называются натуральными уравнениями плоской регулярной кривой и полностью её определяют.
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое «Репер Френе» в других словарях:
-
НАТУРАЛЬНЫЙ РЕПЕР, — трехгранник (или репер) Френе, естественный трехгранник, фигура, составленная из касательной, главной нормали, бинормали и трех плоскостей, попарно содержащих эти прямые. Если ребра Н. р. в данной точке кривой принять за оси прямоугольной… … Математическая энциклопедия
-
Трёхгранник Френе — Репер или трёхгранник Френе или Френе Серре известный также, как естественный, сопровождающий, сопутствующий ортонормированный репер в трёхмерном пространстве, возникающий при изучении бирегулярных кривых. Содержание 1 Определение 2… … Википедия
-
ПЛАСТИЧНОСТИ ТЕОРИЯ — раздел механики, в к ром изучаются законы, отражающие связи между напряжениями и упругопластич. деформациями (физ. основы П. т.), и разрабатываются методы решения задач о равновесии и движении деформируемых тв. тел (матем. П. т.). П. т. явл.… … Физическая энциклопедия
-
Естественный трёхгранник — Репер или трёхгранник Френе или Френе Серре известный также, как естественный, сопровождающий, сопутствующий ортонормированный репер в трёхмерном пространстве, возникающий при изучении бирегулярных кривых. Содержание 1 Определение 2 Формулы Френе … Википедия
-
ПОДВИЖНОГО РЕПЕРА МЕТОД — дифференциально геометрический метод локального исследования подмногообразий различных однородных пространств, исходным моментом к poro является отнесение самого подмногообразия и всех его геометрич. объектов к возможно более общему (подвижному)… … Математическая энциклопедия
-
КРИВИЗНА — количеств. характеристика, описывающая отклонение кривой, поверхности, риманова пространства и др. соответственно от прямой, плоскости, евклидова пространства и др. Обычно понятие К. вводится локально, т. е. в каждой точке. В декартовых… … Физическая энциклопедия
Рассмотрим
гладкую кривую
в пространстве
.
Пусть
— любая точка кривой. Найдем плоскость,
проходящую через
и «ближе всего подходящую» к кривой
в окрестности точки
.
Заметим, что если кривая
— плоская (то есть лежащая в некоторой
плоскости
),
то искомой плоскостью будет плоскость
.
Определение
3.1. Соприкасающейся
плоскостью к
кривой
в точке
называется предел секущей плоскости,
проходящей через точки
кривой
при
стремлении
Более
строго, плоскость
,
проходящая через точку
кривой
,
является соприкасающейся к кривой
в точке
,
если
.
Теорема
3.1.
-гладкая
кривая
имеет в каждой точке
соприкасающуюся плоскость.
Дадим
необходимые разъяснения для кривой
более высокого порядка гладкости.
Пусть
в
пространстве
задана прямоугольная система координат
Оxyz.
Пусть
r
(t)
— одна из гладких параметризаций кривой
:
и
Рассмотрим
произвольную точку
,
близкую к точке
.
Разложим
в ряд Тейлора вектор смещения
:

Пусть
— неколлинеарные векторы.
Тогда
искомая плоскость единственна и проходит
через точку
параллельно векторам
.
Замечание
3.1.
Неколлинеарность векторов
не
зависит от способа параметризации
кривой.
В частности, для любой допустимой замены
параметра
,
где
,
векторы
также будут неколлинеарны.
Пусть
— коллинеарные векторы.
Тогда
соприкасающаяся плоскость не единственна.
В качестве одной из соприкасающихся
плоскостей можно взять любую из
плоскостей, проходящих через касательную
к кривой в точке
.
Определение
3.2. Спрямляющей
плоскостью к
кривой
в точке
называется плоскость, проходящая через
точку
кривой
перпендикулярно
спрямляющей и нормальной плоскостям в
этой точке.
Определение
3.3. Главной
нормалью к
кривой
в точке
называется прямая пересечения
соприкасающейся и нормальной плоскостей,
проведенных в точке
.
Главная
нормаль перпендикулярна спрямляющей
плоскости
.
Определение
3.4. Бинормалью
к
кривой
в точке
называется прямая пересечения спрямляющей
и нормальной плоскостей, проведенных
в точке
.
Бинормаль
перпендикулярна соприкасающейся
плоскости в точке
.
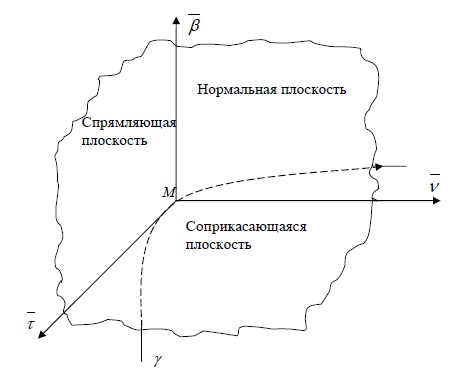
Определение
3.5. Сопровождающим
трехгранником (или
репером
Френе)
кривой
в точке
называется совокупность трех прямых
– касательной, главной нормали и
бинормали, и трех плоскостей – нормальной
спрямляющей и соприкасающейся, проведенных
в точке
.
Рисунок 12.
Пусть
r
(t)
— одна из гладких параметризаций кривой
:
,
и
— любая точка кривой.
Напишем
уравнения всех прямых и всех плоскостей
сопровождающего трехгранника кривой.
Уравнения
касательной прямой и нормальной плоскости
мы уже выписывали в §2.
Если
соприкасающаяся плоскость к кривой
в точке
единственна, то она может быть задана
параметрическими уравнениями
,
где
.
В
качестве направляющего вектора бинормали
возьмем вектор
.
Уравнение бинормали в параметрическом
виде
,
где
.
В
качестве направляющего вектора главной
нормали возьмем вектор
.
Уравнение главной нормали в параметрическом
виде
,
где
.
Уравнение спрямляющей
плоскости в параметрическом виде
,
где
.
Уравнение
соприкасающейся плоскости можно также
написать в общем виде как уравнение
плоскости, проходящей через точку
перпендикулярно вектору
:
.
Аналогично,
так как спрямляющая плоскость проходит
через точку
перпендикулярно вектору
,
то ее общее уравнение имеет вид:
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

 сопоставленную каждой точке бирегулярной кривой
сопоставленную каждой точке бирегулярной кривой  , где
, где связаны соотношениями:
связаны соотношениями:
 называют, соответственно, кривизной и кручением кривой в данной точке. Уравнения вида
называют, соответственно, кривизной и кручением кривой в данной точке. Уравнения вида  где
где  . Дифференцируя по времени находим выражение для ускорения:
. Дифференцируя по времени находим выражение для ускорения:  . Компоненту при векторе
. Компоненту при векторе  называют тангенциальным ускорением, она характеризует изменение модуля скорости точки. Компоненту при векторе
называют тангенциальным ускорением, она характеризует изменение модуля скорости точки. Компоненту при векторе 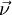 называют нормальным ускорением. Она показывает, как меняется траектория движения точки.
называют нормальным ускорением. Она показывает, как меняется траектория движения точки. , таких что двойка
, таких что двойка 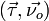 образуют правый базис в каждой точке
образуют правый базис в каждой точке  . Ориентированной кривизной кривой
. Ориентированной кривизной кривой  . В сделанных предположениях имеет место следующая система уравнений, называемая формулами Френе для ориентированной кривизны
. В сделанных предположениях имеет место следующая система уравнений, называемая формулами Френе для ориентированной кривизны .
.