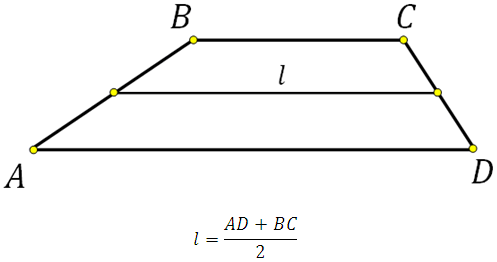
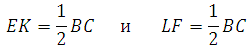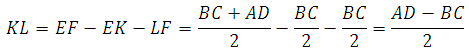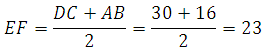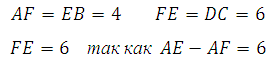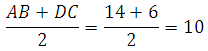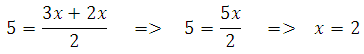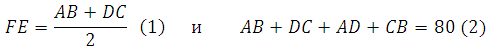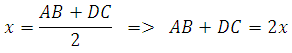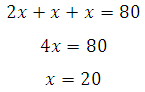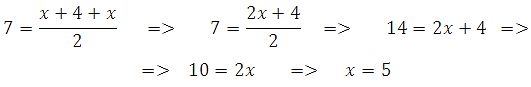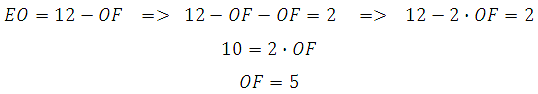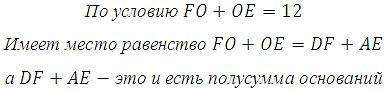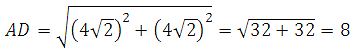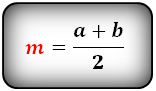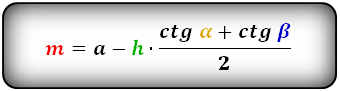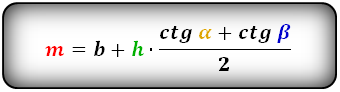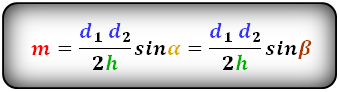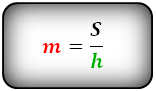В этой статье для вас сделана очередная подборка задач с трапецией. Условия так или иначе связаны с её средней линией. Типы заданий взяты из открытого банка типовых задач. Если есть желание, то можете освежить свои теоретические знания связанные с трапецией. На блоге уже рассмотрены задачи условия которых связаны с площадью трапеции, а также с углами. Кратко о средней линии:
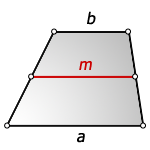
Средняя линия трапеции соединяет середины боковых сторон. Она параллельна основаниям и равна их полусумме.
Перед решением задач давайте рассмотрим теоретический пример.
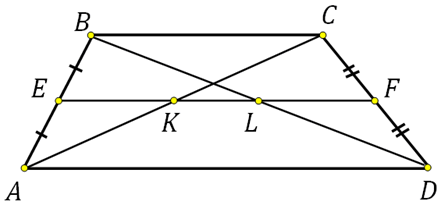
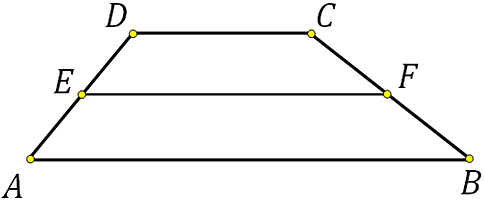
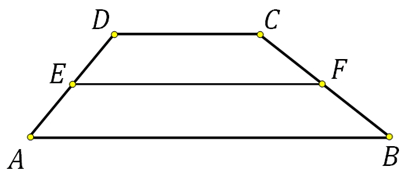
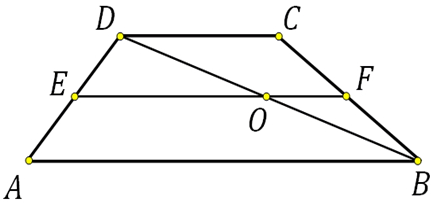
Дана трапеция ABCD. Диагональ АС пересекаясь со средней линией образует точку К, диагональ BD точку L. Доказать, что отрезок KL равен половине разности оснований.
Давайте сначала отметим тот факт, что средняя линия трапеции делит пополам любой отрезок концы которого лежат на её основаниях. Этот вывод напрашивается сам собой. Представьте отрезок соединяющий две точки оснований, он разобьёт данную трапецию на две других. Получится, что отрезок параллельный основаниям трапеции и проходящий через середину боковой стороны на другой боковой стороне пройдёт через её середину.
Так же это основывается на теореме Фалеса:
Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки.
То есть в данном случае К середина АС и L середина BD. Следовательно EK есть средняя линия треугольника АВС, LF есть средняя линия треугольника DCB. По свойству средней линии треугольника:
Можем теперь выразить отрезок KL через основания:
Доказано!
Данный пример приведён не просто так. В задачах для самостоятельного решения имеется именно такая задача. Только в ней не сказано, что отрезок соединяющий середины диагоналей лежит на средней линии. Рассмотрим задачи:
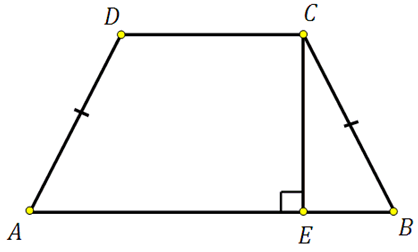
27819. Найдите среднюю линию трапеции, если ее основания равны 30 и 16.
Вычисляем по формуле:
Ответ: 23
27820. Средняя линия трапеции равна 28, а меньшее основание равно 18. Найдите большее основание трапеции.
Выразим большее основание:
Таким образом:
Ответ: 38
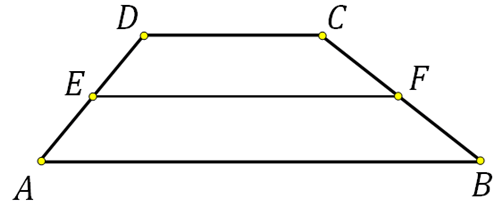
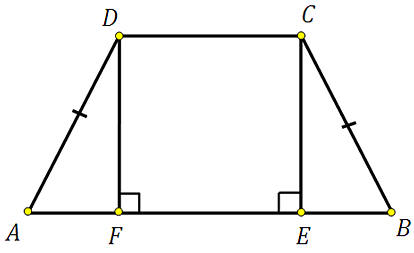
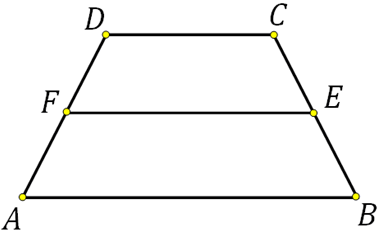
27836. Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 10 и 4. Найдите среднюю линию этой трапеции.
Для того, чтобы найти среднюю линию необходимо знать основания. Основание АВ найти просто: 10+4=14. Найдём DC.
Построим второй перпендикуляр DF:
Отрезки AF, FE и EB будут равны соответственно 4, 6 и 4. Почему?
В равнобедренной трапеции перпендикуляры опущенные к большему основанию разбивают его на три отрезка. Два из них, являющиеся катетами отсекаемых прямоугольных треугольников, равны друг другу. Третий отрезок равен меньшему основанию, так как при построении указанных высот образуется прямоугольник, а в прямоугольнике противолежащие стороны равны. В данной задаче:
Таким образом DC=6. Вычисляем:
Ответ: 10
27839. Основания трапеции относятся 2:3, а средняя линия равна 5. Найдите меньшее основание.
Введём коэффициент пропорциональности х. Тогда АВ=3х, DC=2х. Можем записать:
Следовательно меньшее основание равно 2∙2=4.
Ответ: 4
27840. Периметр равнобедренной трапеции равен 80, ее средняя линия равна боковой стороне. Найдите боковую сторону трапеции.
Исходя из условия можем записать:
Если обозначить среднюю линию через величину х, то получится:
Второе уравнение уже можно записать в виде:
Ответ: 20
27841. Средняя линия трапеции равна 7, а одно из ее оснований больше другого на 4. Найдите большее основание трапеции.
Обозначим меньшее основание (DC) как х, тогда большее (AB) будет равно х+4. Можем записать
Получили, что меньшее основание рано пяти, значит большее равно 9.
Ответ: 9
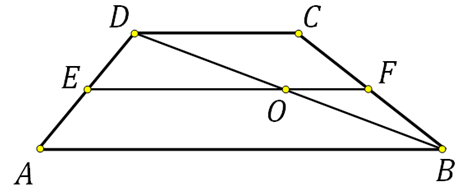
27842. Средняя линия трапеции равна 12. Одна из диагоналей делит ее на два отрезка, разность которых равна 2. Найдите большее основание трапеции.
Большее основание трапеции мы без труда найдём если вычислим отрезок ЕО. Он является средней линией в треугольнике ADB, и АВ=2∙ЕО.
Что имеем? Сказано что средняя линия равна 12 и разность отрезков ЕО и ОF равна 2. Можем записать два уравнения и решить систему:
Понятно, что в данном случае подобрать пару чисел можно без вычислений, это 5 и 7. Но, всё-таки, решим систему:
Значит ЕО=12–5=7. Таким образом, большее основание равно АВ=2∙ЕО=14.
Ответ: 14
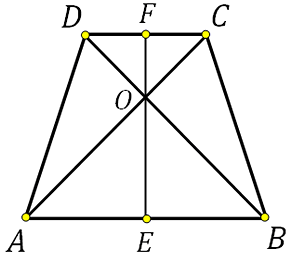
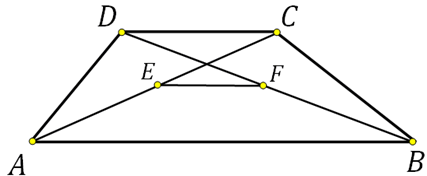
27844. В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию.
Сразу отметим, что высота проведённая через точку пересечения диагоналей в равнобедренной трапеции лежит на оси симметрии и разбивает трапецию на две равные прямоугольные трапеции, то есть основания этой высотой делятся пополам.
Казалось бы, для вычисления средней линии мы должны найти основания. Тут небольшой тупик возникает… Как зная высоту, в данном случае, вычислить основания? А ни как! Таких трапеций с фиксированной высотой и диагоналями пересекающимися по углом 90 градусов можно построить множество. Как быть?
Посмотрите на формулу средней линии трапеции. Ведь нам необязательно знать сами основания, достаточно узнать их сумму (или полусумму). Это мы сделать можем.
Так как диагонали пересекаются под прямым углом, то высотой EF образуются равнобедренные прямоугольные треугольники:
При чём:
Из выше сказанного следует, что FO=DF=FC, а OE=AE=EB. Теперь запишем чему равна высота выраженная через отрезки DF и AE:
Таким образом, средняя линия равна 12.
*Вообще это задачка, как вы поняли, для устного счёта. Но, уверен, представленное подробное объяснение необходимо. А так… Если взглянуть на рисунок (при условии, что при построении соблюдён угол между диагоналями), сразу в глаза бросается равенство FO=DF=FC, а OE=AE=EB.
Ответ: 12
В составе прототипов имеется ещё типы заданий с трапециями. Построена она на листе в клетку и требуется найти среднюю линию, сторона клетки обычно равна 1, но может быть другая величина.
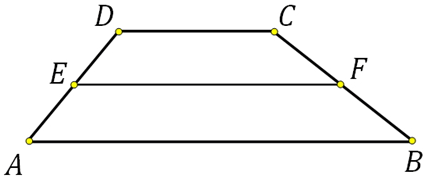
27848. Найдите среднюю линию трапеции ABCD, если стороны квадратных клеток равны 1.
Всё просто, вычисляем основания по клеткам и используем формулу: (2+4)/2=3
Ответ: 3
Если же основания построены под углом к клеточной сетке, то есть два способа. Например!
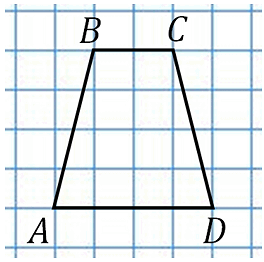
28854.Найдите среднюю линию трапеции ABCD, если стороны квадратных клеток равны √2.
В данном случае видно, что средняя линия трапеции равна трём диагоналям клетки. Диагональ одной клетки по теореме Пифагора будет равна:
Значит средняя линия равна 2∙3=6.
Конечно, есть и другой путь решения.
Если допустить мысль, что основания трапеции могут лежать по отношению к сетке под углом не 45 градусов, а например 30, или другим, то вполне применим следующий метод (таких задач на ЕГЭ не предвидится):
Вычисляем основания используя теорему Пифагора, а далее используем формулу средней линии.
Основание AD при данных условиях это диагональ в прямоугольном треугольнике с катетами равными 4 сторонам клетки, вычисляем:
Основание BC это диагональ в прямоугольном треугольнике катетами равными 2 сторонам клетки, вычисляем:
Средняя линия будет равна (8+4)/2=6.
*То есть при данном подходе, как бы ни была построена трапеция всегда можно вычислить основания.
Ответ: 6
27853. Найдите высоту трапеции ABCD, опущенную из вершины B, если стороны квадратных клеток равны √2.
Высота трапеции равна диагонали клетки. Вычисляем по теореме Пифагора:
Ответ: 2
27821. Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.
Посмотреть решение
27838.Периметр трапеции равен 50, а сумма непараллельных сторон равна 20. Найдите среднюю линию трапеции.
Посмотреть решение
27843. Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.
Посмотреть решение
На этом всё, успеха вам!
С уважением, Александр Крутицких.
P,S: Расскажите о сайте в социальных сетях.
В данной публикации мы рассмотрим определение, свойства и признак средней линии трапеции, а также разберем пример решения задачи для лучшего понимания изложенного материала.
- Определение средней линии трапеции
-
Свойства средней линии трапеции
- Свойство 1
- Свойство 2
- Свойство 3
- Признак средней линии трапеции
- Вторая средняя линия
- Пример задачи
Определение средней линии трапеции
Отрезок, соединяющий середины боковых сторон трапеции, называется ее средней линией.
- LM – средняя линия трапеции ABCD
- L – середина стороны AB, т.е. AL = LB
- M – середина стороны CD, т.е. CM = MD
Свойства средней линии трапеции
Свойство 1
Средняя линия трапеции параллельна ее основаниям и равняется их полусумме.
Для рисунка выше:
Свойство 2
Средняя линия трапеции делит пополам любой отрезок, концы которого лежат на основаниях данной трапеции.
Свойство 3
Средняя линия трапеции делит ее на две другие трапеции, площади которых соотносятся следующим образом (см. первый чертеж публикации):
Признак средней линии трапеции
Если отрезок, выходящий из середины боковой стороны трапеции, пересекает ее вторую боковую сторону и, при этом, параллелен основаниям фигуры, то он является средней линией этой трапеции.
Вторая средняя линия
Иногда дополнительно выделяют вторую среднюю линию трапеции – отрезок, соединяющий середины ее оснований. При этом следует помнить, что к ней не применимы Свойства 1-3 и Признак, рассмотренные выше.
Вторая средняя линия равнобедренной трапеции одновременно является ее высотой.
Пример задачи
Средняя линия трапеции равняется 25 см, а ее высота – 7 см. Найдите площадь фигуры.
Решение
Как мы знаем, площадь трапеции равняется полусумме оснований, умноженной на высоту h: S = (a+b)/2 ⋅ h
В данном случае полусумма оснований – это и есть средняя линия. Обозначим ее буквой m. То есть m = (a+b)/2.
Таким образом, S = m ⋅ h = 25 см ⋅ 7 см = 175 см2.
Средняя линия трапеции
Это отрезок, который соединяет середины 2 боковых сторон трапеции. Существует несколько способов (формул), позволяющих узнать, чему равна средняя линия.
Рассмотрим некоторые из них.
Как найти среднюю линию трапеции через основания
Если известно, чему равны основания трапеции, то среднюю линию найти совсем не сложно.
Она будет равна полусумме оснований.
EF = (AB + CD) / 2.
Например, если основание AB = 10 см, а основание CD = 6 см, то средняя линия равна (10 + 6) / 2 = 8 см.
Как найти среднюю линию трапеции через площадь и высоту
По классической формуле, площадь трапеции равна полусумме оснований умноженной на высоту. А полусумма оснований и есть средняя линия.
Поэтому, если площадь S = EF * DH, то средняя линия EF = S / DH.
Например, если площадь трапеции равна 30 кв. см, а высота — 6 см, то средняя линия = 30 / 6 = 5 см.
Как найти среднюю линию трапеции через высоту, диагонали и угол между ними
Если неизвестна площадь трапеции, но известны диагонали и угол между ними, то можно воспользоваться одной из формул нахождения площади.
А после этого подставить полученное значение в формулу, позволяющую найти среднюю линию через площадь и высоту.
Если даны диагонали d1 и d2, а также угол между ними (например, γ), то S = 0,5 * d1 *d2 * sinγ.
Подставим это в формулу нахождения средней линии: EF = S / DH = (0,5 * AC * BD * sinγ) / DH = AC * BD * sinγ / 2DH.
Например, высота = 6 см, диагонали — 8 и 10 см, угол между ними — 30 градусов.
EF = (8 * 10 * 0,5) / (2 * 6) = 40 / 12 = 3,33 см.
Трапеция это фигура, которая имеет четыре стороны, две из которых параллельны, а две другие, нет. Параллельные стороны называются — верхнее основание и нижнее основание. Две другие, называются боковыми сторонами.
Средняя линия трапеции — отрезок соединяющий середины боковых сторон и расположен параллельно к основаниям. Длина средней линии, равна полу сумме оснований.
1. Формула средней линии трапеции через основания
b — верхнее основание
a — нижнее основание
m— средняя линия
Формула средней линии, (m ):
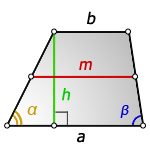
2. Формулы средней линии через основание, высоту и углы при нижнем основании
b — верхнее основание
a — нижнее основание
α, β — углы трапеции
h — высота трапеции
m — средняя линия
Формулы средней линии трапеции, (m):
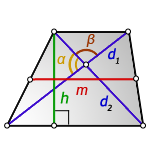
3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями
α, β — углы между диагоналями
d1 , d2 — диагонали трапеции
h — высота трапеции
m — средняя линия
Формулы средней линии трапеции, (m ):
4. Формула средней линии трапеции через площадь и высоту
S — площадь трапеции
h — высота трапеции
m — средняя линия
Формула средней линии трапеции, (m):
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
- Подробности
-
Опубликовано: 24 сентября 2013
-
Обновлено: 13 августа 2021
Термин «трапеция» произошёл от греческого слова «столик». В русском языке от того же слова произошло
понятие «трапеза» — еда.
Средняя линия — отрезок, который прокладывается через противолежащие стороны, и который дробит их
точно на половинки.
Средняя линия трапеции имеет три отличительных черты:
- Она параллельна базовым сторонам четырёхугольника;
- Эквивалентна половинке суммирования оснований;
- Разбивает первоначальный четырёхугольник на две поменьше. Вместе с тем их площади имеют
конкретное соотношение друг к другу.
- Средняя линия трапеции через длины оснований
- Средняя линия трапеции через площадь и высоту
- Средняя линия трапеции через нижнее основание, высоту и
углы при нижнем основании - Средняя линия трапеции через верхнее основание, высоту и
углы при нижнем основании - Средняя линия трапеции через диагонали, высоту и угол между
диагоналями - Средняя линия трапеции через боковые стороны, верхнее
основание и углы при нижнем основании - Средняя линия трапеции через боковые стороны, нижнее
основание и углы при нижнем основании - Средняя линия равнобедренной трапеции через боковую
сторону, нижнее основание и угол между ними - Средняя линия равнобедренной трапеции через боковую
сторону, верхнее основание и угол при нижнем основании - Средняя линия прямоугольной трапеции через нижнее
основание, высоту и острый угол при нижнем основании - Средняя линия прямоугольной трапеции через верхнее
основание, высоту и острый угол при нижнем основании
Через длины оснований
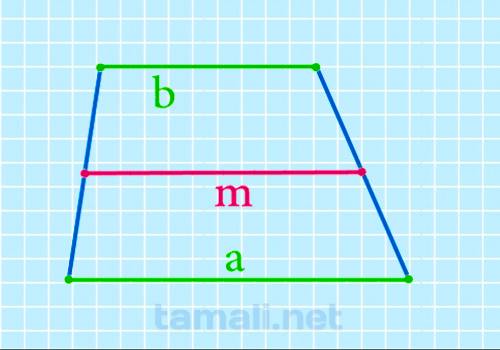
Имеется одно основная формулировка, которая позволяет рассчитывать величину средней линии. Величина
средней линии будет равна сумме базовых сторон фигуры, поделённой напополам. Формула следующая:
M = a + b / 2
где a и b — наибольшая и наименьшая стороны.
Цифр после
запятой:
Результат в:
Пример. Если наибольшая базовая сторона равна 8, а наименьшая — 10, то (8 + 10) / 2 = 9. Или, если
наибольшая базовая сторона равна 15, а наименьшая — 3. Тогда:
(3 + 15) / 2 = 9.
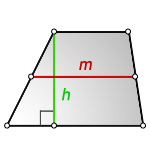
Через площадь и высоту
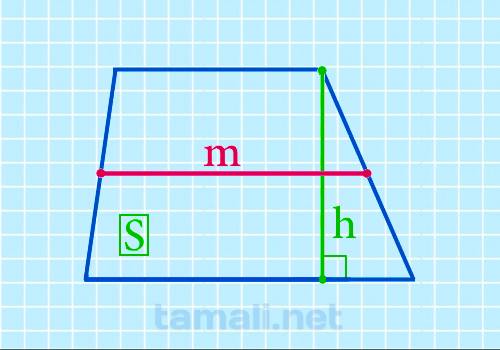
Формулировка поиска величины срединного отрезка через площадь и перпендикуляр:
M = S / h
где S — площадь, h — перпендикуляр.
Цифр после
запятой:
Результат в:
Пример. Если площадь равняется 20, а высота — 5, тогда: M = 20 / 5 = 4. Если площадь равна 50, а
высота равна 5, тогда срединный отрезок:
M = 50 / 5 = 10.
Через верхнее основание, высоту и углы при нижнем основании
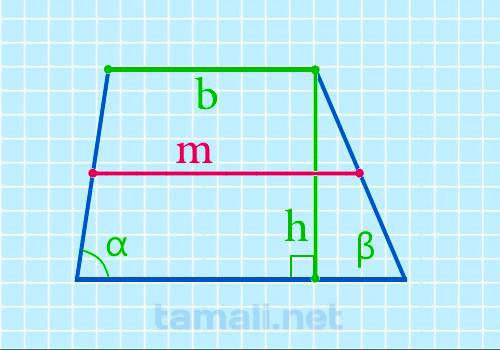
Равенство расчёта величины срединного отрезка через наибольшую базовую сторону, высоту и углы при
наименьшей базовой стороне выглядит:
M = b + h * (ctg α + ctg β)/2
где b — наибольшая базовая сторона, α и β — углы при наименьшей базовой стороне, h — высота.
Цифр после
запятой:
Результат в:
Пример. Наибольшая сторона равняется 15, высота — 6, а углы — 45 и 30. В таком случае:
m = 15 + 6 · (ctg 45 + ctg 30)/2 = 15 + 6 · (1 + √3)/2 ≈ 23,196.
Через диагонали, высоту и угол между диагоналями
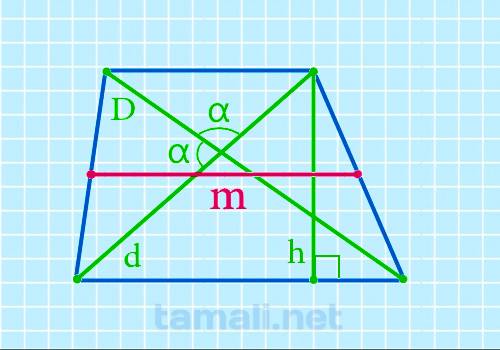
Формулировка исчисления величины срединного отрезка через диагонали, высоту и уголок между
диагоналями описывается:
M = (d1 * d2)/2h * sin α
где d1, d2 — диагонали, α — уголок между диагоналями, h — высота.
Цифр после
запятой:
Результат в:
Пример. Пусть диагонали четырёхугольника равняются 15 и 4, высота — 5, а уголок между диагоналями
фигуры — 30 градусов. Значит:
m = (15 * 4)/(2 * 5) * sin 30 = 6 * 1/2 = 3.
Если в качестве диагоналей взять 20 и 5, высоты — 6, а угла — 30, тогда: m = (20 * 5)/(2 * 6) * sin
30 ≈ 8,33 * 1/2 ≈ 4,167.
Через нижнее основание, высоту и углы при нижнем основании
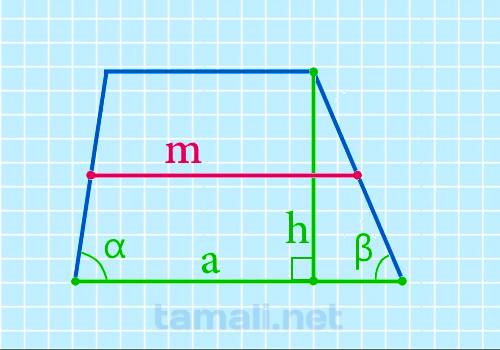
Формулировка нахождения величины срединного отрезка через наименьшую базовую сторону, высоту и углы
при наименьшей базовой стороне приведена далее:
M = a — h * (ctg α + ctg β)/ 2
где a — наименьшая базовая сторона, α и β — углы при наименьшей базовой стороне, h — высота
четырёхугольника.
Цифр после
запятой:
Результат в:
Пример. Если наименьшая базовая сторона четырёхугольника равносильна 5, углы — 45 и 45, а высота — 2,
тогда: 5 – 2 · (ctg 45 + ctg 45)/ 2 = 3.
Через боковые стороны, верхнее основание и углы при нижнем основании
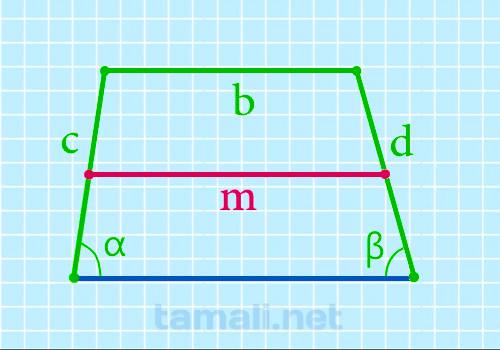
Тождество поиска величины срединного отрезка через вспомогательные стороны, наибольшую сторону и углы
при наименьшей стороне:
m = (2b + c * cos α + d * cos β) / 2
где b — наибольшая сторона, c и d — вспомогательные стороны, α и β — углы при наименьшей стороне.
Цифр после
запятой:
Результат в:
Пример. Если в качестве наибольшей стороны взять 15, наклонных сторон — 7 и 9, а углов при наименьшей
стороне — 60 и 60 градусов. Следовательно: m = (2 * 15 + 7 * cos 60 + 9 * cos 60) / 2 = (30 +
3,5 + 4,5) / 2 = 19.
Через боковые стороны, нижнее основание и углы при нижнем основании
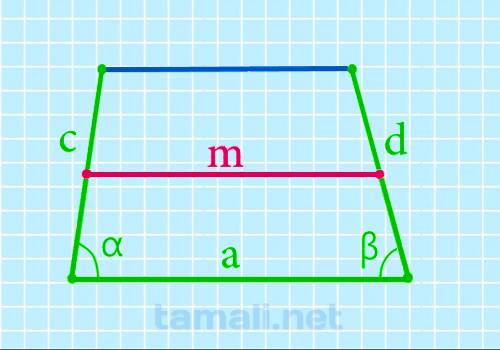
Выражение исчисления величины срединного отрезка через вспомогательные стороны, меньшую сторону и углы при меньшей стороне:
m = (2a — c * cos α — d * cos β) / 2
где a — меньшая сторона, c и d — наклонные стороны, α и β — углы.
Угол (α):
Угол (β):
Цифр после запятой:
Результат в:
К примеру, если нижняя сторона равна 8, боковая сторона 5, а угол при нижней стороне фигуры — 60, тогда:
m = (2 · 8 – 2 · 5 · cos 60) / 2 = 3.
Если же нижняя сторона равняется 12, боковая сторона 6, а угол при нижней стороне — 60, в таком случае:
m = (2 · 12 – 2 · 6 · cos 60) / 2 = 9.
Средняя линия равнобедренной трапеции через боковую сторону, верхнее основание и угол при нижнем
основании
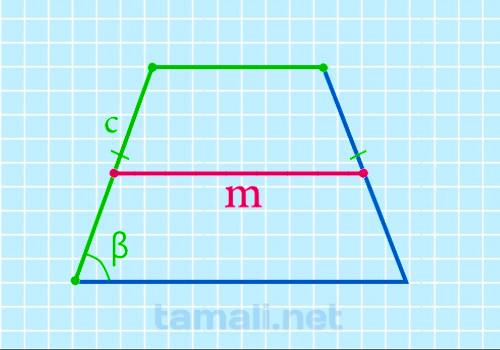
Формула расчёта длины срединного отрезка через боковые стороны, верхнюю сторону и углы при нижней
стороне:
m = (2b + 2c · cos β) / 2
где b — верхняя сторона, c — боковая сторона четырёхугольника, β — угол.
Цифр после
запятой:
Результат в:
Например, если верхняя сторона четырёхугольника равняется 5, боковая сторона 8, а угол при нижней
стороне фигуры — 60, тогда срединный отрезок рассчитывается следующим образом: m = (2 · 5 – 2 ·
8 · cos 60) / 2 = 1.
Если представить верхнюю сторону длиной 6, боковую сторону длиной 5, а угол при нижней стороне
четырёхугольника — 60, в таком случае: m = (2 · 6 – 2 · 5 · cos 60) / 2 = 3,5.
Через боковые стороны, нижнее основание и углы при нижнем основании
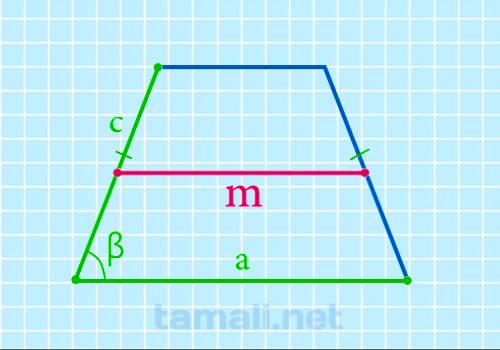
Выражение исчисления величины срединного отрезка через вспомогательные стороны, меньшую сторону и
углы при меньшей стороне:
m = (2a — c * cos α — d * cos β) / 2
где a — меньшая сторона, c и d — наклонные стороны, α и β — углы.
Цифр после
запятой:
Результат в:
К примеру, если нижняя сторона равна 8, боковая сторона 5, а угол при нижней стороне фигуры — 60,
тогда: m = (2 · 8 – 2 · 5 · cos 60) / 2 = 3.
Если же нижняя сторона равняется 12, боковая сторона 6, а угол при нижней стороне — 60, в таком
случае: m = (2 · 12 – 2 · 6 · cos 60) / 2 = 9.
Средняя линия прямоугольной трапеции через нижнее основание, высоту и острый угол при нижнем
основании
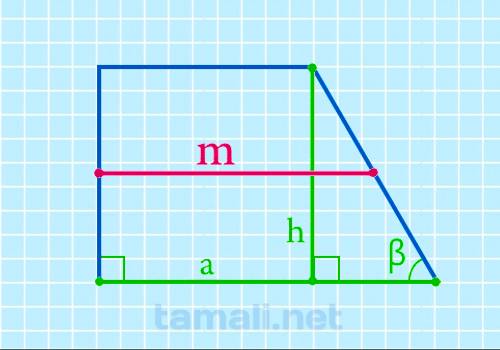
Формула определения длины срединного отрезка через боковые стороны, верхнюю сторону и углы при нижней
стороне:
m = a – h · ctg β / 2
где a — нижняя сторона, h — высота, β — острый уголок при нижней стороне.
Цифр после
запятой:
Результат в:
Пример. Пусть нижняя сторона четырёхугольника равняется 8, высота — 3, а острый уголок — 45, в таком
случае: m = 8 – 3 · ctg 45 / 2 = 6,5.
Средняя линия прямоугольной трапеции через верхнее основание, высоту и острый угол при нижнем
основании
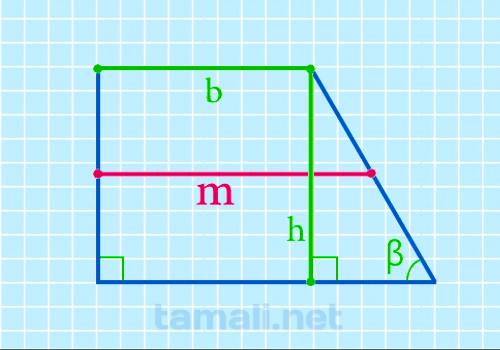
Формула определения длины срединного отрезка через боковые стороны, верхнюю сторону и углы при нижней
стороне:
m = b + h · ctg β / 2
где b — верхняя сторона, h — высота, β — острый угол при нижней стороне.
Цифр после
запятой:
Результат в:
Пример. В качестве верхнего возьмём 4, высоты — 2, острого угла — 45. В таком случае формула
такая: m = 4 + 2 · ctg 45 / 2 = 5.
Общее понятие трапеции
Трапеция — геометрическая фигура, четырёхугольник, две противолежащие стороны которого размещены на
параллельных прямых. В свою очередь, две иные стороны должны быть не параллельными. Нередко в
описании четырёхугольника не обращают внимания на завершающее требование.
Впервые эту фигуру описал математик Древней Греции Евклид в своих работах. В своей книге «Начала» он
таким образом характеризует всякий четырёхугольник, не являющийся параллелограммом.
Описывая трапецию, необходимо выделить следующие элементы:
- Параллельные противолежащие стороны именуются основаниями фигуры;
- Две иные стороны именуют боковыми или наклонными сторонами;
- Отрезок, который объединяет средины вспомогательных сторон, прозвали средней линией
четырёхугольника; - Углом при основании трапеции прозвали её внутренний уголок, который образовало основание с
наклонной стороной.
Выделяют такие характеристики трапеции:
- Срединный отрезок трапеции пролегает параллельно основаниям и равняется половине их
суммирования; - Отрезок, который объединяет средины диагоналей трапеции, равняется половинке разности оснований
и пролегает по средней линии; - Отрезок, который параллелен основаниям и пролегает через точку скрещивания диагоналей,
разделяется последней напополам и равняется 2xy / (x + y) среднему гармоническому (один из
методов, которым можно характеризовать «среднюю» величину определённой совокупности чисел)
величин оснований трапеции; - В трапецию можно вписать окружность, если суммирование величин оснований четырёхугольника
равняется суммированию величин её вспомогательных сторон; - Точка скрещивания диагоналей трапеции, точка скрещивания последующих продлений её
вспомогательных сторон и средины оснований располагаются на единой прямой; - Если суммирование углов при одном из оснований трапеции равняется 90°, в таком случае
продолжения наклонных сторон перекрещиваются под прямым углом, а отрезок, объединяющий средины
оснований, равняется половинке их разности; - Диагонали четырёхугольника разделяют его на четыре треугольника. Два из них, которые прилегают к
основаниям, подобны. Два иных, которые прилегают к вспомогательным сторонам, имеют равную
площадь; - Если отношение оснований равно K, тогда отношение площадей треугольников, которые прилегают к
ним, равняется K2; - Прямая Ньютона (прямая, которая объединяет серединки диагоналей четырёхугольника) для
четырёхугольника сходится с её срединным отрезком.
Рассмотренная версия трапеции — это наиболее популярная разновидность геометрической фигуры. Однако,
выделяют и дополнительные ситуации.
Равнобедренная или равнобокая или равнобочная трапеция — та, у которой наклонные, иными словами,
непараллельные, стороны равняются друг другу. В евклидовой геометрии равнобедренной трапецией
именуется выпуклый четырёхугольник с осью симметрии, которая пролегает через средины двух
противолежащих сторон. Во всякой равнобедренной трапеции два противолежащих основания параллельны,
две наклонные стороны имеют одинаковые величины (характеристика, которой параллелограмм также
соответствует). Диагонали также имеют равносильные величины. Углы при всяком основании равняются
друг другу и углы при разнообразных основаниях считаются смежными, иначе говоря, в сумме
составляющие 180 градусов.
Трапеция является равнобедренной лишь в том случае, когда выполняется одно из таких эквивалентных
условий:
- Прямая, пролегающая через средины оснований, ортогональна ним;
- Перпендикуляр, который проложен из вершины на наиболее протяжённое основание, разделяет его на
две части, одна из которых равняется половине суммирования оснований, а другая — половинке
разности; - Углы при всяком основании равносильны;
- Суммирование противолежащих углов равняется 180 градусам;
- Величины диагоналей равносильны;
- Вокруг следующего четырёхугольника можно описать окружность;
- Вершинами подобного четырёхугольника ещё считаются вершины какого-либо антипараллелограмма или
контрпараллелограмма (плоского четырёхугольника, где всякие две противолежащие стороны равняются
друг другу, но не параллельны, в сравнении с параллелограммом); - Если в равнобедренной трапеции диагонали ортогональны, тогда перпендикуляр равняется половине
суммирования базовых сторон.
Диагонали равнобедренной трапеции равносильны. Иными словами, всякая равнобедренная трапеция
считается равнодиагональным четырёхугольником. Тем не менее диагонали равнобедренной трапеции
разделяются в одинаковой пропорции.
Прямоугольная трапеция — та, где одна из наклонных сторон и основание формируют прямой угол (в 90
градусов).
Иным особенным случаем считается трапеция с тремя равносильными сторонами. В иностранной литературе
её именуют трёхсторонней трапецией или триравнобедренной трапецией. Подобный четырёхугольник
анализируется как отсечение четырёх последовательных вершин от правильного многоугольника, который
имеет пять или больше сторон.
По заданному описанию параллелограмм и прямоугольник — особые случаи трапеции. Тем не менее при
применении подобного термина основная доля характеристик равнобедренной трапеции становится
недействительна, так как параллелограмм становится её особым случаем.
Анализирование трапеции неразрывно связано с окружностью:
- Если суммирование базовых сторон трапеции равносильно суммированию вспомогательных сторон, то в
неё можно вписать окружность. Средняя линия в такой ситуации равносильна суммированию наклонных
сторон, разделённой на два, ведь средняя линия трапеции равносильна половинке суммирования
оснований; - В четырёхугольнике его вспомогательная сторона различима из центра вписанной окружности
ортогонально; - Если четырёхугольник можно вписать в окружность, в такой ситуации она равнобедренная.