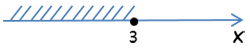Смотрите бесплатные видео-уроки по теме “Неравенства” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Неравенства
Что такое неравенство? Если взять любое уравнение и знак = поменять на любой из знаков неравенства:
> больше,
≥ больше или равно,
< меньше,
≤ меньше или равно,
то получится неравенство.
Линейные неравенства
Линейные неравенства – это неравенства вида:
a x < b a x ≤ b a x > b a x ≥ b
где a и b – любые числа, причем a ≠ 0, x – переменная.
Примеры линейных неравенств:
3 x < 5 x − 2 ≥ 0 7 − 5 x < 1 x ≤ 0
Решить линейное неравенство – получить выражение вида:
x < c x ≤ c x > c x ≥ c
где c – некоторое число.
Последний шаг в решении неравенства – запись ответа. Давайте разбираться, как правильно записывать ответ.
- Если знак неравенства строгий > , < , точка на оси будет выколотой (не закрашенной), а скобка, обнимающая точку – круглой.
Смысл выколотой точки в том, что сама точка в ответ не входит.
- Если знак неравенства нестрогий ≥ , ≤ , точка на оси будет жирной (закрашенной), а скобка, обнимающая точку – квадратной.
Смысл жирной точки в том, что сама точка входит в ответ.
- Скобка, которая обнимает знак бесконечности всегда круглая – не можем мы объять необъятное, как бы нам этого ни хотелось.
Таблица числовых промежутков
| Неравенство | Графическое решение | Форма записи ответа |
|---|---|---|
| x < c |
|
x ∈ ( − ∞ ; c ) |
| x ≤ c |
|
x ∈ ( − ∞ ; c ] |
| x > c |
|
x ∈ ( c ; + ∞ ) |
| x ≥ c |
|
x ∈ [ c ; + ∞ ) |
Алгоритм решения линейного неравенства
- Раскрыть скобки (если они есть), перенести иксы в левую часть, числа в правую и привести подобные слагаемые. Должно получиться неравенство одного из следующих видов:
a x < b a x ≤ b a x > b a x ≥ b
- Пусть получилось неравенство вида a x ≤ b. Для того, чтобы его решить, необходимо поделить левую и правую часть неравенства на коэффициент a.
- Если a > 0 то неравенство приобретает вид x ≤ b a .
- Если a < 0 , то знак неравенства меняется на противоположный, неравенство приобретает вид x ≥ b a .
- Записываем ответ в соответствии с правилами, указанными в таблице числовых промежутков.
Примеры решения линейных неравенств:
№1. Решить неравенство 3 ( 2 − x ) > 18.
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6 − 3 x > 18
− 3 x > 18 − 6 − 3 x > 12 | ÷ ( − 3 )
Делим обе части неравенства на (-3) – коэффициент, который стоит перед x. Так как − 3 < 0 , знак неравенства поменяется на противоположный. x < 12 − 3 ⇒ x < − 4 Остается записать ответ (см. таблицу числовых промежутков).
Ответ: x ∈ ( − ∞ ; − 4 )
№2. Решить неравество 6 x + 4 ≥ 3 ( x + 1 ) − 14.
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6 x + 4 ≥ 3 x + 3 − 14
6 x − 3 x ≥ 3 − 14 − 4
3 x ≥ − 15 | ÷ 3 Делим обе части неравенства на (3) – коэффициент, который стоит перед x. Так как 3 > 0, знак неравенства после деления меняться не будет.
x ≥ − 15 3 ⇒ x ≥ − 5 Остается записать ответ (см. таблицу числовых промежутков).
Ответ: x ∈ [ − 5 ; + ∞ )
Особые случаи (в 14 задании ОГЭ 2019 они не встречались, но знать их полезно).
Примеры:
№1. Решить неравенство 6 x − 1 ≤ 2 ( 3 x − 0,5 ).
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6 x − 1 ≤ 6 x − 1
6 x − 6 x ≤ − 1 + 1
0 ≤ 0
Получили верное неравенство, которое не зависит от переменной x. Возникает вопрос, какие значения может принимать переменная x, чтобы неравенство выполнялось? Любые! Какое бы значение мы ни взяли, оно все равно сократится и результат неравенства будет верным. Рассмотрим три варианта записи ответа.
Ответ:
- x – любое число
- x ∈ ( − ∞ ; + ∞ )
- x ∈ ℝ
№2. Решить неравенство x + 3 ( 2 − 3 x ) > − 4 ( 2 x − 12 ).
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
x + 6 − 9 x > − 8 x + 48
− 8 x + 8 x > 48 − 6
0 > 42
Получили неверное равенство, которое не зависит от переменной x. Какие бы значения мы ни подставляли в исходное неравенство, результат окажется одним и тем же – неверное неравенство. Ни при каких значениях x исходное неравенство не станет верным. Данное неравенство не имеет решений. Запишем ответ.
Ответ: x ∈ ∅
Квадратные неравенства
Квадратные неравенства – это неравенства вида: a x 2 + b x + c > 0 a x 2 + b x + c ≥ 0 a x 2 + b x + c < 0 a x 2 + b x + c ≤ 0 где a, b, c — некоторые числа, причем a ≠ 0, x — переменная.
Существует универсальный метод решения неравенств степени выше первой (квадратных, кубических, биквадратных и т.д.) – метод интервалов. Если его один раз как следует осмыслить, то проблем с решением любых неравенств не возникнет.
Для того, чтобы применять метод интервалов для решения квадратных неравенств, надо уметь хорошо решать квадратные уравнения (см. урок 4).
Алгоритм решения квадратного неравенства методом интервалов
- Решить уравнение a x 2 + b x + c = 0 и найти корни x 1 и x 2 .
- Отметить на числовой прямой корни трехчлена.
Если знак неравенства строгий > , < , точки будут выколотые.
Если знак неравенства нестрогий ≥ , ≤ , точки будут жирные (заштрихованный).
- Расставить знаки на интервалах. Для этого надо выбрать точку из любого промежутка (в примере взята точка A) и подставить её значение в выражение a x 2 + b x + c вместо x.
Если получилось положительное число, знак на интервале плюс. На остальных интервалах знаки будут чередоваться.
Точки выколотые, если знак неравенства строгий.
Точки жирные, если знак неравенства нестрогий.
Если получилось отрицательное число, знак на интервале минус. На остальных интервалах знаки будут чередоваться.
Точки выколотые, если знак неравенства строгий.
Точки жирные, если знак неравенства нестрогий.
- Выбрать подходящие интервалы (или интервал).
Если знак неравенства > или ≥ в ответ выбираем интервалы со знаком +.
Если знак неравенства < или ≤ в ответ выбираем интервалы со знаком -.
- Записать ответ.
Примеры решения квадратных неравенств:
№1. Решить неравенство x 2 ≥ x + 12.
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
x 2 ≥ x + 12
x 2 − x − 12 ≥ 0
x 2 − x − 12 = 0
a = 1, b = − 1, c = − 12
D = b 2 − 4 a c = ( − 1 ) 2 − 4 ⋅ 1 ⋅ ( − 12 ) = 1 + 48 = 49
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 1 ) ± 49 2 ⋅ 1 = 1 ± 7 2 = [ 1 + 7 2 = 8 2 = 4 1 − 7 2 = − 6 2 = − 3
Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 6. Подставляем эту точку в исходное выражение:
x 2 − x − 1 = 6 2 − 6 − 1 = 29 > 0
Это значит, что знак на интервале, в котором лежит точка 6 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
В ответ пойдут два интервала. В математике для объединения нескольких интервалов используется знак объединения: ∪ .
Точки -3 и 4 будут в квадратных скобках, так как они жирные.
Ответ: x ∈ ( − ∞ ; − 3 ] ∪ [ 4 ; + ∞ )
№2. Решить неравенство − 3 x − 2 ≥ x 2 .
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
− 3 x − 2 ≥ x 2
− x 2 − 3 x − 2 ≥ 0
− x 2 − 3 x − 2 = 0
a = − 1, b = − 3, c = − 2
D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ ( − 2 ) = 9 − 8 = 1
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 3 ) ± 1 2 ⋅ ( − 1 ) = 3 ± 1 − 2 = [ 3 + 1 − 2 = 4 − 2 = − 2 3 − 1 − 2 = 2 − 2 = − 1
x 1 = − 2, x 2 = − 1
Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение:
− x 2 − 3 x − 2 = − ( 0 ) 2 − 3 ⋅ 0 − 2 = − 2 < 0
Это значит, что знак на интервале, в котором лежит точка 0 будет − .
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства ≥ , выбираем в ответ интервал со знаком +.
Точки -2 и -1 будут в квадратных скобках, так как они жирные.
Ответ: x ∈ [ − 2 ; − 1 ]
№3. Решить неравенство 4 < x 2 + 3 x .
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
4 < x 2 + 3 x
− x 2 − 3 x + 4 < 0
− x 2 − 3 x + 4 = 0
a = − 1, b = − 3, c = 4
D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ 4 = 9 + 16 = 25
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 3 ) ± 25 2 ⋅ ( − 1 ) = 3 ± 5 − 2 = [ 3 + 5 − 2 = 8 − 2 = − 4 3 − 5 − 2 = − 2 − 2 = 1
x 1 = − 4, x 2 = 1
Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение:
− x 2 − 3 x + 4 = − ( 2 ) 2 − 3 ⋅ 2 + 4 = − 6 < 0
Это значит, что знак на интервале, в котором лежит точка 2, будет -.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства < , выбираем в ответ интервалы со знаком − .
Точки -4 и 1 будут в круглых скобках, так как они выколотые.
Ответ: x ∈ ( − ∞ ; − 4 ) ∪ ( 1 ; + ∞ )
№4. Решить неравенство x 2 − 5 x < 6.
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
x 2 − 5 x < 6
x 2 − 5 x − 6 < 0
x 2 − 5 x − 6 = 0
a = 1, b = − 5, c = − 6
D = b 2 − 4 a c = ( − 5 ) 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 25 + 25 = 49
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 5 ) ± 49 2 ⋅ 1 = 5 ± 7 2 = [ 5 + 7 2 = 12 2 = 6 5 − 7 2 = − 2 2 = − 1
x 1 = 6, x 2 = − 1
Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 10. Подставляем эту точку в исходное выражение:
x 2 − 5 x − 6 = 10 2 − 5 ⋅ 10 − 6 = 100 − 50 − 6 = 44 > 0
Это значит, что знак на интервале, в котором лежит точка 10 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства < , выбираем в ответ интервал со знаком -.
Точки -1 и 6 будут в круглых скобках, так как они выколотые
Ответ: x ∈ ( − 1 ; 6 )
№5. Решить неравенство x 2 < 4.
Решение:
Переносим 4 в левую часть, раскладываем выражение на множители по ФСУ и находим корни уравнения.
x 2 < 4
x 2 − 4 < 0
x 2 − 4 = 0
( x − 2 ) ( x + 2 ) = 0 ⇔ [ x − 2 = 0 x + 2 = 0 [ x = 2 x = − 2
x 1 = 2, x 2 = − 2
Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 3. Подставляем эту точку в исходное выражение:
x 2 − 4 = 3 2 − 4 = 9 − 4 = 5 > 0
Это значит, что знак на интервале, в котором лежит точка 3 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства < , выбираем в ответ интервал со знаком − .
Точки -2 и 2 будут в круглых скобках, так как они выколотые.
Ответ: x ∈ ( − 2 ; 2 )
№6. Решить неравенство x 2 + x ≥ 0.
Решение:
Выносим общий множитель за скобку, находим корни уравнения x 2 + x = 0.
x 2 + x ≥ 0
x 2 + x = 0
x ( x + 1 ) = 0 ⇔ [ x = 0 x + 1 = 0 [ x = 0 x = − 1
x 1 = 0, x 2 = − 1
Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 1. Подставляем эту точку в исходное выражение:
x 2 + x = 1 2 + 1 = 2 > 0
Это значит, что знак на интервале, в котором лежит точка 1 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства ≥ , выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Точки -1 и 0 будут в квадратных скобках, так как они жирные.
Ответ: x ∈ ( − ∞ ; − 1 ] ∪ [ 0 ; + ∞ )
Вот мы и познакомились с методом интервалов. Он нам еще пригодится при решении дробно рациональных неравенств, речь о которых пойдёт ниже.
Дробно рациональные неравенства
Дробно рациональное неравенство – это неравенство, в котором есть дробь, в знаменателе которой стоит переменная, т.е. неравенство одного из следующих видов:
f ( x ) g ( x ) < 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0
Дробно рациональное неравенство не обязательно сразу выглядит так. Иногда, для приведения его к такому виду, приходится потрудиться (перенести слагаемые в левую часть, привести к общему знаменателю).
Примеры дробно рациональных неравенств:
x − 1 x + 3 < 0 3 ( x + 8 ) ≤ 5 x 2 − 1 x > 0 x + 20 x ≥ x + 3
Как же решать эти дробно рациональные неравенства? Да всё при помощи того же всемогущего метода интервалов.
Алгоритм решения дробно рациональных неравенств:
- Привести неравенство к одному из следующих видов (в зависимости от знака в исходном неравенстве):
f ( x ) g ( x ) < 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0
- Приравнять числитель дроби к нулю f ( x ) = 0. Найти нули числителя.
- Приравнять знаменатель дроби к нулю g ( x ) = 0. Найти нули знаменателя.
В этом пункте алгоритма мы будем делать всё то, что нам запрещали делать все 9 лет обучения в школе – приравнивать знаменатель дроби к нулю. Чтобы как-то оправдать свои буйные действия, полученные точки при нанесении на ось x будем всегда рисовать выколотыми, вне зависимости от того, какой знак неравенства.
- Нанести нули числителя и нули знаменателя на ось x.
Вне зависимости от знака неравенства
при нанесении на ось x нули знаменателя всегда выколотые.
Если знак неравенства строгий,
при нанесении на ось x нули числителя выколотые.
Если знак неравенства нестрогий,
при нанесении на ось x нули числителя жирные.
- Расставить знаки на интервалах.
- Выбрать подходящие интервалы и записать ответ.
Примеры решения дробно рациональных неравенств:
№1. Решить неравенство x − 1 x + 3 > 0.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f ( x ) g ( x ) > 0.
- Приравниваем числитель к нулю f ( x ) = 0.
x − 1 = 0
x = 1 — это ноль числителя. Поскольку знак неравенства строгий, ноль числителя при нанесени на ось x будет выколотым. Запомним это.
- Приравниваем знаменатель к нулю g ( x ) = 0.
x + 3 = 0
x = − 3 — это ноль знаменателя. При нанесении на ось x точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x.
При нанесении нулей числителя обращаем внимание на знак неравенства. В данном случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение f ( x ) g ( x ) : x − 1 x + 3 = 2 − 1 2 + 3 = 1 5 > 0,
Это значит, что знак на интервале, в котором лежит точка 2 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Точки -3 и 1 будут в круглых скобках, так как обе они выколотые.
Ответ: x ∈ ( − ∞ ; − 3 ) ∪ ( 1 ; + ∞ )
№2. Решить неравенство 3 ( x + 8 ) ≤ 5.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Привести неравенство к виду f ( x ) g ( x ) ≤ 0.
3 ( x + 8 ) ≤ 5
3 ( x + 8 ) − 5 x + 8 ≤ 0
3 x + 8 − 5 ( x + 8 ) x + 8 ≤ 0
3 − 5 ( x + 8 ) x + 8 ≤ 0
3 − 5 x − 40 x + 8 ≤ 0
− 5 x − 37 x + 8 ≤ 0
- Приравнять числитель к нулю f ( x ) = 0.
− 5 x − 37 = 0
− 5 x = 37
x = − 37 5 = − 37 5 = − 7,4
x = − 7,4 — ноль числителя. Поскольку знак неравенства нестрогий, при нанесении этой точки на ось x точка будет жирной.
- Приравнять знаменатель к нулю g ( x ) = 0.
x + 8 = 0
x = − 8 — это ноль знаменателя. При нанесении на ось x, точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x.
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства нестрогий, значит нули числителя будут жирными. Ну а нули знаменателя выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение f ( x ) g ( x ) :
− 5 x − 37 x + 8 = − 5 ⋅ 0 − 37 0 + 8 = − 37 8 < 0
Это значит, что знак на интервале, в котором лежит точка 0 будет -.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства ≤ , выбираем в ответ интервалы со знаком -.
В ответ пойдут два интервала. Точка -8 будет в круглой скобке, так как она выколотая, точка -7,4 будет в квадратных скобках, так как она жирная.
Ответ: x ∈ ( − ∞ ; − 8 ) ∪ [ − 7,4 ; + ∞ )
№3. Решить неравенство x 2 − 1 x > 0.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f ( x ) g ( x ) > 0.
- Приравнять числитель к нулю f ( x ) = 0.
x 2 − 1 = 0
( x − 1 ) ( x + 1 ) = 0 ⇒ [ x − 1 = 0 x + 1 = 0 [ x = 1 x = − 1
x 1 = 1, x 2 = − 1 — нули числителя. Поскольку знак неравенства строгий, при нанесении этих точек на ось x точки будут выколотыми.
- Приравнять знаменатель к нулю g ( x ) = 0.
x = 0 — это ноль знаменателя. При нанесении на ось x, точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x.
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя и так выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение f ( x ) g ( x ) :
x 2 − 1 x = 2 2 − 1 2 = 4 − 1 2 = 3 2 > 0, Это значит, что знак на интервале, в котором лежит точка 2, будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Все точки будут в круглых скобках, так как они выколотые.
Ответ: x ∈ ( − 1 ; 0 ) ∪ ( 1 ; + ∞ )
Системы неравенств
Сперва давайте разберёмся, чем отличается знак { системы от знака [ совокупности. Система неравенств ищет пересечение решений, то есть те точки, которые являются решением и для первого неравенства системы, и для второго. Проще говоря, решить систему неравенств — это найти пересечение решений всех неравенств этой системы друг с другом. Совокупность неравенств ищет объединение решений, то есть те точки, которые являются решением либо для первого неравенства, либо для второго, либо одновременно и для первого неравенства, и для второго. Решить совокупность неравенств означает объединить решения обоих неравенств этой совокупности. Более подробно об этом смотрите короткий видео-урок.
Системой неравенств называют два неравенства с одной неизвестной, которые объединены в общую систему фигурной скобкой.
Пример системы неравенств:
{ x + 4 > 0 2 x + 3 ≤ x 2
Алгоритм решения системы неравенств
- Решить первое неравенство системы, изобразить его графически на оси x.
- Решить второе неравенство системы, изобразить его графически на оси x.
- Нанести решения первого и второго неравенств на ось x.
- Выбрать в ответ те участки, в которых решение первого и второго неравенств пересекаются. Записать ответ.
Примеры решений систем неравенств:
№1. Решить систему неравенств { 2 x − 3 ≤ 5 7 − 3 x ≤ 1
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
2 x − 3 ≤ 5
2 x ≤ 8 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.
x ≤ 4 ;
Графическая интерпретация:
Точка 4 на графике жирная, так как знак неравенства нестрогий.
- Решаем второе неравенство системы.
7 − 3 x ≤ 1
− 3 x ≤ 1 − 7
− 3 x ≤ − 6 | ÷ ( − 3 ), поскольку − 3 < 0, знак неравенства после деления меняется на противоположный.
x ≥ 2
Графическая интерпретация решения:
Точка 2 на графике жирная, так как знак неравенства нестрогий.
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается на отрезке от 2 до 4. Точки 2 и 4 в ответе буду в квадратных скобках, так как обе они жирные.
Ответ: x ∈ [ 2 ; 4 ]
№2. Решить систему неравенств { 2 x − 1 ≤ 5 1 < − 3 x − 2
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
2 x − 1 ≤ 5
2 x ≤ 6 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.
x ≤ 3
Графическая интерпретация:
Точка 3 на графике жирная, так как знак неравенства нестрогий.
- Решаем второе неравенство системы.
1 < − 3 x − 2
3 x < − 1 − 2
3 x < − 3 | ÷ 3 , поскольку 3 > 0, знак неравенства после деления сохраняется.
x < − 1
Графическая интерпретация решения:
Точка -1 на графике выколотая, так как знак неравенства строгий.
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается на самом левом участке. Точка -1 будет в ответе в круглых скобках, так как она выколотая.
Ответ: x ∈ ( − ∞ ; − 1 )
№3. Решить систему неравенств { 3 x + 1 ≤ 2 x x − 7 > 5 − x
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
3 x + 1 ≤ 2 x
3 x − 2 x ≤ − 1
x ≤ − 1
Графическая интерпретация решения:
- Решаем второе неравенство системы
x − 7 > 5 − x
x + x > 5 + 7
2 x > 12 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.
x > 6
Графическая интерпретация решения:
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечений решений не наблюдается. Значит у данной системы неравенств нет решений.
Ответ: x ∈ ∅
№4. Решить систему неравенств { x + 4 > 0 2 x + 3 ≤ x 2
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
x + 4 > 0
x > − 4
Графическая интерпретация решения первого неравенства:
- Решаем второе неравенство системы
2 x + 3 ≤ x 2
− x 2 + 2 x + 3 ≤ 0
Решаем методом интервалов.
− x 2 + 2 x + 3 = 0
a = − 1, b = 2, c = 3
D = b 2 − 4 a c = 2 2 − 4 ⋅ ( − 1 ) ⋅ 3 = 4 + 12 = 16
D > 0 — два различных действительных корня.
x 1,2 = − b ± D 2 a = − 2 ± 16 2 ⋅ ( − 1 ) = − 2 ± 4 − 2 = [ − 2 − 4 − 2 = − 6 − 2 = 3 − 2 + 4 − 2 = 2 − 2 = − 1
Наносим точки на ось x и расставляем знаки на интервалах. Поскольку знак неравенства нестрогий, обе точки будут заштрихованными.
Графическая интерпретация решения второго неравенства:
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается в двух интервалах. Для того, чтобы в ответе объединить два интервала, используется знак объединения ∪ .
Точка -4 будет в круглой скобке, так как она выколотая, а точки -1 и 3 в квадратных, так как они жирные.
Ответ: x ∈ ( − 4 ; − 1 ] ∪ [ 3 ; + ∞ )
Скачать домашнее задание к уроку 8.
При решении неравенств вы должны свободно владеть понятием числового неравенства, знать, что такое решение неравенства, что значит решить неравенство, помнить свойства неравенств. То же относится и к системам числовых неравенств. Все эти сведения вы можете найти в любом пособии для поступающих в вузы.
Напомним свойства числовых неравенств.
1. Если а > b , то b < а; наоборот, если а < b, то b > а.
2. Если а > b и b > c, то а > c. Точно так же, если а < b и b < c, то а < c.
3. Если а > b, то а + c > b+ c (и а – c > b – c). Если же а < b, то а + c < b+ c (и а – c < b – c). Т. е. к обеим частям неравенства можно прибавлять (или из них вычесть) одну и ту же величину.
4. Если а > b и c > d, то а + c > b + d; точно так же, если а < b и c < d, то а + c < b + d, т. е. два неравенства одинакового смысла можно почленно складывать.
Замечание.
Два неравенства одинакового смысла нельзя почленно вычитать друг из друга, так как результат может быть верным, но может быть и неверным. Например, если из неравенства 11 > 9 почленно вычесть неравенство 3 > 2, то получим верное неравенство 8 > 7. Если из неравенства 11 > 9 почленно вычесть неравенство 7 > 2, то полученное неравенство будет неверным.
5. Если а > b и c < d, то а – c > b – d; если а < b и c > d, то а – c < b – d, т.е. из одного неравенства можно почленно вычесть другое неравенство противоположного смысла, оставляя знак того неравенства, из которого вычиталось другое.
6. Если а > b и m – положительное число, то m а > m b и 
Если же а > b и n – отрицательное число, то n а < n b и 
7. Если а > b и c > d , где а, b, c, d > 0, то а c > b d и если а < b и c < d, где а, b, c, d > 0, то аc < bd, т.е. неравенства одного смысла на множестве положительных чисел можно почленно перемножать.
Следствие. Если а > b, где а, b > 0, то а2 > b2, и если а < b, то а2 < b2, т.е. на множестве положительных чисел обе части неравенства можно возводить в квадрат.
8. Если а > b, где а, b > 0, то 

Виды неравенств и способы их решения
1. Линейные неравенства и системы неравенств
Пример 1. Решить неравенство 
Решение:

Ответ: х < – 2.
Пример 2. Решить систему неравенств 
Решение:

Ответ: (– 2; 0].
Пример 3. Найти наименьшее целое решение системы неравенств
Решение:
Ответ:
2. Квадратные неравенства
Пример 4. Решить неравенство х2 > 4.
Решение:
х2 > 4 (х – 2)∙(х + 2) > 0.
Решаем методом интервалов.
Ответ:
3. Неравенства высших степеней
Пример 5. Решить неравенство (х + 3)∙(х2 – 2х + 1) > 0.
Решение:

Ответ: 
Пример 6. Найти середину отрезка, который является решением неравенства 4х2 – 24х + 24 < 4у2, где 
Решение:
Область определения неравенства: 
С учётом области определения 4х2 – 24х + 24 < 4у2 будет равносильно неравенству
Решаем методом интервалов.
Решение неравенства: 
Середина отрезка: 
Ответ: 
4. Рациональные неравенства
Пример 7. Найти все целые решения, удовлетворяющие неравенству 
Решение:

Методом интервалов:
Решение неравенства: 
Целые числа, принадлежащие полученным полуинтервалам: – 6; – 5; – 4; 1.
Ответ: – 6; – 5; – 4; 1.
5. Иррациональные неравенства
Помните! Начинать решение иррациональных неравенств нужно с нахождения области определения.
Пример 8. Решить неравенство 
Решение:
Область определения: 
Так как арифметический корень не может быть отрицательным числом, то 
Ответ: 
Пример 9. Найти все целые решения неравенства 
Решение:
Область определения 



Целыми числами из этого отрезка будут 2; 3; 4.
Ответ: 2; 3; 4.
Пример 10. Решить неравенство 
Решение:
Область определения: 
Преобразуем неравенство: 


Ответ: 
Пример 11. Решить неравенство 
Решение:
Раскрываем знак модуля.
Объединим решения систем 1) и 2): 
Ответ: 
6. Показательные, логарифмические неравенства и системы неравенств
Пример 12. Решите неравенство 
Решение:

Ответ: 
Пример 13. Решите неравенство 
Решение:

Ответ: 
Пример 14. Решите неравенство 
Решение:
Ответ: 
Пример 15. Решите неравенство 
Решение:
Ответ: 
Задания для самостоятельного решения
Базовый уровень
Целые неравенства и системы неравенств
1) Решите неравенство 2х – 5 ≤ 3 + х.
2) Решите неравенство – 5х > 0,25.
3) Решите неравенство 
4) Решите неравенство 2 – 5х ≥ – 3х.
5) Решите неравенство х + 2 < 5x – 2(x – 3).
6) Решите неравенство
.
7) Решите неравенство (х – 3) (х + 2) > 0.


9) Найдите целочисленные решения системы неравенств 
10) Решить систему неравенств 
11) Решить систему неравенств 
12) Найти наименьшее целое решение неравенства 
13) Решите неравенство 
14) Решите неравенство 
15) Решите неравенство 
16) Решите неравенство 
17) Найдите решение неравенства 

18) Решить систему неравенств 
19) Найти все целые решения системы 
Рациональные неравенства и системы неравенств
20) Решите неравенство 
21) Решите неравенство 
22) Определите число целых решений неравенства 
23) Определите число целых решений неравенства 
24) Решите неравенство 
25) Решите неравенство 2x<16 .
26) Решите неравенство 
27) Решите неравенство 
28) Решите неравенство 
29) Найдите сумму целых решений неравенства 
30) Решите неравенство 
31) Решите неравенство 
Иррациональные неравенства
32) Решите неравенство 
33) Решите неравенство
34) Решите неравенство 
Показательные, логарифмические неравенства и системы неравенств
35) Решите неравенство 
36) Решите неравенство 
37) Решите неравенство 
38) Решите неравенство 
39) Решите неравенство 
40) Решите неравенство 49∙7х < 73х + 3.
41) Найдите все целые решения неравенства 
42) Решите неравенство 
43) Решите неравенство 
44) Решите неравенство 7x+1-7x<42 .
45) Решите неравенство log3(2x2+x-1)>log32 .
46) Решите неравенство log0,5(2x+3)>0 .
47) Решите неравенство 
48) Решите неравенство 
49) Решите неравенство 
50) Решите неравенство logx+112>logx+12 .
51) Решите неравенство logx9<2.
52) Решите неравенство 
Повышенный уровень
53) Решите неравенство |x-3|>2x.
54) Решите неравенство 2│х + 1| > х + 4.
55) Найдите наибольшее целое решение неравенства 
56) Решить систему неравенств 
57) Решить систему неравенств 
58) Решите неравенство 
59) Решите неравенство 25•2x-10x+5x>25 .
60) Решите неравенство 
Ответы
1) х ≤ 8; 2) х < – 0,05; 3) х ≥ 5; 4) х ≤ 1; 5) х > –2; 6) х < 11; 7) 





20) (0; 2); 21) (0; 1,5); 22) 3; 23) 6; 24) (–1; 1,5); 25) х < 4; 26)
; 29) – 10; 30) (0; + ∞); 31)









.
Прежде чем перейти к определению и решению неравенств давайте вспомним, какие знаки используют в математике для
сравнения величин.
| Символ | Название | Тип знака |
|---|---|---|
| > | больше |
строгий знак (число на границе не включается) |
| < | меньше |
строгий знак (число на границе не включается) |
| ≥ | больше или равно |
нестрогий знак (число на границе включается) |
| ≤ | меньше или равно |
нестрогий знак (число на границе включается) |
Теперь мы можем разобраться, что называют линейным неравенством и чем неравенство
отличается от уравнения.
В отличии от уравнения в неравенстве вместо знака равно «=» используют любой
знак сравнения: «>», «<»,
«≤» или «≥».
Запомните!
Линейным
неравенством называют неравенство, в котором неизвестное стоит только в первой степени.
Рассмотрим пример линейного неравенства.
x − 6 < 8
Так как в неравенстве «x − 6 < 8»
неизвестное «x» стоит в первой степени, такое неравенство называют линейным.
Как решить линейное неравенство
Важно!
Чтобы решить неравенство, нужно чтобы в левой части осталось только неизвестное
в первой степени с
коэффициентом «1».
При решении линейных неравенств используют правило переноса и правило деления неравенства на число.
Правило переноса в неравенствах
Также как и в уравнениях,
в неравенствах можно переносить
любой член неравенства из левой части в правую и наоборот.
Запомните!
При переносе из левой части в правую (и наоборот) член неравенства меняет свой знак на
противоположный.
Вернемся к нашему неравенству и используем правило переноса.
x − 6 < 8
x < 8 + 6
x < 14
Итак, мы получили ответ к неравенству «x < 14». Но что означает такой
ответ?
Для того, чтобы понять, что получается при решении неравенства, нам нужно вспомнить,
понятие числовой оси.
Нарисуем числовую ось для неизвестного «x» и отметим на ней число «14».

Запомните!
При нанесении числа на числовую ось соблюдаются следующие правила:
Заштрихуем на числовой оси по полученному ответу «x < 14» все решения неравенства, то есть область
слева от числа «14».
Рисунок выше говорит о том, что любое число из заштрихованной области при подстановке в исходное неравенство
«x − 6 < 8»
даст верный результат.
Возьмем, например число «12» из заштрихованной области и подставим его
вместо «x» в исходное неравенство «x − 6 < 8».
Другими словами, можно утверждать, что любое число из заштрихованной области будет являться решением неравенства.
Важно!
Решить неравенство — это значит найти множество чисел, которые при подстановке в исходное неравенство
дают верный результат.
Решением неравенства
называют множество чисел из заштрихованной области на числовой оси.
В нашем примере ответ «x < 14» можно понимать так: любое число из
заштрихованной области (то есть любое число меньшее
«14») будет являться решением неравенства
«x − 6 < 8».
Правило умножения или деления неравенства на число
Рассмотрим другое неравенство.
2x − 16 > 0
Используем правило переноса и перенесём все числа без неизвестного, в правую часть.
2x − 16 > 0
2x > 16
Теперь нам нужно сделать так, чтобы при неизвестном «x»
стоял коэффициент «1». Для этого достаточно разделить и левую,
и правую часть на число «2».
Запомните!
При умножении или делении неравенства на число, на это число умножается (делится) и левая, и правая часть.
- Если неравенство умножается (делится) на положительное число,
то
знак самого неравенства остаётся прежним. - Если неравенство умножается (делится) на отрицательное число,
то
знак самого неравенства меняется на противоположный.
Разделим «2x > 16» на «2».
Так как «2» —
положительное число, знак неравенства останется прежним.
2x > 16 | (:2)
2x (:2) > 16 (:2)
x > 8
Ответ: x > 8
Рассмотрим другое неравенство.
9 − 3x ≥ 0
Используем правило переноса.
9 − 3x ≥ 0
−3x ≥ −9
Разделим неравенство на «−3».
Так как мы делим неравенство на отрицательное число, знак неравенства поменяется на противоположный.
−3x ≥ −9
−3x ≥ −9 | :(−3)
−3x : (−3) ≤ −9 :(−3)
x ≤ 3
Ответ: x ≤ 3
Примеры решения линейных неравенств
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
16 ноября 2021 в 16:44
Алина Кирщина
Профиль
Благодарили: 0
Сообщений: 1
Алина Кирщина
Профиль
Благодарили: 0
Сообщений: 1
Как правильно написать «больше 15» символом? <15 или >15?
0
Спасибо
Ответить
24 ноября 2021 в 12:56
Ответ для Алина Кирщина
Борис Гуров
Профиль
Благодарили: 1
Сообщений: 28
Борис Гуров
Профиль
Благодарили: 1
Сообщений: 28
> 15 Острый конец символа «птичка» > смотрит в сторону меньшего числа
Еще можно запомнить, как что где больше вершин у символа «птички», там большее число находится. У символа > слева две вершины, а справа одна, значит слева находится большее число.
0
Спасибо
Ответить
29 ноября 2021 в 7:32
Ответ для Алина Кирщина
Фархад Асланов
Профиль
Благодарили: 0
Сообщений: 1
Фархад Асланов
Профиль
Благодарили: 0
Сообщений: 1
>15
0
Спасибо
Ответить
5 марта 2020 в 23:01
Лина Недзвецкая
Профиль
Благодарили: 0
Сообщений: 1
Лина Недзвецкая
Профиль
Благодарили: 0
Сообщений: 1
Решите неравенство:
log3
≤1
0
Спасибо
Ответить
20 августа 2020 в 1:16
Ответ для Лина Недзвецкая
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
0 < (3x − 5)/(x+1) ≤ 3.
(3x − 5)/(x+1) > 0 ⇔ x < − 1 ∪ x > 5/3;
(3x − 5)/(x+1) ≤ 3 ⇔ 8/(x+1) ≥ 0 ⇔ x > − 1.
{(−∞; −1) ∪ (5/3; +∞)} ∩ (−1; +∞) = (5/3; +∞).
0
Спасибо
Ответить
17 июля 2016 в 15:37
Sergey Gurzhiy
Профиль
Благодарили: 0
Сообщений: 1
Sergey Gurzhiy
Профиль
Благодарили: 0
Сообщений: 1
Решите неравенство
2^3-6x<1
0
Спасибо
Ответить
21 сентября 2016 в 13:44
Ответ для Sergey Gurzhiy
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Странно, что для 11класса, но всё же:
23 ? 6x<1
8 ? 6x<1
? 6x< ? 7
x>
1
Спасибо
Ответить
6 июня 2016 в 17:05
Катя Петрова
Профиль
Благодарили: 0
Сообщений: 1
Катя Петрова
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
7 июня 2016 в 2:49
Ответ для Катя Петрова
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Пусть 2x = y > 0.
Неравенство можно записать в виде
? 0.
Откуда y = 2 или 8 ? y < 9.
Стало быть, x = 1 или 3 ? x < log29.
0
Спасибо
Ответить
7 июня 2016 в 13:11
Ответ для Катя Петрова
Хачик Казанджян
Профиль
Благодарили: 0
Сообщений: 1
Хачик Казанджян
Профиль
Благодарили: 0
Сообщений: 1



-Tак как y>0, то сокращаем на y и преобразуем к виду
Учитывая, что y=2x получим x=1 или (3?x<log29) Ответ: (x=1)?(3?x<log2). или так {1?[3;log29)}
0
Спасибо
Ответить
8 июня 2016 в 12:10
Ответ для Катя Петрова
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Списывать нехорошо.
0
Спасибо
Ответить
5 мая 2016 в 10:09
Влада Навдушевич
Профиль
Благодарили: 0
Сообщений: 1
Влада Навдушевич
Профиль
Благодарили: 0
Сообщений: 1
Как решить неравенство (х^2-4х+3)/(х^4-х^6) < или = 0
0
Спасибо
Ответить
8 июня 2016 в 12:28
Ответ для Влада Навдушевич
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
| (x — 1)(x — 3) |
| x4(1 — x)(1 + x) |
? 0.
и метод интервалов.
Ответ: (-oo; -1) U [3; +oo).
0
Спасибо
Ответить
3 августа 2015 в 16:54
Надие Рахимова
Профиль
Благодарили: 0
Сообщений: 1
Надие Рахимова
Профиль
Благодарили: 0
Сообщений: 1
область решения неравенства (х-4)>3х равна? решить
0
Спасибо
Ответить
31 августа 2016 в 10:31
Ответ для Надие Рахимова
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
(x-4)>3x
x-4-3x>0
-4-2x>0
2x+4<0
2x<-4
x<-2
Проверка: Возьмём число меньшее -2, например -3
-3-4>-3 · 3
12>-9 Верно.
Ответ: x<-2
0
Спасибо
Ответить
На этой странице вы узнаете
- Как мы ежедневно расставляем знаки неравенства в жизни?
- Как быстро определить верное обозначение точки на прямой?
- Как правильно чередовать знаки на числовой прямой?
Решая уравнение, мы стремимся к тому, чтобы обе части были равны. Но существуют такие примеры, где мы заведомо знаем, что два выражения не могут быть равны между собой. Они называются неравенствами.
Метод интервалов
Неравенство — это алгебраическое выражение, в котором одна сторона имеет отличное от другой значение. В неравенствах обычно одна сторона больше другой.
Для записи неравенств используют знаки > , < , ≥ , ≤ .
При этом “>” и “<” — это строгие знаки неравенства, а “≥” и “≤” — нестрогие знаки неравенства.
Их отличие в том, что нестрогие знаки неравенства включают граничные точки в итоговый промежуток, а строгие — нет.
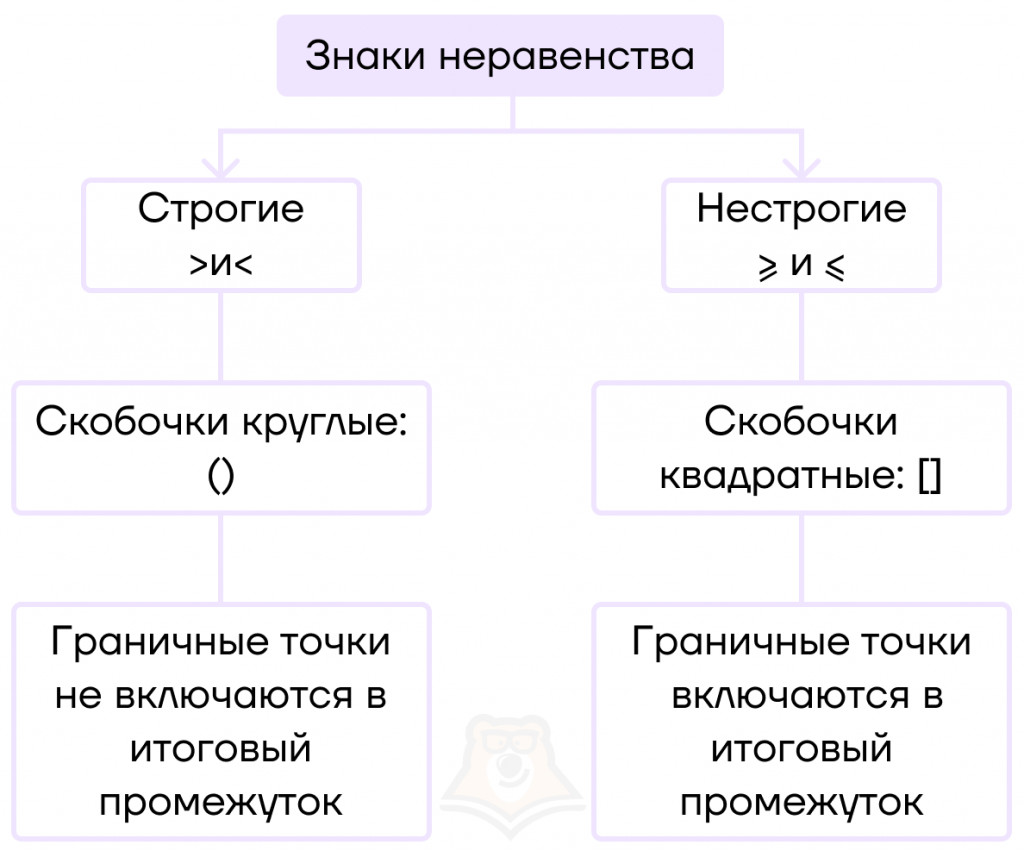
Посмотрим на привычные ситуации с точки зрения строгости знаков неравенства.
Например, возьмем известную игру “Камень, ножницы, бумага”.
Правила игры говорят нам, что камень всегда побеждает ножницы, а бумага побеждает камень. Если перенести это на язык неравенства, то получится:
Теперь зайдем в магазин цифровой техники и попробуем выбрать себе новый мобильный телефон. Задачка непростая, не так ли? Две разные модели могут настолько незначительно отличаться друг от друга своими характеристиками, что будут казаться почти одинаковыми. Тогда мы можем сказать, что они практически равны между собой, то есть неравенство нестрогое. Но один из них всё-таки понравился нам больше.
И каждый наш выбор, каждый шаг – это расстановка знака неравенства в настоящей жизни. Просто по бокам от него не цифры и переменные, а существующие ситуации и вещи.
Рассмотрим пример неравенства (х — 10)(х + 21) > 0.

Его можно решить несколькими способами. Например, вспомним, что положительным будет произведение двух положительных или двух отрицательных множителей, тогда получается совокупность из двух систем.
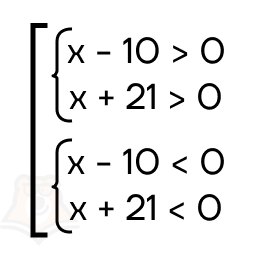
Однако этот способ решения очень трудоемкий и требует много времени. А если множителей будет больше, например, три или четыре, то время на решение в разы увеличивается.
Небольшой секрет тайм-менеджмента: как сократить время при решении неравенств? В таких случаях на помощь приходит метод интервалов.
Метод интервалов — специальный алгоритм решения для сложных неравенств вида f(x) > 0. При этом знак неравенства может быть любым.
Интервал — это промежуток на числовой прямой, ограниченный двумя различными числами.
Алгоритм решения неравенств методом интервалов
1 шаг. Перенести все части неравенства в одну сторону так, чтобы с другой остался только 0.
2 шаг. Найти нули функции, для этого необходимо решить уравнение f(x) = 0.
3 шаг. Начертить числовую прямую и отметить на ней все полученные корни. Таким образом, числовая прямая разобьется на интервалы.
4 шаг. Определить знаки на каждом интервале. Для этого необходимо подставить любое удобное значение в f(x) и определить, какой знак будет иметь функция на данном интервале.
Расставляя полученные корни на прямой, необходимо отмечать их точками. При этом от того, какая отмечена точка (выколотая или закрашенная), будет зависеть ответ.
- Если в неравенстве стоит строгий знак неравенства, то все точки на прямой должны быть выколотыми.
Таким образом, граничные точки не будут включены в итоговый промежуток. Для записи таких точек используют круглые скобочки. Например, в промежуток (2;3) включаются все значения от 2 до 3, но не включаются граничные точки.
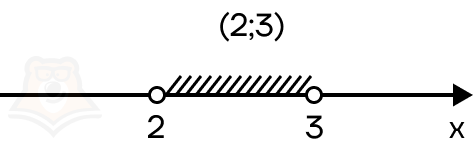
- Если в неравенстве стоит нестрогий знак неравенства, то найденные корни должны быть отмечены закрашенными точками.
Это означает, что мы включаем их в итоговый промежуток. Для записи таких точек используют квадратные скобочки. Например, в промежуток [2;3] включаются все значения от 2 до 3, в том числе и граничные точки.
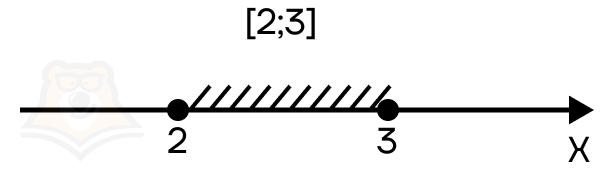
- Если в неравенстве появляются ограничения и некоторые точки нельзя взять в ответ, то такие точки должны быть выколотыми на числовой прямой, при этом знак самого неравенства может быть как строгим, так и нестрогим.
Например, если необходимо решить неравенство с дробью, то нули знаменателя на числовой прямой обязательно должны быть обозначены выколотыми точками.
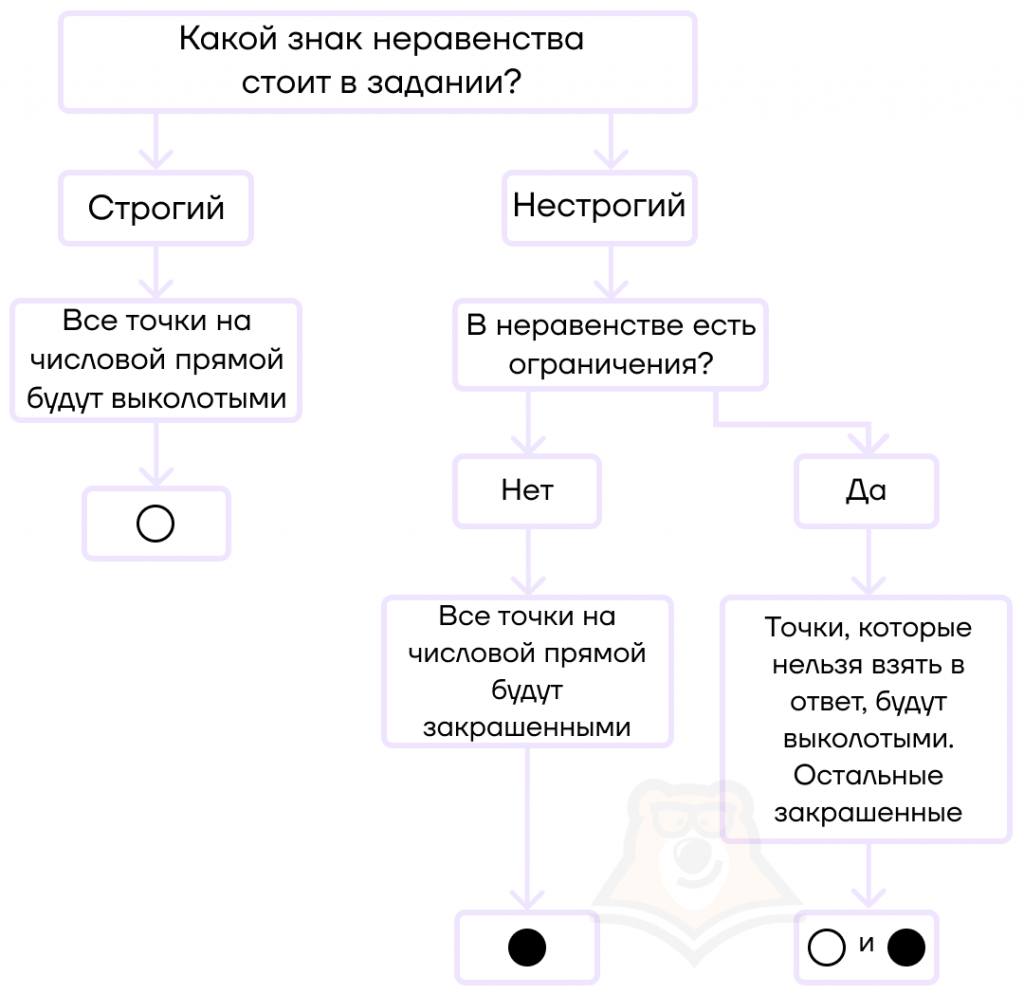
В случае сомнений мы всегда можем проверить себя по простой схеме.
Вывод:
— если знак неравенства строгий, то все точки будут выколотыми;
— если знак неравенства нестрогий, то точки будут закрашенными, кроме тех точек, которые нельзя взять в ответ (например, они не удовлетворяют ОДЗ).
Стоит отметить, что непрерывная функция будет менять знак только в точках, в которых она равна 0. Подробнее узнать про смену знака функции можно в статье «Определение и график функции». Именно поэтому в методе интервалов мы ищем и отмечаем нули функции на прямой — только при переходе через них будет меняться знак функции.
При этом существует способ, с помощью которого можно быстро расставить знаки на прямой. Достаточно определить знак на одном из интервалов, а дальше чередовать знаки при переходе через каждую точку на прямой.
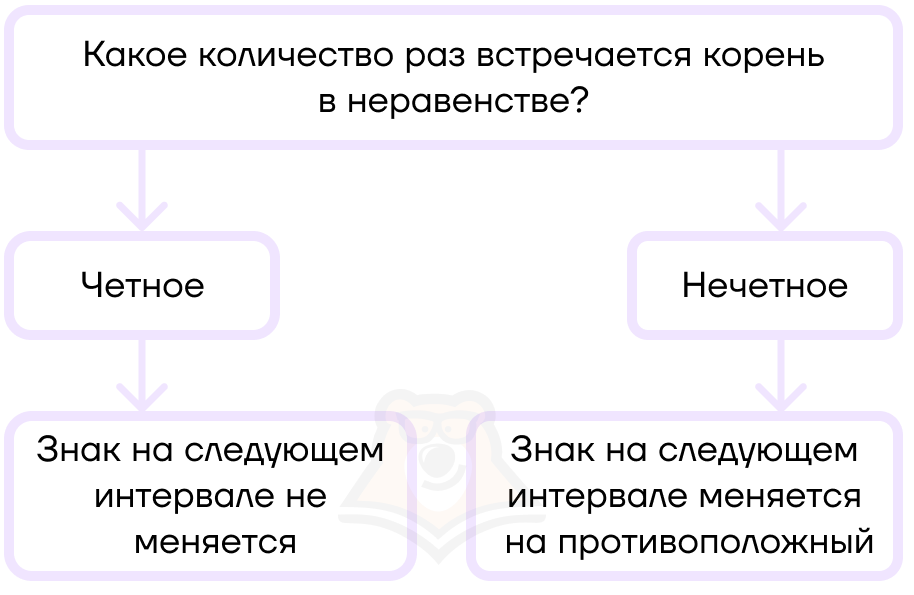
Правила чередования знаков:
- Если корень повторяется нечетное количество раз (то есть его степень нечетная), то знак при переходе на следующий интервал меняется.
- Если корень повторяется четное количество раз (его степень четная), то знак при переходе на следующий интервал не меняется.
Всегда будет нелишним перепроверить знак на каждом интервале, подставив значения в функцию, и убедиться в правильности расстановки знаков на прямой.
Но при расстановке можно пользоваться следующим алгоритмом, что значительно сократит время расстановки знаков.
Методом интервалов можно решить практически любое неравенство в задании 14 из ЕГЭ по профильной математике, также он может понадобиться в заданиях 8, 11 и 17 «профиля» или в задании 17 ЕГЭ по базовой математике.
На ОГЭ данным методом можно воспользоваться при решении неравенств из первой и второй частей — №13 и №20.
Так что осваивайте метод и 2 балла ЕГЭ или 3 балла ОГЭ будут у вас в кармане. Обязательно следуйте алгоритму решения неравенств методом интервалов, тогда вы точно решите неравенство верно.
Практика
Рассмотрим несколько примеров, чтобы на практике разобрать применение метода интервалов для решения неравенств.
Пример 1. Решить неравенство x2 + 8x — 33 > 0.
Шаг 1. Первым шагом необходимо найти нули функции, для этого приравниваем выражение слева к 0: x2 + 8x — 33 = 0.
Шаг 2. Находим корни уравнения, получаем х = 3 и х = -11.
Шаг 3. Расставляем полученные корни на числовой прямой. Поскольку знак неравенства строгий, то точки должны быть выколотыми:

Шаг 4. Дальше необходимо определить знаки на каждом интервале. Для этого подставим х = -12 в x2 + 8x — 33. Получаем:
(-12)2 + 8*(-12) — 33 = 144 — 96 — 33 = 15.
Получается положительное число, следовательно, интервал от минус бесконечности до -11 положительный. Поскольку все корни в неравенстве повторяются нечетное количество раз (по одному разу), то знаки чередуются.
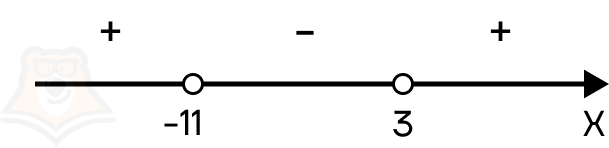
В ответ необходимо записать промежутки с положительным знаком, следовательно, ответом будет х ∈ (-∞; -11) U (3; +∞).
Пример 2. Решить неравенство (frac{2х^2 + 22х — 204}{(х-3)(х+5)} ≤ 0).
1. Находим нули функции.
Нули числителя: 2х2 + 22х — 204 = 0. Решая уравнение, получаем х = 6 и х = -17.
Нули знаменателя: (х — 3)(х + 5) = 0, следовательно, х = 3 и х = -5.
2. Расставляем полученные корни на числовой прямой. Нули числителя будут обозначены закрашенными точками, поскольку знак неравенства нестрогий. А вот нули знаменателя — выколотыми, поскольку знаменатель не может равняться 0, следовательно, и нули знаменателя не должны входить в итоговый промежуток.

3. Определяем знак на крайнем левом промежутке, подставляя х=-20 в дробь:
(frac{2(-20)^2 + 22(-20) — 204}{(-20 -3)(-20 +5)} = frac{2 * 400 — 440 — 204}{(-23) * (-15)} = 156345. )
Следовательно, промежуток положительный.
4. Поскольку каждый корень встречается один раз, то есть нечетное количество раз, то знаки будут чередоваться.

В ответ необходимо включить отрицательные промежутки. Следовательно, ответом будет х ∈ [-17; -5) U (3; 6].
Пример 3. Решить неравенство (frac{1}{х^2} ≥ frac{1}{х+2})
1. Первым делом следует отметить, что знаменатели не могут быть равны 0, следовательно, х2 ≠ 0 и х + 2 ≠ 0, отсюда получаем х ≠ 0 и х ≠ -2.
2. Теперь перенесем все части неравенства влево:
(frac{1}{х^2} — frac{1}{х+2} ≥ 0).
Приведем к общему знаменателю:
(frac{х + 2 — х^2}{х^2 (х + 2)} ≥ 0).
Для решения неравенства будет удобнее, если перед х2 в числителе будет стоять положительный знак, для этого умножим неравенство на -1.
При умножении неравенства на отрицательное число знак неравенства меняется на противоположный.
Получаем:
(frac{х^2 — х — 2}{х^2 (х + 2)} ≤ 0).
Теперь найдем нули функции.
Нули числителя: х2 — х — 2 = 0. Тогда х = -1 и х = 2.
Нули знаменателя: х = 0 и х = -2.
2. Расставим корни на числовой прямой, при этом нули числителя будут обозначены закрашенными точками, а нули знаменателя — выколотыми.

3. Определим знак на крайнем левом промежутке, подставив для этого х = -3 в дробь:
(frac{(-3)^2 — (-3) — 2}{(-3)^2 ((-3) + 2)} = frac{9 + 3 — 2}{9 * (-1)} = frac{10}{-9})
Промежуток отрицательный.
4. Дальше расставляем знаки, чередуя их. При этом следует заметить, что х = 0 — корень, повторяющийся четное количество раз (поскольку у х2 четная степень). Следовательно, при переходе через эту точку знак функции меняться не будет.

В ответ необходимо включить отрицательные промежутки, следовательно: х ∈ (-∞; -2) U [-1; 0) U (0; 2].
Давайте подведем итог. Для чего мы это изучили?
Конечно же, эти знания пригодятся на экзаменах, а также в решении школьных примеров с 8 класса по 11 класс.
Советуем после прочтения этой статьи попрактиковаться в рубрике «Проверь себя», чтобы закрепить полученные знания. После чего можете приступить к решению заданий посложнее, чтобы на экзамене у вас точно получилось решить подобные задания и набрать за них максимум баллов.
Фактчек
- Метод интервалов позволяет упростить решение любого неравенства, а также экономит время, которое ограничено на экзамене.
- Чтобы решить неравенство с помощью метода интервалов необходимо найти нули функции, расставить их на числовой прямой, а после определить знак каждого полученного интервала.
- Нули функции на прямой обозначаются точками, при этом закрашенные точки включают граничные значения в итоговый промежуток, а незакрашенные, напротив, исключают их из промежутка.
- Для определения знака на каждом интервале необходимо подставить любое значение из этого интервала в функцию.
- Для упрощения расстановки знаков можно пользоваться правилами чередования, определив знак только на одном интервале, а дальше менять знаки на каждом следующем. При этом если корень встречается в функции нечетное количество раз, то знак при переходе через эту точку на следующий интервал меняется, а если корень встречается четное количество раз, то знак на следующем интервале не меняется.
Проверь себя
Задание 1.
Какие знаки неравенства существуют?
- Строгие
- Нестрогие
- Строгие и нестрогие
- Больше и меньше
Задание 2.
Какой знак неравенства может встретиться в методе интервалов?
- Только больше или меньше.
- Только “больше или равно” или “меньше или равно”.
- Только “больше” и “больше или равно” или только “меньше” и “меньше или равно”.
- Любой.
Задание 3.
Какое утверждение верное?
- Если в неравенстве строгий знак неравенства, то точки на числовой прямой закрашены.
- Если в неравенстве строгий знак неравенства, то точки на числовой прямой выколоты.
- Если в неравенстве нестрогий знак неравенства, то все точки на числовой прямой закрашены, даже если в неравенстве есть ограничения.
- Если в неравенстве нестрогий знак неравенства, то все точки на числовой прямой выколоты.
Задание 4.
Какое утверждение верное?
- При переходе на числовой прямой на следующий интервал, знак на интервале всегда будет меняться.
- Если корень встречается в неравенстве четное количество раз, то при переходе через него на следующий интервал знак не меняется.
- Если корень встречается в неравенстве нечетное количество раз, то при переходе через него на следующий интервал знак не меняется.
- Невозможно определить правильное чередование знаков на прямой, не подставляя значение из каждого интервала в функцию.
Задание 5.
Если в неравенстве строгий знак неравенства, то какие скобочки могут встретиться в ответе?
- Круглые
- Квадратные
- И круглые, и квадратные
- Ни один из перечисленных вариантов
Ответы: 1. — 3 2. — 4 3. — 2 4. — 2 5. — 1
План урока:
Сравнение чисел
Свойства неравенств
Оценка значений выражений
Доказательство неравенств
Решение неравенств с одной переменной
Решение систем неравенств с одной переменной
Решение совокупностей неравенств
Метод интервалов
Сравнение чисел
Если выбрать любые два различных числа, то одно из них обязательно окажется больше другого. Например, 15 больше, чем 12. Для записи этого факта используются специальные знаки. Символ «<»читается как «меньше». Например, запись
22 < 23
читается как «22 меньше 23» Другой знак, «>», означает «больше». Помимо них для сравнения чисел используются символы «⩾» (больше или равно) и «⩽» (меньше или равно).
Выражения, содержащие знаки сравнения, называются неравенствами. Иногда в учебной литературе может использоваться сокращение: нер-во.
Сравнивать натуральные числа очень легко, однако при сравнении отрицательных, дробных, иррациональных чисел могут возникнуть проблемы. Существует универсальный способ сравнивать числа между собой, основанный на использовании координатной прямой.
Можно заметить, что чем больше число, тем правее оно располагается на координатной прямой. Это правило действует для всех действительных чисел.
Отметим на прямой два числа, а и b, а также расстояние между ними (буква c):
b располагается правее а, а потому
b>a
Расстояние между ними равно c, причем с – положительное число. Очевидно, что
b– а = с
Перенося слагаемые через знак равенства, можно получить
а – b = – с
Получается, что при вычитании из большего меньшего получается положительное число. Если же уменьшаемое меньше вычитаемого, то их разность – отрицательное число. На этом факте основан один из способов сравнения чисел. Чтобы узнать, какое из двух чисел больше, надо лишь вычесть их друг из друга и проанализировать знак получившейся разности.
Пример. Сравните дроби 29/35 и 33/40
Решение. Найдем разность этих двух дробей:
Получили положительное число. Значит, уменьшаемое больше вычитаемого.
Ответ: 29/35 > 33/40.
Свойства неравенств
Рассмотрим основные свойства числовых неравенств, которые в дальнейшем помогут нам решать некоторые задачи.
Докажем это. Если а >b, то тогда и разность (a –b) является положительным числом:
а – b = c
умножив части равенства на (– 1), получим:
– (а – b) = – с
(b– a) = – с
Так как разность (b– a)оказалась равна отрицательному числу (– с), тоb<a.
Для доказательства этого очевидного факта используем координатную прямую:
Ясно, что если b>a, то оно располагается правее. Аналогично и с располагается правее b, так как с >b. Видно, что тогда сбудет находиться правее а, то есть оно больше.
Данное свойство называют транзитивностью. Им обладает не только отношение «больше — меньше», но и ряд других отношений. Например, из геометрии известно, что если отрезок АВ параллелен отрезку CD, а тот в свою очередь параллелен ещё одному отрезку EF, то и АВ параллельно ЕF.
Свойство транзитивности позволяет использовать так называемые двойные неравенства. Например, нам надо указать, что 25 меньше 48, а 48 меньше 94. Это можно записать в виде одного неравенства:
25 < 48 < 94
Можно использовать и более двух знаков сравнения:
365 <366 < 367 < 368 < 369
Другими словами, к обеим частям верного неравенства можно добавить одинаковое число, и оно всё равно останется верным. Действительно, пусть нам надо сравнить величины (а + с) и (b + c). Для этого найдем их разность:
(а + с) – (b + c) = a + c – b – с = а – b
Так как a<b, то и разность а – b отрицательна. Значит, отрицательна разность величин (а + с) и (b + c), из чего следует, что
а + с <b + c
Проиллюстрируем это на примере неравенства
73 < 86
Добавим к обеим частям число 11 и получим другое верное равенство:
73 + 11 < 86 + 11
84 < 97
Снова рассмотрим разность величин ac и bc:
ac– bc = (a– b)c
Разность (а – b) отрицательна при условии а <b. Если с – положительное число, то всё произведение (a– b)c остается отрицательным, т тогда
ас <bc
Если же c– отрицательное число, то произведение (a– b)c становится положительным, а потому
ас <bc
Пусть есть неравенство
100< 200
Если умножить его на положительное число, например, на 3, то получим верное равенство
300 < 600
Если же умножить его на (– 3), то придется «перевернуть» знак сравнения, поставить вместо «<»знак «>»:
– 300 >– 600
Следующее свойство неравенств позволяет их складывать:
Докажем эту теорему. Найдем разность чисел (а + c) и (b + d):
(а + c) – (b + d) = а + с – b – d = (a– b) + (b– d)
Получили сумму двух слагаемых, (a– b) и (b– d). Каждое из них является отрицательным числом, так как a<bи c<d. Сумма двух отрицательных чисел также отрицательна, а потому можно утверждать, что
а + c<b + d
Покажем, как с помощью этого правила можно складывать неравенства. Пусть есть два верных неравенства:
59<62
69<75
Теперь сложим отдельно их правые и левые части:
59 + 69<62 + 75
128 < 137
Однако если у неравенств разные знаки, то для их сложения надо в одном из них поменять местами правую и левую часть. Например, даны неравенства
63 < 99
26> 25
В одном стоит знак «меньше», а в другом «больше», поэтому сразу их складывать нельзя. Сначала «перевернем» второе неравенство
25 < 26
теперь в обоих неравенствах стоит знак «<», поэтому их можно сложить:
63 + 25 < 99 + 26
88 < 125
Последнее правило позволяет перемножать неравенства:
Для доказательства утверждения найдем разность величин ac и bd. При этом добавим к ней слагаемое bc и тут же его вычтем (это необходимо для того, чтобы мы смогли сгруппировать слагаемые):
ac – bd = ac – bd– bc + bc= (ac – bc) + (bc – bd) =
=c(a– b) + b(c– d)
Так как разности (a– b) и (c– d) являются отрицательными числами, c и b – положительными, то и произведения c(a– b) и b(c– d) – это отрицательные величины. Сумма же двух отрицательных величин также отрицательна, поэтому
ac<bd
Покажем на примере использование этого правила. Пусть есть неравенства
7<8
5<6
Перемножив их, получим:
7•5<8•6
35 < 48
Оценка значений выражений
Если известны пределы, в которых может изменяться переменная, то можно найти оценку значения выражения, в которое оно входит.
Пример. Известно, что 43 <v< 47. Оцените значение выражения 3v + 9.
Решение. Умножим каждую часть исходного неравенства на 3:
43 <v< 47
3•43 < 3•v< 3•47
129 < 3v<141
Далее добавим к неравенству девятку:
129 + 9 < 3v + 9 < 141 + 9
138 < 3v + 9 < 150
Получили оценку выражения 3v + 9, которую и требовалось найти
Ответ: 138 < 3v + 9 < 150.
Пример. Сторона квадрата может принимать значения от 16 до 21 см. Оцените величину площади этого квадрата.
Решение. Обозначим сторону квадрата буквой a. Тогда можно записать двойное неравенство
16⩽ а ⩽ 21
Знак «меньше или равно» используется из-за того, что по условию сторона квадрата может в точности равняться значению 16 или 21 см. Площадь квадрата (обозначим ее как S) равна а2. Запишем неравенство из условия дважды, после чего перемножим эти неравенства:
16⩽ а ⩽21
16⩽ а ⩽21
16•16⩽ а•а⩽21•21
256⩽ а2⩽441
Получили оценку для а2, а значит, и для площади S. Отметим, что при решении задач необязательно два раза писать одно и то же неравенство, чтобы потом их перемножать.
Ответ: 256 ⩽S⩽ 441
Пример. Пете надо купить 2 килограмма бананов и пакет молока. Он точно знает, что пакет молока стоит в разных магазинах от 65 до 80 рублей, а стоимость килограмма бананов колеблется от 54 до 69 рублей. Помогите Пете оценить, сколько денег он потратит в магазине.
Решение. Обозначим буквой h стоимость килограмма бананов, а через k – цену пакета молока. Затраты Пети составят 2h + k, при этом можно написать следующие оценки:
54 <h< 69
65 <k< 80
Оценим величину 2h
2•54 < 2h< 2•69
108 < 2h< 138
Сложим получившееся неравенство с 65 <k< 80:
108 + 65 < 2h + k< 138 + 80
173 < 2h + k< 218
Ответ: Петя потратит от 173 до 218 рублей.
Доказательство неравенств
Иногда в неравенствах помимо чисел встречаются переменные величины. При этом некоторые из них верны при любом значении этих переменных. Важно уметь доказывать это. Простейшие случаи связаны с использованием того факта, что квадрат любого числа неотрицателен.
Пример. Докажите, что при любом значении d выполняется неравенство
d2+ 11 >5
Решение. Запишем очевидно верное неравенство
d2⩾ 0
Добавим к нему число 11:
d2 + 11 ⩾ 11
Число 11 больше 5, поэтому можно записать:
d2 + 11 ⩾ 11 > 5
d2 + 11 > 5
Пример. Докажите, что неравенство
n2 – 8n + 19> 0
справедливо для любого n.
Решение.
В левой части стоит квадратный трехчлен, попытаемся преобразовать его с помощью формулы квадрата суммы:
n2 – 8n + 19 = n2 – 2•4n + 19 = n2 – 2•4n +16 – 16 + 19 =
= (n2 – 2•4n + 42) – 16 + 19 = (n– 4)2 + 3
Величина (n – 4)2 является неотрицательным числом, поэтому сумма (n – 4)2 + 3 никак не меньше трех, то есть положительна.
Иногда для доказательства числового неравенства можно определить знак разности выражений, стоящих в правой и левой части.
Пример. Докажите, что при любом значении переменных выполняется условие
2ut⩽u2 + t2
Решение. Запишем разность выражений, стоящих в неравенстве, а потом преобразуем ее:
2ut – (u2 + t2) = 2ut – u2 – t2 = – (u2 – 2ut + t2) = – (u – t)2
Разность получилась неположительной. Значит, между уменьшаемым и вычитаемым можно поставить знак «⩽»:
2ut⩽u2 + t2
Полученное выражение означает, что удвоенное произведение двух чисел не превосходит сумму их квадратов. Этот факт мы используем при решении следующего задания.
Пример. Докажите, что
d2 + s2 + m2⩾ds + dm + sm
Решение. В предыдущем примере мы установили, что сумма квадратов чисел больше или равна их двойному произведению, поэтому можно записать:
d2 + s2⩾ 2ds
s2 + m2⩾ 2sm
d2 + m2⩾ 2dm
Сложим полученные неравенства:
(d2 + s2) + (s2 + m2) + (d2 + m2) ⩾2ds + 2sm + 2dm
2d2 + 2s2 + 2m2⩾2ds + 2sm + 2dm
Осталось поделить на два это неравенство:
d2 + s2 + 2m2⩾ds + sm + dm
Решение неравенств с одной переменной
Очевидно, что не все неравенства справедливы при любом значении входящих в них переменных. Так, нер-во
х – 2 > 0
справедливо для х = 3 (так как 3 – 2 > 0), но несправедливо при х = 1. Такие выражения называют неравенствами с одной переменной. Его решением называют значение переменной, при подстановке которого получается справедливое числовое неравенство.
Так, 3 – это одно из решений для нер-ва
х – 2 > 0
ведь при его подстановке получается справедливое числовое нер-во
3 – 2 > 0
Чтобы решить нер-во, надо указать сразу ВСЕ решения для него. Однако стоит заметить, что почти всегда нер-во, в отличие от уравнения, имеет бесконечное количество решений. Так, решением для нер-ва
х – 2 > 0
является не только число 3, но также числа 4, 5, 6, 7, 8, и т.д. Более того, подойдут и дробные числа, например, 2,5; 2,6; 2,61 и т.д. Поэтому для указания решения нер-в используются особые математические объекты – числовые промежутки.
Отметим на координатной прямой числа а и b, а также точку с, лежащую между ними. Все числа, расположенные между ними, образуют множество, которое называют числовым промежутком:
Числовой промежуток обозначается скобками, в которых указаны его граничные точки: (а;b). В данном случае скобки круглые, это означает, что сами числа a и b НЕ входят в это множество. По этой причине концы промежутка на рисунке показаны незакрашенными точками, которые ещё называют «выколотыми».
Если некоторое число c располагается между числами a и b, то говорят, что с принадлежит промежутку (а; b). Записывается это так:
c∈(a; b)
Естественно, что с принадлежит промежутку в том случае, если выполняется неравенство
а <c<b
Например, число 29 принадлежит промежутку (21; 37), так как 21 < 29<37:
Промежуток, чьи концы НЕ относятся к нему самому, называют интервалом. Если же концы промежутка тоже входят в сам промежуток, то его уже называют отрезком. При этом для его обозначения используются квадратные скобки, а точки на рисунке показывают закрашенными:
Если точка с принадлежит отрезку [a; b], то это означает, что а ⩽ с ⩽b. Другими словами, записи с∈[a; b] и а ⩽ с ⩽b эквиваленты друг другу и означают одно и то же.
Возможны случаи, когда один конец промежутка относится к нему, а другой – нет. В этом случае промежуток называют полуинтервалом. В его записи одна скобка квадратная, а вторая – круглая:
Во всех этих рисунках под графическим изображением промежутка указывается его обозначение, а также двойное неравенство, которое можно написать для любой точки с, принадлежащей этому промежутку.
Наконец, порою надо указать множество чисел, которое ограничено только с одной стороны. Например, все числа, большие a, будут отмечаться так:
Символ ∞ означает «бесконечность». + ∞ – это условно бесконечно большое положительное число, а (– ∞) – это противоположное ему отрицательное число. Грубо говоря, + ∞ – это условная точка, расположенная правее любой другой на числовой прямой, а (– ∞) – условная точка, расположенная левее любой другой. Так как на самом деле таких точек не существует, то при обозначении соответствующего промежутка скобка со стороны знака бесконечности всегда круглая, а не квадратная. Промежутки, ограниченные лишь с одной стороны, называют числовыми лучами.
Теперь посмотрим, как числовые промежутки используются для решения неравенств. Пусть есть нер-во
х > 20
Отметим на числовой прямой число 20 и всё множество решений этого нер-ва:
Решением нер-ва будет промежуток (20; + ∞)
Введем понятие равносильных неравенств:
Более сложные нер-ва можно свести к более простым, но равносильным им, с помощью нескольких приемов:
Эти способы основаны на свойствах нер-в и очень сильно напоминают способы преобразований уравнений. Рассмотрим их использование на примере.
Пример. Найдите решение неравенства с одной переменной
х + 10 > 18
Решение.
Перенесем слагаемое 10 вправо, изменив его знак на противоположный:
х +10> 18
х > 18– 10
х > 8
Получили нер-во, решением которого является интервал (8; + ∞):
Ответ: (8; + ∞).
Пример. Решите нер-во
5у ⩾ 20
Решение. Поделим обе части на число 5. Оно положительное, а потому знак нер-ва не меняется:
5у ⩾ 20
у ⩾ 20/5
у ⩾4
Решением этого нер-ва будет интервал [4; + ∞)
Ответ: [4; + ∞).
Пример. Найдите значения переменной, при которых верна запись
–6z > 42
Решение. Поделим нер-во на (– 6). Так как это число отрицательное, то знак неравенства изменится на противоположный:
– 6z> 42
z< 42/ (– 6)
z<– 7
Решением нер-ва z< – 7 будет интервал (– ∞; – 7).
Ответ: (– ∞; – 7).
Пример. При каких значениях k справедливо нер-во
12k + 26 > 146
Решение. Перенесем слагаемое 26 вправо:
12k> 146 – 26
12k>120
Теперь поделим на 12 правую и левую часть:
k> 120/12
k> 10
Для нер-ваk> 10 решением является промежуток
Ответ: (10; + ∞).
Пример. Решите нер-во
9(h + 2) + 21 < 111 + 6h
Решение. Выполним тождественное преобразование – раскроем скобки в левой части:
9h + 18 + 21 < 111 + 6h
Далее перенесем слагаемое 6h влево, а 18 и 21 вправо:
9h – 6h< 111 – 21 – 18
3h< 72
h< 72/3
h< 24
Множеством решений этого нер-ва является промежуток (24; + ∞).
Ответ: (24; + ∞).
Решение систем неравенств с одной переменной
Из 7 класса мы помним, что помимо отдельных уравнений порою приходиться решать и системы уравнений. Аналогично существуют и системы неравенств.
Для обозначения систем используются фигурные скобки. Можно убедиться подстановкой, что для системы
числа 12 и 13 будут являться решением, а числа 9 и 16 – нет.
Как и в случае с одиночными нер-вами, нам требуется найти числовой промежуток, все числа которого будет решениями системами. Отметим на координатной прямой решений нер-ва х > 10 (штриховка сверху) и х < 15 (штриховка снизу):
Красным цветом выделен промежуток (10; 15), который является решением для обоих нер-в. Именно он и является решением системы
Заметим, что решением системы неравенств является пересечением множеств решений каждого отдельного нер-ва, входящего в его состав. Подробнее о понятии пересечения множеств можно узнать из этого урока.
Для того чтобы решить систему, надо решить каждое отдельное нер-во, а потом найти пересечение полученных решений. Рассмотрим несколько задач.
Пример. Найдите решение системы неравенств
Решение. В первом нер-ве перенесем слагаемое вправо, а второе поделим на 3:
Решением первого нер-ва будет промежуток (3; + ∞), а второго – промежуток (– ∞; 9). Их пересечением будет промежуток (3; 9):
Ответ: (3; 9).
Пример. При каких значениях переменных верна система
Решение. Преобразуем систему:
Решения этих двух нер-в, (8; + ∞) и (– ∞; – 2), не пересекаются:
Таким образом, система не имеет решения. Другими словами, ее решение – пустое множество, обозначаемое символом ∅.
Ответ: ∅
Пример. Укажите решение системы неравенств
Решение:
Решениями этих нер-в являются промежутки (– ∞; 4] и (– ∞; 6), их пересечением является (– ∞; 4] (он является подмножеством (– ∞; 6)):
Ответ: (– ∞; 4].
Решение совокупностей неравенств
Несколько неравенств могут быть объединены не только в системы, но и в совокупности. Отличие совокупности от системы заключается в том, что ее решением является любое число, которое обращает в верное числовое неравенство хотя бы одно из входящих в него нер-в.
Для обозначения совокупности используется квадратная скобка. Так решением совокупности
являются все числа, которые либо больше 10, либо меньше 6:
Можно сказать, что решение совокупности является объединением множеств решений всех входящих в него нер-в. Записывается это так:
(– ∞; 6)⋃(10; + ∞)
Пример. Найдите решение совокупности неравенств
Решение. Преобразуем совокупность
Отметим решения этих нер-в:
Так как мы решаем не систему нер-в, а их совокупность, то ответом будет являться та область числовой прямой, которая заштрихована хотя бы с одной стороны, не обязательно с двух (эта область выделена красным цветом). Получаем, что решением совокупности является луч (– ∞; 1).
Заметим, что если бы мы решали систему, а не совокупность, то ответом был бы луч (– ∞; 0,5).
Ответ: (– ∞; 1).
Метод интервалов
При решении сложных неравенств весьма эффективен метод интервалов. Он работает в том случае, если в одной части нер-ва стоит произведение нескольких множителей (обычно линейных полиномов), а в другой ноль. Тогда знак неравенства можно поменять на «=», и получить уравнение. Далее его следует решить и отметить на координатной прямой полученные корни. Эти корни разобьют числовую прямую на несколько интервалов. Далее надо просто определить, на каких интервалах выполняется неравенство. Рассмотрим этот метод на конкретном примере.
Пример. Решите неравенство
(х – 5)(х – 7)(4 – 2х) > 0
Решение.
Первый шаг – заменим знак «>» на «=»:
(х – 5)(х – 7)(4 – 2х) = 0
Получили уравнение. Вспомним правило: произведение множителей равно нулю, если хоть один из них равен нулю. Поэтому
х – 5 = 0 или х – 7 = 0 или 4 – 2х = 0
Решим каждое из трех полученных линейных уравнений:
- х – 5 = 0
х = 5
- х – 7 = 0
х = 7
- 4 – 2х = 0
– 2х = – 4
х = 2
Получили корни 2, 5 и 7. Отметим их на координатной прямой:
Эти точки разбивают числовую прямую на 4 промежутка:
- (– ∞; 2);
- (2; 5);
- (5; 7);
- (7; + ∞).
В исходном неравенстве слева стоит произведение (х – 5)(х – 7)(4 – 2х). Определим его знак на каждом из этих 4 интервалов. Для этого достаточно взять одно число из интервала и подставить его в выражение:
- Из промежутка (– ∞; 2) возьмем х = 0:
(х – 5)(х – 7)(4 – 2х) = (0 – 5)(0 – 7)(4 – 2•0) = (– 5)•(– 7)•4 = 140
Получили число, большее нуля: 140 > 0
- Из промежутка (2; 5) возьмем х = 3:
(х – 5)(х – 7)(4 – 2х) = (3 – 5)(3 – 7)(4 – 2•3) = (– 2)•(– 4)•(– 2) = – 16
Получили отрицательное число.
- Из промежутка (5; 7) возьмем х = 6:
(х – 5)(х – 7)(4 – 2х) = (6 – 5)(6 – 7)(4 – 2•6) = 1•(– 1)•(– 
Получили положительное число
- Для последнего промежутка возьмем х = 8:
(х – 5)(х – 7)(4 – 2х) = (8 – 5)(8 – 7)(4 – 2•8) = 3•1•(– 12) = – 36
Теперь поставим на числовой прямой знаки, соответствующие каждому интервалу:
Так как в исходном неравенстве стоял знак «>», то в ответ надо записать объединение тех интервалов, на которых левая часть принимает положительные значения.
Ответ: (– ∞; 2)⋃(5; 7)
В этом примере можно заметить, что знаки в интервалах чередовались. Так и должно происходить в том случае, если каждый из множителей в левой части является многочленом первой степени. Напомним, что многочлен 1-ой степени – это выражение вида ах + с, например:
- 5х + 9
- 8х – 13
- 7,56х + 12,35
Пример. Определите, при каких значениях переменной полином
х2 – 8х + 12
принимает отрицательные значения.
Решение. По сути, нам надо решить нер-во
х2 – 8х + 12< 0
Вспомним, что квадратный трехчлен можно разложить на линейные множители. Для этого надо решить уравнение:
х2 – 8х + 12 = 0
D = (– 
Зная х1 и х2, можем записать, что
х2 – 8х + 12 = (х – х1)(х – х2) = (х – 2)(х – 6)
Перепишем исходное нер-во:
(х – 2)(х – 6) > 0
К нему уже можно применить метод интервалов (так как в левой части стоит произведение):
(х – 2)(х – 6) = 0
х – 2 = 0 или х – 6 = 0
х = 2 или х = 6
Естественно, что мы получили те же корни, что и при решении квадратного уравнения выше. Отметим корни на прямой и определим значение трехчлена на каждом из полученных интервалов:
На промежутке (– ∞; 2) при х = 1 имеем (1 – 2)(1 – 6) = (– 1)•(– 5) = 5
Промежуток (2; 6): при х = 3 получаем (3 – 2)(3 – 6) = 1• (– 3) = – 3
На промежутке (6; + ∞) при х = 7 получается (7 – 2)(7 – 6) = 5•1 = 5
В итоге трехчлен отрицателен тогда, когда х принадлежит интервалу (2; 6).
Ответ (2; 6).