Результативного показателя как найти

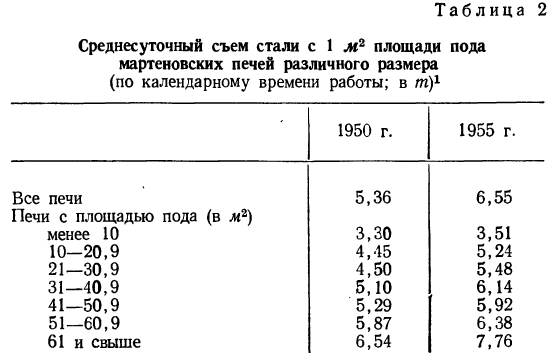
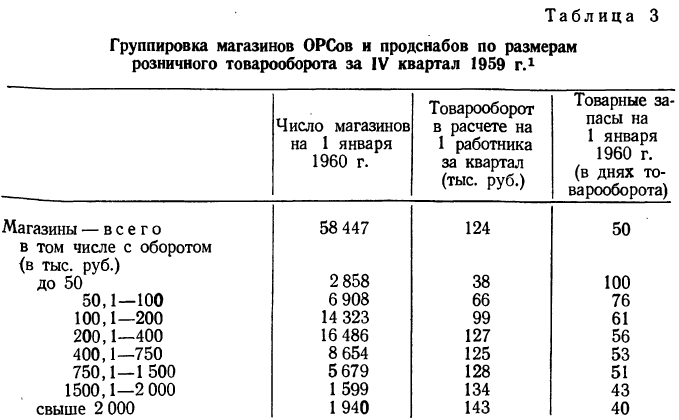
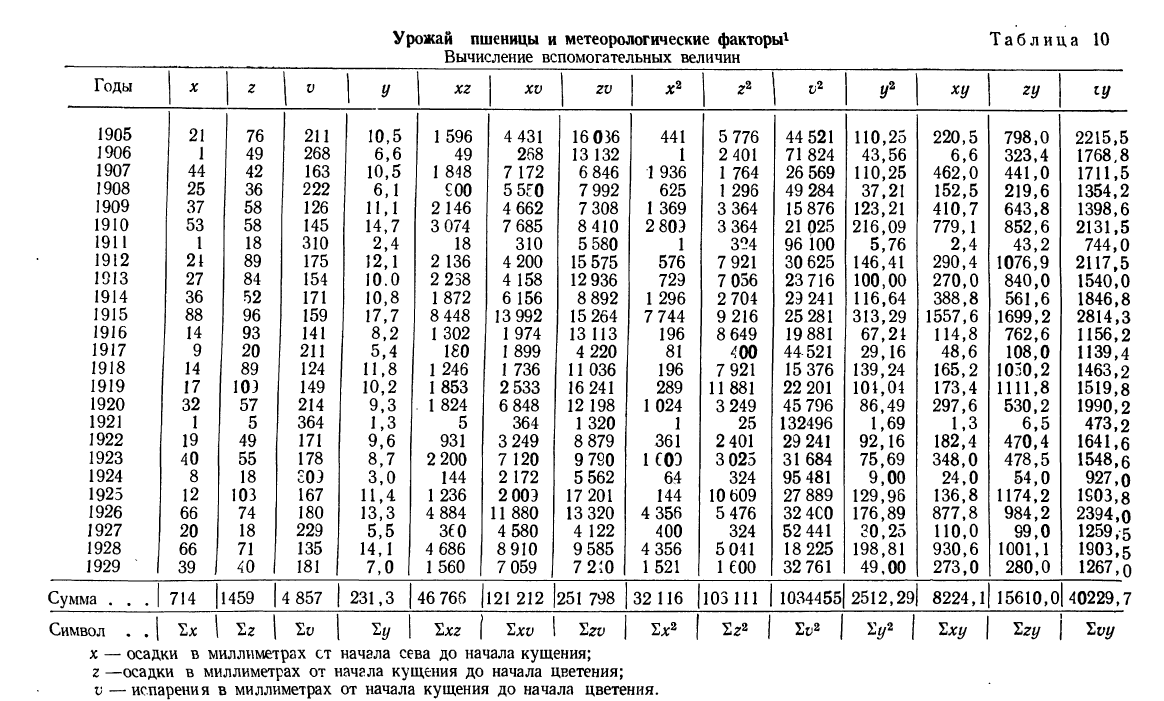
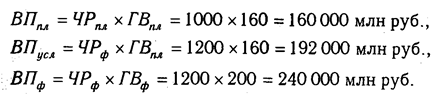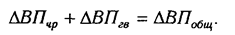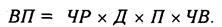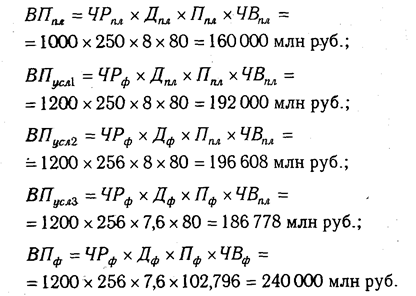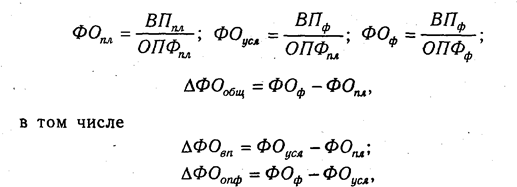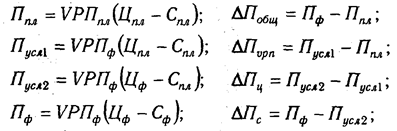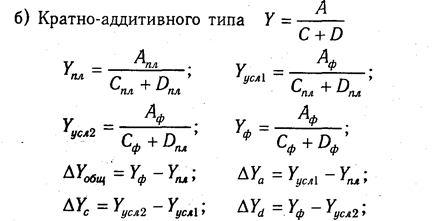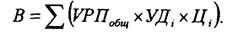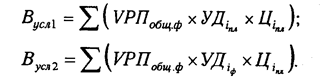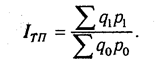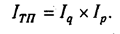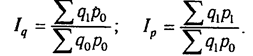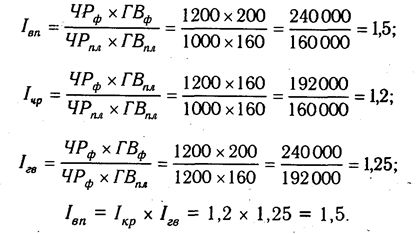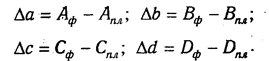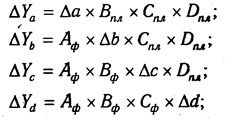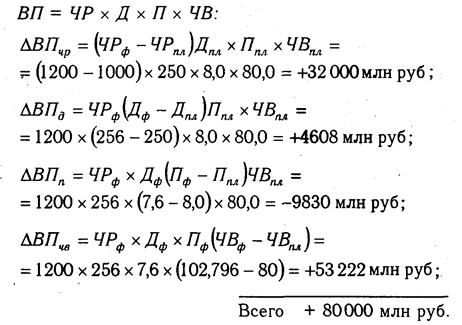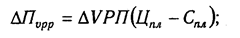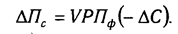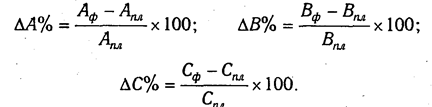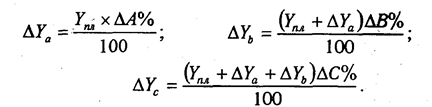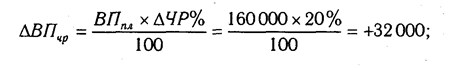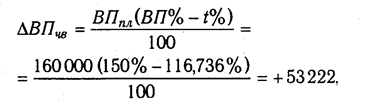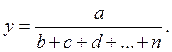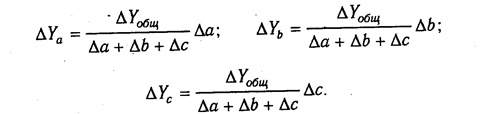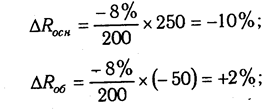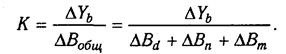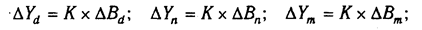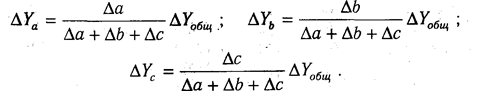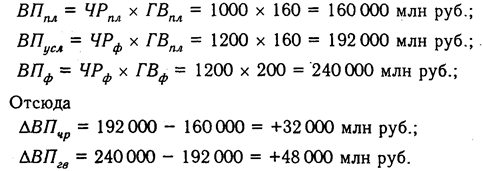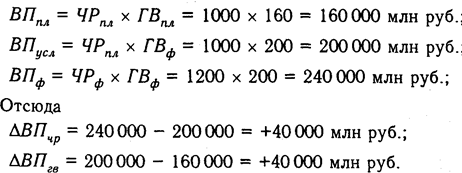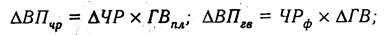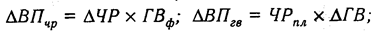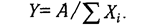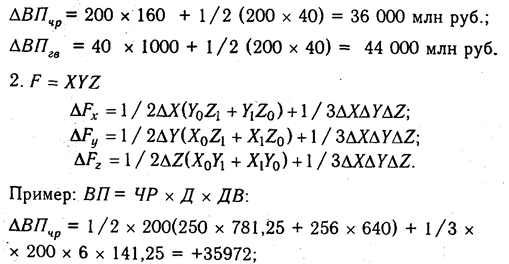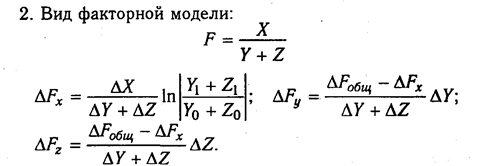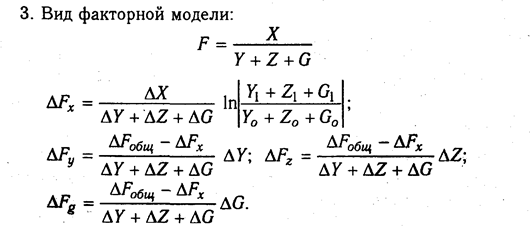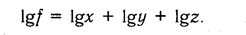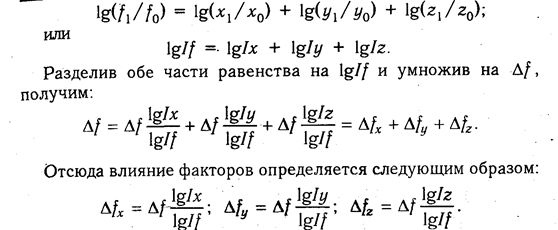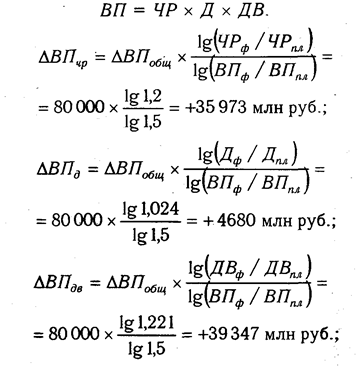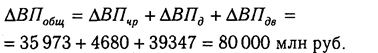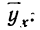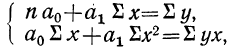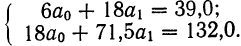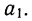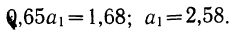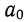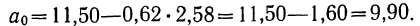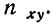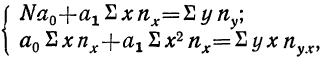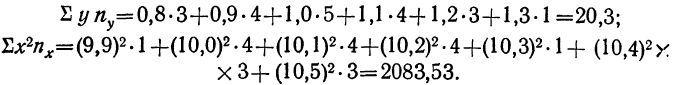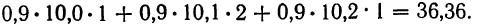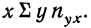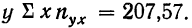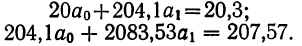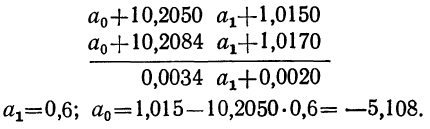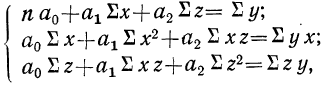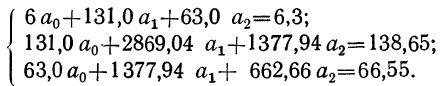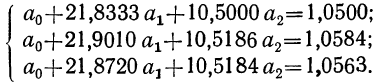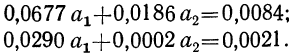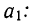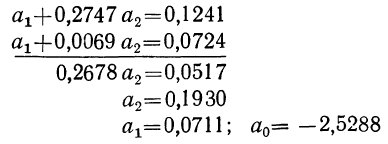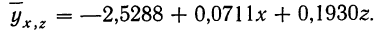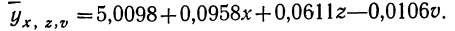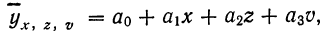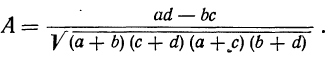Все объекты экономического анализа находят свое отображение в системе показателей плана, учета, отчетности и других источниках информации.

В соответствии с методикой проведения аналитического исследования необходимо выработать систему показателей, которая будет использована в процессе анализа.

Экономические показатели представляют собой один из самых распространенных и эффективных инструментариев описания экономики, используемых в экономической науке и в управлении экономическими процессами.

В наиболее общем виде экономический показатель включает наименование, числовое значение и единицу измерения.

Каждое экономическое явление, процесс или объект, как правило, характеризуется не одним, обособленным, а целым комплексом взаимосвязанных показателей.

Например, эффективность использования основных фондов организации характеризуется показателями фондоотдачи, фондоемкости, фондорентабельности, объемом выпуска продукции на один квадратный метр производственной площади и др.

В связи с этим выбор и обоснование системы показателей для отражения экономических явлений и процессов является важным методологическим вопросом в экономическом анализе.

От того, насколько полно и точно показатели отражают сущность изучаемых объектов, зависят результаты экономического анализа.

Система экономических показателей — это совокупность взаимосвязанных, систематизированных показателей, характеризующих экономику в целом, ее отрасль, регион, сферу экономической деятельности, группу однородных экономических процессов.

На уровне организации система показателей — это множество взаимосвязанных и взаимосогласованных показателей, которые характеризуют различные стороны экономического процесса и экономику организации в целом, эта система является ключевым элементом экономического анализа.

Поскольку при проведении аналитического исследования применяется большое количество разнокачественных показателей, необходима их классификация.

В основе классификации экономических показателей, т.е. их деления на отдельные группы, лежат их отличия в методике определения, расчета числовых значений, цели и задачи, для решения которых эти показатели используются.

Экономические показатели можно классифицировать по следующим признакам.

В соответствии с делением экономической науки на макроэкономику и микроэкономику выделяют обобщенные макроэкономические показатели, характеризующие экономику в целом и ее крупные части, сферы, и микроэкономические показатели, относящиеся в основном к экономике организаций (корпораций, компаний, фирм).

По содержанию выделяют группы количественных (объемных) и качественных показателей.

К количественным показателям относятся показатели, характеризующие изменение ресурсов, которыми располагает организация; объемы деятельности организации.

Например, это сумма прибыли организации, ее производственная мощность, объем реализованной продукции, численность работников, площадь посевов, поголовье скота и т.д.

К качественным показателям относятся показатели, характеризующие существенные особенности и свойства изучаемых объектов.

Примером качественных показателей являются рентабельность капитала, фондоотдача, производительность труда рабочих, себестоимость единицы продукции, оборачиваемость оборотных средств, жирность молока, урожайность культур и др.

Количественные и качественные показатели тесно взаимосвязаны, поскольку изменение количественных показателей, как правило, влечет за собой изменение качественных, и наоборот.

Так, например, увеличение прибыли ведет к росту рентабельности капитала, увеличение численности работников — к снижению производительности труда.

Рост урожайности обеспечивает увеличение валового сбора зерновых культур, ускорение оборачиваемости оборотных средств — уменьшение потребности в капитале.

В структуре экономических показателей различают абсолютные (называемые также количественными) и относительные (называемые также качественными) показатели.

Абсолютные показатели отражают уровень развития явления. Все абсолютные величины измеряются в конкретных единицах и могут быть как положительными, так и отрицательными (прибыль, убытки, потери и т.п.).

Абсолютные показатели выражаются в натуральных (условно-натуральных), стоимостных измерителях или через трудоемкость. Натуральные показатели выражают величину явления в физических единицах измерения (масса, длина, объем и т.д.).

Условно-натуральные показатели применяются для обобщенной характеристики объемов производства и реализации продукции разнообразного ассортимента (например, условные пары обуви в обувной промышленности, тысячи условных банок на консервных предприятиях, условные кормовые единицы в сельском хозяйстве).

Натуральные единицы измерения могут быть простыми (тонны, штуки, метры, литры) и сложными, являющимися комбинацией нескольких разноименных величии (грузооборот автомобильного транспорта выражается в тонно-километрах, производство электроэнергии — в киловатт-часах).

Стоимостные показатели показывают величину сложных по составу явлений в денежном измерении. В трудовых единицах измерения (человеко-днях, человекочасах) учитываются общие затраты труда в организации, трудоемкость отдельных операций.

Поскольку абсолютные показатели — это основа всех форм учета и приемов количественного анализа, то следует разграничивать моментные и интервальные абсолютные величины.

Моментные показатели характеризуют фактическое наличие или уровень явления, развития объекта исследования па определенный момент времени, дату (например, наличие запасов сырья и материалов, кредиторская задолженность, величина незавершенного производства, парк автомобилей и т.д.).

Интервальные показатели характеризуют итоговый накопленный результат за исследуемый период в целом (объем валовой продукции, выручку, прибыль за месяц или год, величину валового сбора зерна за год и т.п.).

Относительные показатели представляют собой соотношения каких-либо двух абсолютных показателей одинаковой или разной размерности.

В первом случае это безразмерные показатели, характеризующие обычно темп изменения экономической величины или соотношения, пропорции однородных экономических величин, получаемые в результате их сравнения, измеряемые в долевом исчислении либо в процентах.

Во втором случае это размерные показатели, характеризующие скорость изменения величины во времени, эффективность использования ресурсов, чувствительность величины по отношению к фактору, обусловившему ее изменение.

Например, показатель эффективности автомобильного двигателя может быть измерен массой расходуемого бензина на один километр пути, а показатель рентабельности — количеством полученной прибыли, приходящейся па один рубль вложенного капитала.

Относительные показатели определяются в процентах, коэффициентах или индексах.

По содержанию выражаемых количественных соотношений выделяют следующие типы относительных показателей:

• выполнения плана;
• динамики;
• структуры;
• координации;
• интенсивности (эффективности);
• сравнения.

Относительный показатель выполнения плана рассчитывается как отношение фактически достигнутого в данном периоде уровня к его уровню по плану (степень выполнения плана). Рассчитывается, как правило, в процентах.

Относительные показатели динамики рассчитываются путем построения временного ряда, т.е. они характеризуют изменение того или иного объекта, явления во времени (отношение, например, выпуска продукции за отчетный год к базисному году). Для их характеристики используют индексы, темпы роста и темпы прироста.

Относительные показатели структуры характеризуют удельный вес части совокупности в ее общем объеме (например, удельный вес собственного капитала во всем капитале организации, доля отдельных видов продукции в выручке организации).

Отражая отношение части совокупности к совокупности, взятой в целом, они наглядно иллюстрируют как всю совокупность, гак и ее часть.

Относительный показатель координации представляет собой соотношение частей совокупности между собой.

Относительные показатели координации характеризуют, во сколько раз одна часть совокупности больше другой либо сколько единиц одной части приходится на 1, 10, 100, 1000 и более единиц другой части (количество единиц одной валюты на 1, 10 единиц другой валюты, количество врачей на 10000 человек и др.).

Относительные показатели интенсивности (эффективности) характеризуют степень распределения или развития данного явления в той или иной среде.

Они представляют собой отношение абсолютного уровня одного показателя, свойственного изучаемой среде, к другому абсолютному показателю, также присущему данной среде и, как правило, являющемуся для первого показателя факторным признаком (например, производство промышленной продукции на 100 руб. основных фондов, сумма оборота торговой организации на 1 м2 торговой площади, оборачиваемость оборотных средств, рентабельность продаж и др.).

Относительные показатели сравнения характеризуют сравнительные размеры одноименных абсолютных величин, относящихся к одному и тому же периоду либо моменту времени, но к различным объектам или территориям.

Посредством этих показателей сопоставляются мощность различных видов оборудования, производительность труда отдельных рабочих, производство продукции определенного вида разными организациями, регионами, странами и т.п.

По масштабам использования различают общие и специфические показатели. Общие показатели используются при анализе деятельности всех отраслей национальной экономики, локальные — только в отдельных отраслях.

К общим показателям можно отнести показатели выручки от продажи продукции (услуг, работ), производительности труда, себестоимости, прибыли, рентабельности и др.

К специфическим показателям для отдельных отраслей, видов деятельности, организаций могут быть отнесены содержание клейковины в муке, удельный расход бензина, жирность молока, урожайность овощных культур и т.д.

Все показатели, которые используются в анализе, взаимосвязаны и взаимообусловлены. Это вытекает из реально существующих связей между экономическими явлениями, которые они описывают.

Поэтому при изучении причинно-следственных связей показатели делятся на факторные и результативные.

Если тот или другой показатель выступает в качестве объекта исследования и рассматривается как результат воздействия одной или нескольких причин, то при изучении взаимосвязей он называется результативным.

Показатели, которые определяют поведение результативного показателя и рассматриваются в качестве причин изменения его величины, называются факторными.

По способу формирования различают следующие показатели:

Нормативные.

Нормативными называют обычно показатели, устанавливаемые органами управления организации или сложившиеся в практике хозяйствования и выражающие нормы затрат ресурсов (сырья, энергии, материалов, труда, денег) на производство единицы продукции, выполнение работы, потребление (нормы потребления).

Показатели в виде норм и нормативов (универсальных норм) отражают также принятые, заданные соотношения, пропорции, такие, например, как норма накопления, сбережений, прибыли, оплаты труда, налогообложения.

Плановые (данные установленных организацией планов экономического развития, плановые задания внутрихозяйственным подразделениям).

Учетные (данные бухгалтерского, статистического, оперативного учета).

Отчетные (данные бухгалтерской, статистической и оперативной отчетности).

Аналитические (оценочные), которые исчисляются в процессе аналитического исследования для оценки результатов и эффективности работы предприятия. К ним относят, прежде всего, относительные показатели.

Все показатели в зависимости от объекта анализа могут быть комплексными и частными. Комплексные показатели позволяют оценить результаты работы организации в целом.

К ним можно отнести показатели ресурсоотдачи, ресурсорентабельности (рентабельности капитала). Частные показатели используются при системном анализе и в зависимости от глубины системного анализа могут быть подразделены на частные показатели первого уровня, второго уровня и т.д.

Например, если в качестве обобщающего показателя рассматривать ресурсоотдачу, то к частным показателям первого уровня можно отнести фондоотдачу и фондоемкость, а к частным показателям второго порядка — фондоотдачу пассивной и активной части основных фондов и т.д.

В зависимости от того, какая стадия экономического (хозяйственного) кругооборота организации изучается, показатели, используемые в аналитическом исследовании, можно разделить на следующие группы:

• показатели исходных условий деятельности организации (наличие финансовых, материальных и трудовых ресурсов для нормального функционирования организации и достижения поставленной перед ней цели, организационно-технический уровень организации, условия и факторы внешней предпринимательской среды, финансовой микросреды и т.и.);
  показатели использования средств труда;
• показатели использования предметов труда;
• показатели использования трудовых ресурсов;
• показатели производства и реализации продукции;
• показатели себестоимости продукции; показатели прибыли и рентабельности организации;
• показатели финансового состояния организации.

Рассмотренная система показателей не является исчерпывающей. Могут применяться и иные классификации показателей. Кроме того, при проведении тематического анализа ряд показателей может быть разработан самой организацией (например, при проведении экспресс-анализа).

Например, при оценке эффективности хозяйственно-финансовой деятельности организации показатели экономической эффективности могут быть разделены на две группы:

• показатели внутренней эффективности (рентабельность совокупного капитала, рентабельность собственного капитала, рентабельность продаж и др.);
• показатели внешней эффективности (доля организации на рынке отдельного вида продукции, региона, показатель лояльности клиентов, коэффициент расширения клиентской базы и др.).

Способы выявления влияния факторов на результативный показатель

Одной
из важнейших методологических задач в
экономическом анализе является
определение величины влияния факторов
на прирост результативных показателей.
В детерминированном факторном анализе
для этого используются следующие методы:
цепной подстановки, абсолютных разниц
относительных разниц, долевого участия,
логарифмический, балансовый и т.д.

Наиболее
распространенным является метод цепной
подстановки.

Данный
способ используется для расчета влияния
факторов во всех типах детерминированных
факторных моделей: аддитивных,
мультипликативных, кратных и
комбинированных. Способ цепных подстановок
заключается в определении ряда
промежуточных значений результативного
показателя путем последовательной
замены базисных значений факторов на
отчетные. Разность промежуточных
значений равна изменению результативного
показателя за счет заменяемого фактора.
Число расчетов результативного показателя
на единицу больше числа факторов. При
расчетах используется следующий порядок.
При наличии количественных и качественных
показателей в первую очередь производится
подсчет количественных факторов, а
затем качественных.

Рассмотрим
пример применения этого способа.

Таблица
5.1.

Показатели, определяющие объем выпуска продукции

Показатель	Условное обозначение	Уровень показателя	Отклонение
базовый	отчетный	абсолютное	относительное, %
Валовая продукция, тыс. руб.	Вп	4800	5920	+1120	+23,3
Среднесписочная численность рабочих, чел.	Чр	15	16	+1	+6,7
Среднегодовая выработка продукции одним рабочим, тыс. руб.	Гв	320	370	+50	15,625
Количество отработанных дней одним рабочим за год	Д	200	205	+5	+2,5
Средняя продолжительность рабочего дня, час.	П	8	7,8	-0,2	-2,5
Среднечасовая выработка продукции одним рабочим, руб.	ЧВ	200	231,4	+31,4	+15,7

Между
показателями данной таблицы существует
взаимосвязь, которая может быть выражена
в виде следующей факторной модели:

ВП
= ЧР ∙ ГВ.

лгоритм
расчета способом цепной подстановки
имеет вид:

ВП₀
= ЧР₀
∙ ГВ₀
= 15 ∙ 320 = 4800 тыс. руб.

ВП_усл
= ЧР₁
∙ ГВ₀
= 16 ∙ 320 = 5120 тыс. руб.

ВП₁
= ЧР₁
∙ ГВ₁
= 16 ∙ 370 = 5920 тыс. руб.

Второй
показатель валовой продукции отличается
от первого тем, что при его расчете взята
численность рабочих текущего периода
вместо базисного. Выработка продукции
одним рабочим и там и там базисная. Можно
сказать, что за счет передержки численности
рабочих выпуск продукции вырос на 320
тыс. руб. (5120 — 4800).

Третий
показатель валовой продукции отличается
от второго тем, что при его расчете
выработка рабочих взята фактическая
вместо базисной. Численность и там и
там фактическая. Таким образом, за счет
роста производительности труда
объем валовой продукции вырос на 800 тыс.
руб. (5920  — 5120).

Следовательно,
рост объема производства произошел за
счет следующих факторов:

1) рост численности	+320 тыс. руб.;
2) повышение уровня производительности труда	+800 тыс. руб.;

Итого

+1120 тыс. руб.

Алгебраическая
сумма влияния факторов обязательно
должна быть равна общему приросту
результативного показателя:

Δ
ВП_чр
+ Δ ВП_гв
= Δ ВП_общ
.

Отсутствие
такого равенства говорит о допущенных
ошибках в расчетах.

Для
определения большего количества
факторов, например, четырех, рассчитывается
пять значений результативного показателя.
Схематически это можно представить
следующим образом (табл. 5.2)

Таблица
5.2.

Схема
расчета пяти значений результативного
показателя

Уровень результативного показателя	Условия расчета результативного показателя
Фактор 1	Фактор 2	Фактор 3	Фактор 4
Базисный	план	план	план	план
Условный 1	факт	план	план	план
Условный 2	факт	факт	план	план
Условный 3	факт	факт	факт	план
Фактический	факт	факт	факт	факт

В
качестве примера рассмотрим четырехфакторную
модель валовой продукции:

ВП
= ЧР ∙ Д ∙ П ∙ ЧВ.

Исходные
данные возьмем из таблицы 5.1:

ВП₀
= ЧР₀
∙ Д₀
∙ П₀
∙ ЧВ₀
= 15 ∙ 200 ∙ 8 ∙ 200 = 4800 тыс. руб.

ВП_усл1
= ЧР₁
∙ Д₀
∙ П₀
∙ ЧВ₀
= 16 ∙ 200 ∙ 8 ∙ 200 = 5120 тыс. руб.

ВП_усл2
= ЧР₁
∙ Д₁
∙ П₀
∙ ЧВ₀
= 16 ∙ 205 ∙ 8 ∙ 200 = 5248 тыс. руб.

ВП_усл3
= ЧР₁
∙ Д₁
∙ П₁
∙ ЧВ₀
= 16 ∙ 205 ∙ 7,8 ∙ 200 = 5116,8 тыс. руб.

ВП₁
= ЧР₁
∙ Д₁
∙ П₁
∙ ЧВ₁
= 16 ∙ 205 ∙ 7,8 ∙ 231,4 = 5920 тыс. руб.

Объем
выпуска продукции
за отчетный период вырос на 1120 тыс. руб.,
в том числе за счет изменения:

1)
численности рабочих:

Δ
ВП(ЧР) = ВП_усл1  — ВП₀ = 5120 —
4800 = +320 тыс. руб.;

2)
количества отработанных дней одним
рабочим за год:

Δ
ВП(Д) = ВП_усл2  — ВП_усл1 =
5248 — 5120 = +128 тыс. руб.;

3)
средней продолжительности рабочего
дня:

Δ
ВП(П) = ВП_усл3  — ВП_усл2 =
5116,8 — 5248 = -131,2 тыс. руб.;

4)
среднечасовой выработки:

Δ
ВП(ЧВ) = ВП₁  — ВП_усл3 = 5920 —
5116,8 = 803,2 тыс. руб.

Итого:
+1120 тыс. руб.

Следовательно,
применение способа цепной подстановки
требует знания взаимосвязи факторов,
их соподчиненности, умения правильно
их классифицировать и систематизировать.

В
мультипликативных моделях детерминированного
факторного анализа применяется способ
абсолютных разниц. Несмотря на
ограниченное использование, благодаря
простоте он получил широкое применение
в экономическом анализе.

Сущность
этого способа заключается в том, что
величина влияния факторов определяется
умножением абсолютного прироста значения
исследуемого фактора на базовую
(плановую) величину факторов, которые
находятся справа от него, и на фактическую
величину факторов, расположенных слева
от него в модели.

Алгоритм
расчета для мультипликативной
четырехфакторной модели валовой
продукции представляет собой следующее.

ВП
= ЧР ∙ Д ∙ П ∙ ЧВ.

Δ
ВП_чр = Δ ЧР ∙ Д₀ ∙ П₀ ∙
ЧВ₀ = (+1) ∙ 200 ∙ 8 ∙ 200 = + 320 тыс. руб.

Δ
ВП_д = ЧР₁ ∙ Δ Д ∙ П₀ ∙
ЧВ₀ = 16 ∙ (+5) ∙ 8 ∙ 200 = + 128 тыс. руб.

Δ
ВП_п = ЧР₁ ∙ Д₁ ∙ Δ П ∙
ЧВ₀ = 16 ∙ 205 ∙ (-0,2) ∙ 200 = -131,2 тыс.
руб.

Δ
ВП_чв = ЧР₁ ∙ Д₁ ∙ П₁
∙ Δ ЧВ = 16 ∙ 205 ∙ 7,8 ∙ (+31,4) = +803,2 тыс. руб.

Итого:
+1120 тыс. руб.

Результаты
с помощью способа абсолютных разниц
получаются те же, что и способом цепной
подстановки. Необходимо иметь в виду,
что если имеется несколько количественных
и качественных факторов, то сначала
исследуется влияние факторов первого
порядка, а затем более низкого.

Данный
способ применяется для измерения влияния
факторов на прирост результативного
показателя только в мультипликативных
моделях. Используются относительные
приросты факторных показателей,
выраженные в виде коэффициентов или
процентов.

Для
расчета влияния первого фактора
необходимо базовую величину результативного
показателя умножить на относительный
прирост первого фактора, выраженного
в виде десятичной дроби.

Для
расчета влияния второго фактора нужно
к базовой величине результативного
показателя прибавить изменение его за
счет первого фактора и затем полученную
сумму умножить на относительный прирост
второго фактора.

Влияние
третьего фактора определяется аналогично:
к базовой величине результативного
показателя необходимо прибавить его
прирост за счет первого и второго
факторов и полученную сумму умножить
на относительный прирост третьего
фактора и т.д.

Рассмотрим
данную методику на примере, приведенном
в

Δ
ВП_чр = ВП₀ ∙ Δ ЧР / ЧР₀
= 4800 ∙ 1 / 15 = +320 тыс. руб.

Δ
ВП_д = (ВП₀ + Δ ВП_чр ) ∙
Δ Д / Д₀ = (4800 + 320) ∙ 5 / 200 = +128 тыс. руб.

Δ
ВП_п = (ВП₀ + Δ ВП_чр + Δ
ВП_д ) ∙ Δ П / П₀ = (4800 + 320 + 128) ∙
-0,2 / 8 = -131,2 тыс. руб.

Δ
ВП_чв = (ВП₀ + Δ ВП_чр + Δ
ВП_д + Δ ВП_п ) ∙ Δ ЧВ / ЧВ₀
= (4800 + 320 + 128 — 131,2) ∙ 31,4 / 200 = 803,2 тыс. руб.

Результаты
расчетов такие же, как и при использовании
предыдущих способов.

Данный
способ удобно применять в тех случаях,
когда требуется рассчитывать влияние
большего количества факторов (8 и более).
Этот способ значительно сокращает число
вычислительных действий, что говорит
о его преимуществе.

Иногда,
чтобы определить влияние факторов на
прирост результативного показателя,
используется метод пропорционального
деления. Он используется, когда мы
имеем дело с аддитивными моделями Y = Σ
x_i и моделями кратно-аддитивного
характера:

Y
= a / b + c + d +….+n; Y = a + b + c +… + n / k.

Когда
имеется одноуровневая модель, например,
Y = a + b + c, расчет проводится следующим
образом:

Δ
Y_a = Δ
Y_общ / Δ
a + Δ b + Δ c ∙
Δ a;

Δ
Y_b = Δ
Y_общ / Δ
a + Δ b + Δ c ∙
Δ b;

Δ
Y_c = Δ
Y_общ / Δ
a + Δ b + Δ c ∙
Δ c.

В
моделях кратно-аддитивного типа сначала
определяем методом цепной подстановки,
как изменился результативный показатель
за счет числителя и знаменателя, а затем
следует расчет влияния факторов второго
порядка
способом пропорционального деления
вышеперечисленными алгоритмами.

Пример.

Уровень
фонда заработной платы повысился на
21,7% в связи с ростом среднегодовой
заработной платы на 3250 руб. Среднегодовая
заработная плата возросла за счет роста
выплат по тарифным ставкам — на 346
руб., за счет роста выплат доплат и
надбавок — на 2129 руб., за счет роста
выплат дополнительной заработной
платы — на 775 руб. Определим, как
изменился фонд заработной платы за счет
каждого фактора.

Δ
ФЗП_тс = +21,7% / 3250 ∙ 346 = +2,3%; Δ ФЗП_дн
= +21,7% / 3250 ∙ 2129 = +14,2%; Δ ФЗП_дз = +21,7%
/ 3250 ∙ 775 = +5,2%.

Для
решения такого типа задач можно
использовать способ долевого участия.

Сначала
определяется доля каждого фактора в
общей сумме их приростов, которая затем
умножается на общий прирост результативного
показателя (табл. 5.3).

Δ
Y_a = Δ а / Δ a + Δ b + Δ c ∙ Δ Y_общ
; Δ Y_c = Δ с / Δ a + Δ b + Δ c ∙ Δ Y_общ
; Δ Y_b = Δ b / Δ a + Δ b + Δ c ∙ Δ Y_общ
.

Таблица
5.3.

Соседние файлы в папке АХД

• #
• #
• #
• #
• #
• #

Способы:

— цепной подстановки;

— индексный;

— абсолютных разниц;

— относительных разниц;

— пропорционального деления;

— долевого участия;

— интегральный;

— логарифмирования.

6.1. Способ цепной подстановки

 Типы детерминированных моделей, в которых применяется способ цепной подстановки. Сущность и правила его применения. Алгоритмы расчета влияния факторов этим  спосбом в различных типах моделей.

Одним из важнейших методологических вопросов в АХД является определение величины влияния отдельных факторов на прирост результативных показателей. В детерминированном факторном анализе (ДФА) для этого используются следующие способы: цепной подстановки, индексный, абсолютных разниц, относительных разниц, пропорционального деления, интегральный, логарифмирования и др.

Первых четыре способа основываются на методе элиминирования. Элиминировать — значит устранить, отклонить, исключить воздействие всех факторов на величину результативного показателя, кроме одного. Этот метод исходит из того, что все факторы изменяются независимо друг от друга: сначала изменяется один, а все другие остаются без изменения, потом изменяются два, затем три и т.д., при неизменности остальных. Это позволяет определить влияние каждого фактора на величину исследуемого показателя в отдельности.

Наиболее универсальным из них является способ цепной подстановки. Он используется для расчета влияния факторов во всех типах детерминированных факторных моделей: аддитивных, мультипликативных, кратных и смешанных (комбинированных). Этот способ позволяет определить влияние отдельных факторов на изменение величины результативного показателя путем постепенной замены базисной величины каждого факторного показателя в объеме результативного показателя на фактическую в отчетном периоде. С этой целью определяют ряд условных величин результативного показателя, которые учитывают изменение одного, затем двух, трех и т.д. факторов, допуская, что остальные не меняются. Сравнение величины результативного показателя до и после изменения уровня того или другого фактора позволяет элиминироваться от влияния всех факторов, кроме одного, и определить воздействие последнего на прирост результативного показателя.

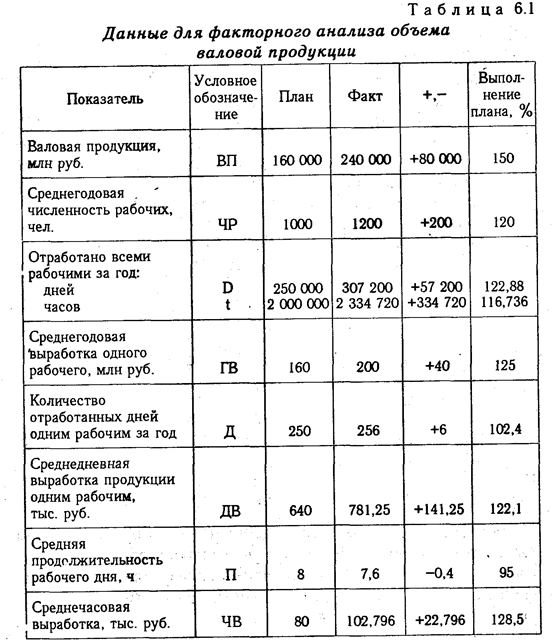
Порядок применения этого способа рассмотрим на следующем примере (табл. 6.1).

Как нам уже известно, объем валовой продукции (ВП) зависит от двух основных факторов первого уровня: численности рабочих (ЧР) и среднегодовой выработки (ГВ). Имеем двухфакторную мультипликативную модель: ВП = ЧР х ГВ.

Алгоритм расчета способом цепной подстановки для этой модели:

Как видим, второй показатель валовой продукции отличается от первого тем, что при его расчете принята фактическая численность рабочих вместо запланированной. Среднегодовая выработка продукции одним рабочим в том и другом случае плановая. Значит за счет увеличения количества рабочих выпуск продукции увеличился на 32 000 млн руб. (192 000 — 160 000).

Третий показатель отличается от второго тем, что при расчете его величины выработка рабочих принята по фактическому уровню вместо плановой. Количество же работников в обоих случаях фактическое. Отсюда за счет повышения производительности труда объем валовой продукции увеличился на 48 000 млн руб. (240 000 — 192 000).

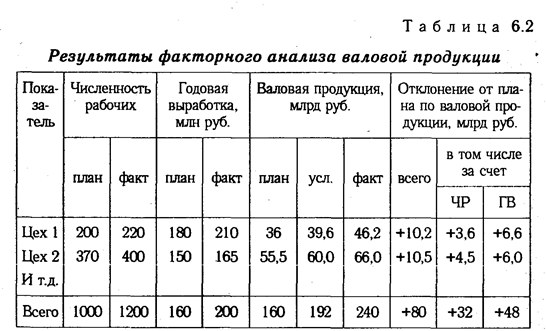
Таким образом, перевыполнение плана по объему валовой продукции явилось результатом влияния следующих факторов:

а) увеличения численности рабочих                                               + 32 000 млн руб.

б) повышения уровня производительности труда                         + 48 000 млн руб.

                                                                                                   Итого   +80 000 млн руб.

Алгебраическая сумма влияния факторов обязательно должна быть равна общему приросту результативного показателя:

Отсутствие такого равенства свидетельствует о допущенных ошибках в расчетах.

Для наглядности результаты анализа приведены в табл. 6.2.

Если требуется определить влияние трех факторов, то в этом случае рассчитывается не один, а два условных дополнительных показателя, т.е. количество условных показателей на единицу меньше числа факторов. Проиллюстрируем это на четырехфакторной модели валовой продукции:

Исходные данные для решения задачи приведены в табл.6.1:

План по выпуску продукции в целом перевыполнен на 80 000 млн руб. (240000 — 160000), в том числе за счет изменения:

а) количества рабочих

Используя способ цепной подстановки, рекомендуется придерживаться определенной последовательности расчетов: в первую очередь нужно учитывать изменение количественных, а затем качественных показателей. Если же имеется несколько количественных и несколько качественных показателей, то сначала следует изменить величину факторов первого уровня подчинения, а потом более низкого. В приведенном примере объем производства продукции зависит от четырех факторов: количества рабочих, количества отработанных дней одним рабочим, продолжительности рабочего дня и среднечасовой выработки. Согласно схеме 5.2, количество рабочих в данном случае — фактор первого уровня подчинения, количество отработанных дней – второго уровня, продолжительность рабочего дня и среднечасовая выработка — факторы третьего уровня. Это и обусловило последовательность размещения факторов в модели и соответственно очередность их исследования.

Таким образом, применение способа цепной подстановки требует знания взаимосвязи факторов, их соподчиненности, умения правильно их классифицировать и систематизировать.

Мы рассмотрели пример расчета влияния факторов на прирост результативного показателя в мультипликативных моделях.

В кратных моделях алгоритм расчета факторов на величину исследуемых показателей следующий:

где ФО — фондоотдача; ВП —валовая продукция; ОПФ — среднегодовая стоимость основных производственных фондов.

Методика расчета влияния факторов в смешанных моделях:

а) Мультипликативно-аддитивного типа П = VPП (Ц — С)

где П — сумма прибыли от реализации продукции; VPП — объем реализации продукции; Ц — цена реализации; С — себестоимость единицы продукции;

Аналогичным образом рассчитывают влияние факторов и по другим детерминированным моделям смешанного типа.

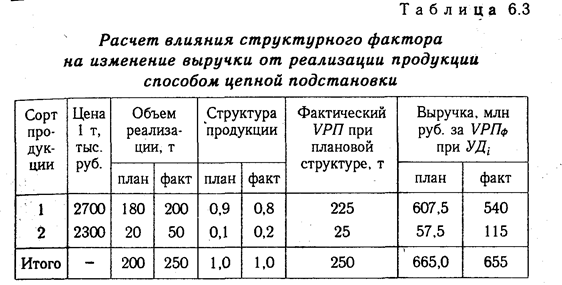
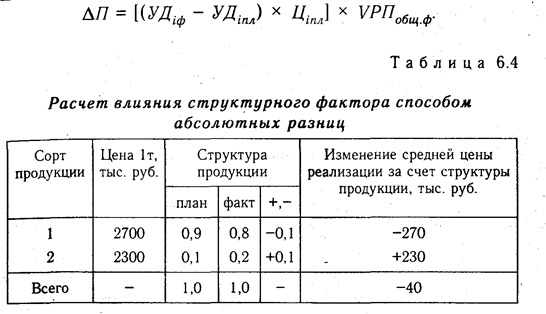
Отдельно необходимо остановиться на методике определения влияния структурного фактора на прирост результативного показателя с помощью этого способа. Например, выручка от реализации продукции (В) зависит не только от цены (Ц) и количества проданной продукции (VPH), но и от ее структуры (УД_i). Если возрастет доля продукции высшей категории качества, которая продается по более высоким ценам, то выручка за счет этого увеличится, и наоборот. Факторная модель этого показателя может быть записана так:

В процессе анализа необходимо элиминироваться от воздействия всех факторов, кроме структуры продукции. Для этого сравниваем следующие показатели выручки:

Разность между этими показателями учитывает изменение выручки от реализации продукции за счет изменения ее структуры (табл. 6.3.).

Из таблицы видно, что в связи с увеличением удельного веса продукции второго сорта в общем объеме его реализации выручка уменьшилась на 10 млн руб. (655 — 665). Это неиспользованный резерв предприятия.

6.2. Индексный метод

Сущность и назначение индексного метода. Алгоритм расчета влияния факторов этим методом для разных моделей.

Индексный метод основан на относительных показателях динамики, пространственных сравнений, выполнения плана, выражающих отношение фактического уровня анализируемого показателя в отчетном периоде к его уровню в базисном периоде (или к плановому или по другому объекту).

С помощью агрегатных индексов можно выявить влияние различных факторов на изменение уровня результативных показателей в мультипликативных и кратных моделях.

Для примера возьмем индекс стоимости товарной продукции:

Он отражает изменение физического объема товарной продукции (q) и цен (р) и равен произведению этих индексов:

Чтобы установить, как изменилась стоимость товарной продукции за счет количества произведенной продукции и за счет цен, нужно рассчитать индекс физического объема Iq и индекс цен 1_p:                                      

В нашем примере объем валовой продукции можно представить в виде произведения численности рабочих и их среднегодовой выработки. Следовательно, индекс валовой продукции 1вп будет равен произведению индекса численности рабочих lчр и индекса среднегодовой выработки 1гв:

Если из числителя вышеприведенных формул вычесть знаменатель, то получим абсолютные приросты валовой продукции в целом и за счет каждого фактора в отдельности, т.е. те же результаты, что и способом цепной подстановки.

6.3. Способ абсолютных разниц

Сущность, назначение и сфера применения способа абсолютных разниц. Порядок и алгоритмы расчета влияния факторов этим способом

Способ абсолютных разниц является одной из модификаций элиминирования. Как и способ цепной подстановки, он применяется для расчета влияния факторов на прирост результативного показателя в детерминированном анализе, но только в мультипликативных и мультипликативно-аддитивных моделях: Y = (а — b)с и У = a(b — с). И хотя его использование ограничено, но благодаря своей простоте он получил широкое применение в АХД. Особенно эффективно применяется этот способ в том случае, если исходные данные уже содержат абсолютные отклонения по факторным показателям.

При его использовании величина влияния факторов рассчитывается умножением абсолютного прироста исследуемого фактора на базовую (плановую) величину факторов, которые находятся справа от него, и на фактическую величину факторов, расположенных слева от него в модели.

Рассмотрим алгоритм расчета для мультипликативной факторной модели типа Y=axbxcxd. Имеются плановые и фактические значения по каждому факторному показателю, а также их абсолютные отклонения:

Определяем изменение величины результативного показателя за счет каждого фактора:

Как видно из приведенной схемы, расчет строится на последовательной замене плановых значений факторных показателей на их отклонения, а затем на фактический уровень этих показателей.

Рассмотрим методику расчета влияния факторов этим способом для четырехфакторной мультипликативной модели валовой продукции:

Таким образом, способ абсолютных разниц дает те же результаты, что и способ цепной подстановки. Здесь также необходимо следить за тем, чтобы алгебраическая сумма прироста результативного показателя за счет отдельных факторов была равна общему его приросту.

 Рассмотрим алгоритм расчета факторов этим способом в смешанных моделях типа V = (а — b)с. Для примера возьмем факторную модель прибыли от реализации продукции, которая уже использовалась в предыдущем параграфе:

П = VРП(Ц — С).

Прирост суммы прибыли за счет изменения объема реализации продукции:

цены реализации:

себестоимости продукции:

Расчет влияния структурного фактора при помощи этого способа проводится следующим образом:

Как видно из табл. 6.4, за счет изменения структуры реализации средняя цена за 1 т молока уменьшилась на 40 тыс. руб., а за весь фактический объем реализации продукции прибыли было получено меньше на 10 млн руб. (40 тыс. руб. х 250 т).

6.4. Способ относительных разниц

Сущность и назначение способа относительных разниц. Сфера его применения. Алгоритм расчета влияния факторов этим способом.

Способ относительных разниц, как и предыдущий, применяется для измерения влияния факторов на прирост результативного показателя только в мультипликативных и аддитивно-мультипликативных моделях типа V = (а — b)с. Он значительно проще цепных подстановок, что при определенных обстоятельствах делает его очень эффективным. Это прежде всего касается тех случаев, когда исходные данные содержат уже определенные ранее относительные приросты факторных показателей в процентах или коэффициентах.

Рассмотрим методику расчета влияния факторов этим способом для мультипликативных моделей типа V = А х В х С. Сначала необходимо рассчитать относительные отклонения факторных показателей:

Тогда изменение результативного показателя за счет каждого фактора определяется следующим образом:

Согласно этому правилу, для расчета влияния первого фактора необходимо базисную (плановую) величину результативного показателя умножить на относительный прирост первого фактора, выраженного в процентах, и результат разделить на 100.

Чтобы рассчитать влияние второго фактора, нужно к плановой величине результативного показателя прибавить изменение его за счет первого фактора и затем полученную сумму умножить на относительный прирост второго фактора в процентах и результат разделить на 100.

Влияние третьего фактора определяется аналогично: к плановой величине результативного показателя необходимо прибавить его прирост за счет первого и второго факторов и полученную сумму умножить на относительный прирост третьего фактора и т.д.

Закрепим рассмотренную методику на примере, приведенном в табл. 6.1:

Как видим, результаты расчетов те же, что и при использовании предыдущих способов.

Способ относительных разниц удобно применять в тех случаях, когда требуется рассчитать влияние большого комплекса факторов (8-10 и более). В отличие от предыдущих способов значительно сокращается количество вычислений.

Разновидностью этого способа является прием процентных разностей. Методику расчета влияния факторов с его помощью рассмотрим на том же примере (табл. 6.1).

Для того чтобы установить, насколько изменился объем валовой продукции за счет численности рабочих, необходимо плановую его величину умножить на процент перевыполнения плана по численности рабочих ЧР%:

Для расчета влияния второго фактора необходимо умножить плановый объем валовой продукции на разность между процентом выполнения плана по общему количеству отрабо­танных дней всеми рабочими D% и процентом выполнения плана по среднесписочной численности рабочих ЧР%:

Абсолютный прирост валовой продукции за счет измене­ния средней продолжительности рабочего дня (внутрисменных простоев) устанавливается путем умножения планового объема валовой продукции на разность между процентами вы­полнения плана по общему количеству отработанных часов всеми рабочими t% и общему количеству отработанных ими дней D%:

Для расчета влияния среднечасовой выработки на изменение объема валовой продукции необходимо разность между процен­том выполнения плана по валовой продукции ВП% и процен­том выполнения плана по общему количеству отработанных часов всеми рабочими t% умножить на плановый объем вало­вой продукции ВПпл:

Преимущество этого способа состоит в том, что при его при­менении не обязательно рассчитывать уровень факторных по­казателей. Достаточно иметь данные о процентах выполнения плана по валовой продукции, численности рабочих и количеству отработанных ими дней и часов за анализируемый период.

6.5. Способ пропорционального деления и долевого участия

Сущность, назначение и сфера применения способа про­порционального деления. Порядок и алгоритмы расчетов влияния факторов этим способом.

В ряде случаев для определения величины влияния факто­ров на прирост результативного показателя может быть исполь­зован способ пропорционального деления. Это касается тех случаев, когда мы имеем дело с аддитивными моделями типа V = 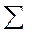Xi и кратно-аддитивного типа

В первом случае, когда имеем одноуровневую модель типа V= а + b + с. расчет проводится следующим образом:

Например, уровень рентабельности снизился на 8% в связи с увеличением капитала предприятия на 200 млн руб. При этом стоимость основного капитала возросла на 250 млн руб., а обо­ротного уменьшилась на 50 млн руб. Значит, за счет первого фактора уровень рентабельности снизился, а за счет второго — повысился:

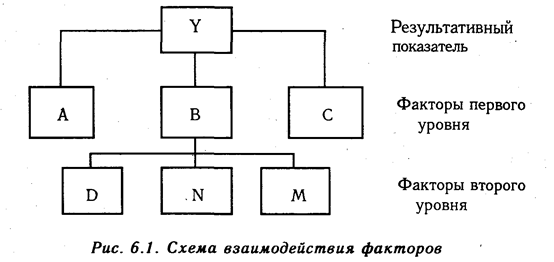
Методика расчета для смешанных моделей несколько слож­нее. Взаимосвязь факторов в комбинированной модели пока­зана на рис. 6.1.

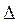
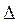
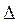
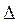
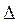
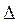
Когда известны Вd, Вп и Вт, а также Yb, то для определения Y_d, Y_n, Y_m можно использовать способ пропорционального деления, который основан на пропорциональном распределении прироста результативного показателя Y за счет изменения фактора В между факторами второго уровня D, N и М соответственно величине их прироста. Пропорциональность этого распределения достигается путем определения постоянного для всех факторов коэффициента, который показывает величину изменения результативного показателя Y за счет изменения фактора В на единицу.

Величина коэффициента (К) определяется следующим образом:

Умножив этот коэффициент на абсолютное отклонение В за счет соответствующего фактора, найдем изменение результативного показателя:

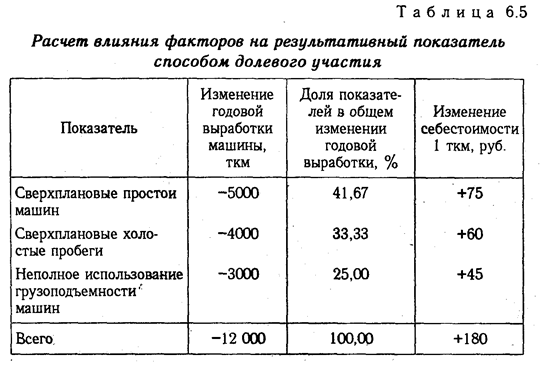
Например, себестоимость 1 ткм за счет снижения среднегодовой выработки автомобиля повысилась на 180 руб. При этом известно, что среднегодовая выработка автомашины снизилась из-за:

а) сверхплановых простоев машин                       -5000 ткм

б) сверхплановых холостых пробегов                  -4000 ткм

в) неполного использования грузоподъемности -3000 ткм

                                                                                 Всего-12000 ткм

 Отсюда можно определить изменение себестоимости под влиянием факторов второго уровня:

Для решения такого типа задач можно использовать также способ долевого участия. Сначала определяется доля каждого фактора в общей сумме их приростов, которая затем умножается на общий прирост результативного показателя (табл. 6.5):

Аналогичных примеров применения этого способа в АХД можно привести очень много, в чем вы сможете убедиться в процессе изучения отраслевого курса анализа хозяйственной деятельности предприятия.

6.6. Интегральный способ в анализе хозяйственной деятельности

Основные недостатки метода элиминирования. Проблема разложения дополнительного прироста от взаимодействия факторов между ними. Сущность интегрального метода и сфера его применения. Алгоритмы расчета влияния факторов в разных моделях интегральным способом.

Элиминирование как способ детерминированного факторного анализа имеет существенный недостаток. При его использовании исходят из того, что факторы изменяются независимо друг от друга. На самом же деле они изменяются совместно, взаимосвязано и от этого взаимодействия получается дополнительный прирост результативного показателя, который при применении способов элиминирования присоединяется к одному из факторов, как правило к последнему. В связи с этим величина влияния факторов на изменение результативного показателя меняется в зависимости от места, на которое поставлен тот или иной фактор в детерминированной модели.

Рассмотрим это на примере, который дан в табл. 6.1. Согласно приведенным в ней данным, количество рабочих на предприятии увеличилось на 20%, производительность труда — на 25%, а объем валовой продукции — на 50%. Это значит, что 5% (50 — 20 — 25), или 8000 млн руб. валовой продукции составляет дополнительный прирост от взаимодействия обоих факторов.

Когда мы подсчитаем условный объем валовой продукции, исходя из фактического количества рабочих и планового уровня производительности труда, то весь дополнительный прирост от взаимодействия двух факторов относится к качественному фактору — изменению производительности труда:

Если же при расчете условного объема валовой продукции взять запланированное количество рабочих и фактический уровень производительности труда, то весь дополнительный прирост валовой продукции относится к количественному фактору, который мы изменяем во вторую очередь:

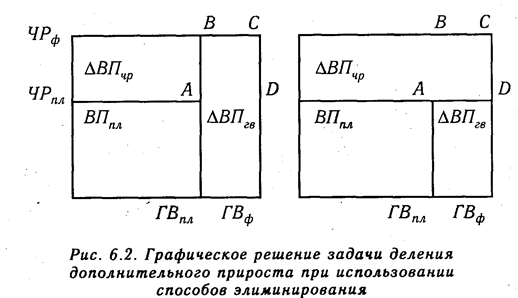
Покажем графическое решение задачи в разных вариантах (рис. 6.2).

В первом варианте расчета условный показатель имеет форму: ВП_усл = ЧРф х ГВ_пл, во втором – ВП_усл = ЧР_пл х ГВф.

Соответственно отклонения за счет каждого фактора в первом случае

во втором

На графиках этим отклонениям соответствуют разные прямоугольники, так как при разных вариантах подстановки величина дополнительного прироста результативного показателя, равная прямоугольнику ABCD, относится в первом случае к величине влияния годовой выработки, а во –втором,  к величине влияния количества рабочих. В результате этого величина влияния одного фактора преувеличивается, а другого — приуменьшается, что вызывает неоднозначность оценки влияния факторов, особенно в тех случаях, когда дополнительный прирост довольно существенный, как в нашем примере.

Чтобы избавиться от этого недостатка, в детерминированном факторном анализе используется интегральный метод, который применяется для измерения влияния факторов в мультипликативных, кратных и смешанных моделях кратно-аддитивного вида

Использование этого способа позволяет получать более точные результаты расчета влияния факторов по сравнению со способами цепной подстановки, абсолютных и относительных разниц и избежать неоднозначной оценки влияния факторов потому, что в данном случае результаты не зависят от местоположения факторов в модели, а дополнительный прирост результативного показателя, который образовался от взаимодействия факторов, раскладывается между ними поровну.

На первый взгляд может показаться, что для распределения дополнительного прироста достаточно взять его половину или часть, соответствующую количеству факторов. Но это сделать чаще всего сложно, так как факторы могут действовать в разных направлениях. Поэтому в интегральном методе пользуются определенными формулами. Приведем основные из них для разных моделей.                            

В нашем примере (см. табл. 6.1) расчет проводится следующим образом:

Для расчета влияния факторов в кратных и смешанных моделях используются следующие рабочие формулы.

Таким образом, использование интегрального метода не требует знания всего процесса интегрирования. Достаточно в готовые рабочие формулы подставить необходимые числовые данные и сделать не очень сложные расчеты с помощью калькулятора или другой вычислительной техники. При этом достигается более высокая точность расчетов.

6.7. Способ логарифмирования в анализе хозяйственной деятельности

Сущность, сфера применения и отличительные черты способа логарифмирования. Алгоритмы расчета влияния факторов этим способом.

Способ логарифмирования применяется для измерения влияния факторов в мультипликативных моделях. В данном случае результат расчета, как и при интегрировании, не зависит от месторасположения факторов в модели и по сравнению с интегральным методом обеспечивается еще более высокая точность расчетов. Если при интегрировании дополнительный прирост от взаимодействия факторов распределяется поровну между ними, то с помощью логарифмирования результат совместного действия факторов распределяется пропорционально доли изолированного влияния каждого фактора на уровень результативного показателя. В этом его преимущество, а недостаток — в ограниченности сферы применения.

В отличие от интегрального метода при логарифмировании используются не абсолютные приросты показателей, а индексы их роста (снижения).

Математически этот метод описывается следующим образом. Допустим, что результативный показатель можно представить в виде произведения трех факторов: f = хуz. Прологарифмировав обе части равенства, получим

Учитывая, что между индексами изменения показателей сохраняется та же зависимость, что и между самими показателями, произведем замену абсолютных их значений на индексы:

Из формул вытекает, что общий прирост результативного показателя распределяется по факторам пропорционально отношениям логарифмов факторных индексов к логарифму индекса результативного показателя. И не имеет значения, какой логарифм используется — натуральный или десятичный.

Используя данные табл. 6.1, вычислим прирост валовой продукции за счет численности рабочих (ЧР), количества отработанных дней одним рабочим за год (Д) и среднедневной выработки (ДВ) по факторной модели:

Сравнив полученные результаты расчета влияния факторов разными способами по данной факторной модели, можно убедиться в преимуществе способа логарифмирования. Это выражается в относительной простоте вычислений и повышении точности расчетов.

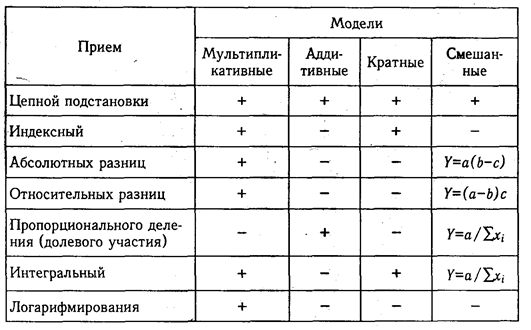
Рассмотрев основные приемы детерминированного факторного анализа и сферу их применения, результаты можно систематизировать в виде следующей матрицы:

Знание сущности данных приемов, области их применения, процедуры расчетов — необходимое условие квалифицированного проведения количественных исследований.

ГБОУ СПО «Пильнинский агропромышленный техникум»

МЕТОДИКА ФАКТОРНОГО АНАЛИЗА

Курс лекций

Составитель:

 преподаватель
спецдисциплин ГБОУ СПО «ПАПТ»

Рыбакова Елена Алексеевна

Пильна

2013

Содержание

1. Метод и методика анализа хозяйственной
деятельности

1.1. Метод анализа финансово-хозяйственной
деятельности, его характерные черты

1.2. Методика анализа финансово-хозяйственной
деятельности

1.3.  Методика факторного анализа

1.4. Факторы в анализе финансово-хозяйственной деятельности

2. Моделирование взаимосвязей в факторном
анализе

3. Способы измерения влияния факторов в
анализе хозяйственной деятельности

3.1. Способ цепной подстановки

3.2. Способ абсолютных разниц

3.3. Способ относительных разниц

3.4. Способы пропорционального деления и долевого
участия

3.5. Интегральный способ в анализе хозяйственной
деятельности

1.     Метод и методика анализа хозяйственной
деятельности

1. 1. Метод анализа хозяйственной
деятельности, его характерные черты

Под методом науки в широком смысле понимают способ
иссле­дования своего предмета. Характерные черты анализа
финансово-хозяйственной деятельности обусловлены положениями диалектического
метода познания:

1. Диалектический метод познания исходит из того, что
все явления и процессы необходимо рассматривать в постоянном движении, изме­нении,
развитии. Здесь исток одной из характерных черт ме­тода АФХД — необходимость
постоянных сравнений. Фактические результаты деятельности сравниваются с
результатами прошлых лет, достижениями других предприятий, плановыми
показателями и т.д.

2. Каждый процесс, каждое явление надо рассматривать
как единство и борьбу противоположностей. Отсюда вы­текает необходимость
изучения внутренних противоречий, положи­тельных и отрицательных сторон каждого
явления, каждого процесса.

3. Изу­чение хозяйственной деятельности предприятий
должно проводиться с учетом всех взаимосвязей. Ни одно явление не может быть
правильно понято, если оно рассматривается изолированно, без связи с другими.

4. Важной методологической чертой анализа является
способность не только устанавливать причинно-следственные связи, но и давать им
количественную характеристику, т.е. обеспечивать измере­ние влияния факторов на
результаты деятельности.

5. Каждый процесс, каждое экономическое явление надо
рассматривать как систему, как совокупность многих элементов, связанных между
собой. Из этого вытекает необходимость системного подхода к изу­чению объектов
анализа. Системный подход предусматривает максимальную детали­зацию изучаемых явлений
и процессов на элементы (собственно ана­лиз), их систематизацию и синтез
(обобщение).

Детализация явлений проводится в степени, которая
необхо­дима для выяснения наиболее существенного и главного в изучае­мом
объекте. Она зависит от объекта и цели анализа. Систематизация элементов
производится на основе изучения их взаимосвязи, взаимодействия,
взаимозависимости и соподчиненно­сти. Это позволяет построить приблизительную
модель изучаемого объекта (системы), определить его главные компоненты, функции,
соподчиненность элементов системы, раскрыть логико-методологи­ческую схему
анализа, которая соответствует внутренним связям изу­чаемых показателей. После
изучения отдельных сторон экономики предприятия, их взаимосвязи, подчиненности
и зависимости надо обобщить весь ма­териал исследования. Для этого из всего множества
изучаемых факторов необходимо выделить типичные, главные и решающие, от которых
зависят результаты деятельности.

6. Разработка и использование системы показателей,
необходимой для комплексного, системного исследования причинно-следственных
связей экономических явле­ний и процессов в хозяйственной деятельности
предприятия.

Таким образом, метод АФХД представляет собой
системное, комп­лексное изучение, измерение и обобщение влияния факторов на резуль­таты
деятельности предприятия путем обработки специальными при­емами системы
показателей плана, учета, отчетности и других источников информации с целью
повышения эффективности функцио­нирования предприятия.

1.2. Методика анализа финансово-хозяйственной
деятельности

Метод АФХД предусматривает использование ряда
конкретных методик аналитического исследования, т.е. совокупности способов,
правил наиболее целесообразного выполнения какой-либо работы.

В экономическом анализе методика — это
совокупность анали­тических способов и правил исследования экономических
явлений и процессов финансово-хозяйственной деятельности, подчиненных
достижению цели анализа.

Различают общую и частные методики анализа. Общая
методика — это система исследования, которая в одинако­вой мере
используется при изучении различных объектов экономичес­кого анализа в
различных отраслях экономики. Частные методики конкретизируют общую
методику применительно к определенным отраслям экономики, типам производства,
объектам исследования, видам анализа.

Любая методика анализа представляет собой указания или
мето­дологические советы относительно выполнения аналитического ис­следования.
Она содержит:

1. Формулировку задач и целей анализа.

2. Объекты анализа.

3. Системы показателей, с помощью которых будет исследовать­ся
каждый объект анализа.

4. Советы относительно последовательности и
периодичности проведения аналитического исследования.

5. Описание способов и методики исследования изучаемых
объектов.

6. Источники данных, на основании которых производится
анализ.

7. Указания по организации анализа (какие лица, службы
будут проводить отдельные части исследования).

8. Технические средства, которые целесообразно
использовать для аналитической обработки информации.

9. Порядок оформления результатов анализа.

10. Перечень пользователей результатов анализа.

Важнейшим элементом методики АФХД являются
всевозможные технические при­емы и способы анализа (инструментарий анализа).
Среди них можно выделить:

традиционные логические способы, которые применяют­ся
для обработки и изучения информации (срав­нение, графический способ,
балансовый, средних и относительных величин, аналитических группировок,
эвристические методы реше­ния экономических задач на основании интуиции,
прошлого опыта, экспертных оценок специалистов и др.);

для изучения влияния факторов на результаты
хозяйствования и подсчета резервов применяются такие способы, как цепные подста­новки,
абсолютные и относительные разницы, интегральный метод, корреляционный,
компонентный, методы линейного, выпуклого программирования, теория массового
обслуживания, теория игр, ис­следования операций и др.;

математи­ческие методы.

1.3. Методика факторного анализа

Все явления и процессы хозяйственной деятель­ности
предприятий взаимосвязаны, взаимозависимы и взаимообуслов­лены. Одни из них
связаны между собой непосредственно, другие — кос­венно. Каждое явление можно
рассматривать и как причину, и как ре­зультат.

Если тот или иной показатель рассматривается как
следствие, как результат действия одной или нескольких причин и выступает в ка­честве
объекта исследования, то при изучении взаимосвязей его на­зывают результативным
показателем.

Показатели, определяющие поведение результативного
призна­ка, называются факторными.

Факторный анализ — это методика комплексного и системного изу­чения и
измерения воздействия факторов на величину результативных показателей.

Задачи факторного анализа:

1. Отбор факторов для анализа исследуемых показателей.

2. Классификация и систематизация их с целью
обеспечения сис­темного подхода.

3. Моделирование взаимосвязей между результативными и
фактор­ными показателями.

4. Расчет влияния факторов и оценка роли каждого из
них в изме­нении величины результативного показателя.

5. Работа с факторной моделью.

В зависимости от характера исследуемых взаимосвязей
различа­ют детерминированный и стохастический факторный анализ.

Детерминированный факторный анализ исследует влияние факто­ров, связь которых с
результативным показателем носит функцио­нальный характер, т.е. когда величина
результативного показателя может быть представлена в виде произведения,
частного или алгеб­раической суммы нескольких факторов.

Стохастический анализ представляет собой методику исследова­ния факторов,
связь которых с результативным показателем, в отли­чие от функциональной,
является неполной, вероятностной (корре­ляционной). Если при функциональной
(полной) зависимости с изменением аргумента всегда происходит соответствующее
измене­ние функции, то при корреляционной связи изменение аргумента может дать
несколько значений прироста функции в зависимости от сочетания других факторов,
определяющих данный показатель.

Различают также прямой и обратный факторный анализ.

Прямой факторный анализ осуществляется дедуктивным способом — от об­щего
к частному. Обратный факторный анализ исследует причинно­-следственные
связи способом логической индукции — от частных, от­дельных факторов к общим.

Факторный анализ может быть одноступенчатым и многосту­пенчатым.
 Первый вид используется для исследования факторов только одного уровня (одной
ступени) подчинения без их детализа­ции на составные части. Например, у = аЬ.
При многоступенчатом факторном анализе проводится детализация факторов а и Ь на
состав­ные элементы с целью изучения их сущности. Детализация факторов может
быть продолжена и дальше. В данном случае изучается влия­ние факторов различных
уровней соподчиненности.

Необходимо различать также статический и динамический
фактор­ный анализ. Первый вид применяется при изучении влияния факторов на
результативные показатели на соответствующую дату. Другой вид представляет
собой методику исследования причинно-следственных связей в динамике.

И, наконец, факторный анализ может быть ретроспективным,
ко­торый изучает причины изменения результатов хозяйственной деятель­ности за прошлые
периоды, и перспективным, который исследует по­ведение факторов и
результативных показателей в перспективе.

1.4. Факторы в анализе хозяйственной
деятельности

Исследуемые в анализе факторы могут быть
классифицированы по разным признакам, что позволяет точнее оценить место и роль
каждого фактора в формировании величины результативных показателей.

По своей природе факторы разделяются на:

1. Природно-климатические факторы оказывают большое
влияние на результаты деятельности в сельском хозяйстве, добывающей про­мышленности,
лесном хозяйстве и других отраслях. Учет их влияния позволяет точнее оценить
результаты работы субъектов хозяйствова­ния.

2. К социально-экономическим факторам относятся
жилищные усло­вия работников, организация культурно-массовой, спортивной и оздоровительной
работы на предприятии, общий уровень культуры и образования персонала и др. Они
способствуют более полному ис­пользованию производственных ресурсов предприятия
и повышению эффективности его работы.

3. Производственно-экономические факторы определяют
полноту и эффективность использования производственных ресурсов предпри­ятия и
конечные результаты его деятельности.

По степени воздействия на результаты хозяйственной деятельно­сти
факторы делятся на:

1. Второстепенные факторы

2. Основные фак­торы, в отличие от второстепенных,
оказывают наиболее существен­ное влияние на результативный показатель.

Один и тот же фактор в зависимости от обстоятельств
может быть и основным, и второстепенным.

По отношению к объекту исследования факторы классифицируются на:

1. Внутренние — зависящие от деятель­ности данного
предприятия.

2. Внешние — не зависящие от деятель­ности данного
предприятия.

Основное внимание при анализе должно уделяться
исследованию внутренних факторов, на которые пред­приятие может воздействовать.

По степени зависимости от субъекта
хозяйствования факторы
разделяют на:

1. Объективные (не зависящие от воли и желания людей,
например стихийное бедствие).

2. Субъективные (зависящие от деятель­ности
юридических и физических лиц).

По степени распространенности факторы делятся на:

1. Общие (дейст­вующие во всех отраслях экономики).

2. Специфические (действующие, в условиях отдельной
отрасли экономики или предприятия).

По продолжительности воздействия на результаты
деятельности раз­личают
факторы:

1. Постоянные (оказывающие влияние на изучаемое яв­ление
беспрерывно на протяжении всего времени).

2. Переменные (воз­действие которых является
периодическим, например освоение новой техники, новых видов продукции, новой
технологии производства и т.д.).

По характеру действия факторы делятся на:

1.                     
Интенсивные, которые
характеризуют степень усилия, напряженности труда в процессе про­изводства
(например, повышение урожайности сельскохозяйственных культур, повышение
продуктивности скота, уровня производительно­сти труда).

2.                     
Экстенсивные, которые
связаны с количественным, а не качественным приростом результативного
показателя (например, уве­личение объема производства продукции путем
расширения посевной площади, увеличения поголовья животных, количества рабочих
и т.д.).

По мере влияния каждого фак­тора на результаты
хозяйственной деятельности их
разделяют на:

1.    
Количественные и
качественные.

Количественные факторы выражают количественную
определен­ность явлений (количество рабочих, оборудования, сырья и т.д.).

Качественные факторы определяют внутренние качества,
призна­ки и особенности изучаемых объектов (производительность труда, качество
продукции, плодородие почвы и т.д.).

2.                     
Сложные (комплекс­ные) и
простые (элементные), которые не раскладываются на составные части..

3.    
Прямые и кос­венные.

Одни факторы оказывают непосредствен­ное, а другие —
косвенное влияние на результативный показатель. По уровню соподчиненности
(иерархии) различают факторы первого, второго, третьего и так далее уровней
подчинения. Факторы первого уровня непосредственно влияют на результативный
показатель. Фак­торы второго уровня определяют результативный показатель косвен­но,
при помощи факторов первого уровня, и т.д.

4.    
Измеримые (параметрические)
и неизмеримые (непараметрические).

Системный подход в АФХД вызывает необходимость
взаимосвя­занного изучения факторов с учетом их внутренних и внешних свя­зей,
взаимодействия и соподчиненности, что достигается с помощью систематизации.

Систематизация — это размещение изучаемых яв­лений или объектов в
определенном порядке с выявлением их взаи­мосвязи и соподчиненности.

Различают детерминированные и стохастические факторные
си­стемы.

Создать детерминированную факторную систему — это значит представить изучаемое явление в
виде алгебраической суммы, част­ного или произведения нескольких факторов,
определяющих его ве­личину и находящихся с ним в функциональной зависимости. Развитие
детерминированной факторной системы достигается за счет детализации комплексных
факторов. С развитием системы комплексные факторы постепенно де­тализируются на
менее общие, те, в свою очередь, — на еще менее общие, постепенно приближаясь
по своему аналитическому содер­жанию к элементным (простым). Элемент­ные
факторы  не расклады­ваются на сомножители, так как по своему содержанию они
одно­родны.  

2. Моделирование взаимосвязей в факторном
анализе

Сущность моделирования заключается в том, что
взаимосвязь ис­следуемого показателя с факторными передается в форме конкрет­ного
математического уравнения.

В детерминированном анализе используются сле­дующие
факторные модели:

1. Мультипликативные. Применяются, когда
результативный показатель представляет собой произведение нескольких факторов.

2. Аддитивные. Используются, когда
результативный показатель представляет собой алгебраическую сумму нескольких
факторных показателей.

3. Кратные. Используются, когда результативный
показатель по­лучают делением величины одного фактора на величину другого.

4. Смешанные (комбинированные) — сочетание в
различных комбина­циях предыдущих моделей.

  ,     ,        и
другие.

Моделирование мультипликативных факторных систем в АФХД
осуществляется путем последовательного расчленения факторов исход­ной системы
на факторы-сомножители.

Если   , то

Аналогичным образом, т.е. путем расчленения факторов
исход­ной модели на составные элементы, осуществляется моделирование аддитивных
факторных систем.

Если    , то

Кратные модели преобразуют следующими методами:

1. Метод удлинения предусматривает удлинение
числителя исходной модели путем замены одного или нескольких факторов суммой од­нородных
показателей.

        Допустим, что                    ,            тогда

, где

, ,

Таким образом, из исходной кратной модели получили
аддитивную модель с новым набором факторов.

2. Метод расширения предусматривает расширение
исходной фактор­ной модели путем умножения числителя и знаменателя на один или
несколько новых показателей.  

Если в исходную модель ввести новый показатель а,
то модель примет вид

Таким образом, получается конечная мультипликативная
модель с новым набором факторов.

3. Метод сокращения — это создание новой
факторной модели пу­тем деления числителя и знаменателя на один и тот же
показатель. В итоге получается конечная модель того же типа, что и исходная,
однако с другим набором факторов.

Таким образом, результативные показатели могут быть
разложены на составные элементы (факторы) различными способами и представ­лены
в виде различных типов детерминированных моделей.

3. Способы измерения влияния факторов в
анализе

хозяйственной деятельности

3.1. Способ цепной подстановки

Способ цепной подстановки используется для расчета
влияния факторов во всех типах детерми­нированных факторных моделей —
аддитивных, мультипликативных, кратных и смешанных (комбинированных). Этот
способ позволяет определить влияние отдельных факторов на изменение величины
результативного показателя путем постепенной замены базового уров­ня каждого
факторного показателя в объеме результативного показа­теля на фактический его
уровень в отчетном периоде. С этой целью определяют ряд условных величин
результативного показателя, ко­торые учитывают изменение одного, затем двух,
трех и последующих факторов, допуская, что остальные не меняются. Сравнение
величи­ны результативного показателя до и после изменения уровня того или
другого фактора позволяет элиминировать влияние всех факторов, кроме одного, и
определить воздействие последнего на прирост ре­зультативного показателя.

Рассмотрим, например, трехфакторную мультипликативную
модель:

.

Алгоритм расчета влияния факторов:

 — значение
результативного показателя в базовом периоде,

 ,

 ,

 — значение
результативного показателя в отчетном периоде,

 — общее изменение
(абсолютное) результативного показателя,

 — изменение
результативного показателя за счет фактора а,

 — изменение
результативного показателя за счет фактора b,

 — изменение
результативного показателя  за счет фактора c.

Алгебраическая сумма влияния факторов обязательно
должна быть равна общему приросту результативного показателя:

 .

Отсутствие такого равенства свидетельствует о
допущенных ошиб­ках в расчетах.

Количество услов­ных величин результативного
показателя на единицу меньше числа факторов.

Используя способ цепной подстановки, необходимо знать
прави­ла последовательности расчетов: в первую очередь нужно учитывать
изменение количественных, а затем качественных показателей. Если же имеется
несколько количественных и несколько качественных по­казателей, то сначала
следует изменить величину факторов первого уровня подчинения, а потом — более
низкого. Применение способа цепной подстановки требу­ет знания взаимосвязи
факторов, их соподчиненности, умения пра­вильно их классифицировать и
систематизировать.

3.2. Способ абсолютных разниц

Данный способ применяется для расчета влияния факторов
на прирост результативного показателя в детерминированном анализе, но только в
мультипликативных моделях и моделях мультипликативно-аддитивного типа. При его
использовании величина влияния факторов рассчитыва­ется умножением абсолютного
прироста значения исследуемого фак­тора на базовую величину факторов, которые
находятся справа от него, и на фактическую величину факторов отчетного периода,
рас­положенных слева от него в модели.

Алгоритм расчета влияния факторов для
мультипликативной трехфакторной модели:

.

 — значение
результативного показателя в базовом периоде,

 — изменение
результативного показателя за счет фактора а,

— изменение
результативного показателя за счет фактора b,

 — изменение
результативного показателя  за счет фактора c,

 — значение
результативного показателя в отчетном периоде,

 — общее изменение
(абсолютное) результативного показателя.

Здесь также необходимо следить за тем, чтобы
алгебраичес­кая сумма прироста результативного показателя за счет отдельных
факторов равнялась его общему приросту:

 .

Рассмотрим алгоритм расчета факторов в моделях
мультипликативно-аддитивного вида. Для примера возьмем трехфактор­ную модель:

,

 ,

 ,

 ,

 .

3.3. Способ относительных разниц

Данный способ применяется для измерения влияния
факторов на прирост результативного показателя только в мультипликативных
моделях. Здесь используются относительные приросты факторных показателей,
выраженные в виде коэффициентов или процентов.

Рассмотрим методику расчета влияния факторов этим
способом для мультипликативных моделей типа:

.

Изменение результативного показателя определяется
следующим образом:

 ,

 ,

 .

То есть для расчета влияния первого фактора необходимо
базовую величину результативного показателя умножить на относительный прирост
первого фактора, выраженного в виде де­сятичной дроби.

Чтобы рассчитать влияние второго фактора, нужно к базовой
ве­личине результативного показателя прибавить его изменение за счет первого
фактора и затем полученную сумму умножить на относитель­ный прирост второго
фактора.

Влияние третьего фактора определяется аналогично: к
базовой величине результативного показателя необходимо прибавить его при­рост
за счет первого и второго факторов и полученную сумму умно­жить на
относительный прирост третьего фактора и т.д.   

3.4. Способы пропорционального деления и
долевого участия

Данный способ применяется для измерения влияния
факторов на прирост результативного показателя в моделях аддитивного и
кратно-аддитивного типа.

1. Способ пропорционального деления

Рассмотрим одноуровневую модель типа у = а+b+с.

Расчет проводится следующим образом:

 ,

 ,

 .

  В моделях кратно-аддитивного вида сначала необходимо
спо­собом цепной подстановки определить, насколько изменился ре­зультативный
показатель за счет числителя и знаменателя, а затем рассчитать влияние факторов
второго порядка способом пропорци­онального деления по приведенным алгоритмам.

2. Способ долевого участия

  Сначала определяется доля каждого фак­тора в общей
сумме их приростов, которая затем умножается на об­щий прирост результативного
показателя:

 ,

 ,

 .

3.5. Интегральный способ

Данный способ применяется для измерения влияния
факторов в мультипликативных, кратных и кратно-аддитивных моделях. Исполь­зование
этого способа позволяет получать более точные результаты расчета влияния
факторов по сравнению со способами цепной под­становки, абсолютных и
относительных разниц, поскольку дополни­тельный прирост результативного
показателя от взаимодействия фак­торов присоединяется не к последнему фактору,
а делится поровну между ними.

Рассмотрим алгоритмы расчетов влияния факторов для
разных моделей.

1.                     
Мультипликативная
модель

 ,

 ,

 .

2.                     
Кратная модель

 ,

 ,

 .

3.                     
Кратно-аддитивная
модель

 ,

 ,

 ,

 .

3.6. Способ логарифмирования

Данный способ применяется для измерения влияния
факторов в мультипликативных моделях. Дополнительный прирост от взаимодействия
факторов распределяется поровну между ними, то с помощью логарифмирования
результат совместного дей­ствия факторов распределяется пропорционально доли
изолирован­ного влияния каждого фактора на уровень результативного показате­ля.
При логарифмировании ис­пользуются не абсолютные приросты показателей, а
индексы их рос­та (снижения).

Рассмотрим трехфакторную модель:

 .

Влияние данных факторов определяется следующим
образом:

 ,

 ,

 .

Из формул следует, что общий прирост результативного
показа­теля распределяется по факторам пропорционально отношениям ло­гарифмов
факторных индексов к логарифму результативного пока­зателя. И не имеет
значения, какой логарифм используется ­натуральный или десятичный.

Метод статистических уравнений зависимостей

Назначение сервиса . С помощью сервиса можно найти следующие показатели:

• уравнение однофакторной линейной связи, уравнение многофакторной линейной связи;
• коэффициент корреляции однофакторный, индекс корреляции (однофакторный и многофакторный), коэффициент устойчивости связи;

• Шаг №1
• Шаг №2
• Видеоинструкция

Пример . Известны следующие данные об удельном весе пашни, лугов и пастбищ в сельскохозяйственных угодьях и уровне рентабельности производства сельскохозяйственной продукции по КСП административных районов области за год.
Определите:
Параметры и критерии метода статистических уравнений зависимостей:
а) параметры уравнений зависимости для каждого фактора; отразите их на графиках;
б) коэффициент и индекс корреляции;
в) сумму минимальных отклонений между теоретическими и эмпирическими значениями результативного признака;
г) коэффициент устойчивости связи для каждого фактора;
д) параметры уравнения множественной зависимости и удельный вес влияния каждого из факторов на результативный признак.
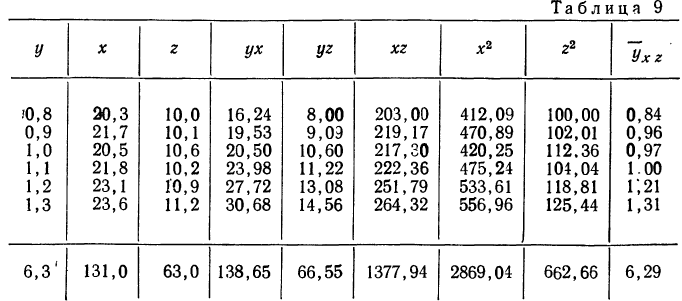
Нормативные уровни факторов и результативного показателя:
а) нормативный уровень результативного показателя (уровня рентабельности) при изменении уровня каждого из факторов на единицу.
б) нормативные уровни факторов для обеспечения изменения результативного показателя (уровня рентабельности) на единицу.

Корреляция — определение и вычисление с примерами решения

Содержание:

Понятие о корреляции:

Марксистская философия учит, что каждое явление природы и общества не возникает само по себе, отдельно от других, а находится в связи с другими явлениями, причем каждое из них представляет собой единство составляющих его частей и свойств. Для того чтобы познать какое-либо явление, необходимо изучить его не только во всех сложных взаимоотношениях с окружающими явлениями-факторами, но также во взаимосвязи всех его сторон.

Если всеобщая связь и взаимозависимость явлений составляют один из наиболее общих законов, то основной задачей науки является изучение этой взаимосвязи.

В математической статистике взаимосвязь явлений изучается методом корреляции. Термин корреляция происходит от английского слова correlation — соотношение, соответствие. Особенность изучения связи явлений методом корреляции состоит в том, что нельзя изолировать влияние посторонних факторов либо потому, что эти факторы неизвестны, либо потому, что их изоляция невозможна. Поэтому метод корреляции применяется для того, чтобы при сложном взаимодействии посторонних влияний выяснить, какова была бы зависимость между результатом фактором, если бы посторонние факторы не изменялись и своим изменением не искажали основную зависимость. При этом небольшое число наблюдений не дает возможности обнаружить закономерность связи.

Первая задача корреляции заключается в выявлении на основе наблюдения над большим количеством фактов того, как изменяется в среднем результативный признак в связи с изменением данного фактора. Это изменение предполагает условие неизменности ряда других факторов, хотя искажающее влияние этих других факторов на самом деле имеет место. Вторая задача заключается в определении степени влияния искажающих факторов.

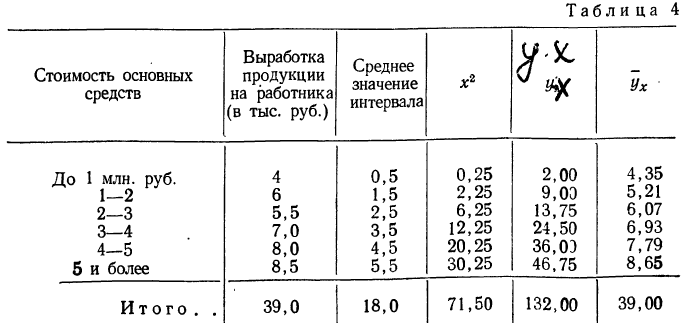
Первая задача решается нахождением уравнения связи.

Вторая задача решается при помощи различных показателей тесноты связи.

Такими показателями являются меры тесноты связи, найденные разными исследователями, а также коэффициент корреляции и корреляционное отношение.

Результативный и факториальный признаки

При изучении влияния одних признаков явлений на другие из цепи признаков, характеризующих данное явление, выделяются два признака — факториальный и результативный. Необходимо установить, какой из признаков является факториальным и какой результативным. В этом помогает прежде всего логический анализ.

Пример. Себестоимость промышленной продукции отдельного предприятия зависит от многих факторов, в том числе от объема продукции на данном предприятии. Себестоимость продукции выступает в этом случае как результативный признак, а объем продукции — как факториальный.

Другой пример. Чтобы судить о преимуществах крупных предприятий перед мелкими, рассмотрим, как увеличивается производительность труда рабочих крупных предприятий, и выявим зависимость производительности труда от увеличения размеров предприятия.

Таблица!

Группировка магазинов Министерства торговли по числу рабочих мест на 1 января 1960 г.1

Группы магазинов по числу рабочих мест Число магазинов Товарооборот в расчете на одного работника за квартал (в тыс. руб.)

Всего 68 375 117

Из них

с числом рабочих мест:

• с 1 19 893 109
• с 2 18 030 108
• с 3—4 16 508 108
• с 5—7 8 321 111
• с 8—10 2 868 118
• с 11 — 15 1 559 122
• с 16 и более 1 196 139
• J

Группировка показывает прямую зависимость производительности труда торговых работников, выражающуюся в товарообороте, приходящегося на одного работника, от размера магазина. Признак группировки — число рабочих мест — является факториальным, товарооборот — результативным признаком.

От размеров производства зависит также производительность оборудования, о чем свидетельствует следующая таблица:

Из таблицы ясно видна связь между размерами печей и их производительностью. Эта связь прямая: чем крупнее печь, тем она производительнее.

Однако зависимость результативного признака (суточного съема стали) от факториального носит не обязательный характер. Если в общей массе мы наблюдаем эту связь, то в отдельных группах бывают и отступления от общей закономерности. Такие отступления—характерная особенность статистической связи вообще, о которой будет рассказано ниже.

Группировки позволяют выявить и зависимость нескольких результативных признаков от одного факториального. Рассмотрим табл. 3.

В этой таблице мы видим зависимость двух результативных признаков: товарооборота на одного работника и товарных запасов—от размеров магазинов. Зависимость товарооборота от размеров магазина прямая, а зависимость товарных остатков от размеров магазина — обратная. В первом случае она растет с ростом размеров магазина, во втором уменьшается. Однако то и другое благоприятно.

Графическое изображение связи

Графическое изображение изучаемых явлений позволяет не только установить наличие или отсутствие связи между ними, но и изучить характер этой связи, иначе говоря изучить форму связи и ее тесноту.

Имея перед собой числовые характеристики факториального и результативного признаков одного и того же явления, можно каждую пару чисел изобразить в виде точки на плоскости. Для этого на плоскости берем две взаимно перпендикулярные линии и образуем систему координат. В этой системе по оси абсцисс откладываем значения факториального признака, а по оси ординат— значения результативного признака. Каждая пара чисел дает при этом точку на плоскости координатного поля.

Возьмем, например, группировку магазинов по числу рабочих мест, данную на стр. 239, и будем откладывать число рабочих мест по горизонтальной оси (оси Ох), а товарооборот в расчете на одного работника — по вертикальной оси (оси Оу). Будем иметь ряд точек, соединив которые получим ломаную линию, которая называется ломаной регрессии (см. график 1).

Как видно из графика, с ростом числа рабочих мест в магазине растет и товарооборот, приходящийся на одного работника, что говорит о связи между этими признаками, причем связи прямой. График подчеркивает эту зависимость ходом ломаной линии из нижнего угла в верхний правый угол.

Такого же рода зависимость будем наблюдать на графике 2, изучая связь между величиной мартеновских печей по площади пода и среднесуточным съемом стали с 1 пода. Как и в предыдущем примере, факториальный признак — величину площади пода — будем откладывать на оси абсцисс, а результативный — среднесуточный съем стали с 1 пода — на оси ординат.

Здесь также ясно выраженная прямая зависимость между результативным и факториальным признаками.

По-другому будет выглядеть график зависимости товарных запасов от размера товарооборота магазина.

Здесь мы наблюдаем ярко выраженную обратную связь между признаками: падение товарных запасов сопровождается ростом размера магазина по товарообороту.

Графический метод наглядно иллюстрирует зависимость, выявленную группировкой. Недостаток графического метода изучения связи заключается в том, что он позволяет выявить связь лишь между двумя признаками.

Функциональные и статистические связи

До сих пор говорилось о связях между явлениями и их признаками без объяснения формы и степени этих связей. В приведенных примерах связи носят логически обоснованный характер, но числовое выражение этих связей говорит о том, что они проявляются не всегда одинаково. В определенных случаях имеются отступления от наблюдаемых общих закономерностей. В приведенной на стр. 240 таблице о среднесуточном съеме стали с 1 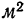пода печи наблюдается зависимость съема стали от размера печи по площади пода, но эта зависимость за 1955 г. искажена показателями 5-й группы, где съем стали значительно ниже, чем в 4-й группе. Если бы рассматривалась при этом каждая печь в отдельности, то это несоответствие установленному правилу зависимости проявлялось бы неоднократно. Но средние величины съема стали, вычисленные на основании данных довольно большого числа печей в группе, говорят о явно выраженной зависимости. Связи между явлениями, или их признаками. проявляющиеся в изменении в зависимости от одного признака характеристик распределения (из которых главная — средняя) другого признака, называются связями статистическими.

Статистические связи характеризуются тем, что в них результативный признак не полностью определяется влиянием признака факториального. Это влияние проявляется лишь в среднем, а в отдельных случаях получаются результаты, даже противоречащие установленной связи.

В отличие от статистических связей связи функциональные характеризуются тем, что при таких связях факториальный признак полностью определяет величину результативного признака.

Функциональные связи почти не встречаются в явлениях общественной жизни, отличающихся сложностью и многообразием существующих и проявляющихся взаимосвязей. Но во многих явлениях в основе статистических связей лежат функциональные связи. Связь функциональная может показывать зависимость между результативным признаком и несколькими аргументами. Так, площадь прямоугольника зависит от длины его двух сторон, путь, проходимый телом, зависит от скорости его движения и времени движения и т. д.

Уравнение связи

Наблюдая статистическую связь между двумя признаками, математическая статистика стремится придать этой связи форму функциональной, т. е. связи, выражаемой при помощи математической функции.

На помощь приходит ее графическое изображение при отыскании нужной функции связи. При этом необходимо стремиться найти такую функцию, которая давала бы наименьшее отклонение от полученных при наблюдении значений их признаков, которая выражала бы основную зависимость, проявляющуюся в эмпирическом материале. Уравнение этой функции будет уравнением связи между результативным и факториальным признаками.

Уравнение связи находится с помощью способа наименьших квадратов, который требует, чтобы сумма квадратов отклонений эмпирических значений от значений, получаемых на основании уравнения связи, была минимальной.

Применение способа наименьших квадратов позволяет находить параметры уравнения связи при помощи решения системы так называемых нормальных уравнений, различных для связи каждого вида.

Чтобы отметить, что зависимость между двумя признаками выражается в среднем, значения результативного признака, найденные по уравнению связи, обозначаются

Зная уравнение связи, можно вычислить заранее среднее значение результативного признака, когда значение факториального признака известно. Таким образом, уравнение связи является методом обобщения наблюдаемых статистических связей, методом их изучения.

Применение той или иной функции в качестве уравнения связи разграничивает связи по их форме: линейную связь и криволинейную связь (параболическую, гиперболическую и др.).

Рассмотрим уравнения связи для зависимостей от одного признака при разных формах связи (линейной, криволинейной параболической, гиперболической) и для множественной связи.

Линейная зависимость

Уравнение связи как уравнение прямой 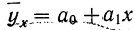применяется в случае равномерного нарастания результативного признака с увеличением признака факториального. Такая зависимость будет зависимостью линейной (прямолинейной).

Параметры уравнения прямой линии 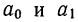находятся путем решения системы нормальных уравнений, получаемых по способу наименьших квадратов:

где n — число полученных при наблюдении пар взаимосвязанных величин; — сумма значений факториального признака;

— сумма квадратов значений факториального признака;

— сумма значений результативного признака; — сумма произведений значений факториального признака на значения результативного признака.

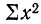
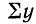
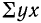
Примером расчета параметров уравнения и средних значений результативного признака 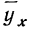может служить следующая таблица, являющаяся результатом группировки по факториальному признаку и подсчета средних по результативному признаку.

Группировка предприятий по стоимости основных средств и подсчет сумм необходимы для уравнения связи.

Из таблицы находим: 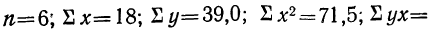132,0. Строим систему двух уравнений с двумя неизвестными:

Поделив каждый член в обоих уравнениях на коэффициенты при получим:

Вычтем из второго уравнения первое: Подставив значения в первое уравнение найдем

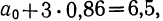
Уравнение связи примет вид: 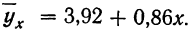Подставив в это уравнение соответствующие х, получим значения результативного признака, отражающие среднюю зависимость у от х в виде корреляционной зависимости.

Заметим, что суммы, исчисленные по уравнению и фактические, равны между собой. Изображение фактических и вычисленных значений на графике 4 показывает, что уравнение связи отображает наблюденную зависимость в среднем.

Параболическая зависимость

Параболическая зависимость, выражаемая уравнением параболы 2-го порядка 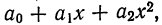имеет место при ускоренном возрастании или убывании результативного признака в сочетании с равномерным возрастанием факториального признака.

Параметры уравнения параболы 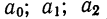вычисляются путем решения системы 3 нормальных уравнений:

Возьмем для примера зависимость месячного выпуска продукции (у) от величины стоимости основных средств (х). Оба показателя округлены до миллионов рублей. Расчеты необходимых сумм приведем в таблице 5.

По данным таблицы, составляем систему уравнений:

После деления всех уравнений на коэффициенты при 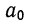получим:

Вычтя из второго уравнения первое и из третьего второе, получим два новых уравнения с двумя неизвестными:

Полученные уравнения снова разделим на коэффициенты при

Следовательно,

Запишем уравнение параболы, выражающей связь между х и у.

Графическое сопоставление опытных данных и данных расчета (см. график 5) показывает почти полное совпадение хода обеих линий, что говорит о хорошем воспроизведении опытных данных расчетными средними значениями результативного признака.

В практике изучения связи между признаками, кроме параболы 2-го порядка, применяются параболы и более высоких порядков. Чем выше порядок параболы, тем точнее он воспроизводит опытные данные.

Если уравнение связи представляет собой параболу 3-го порядка 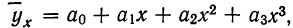то система нормальных уравнений примет вид:

Имея соответствующие хну, можем составить Дополнительную расчетную таблицу по следующей схеме:

которая используется для нахождения нужных сумм. Решив систему 4 уравнений, найдем параметры 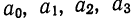и, следовательно, уравнение связи.

Уравнение гиперболы

Обратная связь указывает на убывание результативного признака при возрастании факториального. Такова линейная связь при отрицательном значении 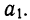В ряде других случаев обратная связь может быть выражена уравнением гиперболы

Параметры уравнения гиперболы 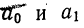находятся из системы нормальных уравнений:

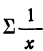
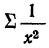
где — сумма величин, обратных значениям факториального признака, а — сумма их квадратов.

Примером расчета обратной связи по гиперболе может служить следующая таблица:

Составив по данным таблицы систему уравнений и разделив каждый член обоих уравнений на коэффициенты при а, получим:

Находим вычитанием из второго уравнения первого величину

Подставив вместо 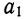его значение, получим

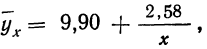
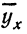
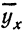
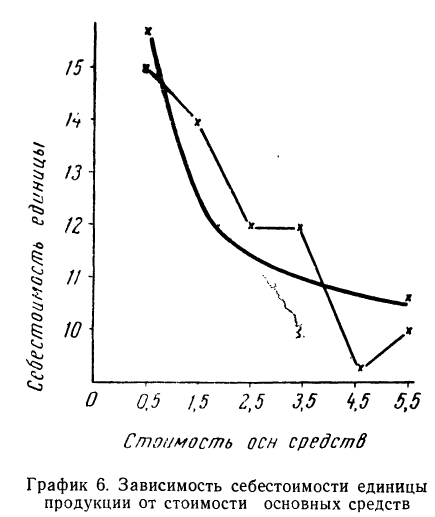
Запишем уравнение связи в общем виде затем, подставив каждое значение х в уравнение, находим по любой строке таблицы. Строим ломаную по парам х и у и кривую по х и . Ломаная и кривая очень близки друг к другу.

Корреляционная таблица

При большом объеме наблюдений, когда число взаимосвязанных пар велико, парные данные легко могут быть расположены в корреляционной таблице, являющейся наиболее удобной формой представления значительного количества пар чисел.

В корреляционной таблице один признак располагается в строках, а другой — в колонка таблицы. Число, расположенное в клетке на пересечении графы и колонки, показывает, как часто встречается данное значение результативного признака в сочетании с данным значением факториального признака.

Для простоты расчета возьмем небольшое число наблюдений на 20 предприятиях за средней месячной выработкой продукции на одного рабочего (тыс. руб. — у) и за стоимостью основных производственных средств (млн. руб. — х).

В обычной парной таблице эти сведения располагаются так:

Сведем эти данные в корреляционную таблицу.

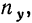
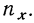
Итоги строк у показывают частоту признака итоги граф х — частоту признака Числа, стоящие в клетках корреляционной таблицы, являются частотами, относящимися к обоим признакам и обозначаются

Корреляционная таблица даже при поверхностном знакомстве дает общее представление о прямой и обратной связи. Если частоты расположены по диагонали вниз направо, то связь между признаками прямая (при увеличивающихся значениях признака в строках и графах). Если же частоты расположены по диагонали вверх направо, то связь обратная.

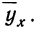
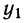
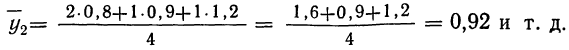
Для предварительного суждения о связи по корреляционной таблице можно для каждого столбца рассчитать средние значения Так, в первом столбце х = 9,9, а имеет лишь одно значение, равное 0,8. Найдем среднее значение для второго столбца. Оно будет равно:

Следовательно, при 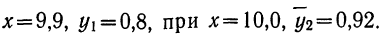Выпишем все значения х и соответствующие им

Зависимость, выраженная в таблице, более ярко и убедительно выступит в «ломаной регрессии», когда каждую пару чисел нанесем на график (см. график 7).

По корреляционной таблице можно вести расчеты параметров уравнения связи, как уравнения прямой, так и уравнений параболы и гиперболы. При этом необходимо учитывать, что сочетание каждой пары значений может встречаться не один, а несколько раз. Сами значения хну необходимо взвешивать, т. е. умножать на соответствующие частоты. Для самого признака х частота будет обозначаться для признака Частоту сочетаний обозначим

Ввиду сказанного мы можем систему нормальных уравнений написать так, чтобы были учтены веса. Тогда для линейной зависимости система нормальных уравнений примет вид:

где N — число произведенных наблюдений (число пар). В приведенной корреляционной таблице N = 20. 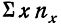будет суммой произведений соответствующих х на их частоты. В данной таблице эта сумма составит:

9,9 +10,0 • 4 +10,1 • 4 + 10,2 • 4 +10,3 • 1 +10,4 • 3 +10,5 • 3 = 204.

—сумма произведений у на соответствующие частоты. В нашем примере она равна:

включает сумму произведений всех х на у и на для тех клеток корреляционной таблицы, в которых записаны частоты. Рассчитаем суммы произведений для 1-й и 2-й строки

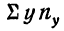
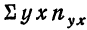
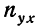
Нетрудно заметить, что в каждой строке у повторяется столько раз, сколько раз мы его суммируем, а, следовательно, у можно вынести за скобку.

• Для 1-й строки: 0,8 (9,9 • 1 +10,0 • 2) =23,92.
• Для 2-й строки:

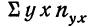
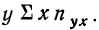
Следовательно, сумма произведений может быть записана при постоянном у, как Заметим, что сумма произведений может быть записана и рассчитана как произведение

Продолжим расчет для последующих строк.

Общая сумма по всем строкам

Система нормальных уравнений может быть записана по результатам подсчета в таком виде:

Для расчета параметров уравнения линейной связи делим каждое из уравнений на коэффициенты при

Уравнение связи 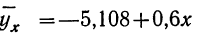определяет среднюю зависимость выработки рабочего от стоимости основных средств. Вычислительная работа облегчается, если в самой корреляционной таблице путем записи дополнительных граф и строк производить нужные подсчеты для решения системы уравнений.

Число наблюдений N может быть подсчитано и по столбцу как его сумма. Она равна итогу по строке Для определения необходимо ввести новую строку Итог этой строки и дает искомую сумму.

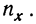
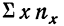
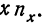
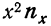
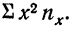
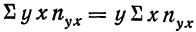
Следующая дополнительная строка представляет возможность определить Далее, и может быть определена на основе расчета двух дополнительных граф:

В корреляционной таблице (см. табл. в последних строках дается расчет для построения ломаной регрессии — для построения прямой (см. график 7).

Корреляционная таблица позволяет вычислять уравнение связи для любой формы: прямой, параболы, гиперболы и др. Однако в подобной таблице видна зависимость результативного признака лишь от одного факториального.

Зависимость результативного признака от двух или более факториальных признаков носит название множественной связи.

Множественная связь

Исследование зависимости результативного признака от двух или нескольких факториальных признаков возможно при помощи уравнения множественной связи.

В простейшем уравнении множественной связи предполагается, что зависимость между признаками линейная. Сначала рассмотрим линейную зависимость результативного признака (у) от двух факториальных (х, z). Уравнение связи в этом случае выразится формулой 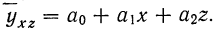Параметры этого уравнения находятся при решении системы нормальных уравнений, получаемых для способа наименьших квадратов

где п — число одновременных наблюдений по трем признакам;

—суммы соответствующих значений по этим признакам.

Все расчеты удобно сосредоточить в специальной таблице, как это делается в приводимом ниже примере.

Рассмотрим зависимость средней урожайности ячменя (у) на равных участках от количества внесенных минеральных удобрений (х) и количества выпавших в период цветения осадков (z).

Средняя урожайность исчислялась по участкам с равным количеством внесенных удобрений и с равным количеством выпавших осадков.

Пользуясь данными таблицы, составляем систему трех уравнений:

Поделив все члены уравнений на коэффициенты при получим:

Вычитая из второго уравнения сначала первое, а затем третье, получим 2 уравнения с двумя неизвестными:

Делим каждый член обоих уравнений на коэффициенты при

Уравнение связи, определяющее зависимость результативного признака (у) от двух факториальных

Вычислив по этому уравнению при соответствующих х и z величины замечаем, что суммы опытных данных (y) и расчетных данных совпадают, а отдельные значения их мало отличаются друг от друга.

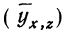
Найдем уравнение связи между урожайностью пшеницы на Безенчукской опытной станции и тремя факторами (х, z, v).

Статистические данные, полученные в результате наблюдения, и расчеты представлены в табл. 10, откуда возьмем необходимые данные для составления системы нормальных уравнений:

Следовательно,, корреляционное уравнение будет:

Расширив число факториальных признаков, можно найти уравнение множественной связи для 4, 5, 6 и т. д. признаков. При этом необходимо брать только такие признаки, которые оказывают существенное влияние на величину результативного признака, ибо учет несущественных, второстепенных признаков лишь увеличивает расчетную работу при нахождении уравнения связи, а не приближает к более полному изучению связи.

Если число факториальных признаков возрастает, возрастает и число членов уравнения связи. Так, для трех факториальных признаков линейное уравнение связи будет записано формулой:

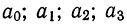
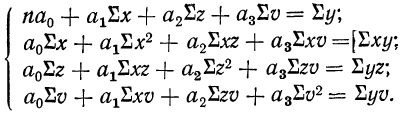
где параметры уравнения находятся путем решения системы четырех нормальных уравнений:

Построив соответствующую таблицу, получим в ней необходимые суммарные данные для приведенной системы уравнений (см. табл. 10).

Мерой существенности влияния того или иного факториального признака на результативный являются показатели тесноты связи.

В настоящем издании мы рассмотрим эмпирические меры тесноты связи, полученные разными исследователями, и меры тесноты связи, основанные на измерении вариации.

Эмпирические меры тесноты связи

Эмпирические меры тесноты связи позволяют оценить степень связи между явлениями или факторами, находящимися в зависимости один от другого. Эмпирические меры получены различными исследователями, занимавшимися статистической обработкой фактического материала. Они получены ранее, чем был открыт метод корреляции. Практическое пользование эмпирическими показателями довольно удобно.

К эмпирическим мерам тесноты относятся:

• а) коэффициент ассоциации:
• б) коэффициенты взаимной напряженности;
• в) коэффициент Фехнера;
• Г) коэффициент корреляции рангов;

Рассмотрим каждый из них.

а) Коэффициент ассоциации. Коэффициент ассоциации как мера тесноты связи применяется для изучения связи двух качественных признаков, состоящих только из двух групп. Для его вычисления строится четырехклеточная таблица корреляции, которая выражает связь между двумя явлениями, каждое из которых, в свою очередь, должно быть альтернативным, т. е. состоящим только из двух видов, качественно отличных друг от друга. Например, при изучении зависимости урожая от количества внесенных в почву удобрений выделяем по урожайности и по количеству внесенных удобрений лишь по две группы. При этом условии можно построить следующую четырехклеточную таблицу.

Числа, стоящие на пересечении строк и граф — a,b,c,d, показывают, сколько участков встречается с тем и другим количеством удобрений, внесенным в почву, с той и другой урожайностью.

Мера тесноты связи — коэффициент ассоциации — исчисляется по формуле:

Заполнив клетки конкретными числовыми данными, получим следующую четырехклеточную таблицу, где числа, стоящие в клетках, — гектары посевов.

Коэффициент ассоциации равен: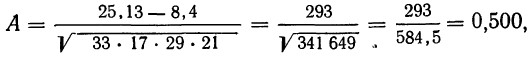
что говорит о достаточно тесной прямой связи между урожайностью и степенью удобрения почв.

Коэффициент ассоциации может иметь и отрицательные значения, когда ad

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Теоретические и прикладные аспекты применения методов статистических уравнений зависимостей и комплексных статистических коэффициентов

д. э.н., профессор Хмельницкого университета управления и права

ТЕОРЕТИЧЕСКИЕ И ПРИКЛАДНЫЕ АСПЕКТЫ ПРИМЕНЕНИЯ МЕТОДОВ СТАТИСТИЧЕСКИХ УРАВНЕНИЙ ЗАВИСИМОСТЕЙ И КОМПЛЕКСНЫХ СТАТИСТИЧЕСКИХ КОЭФФИЦИЕНТОВ

1. Метод статистических уравнений зависимостей

Для изучения зависимостей социально-экономических явлений можно использовать метод статистических уравнений зависимостей, расчет параметров которых основывается на определении коэффициентов сравнения факторных и результативных признаков путем отношения отдельных значений одноименного признака к его минимальному или максимальному уровню[1] 2.

Коэффициенты сравнения показывают степень изменения (увеличения или уменьшения) величины признака по отношению к принятой базе сравнения. При увеличении значений признака коэффициенты сравнения исчисляют от минимального уровня, а при уменьшении — от максимального. На основе этих коэффициентов определяется параметр уравнения зависимости, представляющий собой отношение суммы отклонений от единицы, вычисленных коэффициентов сравнения результативного и факторного признаков.

В отличие от известных в статистике коэффициентов эластичности параметр уравнения зависимости позволяет учесть влияние на результативный признак не только одного фактора, но и совокупного действия многих факторов.

Применение статистических уравнений зависимости для анализа взаимосвязей социально-экономических явлений требует [2]:

1) качественного анализа исследуемых факторных и результативных признаков;

2) однородности изучаемого явления;

3) оценки устойчивости связи между явлениями.

Первое требование предусматривает наличие логической зависимости между факторными и результативными признаками и использование прямых показателей, позволяющих проводить нормативные расчеты.

Второе требование предполагает исключение из расчетов значений признака (минимальных или максимальных), значительно отличающихся (в два-три раза) соответственно от следующей за минимальной или предшествующей максимальной величины.

Оценка устойчивой или неустойчивой связи между факторным и результативным признаком проводится по шкале зависимостей на основе расчета коэффициента устойчивости связи. Исходными данными для расчета этого коэффициента служат табличные модели определения параметров уравнений зависимости.

Статистические уравнения зависимостей выражают различные виды (однофакторные и многофакторные) и направления связи (линейную, криволинейную и др.). Для расчета параметров уравнений зависимостей целесообразно использовать систему формул, например [2]:

1.Однофакторная линейная связь

а) увеличении факторного и результативного признаков

Уx = Уmin

б) уменьшении факторного и результативного признаков

Уx = Уmax

1.2. Обратная при:

а) увеличении факторного признака и уменьшении результативного

Уx = Уmах

б) уменьшении факторного признака и увеличении результативного

Уx = Уmіп

2. Многофакторная линейная связь

а) при увеличении факторных и результативного признаков

Уxz = Уmin.

б) уменьшении факторных и результативного признаков

Уxz = Уmax.

а) увеличении факторных признаков и уменьшении результативного

Уxz = Уmax

б) уменьшении факторных признаков и увеличении результативного

Уxz = Уmin

3. Комбинационная при:

а) прямой зависимости Y от X и обратной зависимости Y от Z :

Уxz = Уmin

б) обратной зависимости Y от X и прямой зависимости Y от Z :

Уxz = Уmin

Расчет коэффициентов сравнения результативного признака осуществляется с учетом изменения его значений:

а) при увеличении ;

б) при уменьшении 1- .

Для расчета параметров зависимости, оценки тесноты и устойчивости связи используем следующие формулы:

b = ;

B =.

Коэффициент корреляции однофакторный

.

Индекс корреляции (однофакторный и многофакторный)

.

Коэффициент устойчивости связи

K = 1-,

Шкала оценки зависимостей

Коэффициент устойчивости связи

1. Неустойчивая связь

2. Устойчивая связь

Ух, Ухz — уравнения зависимостей однофакторной и многофакторной связи;

Уi— эмпирические значения результативного признака;

Уmin, Уmax — эмпирические значения результативного признака (минимальные и максимальные);

Xi, Zi — эмпирические значения факторных признаков;

Хmin, Zmax — эмпирические значения факторных признаков (минимальные и максимальные);

Хо, Zo — значения факторных признаков, соответствующих максимальному значению результативного признака Уmax при прямой параболической зависимости, а при обратной параболической зависимости — минимальному его значению Уmin;

d — знак отклонений;

b1, b2 — параметры уравнений для отдельных факторных признаков;

В — совокупный параметр уравнения множественной зависимости;

ryx — коэффициент корреляции однофакторной связи;

R — индекс корреляции, совместный для всех видов связи;

dx, dy — размер отклонений коэффициентов сравнения факторного и результативного признаков;

dуx — размер отклонений коэффициентов сравнения теоретических значений результативного признака.

Проведение эконометрических расчетов предлагаем осуществлять по следующим формулам:

Нормативные уровни факторов при нормативной, плановой или заданной величине результативного признака

1.Разность коэффициента сравнения результативного признака

при увеличении значений результативного признака

;

при уменьшении значений результативного признака

.

2.Нормативные уровни факторов

Xн= ;

Xн= .

Нормативные уровни результативного признака при известных (нормативных, плановых или заданных) величинах факторов:

1. Разность коэффициента сравнения факторных признаков

а) при увеличении значений результативного признака

;

;

б) при уменьшении значений результативного признака

;

.

2. Размер отклонений коэффициентов сравнения

3. Нормативные уровни результативного признака

а) при увеличении значений результативного признака

б) при уменьшении значений результативного признака

Расчеты параметров статистических уравнений зависимости, показателей тесноты и устойчивости связи осуществляют с применением програмного обеспечения [2, 3].

Статистические уравнения зависимостей позволяют:

1) оценить взаимосвязь между факторными и результативными признаками при наличии малочисленной и многочисленной совокупности единиц наблюдения;

2) установить уровень и, соответственно, размер изменения результативного признака при изменении одного или многих факторов на единицу;

3) установить размер изменения факторных признаков при изменении результативного признака на единицу или же другую заданную величину (обратная задача);

4) определить нормативные уровни факторных признаков, формирующих планируемую, заданную или нормативную величину результативного признака;

5) установить интенсивность использования факторных признаков для достижения средней величины результативного признака путем сопоставления вычисленных оптимальных (нормативных) уровней факторных признаков с их фактическими средними значениями;

6) оценить устойчивость связи между факторными и результативными признаками. Это дает возможность отграничить устойчивую зависимость от неустойчивой;

7) определить средние темпы прироста (снижения) результативного признака в результате действия изучаемых факторов для каждого объекта исследования (организации, предприятия и т. п.);

построить графическое изображение исследуемой зависимости (однофакторной и многофакторной).

Для выполнения расчетов необходимо:

1) отобрать количественные показатели, характеризующие результаты работы организаций и предприятий;

2) вычислить по отобранным показателям средние и относительные величины, дающие качественную характеристику хозяйственно-финансовой деятельности;

3) определить форму (линейную, криволинейную) и направление связи (прямую и обратную) между факторными и результативными признаками;

4) определить параметры однофакторных и многофакторных уравнений зависимости, соответствующие форме и направлению связи;

5) установить сумму отклонений между эмпирическими (У) и теоретическими (Ух) значениями результативного признака;

6) используя модели определения параметров уравнений однофакторной и многофакторной зависимости, вычислить коэффициенты устойчивости связи.

Коэффициент устойчивости связи показывает степень влияния одного или многих факторов на результативный признак. Его вычисляют путем отношения разности отклонений коэффициентов сравнения эмпирических и теоретических значений результативного признака к сумме отклонений коэффициентов сравнения результативного признака с последующим вычитанием от единицы.

Критериями выбора вида уравнения зависимости являются:

1) наименьшая сумма линейных отклонений эмпирических значений результативного признака от его теоретических значений;

2) совпадение значений коэффициента и индекса корреляции (их различие не должно превышать 0,01).

Минимизация суммы отклонений эмпирических значений результативного признака от его теоретических значений при использовании компьютеров осуществляется автоматически перебором четырнадцати (прямой линии, гиперболы, параболы, логической функции) видов и направлений однофакторной связи с выбором наилучшего уравнения зависимости, обеспечивающего минимум суммы отклонений.

Модели расчета параметров статистических уравнений однофакторной зависимости соответствующих видов и направлений связи являются исходными для расчета показателей тесноты связи (коэффициента и индекса корреляции). Их расчет осуществляется как с целью оценки тесноты связи, так и для подтверждения правильности выбора типа уравнения зависимости.

2. Метод комплексных статистических коэффициентов

Эффективное обеспечение политической и экономической безопасности страны и конкурентоспособности хозяйствующих субъектов требует своевременной и объективной комплексной их оценки. Сложность такой оценки заключается в поиске обобщающего показателя социально-экономического развития, с помощью которого можно было бы рациональным способом объединить разнородные показатели в один — комплексный. Для решения этой задачи можно применить метод комплексных статистических коэффициентов [1].

Применение метода комплексных статистических коэффициентов предполагает расчет комплексного коэффициента весомости отклонений уровней абсолютных, относительных и средних показателей социально-экономического развития страны (регионов) и хозяйственно-финансовой деятельности предприятий (организаций) по следующим направлениям [3]:

1) комплексную оценку значимости отклонений абсолютных относительных и средних величин показателей статики и динамики, стандартизированных размахом вариации:

; (1)

2) комплексную оценку весомости отклонений на основе стандартизации уровней показателей от среднего значения по совокупности стран (регионов):

а) при положительном значении росте показателя:

(2)

б) при отрицательном значении росте показателя:

(3)

3) комплексную оценку весомости отклонений относительных величин выполнения задач, планов и нормативов:

. (4)

Выбор формул 1-3 комплексного статистического коэффициента зависит от:

1) формы выражения показателей исходных данных (абсолютные, относительные и средние величины или относительные величины выполнения задач планов или нормативов);

2) наличия в исходных данных соответствующих средних значений показателей по совокупности стран (регионов) или предприятий (организаций).

Обеспечение принципа объективности требует также полноты исходных данных.

Первая формула комплексного статистического коэффициента весомости отклонений абсолютных, относительных и средних величин показателей, стандартизированных размахом вариации применяется в случаях отсутствия средних значений показателей по совокупности стран (регионов) или предприятий (организаций), оценки устойчивости курса валют и т. п. Формула состоит из двух частей, одна из которых применяется для показателей-стимуляторов социально-экономического развития региона (например, прирост объема инвестиций), а другая — для дестимуляторов (например, прирост индекса потребительских цен) [2]:

, (1)

где Квj — коэффициент весомости отклонений значений показателей объекта исследования;

хіj — значение показателя социально-экономического развития страны (региона);

xmax i хmin — соответственно максимальное и минимальное значение показателя социального и экономического развития.

С уменьшением размера отклонений показателя социально-экономического развития в отдельных странах (регионах) от максимального его уровня (при положительном значении рост показателя), минимального уровня (при отрицательном значении рост показателя), в совокупности стран (регионов) комплексный коэффициент весомости отклонений уменьшается. Чем ниже этот коэффициент, тем выше уровень социально-экономического развития страны (региона), что свидетельствует также о высоком месте этого региона в их совокупности.

Применение второй и третьей формулы предусматривает определение рейтинга стран (регионов) по показателям, характеризующим результаты социально-экономического развития, путем расчета отклонений индивидуальных значений показателей от их средних уровней по совокупности последующим формулам [3]:

а) при положительном значении росте показателя:

(2)

б) при отрицательном значении росте показателя:

(3)

где — комплексный коэффициент весомости отклонений абсолютных, относительных и средних величин статики и динамики развития региона (на основе отклонений от средних значений);

— значение показателя социально-экономического развития региона;

— соответственно минимальное и максимальное значение показателя социально-экономического развития региона;

— среднее значение показателя социально-экономического развития по стране;

— значение показателя социально-экономического развития региона, соответственно меньше или равно и более от среднего значения по совокупности регионов.

Уровень весомости отдельных отклонений значений относительных величин интенсивности регионального развития, превышающие средний уровень по совокупности объектов исследования () при положительном значении росте показателя, а также если значение показателя меньше или равно среднему уровню — для показателей-дестимуляторов, возводятся в квадрат. Этим уменьшается значимость отклонений показателя, при положительном росте значений превышает средний по совокупности уровень, а также для отдельного объекта исследования по показателю-дестимулятору, значение которого меньше или равно среднему уровню.

Несмотря на то, что регионы формируют среднее значение показателей социально-экономического развития с разной степенью интенсивности (одни регионы имеют показатели выше средних, другие — ниже среднего уровня), в формулу расчета комплексного коэффициента заложен механизм, который предусматривает улучшение рейтинговой оценки за превышение регионом среднего уровня показателя в их совокупности. Расчеты комплексного коэффициента весомости отклонений от среднего уровня показателей по предлагаемым формулам свидетельствуют: что чем он ниже, тем выше уровень социально-экономического развития региона и является свидетельством высокого места этого региона в их совокупности.

Определение рейтинга объектов комплексной оценки по показателям, выраженными относительными величинами выполнения задания, плана или норматива, осуществляется по четвертой формуле:

(4)

Кв — комплексный коэффициент весомости отклонений показателей выполнения задания, плана или норматива региона;

— значение показателя социально-экономического развития региона;

хmax — максимальное значение показателя.

Уровень весомости отдельных отклонений значения процента выполнения задания или планового (нормативного) показателя хозяйственно-финансовой деятельности, превышает 100 % (),от максимального значения этого показателя в совокупности регионов возвышается к квадрату. Этим уменьшается значимость отклонений процента выполнения показателя, превышает 100% от его максимального значения в совокупности регионов по сравнению с весомостью отклонений, полученных разницей от 100 %.

С уменьшением размера отклонений показателя по отдельным регионам от 100 %, максимального значения показателя при перевыполнении задания, плана или норматива хmax>100 в совокупности регионов комплексный коэффициент весомости отклонений уменьшается. Чем ниже этот коэффициент, тем выше уровень эффективности организационно-управленческой деятельности, что свидетельствует о высоком месте этого региона среди других.

По тем показателям, рост значений которых имеет отрицательный эффект (например, прирост уровня безработицы), следует принять обратные величины выполнения задания, плана или норматива.

Выводы. Оценка уровня социально-экономического развития районов области и городов областного значения проводится аналогично с комплексной оценкой регионов страны с использованием системы показателей по результатам работы местных государственных администраций.

Для разграничения основных и дополнительных показателей можно применить метод статистических уравнений зависимостей, который позволяет определить степень устойчивого или неустойчивого взаимосвязи показателей. При этом основными показателями будут те, для которых наблюдается стойкая зависимость, а дополнительными — ее отсутствие.

Комплексная территориальная оценка методом комплексных статистических коэффициентов результатов социально-экономического развития стран (регионов) предусматривает также осуществление:

1) оценки абсолютных, средних и относительных показателей хозяйственно-финансовой деятельности предприятий, фирм, организаций;

2) оценки выполнения задач (планов) производства (поставки) продукции или услуг;

3) оценки равномерности выполнения заданий (планов) производства (поставки) продукции или услуг;

4) оценки устойчивости курса валют, акций и ценных бумаг.

Комплексная оценка эффективности организационной и производственно-хозяйственной деятельности является действенным средством управления. Она предусматривает выбор и совершенствование методов конструирования обобщающих оценок, а также их использования в практической работе органов государственной статистики, менеджеров и экономистов-аналитиков как на государственном, так и на региональном уровне.

1. Кулинич оценка факторов хозяйственной деятельности заготовительных организаций. – М.: Финансы и статистика, 1983. – 192 с.

2. Кулинич О. І. Теорія статистики: [підруч.] / О. І. Кулинич, Р. О. Кулинич. — [5–тє вид., перероб. і доп.]. — К.: Знання, 20 с.

3. Кулинич Р. О. Статистичні методи аналізу взаємозв’язку показників соціально-економічного розвитку: [монограф.]. — К.: Формат, 20 с.

[1]Относительные величины сравнения определяют соотношением уровней одноименных величин явления за один и тот же период или момент времени по различным объектам (территориям), один из которых принимается за базу сравнения. Их использование позволяет устранить несравнимость в проведении статистических расчетов показателей, выраженных разноименными величинами (кг, шт, %, денежном выражении и т. п.)