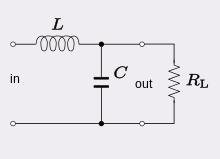
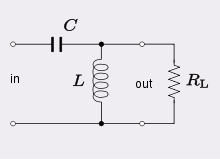
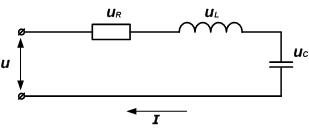
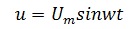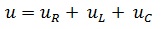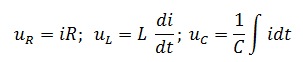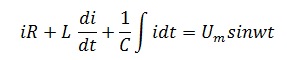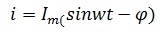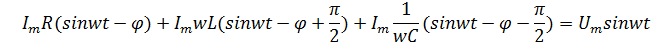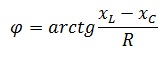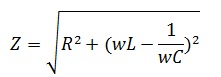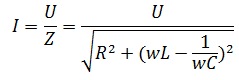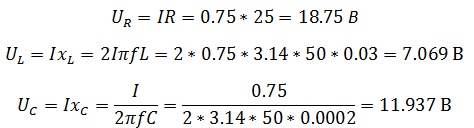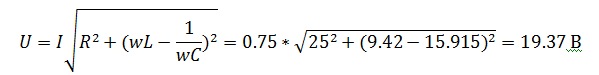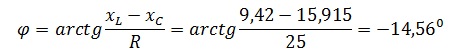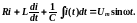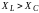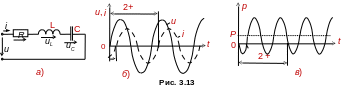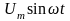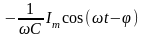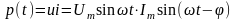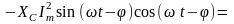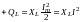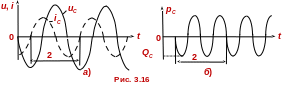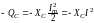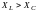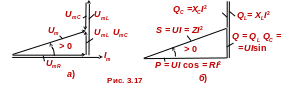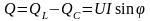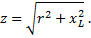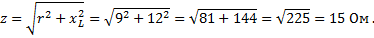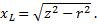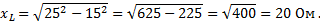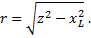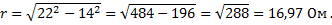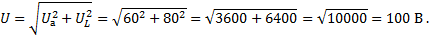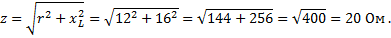Rlc цепь как найти ток - Исправление недочетов и поиск решений вместе с Examum.ru

Рассмотрим цепь, состоящую из последовательно соединенных резистора, конденсатора и катушки индуктивности.

Напряжение на зажимах цепи

или

где

Выполнив подстановку, получим

Подставим в последнее выражение ток в цепи, зная, что он равен

В итоге получим выражение

Из этого выражения можно увидеть сдвиг фаз каждого элемента. У резистора он отсутствует, то есть напряжение и ток совпадают по фазе, у катушки индуктивности напряжение опережает ток на угол π/2, а у конденсатора, напротив, отстает.

Сдвиг фаз RLС-цепи можно определить по формуле

Полное сопротивление RLС-цепи

Амплитудное значение тока

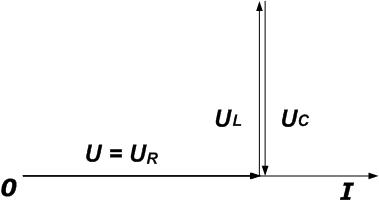
При построении векторной диаграммы RLC-цепи возможны три случая:

1 – Цепь носит активный характер, сдвиг фаз равен нулю, индуктивное и емкостное сопротивления равны. При этом в такой цепи наблюдается резонанс напряжений.

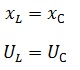
2 – Цепь носит индуктивный характер, в этом случае индуктивное сопротивление больше чем емкостное.

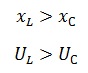
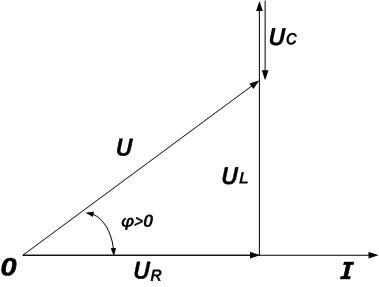
На векторной диаграмме, как правило, сначала откладывают вектор напряжения на катушке индуктивности, а затем из него вычетают напряжение на конденсаторе. После этого проводят вектор общего напряжения и определяют сдвиг фаз φ.

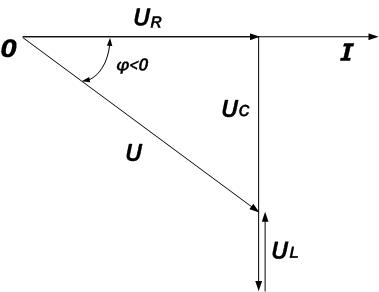
3 – Цепи носит емкостной характер, при этом емкостное сопротивление больше чем индуктивное.

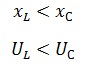
Построение векторной диаграммы выполняется аналогично цепи индуктивного характера, за тем исключением, что здесь сдвиг фаз отрицателен и вычитается индуктивное напряжение из напряжения на емкости.

Пример задачи

Цепь состоит из последовательно включенных резистора сопротивлением 25 Ом, конденсатора емкостью 200 мкФ и катушки индуктивности 30 мГн. Ток, протекающий в цепи, равен 0,75 А. Определите U,U_R,U_L,U_C,φ. Постройте векторную диаграмму и определите характер цепи.

Найдем напряжение на каждом из элементов

И общее в цепи

Сдвиг фаз равен

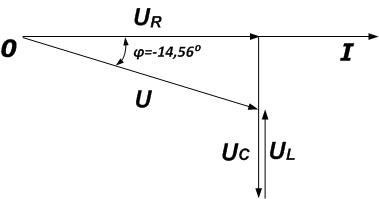
Векторная диаграмма

Из векторной диаграммы можно сделать вывод, что цепь носит емкостной характер.

Источник

A series RLC network (in order): a resistor, an inductor, and a capacitor

An RLC circuit is an electrical circuit consisting of a resistor (R), an inductor (L), and a capacitor (C), connected in series or in parallel. The name of the circuit is derived from the letters that are used to denote the constituent components of this circuit, where the sequence of the components may vary from RLC.

The circuit forms a harmonic oscillator for current, and resonates in a manner similar to an LC circuit. Introducing the resistor increases the decay of these oscillations, which is also known as damping. The resistor also reduces the peak resonant frequency. Some resistance is unavoidable even if a resistor is not specifically included as a component.

RLC circuits have many applications as oscillator circuits. Radio receivers and television sets use them for tuning to select a narrow frequency range from ambient radio waves. In this role, the circuit is often referred to as a tuned circuit. An RLC circuit can be used as a band-pass filter, band-stop filter, low-pass filter or high-pass filter. The tuning application, for instance, is an example of band-pass filtering. The RLC filter is described as a second-order circuit, meaning that any voltage or current in the circuit can be described by a second-order differential equation in circuit analysis.

The three circuit elements, R, L and C, can be combined in a number of different topologies. All three elements in series or all three elements in parallel are the simplest in concept and the most straightforward to analyse. There are, however, other arrangements, some with practical importance in real circuits. One issue often encountered is the need to take into account inductor resistance. Inductors are typically constructed from coils of wire, the resistance of which is not usually desirable, but it often has a significant effect on the circuit.

Basic concepts[edit]

Resonance[edit]

An important property of this circuit is its ability to resonate at a specific frequency, the resonance frequency, f₀. Frequencies are measured in units of hertz. In this article, angular frequency, ω₀, is used because it is more mathematically convenient. This is measured in radians per second. They are related to each other by a simple proportion,

${displaystyle omega _{0}=2pi f_{0},.}$

Resonance occurs because energy for this situation is stored in two different ways: in an electric field as the capacitor is charged and in a magnetic field as current flows through the inductor. Energy can be transferred from one to the other within the circuit and this can be oscillatory. A mechanical analogy is a weight suspended on a spring which will oscillate up and down when released. This is no passing metaphor; a weight on a spring is described by exactly the same second order differential equation as an RLC circuit and for all the properties of the one system there will be found an analogous property of the other. The mechanical property answering to the resistor in the circuit is friction in the spring–weight system. Friction will slowly bring any oscillation to a halt if there is no external force driving it. Likewise, the resistance in an RLC circuit will «damp» the oscillation, diminishing it with time if there is no driving AC power source in the circuit.

The resonant frequency is defined as the frequency at which the impedance of the circuit is at a minimum. Equivalently, it can be defined as the frequency at which the impedance is purely real (that is, purely resistive). This occurs because the impedances of the inductor and capacitor at resonant are equal but of opposite sign and cancel out. Circuits where L and C are in parallel rather than series actually have a maximum impedance rather than a minimum impedance. For this reason they are often described as antiresonators; it is still usual, however, to name the frequency at which this occurs as the resonant frequency.

Natural frequency[edit]

The resonance frequency is defined in terms of the impedance presented to a driving source. It is still possible for the circuit to carry on oscillating (for a time) after the driving source has been removed or it is subjected to a step in voltage (including a step down to zero). This is similar to the way that a tuning fork will carry on ringing after it has been struck, and the effect is often called ringing. This effect is the peak natural resonance frequency of the circuit and in general is not exactly the same as the driven resonance frequency, although the two will usually be quite close to each other. Various terms are used by different authors to distinguish the two, but resonance frequency unqualified usually means the driven resonance frequency. The driven frequency may be called the undamped resonance frequency or undamped natural frequency and the peak frequency may be called the damped resonance frequency or the damped natural frequency. The reason for this terminology is that the driven resonance frequency in a series or parallel resonant circuit has the value.^[1]

${displaystyle omega _{0}={frac {1}{sqrt {L,C~}}},~.}$

This is exactly the same as the resonance frequency of a lossless LC circuit – that is, one with no resistor present. The resonant frequency for a driven RLC circuit is the same as a circuit in which there is no damping, hence undamped resonant frequency. The resonant frequency peak amplitude, on the other hand, does depend on the value of the resistor and is described as the damped resonant frequency. A highly damped circuit will fail to resonate at all, when not driven. A circuit with a value of resistor that causes it to be just on the edge of ringing is called critically damped. Either side of critically damped are described as underdamped (ringing happens) and overdamped (ringing is suppressed).

Circuits with topologies more complex than straightforward series or parallel (some examples described later in the article) have a driven resonance frequency that deviates from ${displaystyle omega _{0}=1/{sqrt {L,C~}} }$ , and for those the undamped resonance frequency, damped resonance frequency and driven resonance frequency can all be different.

Damping[edit]

Damping is caused by the resistance in the circuit. It determines whether or not the circuit will resonate naturally (that is, without a driving source). Circuits that will resonate in this way are described as underdamped and those that will not are overdamped. Damping attenuation (symbol α) is measured in nepers per second. However, the unitless damping factor (symbol ζ, zeta) is often a more useful measure, which is related to α by

${displaystyle zeta ={frac {alpha }{ omega _{0} }} .}$

The special case of ζ = 1 is called critical damping and represents the case of a circuit that is just on the border of oscillation. It is the minimum damping that can be applied without causing oscillation.

Bandwidth[edit]

The resonance effect can be used for filtering, the rapid change in impedance near resonance can be used to pass or block signals close to the resonance frequency. Both band-pass and band-stop filters can be constructed and some filter circuits are shown later in the article. A key parameter in filter design is bandwidth. The bandwidth is measured between the cutoff frequencies, most frequently defined as the frequencies at which the power passed through the circuit has fallen to half the value passed at resonance. There are two of these half-power frequencies, one above, and one below the resonance frequency

${displaystyle Delta omega =omega _{2}-omega _{1},,}$

where Δω is the bandwidth, ω₁ is the lower half-power frequency and ω₂ is the upper half-power frequency. The bandwidth is related to attenuation by

where the units are radians per second and nepers per second respectively.^{[citation needed]} Other units may require a conversion factor. A more general measure of bandwidth is the fractional bandwidth, which expresses the bandwidth as a fraction of the resonance frequency and is given by

${displaystyle B_{mathrm {f} }={frac {Delta omega }{omega _{0}}},.}$

The fractional bandwidth is also often stated as a percentage. The damping of filter circuits is adjusted to result in the required bandwidth. A narrow band filter, such as a notch filter, requires low damping. A wide band filter requires high damping.

Q factor[edit]

The Q factor is a widespread measure used to characterise resonators. It is defined as the peak energy stored in the circuit divided by the average energy dissipated in it per radian at resonance. Low-Q circuits are therefore damped and lossy and high-Q circuits are underdamped and prone to amplitude extremes if driven at the resonant frequency.^[a]
Q is related to bandwidth; low-Q circuits are wide-band and high-Q circuits are narrow-band. In fact, it happens that Q is the inverse of fractional bandwidth

${displaystyle Q={frac {1}{,B_{mathrm {f} },}}={frac {omega _{text{o}}}{,operatorname {Delta } omega ,}};.}$

^[2]

Q factor is directly proportional to selectivity, as the Q factor depends inversely on bandwidth.

For a series resonant circuit (as shown below), the Q factor can be calculated as follows:^[2]

${displaystyle Q={frac {X}{,R;}}={frac {1}{,omega _{text{o}}R,C,}}={frac {,omega _{text{o}}L,}{R}}={frac {1}{,R;}}{sqrt {{frac {L}{,C,}},}}={frac {,Z_{text{o}},}{R;}};,}$

^[2]

where is the reactance either of or of at resonance, and ${displaystyle ,Z_{text{o}}equiv {sqrt {{frac {L}{,C,}},}};.}$

Scaled parameters[edit]

The parameters ζ, B_f, and Q are all scaled to ω₀. This means that circuits which have similar parameters share similar characteristics regardless of whether or not they are operating in the same frequency band.

The article next gives the analysis for the series RLC circuit in detail. Other configurations are not described in such detail, but the key differences from the series case are given. The general form of the differential equations given in the series circuit section are applicable to all second order circuits and can be used to describe the voltage or current in any element of each circuit.

Series circuit[edit]

Figure 1: RLC series circuit

V, the voltage source powering the circuit
I, the current admitted through the circuit
R, the effective resistance of the combined load, source, and components
L, the inductance of the inductor component
C, the capacitance of the capacitor component

In this circuit, the three components are all in series with the voltage source. The governing differential equation can be found by substituting into Kirchhoff’s voltage law (KVL) the constitutive equation for each of the three elements. From the KVL,

${displaystyle V_{mathrm {R} }+V_{mathrm {L} }+V_{mathrm {C} }=V(t),,}$

where V_R, V_L and V_C are the voltages across R, L, and C, respectively, and V(t) is the time-varying voltage from the source.

Substituting ${displaystyle V_{R}=R I(t),,}$ ${displaystyle ,V_{mathrm {L} }=L{frac {mathrm {d} I(t)}{mathrm {d} t}},}$ and ${displaystyle ,V_{mathrm {C} }=V(0)+{frac {1}{,C,}}int _{0}^{t}I(tau ),mathrm {d} tau ,}$ into the equation above yields:

${displaystyle RI(t)+L{frac {,mathrm {d} I(t),}{mathrm {d} t}}+V(0)+{frac {1}{,C,}}int _{0}^{t}I(tau ),mathrm {d} tau =V(t);.}$

For the case where the source is an unchanging voltage, taking the time derivative and dividing by L leads to the following second order differential equation:

${displaystyle {frac {d^{2}}{dt^{2}}}I(t)+{frac {R}{,L,}}{frac {mathrm {d} }{mathrm {d} t}}I(t)+{frac {1}{,L,C,}}I(t)=0;.}$

This can usefully be expressed in a more generally applicable form:

${displaystyle {frac {mathrm {d} ^{2}}{mathrm {d} t^{2}}}I(t)+2alpha {frac {mathrm {d} }{mathrm {d} t}}I(t)+omega _{0}^{2}I(t)=0;.}$

α and ω₀ are both in units of angular frequency. α is called the neper frequency, or attenuation, and is a measure of how fast the transient response of the circuit will die away after the stimulus has been removed. Neper occurs in the name because the units can also be considered to be nepers per second, neper being a logarithmic unit of attenuation. ω₀ is the angular resonance frequency.^[3]

For the case of the series RLC circuit these two parameters are given by:^[4]

${displaystyle {begin{aligned}alpha &={frac {R}{,2L,}}\omega _{0}&={frac {1}{,{sqrt {L,C,}},}};.end{aligned}}}$

A useful parameter is the damping factor, ζ, which is defined as the ratio of these two; although, sometimes ζ is not used, and α is referred to as damping factor instead; hence requiring careful specification of one’s use of that term.^[5]

${displaystyle zeta equiv {frac {alpha }{,omega _{0},}};.}$

In the case of the series RLC circuit, the damping factor is given by

${displaystyle zeta ={frac {,R,}{2}}{sqrt {{frac {C}{,L,}},}}={frac {1}{ 2Q }}~.}$

The value of the damping factor determines the type of transient that the circuit will exhibit.^[6]

Transient response[edit]

Plot showing underdamped and overdamped responses of a series RLC circuit to a voltage input step of 1 V. The critical damping plot is the bold red curve. The plots are normalised for L = 1, C = 1 and ω₀ = 1.

The differential equation has the characteristic equation,^[7]

${displaystyle s^{2}+2alpha s+omega _{0}^{2}=0,.}$

The roots of the equation in s-domain are,^[7]

${displaystyle {begin{aligned}s_{1}&=-alpha +{sqrt {alpha ^{2}-omega _{0}^{2},}}=-omega _{0}left(zeta -{sqrt {zeta ^{2}-1,}}right)={frac {-omega _{0}}{ zeta +{sqrt {zeta ^{2}-1 }} }} ,\s_{2}&=-alpha -{sqrt {alpha ^{2}-omega _{0}^{2},}}=-omega _{0}left(zeta +{sqrt {zeta ^{2}-1,}}right);.end{aligned}}}$

The general solution of the differential equation is an exponential in either root or a linear superposition of both,

${displaystyle I(t)=A_{1}e^{s_{1}t}+A_{2}e^{s_{2}t};.}$

The coefficients A₁ and A₂ are determined by the boundary conditions of the specific problem being analysed. That is, they are set by the values of the currents and voltages in the circuit at the onset of the transient and the presumed value they will settle to after infinite time.^[8] The differential equation for the circuit solves in three different ways depending on the value of ζ. These are overdamped (ζ > 1), underdamped (ζ < 1), and critically damped (ζ = 1).

Overdamped response[edit]

The overdamped response (ζ > 1) is^[9]

${displaystyle I(t)=A_{1}e^{-omega _{0}left(zeta +{sqrt {zeta ^{2}-1}}right)t}+A_{2}e^{-omega _{0}left(zeta -{sqrt {zeta ^{2}-1}}right)t};.}$

The overdamped response is a decay of the transient current without oscillation.^[10]

Underdamped response[edit]

The underdamped response (ζ < 1) is^[11]

${displaystyle I(t)=B_{1}e^{-alpha t}cos(omega _{mathrm {d} }t)+B_{2}e^{-alpha t}sin(omega _{mathrm {d} }t),.}$

By applying standard trigonometric identities the two trigonometric functions may be expressed as a single sinusoid with phase shift,^[12]

${displaystyle I(t)=B_{3}e^{-alpha t}sin(omega _{mathrm {d} }t+varphi );.}$

The underdamped response is a decaying oscillation at frequency ω_d. The oscillation decays at a rate determined by the attenuation α. The exponential in α describes the envelope of the oscillation. B₁ and B₂ (or B₃ and the phase shift φ in the second form) are arbitrary constants determined by boundary conditions. The frequency ω_d is given by^[11]

${displaystyle omega _{mathrm {d} }={sqrt {omega _{0}^{2}-alpha ^{2}}}=omega _{0}{sqrt {1-zeta ^{2},}};.}$

This is called the damped resonance frequency or the damped natural frequency. It is the frequency the circuit will naturally oscillate at if not driven by an external source. The resonance frequency, ω₀, which is the frequency at which the circuit will resonate when driven by an external oscillation, may often be referred to as the undamped resonance frequency to distinguish it.^[13]

Critically damped response[edit]

The critically damped response (ζ = 1) is^[14]

${displaystyle I(t)=D_{1}te^{-alpha t}+D_{2}e^{-alpha t};.}$

The critically damped response represents the circuit response that decays in the fastest possible time without going into oscillation. This consideration is important in control systems where it is required to reach the desired state as quickly as possible without overshooting. D₁ and D₂ are arbitrary constants determined by boundary conditions.^[15]

Laplace domain[edit]

The series RLC can be analyzed for both transient and steady AC state behavior using the Laplace transform.^[16] If the voltage source above produces a waveform with Laplace-transformed V(s) (where s is the complex frequency s = σ + jω), the KVL can be applied in the Laplace domain:

${displaystyle V(s)=I(s)left(R+L,s+{frac {1}{,C,s,}}right),,}$

where I(s) is the Laplace-transformed current through all components. Solving for I(s):

${displaystyle I(s)={frac {1}{,R+L,s+{frac {1}{,C,s,}},}}V(s);.}$

And rearranging, we have

${displaystyle I(s)={frac {s}{,L left(s^{2}+{frac {R}{,L,}}s+{frac {1}{,L,C,}}right),}}V(s);.}$

Laplace admittance[edit]

Solving for the Laplace admittance Y(s):

${displaystyle Y(s)={frac {I(s)}{,V(s),}}={frac {s}{,L left(s^{2}+{frac {R}{,L,}}s+{frac {1}{,L,C,}}right),}},.}$

Simplifying using parameters α and ω₀ defined in the previous section, we have

${displaystyle Y(s)={frac {I(s)}{,V(s),}}={frac {s}{,L left(s^{2}+2alpha s+omega _{0}^{2}right),}};.}$

Poles and zeros[edit]

The zeros of Y(s) are those values of s where Y(s) = 0:

{displaystyle s=0quad {mbox{and}}quad |s|rightarrow infty ;.}

The poles of Y(s) are those values of s where Y(s) → ∞. By the quadratic formula, we find

${displaystyle s=-alpha pm {sqrt {alpha ^{2}-omega _{0}^{2},}};.}$

The poles of Y(s) are identical to the roots s₁ and s₂ of the characteristic polynomial of the differential equation in the section above.

General solution[edit]

For an arbitrary V(t), the solution obtained by inverse transform of I(s) is:

where ω_r = √α² − ω₀², and cosh and sinh are the usual hyperbolic functions.

Sinusoidal steady state[edit]

Bode magnitude plot for the voltages across the elements of an RLC series circuit. Natural frequency ω₀ = 1 rad/s, damping ratio ζ = 0.4.

Sinusoidal steady state is represented by letting s = jω, where j is the imaginary unit. Taking the magnitude of the above equation with this substitution:

${displaystyle {big |}Y(jomega ){big |}={frac {1}{{sqrt {R^{2}+left(omega L-{frac {1}{,omega C,}}right)^{2}}},}};.}$

and the current as a function of ω can be found from

{displaystyle {big |}I(jomega ){big |}={big |}Y(jomega ){big |}cdot {bigl |}V(jomega ){bigr |};.}

There is a peak value of |I(jω)|. The value of ω at this peak is, in this particular case, equal to the undamped natural resonance frequency.^[17] This means that the maximum voltage across the resistor, and thus maximum heat dissipation, occurs at the natural frequency.

${displaystyle omega _{0}={frac {1}{,{sqrt {L C }},}};.}$

From the frequency response of the current, the frequency response of the voltages across the various circuit elements can also be determined (see figure). Moreover, the maximum voltage across the capacitor happens at a frequency

${displaystyle omega _{C}={frac { {sqrt {{tfrac {L}{ C }}-{tfrac {1}{2}}R^{2}}} }{L}};,}$

whereas the maximum voltage across the inductor occurs at

${displaystyle omega _{L}={frac {1}{ C{sqrt {{tfrac {L}{ C }}-{tfrac {1}{2}}R^{2} }} }};.}$

It holds: ${displaystyle omega _{C}<omega _{0}<omega _{L}}$ .

Parallel circuit[edit]

Figure 2. RLC parallel circuit
V – the voltage source powering the circuit
I – the current admitted through the circuit
R – the equivalent resistance of the combined source, load, and components
L – the inductance of the inductor component
C – the capacitance of the capacitor component

The properties of the parallel RLC circuit can be obtained from the duality relationship of electrical circuits and considering that the parallel RLC is the dual impedance of a series RLC. Considering this, it becomes clear that the differential equations describing this circuit are identical to the general form of those describing a series RLC.

For the parallel circuit, the attenuation α is given by^[18]

${displaystyle alpha ={frac {1}{,2,R,C,}}}$

and the damping factor is consequently

${displaystyle zeta ={frac {1}{,2,R,}}{sqrt {{frac {L}{C}}~}},~.}$

Likewise, the other scaled parameters, fractional bandwidth and Q are also reciprocals of each other. This means that a wide-band, low-Q circuit in one topology will become a narrow-band, high-Q circuit in the other topology when constructed from components with identical values. The fractional bandwidth and Q of the parallel circuit are given by

${displaystyle {begin{aligned}B_{mathrm {f} }&={frac {1}{,R,}}{sqrt {{frac {L}{C}}~}}\Q&=R{sqrt {{frac {C}{L}}~}},~.end{aligned}}}$

Notice that the formulas here are the reciprocals of the formulas for the series circuit, given above.

Frequency domain[edit]

Figure 3. Sinusoidal steady-state analysis. Normalised to R = 1 Ω, C = 1 F, L = 1 H, and V = 1 V.

The complex admittance of this circuit is given by adding up the admittances of the components:

${displaystyle {begin{aligned}{frac {1}{,Z,}}&={frac {1}{,Z_{L},}}+{frac {1}{,Z_{C},}}+{frac {1}{,Z_{R},}}\&={frac {1}{,j,omega ,L,}}+j,omega ,C+{frac {1}{,R,}},.end{aligned}}}$

The change from a series arrangement to a parallel arrangement results in the circuit having a peak in impedance at resonance rather than a minimum, so the circuit is an anti-resonator.

The graph opposite shows that there is a minimum in the frequency response of the current at the resonance frequency ${displaystyle ~omega _{0}=1/{sqrt {,L,C~}}~}$ when the circuit is driven by a constant voltage. On the other hand, if driven by a constant current, there would be a maximum in the voltage which would follow the same curve as the current in the series circuit.

Other configurations[edit]

Figure 4. Series RL, parallel C circuit with resistance in series with the inductor is the standard model for a self-resonant inductor

A series resistor with the inductor in a parallel LC circuit as shown in Figure 4 is a topology commonly encountered where there is a need to take into account the resistance of the coil winding and its self-capacitance. Parallel LC circuits are frequently used for bandpass filtering and the Q is largely governed by this resistance. The resonant frequency of this circuit is^[19]

${displaystyle omega _{0}={sqrt {{frac {1}{ LC }}-left({frac {R}{ L }}right)^{2}~}} .}$

This is the resonant frequency of the circuit defined as the frequency at which the admittance has zero imaginary part. The frequency that appears in the generalised form of the characteristic equation (which is the same for this circuit as previously)

${displaystyle s^{2}+2alpha s+{omega '_{0}}^{2}=0 }$

is not the same frequency. In this case it is the natural, undamped resonant frequency:^[20]

${displaystyle omega '_{0}equiv {frac {1}{ {sqrt {LC~}} }} .}$

The frequency ω_max, at which the impedance magnitude is maximum, is given by^[21]

${displaystyle omega _{mathrm {max} }=omega '_{0} {sqrt {-{frac {1}{ Q_{L}^{2} ~}}+{sqrt {1+{frac {2}{ Q_{L}^{2} }}~}}~}} ,}$

where Q_L ≡ ω′₀L/R is the quality factor of the coil. This can be well approximated by^[21]

${displaystyle omega _{mathrm {max} }approx omega '_{0} {sqrt {1-{frac {1}{ 2Q_{L}^{4} }}~}} .}$

Furthermore, the exact maximum impedance magnitude is given by^[21]

${displaystyle |Z|_{mathrm {max} }={frac {RQ_{L}^{2}}{ {sqrt {2Q_{L}{sqrt {Q_{L}^{2}+2 }}-left(2Q_{L}^{2}+1right)~}} }}={frac {RQ_{L}}{ {sqrt {2{sqrt {1+2/Q_{L}^{2} }}-left(2+1/Q_{L}^{2}right)~}} }} .}$

For values of ${displaystyle Q_{L}gg 1 ,}$ this can be well approximated by^[21]

${displaystyle |Z|_{mathrm {max} }approx RQ_{L}^{2} .}$

Figure 5. Parallel RC, series L circuit with resistance in parallel with the capacitor

In the same vein, a resistor in parallel with the capacitor in a series LC circuit can be used to represent a capacitor with a lossy dielectric. This configuration is shown in Figure 5. The resonant frequency (frequency at which the impedance has zero imaginary part) in this case is given by^[22]

${displaystyle omega _{0}={sqrt {{frac {1}{ LC }}-{frac {1}{ (RC)^{2} }} }} ,}$

while the frequency ω_m at which the impedance magnitude is minimum is given by

${displaystyle omega _{mathrm {m} }=omega '_{0} {sqrt {-{frac {1}{ Q_{C}^{2} }}+{sqrt {1+{frac {2}{ Q_{C}^{2} }} }} }} ,}$

where Q_C = ω′₀RC.

History[edit]

The first evidence that a capacitor could produce electrical oscillations was discovered in 1826 by French scientist Felix Savary.^[23]^[24] He found that when a Leyden jar was discharged through a wire wound around an iron needle, sometimes the needle was left magnetized in one direction and sometimes in the opposite direction. He correctly deduced that this was caused by a damped oscillating discharge current in the wire, which reversed the magnetization of the needle back and forth until it was too small to have an effect, leaving the needle magnetized in a random direction.

American physicist Joseph Henry repeated Savary’s experiment in 1842 and came to the same conclusion, apparently independently.^[25]^[26] British scientist William Thomson (Lord Kelvin) in 1853 showed mathematically that the discharge of a Leyden jar through an inductance should be oscillatory, and derived its resonant frequency.^[23]^[25]^[26]

British radio researcher Oliver Lodge, by discharging a large battery of Leyden jars through a long wire, created a tuned circuit with its resonant frequency in the audio range, which produced a musical tone from the spark when it was discharged.^[25] In 1857, German physicist Berend Wilhelm Feddersen photographed the spark produced by a resonant Leyden jar circuit in a rotating mirror, providing visible evidence of the oscillations.^[23]^[25]^[26] In 1868, Scottish physicist James Clerk Maxwell calculated the effect of applying an alternating current to a circuit with inductance and capacitance, showing that the response is maximum at the resonant frequency.^[23]

The first example of an electrical resonance curve was published in 1887 by German physicist Heinrich Hertz in his pioneering paper on the discovery of radio waves, showing the length of spark obtainable from his spark-gap LC resonator detectors as a function of frequency.^[23]

One of the first demonstrations of resonance between tuned circuits was Lodge’s «syntonic jars» experiment around 1889^[23]^[25] He placed two resonant circuits next to each other, each consisting of a Leyden jar connected to an adjustable one-turn coil with a spark gap. When a high voltage from an induction coil was applied to one tuned circuit, creating sparks and thus oscillating currents, sparks were excited in the other tuned circuit only when the inductors were adjusted to resonance. Lodge and some English scientists preferred the term «syntony» for this effect, but the term «resonance» eventually stuck.^[23]

The first practical use for RLC circuits was in the 1890s in spark-gap radio transmitters to allow the receiver to be tuned to the transmitter. The first patent for a radio system that allowed tuning was filed by Lodge in 1897, although the first practical systems were invented in 1900 by Anglo Italian radio pioneer Guglielmo Marconi.^[23]

Applications[edit]

Variable tuned circuits[edit]

A very frequent use of these circuits is in the tuning circuits of analogue radios. Adjustable tuning is commonly achieved with a parallel plate variable capacitor which allows the value of C to be changed and tune to stations on different frequencies. For the IF stage in the radio where the tuning is preset in the factory, the more usual solution is an adjustable core in the inductor to adjust L. In this design, the core (made of a high permeability material that has the effect of increasing inductance) is threaded so that it can be screwed further in, or screwed further out of the inductor winding as required.

Filters[edit]

Figure 6. RLC circuit as a low-pass filter	Figure 7. RLC circuit as a high-pass filter
Figure 8. RLC circuit as a series band-pass filter in series with the line	Figure 9. RLC circuit as a parallel band-pass filter in shunt across the line
Figure 10. RLC circuit as a series band-stop filter in shunt across the line	Figure 11. RLC circuit as a parallel band-stop filter in series with the line

In the filtering application, the resistor becomes the load that the filter is working into. The value of the damping factor is chosen based on the desired bandwidth of the filter. For a wider bandwidth, a larger value of the damping factor is required (and vice versa). The three components give the designer three degrees of freedom. Two of these are required to set the bandwidth and resonant frequency. The designer is still left with one which can be used to scale R, L and C to convenient practical values. Alternatively, R may be predetermined by the external circuitry which will use the last degree of freedom.

Low-pass filter[edit]

An RLC circuit can be used as a low-pass filter. The circuit configuration is shown in Figure 6. The corner frequency, that is, the frequency of the 3 dB point, is given by

${displaystyle omega _{mathrm {c} }={frac {1}{sqrt {LC}}},.}$

This is also the bandwidth of the filter. The damping factor is given by^[27]

${displaystyle zeta ={frac {1}{2R_{L}}}{sqrt {frac {L}{C}}},.}$

High-pass filter[edit]

A high-pass filter is shown in Figure 7. The corner frequency is the same as the low-pass filter:

${displaystyle omega _{mathrm {c} }={frac {1}{sqrt {LC}}},.}$

The filter has a stop-band of this width.^[28]

Band-pass filter[edit]

A band-pass filter can be formed with an RLC circuit by either placing a series LC circuit in series with the load resistor or else by placing a parallel LC circuit in parallel with the load resistor. These arrangements are shown in Figures 8 and 9 respectively. The centre frequency is given by

${displaystyle omega _{mathrm {c} }={frac {1}{sqrt {LC}}},,}$

and the bandwidth for the series circuit is^[29]

${displaystyle Delta omega ={frac {R_{L}}{L}},.}$

The shunt version of the circuit is intended to be driven by a high impedance source, that is, a constant current source. Under those conditions the bandwidth is^[29]

${displaystyle Delta omega ={frac {1}{CR_{L}}},.}$

Band-stop filter[edit]

Figure 10 shows a band-stop filter formed by a series LC circuit in shunt across the load. Figure 11 is a band-stop filter formed by a parallel LC circuit in series with the load. The first case requires a high impedance source so that the current is diverted into the resonator when it becomes low impedance at resonance. The second case requires a low impedance source so that the voltage is dropped across the antiresonator when it becomes high impedance at resonance.^[30]

Oscillators[edit]

For applications in oscillator circuits, it is generally desirable to make the attenuation (or equivalently, the damping factor) as small as possible. In practice, this objective requires making the circuit’s resistance R as small as physically possible for a series circuit, or alternatively increasing R to as much as possible for a parallel circuit. In either case, the RLC circuit becomes a good approximation to an ideal LC circuit. However, for very low-attenuation circuits (high Q-factor), issues such as dielectric losses of coils and capacitors can become important.

In an oscillator circuit

${displaystyle alpha ll omega _{0},,}$

or equivalently

As a result,

${displaystyle omega _{mathrm {d} }approx omega _{0},.}$

Voltage multiplier[edit]

In a series RLC circuit at resonance, the current is limited only by the resistance of the circuit

${displaystyle I={frac {V}{R}},.}$

If R is small, consisting only of the inductor winding resistance say, then this current will be large. It will drop a voltage across the inductor of

${displaystyle V_{L}={frac {V}{R}}omega _{0}L,.}$

An equal magnitude voltage will also be seen across the capacitor but in antiphase to the inductor. If R can be made sufficiently small, these voltages can be several times the input voltage. The voltage ratio is, in fact, the Q of the circuit,

${displaystyle {frac {V_{L}}{V}}=Q,.}$

A similar effect is observed with currents in the parallel circuit. Even though the circuit appears as high impedance to the external source, there is a large current circulating in the internal loop of the parallel inductor and capacitor.

Pulse discharge circuit[edit]

An overdamped series RLC circuit can be used as a pulse discharge circuit. Often it is useful to know the values of components that could be used to produce a waveform. This is described by the form

${displaystyle I(t)=I_{0}left(,e^{-alpha ,t}-e^{-beta ,t}right),.}$

Such a circuit could consist of an energy storage capacitor, a load in the form of a resistance, some circuit inductance and a switch – all in series. The initial conditions are that the capacitor is at voltage, V₀, and there is no current flowing in the inductor. If the inductance L is known, then the remaining parameters are given by the following – capacitance:

${displaystyle C={frac {1}{~L,alpha ,beta ,~}},,}$

resistance (total of circuit and load):

initial terminal voltage of capacitor:

${displaystyle V_{0}=-I_{0}L,alpha ,beta ,left({frac {1}{beta }}-{frac {1}{alpha }}right),.}$

Rearranging for the case where R is known – capacitance:

${displaystyle C={frac {~alpha +beta ~}{R,alpha ,beta }},,}$

inductance (total of circuit and load):

${displaystyle L={frac {R}{,alpha +beta ~}},,}$

initial terminal voltage of capacitor:

${displaystyle V_{0}={frac {,-I_{0}R,alpha ,beta ~}{alpha +beta }}left({frac {1}{beta }}-{frac {1}{alpha }}right),.}$

Footnotes[edit]

^
RLC response to driving voltage occurs at the frequency for lossless oscillation, ${displaystyle {frac {1}{ 2pi {sqrt {LC }} }} ,}$ even though loss resistance R may be present. The driven resonance does not occur at the damped free oscillation frequency, with a more complicated formula (see below) that produces a reduced value due to damping (R) which only applies to free oscillations (no driving signal).

References[edit]

^ Kaiser, pp. 7.71–7.72
^ ^a ^b ^c Long, Steve (2004-04-15) [2002-01-17]. Rodwell, Mark (ed.). «Resonant circuits – resonators and Q» (PDF). ECE145B / ECE 218B. ece.ucsb.edu (course notes). Electrical & Computer Engineering. Santa Barbara, CA: U.C. Santa Barbara. Retrieved 2016-10-21.
^ Nilsson and Riedel, p. 308.
^ Agarwal and Lang, p. 641.
^ Agarwal and Lang, p. 646.
^ Irwin, pp. 217–220.
^ ^a ^b Agarwal and Lang, p. 656.
^ Nilsson and Riedel, pp. 287–288.
^ Irwin, p. 532.
^ Agarwal and Lang, p. 648.
^ ^a ^b Nilsson and Riedel, p. 295.
^ Humar, pp. 223–224.
^ Agarwal and Lang, p. 692.
^ Nilsson and Riedel, p. 303.
^ Irwin, p. 220.
^ This section is based on Example 4.2.13 from Debnath, Lokenath; Bhatta, Dambaru (2007). Integral Transforms and Their Applications (2nd ed.). Chapman & Hall/CRC. pp. 198–202. ISBN 978-1-58488-575-7. (Some notations have been changed to fit the rest of this article.)
^ Kumar and Kumar, Electric Circuits & Networks, p. 464.
^ Nilsson and Riedel, p. 286.
^ Kaiser, pp. 5.26–5.27
^ Agarwal & Lang, p. 805.
^ ^a ^b ^c ^d Cartwright, K.V.; Joseph, E.; Kaminsky, E.J. (2010). «Finding the exact maximum impedance resonant frequency of a practical parallel resonant circuit without calculus» (PDF). The Technology Interface International Journal. 11 (1): 26–34.
^ Kaiser, pp. 5.25–5.26.
^ ^a ^b ^c ^d ^e ^f ^g ^h Blanchard, Julian (October 1941). «The History of Electrical Resonance». Bell System Technical Journal. USA: AT&T. 20 (4): 415. doi:10.1002/j.1538-7305.1941.tb03608.x. S2CID 51669988. Retrieved 2013-02-25.
^ Savary, Felix (1827). «Memoirs sur l’Aimentation». Annales de Chimie et de Physique. Paris: Masson. 34: 5–37.
^ ^a ^b ^c ^d ^e Kimball, Arthur Lalanne (1917). A College Text-book of Physics (2nd ed.). New York: Henry Hold. pp. 516–517.
^ ^a ^b ^c Huurdeman, Anton A. (2003). The Worldwide History of Telecommunications. USA: Wiley-IEEE. pp. 199–200. ISBN 0-471-20505-2.
^ Kaiser, pp. 7.14–7.16.
^ Kaiser, p. 7.21.
^ ^a ^b Kaiser, pp. 7.21–7.27.
^ Kaiser, pp. 7.30–7.34.

Bibliography[edit]

Agarwal, Anant; Lang, Jeffrey H. (2005). Foundations of Analog and Digital Electronic Circuits. Morgan Kaufmann. ISBN 1-55860-735-8.
Humar, J. L. (2002). Dynamics of Structures. Taylor & Francis. ISBN 90-5809-245-3.
Irwin, J. David (2006). Basic Engineering Circuit Analysis. Wiley. ISBN 7-302-13021-3.
Kaiser, Kenneth L. (2004). Electromagnetic Compatibility Handbook. CRC Press. ISBN 0-8493-2087-9.
Nilsson, James William; Riedel, Susan A. (2008). Electric Circuits. Prentice Hall. ISBN 978-0-13-198925-2.

Источник

П
ри
последовательном
соединении элементов R,
L
и C
(рис. 3.10) приложенное к зажимам цепи
напряжение

равно сумме напряжений на элементах
цепи:

u
= u_R+
u_L+
u_С
=

После
подстановки тока

)
имеем

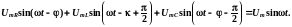
Вид
векторной диаграммы напряжений
и тока и характер электрических
процессов, протекающих в цепи,
зависят от соотношения сопротивлений
X_Lи
X_C:


при

(X_L>
X_C)
и U_mL>
U_mCцепь
носит
активно-индуктивный
характер;
ток
i
отстает по фазе от напряжения u
на угол 
(рис. 3.11а);

 при

(X_L<
X_C)
и
U_mL<
U_mC
цепь
носит
активно-ёмкостный
характер;
ток
i
опережает по фазе напряжение u
на угол 

(рис. 3.11б);

 при

(X_L=
X_C)
и U_mL=
U_mCцепь
для источника энергии 
чисто
активная
нагрузка;
вследствие
возникшего в цепи резонанса напряжений
угол между входным током и напряжением

=
0
(рис. 3.11в).

з
треугольников напряжения (см. рис. 3.11а,
б)
следует, что

откуда
амплитуда тока

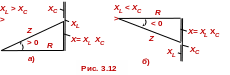
Из
треугольников сопротивлений (рис.
3.12а,
б)
следует, что полное
сопротивление
последовательной RLC-цепи
равно

где


полное
реактивное
сопротивление
RLC-цепи.

Сдвиг
фаз
между напряжением u(t)
и током i(t)
в
RLC-цепи
(рис. 3.12)




алгебраическая
величина, зависящая от соотношения
сопротивлений X_L,
X_C
и R.

3.4. Мощности цепи синусоидального тока

При
синусоидальном напряжении

приложенном к зажимам RLC-цепи
(рис. 3.13а),
и установившемся в ней токе

(при

,
рис. 3.13б)
выражение мгновенной мощности
имеет вид

p(t)
= dW/dt
= u(t)i(t)
= (u_R+
u_L+
u_С
)i
=

После
подстановки тока i
и
напряжения

u
=

получим

=

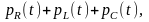
график
которой приведён на рис. 3.13в.

Проведём
анализ каждой составляющей мощности
р(t)
цепи.

Активная
мощность цепи.
Анализируя выражение мгновенной
мощности

=
в
резистивном
элементе R
(рис. 3.14а,
б),
замечаем, что она знакоположительная
функция.
Это
означает, что электрическая
энергия источника необратимо
преобразуется в элементе R
в другие виды,
например, в тепловую энергию. Такую
мощность называют активной
и
измеряют в ваттах [Вт].
Степень
необратимого преобразования
энергии в цепи оценивают средним
значением мгновенной
мощности р(t)
за
период T
и
обозначают символом P:

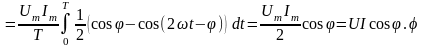
Примечание.
Напомним, что интеграл от гармонических
функций типа sint,
cost,

cos2t,
cos(t

),
cos(2t

)
и т. д. за период Т
равен
нулю.

Итак,
активная
мощность
цепи синусоидального тока есть
среднее значение общей мощности
р(t)
за период T.
Она равна произведению действующих
значений приложенного к цепи напряжения
U
и тока I,
умноженному на
cos,
т. е.

P
= UI
cos
= RI².

Реактивная
индуктивная мощность.
Анализ мгновенной мощности в
индуктивном
элементе
L

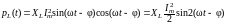
показывает,
что это
знакопеременная
функция,
изменяющаяся с двойной частотой
по отношению к частоте изменения
напряжения u_Lи
тока i_L
в цепи
(рис. 3.15б).
Среднее значение мощности p_L(t)
за период T
равно нулю.

В
индуктивном
элементе
в первую четверть периода T
(см. рис. 3.15а)
напряжение
u_L
и ток i_L
имеют
знак плюс, поэтому мощность p_L
= u_Li_L
> 0,
т.е. индуктивный элемент
потребляет
электрическую энергию источника
и преобразовывает её в магнитную,
накапливая её в магнитном поле катушки.
Во вторую четверть периода напряжение
u_L
и
ток
i_L
имеют
противоположные знаки,
поэтому мощность p_L
= u_Li_L
< 0.
В это время накопленная магнитная
энергия возвращается
источнику,
преобразовываясь в электрическую
энергию. В третьей четверти
происходит накопление энергии в
магнитном поле элемента L,
в четвертой 
её возврат источнику энергии.

нтенсивность
преобразования электрической энергии
источника в магнитную в
элементе
L
и
обратно оценивается реактивной
индуктивной
мощностью
+Q_L,
которая равна амплитуде мощности

(см. рис. 3.15б),
всегда
берётся со знаком плюс
и
измеряется в
варах (вольт-ампер
реактивный)
[вар],
т.е.

Реактивная
ёмкостная мощность цепи.
Анализируя мгновенную мощность в
ёмкостном
элементе

заключаем,
что это
знакопеременная
функция времени
(рис. 2.16б),
изменяющаяся
с частотой 2
и находящаяся в противофазе
с реактивной индуктивной
мощностью p_L(t)
(см.
рис. 3.16б).
Среднее
значение мощности p_С(t)

за
период T
равно нулю.

В
ёмкостном
элементе
в первую четверть периода T
напряжение u_С
и ток i_С
имеют разные знаки (см. рис. 3.16а),
что означает, что ёмкостный элемент
возвращает
накопленную в электрическом
поле конденсатора электрическую
энергию источнику
(конденсатор разряжается).
Во вторую четверть периода ток i_С
и напряжение u_С
имеют одинаковое направление. В этом
случае ёмкостный элемент (конденсатор)
потребляет
энергию источника
и накапливает её в электрическом
поле (конденсатор заряжается). В третью
четверть периода накопленная в
электрическом поле конденсатора энергия
возвращается источнику, в четвертую

конденсатор вновь заряжается
(потребляет энергию источника).

Интенсивность
преобразования энергии в конденсаторе
оценивается
реактивной
ёмкостной мощностью
—Q_C,
которая
равна амплитуде
p_С
(см.
рис. 3.14б),
всегда берётся со знаком минус
и
измеряется в варах
[вар],
т.е.

Полная
мощность цепи синусоидального тока.
Для определения значения
полной
мощности

и соотношений между полной, активной
и реактивной мощностями последовательной
RLC-цепи
(рис. 3.13а)
при

построим векторную диаграмму
напряжений цепи (рис.
3.17а).

Умножив
все стороны треугольника напряжений
на значение тока I_m/2,
получим подобный треугольник мощностей
(рис.
3.17б),
в котором полная
мощность

т.е.
полная
мощность S
цепи
равна произведению действующих значений
напряжения и тока на её зажимах.
Eё
измеряют в вольт-амперах [ВА]
или в киловольт-амперах
[кВА].

Реактивная
мощность цепи

Мощности
P,
Q
и S,
потребляемые
цепью
синусоидального тока, связаны соотношением

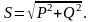
Отметим,
что
накопление энергии в индуктивном и
ёмкостном элементах происходит
в разное время: если в магнитном поле
индуктивной катушки накапливается
магнитная энергия, то в это время
электрическая энергия, запасённая в
электрическом поле конденсатора,
возвращается источнику и обратно.

Соседние файлы в папке Лекции

Источник

Теория / 5.5. Параллельное соединение RLC элементов

Рассмотрим схему, в которой резистор, индуктивность
и емкость подключены к источнику
синусоидального напряжения

Состояние параллельной цепи описывается первым законом
Кирхгофа:

Выразим токи в ветвях через напряжение:

Подставим эти выражения в первый закон Кирхгофа:

Для упрощения расчетов перейдем к символической форме
записи:

Здесь Y – полная комплексная проводимость цепи:

Построим векторную диаграмму (рис. 5.15).

Поскольку ко всем элементам цепи приложено одно и то
же напряжение, то сначала строим вектор напряжения U, затем последовательно суммируем вектора токов, учитывая,
что ток в резистивном элементе совпадает по фазе с напряжением, ток в
индуктивности отстает от напряжения на 90^о, ток в емкости опережает
напряжение на 90^о.

Из векторной диаграммы можно получить треугольник токов
(рис. 5.16).

Этот треугольник векторный, сторонами его являются
активная составляющая тока Ir, реактивная Ib = Il+Ic, модуль которой равен Ib = Il-Ic и общий ток цепи I.

Из треугольника токов можно найти: модуль общего тока

угол сдвига фаз между напряжением и током

Поделив все стороны треугольника токов на напряжение,
получим подобный ему треугольник проводимостей, катетами которого являются
активная проводимость g, реактивная проводимость, равная разности индуктивной
и емкостной проводимостей b = b_L – b_C , а гипотенузой – модуль полной проводимости цепи у (рис. 5.17).

Из треугольника проводимостей можно определить: полную проводимость цепи

сдвиг фаз между напряжением и током

активную проводимость

реактивную проводимость

Источник

Анализ цепи с последовательным соединением

Содержание:

Схема цепи с последовательным соединением элементов

В общем случае любое реальное устройство, содержащееся в электрической цепи, может быть представлено в схеме замещения тремя идеальными элементами. Поэтому целесообразно при анализе цепей синусоидального тока знать соотношение тока и напряжения для участка цепи с тремя последовательно соединенными элементами: резистором, идеальным индуктивным и идеальным емкостным элементами.

Схема замещения такой неразветвленной цепи показана на рис. 23.

Рис. 23. Схема цепи с последовательным соединением элементов R, L, С.

Под действием синусоидального напряжения в цепи возникает синусоидальный ток . Необходимо определить соотношение между синусоидальными током и напряжением этой цепи по величине и по фазе.

Синусоидальный ток с амплитудой и начальной фазой , изображается в виде:

или в комплексной форме:

По второму закону Кирхгофа для контура рассматриваемой цепи полное напряжение цепи соотносится с напряжениями на отдельных элементах в виде:

Как показано ранее (51), (71), (90), напряжение на каждом из элементов соотносятся с током в соответствии с законом Ома:

Ток во всех элементах при их последовательном соединении одни и тот же. Тогда выражение (98) может быть представлено в виде:

или

Здесь

— комплексное полное сопротивление цепи с тремя последовательно соединенными элементами.

Таким образом выражение (103) определяет соотношение между комплексным током и комплексным напряжением также в форме закона Ома: комплексный ток в цепи с тремя последовательно соединенными элементами прямо пропорционален комплексному напряжению и обратно пропорционален комплексному полному сопротивлению этой цепи.

Возможно вам будут полезны данные страницы:

Модуль и аргумент комплексного полного сопротивления определяются параметрами отдельных элементов.

Исходя из (104), модуль комплексного полного сопротивления

где — реактивное сопротивление цепи.

Аргумент комплексного полного сопротивления

В соответствии с законом Ома в комплексном виде для этой цепи (103),

Исходя из полученного выражения (107), действующее значение тока

начальная фаза тока

или

Как видно, действующие значения тока и напряжения в этой цепи также определяется полным сопротивлением Z в форме закона Ома. По фазе напряжение опережает ток на угол . При этом полное сопротивление и разность фаз определяются соотношением сопротивлений трех элементов в соответствии выражениями (105) и (106).

Тот же результат может быть получен посредством наглядного графического изображения тока и напряжений на векторной диаграмме.

Векторная диаграмма

Векторная диаграмма для рассматриваемой цепи показана на рис. 24.

Здесь начальная фаза тока принята произвольно равной нулю . При этом вектор тока направлен вдоль вещественной оси комплексной плоскости.

Рис. 24. Векторная диаграмма цепи с последовательным соединением элементов L, R, С.

Вектор напряжения индуктивного элемента повернут относительно вектора тока на в сторону опережения в соответствии со свойствами этого элемента (66). Вектор напряжения резистора направлен вдоль вектора тока в соответствии с характеристиками резистора (47). Вектор напряжения емкостного элемента повернут на угол относительно вектора тока в сторону отставания в соответствии со свойствами емкостного элемента (85). Длина векторов напряжений определяется их действующими значениями по закону Ома для каждого из элементов в соответствии с (67), (46), (83).

Соотношение напряжений по второму закону Кирхгофа (98) на векторной диаграмме соответствует векторному сложению. При этом вектор полного напряжения цепи на рис. 24 определяется суммой трех векторов напряжений на отдельных элементах:

Из построенной векторной диаграммы возможен анализ соотношения тока и полного напряжения цепи. Для этого выделим на векторной диаграмме прямоугольный треугольник ОАВ (рис. 25).

Треугольник напряжений цепи с последовательным соединением элементов

Треугольник напряжений цепи с последовательным соединением элементов. Обозначить ОАВ

Нижний катет треугольника пропорционален напряжению резистора, которое определяется его активным сопротивлением, и его называют активной составляющей напряжения . Правый катет треугольника пропорционален разности напряжений двух реактивных элементов: индуктивного и емкостного, и его называют реактивной составляющей напряжения:

Гипотенуза треугольника пропорциональна величине полного напряжения цепи U. Угол определяет разность фаз всей цепи.

Этот треугольник называют треугольником напряжений и используют для наглядного представления соотношения между отдельными составляющими напряжений при анализе цепи с последовательным соединением R,L,C -элементов.

Поделим стороны треугольника напряжений на величину тока . При этом получается подобный треугольник (рис. 26) со сторонами:

Рис. 26. Треугольник сопротивлений цепи с последовательным соединением элементов.

— активное сопротивление резистора;

— реактивное сопротивление, определяемое разностью индуктивного и емкостного сопротивлений;

— полное сопротивление цепи, определяющее соотношение по величине тока и полного напряжения.

Угол определяет разность фаз всей цепи.

Этот треугольник называют треугольником сопротивлений и используют для наглядного представления соотношения между сопротивлениями отдельных элементов и полным сопротивлением цепи с последовательным соединением R,L,C — элементов.

По теореме Пифагора для треугольника сопротивлений модуль полного сопротивления

Он определяет соотношение по величине между током и полным напряжением.

Из того же треугольника разность фаз для всей цепи

Она описывает соотношение по фазе между током и полным напряжением и определяет аргумент комплексного полного сопротивления.

Таким образом, комплексное полное сопротивление может быть записано в виде:

Оно определяет соотношение между током и напряжением по закону Ома в комплексном виде:

При этом модуль комплексного полного сопротивления Z определяет соотношение по величине действующих значений напряжения и тока: , а аргумент комплексного сопротивления определяет соотношение синусоидальных напряжения и тока по фазе:

Полученные при графическом анализе выражения (112) — (115) соответствуют записанным ранее (105) — (107).

Эти выражения справедливы для цепи, содержащей в общем случае три идеальных элемента, соединенные последовательно. В частности, реальное устройство может быть представлено эквивалентной схемой с двумя или одним идеальным элементом. В этом случае полученное выражение также верно. Следует лишь формально принять сопротивление отсутствующего элемента равным нулю.

Пример задачи с решением

Для цепи на рис. 21 определить напряжение источника, используя понятие полного комплексного сопротивления.

Рассматривая эту цепь как частный случай цепи с тремя идеальными элементами, можно принять емкостное сопротивление равным нулю . При этом комплексное полное сопротивление

Напряжение всего участка по закону Ома в комплексном виде:

Аналогичным образом можно определять комплексное полное сопротивление участка цепи, содержащего два других идеальных элемента, или один из них.

Используя графические изображения в форме треугольников напряжений и сопротивлений, можно записать выражения, полезные при расчете и анализе такой электрической цепи:

Для анализа энергетических соотношений в цепи с последовательным соединением R, L, С — элементов определим характер изменения мгновенной мощности в этой цепи:

Или, используя действующие значения тока и напряжения,

Как видно из полученного выражения (121), мощность в рассматриваемой цепи изменяется во времени по гармоническому закону с двойной частотой. При этом колебания мощности происходят вокруг среднего значения, определяемого первым слагаемым в правой части этого выражения.

Среднее значение мощности определяет активную мощность. Тогда активная мощность

или

Как видно, активная мощность определяется мощностью резистора. Произведение действующих значений тока и полного напряжения цепи называют полной мощностью

Единица полной мощности — ВА, кВА, МВА.

Исходя из (123 ) и (124) соотношение активной и полной мощностей:

, или

Активная мощность определяет необратимое преобразование электрической энергии в другие виды энергии, т.с. полезную работу, совершаемую током в электрической цепи. В общем случае активная мощность является частью общего значения тока и определяется произведением текущего значения тока на общее напряжение. Этот процент активной мощности определяется по уравнению (125). Отношение активной мощности к полной называется коэффициентом мощности. Принимая во внимание выражение (125), коэффициент мощности обозначают

Коэффициент мощности можно определить соотношением сопротивлений отдельных элементов, например, исходя из треугольника сопротивлений (рис. 26):

Графически соотношение активной и полной мощности отображается треугольником мощностей. Для построения треугольника мощностей умножим треугольник напряжений на действующее значение тока. При этом образуется подобный прямоугольный треугольник (рис. 27).

Рис. 27. Треугольник мощностей цепи с последовательным соединением элементов.

Нижний катет треугольника пропорционален активной мощности:

Правый катет треугольника пропорционален величине:

Это реактивная мощность всей цепи.

Гипотенуза треугольника оказывается равной полной мощности:

Из треугольника мощностей:

или

Что соответствует полученным ранее выражениям.

При выполнении расчетов в комплексном виде комплексное значение полной мощности определяется произведением комплексного напряжения на сопряженный комплексный ток:

Здесь сопряженный комплексный ток. Тогда:

В рассматриваемой цепи с последовательным соединением R, L, С — элементов при разном соотношении сопротивлений элементов создается разный режим работы. При этом характер цепи определяется разностью фаз (/>, значения которой могут быть положительными или отрицательными в диапазоне от

Ниже рассматриваются режимы работы цепи при разных соотношениях индуктивного и емкостного сопротивлений.

Показанная на рис. 24 векторная диаграмма построена в предположении, что индуктивное сопротивление больше емкостного . Реактивное сопротивление всей цепи положительно:

При этом в соответствии с законом Ома напряжение на индуктивном элементе больше емкостного:

Разность фаз всей цепи оказывается положительной, т.е. полное напряжение опережает по фазе ток на угол , больший нуля:

Треугольник сопротивлений и треугольник мощностей для этого режима имеют вид, показанный на рис. 26,27.

В этом режиме цепь характеризуется активной мощностью Р и положительной реактивной мощностью Положительное значение реактивной мощности свидетельствует о том, что индуктивная мощность больше емкостной, т.е. индуктивный элемент преобладает над емкостным элементом.

В этом режиме характер цепи называют активно-индуктивным.

При сопротивлении индуктивного элемента, меньшим емкостного,

При этом в соответствии с законом Ома напряжение на индуктивном элементе меньше емкостного:

Векторная диаграмма для этого режима показана на рис. 28.

Рис. 28. Векторная диаграмма неразветвленной цепи при

Разность фаз всей цепи оказывается отрицательной, т.е. полное напряжение отстает по фазе от тока:

Треугольник сопротивлений и треугольник мощностей для этого режима показаны на рис. 29.

Рис. 29. Треугольник сопротивлений и треугольник мощностей при

В этом режиме цепь характеризуется активной мощностью Р и отрицательной реактивной мощностью Отрицательное значение реактивной мощности свидетельствует о том, что индуктивная мощность меньше емкостной, т.е. емкостный элемент преобладает над индуктивным элементом.

В этом режиме характер цепи называют активно-емкостным.

Особый режим работы цепи возникает при равенстве индуктивного и емкостного сопротивлений:

Реактивное сопротивление всей цепи оказывается равным нулю:

При этом в соответствии с законом Ома напряжения на индуктивном и емкостном элементах равны между собой:

а реактивное напряжение равно нулю:

Векторная диаграмма для этого режима показана на рис. 30.

Рис. 30. Векторная диаграмма неразветвленной цепи при

Разность фаз всей цепи оказывается равной нулю, т.е. полное напряжение совпадает по фазе с током:

Треугольник сопротивлений и треугольник мощностей для этого режима вырождаются в отрезок, поскольку один катет становится равным нулю.

В этом режиме цепь характеризуется активной мощностью Р . Реактивная мощность равна нулю . При этом активная мощность равна полной мощности:

а коэффициент мощности равен

Отсутствие реактивной мощности при наличии в цепи индуктивного и емкостного элементов свидетельствует о том, что реактивная индуктивная мощность и реактивная емкостная мощность взаимно компенсируются. При этом цепь имеет активный характер, поскольку обладает лишь активной мощностью.

Явление, возникающее в неразветвленной цепи с элементами L, R, С, когда полное напряжение и ток совпадают по фазе, называется резонансом напряжений.

Условие резонанса напряжений:

Создать резонанс напряжений в цепи можно изменяя параметры L или С при неизменной частоте, или изменяя частоту при заданных параметрах L и С.

Рассмотрим случай, когда £ и С неизменны при изменении частоты. На рис. 31 показаны зависимости сопротивлений и тока цепи от частоты

Рис. 31. Зависимости от частоты.

В точке . При этом полное сопротивление минимально и определяется лишь активным сопротивлением резистора:

Эта точка определяет резонансную частоту

Ток цепи в этом режиме наибольший:

Активная мощность определяется величиной резонансного тока:

Аналогичным образом возникает режим резонанс напряжений при неизменной частоте и изменении индуктивности индуктивного элемента, либо емкости емкостного элемента. При установлении равенства индуктивного и емкостного сопротивлений возникает резонанс напряжений. При этом полное сопротивление цепи минимально, а ток максимальный.

Признаком резонанса напряжений в цепи является максимальное значение тока и активной мощности

Резонанс напряжений используется в радиотехнических цепях при построении схем резонансных фильтров. При этом свойства цепи оказываются различными для сигналов разных частот.

В электротехнических установках частота неизменна. Здесь возникновение резонанса напряжений обусловлено изменением параметров элементов. При при резонансе напряжений возможны перенапряжения на отдельных участках цепи.

На странице -> решение задач по электротехнике собраны решения задач и заданий с решёнными примерами по всем темам теоретических основ электротехники (ТОЭ).

Услуги:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Треугольник сопротивлений

Автор: Евгений Живоглядов.
Дата публикации: 01 апреля 2015 .
Категория: Статьи.

Если стороны треугольника напряжений (рисунок 1, а) разделить на ток I (рисунок 1, б), то углы треугольника от этого не изменятся, и мы получим новый треугольник, подобный первому – треугольник сопротивлений (рисунок 1, в).

Рисунок 1. Получение треугольника сопротивлений

В треугольнике сопротивления, показанном отдельно на рисунке 2, все стороны обозначают сопротивления, причем гипотенуза его является полным или кажущимся сопротивлением цепи.

Из треугольника сопротивлений видно, что полное или кажущееся сопротивление z равно геометрической сумме активного r и индуктивного x_L сопротивлений.

Применяя теорему Пифагора к треугольнику сопротивлений, получаем:

Если одно из сопротивлений цепи (активное или реактивное), например, в 10 и более раз меньше другого, то меньшим можно пренебречь, в чем легко можно убедиться непосредственным расчетом.

Пример 1. Определить полное сопротивление цепи, в которой r = 9 Ом и x_L = 12 Ом.

Было бы совершенно неправильно, если бы для определенного полного сопротивления были арифметически сложены оба сопротивления r и x_L, так как

Результат, как мы видим, в этом случае получается неверный.

Пример 2. Полное сопротивление обмотки электромагнита z = 25 Ом. Активное сопротивление обмотки r = 15 Ом. Определить индуктивное сопротивление.

Пример 3. Индуктивное сопротивление обмотки электродвигателя переменного тока равно 14 Ом. Полное сопротивление ее равно 22 Ом. Найти активное сопротивление.

Пример 4. В цепи, изображенной на рисунке 3, определить показание вольтметра.

Рисунок 3. К примеру 4

Определим общее сопротивление:

Если умножить z на ток I, получим:

то есть тот же результат, что и выше.

Источник: Кузнецов М. И., «Основы электротехники» — 9-е издание, исправленное — Москва: Высшая школа, 1964 — 560 с.

Анализ линейных электрических цепей (стр. 3 )

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3

Сравнение реактивного (1.22) и комплексного (1.31) сопротивлений индуктивности показывает, что на комплексной плоскости реактивное (индуктивное) сопротивление катушки откладывают на положительной вертикальной полуоси (рис. 1.32, б), потому что эта величина мнимая и положительная.

Запишем выражения комплексных амплитуд тока и напряжения для цепи, содержащей емкость. Из (1.16) и (1.26) следует, что:

где UmC и Im, а также ju и ji связаны соотношениями (1.27). Векторы напряжения на емкости и тока в ней сдвинуты друг относительно друга на –90°, при этом ток опережает напряжение (рис. 1.31, в).

Комплексное сопротивление емкости найдем как:

Здесь учтено, что .

Очевидно, что реактивное сопротивление емкости является мнимым отрицательным числом, на комплексной плоскости оно откладывается на отрицательной вертикальной полуоси (рис. 1.32, в).

Мы уже знаем, что любое комплексное число, записанное в алгебраической форме , имеет вещественную а и мнимую jb составляющие, а число, записанное в показательной форме – модуль A и аргумент j.

Анализ выражений (1показывает, что комплексное сопротивление резистора является вещественным и не содержит мнимой составляющей, его аргумент равен нулю; комплексное сопротивление индуктивности, наоборот, является мнимым, его аргумент равен +90°; комплексное сопротивление емкости также мнимое, но аргумент его равен –90°.

На рис. 1.33, а и 1.34, а показаны последовательные RL и RC цепи. Комплексное сопротивление последовательной RL цепи в алгебраической форме содержит сумму положительного вещественного резистивного сопротивления R и положительного мнимого индуктивного сопротивления jXL (рис. 1.33, б):

где .

В показательной форме это сопротивление запишется в виде:

где модуль ZRL называется полным сопротивлением последовательной RL цепи, а аргумент jZ – углом этого сопротивления. Полное сопротивление ZRL и аргумент jZ подсчитываются, как это следует из рис. 1.33, б, по формулам

Пример 1.11. Определим комплексное сопротивление цепи, изображенной на рис. 1.33, а, на частоте 50 Гц для R = 10 Ом и L = 100 мГн.

Рассчитаем значение индуктивного сопротивления цепи, используя (1.31),

Комплексное сопротивление RL-цепи

В показательной форме комплексное сопротивление RL-цепи

Комплексное сопротивление последовательной RC цепи в алгебраической форме состоит из положительного вещественного резистивного сопротивления R и отрицательного мнимого емкостного (рис. 1.34, б):

где

В показательной форме это комплексное число выглядит как

где – полное сопротивление последовательной RC цепи;

– угол этого сопротивления.

Комплексное сопротивление ZRC изображено на рис. 1.34, б в виде вектора на комплексной плоскости. Там же показаны его проекции на вещественную и мнимую оси.

Прямоугольный треугольник, составленный из резистивного, реактивного и полного сопротивлений (рис. 1.35), называется треугольником сопротивлений.

Пример 1.12. Определим комплексное сопротивление цепи, изображенной на рис. 1.34, а, на частоте 5 кГц для R = 100 Ом, С = 318 нФ.

Рассчитаем значение емкостного сопротивления цепи

Комплексное сопротивление RC-цепи

Вектор комплексного сопротивления RC-цепи изображен на рис. 1.36.

Запишем комплексное сопротивление последовательной RLC цепи (рис. 1.37, а). Оно будет содержать положительное вещественное резистивное сопротивление R и мнимое сопротивление , знак которого будет зависеть от соотношения индуктивного XL и емкостного XC сопротивлений, следовательно:

где .

Напомним, что значения XL и XC зависят от частоты и от соответствующих элементов L и С, поэтому может случиться так, что на определенной частоте и при определенных значениях L и С значение XL будет больше значения XC, как это показано на рис. 1.37, б, или наоборот, значение XC будет больше, чем XL (рис. 1.37, в).

Из треугольника сопротивлений легко вычислить резистивное и реактивное сопротивления, зная полное сопротивление и его угол:

Случай, когда реактивное сопротивление Х = 0, т. е. XL = XC, является особым. Когда это имеет место, то говорят, что в последовательной RLC цепи возникает резонанс напряжений. Частота, на которой индуктивное и емкостное сопротивления оказываются равными, называется частотой резонанса напряжений. Комплексное сопротивление всей RLC цепи равно при этом резистивному сопротивлению R. В дальнейшем явление резонанса напряжений будет рассмотрено более детально.

Пример 1.13. Определим резистивное и реактивное сопротивления последовательной RLC цепи, комплексное сопротивление которой

Сопротивление X = XL – XC положительное, т. е. XL > XC, треугольник сопротивлений такой цепи изображен на рис. 1.38.

При параллельном соединении элементов удобнее иметь дело не с сопротивлениями, а с проводимостями – резистивной G = 1/R, реактивными и , полной Y = 1/Z и комплексной Y = 1/Z. Если при последовательном соединении элементов складыва
лись их комплексные сопротивления, то при параллельном соединении складываются их проводимости.

Для параллельной RLC цепи (рис. 1.39, а) ее комплексная проводимость запишется в виде:

где G = 1/R – резистивная проводимость;

– емкостная проводимость;

– индуктивная проводимость;

– реактивная проводимость;

– полная проводимость;

– угол проводимости.

Резистивную и реактивную проводимости можно найти из треугольника проводимостей (рис. 1.39, б):

Случай, когда реактивная проводимость В равна нулю, т. е. когда также представляет особый интерес. В этот момент в параллельной RLC цепи наступает резонанс токов. Поэтому частота, на которой происходит совпадение реактивных проводимостей ветвей получила название частоты резонанса токов. Комплексная проводимость всей цепи при резонансе становится равной резистивной проводимости G. Более подробно явление резонанса токов будет рассмотрено позднее.

Пример 1.14. Определить комплексное сопротивление параллельной RLC цепи (рис. 1.39, а) на частоте f = 1 кГц для R = 100 Ом, L = 10 мГн, С = 10 мкФ.

Элементы цепи соединены параллельно, поэтому рассчитаем вначале комплексную проводимость YRLC, используя выражение (1.36).

Комплексная проводимость цепи

Комплексное сопротивление цепи обратно пропорционально комплексной проводимости, поэтому

Из данного раздела мы узнали, что:

1.3. Расчет реакций цепи в символической
форме

Расчет реакций в цепи с одним источником. Используется следующий порядок расчета:

1. Цепь, содержащую источник гармонических колебаний, преобразуют, заменяя ее элементы их комплексными сопротивлениями, а мгновенные значения эдс, токов и напряжений записывая в комплексной (символической) форме.

2. Рассчитывают комплексные значения токов в ветвях и напряжений на сопротивлениях, используя закон Ома и законы Кирхгофа.

3. Определяют соответствующие мгновенные значения токов и напряжений в цепи.

Пример 1.15. Определим мгновенные значения тока и напряжений на элементах цепи, содержащей источник гармонического напряжения В, сопротивление R = 300 Ом, индуктивность L = 0,6 Гн и емкость С = = 0,625 мкФ (рис. 1.40).

В соответствии с порядком расчета реакции в цепи с одним источником заменяем элементы цепи их комплексными сопротивлениями.

Анализируя выражение для мгновенного значения напряжения u(t), определяем, что круговая частота w = 2000 рад/с, т. е. частота колебаний f = w/(2p) = = 318,3 Гц. Сопротивление R = 300 Ом остается неизменным. Индуктивность L = 0,6 Гн заменяется сопротивлением

Емкость С = 0,625 мкФ заменяется сопротивлением

Гармоническое напряжение представим в показательной форме записи в виде

В результате получаем схему, изображенную на рис. 1.41.

Для определения тока и напряжений в этой схеме рассчитаем вначале комплексное сопротивление цепи Z относительно зажимов источника. Все сопротивления включены последовательно, поэтому

Отметим, что индуктивное и емкостное сопротивления цепи частично компенсировали друг друга и что реактивное сопротивление цепи меньше по величине, чем сопротивление любого из реактивных элементов.

Фактически возможно полностью исключить наличие реактивного сопротивления в цепи, изменив частоту генератора напряжения до выполнения условия |ZL| = |ZC|.

В рассматриваемом примере сопротивление цепи имеет индуктивный характер, поскольку реактивная составляющая комплексного сопротивления цепи имеет знак «плюс».

Комплексный ток Im в цепи определим, используя закон Ома для комплексного напряжения Um источника и комплексного сопротивления Z. Имеем:

Преобразуя комплексное сопротивление Z в показательную форму для упрощения деления комплексных чисел, получаем

Амплитудное значение тока равно 0,02 А, а начальная фаза равна –53°.

Напряжения на сопротивлениях цепи определяем, умножая ток Im на соответствующие сопротивления.

Ток Im имеет начальную фазу (–53°), напряжение UmR имеет такую же начальную фазу, т. е. векторы Im и UmR направлены по одной прямой на векторной диаграмме, изображенной на рис. 1.42.

Напряжение на индуктивности опережает ток на 90°, таким образом, UmL опережает вектор на горизонтальной оси рис. 1.42 на 37°.

Напряжение на емкости отстает от тока на 90°, а от горизонтальной оси на 143°.

Отметим также, что сдвиг фаз между UmL и UmС составляет 180°.

В соответствии с законом напряжений Кирхгофа

Последние два слагаемых представляют собой сумму напряжений на индуктивности и емкости, и этот суммарный вектор может быть направлен либо по UmL, либо по UmС в зависимости от того, какое из этих напряжений больше по величине. В нашем случае он имеет направление UmL.

Вектор UmR может быть добавлен к сумме UmL + UmС и результатом является вектор Um, как показано на рис. 1.42.

Мгновенные значения тока и напряжений на элементах цепи можно записать в виде

Векторная диаграмма часто бывает полезна при объяснении и интерпретации результатов расчета.

Пример 1.16. Найдем токи и напряжения в цепи, изображенной на рис. 1.43, если заданы значения R1 = 2 Ом, R2 = 2 Ом, ХL = 4 Ом, ХС = 2 Ом, .

Во-первых, определим комплексное сопротивление Zаб параллельного соединения резистора R2 и емкостного сопротивления ХС:

Сопротивление Zаб можно представить в виде Zаб = = Rаб – jXаб.

Получаем эквивалентную схему, изображенную на рис. 1.44.

Эквивалентное комплексное сопротивление цепи определяется как

Ток (рис. 1.45) определяется по закону Ома:

Токи Im1 и Im2 определяем по формулам разброса:

Следует отметить, что согласно закону токов Кирхгофа, Im1 + Im2 = Im. Векторная диаграмма токов приведена на рис. 1.46.

Определим напряжения на элементах цепи (рис. 1.43):

Согласно закону напряжений Кирхгофа (рис. 1.47)

Расчет реакций в цепи с несколькими источниками. Все методы расчета цепей в режиме постоянного тока применимы и к расчету цепей при гармоническом воздействии. Методы наложения, узловых напряжений, контурных токов, эквивалентного генератора используются для определения реакций в цепи с несколькими источниками гармонических колебаний.

Расчет выполняется для символической формы записи токов, напряжений и сопротивлений цепи.

Пример 1.17. Методом наложения определим токи в ветвях цепи, изображенной на рис. 1.48, если заданы значения R1 = 2 Ом, ХL = 4 Ом, ХС = 2 Ом,

Выберем направления токов в ветвях цепи (рис. 1.48). Поскольку в схеме два источника, то истинные направления токов неизвестны, поэтому выбираем их произвольно.

Метод наложения основан на принципе суперпозиции, согласно которому реакция линейной цепи на сумму воздействий равна алгебраической сумме реакций от каждого воздействия в отдельности.

Частичные схемы, в каждой из которых оставлен только один источник, а другой заменен его внутренним сопротивлением, изображены на рис. 1.49, а и 1.49, б.

Рассчитаем токи в первой частичной схеме (рис. 1.49, а). Внутреннее сопротивление источника тока равно бесконечности, поэтому . По закону Ома

Рассмотрим вторую частичную схему (рис. 1.49, б). Ток равен току источника тока, т. е.

Токи и рассчитываем, используя формулу разброса,

Токи в ветвях исходной схемы

Пример 1.18. Методом узловых напряжений определим токи в ветвях цепи, изображенной на рис. 1.48.

Заземляем узел 2. Потенциал этого узла равен нулю, Vm2 = 0.

Для узла 1 составляем уравнение состояния:

В этом уравнении Y11 – это собственная проводимость 1 узла, т. е. сумма проводимостей всех ветвей, подсоединенных к узлу 1:

Y12 – взаимная проводимость узлов 1 и 2, совпадающая в рассматриваемом примере с величиной Y11;

Из уравнения состояния находим потенциал первого узла

Токи в ветвях находим по закону Ома:

Значения токов в ветвях цепи рис. 1.48 те же самые, что и при расчете методом наложения.

Пример 1.19. Методом контурных токов определим токи в ветвях цепи, изображенной на рис. 1.48.

Выберем направления обхода контуров в цепи (рис. 1.50).

Для определения контурного тока составляем уравнение состояния:

В этом уравнении Z11 – собственное сопротивление 1 контура, равное сумме сопротивлений всех ветвей, образующих этот контур:

Z12 – взаимное сопротивление 1 и 2 контуров:

Из уравнения состояния находим контурный ток Imк1:

Зная контурные токи, находим токи ветвей,

Значения токов совпадают с теми, которые были получены при расчете цепи методами наложения и узловых напряжений.

Пример 1.20. Методом эквивалентного генератора определим ток Im1 в цепи, изображенной на рис. 1.48.

Разомкнем ветвь с емкостью и для определения напряжения холостого хода Umхх составим уравнение по второму закону Кирхгофа

В режиме холостого хода ток Imхх = –Imг, поэтому

Сопротивление эквивалентного генератора Zэг равно

Ток Im1 найдем по формуле

Получаем то же самое значение Im1, что и при применении других методов расчета.

Из данного раздела мы узнали, что

1.4. Комплексный коэффициент передачи

Рассмотрим электрическую цепь, изображенную на рис. 1.51.

Нас может интересовать любая реакция цепи (напряжение или ток в любом элементе или ветви цепи) на любое из приложенных воздействий. В этом случае цепь удобно представить четырехполюсником, на входе которого включен источник с заданным воздействием, а на выходе – интересующий нас элемент, например, как это сделано на рис. 1.52.

Символическое изображение напряжений и токов на входе и выходе четырехполюсника, показано на рис. 1.53.

Важнейшей характеристикой линейной электрической цепи является комплексный коэффициент передачи Н. Он определяется отношением комплексной амплитуды реакции к комплексной амплитуде воздействия.

В зависимости от того, что считается реакцией и воздействием, различают следующие виды коэффициентов передачи.

1. Комплексный коэффициент передачи по напряжению

2. Комплексный коэффициент передачи по току

3. Комплексное передаточное сопротивление

4. Комплексная передаточная проводимость

Комплексное число H может быть представлено в показательной форме

где Н – модуль передаточной функции, а j – ее аргумент.

Действительно, рассмотрим передаточную функцию

Модуль передаточной функции

представляет собой отношение амплитуды гармонической реакции цепи к амплитуде гармонического воздействия, т. е. показывает во сколько раз амплитуда гармонического колебания на входе цепи изменилась при прохождении колебания через цепь. Поэтому величину Hu называют коэффициентом передачи по напряжению.

Аргумент передаточной функции

показывает изменение начальной фазы входного колебания после передачи этого колебания по цепи и называется фазовым сдвигом.

Знание комплексного коэффициента передачи цепи позволяет вычислить реакцию цепи на гармоническое воздействие. Амплитуда реакции равна

а начальная ее фаза

Другими словами, чтобы найти амплитуду гармонического колебания на выходе цепи, нужно амплитуду входного гармонического колебания умножить на коэффициент передачи по напряжению, а чтобы найти начальную фазу выходного гармонического колебания, нужно к начальной фазе входного гармонического колебания добавить фазовый сдвиг, вносимый цепью.

В символической форме записи комплексная амплитуда гармонического колебания на выходе цепи определяется из соотношения:

Аналогичным образом вычисляют коэффициент передачи по току

и сдвиг фаз колебания тока

полное передаточное сопротивление цепи

и фазовый угол этого сопротивления

а также полную передаточную проводимость

и ее фазовый угол

В общем виде можно записать

Очевидно, что в схеме рис. 1.51 в качестве реакции может выступать напряжение или ток в любом элементе или любой ветви цепи, а в качестве воздействия использоваться не только напряжения или токи источников, но и любые напряжения или токи элементов (ветвей) цепи.

Пример 1.21. Найдем комплексный коэффициент передачи по напряжению цепи, приведенной в Примере 1.15, если реакцией цепи является напряжение на емкости uC(t).

При решении Примера 1.15 воздействие было записано в символической форме

Напряжение на емкости, т. е. реакция цепи, также было определено:

Комплексный коэффициент передачи

Коэффициент передачи по напряжению

показывает, что при прохождении по цепи амплитуда воздействия уменьшилась в 10 раз.

показывает, что напряжение на емкости отстает от входного колебания на 143°.

Пример 1.22. Найдем комплексный коэффициент передачи по току цепи, изображенной на рис. 1.54, если Imг = 5ej90°, А, R2 = 10 Ом, L = 30 мГн, f = 50 Гц, реакцией цепи является ток в индуктивности.

Для расчета комплексного коэффициента передачи по току

необходимо определить ток в индуктивности. Используя формулу разброса, получаем:

Комплексный коэффициент передачи по току

Очевидно, что комплексный коэффициент передачи цепи определяется значениями элементов цепи R2, L и частоты f.

Пример 1.23. Найдем напряжение на индуктивности uL(t) в цепи, приведенной в Примере 1.22, если комплексное передаточное сопротивление HZ = 6,86ej46,8° Ом.

Амплитуда напряжения на индуктивности

Начальная фаза напряжения на индуктивности

Мгновенное значение напряжения

Из данного раздела мы узнали, что

Вопросы и задания для самоконтроля

1. Какие колебания называются гармоническими?

2. Какие параметры характеризуют гармоническое колебание?

3. Как определяется величина и знак начальной фазы гармонического колебания по его графику?

4. Как связаны частота и период гармонического колебания?

5. Записать выражение для мгновенного значения тока, график которого изображен на рис. 1.5, б, если период колебания Т = 2 с. Определить значение тока в момент времени t1 = T/8.

6. Построить в одной системе координат графики напряжений u1(t) = , u2(t) = .

7. Какая связь между векторным и временным представлением гармонических колебаний?

8. Построить векторы гармонических колебаний, приведенных в п. 6.

9. Построить в одной системе координат графики гармонических колебаний, которым соответствуют векторы и , вращающиеся с одинаковой частотой. Определить сдвиг фаз этих колебаний.

10. Какая связь между параметрами комплексного и временного представления гармонических колебаний?

11. Сформулировать закон Ома для резистивной, индуктивной и емкостной цепей.

12. Какой сдвиг фаз между напряжением и током в резисторе (емкости, индуктивности)?

13. Как рассчитывается комплексное сопротивление последовательного соединения R, L, C элементов?

14. Как рассчитывается комплексная проводимость параллельного соединения R, L, C элементов?

15. Определить комплексное сопротивление цепи, изображенной на рис. 1.55, если

R1 = 20 Ом, R2 = 40 Ом,

Построить треугольник сопротивления цепи.

16. Какие методы используются для расчета цепей с источниками гармонических колебаний?

17. Рассчитать токи в ветвях цепи, изображенной на рис. 1.55, если на вход подается напряжение , В. Построить векторную диаграмму токов.

18. Рассчитать ток Im2 в цепи, изображенной на рис. 1.56, методом наложения и методом эквивалентного генератора, если заданы сопротивления R = 10 Ом, ХL = 30 Ом, ХС = 20 Ом и Um = 10ej0° В, Imг = ej270° А.

19. Что такое комплексный коэффициент передачи? Какие виды комплексных коэффициентов передачи известны?

20. Определить коэффициенты передачи в цепи Примера 1.16, если реакцией является Im2.

* Следует различать резисторы, катушки индуктивности и конденсаторы как физические элементы электрической цепи и резистивные, индуктивные и емкостные элементы как идеализированные элементы, обладающие свойствами необратимого рассеяния энергии или свойствами накопления энергии магнитного и электрического полей. В инженерной практике резистивный, индуктивный и емкостной элементы часто называют просто сопротивлением, индуктивностью и емкостью, отождествляя по существу элемент с его параметром. В дальнейшем для простоты, где это не приведет к недоразумению, мы также будем пользоваться этой терминологией.

источники:

http://kratko-obo-vsem.ru/articles/658-triangle-resistance.html

http://pandia.ru/text/78/272/83148-3.php

Источник

Basic concepts[edit]

Resonance[edit]

Natural frequency[edit]

Damping[edit]

Bandwidth[edit]

Q factor[edit]

Scaled parameters[edit]

Series circuit[edit]

Transient response[edit]

Overdamped response[edit]

Underdamped response[edit]

Critically damped response[edit]

Laplace domain[edit]

Laplace admittance[edit]

Poles and zeros[edit]

General solution[edit]

Sinusoidal steady state[edit]

Parallel circuit[edit]

Frequency domain[edit]

Other configurations[edit]

History[edit]

Applications[edit]

Variable tuned circuits[edit]

Filters[edit]

Low-pass filter[edit]

High-pass filter[edit]

Band-pass filter[edit]

Band-stop filter[edit]

Oscillators[edit]

Voltage multiplier[edit]

Pulse discharge circuit[edit]

See also[edit]

Footnotes[edit]

References[edit]

Bibliography[edit]

3.4. Мощности цепи синусоидального тока

Анализ цепи с последовательным соединением

Схема цепи с последовательным соединением элементов

Векторная диаграмма

Треугольник напряжений цепи с последовательным соединением элементов

Пример задачи с решением

Треугольник сопротивлений

Анализ линейных электрических цепей (стр. 3 )

1.3. Расчет реакций цепи в символической форме

1.4. Комплексный коэффициент передачи

Вопросы и задания для самоконтроля

1.3. Расчет реакций цепи в символической
форме