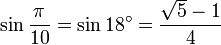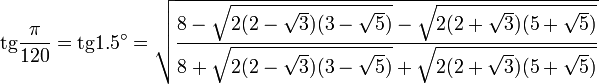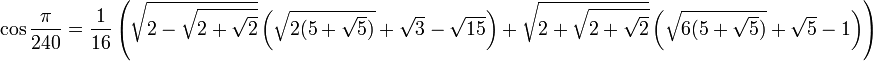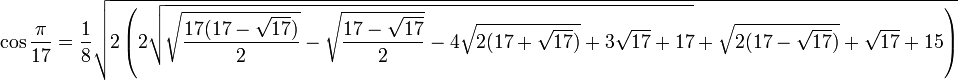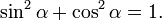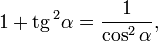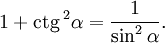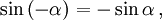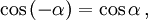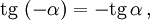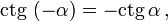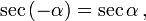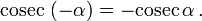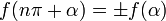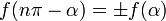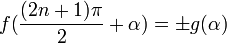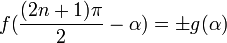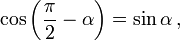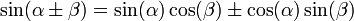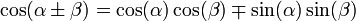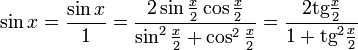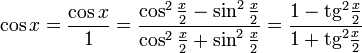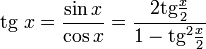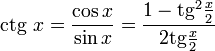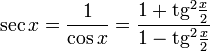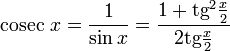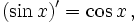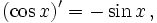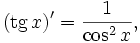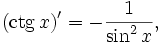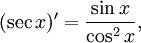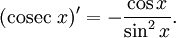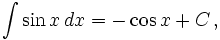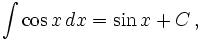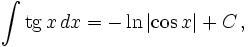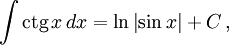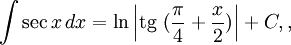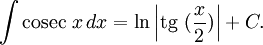
|
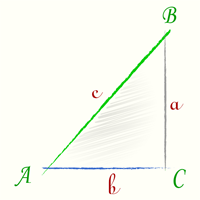
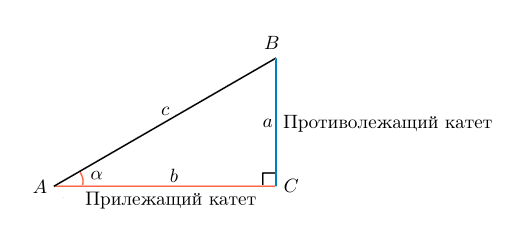
Секанс угла sec(A) — есть отношение [ sec(A) = frac{c}{b} ] |
Секанс угла — sec(A), таблица
|
0° Секанс угла 0 градусов |
$ sec(0°) = sec(0) = 1 $ |
1.000 |
|
30° Секанс угла 30 градусов |
$ sec(30°) = secBig(Largefrac{pi}{6}normalsizeBig) = Largefrac{2}{sqrt{3}}normalsize $ |
1.155 |
|
45° Секанс угла 45 градусов |
$ sec(45°) = secBig(Largefrac{pi}{4}normalsizeBig) = sqrt{2} $ |
1.414 |
|
60° Секанс угла 60 градусов |
$ sec(60°) = secBig(Largefrac{pi}{3}normalsizeBig) = 2 $ |
2.000 |
|
90° Секанс угла 90 градусов |
$ sec(90°) = secBig(Largefrac{pi}{2}normalsizeBig) = infin $ |
∞ |
Вычислить, найти секанс угла sec(A) и угол, в прямоугольном треугольнике
Вычислить, найти секанс угла sec(A) по углу A в градусах
Вычислить, найти секанс угла sec(A) по углу A в радианах
Секанс угла — sec(A) |
стр. 226 |
|---|
Секанс принято определять как отношение единицы и косинуса. То есть:
secα=1cosαsecalpha=frac{1}{cosalpha}
Секанс вместе с косинусом являются единственными четными функциями из всех представленных тригонометрических функций.
В случае с рисунком, описанным выше возможен такой вариант записи секанса:
secα=cbsecalpha=frac{c}{b}
Отсюда следует, что секанс — отношение гипотенузы к прилежащему катету в прямоугольном треугольнике.
Косинус угла в треугольнике равен 0.050.05. Найдите секанс этого угла.
Решение
cosα=0.05cosalpha=0.05
secα=1cosα=10.05=20secalpha=frac{1}{cosalpha}=frac{1}{0.05}=20
Ответ
2020
Прилежащий к углу катет равен 4 см4text{ см}. Гипотенуза равна 5 см5text{ см}. Найдите секанс этого угла.
Решение
b=4b=4
c=5c=5
secα=cb=54=1.25secalpha=frac{c}{b}=frac{5}{4}=1.25
Ответ
1.251.25
Не знаете, где заказать работу по математике онлайн? Наши эксперты готовы вам помочь!
Тест по теме «Вычисление секанса»
Что такое секанс угла
Пусть задан прямоугольный треугольник ABC с острым углом α, тогда косинусом угла α будет отношение гипотенузы к прилежащему катету sec α = AC/AB.
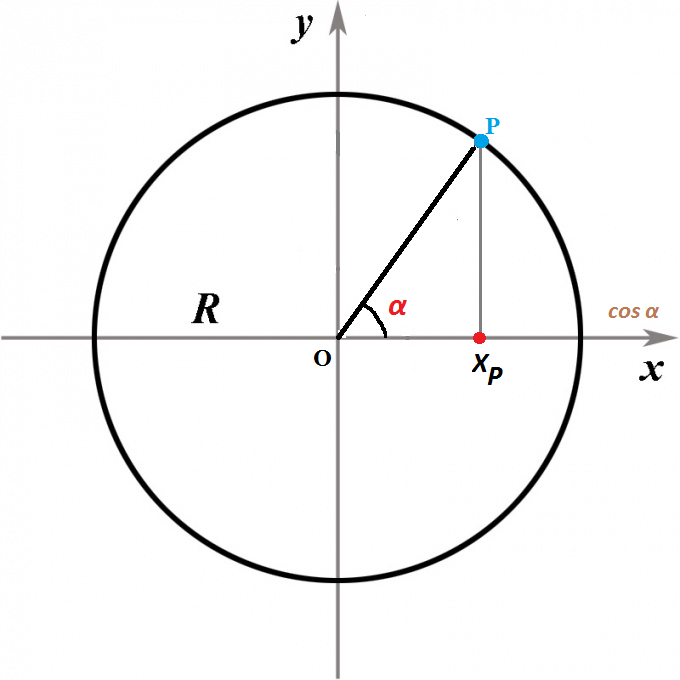
Так же для определения секанса угла можно воспользоваться окружностью, построенной в декартовой системе координат, радиуса R и центром в начале координат O.
На окружности отметим точку P с координатами (1;0), теперь повернем луч OP на некоторый угол α. Направление против часовой стрелки считается положительным, по часовой стрелки – отрицательным.
Секансом угла α будет отношение радиуса окружности к абсциссе точки XP
sec α = R/XP, в случае, если окружность единичная (радиус окружности = 1), формула примет вид sec α = 1/XP и так как косинус угла равен абсциссе точки XP, можно записать sec α = 1/cos α.
|
Секанс — определение, формула Что такое секанс? Секанс — это величина, обратная косинусу, т.е. sec(a)=1/cos(a). Если рассматривать на прямоугольном треугольнике, то секанс — это отношение гипотенузы к катету, являющемуся стороной рассматриваемого угла (к прилежащему катету). автор вопроса выбрал этот ответ лучшим Лара Изюминка 2 года назад Секанс — это величина, используемая в тригонометрии. Это величина обратная косинусу, то есть это 1 / соs . зная, что косинус это в прямоугольном треугольнике отношение прилежащего к углу катета к гипотенузе, а тогда определение секанса — отношение гипотенузы к катету. Иногда используется в тригонометрии эта величина для сокращения записи формулы. Чтобы формула была более наглядна. Анатолий-тдр5 6 лет назад Для запоминания можно простенькую формулу использовать sc=1 (я называю её структурной). Отсюда следует всё, что угодно: sec=1/cos, cosec=1/sin, cos=1/sec, sin=1/cosec. Обл.определения для sec и cosec определяется из условий cos≠0 и sin≠0, обл.значений (-∞;-1]U[1;+∞). Другие свойства и графики можно в справочниках посмотреть. Знаете ответ? |
Рис. 1
Графики тригонометрических функций: синуса, косинуса, тангенса, секанса, косеканса, котангенса
Тригонометрические функции — вид элементарных функций. Обычно к ним относят синус (sin x), косинус (cos x), тангенс (tg x), котангенс (ctg x), секанс (sec x) и косеканс (cosec x), последняя пара функций в настоящее время сравнительно малоупотребительна (про ещё менее употребляемые функции см. здесь). В англоязычной литературе тангенс, котангенс и косеканс обозначаются tan x, cot x, csc x. Обычно тригонометрические функции определяются геометрически, но можно определить их аналитически через суммы рядов или как решения некоторых дифференциальных уравнений, что позволяет расширить область определения этих функций на комплексные числа.
Содержание
- 1 Способы определения
- 1.1 Геометрическое определение
- 1.1.1 Определение тригонометрических функций для острых углов
- 1.2 Определение тригонометрических функций как решений дифференциальных уравнений
- 1.3 Определение тригонометрических функций как решений функциональных уравнений
- 1.4 Определение тригонометрических функций через ряды
- 1.1 Геометрическое определение
- 2 Значения тригонометрических функций для некоторых углов
- 2.1 Значения тригонометрических функций нестандартных углов
- 3 Свойства тригонометрических функций
- 3.1 Простейшие тождества
- 3.2 Чётность
- 3.3 Периодичность
- 3.4 Формулы приведения
- 3.5 Формулы сложения
- 3.6 Однопараметрическое представление
- 4 Производные и интегралы
- 5 История
- 6 См. также
- 7 Ссылки
Способы определения
Геометрическое определение
Рис. 2
Определение тригонометрических функций
Обычно тригонометрические функции определяются геометрически. Пусть дана декартова система координат на плоскости и построена окружность радиуса R с центром в начале координат O. Будем измерять углы как повороты от положительного направления оси абсцисс до луча OB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным. Абсциссу точки В обозначим xB, ординату обозначим yB (см. рисунок.)
Рис. 3.
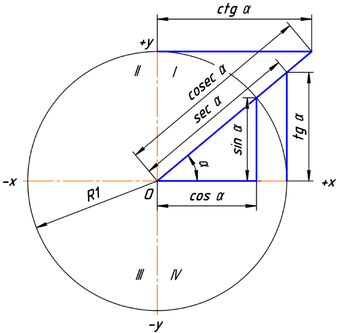
Тригонометрические функции угла α в тригонометрической окружности с радиусом, равным единице.
Ясно, что значения тригонометрических функций не зависят от величины радиуса окружности R в силу свойств подобных фигур. Часто этот радиус принимают равным величине единичного отрезка, тогда синус равен просто ординате yB, а косинус — абсциссе xB. На рисунке 3 показаны величины тригонометрических функций для единичной окружности.
Если α — действительное число, то синусом α в математическом анализе называется синус угла, радианная мера которого равна α, аналогично для прочих тригонометрических функций.
Определение тригонометрических функций для острых углов
Рис. 4.
Тригонометрические функции острого угла
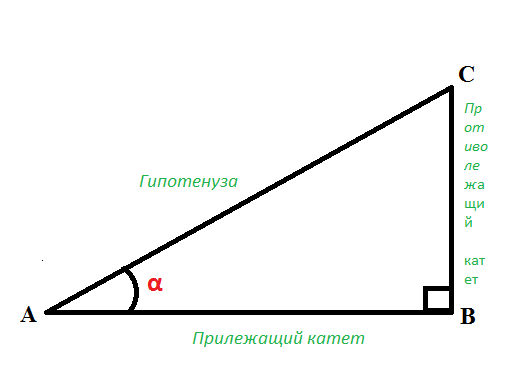
Во многих учебниках элементарной геометрии до настоящего времени тригонометрические функции острого угла определяются как отношения сторон прямоугольного треугольника. Пусть OAB — треугольник с углом α. Тогда:
- Синусом α называется отношение AB/OB (противолежащего катета к гипотенузе)
- Косинусом α называется отношение ОА/OB (прилежащего катета к гипотенузе)
- Тангенсом α называется отношение AB/OA (отношение противолежащего катета к прилежащему)
- Котангенсом α называется отношение ОА/AB (отношение прилежащего катета к противолежащему)
- Секансом α называется отношение ОB/OA (гипотенузы к прилежащему катету)
- Косекансом α называется отношение ОB/AB (гипотенузы к противолежащему катету)
Построив систему координат с началом в точке O, направлением оси абсцисс вдоль OA и в случае необходимости изменив ориентацию (перевернув) треугольник так, чтобы он находился в первой четверти системы координат, и затем, построив окружность с радиусом, равным гипотенузе, сразу находим, что такое определение функций приводит к тому же результату, что и предыдущее. Данное определение имеет некоторое педагогическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач про тупоугольные треугольники (см. Теорема синусов, Теорема косинусов).
Определение тригонометрических функций как решений дифференциальных уравнений
Функции косинус и синус можно определить как чётное (косинус) и нечётное (синус) решение дифференциального уравнения
с начальными условиями cos(0) = sin'(0) = 1, то есть как функций одной переменной, вторая производная которых равна самой функции, взятой со знаком минус:
Определение тригонометрических функций как решений функциональных уравнений
Функции косинус и синус можно определить как непрерывные решения (f и g соответственно) системы функциональных уравнений:
Определение тригонометрических функций через ряды
Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу и что производная косинуса равна минус синусу. Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде суммы степенны́х рядов:
Пользуясь этими формулами, а также уравнениями 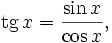
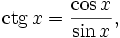
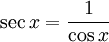
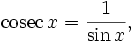
где Bn — числа Бернулли.
где En — числа Эйлера.
Значения тригонометрических функций для некоторых углов
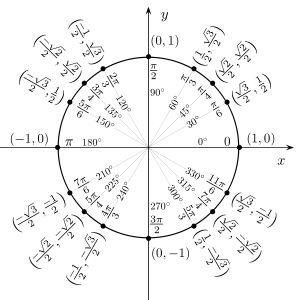
Значения синуса, косинуса, тангенса, котангенса, секанса и косеканса для некоторых углов приведены в таблице.
Значения косинуса и синуса на окружности.
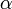 |
0°(0 рад) | 30° (π/6) | 45° (π/4) | 60° (π/3) | 90° (π/2) | 180° (π) | 270° (3π/2) | 360° (2π) |
|---|---|---|---|---|---|---|---|---|
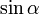 |
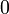 |
 |
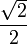 |
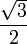 |
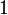 |
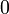 |
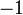 |
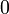 |
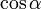 |
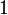 |
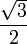 |
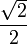 |
 |
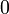 |
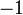 |
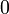 |
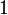
|
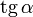 |
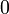 |
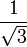 |
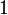 |
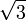 |
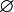 |
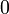 |
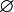 |
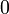 |
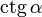 |
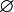 |
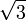 |
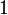 |
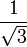 |
 |
 |
 |
 |
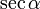 |
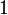 |
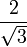 |
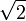 |
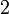 |
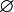 |
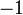 |
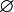 |
 |
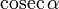 |
 |
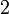 |
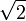 |
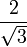 |
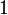 |
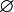 |
 |
 |
Значения тригонометрических функций нестандартных углов
Свойства тригонометрических функций
Простейшие тождества
Так как синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α то, согласно уравнению единичной окружности или теореме Пифагора, имеем:
Деля это уравнение на квадрат косинуса и синуса соответственно имеем далее:
Чётность
Косинус и секанс — чётные. Остальные четыре функции — нечётные, то есть:
Периодичность
Функции y = sin α, y = cos α, y = sec α, y = cosec α — периодические с периодом 2π. Функции: y = tg α, y = ctg α — c периодом π
Формулы приведения
Здесь f — любая тригонометрическая функция, g — соответствующая ей другая функция из пары (то есть косинус для синуса, синус для косинуса и аналогично для остальных функций). Нужный знак в правой части равенства определяется следующим образом: предположим что угол α находится в первой четверти, тогда определяем знаки значений функций в левой и правой части равенства и в случае их несовпадения перед правой частью пишем знак -, например:
Формулы сложения
Другие тригонометрические тождества.
Однопараметрическое представление
Все тригонометрические функции можно выразить через тангенс половинного угла.
Производные и интегралы
Все тригонометрические функции непрерывно дифференцируемы на всей области определения:
Интегралы тригонометрических функций на области определения выражаются через элементарные функции следующим образом:
- См. также Список интегралов от тригонометрических функций
История
Линия синуса у индийских математиков первоначально называлась «арха-джива» («полутетива»), затем слово «арха» было отброшено и линию синуса стали называть просто «джива». Арабские переводчики не перевели слово «джива» арабским словом «ватар», обозначающим тетиву и хорду, а транскрибировали арабскими буквами и стали называть линию синуса «джиба». Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса «джайб», что буквально обозначает «впадина», «пазуха». При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.
Современное обозначение синуса sin и косинуса cos введено Леонардом Эйлером в XVIII веке.
Термины «тангенс» (от лат. tangens — касающийся) и «секанс» (лат. secans — секущий) были введены датским математиком Томасом Финке (1561—1656) в его книге «Геометрия круглого» (Geometria rotundi, 1583)
Сам термин тригонометрические функции введён Клюгелем в 1770.
См. также
- Гиперболические функции
- Обратные тригонометрические функции
- Редко используемые тригонометрические функции
- Эллиптические функции
- Теорема косинусов
- Теорема синусов
- Тригонометрические формулы
- Четырёхзначные математические таблицы (Таблицы Брадиса)
- Функция Гудермана связывает тригонометрические функции и гиперболические функции без привлечения комплексных чисел.
Ссылки
- GonioLab: Проясненная Единичная Окружность, Тригонометрические и Гиперболические функции (Java Web Start)
- Weisstein, Eric W. Тригонометрические функции на сайте Wolfram MathWorld.(англ.)
- Онлайн калькулятор: вычисление значений тригонометрических функций
Wikimedia Foundation.
2010.


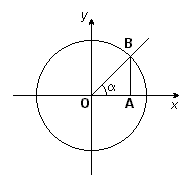

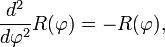
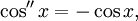
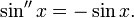
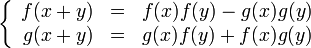
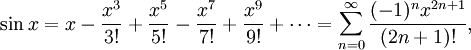
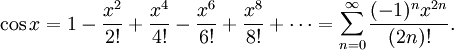
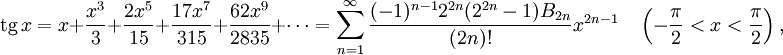 где
где 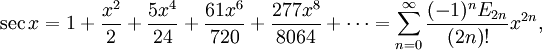 где
где