24.2 Матрицы и графы. Нахождение путей и сечений
с помощью структурной матрицы
Трудно переоценить роль матриц в теории графов (в частности, матрицы полезны, чтобы данный граф более “легко” воспринимался компьютером). Перечислим наиболее известные матрицы.
- Матрица смежности. Это квадратная матрица порядка п (п – число вершин), в которой нули стоят по главной диагонали (если в графе нет петель, а если петли есть в вершине k (и число этих петель равно р), то на главной диагонали в строчке с номером k стоит число р). Если вершина i связана с вершиной j одним ребром, то элемент матрицы смежности aij равен 1, если эти вершины связаны s ребрами, то аij= s. Аналогичным образом строятся матрицы смежности для орграфов и для мультиграфов.
Легко видеть, что матрица В =А2 = АА составлена из целых чисел bij, которые равны числу путей длины 2, соединяющих вершины i и j. Понятно, что А3 составлена из чисел, равных числу путей длины 3 (т. е. путей из 3-х ребер) из вершины i в вершину j и т. д.
- Матрица инциденций – это матрица размера n´ m, где n – число вершин, а m – число ребер графа, при этом ее элементы kij равны 1, если вершина с номером i является для ребра с номером j начальной или конечной (если ребро неориентировано) и начальной для ориентированных ребер. Заметим, что матрица инциденций сравнительно редко используется, так как в современных условиях (где число ребер часто очень велико) она имеет слишком большое число столбцов.
- Структурная матрица. Именно эта матрица имеет особое значение в теории сетей связи. Структурная матрица – это символьная матрица порядка п. Она составляется следующим образом: на главной диагонали стоит 1, т. е. aii = 1, остальные элементы – это символьные обозначения ребер (если вершины i и j не соединены ребром, то aii = 0). При этом, если при i<j вершины i и j соединены ребром а, то элемент sij = a, при i>j – это отрицание а, которое обычно отмечается чертой сверху. Если связи вершины i c вершиной j нет, то соответствующий элемент равен 0, структурная матрица может составляться и для орграфа и для мультиграфа без петель (здесь если два ребра а и b соединяют две вершины, то соответствующий элемент при i <j равен aÚ b, а при i>j этот элемент равен
Отметим, что в учебных целях, когда действия с матрицами осуществляются студентами “вручную” (число вершин в графе невелико), можно обозначать ребра латинскими буквами без индексов a, b, c и т. д., но при использовании компьютера гораздо удобнее обозначать ребра а(i,j), если это ребро соединяет вершины i и j при i<j и с чертой сверху, если i>j.
Теорема. Для того чтобы найти все пути (простые) из вершины i в вершину j достаточно раскрыть минор M(j,i) структурной матрицы методами булевой алгебры. При этом раскрытие минора производится обычными действиями с определителями, но при этом сложение заменяется дизъюнкцией, умножение – конъюнкцией, знаки умножения на числа не используются.
Подробно доказывать эту теорему не будем, но отметим, что определитель равен сумме (в данном случае дизъюнкции) элементов, взятых по одному из каждой строчки и каждого столбца с определенным знаком. В нашем случае знаки не присутствуют, а значит, любой член раскрытия определителя всей структурной матрицы S соответствует циклу в графе. Если же брать минор M(j,i), то его раскрытие соответствует тем членам определителя, в которых имелся элемент s(j,i), но без самого этого элемента (таким образом, индексы i и j встречаются вместо двух только один раз). Это и означает, что получаем маршрут от вершины с номером i к вершине с номером j.
Понятно, что раскрытие минора методами булевой алгебры предусматривает, что верны следующие соотношения: 1Ú a = 1, (это свойство нужно, для того чтобы не проходить по одному ребру дважды в противоположных направлениях), а также используется правило простого поглощения (хÚ ху = х). Видно, что если не использовать правило поглощения, то получим все маршруты (без повторения ребер), связывающие вершины i и j.
Примечание. 1. Если граф не ориентирован, то миноры M(j,i) и M(i,j) совпадают.
2. После получения ответа, черточки над обозначениями ребер (т. е. отрицания) можно убрать (на самом деле “черта” над ребром означает, что ребро проходится от вершины с большим номером к вершине с меньшим номером). Затем рекомендуется записать каждый путь по порядку прохождения ребер (в этом случае удобны обозначения ребер с индексами вершин).
Сечением (разрезом) между вершинами i и j называется неизбыточный набор ребер, при удалении которых из графа теряется связь между данными вершинами (не существует пути из вершины i в вершину j). Заметим, что сечений между данными вершинами может быть много, и они могут содержать разное количество ребер.
Слово “неизбыточный” означает, что если любое ребро из сечения снова возвратить в граф, то связь восстановится.
Естественно, что если известны все пути из вершины i в вершину j, причем эти пути заданы в виде ДНФ, т. е. дизъюнктивной нормальной формы (а именно такой вид получается после раскрытия соответствующего минора структурной матрицы), то все сечения между этими вершинами можно получить отрицанием этих путей (по правилу де Моргана конъюнкцию заменить на дизъюнкцию и наоборот), затем полученное выражение снова привести к ДНФ, используя раскрытие скобок по обычным правилам, при этом правило поглощения обеспечит неизбыточность набора ребер в каждом сечении. Ясно, что знаки отрицания (черточки над символами ребер) можно опустить.
Трудно
переоценить роль матриц в теории графов
(в частности, матрицы полезны, чтобы
данный граф более “легко” воспринимался
компьютером). Перечислим наиболее
известные матрицы.
-
Матрица
смежности.
Это квадратная матрица порядка п
(п –
число
вершин), в которой нули стоят по главной
диагонали (если в графе нет петель, а
если петли есть в вершине k
(и
число этих петель равно р),
то
на главной диагонали в строчке с номером
k
стоит
число р).
Если
вершина i
связана
с вершиной j
одним
ребром,
то элемент матрицы смежности aij
равен
1, если эти вершины
связаны
s
ребрами,
то аij= s.
Аналогичным
образом строятся матрицы смежности
для орграфов и для мультиграфов.
Легко
видеть, что матрица В
=А2
= АА составлена
из целых чисел bij,
которые
равны числу путей длины 2, соединяющих
вершины i
и j. Понятно,
что А3
составлена
из чисел, равных числу путей длины 3
(т. е. путей из 3-х ребер) из вершины i
в
вершину
j
и
т. д.
-
Матрица
инциденций
– это матрица размера n
m,
где
n
– число
вершин, а m
– число
ребер графа, при этом ее элементы kij
равны
1, если вершина с номером i
является
для ребра с номером j
начальной
или конечной (если ребро неориентировано)
и начальной для ориентированных ребер.
Заметим, что матрица инциденций
сравнительно редко используется, так
как в современных условиях (где число
ребер часто очень велико) она имеет
слишком большое число столбцов. -
Структурная
матрица.
Именно эта матрица имеет особое значение
в теории сетей связи. Структурная
матрица – это символьная матрица
порядка п.
Она составляется следующим образом:
на главной диагонали стоит 1, т. е.
aii = 1,
остальные элементы – это символьные
обозначения ребер (если вершины i
и
j
не
соединены ребром, то aii = 0).
При этом, если при i<j
вершины
i
и
j
соединены
ребром а,
то
элемент sij = a,
при
i>j – это
отрицание а,
которое обычно отмечается чертой
сверху. Если связи вершины i
c
вершиной j
нет,
то соответствующий элемент равен 0,
структурная матрица может составляться
и для орграфа и для мультиграфа без
петель (здесь если два
ребра
а
и
b
соединяют
две вершины, то соответствующий элемент
при i
<j равен
a
b,
а
при
i>j
этот
элемент равен
Отметим,
что в учебных целях, когда действия с
матрицами осуществляются студентами
“вручную” (число вершин в графе
невелико), можно обозначать ребра
латинскими буквами без индексов a, b, c
и
т. д., но при использовании компьютера
гораздо удобнее обозначать ребра а(i,j),
если это ребро соединяет вершины i
и
j
при
i<j
и
с чертой сверху, если i>j.
Теорема.
Для того чтобы найти все пути (простые)
из вершины i в вершину j достаточно
раскрыть минор M(j,i)
структурной матрицы методами булевой
алгебры. При этом раскрытие минора
производится обычными действиями с
определителями, но при этом сложение
заменяется дизъюнкцией, умножение –
конъюнкцией, знаки умножения на числа
не используются.
Подробно
доказывать эту теорему не будем, но
отметим, что определитель равен сумме
(в данном случае дизъюнкции) элементов,
взятых по одному из каждой строчки и
каждого столбца с определенным знаком.
В нашем случае знаки не присутствуют,
а значит, любой член раскрытия определителя
всей структурной матрицы S
соответствует циклу
в
графе. Если же брать минор M(j,i),
то
его раскрытие соответствует тем членам
определителя, в которых имелся элемент
s(j,i),
но
без
самого
этого элемента (таким образом, индексы
i
и
j
встречаются
вместо
двух только один раз). Это и означает,
что получаем маршрут
от
вершины с номером i
к
вершине с номером j.
Понятно,
что раскрытие минора методами булевой
алгебры предусматривает, что верны
следующие соотношения: 1
a = 1,
(это
свойство нужно, для того чтобы не
проходить по одному ребру дважды в
противоположных направлениях), а также
используется правило простого поглощения
(х
ху = х).
Видно,
что если не использовать правило
поглощения, то получим все маршруты
(без
повторения ребер), связывающие вершины
i
и
j.
Примечание.
1. Если граф не ориентирован, то миноры
M(j,i)
и
M(i,j)
совпадают.
2. После
получения ответа, черточки над
обозначениями ребер (т. е. отрицания)
можно убрать (на самом деле “черта”
над ребром означает, что ребро проходится
от вершины с большим номером к вершине
с меньшим номером). Затем рекомендуется
записать каждый путь по порядку
прохождения ребер (в этом случае удобны
обозначения ребер с индексами вершин).
Сечением
(разрезом) между
вершинами
i и
j
называется
неизбыточный набор ребер, при удалении
которых из графа теряется связь между
данными вершинами (не существует пути
из вершины i
в
вершину j).
Заметим, что сечений между данными
вершинами может быть много, и они могут
содержать разное количество ребер.
Слово
“неизбыточный” означает, что если
любое ребро из сечения снова возвратить
в граф, то связь восстановится.
Естественно,
что если известны все пути из вершины
i
в
вершину j,
причем
эти пути заданы в виде ДНФ, т. е.
дизъюнктивной нормальной формы (а именно
такой вид получается после раскрытия
соответствующего минора структурной
матрицы), то все сечения
между
этими вершинами можно получить
отрицанием этих
путей (по правилу де Моргана конъюнкцию
заменить на дизъюнкцию и наоборот),
затем полученное выражение снова
привести к ДНФ, используя раскрытие
скобок по обычным правилам, при этом
правило поглощения обеспечит неизбыточность
набора ребер в каждом сечении. Ясно, что
знаки отрицания (черточки над символами
ребер) можно опустить. Пример на эту
тему приведен в разд. 15 (примеры решения
типовых задач).
Соседние файлы в папке Дискретная математика
- #
- #
- #
- #
- #
Трудно переоценить роль матриц в теории графов (в частности, матрицы полезны, чтобы данный граф более “легко” воспринимался компьютером). Перечислим наиболее известные матрицы.
- Матрица смежности. Это квадратная матрица порядка п (п – число вершин), в которой нули стоят по главной диагонали (если в графе нет петель, а если петли есть в вершине k (и число этих петель равно р), то на главной диагонали в строчке с номером k стоит число р). Если вершина i связана с вершиной j одним ребром, то элемент матрицы смежности aij равен 1, если эти вершины связаны s ребрами, то аij= s. Аналогичным образом строятся матрицы смежности для орграфов и для мультиграфов.
Легко видеть, что матрица В =А2 = АА составлена из целых чисел bij, которые равны числу путей длины 2, соединяющих вершины i и j. Понятно, что А3 составлена из чисел, равных числу путей длины 3 (т. е. путей из 3-х ребер) из вершины i в вершину jи т. д.
- Матрица инциденций – это матрица размера nґ m, где n – число вершин, а m – число ребер графа, при этом ее элементы kij равны 1, если вершина с номером i является для ребра с номером j начальной или конечной (если ребро неориентировано) и начальной для ориентированных ребер. Заметим, что матрица инциденций сравнительно редко используется, так как в современных условиях (где число ребер часто очень велико) она имеет слишком большое число столбцов.
- Структурная матрица. Именно эта матрица имеет особое значение в теории сетей связи. Структурная матрица – это символьная матрица порядка п. Она составляется следующим образом: на главной диагонали стоит 1, т. е. aii = 1, остальные элементы – это символьные обозначения ребер (если вершины i и j не соединены ребром, то aii = 0). При этом, если при i<j вершины i и j соединены ребром а, то элемент sij = a, при i>j – это отрицание а, которое обычно отмечается чертой сверху. Если связи вершины i c вершиной j нет, то соответствующий элемент равен 0, структурная матрица может составляться и для орграфа и для мультиграфа без петель (здесь если два ребра а и b соединяют две вершины, то соответствующий элемент при i <j равен aЪ b, а при i>j этот элемент равен
Отметим, что в учебных целях, когда действия с матрицами осуществляются студентами “вручную” (число вершин в графе невелико), можно обозначать ребра латинскими буквами без индексов a, b, c и т. д., но при использовании компьютера гораздо удобнее обозначать ребра а(i,j), если это ребро соединяет вершины i и j при i<j и с чертой сверху, если i>j.
Теорема. Для того чтобы найти все пути (простые) из вершины i в вершину j достаточно раскрыть минор M(j,i) структурной матрицы методами булевой алгебры. При этом раскрытие минора производится обычными действиями с определителями, но при этом сложение заменяется дизъюнкцией, умножение – конъюнкцией, знаки умножения на числа не используются.
Подробно доказывать эту теорему не будем, но отметим, что определитель равен сумме (в данном случае дизъюнкции) элементов, взятых по одному из каждой строчки и каждого столбца с определенным знаком. В нашем случае знаки не присутствуют, а значит, любой член раскрытия определителя всей структурной матрицы S соответствует циклу в графе. Если же брать минор M(j,i), то его раскрытие соответствует тем членам определителя, в которых имелся элемент s(j,i), но без самого этого элемента (таким образом, индексы i и j встречаются вместо двух только один раз). Это и означает, что получаем маршрут от вершины с номером i к вершине с номером j.
Понятно, что раскрытие минора методами булевой алгебры предусматривает, что верны следующие соотношения: 1Ъ a = 1, 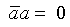
Примечание. 1. Если граф не ориентирован, то миноры M(j,i) и M(i,j) совпадают.
2. После получения ответа, черточки над обозначениями ребер (т. е. отрицания) можно убрать (на самом деле “черта” над ребром означает, что ребро проходится от вершины с большим номером к вершине с меньшим номером). Затем рекомендуется записать каждый путь по порядку прохождения ребер (в этом случае удобны обозначения ребер с индексами вершин).
Сечением (разрезом) между вершинами i и j называется неизбыточный набор ребер, при удалении которых из графа теряется связь между данными вершинами (не существует пути из вершины i в вершину j). Заметим, что сечений между данными вершинами может быть много, и они могут содержать разное количество ребер.
Слово “неизбыточный” означает, что если любое ребро из сечения снова возвратить в граф, то связь восстановится.
Естественно, что если известны все пути из вершины i в вершину j, причем эти пути заданы в виде ДНФ, т. е. дизъюнктивной нормальной формы (а именно такой вид получается после раскрытия соответствующего минора структурной матрицы), то всесечения между этими вершинами можно получить отрицанием этих путей (по правилу де Моргана конъюнкцию заменить на дизъюнкцию и наоборот), затем полученное выражение снова привести к ДНФ, используя раскрытие скобок по обычным правилам, при этом правило поглощения обеспечит неизбыточность набора ребер в каждом сечении. Ясно, что знаки отрицания (черточки над символами ребер) можно опустить. Пример на эту тему приведен в разд. 15 (примеры решения типовых задач).
ПРИКЛАДНАЯ ДИСКРЕТНАЯ МАТЕМАТИКА
2008 Математические основы надежности вычислительных и управляющих систем № 2(2)
УДК 519.17: 681.3
ПОИСК ВЕРШИННЫХ (s, 0-СЕЧЕНИЙ ГРАФА ВЫЧИСЛИТЕЛЬНОЙ СИСТЕМЫ С ОГРАНИЧЕНИЕМ ПО ДИАМЕТРУ КОМПОНЕНТ СВЯЗНОСТИ1
В.А. Мелентьев
Институт физики полупроводников СО РАН, г. Новосибирск E-mail: melva@isp.nsc.ru
В рамках задачи поиска d-ограниченной связности графа вычислительной системы (ВС) предложен подход к решению проблемы поиска множества минимальных d-ограниченных (s, ¿)-сечений, базирующийся на скобочной форме представления проекций и образов графа.
Ключевые слова: структурная отказоустойчивость вычислительной системы, диаметр компоненты связности.
Отказоустойчивость системы базируется на ее структурной конъюнктуре, заключающейся в наличии достаточного для сохранения работоспособности числа вершин в графе ВС и в обеспечении заданного критерия их связанности. В качестве последнего здесь определено значение максимально допускаемого в системе эксцентриситета вершин, или диаметра компоненты связности графа ВС при ее деградации вследствие происходящих в системе отказов. Задача оценки структурной отказоустойчивости ВС с критическими значениями числа n вершин и диаметра d впервые поставлена в [1]. Как указано в [2], суть этой задачи состоит
7*
в выявлении наименьшего числа l вершин, удаление которых переводит диаметр компоненты связности в закритическую область d(G’) > d, или при сохранении диаметра в докритической области d(G’) < d уменьшает число вершин в компоненте более чем на l. В обоих случаях N’ < N — l, и значение l = Kd(G) является d-ограниченной связностью графа G. Если при этом l > lmax, т.е. Vl < lmax, N’ = N — l, то отказоустойчивость системы достигается уже при N = n + lmax элементарных машин, т.е. при нулевой вершинной избыточности = N — (n + lmax). Здесь lmax — максимально допускаемое в системе значение кратности отказов, при которой существенные для ее работоспособности критерии качества находятся в заданных пределах. Структурная отказоустойчивость системы в этом случае достигается только за счет избыточной связности ее графа. Если же l < lmax, т.е. Vl > l < lmax, n < N'(l) < N — l, то система также отказоустойчива, но достигается это свойство не только за счет коммуникационной избыточности, недостаточной для = 0: система должна быть дополнена некоторым избыточным числом ЭМ, т.е. должно быть N > n + lmax и Шг > 0.
Итак, одной из первых задач, возникающих при анализе структурной отказоустойчивости системы, является задача поиска d-ограниченной связности ее графа — l = K/(G). Решение этой задачи базируется на поиске множества минимальных (s, ^-сечений графа G(V, E), представляющих собой VseV, VteV N[s] минимальное множество вершин V e V-s, t, удаление которых приводит к появлению d-компоненты связности G d e G(V V*, E E*V*) такой, что s г G’d ^ t e G’d и s e G’d ^ t г G’d, причем d(s, t) > d. Здесь N[s] = N(s) u s — замкнутая окрестность вершины s, а N(s) — ее окрестность. Поиск минимального d-ограниченного вершинного (s, ^-сечения графа G(V, E) основан на использовании аппарата скобочных образов графа, предложенного автором в [3], и операций над образами, описанных в [4]. В работе предложен и продемонстрирован на примерах подход к реализации такого поиска.
Поиск вершинного (s, ¿)-сечения графа ВС
Проблема поиска (s, ^-сечений достаточно широко представлена в теории графов. В основе алгоритмизации поиска лежит, как правило, теорема Форда — Фалкерсона [5], в соответствии с которой максимальный поток между вершинами t и s равен величине минимального сечения между этими вершинами. Вероятно, для решения задачи, в постановку которой нами введено ограничение на длину простого пути между s и t, можно приспособить одну из известных модификаций алгоритма поиска максимального потока, но в данной работе мы используем введенный автором в [6] и достаточно хорошо показавший себя в [7, 8] аппарат скобочных образов.
Итак, структура изначально работоспособной ВС задана неориентированным невзвешенным связным графом G(V, E), в котором множеству V вершин поставлено в однозначное соответствие множество ЭМ, а множеству E ребер также однозначно поставлены в соответствие линии связи между ЭМ. Граф G(V, E)
1 Работа выполнена при поддержке Российского фонда фундаментальных исследований (проект 05-08-01301а).
представим его проекцией Рк{у°еУ); вершина у° здесь является ракурсной, а индекс к определяет число уровней проекции.
Напомним, что в соответствии с [6] образ графа G(V, Е) определен вектором Р(О) = {Р(у,) |у;еР}, представляющим собой множество его проекций Р(у;) в множестве ракурсов {у,ер}. Проекцию Р(У;) графа 0(У, Е с ракурсной вершиной у¡e V называем у-й проекцией, либо у-м ракурсом этого графа. Полная проекция Р(уг) графа О(У, Е) содержит всю необходимую для его построения информацию. Описание проекции представлено в виде конечного множества уровней. Ракурсная вершина (здесь у0 = я) помещена на нулевом уровне, смежные ей вершины заключены внутри скобок 1-го уровня и т.д. Таким образом, 1-й уровень проекции образа графа включает в себя окрестность начальной вершины — N (у0). Правило включения множества потомков произвольной у-й вершины г-го уровня в (г+1)-й уровень проекции графа определено выражением … у- (^(у- ) С(у-)}), а совокупность 5 г+1 вершин любого (г + 1)-го уровня проекции определяется
выражением 5 г+1 = ({N () С()}, {N( у2 ) С(у2)}, ., {N ( у^,|) С(у^,• |)}) [6]. Здесь у- — произвольная
у-я вершина из совокупности вершин г-го уровня проекции; у = 1, | 5′ |, а | 5′ | — число элементов совокупности 5 ‘; N(у-) — окрестность вершины у- ; С (у-)- множество вершин в составе простой цепи между начальной (у0 = я) и у-й (у- ) вершиной г-го уровня, включающее у0 и у- .
Далее будут использованы следующие обозначения: Ма(я, г) = {М1а (я, г)} — множество ^-ограниченных (я, г)-маршрутов (простых путей между я и г), при этом по умолчанию концевые вершины в множествах вершин, составляющих эти маршруты, опущены, а индекс г идентифицирует маршрут в множестве Ма (я, г):
г = 1,| Ма (я,г) |; Vа (я, г) = {у;} = ^ (.5, г) — множество вершин из Ма (я, г), У^ (я, г) — множество вершин
из М1а (я, г); б^я, г) = { Б1а (я, г)} — множество минимальных и равномощных ^-ограниченных (я, г)-сечений
графа, (я, г) — множество вершин, составляющих г-е сечение из Ба(я, г); т; — кратность вершины у;е Vd(s, г), равная числу содержащих эту вершину маршрутов из Ма(я, г).
Отметим некоторые используемые при поиске положения, справедливые при С(я, г) < С и не требующие доказательства из-за их очевидности.
1. Множество вершинных (я, г)-сечений пусто при С(я, г) = 1 (вершины я и г смежны): С(я, г) = 1^5а(я, г) = 0. Учитывая это, из множества вершин, которые составляют пары с вершиной я и для которых допустимо искать сечение, можно изначально исключить ^^-замкнутую окрестность вершины я.
2. г(я, г)еБ(я, г) ^ (я) п N(t)}е {5 г(я, г)}. Здесь индекс ограничения по диаметру С опущен, так как утверждение справедливо вне зависимости от ограничивающего связанность диаметра. Заметим, что N (я) п N (г) ^ 0 только при С(я, г) = 2. В этом случае множество вершин, составляющих любое из множеств всех (я, г)-сечений графа, обязательно включает в себя вершины пересечения окрестностей N(s) и N (г). Это позволяет производить поиск С-ограниченных (я, г)-сечений графа, изначально включив вершины пересечения в составы искомых сечений и исключив из М^я, г) все маршруты, содержащие эти вершины, соответствующим образом скорректировав при этом множество Ví¡(s, г) и кратности т; составляющих его вершин у; е V¿я, г).
3. Если сумма кратностей вершин подмножества из множества Vd(s, г) не превышает числа маршрутов
|Ма(я, г)|, то таких вершин недостаточно для С-ограниченного (я, г)-рассечения графа. Это утверждение дает основания для первоначального в процессе поиска выбора удаляемой из графа вершины: 1) связность ка(О) не может быть меньше наименьшего числа вершин из Vd(s, г), сумма кратностей которых превосходит число маршрутов в множестве Ма(я, г); 2) кратность очередной выбираемой в процессе поиска из Vd(s,t) вершины не может быть менее округляемого вверх отношения
ГмДя, г) / *-¿(0)1.
На рис. 1 представлена тороидальная структура ВС, на примере которой будет продемонстрирован предлагаемый здесь подход к поиску минимальных (я, г)-сечений. Эта структура достаточно распространена в практике создания ВС из-за удобства в адресной организации и простоты алгоритмов маршрутизации. Помимо этого, в подобных этой структурах можно ограничиться исследованием коммуникационных Рис. 1. ВС с тороидальной структурой свойств лишь (Ы — 1)-й пары вершин из СN возможных.
В [6] доказано, что число к уровней проекции, необходимое для полного описания графа, равно эксцентриситету е(у°) ракурсной вершины у°, если множество вершин, равноудаленных от нее на величину максимального эксцентриситета, не является связанным, и к = е(у°) + 1, если хотя бы одна пара вершин из этого множества смежна. Заметим, что значение эксцентриситета е(у°) не требует вычислений, предваряющих процесс построения проекции, а получается в нем автоматически как номер уровня, которым множество вершин, включенных в предшествующие уровни, дополняется до V. В нашем примере для полноты описания было бы достаточно 4-х уровней (с1(О) = 4), но так как принятое нами выше ограничение на диаметр компоненты связности С = 5, то проекцию графа из вершины 00 представим 5-ю уровнями:
Р5(00) =
00(01(02(03(13(10, 12, 23), 43(33, 40, 42)), 12(11(10, 21), 13(03, 10, 23), 22(21, 23, 32)), 42(32(22, 31, 33), 41(31, 40), 43(03, 33, 40))), 11(10(13(03, 12, 23), 20(21, 23, 30)), 12(02(03, 42), 13(03, 10, 23), 22(21, 23, 32)), 21(20(10, 23, 30), 22(12, 23, 32), 31(30, 32, 41))),
41(31(21(11, 20, 22), 30(20, 33, 40), 32(22, 33, 42)), 40(30(20, 31, 33), 43(03, 33, 42)), 42(02(03, 12), 32(22, 31, 33), 43(03, 33, 40)))),
03(02(01(11(10, 12, 21), 41(31, 40, 42)), 12(11(01, 10, 21), 13(10, 23), 22(21, 23, 32)), 42(32(22, 31, 33), 41(01,
31, 40), 43(33, 40))), 13(10(11(01, 12, 21), 20(21, 23, 30)), 12(02(01, 42), 11(01, 10, 21), 22(21, 23, 32)), 23(20(10, 21, 30), 22(12, 21, 32), 33(30, 32, 43))),
43(33(23(13, 20, 22), 30(20, 31, 40), 32(22, 31, 42)), 40(30(20, 31, 33), 41(01, 31, 42)), 42(02(01, 12), 32(22, 31, 33), 41(01, 31, 40)))),
10(11(01(02(03, 12, 42), 41(31, 40, 42)), 12(02(01, 03, 42), 13(03, 23), 22(21, 23, 32)), 21(20(23, 30), 22(12, 23,
32), 31(30, 32, 41))), 13(03(02(01, 12, 42), 43(33, 40, 42)), 12(02(01, 03, 42), 11(01, 21), 22(21, 23, 32)), 23(20(21, 30), 22(12, 21, 32), 33(30, 32, 43))),
20(21(11(01, 12), 22(12, 23, 32), 31(30, 32, 41)), 23(13(03, 12), 22(12, 21, 32), 33(30, 32, 43)), 30(31(21, 32, 41), 33(23,
32, 43), 40(41, 43)))),
40(30(20(10(11, 13), 21(11, 22, 31), 23(13, 22, 33)), 31(21(11, 20, 22), 32(22, 33, 42), 41(01, 42)), 33(23(13, 20, 22), 32(22, 31, 42), 43(03, 42))), 41(01(02(03, 12, 42), 11(10, 12, 21)), 31(21(11, 20, 22), 30(20, 33), 32(22, 33, 42)), 42(02(01,
03, 12), 32(22, 31, 33), 43(03, 33))),
43(03(02(01, 12, 42), 13(10, 12, 23)), 33(23(13, 20, 22), 30(20, 31), 32(22, 31, 42)), 42(02(01, 03, 12), 32(22, 31,
33), 41(01, 31))))).
Отсутствие здесь возможностей цветовой разметки уровней проекции затрудняет ее структурное восприятие, поэтому 4 части, каждая из которых содержит в себе одну из вершин окрестности начальной вершины, выделены интервально, а разбиение этих частей на строки выделяет вершины 2-го уровня проекции с их потомками.
Множество вершин, составляющих пары с вершиной 00, для которых допустимо искать сечение, не может включать в себя замкнутую окрестность вершины 00 и представляет собой V N[00] = {20, 30, 11, 21, 31, 41, 02, 12, 22, 32, 42, 13, 23, 33, 43}. Продемонстрируем процесс поиска минимального сечения для пары, составленной из вершины 00 и одной из вершин этого множества, к примеру, (00, 32)-сечения. Из того, что множество возможных сечений в графе включает в себя N окрестностей каждой из вершин графа и в соответствии с расширенным в [2] неравенством Уитни, ка(О) < к(О) < 4.
Трансформируя проекцию Р5(00) графа удалением из нее всех концевых вершин, кроме 32-й, получим проекцию Р5(00, 32), содержащую множество простых путей к этой вершине из вершины 00, длина которых не превышает 5; число таких путей в нашем графе равно 31:
00 001(202(з12(422(5325)4), 42(4324)3), 11(312(422(5325)4), 21(422(5325), 31(5325)4)3), 41031(432Д 42(4324)3)2), 03(202(з42(4324)з), 13(312(422(5325)4), 23(422(5325), 33(5325)4)3), 43(з33^324), 42(4324)3)2), 10(211(312(422(5325)4), 21(422(5325), 31(5325)4)3), 13(з12(422(5325)4), 23(422(5325), 33(5325)4)3), 20(з21(422(53 25), 31(5325)4), 23(422(53 25), 33(5325)4), 30(431(53 25), 33(5325)4)3)2),
40(230(з31(4324), 33(4324)з), 41(з31(4324), 42(4324)3), 43(з33(4324), 42(4324)3)2)1).
Здесь для удобства визуального восприятия концевая вершина выделена затенением, а открывающиеся/закрывающиеся скобки снабжены индексом соответствия их содержимого номеру уровня (длине маршрута до любой вершины уровня). Перечислим полученные пути в явном виде, оставив в множестве М5(00, 32) — индекс здесь соответствует предельной длине маршрутов, лишь транзитные вершины:
{01-02-12-22, 01-02-42, 01-11-12-22, 01-11-21-22, 01-11-21-31, 01-41-31, 01-41-42,
03-02-42, 03-13-12-22, 03-13-23-22, 03-13-23-33, 03-43-33, 03-43-42,
10-11-12-22, 10-11-21-22, 10-11-21-31, 10-13-12-22, 10-13-23-22, 10-13-23-33, 10-20-21-22, 10-20-21-31, 10-2023-22, 10-20-23-33, 10-20-30-31, 10-20-30-33,
40-30-31, 40-30-33, 40-41-31, 40-41-42, 40-43-33, 40-43-42}.
Сформируем множество ^(00, 32) = {уу(ту)} транзитных вершин уу е М5(00, 32), входящих в состав М5(00, 32), и выявим кратности ту их использования — у/ту-):
^(00, 32) = {01(7), 02(3), 03(6), 10(12), 11(6), 12(5), 13(6), 20(6),21(6), 22(11), 23(6), 30(4), 31(7), 33(7), 40(6), 41(4), 42(6), 43(4)}.
Как указано выше, для получения сечения из трех вершин необходимо, как минимум, чтобы сумма кратностей удаляемых вершин была не менее числа маршрутов. Поскольку таковых в нашем случае нет (12 + 11 + 7 < 31) и минимальный набор вершин, сумма кратностей которых превышает число маршрутов, состоит из 4 вершин, то мощность минимального сечения не может быть менее 4. Удалив используемую в 12 маршрутах вершину 10 и соответствующие ей маршруты, модифицируем кратности использования вершин в оставшихся 19 путях:
{01-02-12-22, 01-02-42, 01-11-12-22, 01-11-21-22, 01-11-21-31, 01-41-31, 01-41-42,
03-02-42, 03-13-12-22, 03-13-23-22, 03-13-23-33, 03-43-33, 03-43-42,
40-30-31, 40-30-33, 40-41-31, 40-41-42, 40-43-33, 40-43-42}
01(7), 02(3), 03(6), 11(3), 12(3), 13(3), 20(0),21(2), 22(5), 23(2), 30(2), 31(4), 33(4), 40(6), 41(4), 42(6), 43(4).
Для рассечения оставшихся 19 маршрутов тремя вершинами кратность использования следующей удаляемой из этих маршрутов вершины должна быть не менее 7. Такой вершиной является вершина 01, после удаления которой число оставшихся маршрутов уменьшится до 12. Модифицируем множество оставшихся маршрутов и кратности используемых в них вершин; вершины с кратностью менее [19/3] = 6 исключаем из рассмотрения:
{03-02-42, 03-13-12-22, 03-13-23-22, 03-13-23-33, 03-43-33, 03-43-42,
40-30-31, 40-30-33, 40-41-31, 40-41-42, 40-43-33, 40-43-42}
03(6), 40(6), 42(4).
Удаление вершин 03 и 40 завершает процедуру поиска для выбора вершины 10 в качестве 1-й удаляемой. В результате поиска найдено сечение с мощностью, равной 4: {10, 12, 03, 40}. Вернувшись к выбору 1-й удаляемой вершины, начнем теперь с удаления вершины 22 с кратностью, равной 11. Описание всех оставшихся при этом маршрутов из вершины 00 в вершину 32 получим аналогично вышеописанному:
{01-02-42, 01-11-21-31, 01-41-31, 01-41-42,
03-02-42, 03-13-23-33, 03-43-33, 03-43-42,
10-11-21-31, 10-13-23-33, 10-20-21-31, 10-20-23-33, 10-20-30-31, 10-20-30-33,
40-30-31, 40-30-33, 40-41-31, 40-41-42, 40-43-33, 40-43-42}
01(4), 02(2), 03(4), 10(6), 11(2), 12(0), 13(2), 20(4),21(3), 22(0), 23(3), 30(4), 31(7), 33(7), 40(6), 41(4), 42(6), 43(4).
Очевидно, что для получения сечения с мощностью, равной 4, кратности следующих двух удаляемых вершин из оставшихся 20 маршрутов должны быть не меньшими 7, а кратность последней из удаляемых при этом не может быть менее 6. Первому из этих условий удовлетворяют только вершины 31(7), 33(7), — удалим их:
{01-02-42, 01-41-42,
03-02-42, 03-43-42,
40-41-42, 40-43-42}
10(0), 40(2), 42(6).
Осталась единственная вершина 42 с кратностью, не меньшей числа оставшихся маршрутов. Удалив ее, получим искомое сечение: {22, 31, 33, 42}. Как видим, множество минимальных (00, 32)-сечений включает 2 сечения мощности 4, совпадающие с окрестностями разделяемых ими вершин. Чтобы показать, что совпа-
дение множества (я, ї)-сечений только с окрестностями вершин я и ї является здесь случайным, приведем множество (00, 11)-сечений: $¡(00, 11) = {(01, 10, 03, 40), (01, 10, 12, 40), (01, 10, 03, 21), (01, 10, 12, 21)} = = {(01 л 10 л ((03 V 12) л (40 V 21)))}. На рис. 2 приведены подграфы исходного графа, полученные в результате этих сечений; вершины я = 00 и ї = 11 помечены на рисунке концентрическими окружностями.
{01, 10, 03, 40}
{01, 10, 12, 40} Рис. 2. ¿-ограниченные (00, 11)-сечения графа при <і = 5
Проверив полученные в результате сечений компоненты связностей на их соответствие ограничению по диаметру ¡С < 5, выделим в них ^-ограниченные компоненты связностей. Как было указано выше, для этого достаточно получить минимальные полные проекции [6] образовавшихся подграфов, в процессе построения которых и будут получены диаметры описанного каждой проекцией подграфа и их размеры. Нетрудно убедиться, что проекции Р5′(11) и Р5′(10) С-ограниченных компонент связности для сечений (01, 10, 03, 40) и (01, 10, 12, 21) совпадают с соответствующими компонентами Р'(11) и Р'(10), так как эти сечения изолируют только одну из концевых вершин. Размеры таких компонент У5′ = V’ = Л»[х] = 15, где х = я V I.
Ниже приведены проекции Р6′(11) и Р6»(11) компонент, образующихся в результате рассечения графа подмножествами вершин {01, 10, 12, 40} и {01, 10, 03, 21} соответственно:
Рб'(11) = 11 (х21 (220(з23(4 13(503(б00б>5>, 22(5325), 33(530, 32, 435)4), 30(431(532, 415), 33(523, 32, 435)4)3),
22(з23(413(503(6006)5), 20(5305), 33(530, 32, 435)4), 32(431(530, 415), 33(523, 30, 435), 42(502, 41, 435)4)3),
31(з30(420(5235), 33(523, 32, 435)4), 32(422(5235), 33(523, 30, 435), 42(502, 41, 435)4), 41(442(502, 32, 435)4)3)2),
Рб»(11) = 11(:12(202(з42(432(522, 31, 335), 41(531, 40(б00б)5), 43(533, 40(б00бШз),
13(з23(420(5305), 22(5325), 33(530, 32, 435)4)3),
22(з23(413, 20(5305), 33(530, 32, 435)4), 32(431(530, 415), 33(523, 30, 435), 42(502, 41, 435)4)3)2)1).
Данные проекции являются полными, так как 6-й уровень (выделенный в проекциях затенением) включает в себя последнюю из не определенных нижерасположенными уровнями вершин. Диаметры этих компонент одинаковы и равны 6, а число вершин в них N = 16, изолированных вершин нет. Хотя подмножества удаленных вершин не являются здесь (00, 11)-сечениями в общеупотребительной терминологии, тем не менее удаление этих подмножеств приводит к утрате связанности некоторых вершин не только из-за их физической изолированности, но и из-за заданного ограничения достижимости, что соответствует введенному нами определению С-ограниченного (я, ?)-сечения. Из рис. 2 видно, что хотя компонента связности включает в себя вершину 00, в состав проекций 5-ограниченных компонент связности графа, получаемых из Р6′(11) и Р6»(11) удалением 6-го уровня, эта вершина не входит. Ребра, увеличивающие диаметр компоненты связности до С(О’), показаны здесь штриховыми линиями.
Описанный выше подход позволяет выявлять не только минимальные С-ограниченные (я, ?)-сечения, но и сечения большей мощности. При этом одновременно с задачей поиска множества сечений заданной мощности решается задача выявления компонент связности, их размеров и диаметров. Последовательное применение такого поиска на множестве пар вершин в графе позволяет выявить в множестве сечений заданной мощности эквивалентные с тем, чтобы использовать эту информацию в построении функций структурной отказоустойчивости и структурной живучести системы.
Заключение
Отказоустойчивость системы базируется на ее структурной конъюнктуре, заключающейся в наличии достаточного числа вершин в графе ВС и в обеспечении заданного критерия их связанности. В качестве последнего определено значение максимально допускаемого в системе эксцентриситета вершин, или диаметра компоненты связности графа ВС при ее деградации. Поставлена и решена задача выявления наименьшего числа 1* вершин, удаление которых переводит диаметр компоненты связности в закритическую область, или при сохранении диаметра в докритической области уменьшает число вершин в компоненте более чем на 1*.
Сформулированы используемые при поиске положения и предложен подход к решению проблемы, основанный на использовании формальных описаний структур ВС в виде скобочных образов и проекций соот-
ветствующих графов. Подход позволяет выявлять не только минимальные С-ограниченные (я, ?)-сечения, но и сечения большей мощности. Одновременно с задачей поиска множества сечений заданной мощности решается задача выявления компонент связности, их размеров и диаметров. Последовательное применение такого поиска на множестве пар вершин в графе позволяет выявить в множестве сечений заданной мощности эквивалентные для построении функций структурной отказоустойчивости и структурной живучести системы. Параллельная алгоритмизация предложенного подхода сразу для множества (я, г)-сечений выглядит при этом вполне естественной; вполне допустимы и варианты поиска С-ограниченных сечений между подмножествами вершин в графе с использованием, к примеру, известного приема стягивания ребер внутри каждого из подмножеств.
ЛИТЕРАТУРА
1. Мелентьев В.А. Толерантность графов и структурная отказоустойчивость вычислительных систем // Вестник ТГУ. Приложение. 2004. № 9(1). С.144 — 150.
2. Мелентьев В.А. Функция структурной отказоустойчивости и ¿-ограниченная компонента связности графа вычислительной системы // Наст. сборник. С. 102 — 106.
3. Мелентьев В.А. Формальный подход к исследованию структур вычислительных систем // Вестник ТГУ. Приложение. 2005. № 14. С. 167 — 172.
4. Мелентьев В.А. Операции над проекциями графов и актуализация описаний отказоустойчивых систем // Вестник ТГУ. Приложение. 2006. № 17. С. 208 — 213.
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
5. Харари Ф. Теория графов. М.: Мир, 1973.
6. Мелентьев В.А. Формальные основы скобочных образов в теории графов // Труды II Междунар. конф. «Параллельные вычисления и задачи управления» РАС0’2004. 2004. С. 694 — 706.
7. Мелентьев В.А. Изоморфизм графов и их образов в исследованиях отказоустойчивости систем // Вестник ТГУ. Приложение. 2005. № 14. С. 182 — 190.
8. Мелентьев В.А. Образ графа и поиск гамильтоновых путей // Вестник ТГУ. Приложение. 2005. № 14. С. 172 — 181.
А.С. Шандриков
Витебский государственный
политехнический колледж учреждения образования «Витебский государственный
технологический университет»
РАЗРЕЗАНИЕ ГРАФА ИТЕРАЦИОННЫМ МЕТОДОМ
СЕЧЕНИЙ
На этапе компоновки радиоэлектронных средств (РЭС)
решается задача распределения элементов i-го уровня по элементам (i
+ 1)-го уровня конструктивной
иерархии. На самом низком – первом уровне, находятся минимальные конструктивные
единицы – радиоэлектронные компоненты (РЭК) – микросхемы, транзисторы,
конденсаторы и т.п., которые в процессе эксплуатации РЭС можно заменить в
случае их выхода из строя [1]. Решение данной задачи осуществляется с
использованием математической модели принципиальной электрической схемы в виде
графа G = (X, U), где множество вершин X – совокупность всех РЭК, входящих в
состав проектируемого РЭС, а множество U – совокупность
соединений между РЭК в соответствии с принципиальной электрической схемой.
Разрезание графа на заданное количество связанных между собой кусков
моделирует процесс компоновки.
Для решения задачи компоновки разработано
множество эвристических алгоритмов разрезания графа, отличающихся друг от друга
структурой, объёмом, критериями оптимальности [2]. Разрезание графа как
моделирование процесса компоновки РЭС не может иметь общего алгоритма
автоматизированного проектирования из-за большого количества и разнообразия
условий компоновки, а также из-за трудности формализации совокупности критериев,
используемых для оценки качества полученных результатов [3]. По этой причине
разработка новых методик представляет большой интерес как с теоретической, так
и с практической точек зрения.
В данной работе описывается разрезание графа
итерационным методом сечений. Описываемый метод использует процедуру отсечения
кусков, содержащих заданное количество вершин, и обеспечивает получение
наиболее приемлемых результатов при разрезании мультиграфов с большим
количеством пар вершин, связанных кратными рёбрами. Разработанный метод основан
на использовании результатов направленной оптимизации текущего размещения
вершин графа в координатной решётке заданных размеров Gr = s × t, где s – количество узлов координатной решётки по
оси абсцисс, t — количество узлов координатной решётки по
оси ординат. Математическое обоснование направленной оптимизации размещения графа
в решётке подробно описано в [4].
Реализация метода осуществляется в следующем
порядке.
1. Исходный граф произвольно отобразить в
одномерную координатную решётку Gr = n × 1, где n – количество вершин графа.
2. Построить матрицу смежности графа R
= ||rij|| и матрицу расстояний между узлами заданной координатной решётки D
= ||dij|. Шаг решётки, т.е. расстояние между двумя соседними позициями, в
которых размещаются вершины графа, принимается равным единице.
3. Вычислить величины приращений суммарной длины
связей для всех возможных парных перестановок по формуле [4]:

где – длина
связей вершины xi с вершиной xm;
– длина связей вершины xj с вершиной xn;
– длина связей между вершинами xi и xj;
M – количество вершин, связанных с вершиной xi;
N – количество вершин, связанных с вершиной xj;
– суммарная длина связей вершин xi и xj со всеми остальными вершинами графа до их
парной перестановки;
– суммарная длина связей вершины xi и xj со всеми остальными вершинами графа
после их парной перестановки.
По результатам полученных
вычислений построить матрицу приращений суммарной длины связей для всех
возможных парных перестановок.
Отрицательное значение ΔLij означает
уменьшение суммарной длины связей.
4. Из множества пар вершин,
перестановка которых даёт отрицательные приращения суммарной длины связей, выбрать
подмножество, обеспечивающее выполнение следующих условий:
— выбранное подмножество
перестановок максимально уменьшает суммарную длину связей;
— любая пара вершин из
выбранного подмножества не должна иметь связей с другими парами.
Несоблюдение указанных условий
может ухудшить результат размещения по сравнению с первоначальным на любой
итерации. В [4] приводится ещё одно условие: любая вершина может менять свою
позицию только один раз, однако автор в процессе чтения лекций, освещающих
вопросы алгоритмизации размещения РЭС по курсу «Системы автоматизированного
проектирования», неоднократно доказывал, в том числе и на примерах, что данное условие
деструктивно. Недопустимой следует считать повторную перестановку одной и
той же пары вершин. Такая перестановка свидетельствует о зацикливании
программы для автоматизированного решения задачи размещения из-за текстовой
ошибки при её написании. Повторная и, возможно неоднократная, перестановка
одной вершины с вершиной (вершинами) из другой пары способствует минимизации суммарной
длины связей между размещаемыми элементами любого иерархического уровня [5].
5. Выполнить перестановку
выбранных подмножеств. В матрице смежности разрезаемого графа переставить
строки и столбцы, соответствующие переставляемым вершинам.
6. Повторно вычислить величины
приращений суммарной длины связей для всех возможных парных перестановок по
формуле (1).
Описанные действия повторяются
до тех пор, пока в матрице приращений суммарной длины связей не останется ни
одного отрицательного перестановочного коэффициента.
7. Провести сечения между всеми рядом расположенными узлами di и dj координатной сетки в диапазоне
, где nmin – количество вершин, заданное для наименьшего куска
требуемого разрезания.
8. Подсчитать количество рёбер
в каждом сечении.
9. Выбрать сечение с минимальным
количеством находящихся в нём рёбер. Это сечение будем считать входным.
10. Выделить подмножество
вершин с мощностью, равной количеству вершин, заданному для формируемого куска.
Выделение такого подмножества следует осуществлять в направлении расположения
выходного сечения с минимальным количеством содержащихся в нём рёбер. Выходным
сечением будем считать сечение, расположенное до или после входного сечения на
расстоянии ni шагов и содержащее наименьшее количество рёбер.
Если граф разрезается на неравные
по количеству вершин куски, то имеется возможность выбора количества выделяемых
вершин по критерию минимума рёбер в сечении, что в конечном итоге обеспечит
минимум внешних связей между полученными кусками.
11. Удалить из матрицы
смежности строки и столбцы, соответствующие выбранным вершинам. В результате
будет получена матрица смежности R´.
12. Построить новую матрицу
расстояний D´ = ||d´ij||, размерность
которой соответствует размерности матрицы смежности R´.
13. Повторно выполнить действия
3-11. Описанные действия повторяются до тех пор, пока не будет получено
заданное разрезание.
Реализацию данного метода
разрезания графа рассмотрим на примере.
На рис. 1 представлен граф G
= (X, U), содержащий 12 вершин и 36 рёбер, который необходимо разрезать на три
куска, содержащие 3, 4 и 5 вершин.
Рис. 1
Решение данной задачи описанным
методом выполняется в следующей последовательности.
1) Отобразить граф в координатную решётку
размерностью 12 × 1. Результат отображения графа в координатную решётку представлен
на рис. 2.
Рис. 2
2) Построить матрицу смежности графа.
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
x8 |
x9 |
x10 |
x11 |
x12 |
||||
|
x1 |
0 |
0 |
0 |
0 |
0 |
0 |
3 |
1 |
0 |
1 |
0 |
0 |
|||
|
x2 |
0 |
3 |
4 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||
|
x3 |
0 |
1 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||
|
x4 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||
|
x5 |
0 |
4 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
|
R = |
x6 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
(2) |
||||||
|
x7 |
0 |
1 |
1 |
0 |
1 |
0 |
|||||||||
|
x8 |
0 |
0 |
4 |
0 |
0 |
||||||||||
|
x9 |
0 |
0 |
3 |
3 |
|||||||||||
|
x10 |
0 |
0 |
0 |
||||||||||||
|
x11 |
0 |
2 |
|||||||||||||
|
x12 |
0 |
3) Построить матрицу расстояний
для заданного набора позиций.
|
d1 |
d2 |
d3 |
d4 |
d5 |
d6 |
d7 |
d8 |
d9 |
d10 |
d11 |
d12 |
||
|
d1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
|
d2 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
|
d3 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|||
|
d4 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
||||
|
d5 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|||||
|
D |
d6 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|||||
|
d7 |
0 |
1 |
2 |
3 |
4 |
5 |
|||||||
|
d8 |
0 |
1 |
2 |
3 |
4 |
||||||||
|
d9 |
0 |
1 |
2 |
3 |
|||||||||
|
d10 |
0 |
1 |
2 |
||||||||||
|
d11 |
0 |
1 |
|||||||||||
|
d12 |
0 |
Матрица смежности графа R и
матрица расстояний между узлами заданной координатной решётки D симметричны,
поэтому можно ограничиться треугольными подматрицами, расположенными над
главной диагональю.
4) По формуле (1) вычислить
величины приращений суммарной длины связей для всех возможных парных
перестановок и по результатам вычислений построить матрицу перестановочных
коэффициентов. После первой итерации матрица перестановочных коэффициентов
имеет вид:
|
l1 |
l2 |
l3 |
l4 |
l5 |
l6 |
l7 |
l8 |
l9 |
l10 |
l11 |
l12 |
||
|
l1 |
0 |
2 |
–4 |
–18 |
–4 |
–3 |
10 |
11 |
28 |
6 |
22 |
20 |
|
|
l2 |
0 |
–1 |
0 |
9 |
22 |
16 |
42 |
73 |
42 |
75 |
76 |
||
|
l3 |
0 |
–3 |
14 |
18 |
16 |
38 |
64 |
37 |
66 |
67 |
|||
|
l4 |
0 |
7 |
14 |
16 |
34 |
55 |
32 |
57 |
58 |
||||
|
l5 |
0 |
4 |
4 |
20 |
38 |
21 |
44 |
47 |
|||||
|
ΔL |
l6 |
0 |
3 |
12 |
30 |
12 |
32 |
36 |
|||||
|
l7 |
0 |
5 |
16 |
2 |
26 |
24 |
|||||||
|
l8 |
0 |
2 |
2 |
2 |
6 |
||||||||
|
l9 |
0 |
–9 |
0 |
5 |
|||||||||
|
l10 |
0 |
3 |
4 |
||||||||||
|
l11 |
0 |
1 |
|||||||||||
|
l12 |
0 |
В полученной матрице ΔL
отрицательные перестановочные коэффициенты имеют 7 элементов. Оптимальное для
парной перестановки значение имеет элемент ΔL(l1, l4) = –18. Парная перестановка вершин x1 и x4 сократит суммарную длину связей между вершинами графа
на 18 шагов. Больше в матрице ΔL не содержится ни одного отрицательного
перестановочного коэффициента, соответствующего вершинам, не связанным с вершинами
x1
и x4.
5) Переставить в матрице
смежности (2) x1 и x4 строки и столбцы и повторно вычислить перестановочные
коэффициенты для всех возможных парных перестановок вершин графа и пересчитать
элементы матрицы приращений. Процедура повторяется до тех пор, пока в матрице
приращений не останется ни одного отрицательного элемента.
Для решения данной задачи
потребовалось выполнить четыре итерации. По результатам вычислений на второй
итерации были переставлены x9 и x10,
на третьей итерации – вершины x1 и x6
и на четвёртой итерации – вершины x6 и x5.
Как видно из результатов выполнения итерационной части описываемого метода, на
третьей итерации была повторно переставлена вершина x1, а на четвёртой итерации – вершина x6, но эти перестановки были выполнены в паре с
другими вершинами. Это подтверждает несостоятельность запрета на повторную перестановку
какой-либо вершины в процессе оптимизации текущего размещения вершин графа в
узлах координатной решётки, изложенного в [4, с 57].
В результате выполнения парных перестановок
было получено отображение графа в решётку, представленное на рис. 3. Суммарная
длина связей между вершинами графа сократилась при этом со 102 до 47 шагов.
Рис. 3
6) Провести сечения между
соседними узлами координатной решётки. Так как минимальный кусок заданного
разрезания графа должен содержать три вершины, то первое сечение следует
провести между третьим и четвёртым узлами. Последнее сечение должно быть
проведено между девятым и десятым узлами. Данный диапазон соседних узлов
координатной решётки, между которыми проводятся сечения, обеспечивает отсчёт
количества вершин, заданного для минимального куска, от первого (влево) и от
последнего (вправо) узла. Количество соединений между вершинами графа в каждом
сечении показано на рис. 3.
7) Минимальное количество рёбер
umin = 2 содержится в сечениях s(d3, d4) и s(d5, d6). Сечения s(d3, d4) и s(d5, d6)
отсекают влево три и пять вершин соответственно, удаление которых из решётки обеспечивает
формирование минимального и максимального куска заданного разрезания. С целью
минимизации временных затрат на выполнение процесса разрезания графа
рекомендуется выбрать сечение s(d5, d6),
отсекающее наибольшее количество вершин, входящих в состав одного из
формируемых кусков, в данном примере в кусок G3=(X3, U3),
где X3 = {x2, x3, x4, x5, x6}.

X3
из координатной решётки и соответствующие им строки и столбцы из матрицы
смежности (2). Матрица смежности графа после удаления указанных строк и
столбцов имеет вид:
|
x1 |
x7 |
x8 |
x10 |
x9 |
x11 |
x12 |
||
|
x1 |
0 |
3 |
1 |
1 |
0 |
0 |
0 |
|
|
x7 |
0 |
1 |
0 |
1 |
1 |
0 |
||
|
x8 |
0 |
4 |
0 |
0 |
0 |
|||
|
R´ = |
x10 |
0 |
0 |
0 |
0 |
|||
|
x9 |
0 |
3 |
3 |
|||||
|
x11 |
0 |
2 |
||||||
|
x12 |
0 |
9) После удаления вершин
подмножества X3 сократился набор позиций координатной решётки для
отображения графа G´ = (X´, U´), где X´ = XX3. Матрица расстояний D´ имеет вид:
|
d1 |
d2 |
d3 |
d4 |
d5 |
d6 |
d7 |
||
|
d1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
d2 |
0 |
1 |
2 |
3 |
4 |
5 |
||
|
d3 |
0 |
1 |
2 |
3 |
4 |
|||
|
D´ |
d4 |
0 |
1 |
2 |
3 |
|||
|
d5 |
0 |
1 |
2 |
|||||
|
d6 |
0 |
1 |
||||||
|
d7 |
0 |
Отображение графа в
координатную решётку после удаления вершин подмножества X3 представлено
на рис. 4.
Рис. 4
10) Для полученного отображения
графа вычислить величины приращений суммарной длины связей для всех возможных
парных перестановок и по результатам вычислений построить матрицу
перестановочных коэффициентов.
Минимизация суммарной длины
связей между вершинами графа G´ была достигнута после первой итерации путём парной перестановки вершин
x9
и x11. Результат представлен на рис. 5.
Рис. 5
11) Провести сечения между
соседними узлами координатной решётки. Так как минимальный кусок заданного
разрезания графа должен содержать три вершины, и к настоящему моменту ещё не
сформирован, то первое сечение следует провести между третьим и четвёртым
узлами. Второе сечение должно быть проведено между четвёртым и пятым узлами.
Данный диапазон соседних узлов координатной решётки, между которыми проводятся
сечения, обеспечивает отсчёт количества вершин, заданного для первого и второго
кусков заданного разрезания.
Минимальное количество рёбер umin = 2
содержится в сечении s(d4, d5),
которое отсекает вершины множества X1 = {x9, x11, x12},
входящие в первый кусок. Остальные вершины образуют множество X2 = {x1, x7, x8, x10}, назначаемое во второй кусок. На этом
разрезание графа считается законченным. Результат разрезания графа представлен
на рис. 6.
Рис. 6
Литература
1. Автоматизация проектирования
радиоэлектронных средств : Учеб. пособие для вузов / О.В. Алексеев, А.А.
Головков, И.Ю. Пивоваров [и др.] ; под ред. О.В. Алексеева. – М. : Высш. шк.,
2000. – 479 с. : ил. – ISBN 5-06-002691-4.
2. Абрайтис, Л.Б. Автоматизация
проектирования ЭВМ : Автоматизированное техническое проектирование
конструктивных узлов цифровых устройств / Л.Б. Абрайтис, Р.И. Шейнаускас, В.А.
Жилевичюс ; под ред. Л.Б. Абрайтиса. – М. : Сов. радио, 1978. – 272 с. : ил.
3. Автоматизация схемотехнического
проектирования : Учеб. пособие для вузов / В.Н. Ильин, В.Т. Фролкин, А.И. Бутко
[и др.] ; под ред. В.Н. Ильина. – М. : Радио и связь, 1987. – 368 с. : ил.
4. Конструирование и технология
печатных плат : Учеб. пособие для радиотехнических специальностей вузов / А.Т.
Жигалов, Е.П. Котов, К.Н. Шихаев [и др.]. – М. : Высш. шк., 1973. – 216 с. :
ил.
5. Шандриков, А.С. Разрезание графа итерационным методом сечений // IX
Всероссийская конференция молодых ученых по математическому моделированию и
информационным технологиям : 28-30 октября 2008 года, г. Кемерово [Электрон. ресурс] – Режим доступа: http://www.nsc.ru/ws/show_abstract.dhtml?ru+189+14257.