Шар в конусе как найти точки - Исправление недочетов и поиск решений вместе с Examum.ru

Рассмотрим некоторые соотношения, которые полезны при решении задач на шар, вписанный в конус.

В любой конус можно вписать шар. Вписанный в конус шар (или сфера, вписанная в конус) касается основания конуса в его центре, а боковой поверхности — по окружности. Центр шара (сферы) лежит на оси конуса.

При решении задач на шар, вписанный в конус, удобнее всего рассмотреть сечение комбинации тел плоскостью, проходящей через ось конуса и центр шара.

Это сечение представляет собой равнобедренный треугольник, боковые стороны которого — образующие конуса, а основание — диаметр конуса. Вписанный в этот треугольник круг — большой круг шара (то есть круг, радиус которого равен радиусу шара).

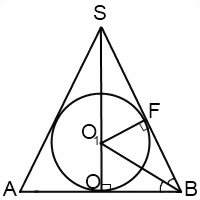
Для данного рисунка образующие SA=SB=l, высота конуса SO=H, радиус вписанного шара OO1=O1F=R. Так как центр вписанного круга — точка пересечения биссектрис треугольника, то ∠OBO1=∠FBO1, OB=r — радиус конуса.

Рассмотрим прямоугольный треугольник SOB. По свойству биссектрисы треугольника:

$[frac{{SB}}{{S{O_1}}} = frac{{OB}}{{O{O_1}}}, Rightarrow frac{l}{{H - R}} = frac{r}{R}]$

$[R = frac{{Hr}}{{I + r}}.]$

По теореме Пифагора

$[SB = sqrt {S{O^2} + O{B^2}} , Rightarrow l = sqrt {{H^2} + {r^2}} ]$

Отсюда

$[frac{{sqrt {{H^2} + {r^2}} }}{{H - R}} = frac{r}{R}.]$

Рассмотрим прямоугольный треугольник OO1B.

$[O{O_1} = OB cdot tgangle OB{O_1}]$

Если ∠OBS=α, то ∠OBO1=α/2. Отсюда

$[R = r cdot tgfrac{alpha }{2}.]$

Если сначала выразить радиус конуса через его высоту из прямоугольного треугольника SOB

то из треугольника OO1B выражаем радиус шара через высоту конуса:

$[r = H cdot ctgalpha cdot tgfrac{alpha }{2}.]$

Источник

Наверх

Пересечение конуса и сферы в данной статье выполняется методом вспомогательных секущих плоскостей. Ниже представлено задание на определение линии пересечения фигур.

Порядок построения на пересечение конуса и сферы:

Первоначально находятся точки в нижнем изображении, затем полученные точки переносятся в верхнее изображение.

1.) Чертятся фигуры согласно заданию.

2.) Строятся и подписываются вспомогательные секущие плоскости. Можно указать первую точку, она находится в верхней части соприкосновения фигур. Смотрите на рисунок снизу.

3.) Плоскость «а» пересекает две фигуры (обозначено синим цветом). Чертятся окружности (синим цветом показаны) на нижнем изображении, опущенные от крайних точек фигур. В месте пересечения ставятся точки.

4.) Плоскость «m» (имеет сиреневый цвет) пересекла данные фигуры. В нижнем изображении также чертятся окружности (сиреневый цвет) и в месте пересечения указываются точки.

5.) Плоскость «n». Повторяются операции выполняемых в пунктах 4 и 3.

6.) Указывают последнюю точку, расположенная в нижней части пересечения фигур

7.) Все найденные точки переносятся из нижнего изображения в верхнее. Для более понятного представления я не зря показал линии разными цветами.

8.) Соединяются точки плавной линией. Соединив, можно уже увидеть как выглядит линия пересечения.

9.) Завершающим шагом является удаление всех дополнительных линий с последующим обведением контуров фигур.

Не стоит забывать про видимые и невидимые линии чертежа и их применение.

Кода все сделано, можно взглянуть на полученный чертеж.

Просмотрели 734

Источник

В данной публикации мы рассмотрим, как найти радиус вписанного в конус шара (сферы), а также площадь его поверхности и объем.

Нахождение радиуса шара/сферы
Формулы площади и объема шара/сферы

Нахождение радиуса шара/сферы

В любой конус можно вписать шар (сферу). Другими словами, вокруг любого шара можно описать конус.

Чтобы найти радиус шара (сферы), вписанного в конус, чертим осевое сечение конуса. Таким образом, мы получаем равнобедренный треугольник (в нашем случае – ABC), в который вписана окружность радиусом r.

Радиус основания конуса (R) равняется половине основания данного треугольника (AC), а образующие (l) являются его боковыми сторонами (AB и BC).

Радиус окружности, вписанной в равнобедренный треугольник ABC, в том числе, является радиусом шара, вписанного в конус. Он находится по формуле:

Формулы площади и объема шара/сферы

Зная радиус (r) можно найти площадь поверхности (S) сферы и объем (V) шара, ограниченного этой сферой:

Примечание: π округленно равняется 3,14.

Источник

Шар является описанным около куба, если все вершины куба находятся на поверхности шара.

Центр шара (O) — точка пересечения диагоналей куба.

Около любого куба можно описать шар.

Общие точки шара и куба — восемь вершин куба.

Чертится диагональное сечение.

AC1

CA1

— диагонали куба.

Радиус шара равен половине диагонали куба.

Шар является вписанным в куб, если он касается всех его граней.

Центр шара (O) находится в точке пересечения диагоналей куба.
В любой куб можно вписать шар.
Общие точки шара и куба — центры шести граней куба (точки касания шара и куба).

Чертится сечение плоскостью, которая параллельна грани куба и проходит через центр шара.

Радиус шара — половина стороны куба.

Шар является описанным около цилиндра, если окружности оснований цилиндра лежат на поверхности шара.

Центр шара (O) находится в середине высоты цилиндра.

Общие элементы — две окружности.

Около любого цилиндра можно описать шар.

Чертится осевое сечение.

Радиус шара — половина диагонали осевого сечения цилиндра.

Шар является вписанным в цилиндр, если касается оснований цилиндра и всех его образующих.

Центр шара (O) — середина высоты цилиндра.

Осевое сечение — квадрат с вписанной в него окружностью.

Радиус шара равен радиусу цилиндра и половине высоты цилиндра.

Источник

Уже древние греки занимались изучением эллипса, гиперболы и параболы, рассматривая их как конические сечения.
Аполлоний (262 до н. э. — 190 до н. э., родом из Перги, но работавший в Александрии,
современник Архимеда) написал труд «Конические сечения» в восьми книгах. Термин «фокус» (лат. «очаг, огонь»)
⁠⁠был введён Иоганном Кеплером
в сочинении «Оптическая часть астрономии» («Astronomiæ pars optica», 1604). А элегантную идею сфер придумал
в 1822 году бельгийский математик и механик Жерминаль Данделен.

Обучаясь в лицее, Жерминаль Пьер Данделен (1794—1847) подружился с Адольфом Кетле (1796—1874); потом они будут помогать друг другу в жизни, иметь общие математические интересы и даже напишут совместную оперу.

В 1822 году Данделен опубликовал работу, в которой привёл конструкцию со сферами, вписанными в конус и касающимися плоскости конического сечения. На примере эллипса он показал равенство суммы расстояний до фокусов длине отрезка образующей. В 1826 году Данделен обобщил свою конструкцию на случай однополостного гиперболоида вращения.

Отметим, что за несколько лет до этого, в 1819 году, Адольф Кетле написал диссертацию по коническим сечениям (Dissertatio Mathematica Inauguralis, De Quibusdam Locis Geometricis, Nec Non De Curva Focali). В работе изучалась кривая, на которой лежат фокусы конических сечений, имеющих фиксированную точку конуса как вершину (т.е при изменении угла наклона плоскости сечения). И большая часть работы Данделена 1822 года посвящена именно этой кривой.

Тот факт, что прямые пересечения секущей плоскости с плоскостями, содержащими окружности касания сфер Данделена и конуса, являются директрисами эллипса, самим Данделеном отмечен не был. Это наблюдение опубликовал ирландский математик и астроном Пирс Мортон в своей статье 1829 года, где он привёл конструкцию сфер, но без ссылки на работы Данделена.

Никто из упомянутых авторов не ссылается и на трактат «De Sectionibus Conicis: Tractatus Geometricus» 1758 года ирландского математика и епископа Хью Гамильтона (1729—1805). И хотя Гамильтон не дошёл до идеи вписанных в конус сфер, касающихся плоскости сечения, он рассматривал окружности касания таких сфер и конуса. Определял он такую окружность как окружность конуса, лежащую на том же расстоянии вдоль образующей от вершины конического сечения, на котором от неё находится фокус. Для такой окружности он доказал оба факта: для любой точки конического сечения длина образующей до окружности равна расстоянию до фокуса; плоскость, содержащая такую окружность, пересекается с плоскостью сечения по директрисе. Причём доказал для всех трёх типов конических сечений — эллипса, параболы и гиперболы. По словам писателя Джеймса Уиллса, в этой книге Гамильтон «был первым, кто вывел свойства конического сечения из свойств конуса с помощью общих демонстраций, не обременённых леммами и протекающих в более естественном и наглядном порядке». Трактат получил признание за ясность изложения, а Леонард Эйлер назвал его идеальной книгой.

Источник