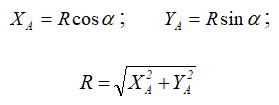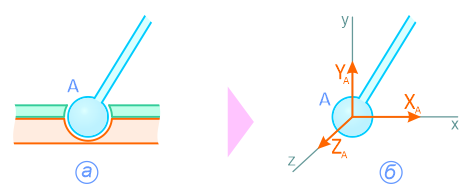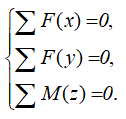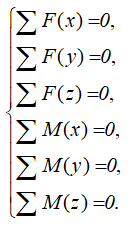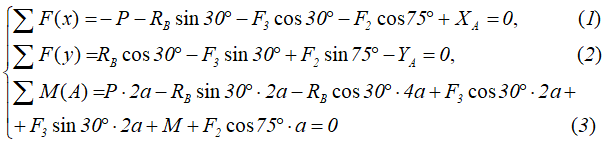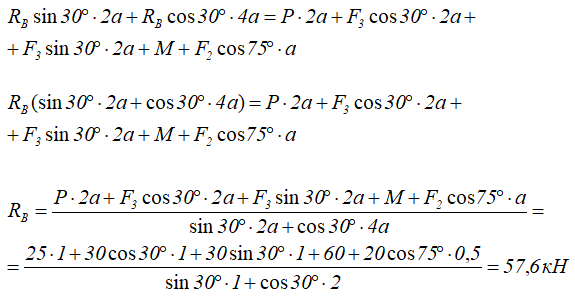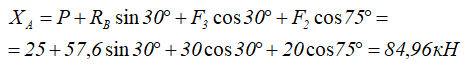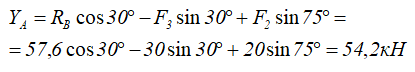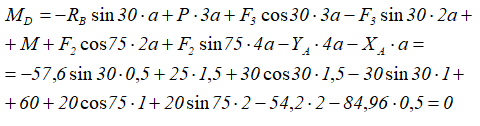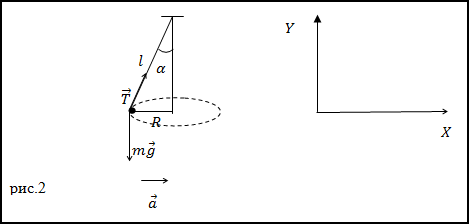Сила натяжения нити, теория и онлайн калькуляторы
Сила натяжения нити
Понятие силы натяжения нити
Пусть тело прикреплено к нити, тогда силой натяжения нити называют силу, действующую на рассматриваемое тело, равную по величине и противоположную по направлению равнодействующей, приложенной к нити. Силу натяжения нити обозначают по-разному, чаще всего: $overline{N}$, $overline{T}, overline{F}$. Если равнодействующую, приложенную к нити обозначить как $overline{R}$, то в соответствии с третьим законом Ньютона имеем:
[overline{N}=-overline{R}left(1right).]
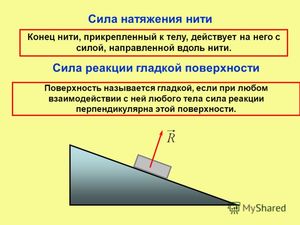
Сила натяжения нити является реакцией подвеса (нити), на действие со стороны тела на подвес. Сила натяжения нити всегда имеет направление вдоль нити.
Очень часто при решении задач указывают, что нить является невесомой (массой нити в сравнении с массой груза можно пренебречь). Если нить невесома и нерастяжима, то такую нить рассматривают как проводник силы.
Если следует учитывать растяжение нити, при этом нагрузки малы, а нить упругая, то при вычислении силы натяжения используют закон Гука:
[overline{N}={overline{F}}_u=kDelta overline{l}left(2right),]
где ${overline{F}}_u$ — сила упругости нити;$ k$ — коэффициент упругости нити; $Delta l$ — удлинение нити.
Единицей измерения силы натяжения нити в Международной системе единиц (СИ) (как и для любой другой силы) является ньютон:
[left[Nright]=H=frac{кгcdot м}{с^2}.]
Примеры задач на силу натяжения нити
Пример 1
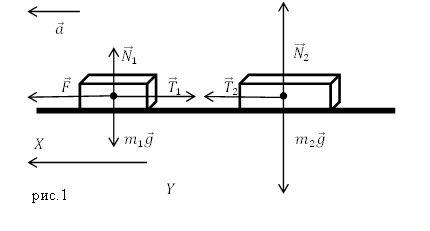
Задание. Какой будет сила натяжения нерастяжимой нити, связывающей два груза находящихся на горизонтальной гладкой поверхности (рис.1), если массы грузов равны $m_1$ и $m_2. $К одному из грузов приложена горизонтальная сила $F.$ Трение брусков о поверхность не учитывать. Нить считать невесомой.
Решение. Рассмотрим силы, которые приложены к первому грузу, запишем второй закон Ньютона для этого тела:
[overline{F}+m_1overline{g}+{overline{N}}_1+{overline{T}}_1=m_1overline{a}left(1.1right),]
$m_1overline{g}$ — сила тяжести, действующая на первый груз; ${overline{N}}_1$ — сила реакции горизонтальной опоры; ${overline{T}}_1$ — сила натяжения нити.
Проектируя на оси X и Y уравнение (1.1) получаем:
[left{ begin{array}{c}
X:F-T_1=m_1aleft(1.2right). \
m_1g=N_1left(1.3right). end{array}
right.]
Рассмотрим силы, действующие на второй груз, запишем второй закон Ньютона для этих сил:
[overline{F}+m_2overline{g}+{overline{N}}_2+{overline{T}}_2=m_2overline{a}left(1.4right).]
В проекциях на оси X и Y получаем систему уравнений:
[left{ begin{array}{c}
X:T_2=m_2aleft(1.5right). \
m_2g=N_2left(1.6right). end{array}
right.]
Так как нить считаем невесомой, то имеем:
[T_1=T_2=Tleft(1.7right).]
Из уравнения (1.5) выразим ускорение и подставим его в (1.2)получим величину силы натяжения нити:
[F-T=m_1frac{T}{m_2}to T=frac{Fm_2}{m_1+m_2}.]
Ответ. $T=frac{Fm_2}{m_1+m_2}$
Пример 2
Задание. К нерастяжимой нити подвешен массивный шарик. Шарик подняли так, что нить приняла горизонтальное положение, затем шарик отпустили. Какова сила натяжения нити в момент, когда шарик проходит положение равновесия? Какой угол составляет нить с вертикалью, если сила натяжения равна силе тяжести, действующая на шарик?
Решение. Сделаем рисунок.
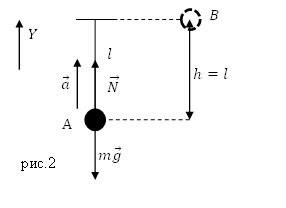
1) Силы, действующие на шарик в момент прохождения положения равновесия (положение А на рис.2): сила тяжести и сила натяжения нити. Для них запишем второй закон Ньютона:
[moverline{g}+overline{N}=moverline{a}left(2.1right).]
Запишем проекцию выражения (2.1) на ось Y:
[N-mg=ma_nleft(2.2right),]
где шарик движется с центростремительным ускорением, равным:
[a_n=frac{v^2}{l}left(2.3right),]
$l$ — длина нити; $v$ — величина скорости движения шарика в точке А.
Скорость $v$ найдем из закона сохранения энергии (см. рис.2 $h=l$), который запишем для положений B (максимальная потенциальная энергия шара) и A (максимальная кинетическая энергия шара):
[mgl=mfrac{v^2}{2}to v^2=2gl left(2.4right).]
Выразим силу натяжения нити из (2.2), подставим найденное ускорение, учитывая (2.4):
[N=mg-mfrac{v^2}{l}=mg+mfrac{2gl}{l}=3mg.]
2)
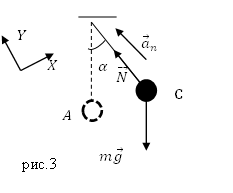
Ось Y направим по нити, ось X перпендикулярно оси Y (рис.3).
Запишем проекцию уравнения (2.1) на новую ось Y:
[N-mg{cos alpha }=ma_{n }left(2.5right).]
Выразим силу натяжения нити:
[N=ma_{n }+mg{cos alpha }left(2.6right).]
Учитывая (2.3), получим:
[N=mfrac{v^2}{l}+mg{cos alpha }left(2.7right).]
Потенциальная энергия шарика в положении C равна $E_p=mgl{cos alpha }$, она переходит полностью в кинетическую энергию положения А ($E_k=mfrac{v^2}{2}$):
[mfrac{v^2}{2}=mgl{cos alpha }left(2.8right).]
Из (2.6) выразим $v^2$, имеем:
[v^2=2gl{cos alpha }left(2.9right).]
Подставим результат (2.9) в формулу (2.7), получили:
[N=mfrac{2gl{cos alpha }}{l}+mg{cos alpha } left(2.10right).]
Приравниваем по условию силу натяжения нити к силе тяжести, выражаем величину угла:
[mg=mfrac{2gl{cos alpha }}{l}+mg{cos alpha }to 1=3{cos alpha to alpha =arc{cos frac{1}{3} } }.]
Ответ. 1) $N=3mg$. 2) $alpha =arc{cos frac{1}{3} }$
Читать дальше: сообщающиеся сосуды.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Связями называют тела, ограничивающие свободу перемещения рассматриваемого тела.
Реакции связей — это усилия, с которыми связи действуют на данное тело.
Тела в природе бывают свободными и несвободными. Тела, свобода перемещения которых ничем не ограничена, называются свободными.
Одним из основных положений механики является принцип освобождаемости от связей, согласно которому несвободное тело можно рассматривать как свободное, если отбросить действующие на него связи и заменить их силами – реакциями связей.
Очень важно правильно расставить реакции связей, иначе написанные уравнения окажутся неверными.
Рассмотрим реакции связей основных типов, встречающихся при решении задач: гладкой поверхности, ребра, гибкой нити, стержня, шарнирных опор и заделок, а также примеры замены связей их реакциями.
Реакции гладкой поверхности и ребра
Ниже приведены примеры замены связей гладкой поверхности и ребра их реакциями.
На рисунках 1.1–1.8 показаны примеры замены реакциями сил, расположенных в плоскости.
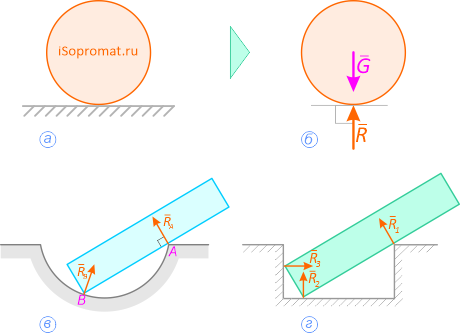
а – тело весом G на гладкой поверхности;
б – действие поверхности заменено реакцией – силой R;
в – в точке А связь «опорная точка» или ребро;
г – реакции направлены перпендикулярно
опираемой или опирающейся плоскостям
Рисунок 1.1
Реакция гладкой поверхности всегда направлена по нормали к этой поверхности (рисунок 1.1).
Реакции связей нити и стержня
Реакция «невесомого» троса (нити, цепи, стержня) всегда направлена вдоль самого троса (нити, цепи, стержня) (рисунок 1.2).
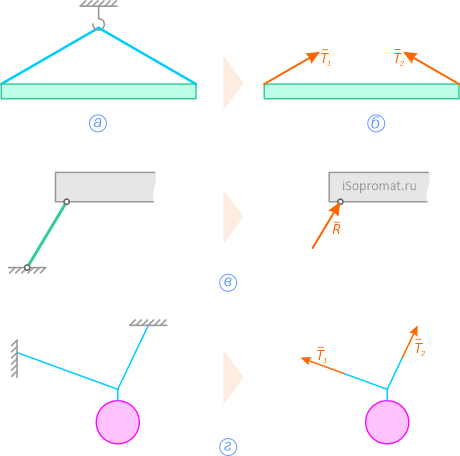
а – балка висит на двух тросах;
б – действие тросов заменено силами Т1 и Т2;
в – связь «идеальный стержень»;
г – связь «идеальная нить»
Рисунок 1.2
Реакции связей шарнирных опор
Шарнирные опоры допускают вращение относительно шарнира, поэтому в них не возникает вращающий момент.
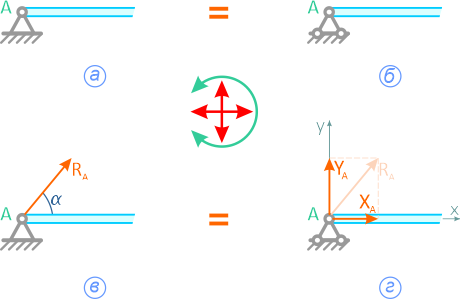
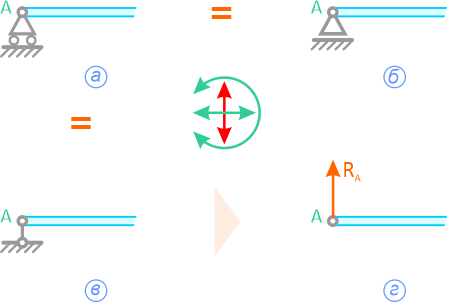
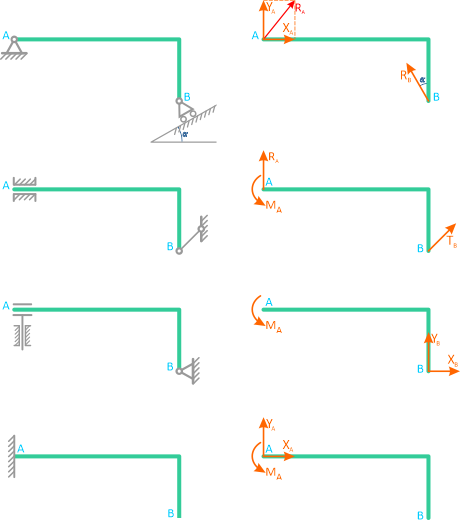
Шарнирно-неподвижная опора может изображаться по-разному (рисунок 1.3,а или 1.3,б). Она может быть заменена либо силой R с углом α (рисунок 1.3,в), либо двумя силами, например, XA и YA (рисунок 1.3,г).
Рисунок 1.3
Всегда можно перейти от R и α к XA и YA (и наоборот):
Шарнирно-подвижная опора (рисунок 1.4,а, б, в) допускает (в данном случае) горизонтальное перемещение и не допускает вертикальное.
Реакция R может быть направлена только по нормали к опорной поверхности (рисунок 1.4, г).
Рисунок 1.4
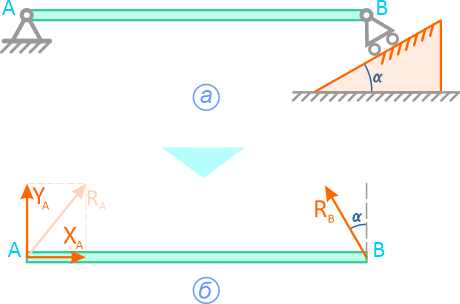
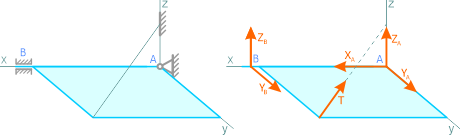
В следующем примере, связи шарнирно-неподвижной опоры в точке A и шарнирно-подвижной опоры в точке B отброшены (рисунок 1.5, б), а их действие заменено силами XA, YA и RB.
Рисунок 1.5
Подробнее про связи и реакции связей смотрите в нашем видео:
Другие видео
Реакции связи в заделках
Все виды заделок исключают поворот, поэтому в них всегда возникает связь «момент».
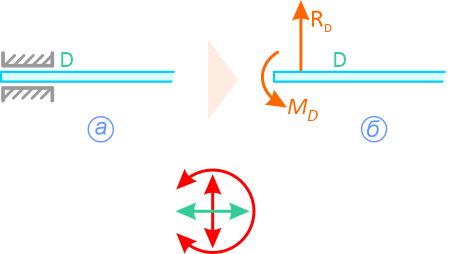
Соединение стержня и втулки в плоскости (рисунок 1.6) – скользящая заделка. Отбросив втулку – получаем действие на стержень силы RD и момента MD.
Рисунок 1.6
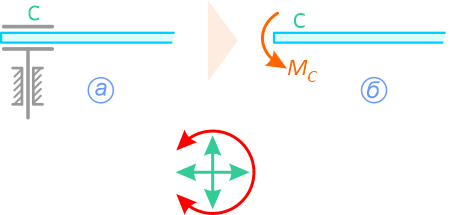
На рисунке 1.7, а изображена бискользящая заделка. В плоскости данная опора допускает поступательное перемещение стержня как по горизонтали, так и по вертикали, но препятствует повороту (в плоскости). Реакцией такой опоры будет только момент MC (рисунок 1.7, б).
Рисунок 1.7
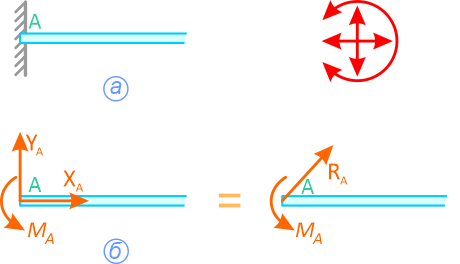
Консоль (глухая или жесткая заделка) не допускает никакого перемещения детали. Реакцией такой опоры являются неизвестная по величине и направлению сила RA с углом α (или XA и YA) и момент ΜA (рисунок 1.8).
Рисунок 1.8
Реакции пространственных связей
Трехмерная шарнирно-неподвижная опора, или сферический шарнир (рисунок 1.9, а), заменяется системой сил (рисунок 1.9, б) XA, YA и ZA, т.е. силой, неизвестной по величине и направлению.
Рисунок 1.9
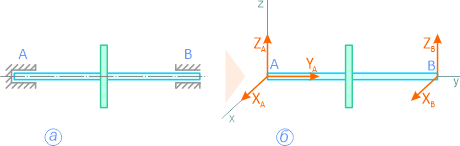
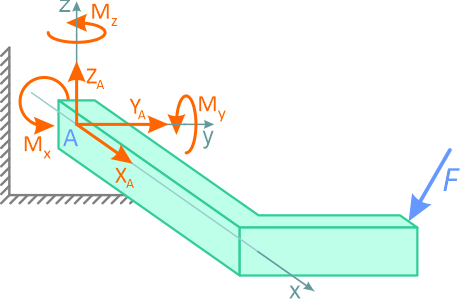
На рисунке 1.10, а показан вал с колесом, закрепленный в опорах: в точке A – подпятник или стакан, в точке B – втулка или подшипник. Действие опор заменено силами XA, YA, ZA и XB, ZB (рисунок 1.10, б).
Рисунок 1.10
На следующих рисунках показаны примеры замены различных типов связей их реакциями.
Рисунок 1.11
Трехмерная система удерживаемая в равновесии тремя типами связей: скользящей заделкой, шарнирно неподвижной опорой и тросом.
Рисунок 1.12
В общем случае пространственного нагружения, в глухой заделке может возникать до шести реакций связей: три силы и три момента.
Рисунок 1.13
Величина и истинное направление сил реакций связей определяются из уравнений равновесия рассматриваемой системы.
Для плоской системы сил составляется 3 уравнения
Для пространственной системы — до шести уравнений статики.
Из которых выражаются и рассчитываются искомые реакции.
Пример определения сил реакций связей
Задача
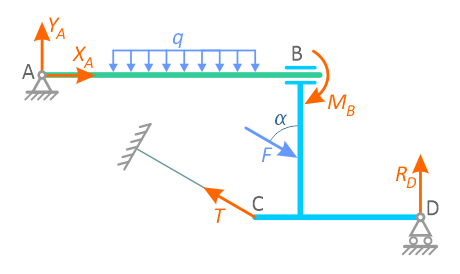
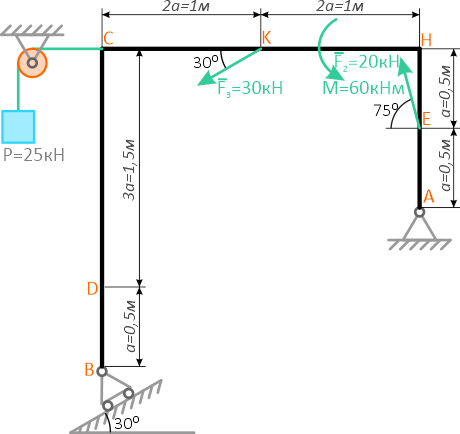
Жесткая рама закреплена в точке A шарнирной связью, а в точке B удерживается в состоянии статического равновесия опорой на катках, с упором в наклонную плоскость под углом 30°.
В точке C к раме привязан трос, перекинутый через блок и несущий на конце груз весом P=25кН.
На раму действует пара сил с моментом M=60кНм и две силы F2 и F3 приложенные в точках K и E и расположенные под углами 30° и 75° к горизонтальной оси.
Требуется определить реакции связей в точках A и B, вызываемые заданными действующими нагрузками.
При расчетах, принять размер a=0,5м.
Решение
Рассмотрим равновесие рамной пластины.
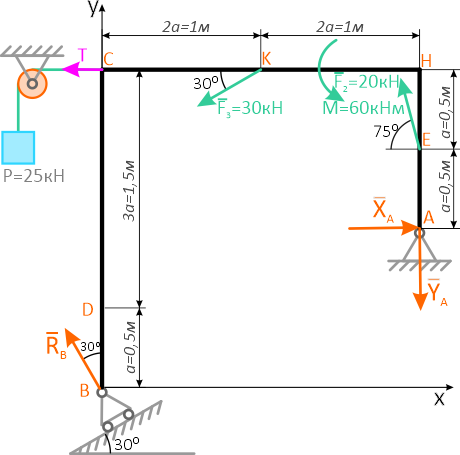
Проведем координатные оси x-y и изобразим действующие на пластину внешние нагрузки: силы F, пару сил с моментом M, натяжение троса T (по модулю T=P) и реакции связей XA, YA, RB.
Реакцию неподвижной шарнирной опоры A изображаем двумя составляющими её связями. Реакция на катке направлена перпендикулярно опорной плоскости.
Для полученной плоской системы сил составим три уравнения равновесия системы.
При вычислении моментов сил F относительно точки A воспользуемся теоремой Вариньона, т.е. разложим силы на составляющие Fx=Fcosα и Fy=Fsinα и учтём что mA(F)=mA(Fx)+mA(Fy).
Запишем уравнения сумм проекций сил на оси x и y, а также суммы моментов относительно любой точки системы, например, точки A.
Решая полученную систему уравнений, определяем неизвестные реакции связей катка и шарнирно-неподвижной опоры.
Из уравнения (3) находим реакцию катка
Из уравнения (1) горизонтальную реакцию в точке A
Из уравнения (2) — вертикальную.
Положительные значения найденных реакций говорят о том, что направление связей было выбрано, верно.
Проверку можно выполнить, составив уравнение суммы моментов, в котором будут записаны все искомые реакции, например, относительно точки D:
Ноль, полученный в ответе, означает правильность составления и решения уравнений
Ответ: Получены следующие значения сил реакций связей: в катке RB=57,6кН, в шарнирной опоре XA=84,96кН и YA=54,2кН.
Другие примеры решения задач >
Проекция силы на ось >
Сила — реакция — нить
Cтраница 1
Сила реакции нити 56 примерно равна 14 н; 2) масса второго груза примерно равна 2 9 кг.
[2]
Сила реакции нити 5С примерно равна 14 н; 2) масса второго груза примерно равна 2 9 кг.
[3]
Вектор силы реакции нити К направлен по нити к точке подвеса.
[4]
Мы получили силу реакции нити; искомая сила натяжения равна ей по модулю и направлена в противоположную сторону.
[5]
Мы получили силу реакции нити, искомая сила натяжения равна ей по величине и направлена в противоположную сторону.
[6]
В этот момент на шарик подействует сила реакции нити, которую можно рассматривать по аналогии с силой реакции стенки, действующей на мячик, ударяющийся о стенку. При этом своеобразном отражении должно выполняться правило равенства углов падения и отражения. Теперь рассмотрим второй случай: мы сначала натянем нить, а затем осторожно выпустим шарик из руки. Сообщим шарику некоторую скорость v0, направленную перпендикулярно к нити. В результате шарик начнет равномерно вращаться на нити. Плоскость вращения задается нитью и вектором скорости, сообщенной шарику. Требуется найти период колебаний маятника, находящегося в системе, которая движется с некоторым ускорением. Однако в отличие от предыдущих задач с лифтом ускорение системы направлено под некоторым углом к ускорению земного тяготения. Поэтому в данном случае возникает дополнительный вопрос: каково равновесное направление нити маятника.
[7]
Изображаем — вес материальной точки Р и силу реакции нити К. Момент силы реакции нити К относительно оси г равен нулю, а момент веса Р равен — РН — Р1 зш ср. Момент отрицателен, так как его направление противоположно направлению положительного отсчета угла поворота ср.
[8]
К маятнику приложены следующие силы: вес маятника Р и сила реакции нити К.
[9]
И точке В на тело действуют сила тяжести mg и сила реакции нити / V Разложим силу тяжести на нормальную mgn и тангенциальную / и составляющие.
[10]
Поэтому к телу приложены две силы: сила тяжести и сила реакции нити. Между прочим, о последней из этих двух сил Вы говорили как о силе натяжения нити, забывая, что сила натяжения нити — это сила, приложенная к нити со стороны тела, тогда как сила, приложенная к телу со стороны нити, есть сила резкими нити.
[11]
Автор: Это требование не нужно, если рассматривается энергия шарика или сила реакции нити. В данном случае речь идет фактически не о маятнике, а о движении шарика по окружности в вертикальной плоскости. Так, например, в задаче 14.2 условие малости угла отклонения маятника несущественно, тогда как в задаче 14.3 это условие крайне важно.
[12]
Автор: Этого требования не нужно, если рассматривается энергия шарика или сила реакции нити. В данном случае речь идет фактически не о маятнике, а о движении шарика по окружности в вертикальной плоскости. Однако если в задаче участвует формула периода колебаний ( 75), то колебания маятника обязательно должны быть гармоническими и, следовательно, угол отклонения нити должен быть мал. Так, например, в задаче 56 условие малости угла отклонения маятника несущественно, тогда как в задаче 57 это условие крайне важно.
[13]
В данном случае электрическая сила направлена все время вдоль нити, и поэтому она все время уравновешивается силой реакции нити. Отсюда следует, что электрическая сила не приводит к появлению возрастающей силы и, следовательно, не может влиять на период колебаний маятника.
[14]
В данном случае электрическая сила направлена все время вдоль нити, и поэтому она вес время уравновешивается силой реакции нити. Отсюда следует, что электрическая сила не приводит к появлению возрастающей силы и, следовательно, не может влиять на период колебаний маятника.
[15]
Страницы:
1
2
3
Вес тела. Сила реакции опоры. Сила натяжения нити
Многие из вас пользуются или пользовались обычной проводной компьютерной мышкой. Если такая проводная мышка рядом с вами, то посмотрите на нее (а если ее нет рядом — то представьте). Мы знаем, что, как и на все тела на Земле, на нее действует сила тяжести F т я г о т е н и я = m ⋅ g F_<тяготения>=mcdot g F т я г о т е н и я = m ⋅ g .
Почему же она не падает вниз, а находится в состоянии покоя? Мы помним из 1-го закона Ньютона, что в инерциальных системах тело может находиться в состоянии покоя, если на него не действуют никакие силы (не наш случай) или действие всех сил скомпенсировано. Значит, что-то компенсирует действие силы тяжести. Но что? Мы забыли, что мышка лежит на столе. Мышка, на которую действует сила тяжести m ⋅ g ⃗ mcdotvec m ⋅ g ⃗ , в свою очередь давит на стол с силой, которую называют вес тела . Обычно вес тела обозначается P ⃗ vec
P ⃗ . Но из 3-го закона Ньютона мы знаем: с какой силой мышка давит на стол ( мышка → rightarrow → стол ), с точно такой же по величине силой стол давит на мышку ( стол → rightarrow → мышка ). Сила, с которой стол давит на мышку, называется силой реакции опоры. Чаще всего она обозначается N ⃗ vec N ⃗ . Из 3-го закона Ньютона следует, что N ⃗ = − P ⃗ . vec=-vec
<.>N ⃗ = − P ⃗ .
Заметьте, что сил три:
Ее не существует, поэтому ее нельзя найти
Равнодействующая равна нулю, поскольку N ⃗ = − P ⃗ vec=-vec
N ⃗ = − P ⃗
Тело в состоянии покоя может не лежать на столе, а, например, висеть на веревке.
Ту же компьютерную мышку можно было бы подвесить на ее же шнуре (если она у вас проводная). Ситуация очень похожа на случай с лежащей мышкой. Только в случае с висящей мышкой падать под действием силы тяжести ей не дает нить, а точнее — сила натяжения нити. Обычно ее обозначают буквой T ⃗ vec T ⃗ .
В этом случае весом называют силу, с которой тело (мышка) растягивает нить подвеса. Вообще
вес — это сила, с которой тело давит на опору или растягивает нить подвеса.
Соответственно, если тело ни на что не давит и ничего не тянет — то оно находится в состоянии невесомости.
Каждый из вас может оказаться в состоянии невесомости, если (отметьте все правильные варианты)
Формула силы натяжения нити
Определение и формула силы натяжения нити
Силу натяжения определяют как равнодействующую сил $(bar)$, приложенных к нити, равную ей по модулю, но противоположно направленную. Устоявшегося символа (буквы), обозначающего силу натяжения нет. Ее обозначают и просто $bar$ и $bar$, и $bar$ . Математически определение для силы натяжения нити можно записать как:
где $bar$ = векторная сумма всех сил, которые действуют на нить. Сила натяжения нити всегда направлена по нити (или подвесу).
Чаще всего в задачах и примерах рассматривают нить, массой которой можно пренебречь. Ее называют невесомой.
Еще одним важной характеристикой нити при расчете силы натяжения является ее растяжимость. Если исследуется невесомая и нерастяжимая нить, то такая нить считается просто проводящей через себя силу. В том случае, когда необходимо учитывать растяжение нити, применяют закон Гука, при этом:
где k – коэффициент жесткости нити, $Delta l$ – удлинение нити при растяжении.
Единицы измерения силы натяжения нити
Основной единицей измерения силы натяжения нити (как и любой силы) в системе СИ является: [T]=Н
Примеры решения задач
Задание. Невесомая, нерастяжимая нить выдерживает силу натяжения T=4400Н. С каким максимальным ускорением можно поднимать груз массой m=400 кг, который подвешивают на эту нить, чтобы она не разорвалась?
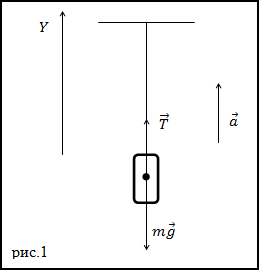
Решение. Изобразим на рис.1 все силы, действующие на груз, и запишем второй закон Ньютона. Тело будем считать материальной точкой, все силы приложенными к центру масс тела.
где $bar$ – сила натяжения нити. Запишем проекцию уравнения (1.1) на ось Y:
Из выражения (1.2) получим ускорение:
Все данные в задаче представлены в единицах системы СИ, проведем вычисления:
Ответ. a=1,2м/с 2
Задание. Шарик, имеющий массу m=0,1 кг прикрепленный к нити (рис.2) движется по окружности, расположенной в горизонтальной плоскости. Найдите модуль силы натяжения нити, если длина нити l=5 м, радиус окружности R=3м.
Решение. Запишем второй закон Ньютона для сил, приложенных к шарику, который вращается по окружности с центростремительным ускорением:
Найдем проекции данного уравнения на обозначенные на рис.2 оси X и Y:
$$ begin X: quad T sin alpha=m a=m omega^ <2>R(2.2) \ Y: quad-m g+T cos alpha=0 end $$
Из уравнения (2.3) получим формулу для модуля силы натяжения нити:
Из рис.2 видно, что:
Подставим (2.5) вместо $cos alpha$ в выражение (2.4), получим:
Так как все данные в условиях задачи приведены в единицах системы СИ, проведем вычисления:
Сила натяжения нити и применение формулы в бытовых ситуациях
Силой натяжения называют ту, что действует на объект, сравнимый с проволокой, шнуром, кабелем, ниткой и так далее. Это могут быть несколько объектов сразу, в таком случае сила натяжения будет действовать на них и необязательно равномерно. Объектом натяжения называют любой предмет, подвешенный на все вышеперечисленное. Но кому это нужно знать? Несмотря на специфичность информации, она может пригодиться даже в бытовых ситуациях.
Например, при ремонте дома или квартиры. Ну и, конечно же, всем людям, чья профессия связана с расчетами:
- инженерам;
- архитекторам;
- проектировщикам и пр.
Натяжения нити и подобных объектов
А зачем им это знать и какая от этого практическая польза? В случае с инженерами и конструкторами знания о мощи натяжения позволят создавать устойчивые конструкции. Это означает, что сооружения, техника и прочие конструкции смогут дольше сохранять свою целостность и прочность. Условно, эти расчеты и знания можно разделить на 5 основных пунктов, чтобы в полной мере понять, о чем идет речь.
1 Этап
Задача: определить силу натяжения на каждом из концов нити. Эту ситуацию можно рассматривать как результат воздействия сил на каждый конец нити. Она равняется массе, помноженной на ускорение свободного падения. Предположим, что нить натянута туго. Тогда любые воздействия на объект приведет к изменению натяжения (в самой нити). Но даже при отсутствии активных действий, по умолчанию будет действовать сила притяжения. Итак, подставим формулу: Т=м*g+м*а, где g – ускорение падения (в данном случае подвешенного объекта), а – любое иное ускорение, действующее извне.
Есть множество сторонних факторов, влияющих на расчеты – вес нити, ее кривизна и так далее. Для простых расчетов это мы не будем пока что учитывать. Иными словами – пусть нить будет идеальна с математической точки зрения и «без изъянов».
Возьмем «живой» пример. На балке подвешена прочная нить с грузом в 2 кг. При этом отсутствует ветер, покачивания и прочие факторы, так или иначе влияющие на наши расчеты. Тогда мощь натяжения равна силе тяжести. В формуле это можно выразить так: Fн=Fт=м*g, в нашем случае это 9,8*2=19,6 ньютона.
2 Этап
Заключается он в вопросе об ускорении. К уже имеющейся ситуации давайте добавим условие. Суть его в том, чтобы на нить действовало еще и ускорение. Возьмем пример попроще. Представим, что нашу балку теперь поднимают вверх со скоростью 3 м/с. Тогда, к натяжению прибавится ускорение груза и формула примет следующий вид: Fн=Fт+уск*м. Ориентируясь на прошлые расчеты получаем: Fн=19,6+3*2=25,6 ньютона.
3 Этап
Тут уже посложнее, так как речь идет об угловом вращении. Следует понимать, что при вращении объекта вертикально, сила, воздействующая на нить, будет намного больше в нижней точке. Но давайте возьмем пример с несколько меньшей амплитудой качания (по типу маятника). В этом случае для расчетов нужна формула: Fц=м* v²/r. Тут искомое значение обозначает дополнительную мощь натяжения, v – скорость вращения подвешенного груза, а r – радиус окружности, по которому вращается груз. Последнее значение фактически равняется длине нити, пускай она составляет 1,7 метра.
Итак, подставляя значения, находим центробежные данные: Fц=2*9/1,7=10,59 ньютона. А теперь, чтобы узнать полную силу натяжения нити, надо к имеющимся данным о состоянии покоя прибавить центробежную силу: 19,6+10,59=30,19 ньютона.
4 Этап
Следует учитывать меняющуюся силу натяжения по мере прохождения груза через дугу. Иными словами – независимо от постоянной величины притяжения, центробежная (результирующая) сила меняется по мере того, как качается подвешенный груз.
Чтобы лучше понять этот аспект, достаточно представить себе привязанный груз к веревке, которую можно свободно вращать вокруг балки, к которой она закреплена (как качели). Если веревку раскачать достаточно сильно, то в момент нахождения в верхнем положении сила притяжения будет действовать в «обратную» сторону относительно силы натяжения веревки. Иными словами – груз станет «легче», из-за чего ослабнет и натяжение на веревку.
Предположим, что маятник отклоняется на угол, равный двадцати градусам от вертикали и движется со скоростью 1,7 м/с. Сила притяжения (Fп) при этих параметрах будет равна 19,6*cos(20)=19,6*0,94=18,424 Н; центробежная сила (F ц=mv²/r)=2*1,7²/1,7=3,4 Н; ну а полное натяжение (Fпн) будет равняться Fп+ Fц=3,4+18,424=21,824 Н.
5 Этап
Его суть заключается в силе трения между грузом и другим объектом, что в совокупности косвенно влияет на натяжение веревки. Иначе говоря – сила трения способствует увеличению силы натяжения. Это хорошо видно на примере перемещения объектов по шершавой и гладкой поверхностях. В первом случае трение будет большим, поэтому и сдвигать предмет становится тяжелее.
Общее натяжение в данном случае вычисляется по формуле: Fн=Fтр+Fу, где Fтр – трение, а Fу – ускорение. Fтр=мкР, где мк – трение между объектами, а Р – сила взаимодействия между ними.
Чтобы лучше понять данный аспект, рассмотрим задачу. Допустим, у нас груз 2 кг и коэффициент трения равен 0,7 с ускорением движения 4м/с постоянной скорости. Теперь задействуем все формулы и получаем:
- Сила взаимодействия — Р=2*9,8=19,6 ньютона.
- Трение — Fтр=0,7*19,6=13,72 Н.
- Ускорение — Fу=2*4=8 Н.
- Общая сила натяжения — Fн=Fтр+Fу=13,72+8=21,72 ньютона.
Теперь вы знаете больше и можете сами находить и рассчитывать нужные значения. Конечно, для более точных расчетов нужно учитывать больше факторов, но для сдачи курсовой и реферата этих данных вполне достаточно.
Видео
Это видео поможет вам лучше разобраться в данной теме и запомнить ее.
http://www.webmath.ru/poleznoe/formules_21_30_sila_natjazhenija_niti.php
http://liveposts.ru/articles/education-articles/fizika/sila-natyazheniya-niti-i-primenenie-formuly-v-bytovyh-situatsiyah
В задачах статики почти всегда приходится рассматривать равновесие несвободного тела, то есть тела, так или иначе закрепленного или имеющего ту или иную опору. В зависимости от вида или типа опоры можно указать следующие основные типы связей:
— гладкая поверхность (без трения);
— гладкий выступ;
— гибкая невесомая нить;
— невесомый стержень с шарнирно закрепленными концами;
— подвижный шарнир без трения (каток);
— неподвижный шарнир.
Рассмотрим каждый тип реакций связей подробнее.
Гладкая поверхность
Пусть тело опирается на гладкую поверхность и соприкасается с ней в некоторой точке. Реакция гладкой поверхности приложена в точке касания и направлена по нормали к поверхности. Обычно такие силы называются нормальными силами или нормальными реакциями опоры и обозначаются буквой или
.
На рис.С.6. приведены примеры реакции гладкой поверхности.
Пусть балка DE опирается в точке D о гладкую поверхность, а в точке E о гладкий выступ. Реакция гладкой поверхности приложена в точке касания и направлена по нормали к поверхности, в то время как реакция гладкого выступа приложена в точке опоры балки и направлена по нормали к оси балки.
Гибкая невесомая нить
Пусть некоторый груз весом подвешен на гибкой нерастяжимой и невесомой нити. Связь, осуществленная в виде гибкой нерастяжимой нити, не дает грузу удаляться от точки крепления нити к грузу. В этом случае реакция гибкой нерастяжимой и невесомой нити приложена к точке крепления нити к телу D и направлена вдоль нити (рис.С.8). Реакцию связи нити иногда называют натяжением нити и обозначают буквой
. В точке А реализуется опирание на гладкую поверхность без трения с реакцией
.

Невесомый прямолинейный стержень с шарнирно закрепленными концами
Пусть груз Q весом закреплен в точке В прямолинейным невесомым стержнем. Трением в шарнирах можно пренебречь. Реакция невесомого стержня с шарнирно закрепленными концами приложена к точке крепления стержня с грузом и направлена по оси стержня.
Если стержень под действием нагрузки подвергается растяжению, то реакция стержня направлена в сторону, указанную на рис.С.9а. Если стержень под действием нагрузки подвергается сжатию, то реакция стержня
направлена в сторону, указанную на рис.С.9б.
При решении задач, в которых связью служит невесомый стержень с шарнирно закрепленными концами, вначале указываем предположительное направление силы . Если после решения задачи окажется, что числовое значение реакции
, т.е. проекция реакции связи
на направление
положительно, то это означает, что сила
направлена на чертеже правильно.

Если после решения задачи окажется, что числовое значение реакции , т.е. проекция реакции связи
на направление
отрицательно, то это означает, что сила
направлена на чертеже в противоположную сторону.
Подвижный шарнир без трения (каток)
Пусть тело весом опирается точкой С на подвижный каток, который может перемещаться по гладкой плоской поверхности
(рис.С.10).
Поскольку данная опора допускает возможность перемещения по направлению поверхности , то в этом направлении отсутствует компонента реакции шарнира.
Таким образом, реакция подвижного шарнира , как показано на рис.С.10, приложена в точке
и направлена по нормали к поверхности перемещения катка
.
Неподвижный шарнир
Пусть тело весом
опирается точкой D на неподвижный шарнир (рис.С.11). Реакция неподвижного шарнира приложена в точке касания тела D с осью шарнира. Направление реакции неподвижного шарнира заранее неизвестно.
При решении задач реакцию неподвижного шарнира обычно раскладывают на две составляющие, соответствующие проекциям на оси координат. При этом могут быть случаи, когда реакцию неподвижного шарнира удобнее раскладывать по другим направлениям.
Составляющие реакции неподвижного шарнира обычно обозначают символами и
.
Направления каждой из составляющих реакции неподвижного шарнира обычно заранее неизвестно, поэтому, как показано на рис.С.11, при решении задач вначале указывают предполагаемые направления составляющих реакции шарнира.
Если после решения задачи окажется, что проекция силы реакции и
то это означает, что обе составляющие на чертеже указаны правильно. В противном случае, проекция составляющей реакции, имеющей отрицательный знак, должна быть направлена в противоположную сторону.
В точке Е реализуется свободное опирание балки с реакцией .
Пример.
Брус DE закреплен в точке D неподвижным шарниром, а в точке Е опирается на гладкую поверхность стены (рис.С.12а).
Для бруса DE связями служат два тела: неподвижный шарнир D и гладкая поверхность стены.
Раскладываем реакцию неподвижного шарнира на две составляющие и
и показываем на чертеже предполагаемые направления этих составляющих.
Реакция гладкой стены приложена в точке Е касания балки и стены и направлена по нормали к стене (рис.С.12б).
На рис.С.13 приведен также пример использования опирания на неподвижный шарнир и гладкий выступ.
Таковы основные типы опор и их реакций.