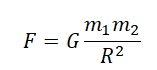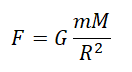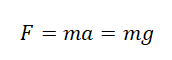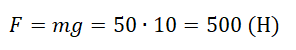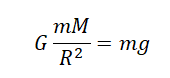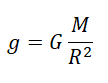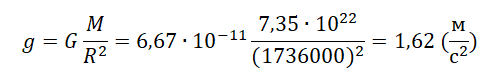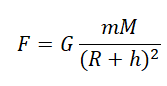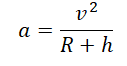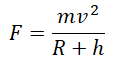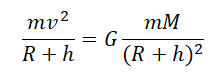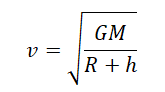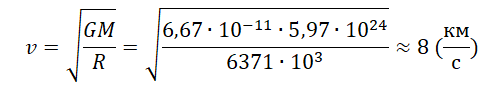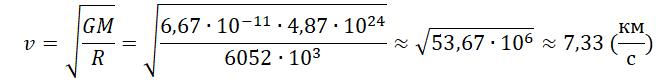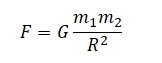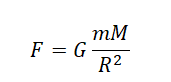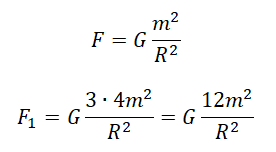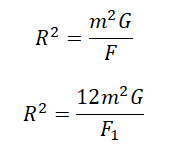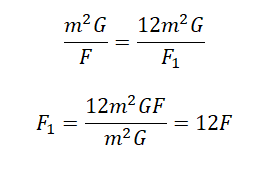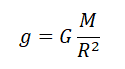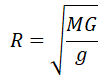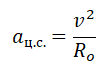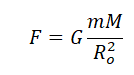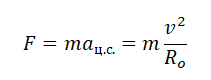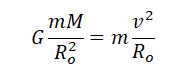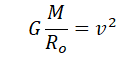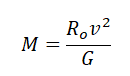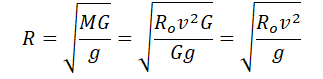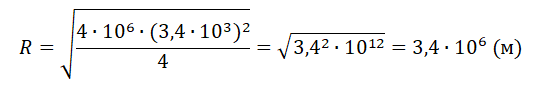Напомню, что такие задачи решаются на ОГЭ несложно, простой подстановкой данных в формулу. Есть два варианта — сначала подставить данные, затем решать уравнение, или сначала выразить из формулы искомую величину, а затем подставить данные. Разберём оба варианта:
1) F=(GmM)/r² Подставляем данные:
0,00667=6,67⋅10⁻¹¹*m*5⋅10⁸/5²
0,00667=6,67*10⁻³*m/5
0,00667*m=0,00667*5
m=5 кг
2) А теперь выразим массу m из формулы:
m=F*r²/G*M
Подставим данные в получившуюся формулу:
m=0,00667*5²/6,67⋅10⁻¹¹*5⋅10⁸=0,00667*5/0,00667=5 кг
Способ решения, который Вы выберете, значения не имеет. Результат при этом получается одинаковый.
Ответ: 5 кг.
Все тела взаимодействуют друг с другом. Так, две материальные точки, обладающие массой, притягиваются друг к другу с некоторой силой, которую называют гравитационной, или силой всемирного тяготения.
Сила всемирного тяготения — сила, с которой все тела притягиваются друг к другу.
Закон всемирного тяготения
Сила взаимного притяжения двух тел прямо пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними.
F — сила всемирного тяготения, m1 и m2 — массы двух притягивающихся друг к другу тел, R — расстояние между этими телами, G — гравитационная постоянная (G = 6,67∙10–11 Н ∙ м2/кг2).
Сила всемирного тяготения направлена по линии, соединяющей центры двух тел.
Гравитационная постоянная численно равна силе притяжения между двумя точечными телами массой 1 кг каждое, если расстояние между ними равно 1 м. Если R = 1 м, m1 = 1 кг и m2 = 1 кг, то F = G.
G = 6,67∙10–11 Н ∙ м2/кг2.
Сила тяжести
Согласно закону всемирного тяготения, все тела притягиваются между собой. Так, Земля притягивает к себе падающий на нее мяч, а мяч притягивает к себе Землю.
Сила тяжести — сила, с которой Земля притягивает к себе тела.
Сила тяжести действует на все тела, находящиеся в поле притяжения Земли. Она всегда направлена к центру нашей планеты.
Расчет силы тяжести на Земле
Силу тяжести можно рассчитать с помощью закона всемирного тяготения. Тогда одна из масс будет равна массе земли. Обозначим ее большой буквой M. Вторая масса будет принадлежать телу, притягивающемуся к Земли. Обозначим его m. В качестве R будет служить радиус Земли. В таком случае сила тяжести будет определяться формулой:
Вывод формулы ускорения свободного падения
Согласно второму закону Ньютона, сила, которая действует на тело, сообщает ему ускорение. Поэтому силу тяжести также можно выразить через это ускорение. Обозначим его g — ускорение свободного падения.
Пример №1. Мальчик массой 50 кг прыгнул под углом 45 градусов к горизонту. Найти силу тяжести, действующую на него во время прыжка.
Сила тяжести зависит только от массы тела и ускорения свободного падения. Направлена она всегда к центру Земли, и от характера движения тела не зависит. Поэтому:
Мы получили две формулы для вычисления силы тяжести: одну — исходя из закона всемирного тяготения, вторую — исходя из второго закона Ньютона. Приравняем правые части формул и получим:
Отсюда:
Формула расчета ускорения свободного падения
Вместо массы и радиуса Земли можно взять массы и радиусы любых планет. Так можно рассчитать ускорение свободного падения для любого космического тела.
Пример №2. Рассчитать ускорение свободного падения на Луне. Считать, что радиус Луны равен 1736 км, а ее масса — 7,35∙1022 кг.
Переведем километры в метры: 1736 км = 1736000 м.
Первая космическая скорость
Исаак Ньютон смог доказать, что причиной падения тел на Землю, движения Луны вокруг Земли и движения Земли вокруг Солнца является сила тяготения. Если камень бросить в горизонтальном направлении, его траектория будет отклонена от прямой линии под действием земной силы тяжести. Если же придать этому камню большую скорость, камень приземлится на большем расстоянии. Значит, существует такая скорость, при которой камень не приземлится, а начнет бесконечно вращаться вокруг Земли.
ОпределениеПервая космическая скорость — минимальная (для заданной высоты над поверхностью планеты) горизонтальная скорость, которую необходимо придать объекту, чтобы он совершал движение по круговой орбите вокруг планеты.
Вывод формулы первой космической скорости
Когда тело массой m вращается на некоторой высоте h, расстояние между ним и центром Земли равно сумме этой высоты и радиуса Земли. Поэтому сила тяготения между этим телом и Землей будет равна:
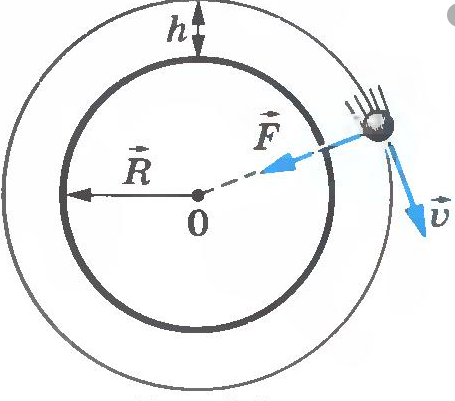
Движение тела вокруг планеты — частный случай движения тела по окружности с постоянной по модулю скоростью. Мы уже знаем, что такое тело движется с центростремительным ускорением, направленным к центру окружности. В данном случае центростремительное ускорение будет направлено к центру Земли. Это ускорение сообщает телу сила тяготения.
Так как тело движется на некоторой высоте h от поверхности Земли, центростремительное ускорение будет определяться формулой:
Подставив это ускорение в формулу второго закона Ньютона, получим силу, с которой Земля притягивает к себе тело массой m:
Приравняем правые части формул, следующих из закона всемирного тяготения и второго закона Ньютона, и получим:
Отсюда скорость, с которой должно тело массой m бесконечно вращаться вокруг Земли на высоте h, равна:
Скорость бесконечно вращающегося вокруг Земли тела не зависит от его массы. Она зависит только от высоты, на которой оно находится. Чем выше высота, тем меньше скорость его вращения.
Тело, вращающееся вокруг планеты, называется ее спутником. Чтобы любое тело стало спутником Земли, нужно сообщить ему некоторую скорость на поверхности планеты в горизонтальном направлении. Высота h в этом случае равна 0. Тогда эта скорость будет равна:
8 км/с — первая космическая скорость Земли.
Пример №3. Рассчитать первую космическую скорость для Венеры. Считать, что масса Венеры равна 4,87∙1024 кг, а ее радиус равен 6052 км.
Задание EF18521
Сила гравитационного притяжения между двумя шарами, находящимися на расстоянии 2 м друг от друга, равна 9 нН. Какова будет сила притяжения между ними, если расстояние увеличить до 6 м? Ответ выразите в наноньютонах (нН).
Алгоритм решения
- Записать исходные данные.
- Записать закон всемирного тяготения.
- Установить зависимость между силой гравитационного притяжения и расстоянием между телами.
- На основании вывода о зависимости двух величин вычислить гравитационное притяжение между двумя шарами при изменении расстояния между ними.
Решение
Запишем исходные данные:
- Расстояние между двумя шарами в первом случае: R1 = 2 м.
- Расстояние между двумя шарами во втором случае: R2 = 6 м.
- Сила гравитационного притяжения между двумя шарами в первом случае: F1 = 9 нН.
Запишем закон всемирного тяготения:
Из формулы видно, что сила гравитационного притяжения обратно пропорционально квадрату расстояния между телами массами m1 и m2.
R2 больше R1 втрое (6 больше 2 в 3 раза). Следовательно, расстояние между шарами тоже увеличилось втрое. В таком случае сила гравитационного притяжения между ними уменьшится в 32 раз, или в 9 раз. Так как в первом случае эта сила была равна 1 нН, то во втором она составит в 9 раз меньше, или 1 нН.
Ответ: 1
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17569
Две звезды одинаковой массы m притягиваются друг к другу с силами, равными по модулю F. Чему равен модуль сил притяжения между другими двумя звёздами, если расстояние между их центрами такое же, как и в первом случае, а массы звёзд равны 3m и 4m?
а) 7F
б) 9F
в) 12F
г) 16F
Алгоритм решения
1.Записать закон всемирного тяготения.
2.Применить закон всемирного тяготения для первой и второй пары звезд.
3.Из каждого выражения выразить расстояние между звездами.
4.Приравнять правые части уравнений и вычислить силу притяжения между второй парой звезд.
Решение
Закон всемирного тяготения выглядит так:
Примерим этот закон для первой и второй пары звезд:
Выразим квадраты радиусов, так как они в обоих случаях одинаковые:
Приравняем правые части выражений и выразим силу притяжения во втором случае:
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18678
Высота полёта искусственного спутника над Землёй увеличилась с 400 до 500 км. Как изменились в результате этого скорость спутника и его потенциальная энергия?
Для каждой величины определите соответствующий характер изменения:
| 1) | увеличилась |
| 2) | уменьшилась |
| 3) | не изменилась |
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Скорость
спутника |
Потенциальная энергия спутника |
Алгоритм решения
1.Записать закон всемирного тяготения и формулу центростремительного ускорения для движения тела по окружности с постоянной по модулю скоростью.
2.Установить зависимость скорости от высоты спутника над поверхностью Земли.
3.Записать формулу потенциальной энергии и установить, как она зависит от высоты.
Решение
На спутник действует сила притяжения Земли, которая сообщает ему центростремительное ускорение:
F=maц=GmM(R+h)2
Отсюда центростремительное ускорение равно:
aц=GM(R+h)2
Но центростремительное ускорение также равно:
aц=v2(R+h)
Приравняем правые части выражений и получим:
GM(R+h)2=v2(R+h)
v2=MG(R+h)(R+h)2=MG(R+h)
Квадрат скорости спутника обратно пропорционален радиусу вращения. Следовательно, при увеличении высоты увеличивается радиус вращения, а скорость уменьшается.
Потенциальная энергия спутника определяется формулой:
Ep = mgh
Видно, что потенциальная энергия зависит от высоты прямо пропорционально. Следовательно, при увеличении высоты потенциальная энергия спутника тоже увеличивается.
Верная последовательность цифр в ответе: 21.
Ответ: 21
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17578
Искусственный спутник обращается вокруг планеты по круговой орбите радиусом 4000 км со скоростью 3,4 км/с. Ускорение свободного падения на поверхности планеты равно 4 м/с2. Чему равен радиус планеты? Ответ запишите в километрах.
Алгоритм решения
1.Записать исходные данные. Перевести единицы измерения в СИ.
2.Записать формулу ускорения свободного падения и выразить через нее радиус планеты.
3.Записать формулу, раскрывающая взаимосвязь между линейной скоростью и радиусом окружности, по которой движется тело.
4.Записать закон всемирного тяготения применительно к спутнику.
5.Вывести формулу для расчета радиуса планеты.
6.Подставить известные данные и произвести вычисление.
Решение
Запишем исходные данные:
• Линейная скорость спутника: v = 3,4 км/с, или 3,4∙103 м/с.
• Радиус орбиты спутника: Rо = 4000 км, или 4∙106 м.
• Ускорение свободного падения у поверхности планеты: g = 4 м/с2.
Ускорение свободного падения определяется формулой:
Отсюда радиус равен:
Линейная скорость и радиус орбиты связываются формулой:
Используя закон всемирного тяготения, запишем силы, с которой притягивается спутник к планете:
Согласно второму закону Ньютона, сила — это произведение массы на ускорение тела. Следовательно:
Отсюда:
Поделим обе части выражения на массу спутника и радиус его орбиты. Получим:
Из этой формулы выразим массу планеты:
Подставим массу планеты в формулу для нахождения ее радиуса:
Подставляем известные данные и вычисляем:
Этот радиус соответствует 3400 км.
Ответ: 3400
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 18k
Все тела в природе притягиваются, это свойство тел, имеющих массу. Сила, с которой тела притягиваются, называется силой гравитации (силой притяжения).
Формула закона всемирного тяготения с объяснениями
Зная массы двух тел и расстояние между ними, можно рассчитать силу их взаимного притяжения с помощью такой формулы:
[ large boxed { F = G cdot frac{m_{1} cdot m_{2}}{R^{2}} } ]
(F left( text{Н} right)) (Ньютоны) — сила, с которой два шарообразных тела притягиваются
( m_{1} left( mbox{кг} right) ) (килограммы) — масса первого тела
( m_{2} left( text{кг} right) ) (килограммы) — масса второго тела
( R left( text{м} right) ) (метры) — расстояние между центрами тел
(G = 6{,}67 cdot 10^{-11} left( text{Н} cdot frac{text{м}^2}{text{кг}^2} right)) — гравитационная постоянная
Примечания:
- формула позволяет точно рассчитать притяжение между двумя однородными шарами;
- если тела не шарообразные, или не однородные, то силу притяжения получим с погрешностью;
- чем больше расстояние между телами, тем меньше будет погрешность;
Словесная формулировка закона всемирного тяготения
Закон всемирного тяготения словами можно сформулировать так:
Два тела притягиваются с силой
прямо пропорциональной
массам этих тел
и обратно пропорциональной
квадрату расстояния между телами.
Пояснения к закону всемирного тяготения
Сила прямо пропорциональна массам тел. Математики прямую пропорциональность записывают так:
[ F sim m_{1} cdot m_{2} ]
Прямая пропорциональность означает: чем больше массы, тем больше сила притяжения.
Сила обратно пропорциональна расстоянию в квадрате. Математики обратную пропорциональность записывают с помощью дроби. В знаменателе этой дроби находится величина, обратно пропорциональная величине, находящейся в левой части выражения:
[ F sim frac{1}{R^{2}} ]
Обратная пропорциональность означает: чем больше расстояние между телами, тем меньше сила притяжения.
Что такое гравитационная постоянная
Физики часто употребляют термин: «Физический смысл». Физический смысл для чего-то – это ответ на вопрос: Что это такое с точки зрения физики?
Физический смысл гравитационной постоянной:
Гравитационная постоянная — это сила, с которой притягиваются два однородных шара, по 1-му килограмму каждый, когда они находятся на расстоянии 1-го метра один от другого.
(G = 6{,}67 cdot 10^{-11} left( text{Н} cdot frac{text{м}^2}{text{кг}^2} right)) — гравитационная постоянная
Как видно, это очень незначительная сила, поэтому в повседневной жизни мы ее не замечаем.
Куда направлена сила притяжения
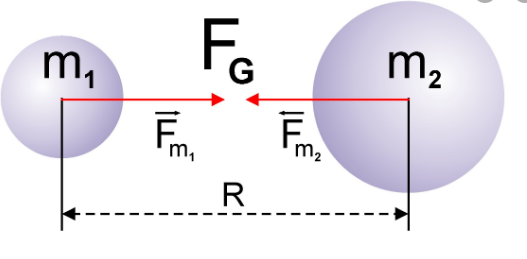
Соединим прямой линией центы притягивающихся тел. Вдоль этой линии и будут направлены силы, с которыми тела притягиваются. Физики часто заменяют фразу «действие одного тела на другое» словом «взаимодействие».
Рис.1. Направление сил взаимодействия двух шаров.
( F_{1} ) – это сила, с которой большой шар притягивается к маленькому шарику;
( F_{2} ) – это сила, с которой маленький шарик притягивается к большому шару;
Из третьего закона Ньютона известно, что тела взаимодействуют с одинаковыми по модулю силами. Это значит, что ( | F_{1} | = | F_{2} | ). То есть, силы равны.
У физиков есть такой шуточный вопрос: «Что сильнее притягивает – Луна Землю, или Земля Луну?». Правильный ответ: «Они притягиваются с одинаковыми силами».
Как правильно выбирать расстояние для подстановки в формулу
Центр масс тела — это точка, которой мы заменяем тело для упрощения задачи.
Если тело однородное и шарообразное, то центр масс — это точка, расположенная в центре шара.
Расстояние между телами — это расстояние между центрами масс.
Рассмотрим несколько поясняющих примеров:
Пример 1. Притяжение между планетой и звездой
Рис.2. Звезда и планета притягиваются
( R = left( r_{1} + h + r_{2} right) )
Складываем радиусы шаров и расстояние между их поверхностями, получаем расстояние между центрами тел. Это расстояние и подставляем в знаменатель формулы.
Пример 2. Два шарообразных тела соприкасаются
Рис. 3. Два шара соприкасаются
( R = left( r_{1} + r_{2} right) )
В формулу нужно подставить расстояние между центрами масс шаров. Складываем радиусы шаров и результат подставляем в формулу вместо R.
Пример 3. Малое тело покоится на поверхности планеты
Рис. 4. Камень находится на поверхности планеты.
( R = r )
Расстояние между телами — это радиус планеты. Радиус камня очень мал по сравнению с радиусом планеты, поэтому, мы радиус камня не учитываем.
Пример 4. Малое тело находится на некотором расстоянии от планеты
Рис. 5. Искусственный спутник находится на некотором расстоянии от планеты
( R = left( r + h right) )
Складываем радиус планеты и расстояние от спутника до поверхности планеты. Полученное число является расстоянием между телами. Размеры спутника не учитываем, так как они очень малы по сравнению с радиусом планеты.
Вам будет интересно почитать:
Первая космическая скорость
Движение по окружности, центростремительная сила и центростремительное ускорение
Ускорение свободного падения



Калькулятор расчётов по закону всемирного тяготения Ньютона
Условные обозначения формулы: F — сила гравитации, m1,m2 — масса двух тел, G — гравитационная константа, приблизительно 6.67384 (80) x10^-11, R — расстояние между телами.
Формула расчёта силы гравитации: F=G*m1*m2/R2. Гравитационная константа, умноженная на массы двух тел и разделённая на расстояние в квадрате.
Формула расчёта массы одного из тел: m1=(F*R2*10^11)/(G/m2). Силу гравитации, умножаем на расстояние, в квадрате, на 10 в 11 степени, и делим на гравитационную константу умноженную на массу другого тела.
Формула расчёта расстояния между телами: R=[квадратный корень][(G*m1*m2)/(F*10^11)]. Гравитационную константу умноженную на массы тел, делим на силу гравитации, умноженную на 10 в 11 степени и извлекаем квадратный корень.
Понравилась страница? Поделитесь ссылкой в социальных сетях. Поддержите проект!
Нет комментариев.
В статье обсуждаются несколько подходов и некоторые примеры проблем о том, как вычислить массу по гравитационной силе.
Каждый объект с массой во Вселенной оказывает гравитационное воздействие на другой. Вот почему сила тяжести прямо пропорциональна массе объекта. Таким образом, используя различные формулы, связанные с гравитационной силой, мы можем вычислить ненулевую массу объекта.
Узнайте больше о Как рассчитать массу по силе и расстоянию.
Как рассчитать массу по гравитационной силе, используя второй закон движения Ньютона
Рассчитаем массу, используя второй закон движения Ньютона:
Во втором законе движения Ньютон описывает, что сила действует на объект с ненулевой массой, чтобы ускорить его в том же направлении. Гравитационная сила — это естественная сила, которая всегда действует вниз на каждый объект, чтобы ускорить его, в зависимости от его массы.
Мы уже изучили два основных типа сил которые действуют на тела. гравитационная сила или гравитация, бесконтактная сила, всегда действует между массами каждого объекта.
Согласно второму закону Ньютона,
F = ма ………………… (*)
Когда действует сила тяжести, каждый объект ускоряется в соответствии со вторым законом движения. Ускорение, вызванное силой тяжести, постоянно, называется ускорение силы тяжести ‘грамм’. Поскольку гравитация всегда действует на нас, возникла идея нашего «веса» как «mg», который включает нашу массу m и ускорение «a». По этой причине гравитационную силу также называют силой тяжести. сила веса.
(Кредит: Shutterstock)
Следовательно, формула второго закона Ньютона принимает следующий вид:
Fg = мг …………………………. (1)
Согласно уравнениям (*) и (1),
Чтобы поднять более тяжелое тело, мы должны создать восходящую силу (ма), превышающую силу тяжести (мг).
Поскольку g имеет постоянное значение 9.8 м / с2, гравитационная сила Fg зависит только от массы объекта m. Чем массивнее объект, тем больше силы требуется для его ускорения.
Если к объекту приложена сила тяжести, мы можем вычислить его массу по формуле второго закона движения Ньютона..
Узнайте больше о Законы движения Ньютона.
Сила тяжести, действующая на бегающую в парке девушку, равна 490. Вычислите массу девушки.
Данный:
Fg = 490 Н
g = 9.8 м / с
Найти: м =?
Формула:
F = ma
Решение:
Масса девушки рассчитывается с помощью Второй закон движения Ньютона формула,
F = ma
Компания сила гравитации дан кем-то,
Fg = мг
m=Fg/g
м=490/9.8
m = 50 кг …………………………………. а)
Масса бегущей в парке девушки 50 кг.
Как найти массу с гравитационной силой и радиусом?
Давайте вычислим массу с гравитационной силой, используя закон тяготения Ньютона следующим образом:
Закон тяготения обнаруживает, что гравитационная сила между двумя объектами прямо пропорциональна их массам и обратно пропорциональна квадрату радиуса между их центрами масс. Если второй объект — Земля с фиксированной массой, мы можем вычислить массу первого объекта.
Согласно закону всемирного тяготения Ньютона,
Fg=G(мМ/р2)……………..(2)
Вся масса объекта сосредоточена в одной конкретной точке, в основном в его центральной точке, называемой его центр масс (см). Радиус r измеряет расстояние или разделение между центрами масс двух объектов.
Небольшая масса в 1 кг, разделенная радиусом 1, испытывала небольшую гравитационную силу 6.67 x 10-11 Нм.2/ кг2, совместимый с каждым объектом. Следовательно, это постоянное значение является значением постоянной пропорциональности в законе всемирного тяготения, также называемой величиной Универсальная гравитационная постоянная G.
Проще вычислить Fg между объектом и Землей как планетой с фиксированной массой M = 5.98 x 1024 кг, а также фиксированный радиус r от центра земли, r = 6.38 x 106m
Сила тяжести, действующая на девушку, бегающую трусцой в парке, равна 490. Вычислите массу девушки, используя закон всемирного тяготения Ньютона.
Данный:
Fg = 490 Н
М = 5.98 х 1024 kg
г = 6.38 х 106m
G = 6.67 х 10-11 nm2/ кг2
Найти: м =?
Формула:
Fg=G(мМ/р2)
Решение:
Масса девушки рассчитывается по Закон всемирного тяготения Ньютона является,
Fg=G(мМ/р2)
Переставляем на массу m,
м=Fgr2/ГМ
Подставляя все значения,
Из (а) и (б) мы заметили расчетная масса с использованием второго закона Ньютона и формулы закона всемирного тяготения такая же.
Закон всемирного тяготения может применяться к двум объектам, имеющим одинаковые или разные массы.
имея разные массы
(Кредит: Shutterstock)
Сила притяжения между вами и вашим коллегой составляет 3 x 10.-7 N, когда вы оба приближаетесь на расстоянии 1 м друг от друга в школьном коридоре. Поскольку ваша масса 60 кг, рассчитайте массу вашего коллеги.
Данный:
Fg = 3 x 10-7 N
г = 1 м
m1 = 60 кг
G = 6.67 х 10-11 nm2/ кг2
Найти: м2 =?
Формула:
Fg=G(м1m2/r2)
Решение:
Масса коллеги рассчитывается по формуле Закон всемирного тяготения Ньютона является,
Fg=G(м1m2/r2)
Перестановка на массу m2,
m2=Fgr2/Гм1
Подставляя все значения,
Масса вашего коллеги 75 кг.
Как рассчитать массу по гравитационной силе, используя формулу центростремительной силы?
Рассчитаем массу с гравитационной силой, используя центростремительная сила формула следующим образом:
Когда объект движется по кругу, его скорость постоянно меняется в зависимости от его направления. Направление ускорения — к центру, вызванное центростремительной силой. Поскольку масса всего объекта сосредоточена в его центре, мы можем рассчитать ее по формуле центростремительной силы.
Центростремительная сила получается из второго закона движения Ньютона.
Поскольку ускорение — это круговой путь, нам нужно учитывать радиус; вот почему ускорение становится
v2/r
Следовательно, согласно уравнению (*) центростремительная сила определяется как
Fc=мв2/r
Центростремительная сила — это центристская сила который действует на объект, чтобы двигаться по кругу к его центру. Земля оказывает центростремительное сила, действующая на спутник, чтобы поддерживать его круговое движение вокруг.
Спутник непрерывно движется по орбите вокруг Земли со скоростью 20 м / с. Гравитационная сила между Землей и спутником составляет 500 Н, что создает центростремительную силу около 200 Н. Вычислите массу спутника.
Данный:
Fg = 500 Н
Fc = 200 Н
v = 20 м / с
M = масса Земли = 5.98 x 1024 kg
G = 6.67 х 10-11 nm2/ кг2
Найти: м =?
Формула:
Fg=G(мМ/р2)
Fc=мв2/r
Решения:
Масса спутника рассчитывается по формуле закон всемирного тяготения Ньютона,
Fg=G(мМ/р2)
Компания центростремительная сила на спутнике есть,
Fc=мв2/r
Решая формулу для радиуса r,
г=мв2/Fc
Подставляя вышеприведенное уравнение в закон всемирного тяготения Ньютона, получаем
Fg=Fc2[ГМ/мв4]
Решая массу m,
Подставляя все значения,
м=159.4/8
м = 19.94 примерно 20 кг
Масса спутника, движущегося вокруг Земли, составляет 20 кг.