Симметричные числа как найти

Симметрия чисел

Симметрия чисел
1. Введение
В нашем мире все взаимосвязано, похоже друг на друга, имеет одинаковые или схожие параметры. Часто эти свойства называют симметрией. В «Кратком Оксфордском словаре» симметрия определяется как «Красота, обусловленная пропорциональностью частей тела или любого целого, равновесием, подобием, гармонией, согласованностью». [1 ] Очень часто симметрия проявляется в математике и физике. В физике свойства симметрии ярко проявляются в квантовой механике и ее математическом аппарате, например Уравнении Шредингера [ 2]. В математике существует специальный математический аппарат, оперирующий понятиями подобия и симметрии. Этот математический аппарат называется теорией групп [3]. Одним из практических применений симметрии в математике, является шифрование с открытым ключом “RSA” [4].

2. Матрица остатков простого числа

Рассмотрим определение вычета и сравнения по модулю. Вот определение, приведенное в современном толковом словаре. Число “ a “ называется вычетом числа “ b “ по модулю “ m “, если разность “ a – b “ делится на “ m “ ( a, b, m > 0 – целые числа ). То есть “ a “ сравнимо с “ b “ по модулю “ m “.

a ≡ b(mod m)

Это означает, что если “ a “ не делится нацело на “ m ”, то “ b “ остаток от деления “ a “ на “ m “. Два целых числа “ a “ и “ b “ сравнимы по модулю натурального числа “ m “, если при делении на “ m “ они дают одинаковые остатки.
Возьмем простое целое число и обозначим его “ b ”. Множество целых чисел в интервале (1,2,3,…b-1) обозначим “ B “. Если это множество записать в виде столбца, в порядке возрастания снизу вверх, то получим матрицу столбец. Все числа в этом столбце расположены одно за другим, их количество равно “ b – 1 “. Обозначим этот столбец номером “ 1 “. Каждое число из множества “ B “ возведем в квадрат и разделим на “ b “ с остатком. Полученные в результате деления остатки запишем в столбец. Обозначим этот столбец номером “ 2 “ и расположим его справа от столбца номер “ 1 “. Нужно расположить остатки так, чтобы они соответствовали числам, возводимым в квадрат, и находились с ними на одной прямой. После этого каждое число из множества “ B “ возведем в третью степень и разделим на “ b “ с остатком. Из полученных остатков сформируем столбец под номером “ 3 “, по аналогии со столбцом номер “ 2 “. Далее по аналогии возводим в следующую степень и находим остатки от деления на “ b “. Действия выполняем до тех пор, пока показатель степени, в которую возводим числа из множества “ B “, меньше “ b “. В результате получим квадратную матрицу размером (b-1) x (b-1).

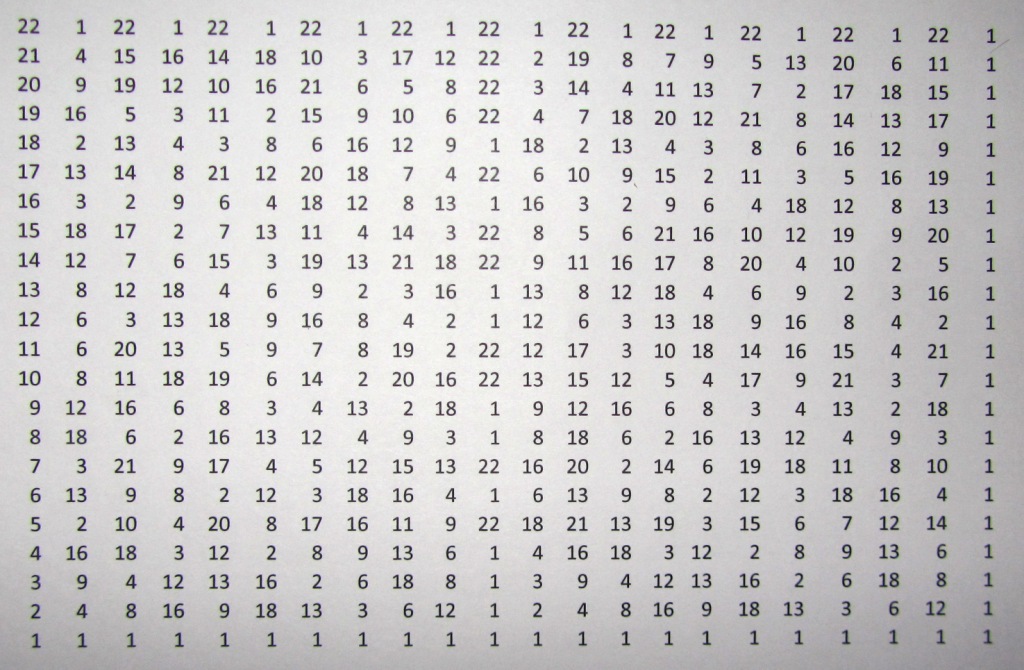
Пример такой квадратной матрицы для простого целого числа “ b = 23 “ представлен на рис.1.

Рис. 1 Матрица остатков простого целого числа b = 23.

Полученная матрица обладает удивительными свойствами:

— Наглядно видно, что последний столбец матрицы состоит из одних единиц. Это полностью соответствует тесту простоты Ферма. A n-1 ≡ 1(mod N) [5].
— Следует отметить, что столбец с номером (b-1)/2 ( “ b “ минус 1 деленное на 2 ) состоит только из двух значений множества “ B “. Это значения 1 и ( b-1).
— Значения чисел, множества “ B “, в столбцах, симметричны относительно середины интервала, т.е. пары значений (b-1)/2 и (b+1)/2.
— Виды симметрии для различных столбцов различны.
— Для столбцов с четными номерами, значения равноудаленные от середины интервала, т.е. пары значений (b-1)/2 и (b+1)/2, совпадают. Для матрицы, изображенной на рис. 1, остаток от 11 в квадрате, деленное на 23 и остаток от 12 в квадрате, деленное на 23, совпадают и равны 6.
— Для столбцов с нечетными номерами, значения, равноудаленные от середины интервала, т.е. пары значений (b-1)/2 и (b+1)/2, в сумме всегда равны “ b “. Для матрицы, изображенной на рис. 1, остаток от 11 в третьей степени, деленное на 23, равен 20, остаток от 12 в третьей степени, деленное на 23, равен 3. В сумме эти два остатка равны 23, т.е. равны “ b “.

Все свойства, описанные выше и рассмотренные для матрицы, изображенной на рис. 1, присущи матрицам, построенным по таким же правилам для других простых целых чисел.

3. Матрица остатков составного числа

Матрица, рассмотренная в разделе 2, характеризует симметрию простых чисел. Для составных чисел матрица, построенная по тем же самым правилам, существенно отличается. Она наследует свойства матрицы простого числа, но приобретает и новые свойства. Рассмотрим составное число, являющееся произведением двух простых чисел “ x “ и “ y “. Точно так же величину числа обозначим “ b “, а множество всех чисел, в интервале (1,b-1), обозначим “ B “. Рассмотрим составное число “ b = 35 “, являющееся результатом перемножения простых чисел “ x = 5 “ и “ y = 7 “. Построим матрицу остатков различных степеней, для числового интервала (35-1). Матрица остатков представлена на рис. 2

Рис. 2 Матрица остатков составного числа b = 35.
Часть свойств унаследована от матрицы остатков простого числа. Так например, значения чисел, присутствующих в столбцах, симметричны относительно середины значений числового интервала, т.е. значений (b-1)/2 и (b+1)/2.

Матрица, изображенная на рис. 2, несет в себе новые свойства:

— Значения строк матрицы, у которых в первом столбце присутствуют величины кратные делителям составного числа, принимают числовые значения кратные делителям составного числа и никогда не равны 1. Например, в матрице рис. 2, строка 5, во втором столбце, имеет значение 25, в третьем 20, в четвертом 30 и так далее. Все эти значения кратны 5.
— Если исключить строки, значения которых кратны делителям числа “ b “, то обязательно найдутся два столбца, в которых остальные значения равны 1. Например, на рис. 2 это столбцы с номерами 12, 24.
— Из этих двух выбранных столбцов, наибольший номер столбца равен произведению (x-1) на (y-1). Т.е. если от каждого из сомножителей, вычесть 1 и перемножить их, то получим номер наибольшего выбранного столбца. Для матрицы на рис. 2 сомножители числа “ b “ равны 5 и 7. Если от каждого из них отнять 1 и перемножить, то получим (5-1) x (7-1) = 24. Это как раз номер наибольшего выбранного столбца. Следует отметить, что в данном случае, номер столбца равен функции Эйлера, значение которой равно (x-1) x (y-1) = ѱ(n). [6].
— Во втором столбце обязательно присутствуют четыре значения равные 1. Для матрицы остатков простого числа и значений множества “ B “равных (1,b-1), величины во втором столбце принимают значение 1. Для матрицы остатков составного числа, обязательно существуют еще два числа множества “ B “, при возведении которых в квадрат и делении на “ b “, остаток равен 1. На рис. 2 это числа 6 и 29.
— Всегда присутствуют пары чисел, множества “ B “, следующих друг за другом, значения которых, кратны делителям “ x “ и “ y “ числа “ b”. Для матрицы на рис. 2 это пары ( 14, 15 ) и ( 20, 21 ).

Все свойства, описанные выше и рассмотренные для матрицы, изображенной на рис. 2, присущи матрицам, построенным по таким же правилам для других составных целых чисел.

4. Факторизация чисел

Если рассмотреть метод шифрования с открытым ключом RSA [4], то его использование основано на существовании взаимно противоположных отображений в матрице остатков составного числа. Если взять составное число “ b “, в его матрице остатков всегда существуют два столбца “ c “ и “ d “, для которых выполняются следующие условия:

(b1**c) ≡ c1( mod b); (c1**d) ≡ d1( mod b ); b1 = d1

где b1, c1, d1 числовые значения в столбцах 1, c, d.

То есть для составного числа “ b “ всегда существует два числа “ c “, “ d “ из диапазона (1,b-1), для которых справедлива последовательность действий:
— Определим остаток любого числа “ b1 “, из диапазона (1,b-1), возведенного в степень “ c “ и деленного на “ b “. Обозначим этот остаток “ c1 “.
— Полученный остаток “ c1 “ возведем в степень “ d “ и разделим на “ b “ с остатком. Обозначим этот остаток “ d1 “.
— Полученный остаток “ d1 “ всегда равен “ b1 “.
Для алгоритма шифрования RSA, (c,b) – открытый ключ, (d,b) – секретный ключ.

Рис. 3 Матрица остатков составного числа b = 33.

Рассмотрим матрицу остатков числа b = 33, рис. 3. Для этого числа c = 3, d =7. Возьмем любое число из первого столбца, например 8 и возведем его в 3 степень, остаток равен 17. Число 17 возведем в степень 7, остаток равен 8, т.е. этот остаток равен исходному числу из первого столбца.
RSA один из распространенных алгоритмов шифрования с открытым ключом. Вместе с совершенствованием методов шифрования, совершенствуются методы дешифровки секретных сообщений.
Часто задачу дешифровки для RSA, пытаются решить в лоб, т.е. найти делители базового составного числа. Эти методы называются факторизацией чисел. Кроме простого перебора значений и проверки чисел, используют метод квадратичного решета.

Основы этого метода в том, что часть остатков от возведения в квадрат и деления на число “ b “, являются полными квадратами чисел. На рис. 2 полными квадратами являются квадратичные остатки чисел (11, 12, 17), из первого столбца. Для нахождения делителей числа “ b “, необходимо из квадратичного остатка извлечь квадратный корень. Результат, т.е. квадратный корень, вычесть из числа “ b “ или сложить с числом “ b “. Будут получены числа кратные делителям числа “ b”. Используя алгоритм Евклида можно найти делители числа “ b “.
На рис. 2, для числа 11, квадратичный остаток равен 16. Извлекаем из 16 корень квадратный, он равен 4. К 11 прибавляем 4, получаем 15, число кратное делителю 5. От 11 отнимаем 4, получаем 7, число равное делителю 7.

Одним из самых современных методов факторизации чисел, является метод решета числового поля [7]. Этот метод позволяет сократить количество проверяемых значений и уменьшить время проведения вычислений. Использование метода решета числового поля и свойств матрицы остатков составного числа, позволяет достичь еще более весомых результатов.

Для экспериментальной проверки методов факторизации чисел можно использовать, так называемые, числа Мерсенна [8]. Эти числа представляют собой число 2 в степени “ n “, минус 1, где “ n “ натуральное число. Только ограниченное количество чисел Мерсенна являются простыми, остальные разлагаются на конечное количество делителей.
Как наглядный пример, один из делителей, числа 2 в степени 4099, минус 1, равен –
431654595928296534254101974033397155588925169723783332084380283993261
209600632883153055473166663136594966053411838575253500155337120152873
781979635198920643526624304319945635699208877607737201529464080041890
547345467573782661041054825447947267620282789541695832747170633177331
920343746996221855049648583763367504662477325712779883313257418325242
923223374882540094860518718525171060169694349915604794431233943848839
032331927197514745282594881581533286782002526616104836932259305133211
436643050243706215479754994805351437606942854754835739144357537526269
041212016993538655106720507482318994547865735219931202814880677303379
021540170667630675512896640229254326407201860556265718380698467494757
374722667518146123812589844575734597771351069823560862537030159862538
798769879690913001816439118925869829536250846639469310212937581855933
518710668619729641309263324784218037304674615635505157625365285797298
443305108038716358762651248086440048468372406494047491988831492829285
161751678332086837187972136968851829414833128243888620308340321378185
123642015152620056914762030047166652837911735649104226834442937368573
819974224203735488718107356908123314371578553175076071717675764345142
549580867720367836084289513946899287311856029114297

4. Литература

[1] Д Эллиот, П. Добер “ Симметрия в физике т. 1 “, Издательство МИР,1983 г.
[2] “ Уравнение Шредингера “, ru.wikipedia.org/wiki/Уравнение_Шредингера.
[3] П.С. Александров “ Введение в теорию групп “, Москва НАУКА, ГРФМЛ, 1980г.
[4] “ RSA “, ru.wikipedia.org/wiki/RSA.
[5] “ Тест Ферма “, ru.wikipedia.org/wiki/Тест_Ферма.
[6] “ Функция Эйлера “,http://ru.wikipedia.org/wiki/Функция_Эйлера.
[7] “ Общий метод решета числового поля “, ru.wikipedia.org/wiki/Общий_метод_решета_числового_поля.
[8] “ Числа Мерсенна “,http://ru.wikipedia.org/wiki/Числа_Мерсенна.

Symmetry occurs not only in geometry, but also in other branches of mathematics. Symmetry is a type of invariance: the property that a mathematical object remains unchanged under a set of operations or transformations.^[1]

Given a structured object X of any sort, a symmetry is a mapping of the object onto itself which preserves the structure. This can occur in many ways; for example, if X is a set with no additional structure, a symmetry is a bijective map from the set to itself, giving rise to permutation groups. If the object X is a set of points in the plane with its metric structure or any other metric space, a symmetry is a bijection of the set to itself which preserves the distance between each pair of points (i.e., an isometry).

In general, every kind of structure in mathematics will have its own kind of symmetry, many of which are listed in the given points mentioned above.

Symmetry in geometry[edit]

The types of symmetry considered in basic geometry include reflectional symmetry, rotation symmetry, translational symmetry and glide reflection symmetry, which are described more fully in the main article Symmetry (geometry).

Symmetry in calculus[edit]

Even and odd functions[edit]

Even functions[edit]

Let f(x) be a real-valued function of a real variable, then f is even if the following equation holds for all x and -x in the domain of f:

Geometrically speaking, the graph face of an even function is symmetric with respect to the y-axis, meaning that its graph remains unchanged after reflection about the y-axis. Examples of even functions include |x|, x², x⁴, cos(x), and cosh(x).

Odd functions[edit]

Again, let f be a real-valued function of a real variable, then f is odd if the following equation holds for all x and -x in the domain of f:

That is,

Geometrically, the graph of an odd function has rotational symmetry with respect to the origin, meaning that its graph remains unchanged after rotation of 180 degrees about the origin. Examples of odd functions are x, x³, sin(x), sinh(x), and erf(x).

Integrating[edit]

The integral of an odd function from −A to +A is zero, provided that A is finite and that the function is integrable (e.g., has no vertical asymptotes between −A and A).^[3]

The integral of an even function from −A to +A is twice the integral from 0 to +A, provided that A is finite and the function is integrable (e.g., has no vertical asymptotes between −A and A).^[3] This also holds true when A is infinite, but only if the integral converges.

Series[edit]

• The Maclaurin series of an even function includes only even powers.
• The Maclaurin series of an odd function includes only odd powers.
• The Fourier series of a periodic even function includes only cosine terms.
• The Fourier series of a periodic odd function includes only sine terms.

Symmetry in linear algebra[edit]

Symmetry in matrices[edit]

In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose (i.e., it is invariant under matrix transposition). Formally, matrix A is symmetric if

By the definition of matrix equality, which requires that the entries in all corresponding positions be equal, equal matrices must have the same dimensions (as matrices of different sizes or shapes cannot be equal). Consequently, only square matrices can be symmetric.

The entries of a symmetric matrix are symmetric with respect to the main diagonal. So if the entries are written as A = (a_ij), then a_ij = a_ji, for all indices i and j.

For example, the following 3×3 matrix is symmetric:

Every square diagonal matrix is symmetric, since all off-diagonal entries are zero. Similarly, each diagonal element of a skew-symmetric matrix must be zero, since each is its own negative.

In linear algebra, a real symmetric matrix represents a self-adjoint operator over a real inner product space. The corresponding object for a complex inner product space is a Hermitian matrix with complex-valued entries, which is equal to its conjugate transpose. Therefore, in linear algebra over the complex numbers, it is often assumed that a symmetric matrix refers to one which has real-valued entries. Symmetric matrices appear naturally in a variety of applications, and typical numerical linear algebra software makes special accommodations for them.

Symmetry in abstract algebra[edit]

Symmetric groups[edit]

The symmetric group S_n (on a finite set of n symbols) is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself.^[4] Since there are n! (n factorial) possible permutations of a set of n symbols, it follows that the order (i.e., the number of elements) of the symmetric group S_n is n!.

Symmetric polynomials[edit]

A symmetric polynomial is a polynomial P(X₁, X₂, …, X_n) in n variables, such that if any of the variables are interchanged, one obtains the same polynomial. Formally, P is a symmetric polynomial if for any permutation σ of the subscripts 1, 2, …, n, one has P(X_σ(1), X_σ(2), …, X_σ(n)) = P(X₁, X₂, …, X_n).

Symmetric polynomials arise naturally in the study of the relation between the roots of a polynomial in one variable and its coefficients, since the coefficients can be given by polynomial expressions in the roots, and all roots play a similar role in this setting. From this point of view, the elementary symmetric polynomials are the most fundamental symmetric polynomials. A theorem states that any symmetric polynomial can be expressed in terms of elementary symmetric polynomials, which implies that every symmetric polynomial expression in the roots of a monic polynomial can alternatively be given as a polynomial expression in the coefficients of the polynomial.

Examples[edit]

In two variables X₁ and X₂, one has symmetric polynomials such as:

and in three variables X₁, X₂ and X₃, one has as a symmetric polynomial:

• 

Symmetric tensors[edit]

In mathematics, a symmetric tensor is tensor that is invariant under a permutation of its vector arguments:

for every permutation σ of the symbols {1,2,…,r}.
Alternatively, an r^th order symmetric tensor represented in coordinates as a quantity with r indices satisfies

The space of symmetric tensors of rank r on a finite-dimensional vector space is naturally isomorphic to the dual of the space of homogeneous polynomials of degree r on V. Over fields of characteristic zero, the graded vector space of all symmetric tensors can be naturally identified with the symmetric algebra on V. A related concept is that of the antisymmetric tensor or alternating form. Symmetric tensors occur widely in engineering, physics and mathematics.

Galois theory[edit]

Given a polynomial, it may be that some of the roots are connected by various algebraic equations. For example, it may be that for two of the roots, say A and B, that A² + 5B³ = 7. The central idea of Galois theory is to consider those permutations (or rearrangements) of the roots having the property that any algebraic equation satisfied by the roots is still satisfied after the roots have been permuted. An important proviso is that we restrict ourselves to algebraic equations whose coefficients are rational numbers. Thus, Galois theory studies the symmetries inherent in algebraic equations.

Automorphisms of algebraic objects[edit]

In abstract algebra, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism group. It is, loosely speaking, the symmetry group of the object.

Examples[edit]

• In set theory, an arbitrary permutation of the elements of a set X is an automorphism. The automorphism group of X is also called the symmetric group on X.
• In elementary arithmetic, the set of integers, Z, considered as a group under addition, has a unique nontrivial automorphism: negation. Considered as a ring, however, it has only the trivial automorphism. Generally speaking, negation is an automorphism of any abelian group, but not of a ring or field.
• A group automorphism is a group isomorphism from a group to itself. Informally, it is a permutation of the group elements such that the structure remains unchanged. For every group G there is a natural group homomorphism G → Aut(G) whose image is the group Inn(G) of inner automorphisms and whose kernel is the center of G. Thus, if G has trivial center it can be embedded into its own automorphism group.^[5]
• In linear algebra, an endomorphism of a vector space V is a linear operator V → V. An automorphism is an invertible linear operator on V. When the vector space is finite-dimensional, the automorphism group of V is the same as the general linear group, GL(V).
• A field automorphism is a bijective ring homomorphism from a field to itself. In the cases of the rational numbers (Q) and the real numbers (R) there are no nontrivial field automorphisms. Some subfields of R have nontrivial field automorphisms, which however do not extend to all of R (because they cannot preserve the property of a number having a square root in R). In the case of the complex numbers, C, there is a unique nontrivial automorphism that sends R into R: complex conjugation, but there are infinitely (uncountably) many «wild» automorphisms (assuming the axiom of choice).^[6] Field automorphisms are important to the theory of field extensions, in particular Galois extensions. In the case of a Galois extension L/K the subgroup of all automorphisms of L fixing K pointwise is called the Galois group of the extension.

Symmetry in representation theory[edit]

Symmetry in quantum mechanics: bosons and fermions[edit]

In quantum mechanics, bosons have representatives that are symmetric under permutation operators, and fermions have antisymmetric representatives.

This implies the Pauli exclusion principle for fermions. In fact, the Pauli exclusion principle with a single-valued many-particle wavefunction is equivalent to requiring the wavefunction to be antisymmetric. An antisymmetric two-particle state is represented as a sum of states in which one particle is in state and the other in state :

and antisymmetry under exchange means that A(x,y) = −A(y,x). This implies that A(x,x) = 0, which is Pauli exclusion. It is true in any basis, since unitary changes of basis keep antisymmetric matrices antisymmetric, although strictly speaking, the quantity A(x,y) is not a matrix but an antisymmetric rank-two tensor.

Conversely, if the diagonal quantities A(x,x) are zero in every basis, then the wavefunction component:

is necessarily antisymmetric. To prove it, consider the matrix element:

This is zero, because the two particles have zero probability to both be in the superposition state . But this is equal to

The first and last terms on the right hand side are diagonal elements and are zero, and the whole sum is equal to zero. So the wavefunction matrix elements obey:

.

or

Symmetry in set theory[edit]

Symmetric relation[edit]

We call a relation symmetric if every time the relation stands from A to B, it stands too from B to A.
Note that symmetry is not the exact opposite of antisymmetry.

Symmetry in metric spaces[edit]

Isometries of a space[edit]

An isometry is a distance-preserving map between metric spaces. Given a metric space, or a set and scheme for assigning distances between elements of the set, an isometry is a transformation which maps elements to another metric space such that the distance between the elements in the new metric space is equal to the distance between the elements in the original metric space. In a two-dimensional or three-dimensional space, two geometric figures are congruent if they are related by an isometry: related by either a rigid motion, or a composition of a rigid motion and a reflection. Up to a relation by a rigid motion, they are equal if related by a direct isometry.

Isometries have been used to unify the working definition of symmetry in geometry and for functions, probability distributions, matrices, strings, graphs, etc.^[7]

Symmetries of differential equations[edit]

A symmetry of a differential equation is a transformation that leaves the differential equation invariant. Knowledge of such symmetries may help solve the differential equation.

A Line symmetry of a system of differential equations is a continuous symmetry of the system of differential equations. Knowledge of a Line symmetry can be used to simplify an ordinary differential equation through reduction of order.^[8]

For ordinary differential equations, knowledge of an appropriate set of Lie symmetries allows one to explicitly calculate a set of first integrals, yielding a complete solution without integration.

Symmetries may be found by solving a related set of ordinary differential equations.^[8] Solving these equations is often much simpler than solving the original differential equations.

Symmetry in probability[edit]

In the case of a finite number of possible outcomes, symmetry with respect to permutations (relabelings) implies a discrete uniform distribution.

In the case of a real interval of possible outcomes, symmetry with respect to interchanging sub-intervals of equal length corresponds to a continuous uniform distribution.

In other cases, such as «taking a random integer» or «taking a random real number», there are no probability distributions at all symmetric with respect to relabellings or to exchange of equally long subintervals. Other reasonable symmetries do not single out one particular distribution, or in other words, there is not a unique probability distribution providing maximum symmetry.

There is one type of isometry in one dimension that may leave the probability distribution unchanged, that is reflection in a point, for example zero.

A possible symmetry for randomness with positive outcomes is that the former applies for the logarithm, i.e., the outcome and its reciprocal have the same distribution. However this symmetry does not single out any particular distribution uniquely.

For a «random point» in a plane or in space, one can choose an origin, and consider a probability distribution with circular or spherical symmetry, respectively.

See also[edit]

• Use of symmetry in integration
• Invariance (mathematics)

References[edit]

Bibliography[edit]

• Weyl, Hermann (1989) [1952]. Symmetry. Princeton Science Library. Princeton University Press. ISBN 0-691-02374-3.
• Ronan, Mark (2006). Symmetry and the Monster. Oxford University Press. ISBN 978-0-19-280723-6. (Concise introduction for lay reader)
• du Sautoy, Marcus (2012). Finding Moonshine: A Mathematician’s Journey Through Symmetry. Harper Collins. ISBN 978-0-00-738087-9.

Вроде бы все должно работать, но система не пропускает.

Дано четырехзначное число. Определите, является ли его десятичная запись симметричной.
Если число симметричное, то выведите 1, иначе выведите любое другое целое число.
Число может иметь меньше четырех знаков, тогда нужно считать, что его десятичная запись дополняется слева нулями. Десятичная запись числа симметрична, если при прочтении слева направо и справа налево получается одно и то же число.

При решении задачи можно пользоваться только целочисленными арифметическими операциями. Нельзя пользоваться нелинейными конструкциями: ветвлениями, циклами, функциями.

H = int(input())

f1 = (H // 1000)                                # первое число в четырехзначном
f12 = (H % 10)                                  # последнее число в четырехзначном
s1 = (H - (f1 * 1000)) // 100                   # второе слева число
w1 = (H - (f1 * 1000) - (s1 * 100)) // 10       # третье число слева
q = (f12 * 1000) + (w1 * 100) + (s1 * 10) + f1  # обираем с конца

print(H // q)

Помогите решить. Где моя ошибка?

алгебра — Симметричные числа