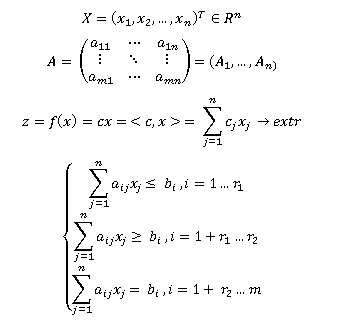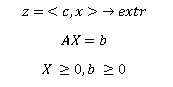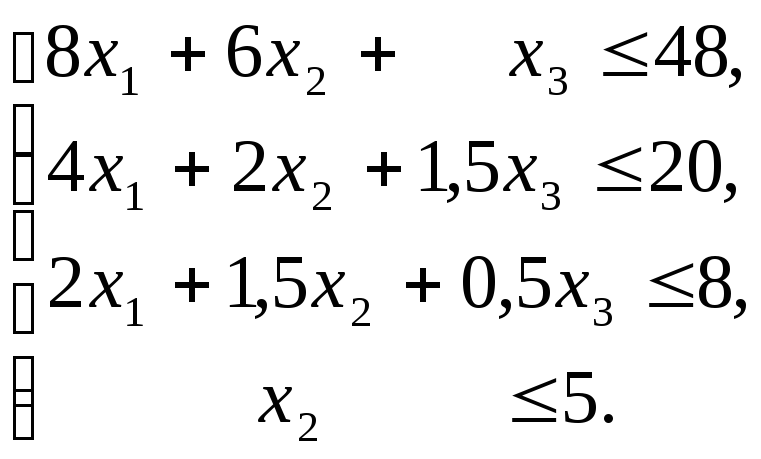Подробный разбор симплекс-метода
Время на прочтение
6 мин
Количество просмотров 192K
Пролог
Недавно появилась необходимость создать с нуля программу, реализующую алгоритм симплекс-метода. Но в ходе решения я столкнулся с проблемой: в интернете не так уж много ресурсов, на которых можно посмотреть подробный теоретический разбор алгоритма (его обоснование: почему мы делаем те или иные шаги) и советы по практической реализации — непосредственно, алгоритм. Тогда я дал себе обещание — как только завершу задачу, напишу свой пост на эту тему. Об этом, собственно, и поговорим.
Замечание. Пост будет написан достаточно формальным языком, но будет снабжен комментариями, которые должны внести некоторую ясность. Такой формат позволит сохранить научный подход и при этом, возможно, поможет некоторым в изучении данного вопроса.
§1. Постановка задачи линейного программирования
Определение:
Линейное программирование – математическая дисциплина, посвященная теории и методам решения экстремальных задач на множествах n- мерного пространства, задаваемых системами линейными уравнений и неравенств.
Общая задача линейного программирования (далее – ЛП) имеет вид:
§2. Каноническая форма задачи ЛП
Каноническая форма задачи ЛП:
Замечание:
Любая задача ЛП сводится к канонической.
Алгоритм перехода от произвольной задачи ЛП к канонической форме:
- Неравенства с отрицательными
умножаем на (-1).
- Если неравенство вида (≤), то к левой части добавляем
– добавочную переменную, и получаем равенство.
- Если неравенство вида (≥), то из левой части вычитаем
, и получаем равенство.
- Делаем замену переменных:
Замечание:
Будем нумеровать
по номеру неравенства, в которое мы его добавили.
Замечание:
≥0.
§3. Угловые точки. Базисные/свободные переменные. Базисные решения
Определение:
Точка
называется угловой точкой, если представление
возможно только при
.
Иными словами, невозможно найти две точки в области, интервал проходящий через которые содержит
(т.е.
– не внутренняя точка).
Графический способ решения задачи ЛП показывает, что нахождение оптимального решения ассоциируется с угловой точкой. Это является основной концепцией при разработке симплекс-метода.
Определение:
Пусть есть система m уравнений и n неизвестных (m < n). Разделим переменные на два множества: (n-m) переменные положим равными нулю, а остальные m переменных определяются решением системы исходных уравнений. Если это решение единственно, то тогда ненулевые m переменных называют базисными; нулевые (n-m) переменных – свободными (небазисными), а соответствующие результирующие значения переменных называют базисным решением.
§4. Симплекс-метод
Симплекс-метод позволяет эффективно найти оптимальное решение, избегая простой перебор всех возможных угловых точек. Основной принцип метода: вычисления начинаются с какого-то «стартового» базисного решения, а затем ведется поиск решений, «улучшающих» значение целевой функции. Это возможно только в том случае, если возрастание какой-то переменной приведет к увеличению значения функционала.
Необходимые условия для применения симплекс-метода:
- Задача должна иметь каноническую форму.
- У задачи должен быть явно выделенный базис.
Определение:
Явно выделенным базисом будем называть вектора вида:
, т.е. только одна координата вектора ненулевая и равна 1.
Замечание:
Базисный вектор имеет размерность (m*1), где m – количество уравнений в системе ограничений.
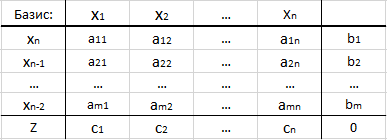
Для удобства вычислений и наглядности обычно пользуются симплекс-таблицами:
- В первой строке указывают «наименование» всех переменных.
- В первом столбце указывают номера базисных переменных, а в последней ячейке – букву Z (это строка функционала).
- В «середине таблицы» указывают коэффициенты матрицы ограничений — aij.
- Последний столбец – вектор правых частей соответствующих уравнений системы ограничений.
- Крайняя правая ячейка – значение целевой функции. На первой итерации ее полагают равной 0.
Замечание:
Базис – переменные, коэффициенты в матрице ограничений при которых образуют базисные вектора.
Замечание:
Если ограничения в исходной задаче представлены неравенствами вида ≤, то при приведении задачи к канонической форме, введенные дополнительные переменные образуют начальное базисное решение.
Замечание:
Коэффициенты в строке функционала берутся со знаком “-”.
Алгоритм симплекс-метода:
1. Выбираем переменную, которую будем вводить в базис. Это делается в соответствии с указанным ранее принципом: мы должны выбрать переменную, возрастание которой приведет к росту функционала. Выбор происходит по следующему правилу:
- Если задача на минимум – выбираем максимальный положительный элемент в последней строке.
- Если задача на максимум – выбираем минимальный отрицательный.
Такой выбор, действительно, соответствует упомянутому выше принципу: если задача на минимум, то чем большее число вычитаем – тем быстрее убывает функционал; для максимума наоборот – чем большее число добавляем, тем быстрее функционал растет.
Замечание:
Хотя мы и берем минимальное отрицательное число в задаче на максимум, этот коэффициент показывает направление роста функционала, т.к. строка функционала в симплекс-таблице взята со знаком “-”. Аналогичная ситуация с минимизацией.
Определение:
Столбец симплекс-таблицы, отвечающий выбранному коэффициенту, называется ведущим столбцом.
2. Выбираем переменную, которую будем вводить в базис. Для этого нужно определить, какая из базисных переменных быстрее всего обратится в нуль при росте новой базисной переменной. Алгебраически это делается так:
- Вектор правых частей почленно делится на ведущий столбец
- Среди полученных значений выбирают минимальное положительное (отрицательные и нулевые ответы не рассматривают)
Определение:
Такая строка называется ведущей строкой и отвечает переменной, которую нужно вывести из базиса.
Замечание:
Фактически, мы выражаем старые базисные переменные из каждого уравнения системы ограничений через остальные переменные и смотрим, в каком уравнении возрастание новой базисной переменной быстрее всего даст 0. Попадание в такую ситуацию означает, что мы «наткнулись» на новую вершину. Именно поэтому нулевые и отрицательные элементы не рассматриваются, т.к. получение такого результата означает, что выбор такой новой базисной переменной будет уводить нас из области, вне которой решений не существует.
3. Ищем элемент, стоящий на пересечении ведущих строки и столбца.
Определение:
Такой элемент называется ведущим элементом.
4. Вместо исключаемой переменной в первом столбце (с названиями базисных переменных) записываем название переменной, которую мы вводим в базис.
5. Далее начинается процесс вычисления нового базисного решения. Он происходит с помощью метода Жордана-Гаусса.
- Новая Ведущая строка = Старая ведущая строка / Ведущий элемент
- Новая строка = Новая строка – Коэффициент строки в ведущем столбце * Новая Ведущая строка
Замечание:
Преобразование такого вида направлено на введение выбранной переменной в базис, т.е. представление ведущего столбца в виде базисного вектора.
6. После этого проверяем условие оптимальности. Если полученное решение неоптимально – повторяем весь процесс снова.
§5. Интерпретация результата работы симплекс-метода
1. Оптимальность
Условие оптимальности полученного решения:
- Если задача на максимум – в строке функционала нет отрицательных коэффициентов (т.е. при любом изменении переменных значение итогового функционала расти не будет).
- Если задача на минимум – в строке функционала нет положительных коэффициентов (т.е. при любом изменении переменных значение итогового функционала уменьшаться не будет).
2. Неограниченность функционала
Однако, стоит отметить, что заданный функционал может не и достигать максимума/минимума в заданной области. Алгебраический признак этого можно сформулировать следующим образом:
При выборе ведущей строки (исключаемой переменной) результат почленного деления вектора правых частей на ведущий столбец содержит только нулевые и отрицательные значения.
Фактически, это значит, что какой бы рост мы не задавали новой базисной переменной, мы никогда не найдем новую вершину. А значит, наша функция не ограничена на множестве допустимых решений.
3. Альтернативные решения
При нахождении оптимального решения возможен еще один вариант – есть альтернативные решения (другая угловая точка, дающая то же самое значение функционала).
Алгебраический признак существования альтернативы:
После достижения оптимального решения имеются нулевые коэффициенты при свободных переменных в строке функционала.
Это значит, что при росте соответствующей переменной с нулевым коэффициентом значение функционала не изменится и новое базисное решение будет также давать оптимум функционала.
Эпилог
Данная статья направлена на более глубокое понимание теоретической части. В замечаниях и пояснениях здесь можно получить ответы на вопросы, которые обычно опускают при изучении этого метода и принимают априори. Однако, надо понимать, что многие методы численной оптимизации основаны на симплекс-методе (например, метод Гомори, М-Метод) и без фундаментального понимания вряд ли получится сильно продвинуться в дальнейшем изучении и применении всех алгоритмов этого класса.
Чуть позже напишу статью о практической реализации симплекс-метода, а также несколько статей о Методе искусственных переменных (М-Метод), Методе Гомори и Методе ветвей и границ.
Спасибо за внимание!
P.S.
Если уже сейчас Вы мучаетесь с реализацией симплекс-метода, советую почитать книгу А. Таха Введение в исследование операций — там все неплохо разобрано и в теории, и на примерах; а также посмотрите примеры решения задач matburo.ru — это поможет с реализацией в коде.
Калькулятор симплекс-метода
Количество переменных:
Количество ограничений:
Очистить
Решить
В двойственную
Выполнено действий:
Как пользоваться калькулятором
- Задайте количество переменных и ограничений
- Введите коэффициенты целевой функции
- Введите коэффициенты ограничений и выберите условия (≤, = или ≥)
- Выберите тип решения
- Нажмите кнопку «Решить»
Что умеет калькулятор симплекс-метода
- Решает основную задачу линейного программирования
- Позволяет получить решение с помощью основного симплекс-метода и метода искусственного базиса
- Работает с произвольным количеством переменных и ограничений
Что такое симплекс-метод
Задача линейного программирования — это задача поиска неотрицательных значений параметров, на которых заданная линейная функция достигает своего максимума или минимума при заданных линейных ограничениях.
Симплекс-метод — алгоритм решения оптимизационной задачи линейного программирования путём перебора вершин выпуклого многогранника в многомерном пространстве. Алгоритм является универсальным методом, которым можно решить любую задачу линейного программирования.
Если вам тоже ничего не понятно из этого определения, то вы на верном пути. Чаще всего статьи про симплекс-метод очень сильно углубляются в дебри теории задачи линейного программирования, из-за чего очень легко потерять суть и так ничего и не понять. Мы постараемся описать алгоритм симплекс-метода так, чтобы показать, что в нём нет ничего страшного и на самом деле он весьма простой. Но сначала нам всё-таки потребуется ввести несколько определений.
Целевая функция — функция, максимум (или минимум) которой нужно найти. Представляет собой сумму произведений коэффициентов на значения переменных: F = c1·x1 + c2·x2 + … + cn·xn
Ограничение — условие вида a1·x1 + a2·x2 + … + an·xn v b, где вместо v ставится один из знаков: ≤, = или ≥
План — произвольный набор значений переменных x1 … xn.
Алгоритм решения основной задачи ЛП симплекс-методом
Пусть в задаче есть m ограничений, а целевая функция заивисит от n основных переменных. Первым делом необходимо привести все ограничения к каноническому виду — виду, в котором все условия задаются равенствами. Для этого предварительно все неравенства с ≥ умножаются на -1, для получения неравенств с ≤.
Чтобы привести ограничения с неравенствами к каноническому виду, для каждого ограничения вводят переменную, называемую дополнительной с коэффициентом 1. В ответе эти переменные учитываться не будут, однако сильно упростят начальные вычисления. При этом дополнительные переменные являются базисными, а потому могут быть использованы для формирования начального опорного решения.
Пример 1
Привести к каноническому виду ограничения:
2·x1 + 3·x2 + 6·x3 ≤ 240
4·x1 + 2·x2 + 4·x3 = 200
4·x1 + 6·x2 + 8·x3 ≥ 160
Меняем знаки у ограничений с ≥, путём умножения на -1 и добавляем дополнительные переменные к ограничениям с неравенством:
2·x1 + 3·x2 + 6·x3 + x4 = 240
4·x1 + 2·x2 + 4·x3 = 200
-4·x1 — 6·x2 — 8·x3 + x5 = -160
Формирование начального базиса
После того как задача приведена к каноническому виду, необходимо найти начальный базис для формирования первого опорного решения. Если в процессе приведения были добавлены дополнительные переменные, то они становятся базисными.
Иначе необходимо выделить среди коэффициентов ограничений столбец, который участвует в формировании единичной матрицы в заданной строке (например, если требуется определить вторую базисную переменную, то необходимо искать столбец, в котором второе число равно 1, а остальные равны нулю). Если такой столбец найден, то переменная, соответствующая этому столбцу, становится базисной.
В противном случае можно поискать столбец, в котором все значения кроме числа в заданной строке равны нулю, и, если он будет найден, то разделить все значения строки на число, стоящее на пересечении этих строки и столбца, тем самым образовав столбец, участвующий в формировании единичной матрицы.
Пример 2
9·x1 + 5·x2 + 4·x3 + 3·x4 + 2·x5 → max
x1 — 2·x2 + 2·x3 ≤ 6
x1 + 2·x2 + x3 + x4 = 24
2·x1 + x2 — 4·x3 + 2·x5 = 30
Для ограничения с неравенством добавляем дополнительную переменную x6.
Перепишем ограничения в каноническом виде:
x1 — 2·x2 + 2·x3 + x6 = 6
x1 + 2·x2 + x3 + x4 = 24
2·x1 + x2 — 4·x3 + 2·x5 = 30
Ищем начальное базисное решение:
Ограничение 1 содержит неравенство, базисной будет добавленная дополнительная переменная x6
Столбец 4 является частью единичной матрицы. Переменная x4 входит в начальный базис
В пятом столбце все значения кроме третьего равны нулю. Поэтому в качестве третьей базисной переменной берём x5, предварительно разделив третью строку на 2.
Симплекс-таблица
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x6 | 1 | -2 | 2 | 0 | 0 | 1 | 6 |
| x4 | 1 | 2 | 1 | 1 | 0 | 0 | 24 |
| ? | 2 | 1 | -4 | 0 | 2 | 0 | 30 |
После преобразования получаем следующую таблицу:
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x6 | 1 | -2 | 2 | 0 | 0 | 1 | 6 |
| x4 | 1 | 2 | 1 | 1 | 0 | 0 | 24 |
| x5 | 1 |
1 2 |
-2 | 0 | 1 | 0 | 15 |
Если такой столбец отсутствует, то для формирования базиса необходимо применить исключение Гаусса для первого ненулевого столбца, который ещё не является базисным. Для этого вся строка делится на элемент в найденном столбце, а из остальных строк вычитается полученная строка, разделённая на значение, стоящее в этом же столбце. После этой операции все значения вне данной строки будут обнулены, и столбец можно будет считать базисным.
Пример 3
4·x1 + 5·x2 + 4·x3 → max
2·x1 + 3·x2 + 6·x3 ≤ 240
4·x1 + 2·x2 + 4·x3 = 160
4·x1 + 6·x2 + 8·x3 ≤ 200
Для каждого ограничения с неравенством добавляем дополнительные переменные x4 и x5.
Перепишем ограничения в каноническом виде:
2·x1 + 3·x2 + 6·x3 + x4 = 240
4·x1 + 2·x2 + 4·x3 = 160
4·x1 + 6·x2 + 8·x3 + x5 = 200
Ищем начальное базисное решение:
Ограничение 1 содержит неравенство, базисной будет добавленная дополнительная переменная x4
Ограничение 3 содержит неравенство, базисной будет добавленная дополнительная переменная x5
Начальная симплекс-таблица
| базис | x1 | x2 | x3 | x4 | x5 | b |
|---|---|---|---|---|---|---|
| x4 | 2 | 3 | 6 | 1 | 0 | 240 |
| ? | 4 | 2 | 4 | 0 | 0 | 160 |
| x5 | 4 | 6 | 8 | 0 | 1 | 200 |
Для определения второй базисной переменной ищем первый ненулевой столбец, который ещё не является базисным. Первый столбец не нулевой и не является базисным. Выполняем исключение Гаусса: делим строку 2 на 4, а из первой и третьей строк вычитаем вторую, умноженную на соответствующий элемент в первом столбце.
| базис | x1 | x2 | x3 | x4 | x5 | b |
|---|---|---|---|---|---|---|
| x4 | 2 | 3 | 6 | 1 | 0 | 240 |
| x1 | 4 | 2 | 4 | 0 | 0 | 160 |
| x5 | 4 | 6 | 8 | 0 | 1 | 200 |
После исключения получаем следующую таблицу:
| базис | x1 | x2 | x3 | x4 | x5 | b |
|---|---|---|---|---|---|---|
| x4 | 0 | 2 | 4 | 1 | 0 | 160 |
| x1 | 1 |
1 2 |
1 | 0 | 0 | 40 |
| x5 | 0 | 4 | 4 | 0 | 1 | 40 |
После того как базис сформирован, нужно построить начальную симплекс-таблицу. Она строится следующим образом:
- Для удобства в первой строке можно записать коэффициенты Ci целевой функции (для дополнительных переменных эти коэффициенты равны нулю)
- Вторая строка формирует шапку таблицы. В ней первый столбец называется базис, а остальные перечисляют основные переменные x1..xn и дополнительные xn+1..xn+k
- Затем построчно перечисляются базисные переменные и коэффициенты ограничений
Схематично начальная таблица будет выглядеть примерно так:
| C | с1 | c2 | … | cn | 0 | 0 | … | 0 | 0 |
|---|---|---|---|---|---|---|---|---|---|
| базис | x1 | x2 | … | xn | xn+1 | xn+2 | … | xn+k | b |
| xe1 | a11 | a12 | … | a1n | a1n+1 | a1n+2 | … | a1n+k | b1 |
| xe2 | a21 | a22 | … | a2n | a2n+1 | a2n+2 | … | a2n+k | b2 |
| … | … | … | … | … | … | … | … | … | … |
| xem | am1 | am2 | … | amn | amn+1 | amn+2 | … | amn+k | bm |
Избавляемся от отрицательных свободных коэффициентов
После приведения к каноническому виду или после алгебраических преобразований при формировании базиса некоторые из свободных коэффициентов (bi) могли стать отрицательными, что не позволяет перейти к дальнейшим вычислениям. Чтобы избавиться от отрицательных значений b необходимо:
- Найти строку, в которой находится максимальное по модулю значение b. Пусть это будет строка i;
- Найти максимальный по модулю элемент в этой строке. Пусть он находится в столбце j;
- Строку i разделить на элемент, стоящий на пересечении i-ой строки и j-го столбца;
- Из каждой оставшейся строки k вычесть строку i, умноженную на элемент строки k и столбца j;
- Переменную, соответствующую найденному столбцу j, сделать базисной (добавить в базис вместо переменной, находящейся в строке i).
Этот шаг необходимо повторять до тех пор, пока все отрицательные b не станут положительными или в строке не останется отрицательных элементов. Если строка с максимальным по модулю bi не содержит отрицательных элементов, то такая задача не имеет решений и на этом алгоритм заканчивает свою работу. В противном случае все bi положительны и алгоритм переходит к следующему этапу — расчёту дельт.
Пример 4
20·x1 + 20·x2 + 10·x3 → min
4·x1 + 3·x2 + 2·x3 ≥ 33
3·x1 + 2·x2 + x3 ≥ 23
x1 + x2 + 2·x3 ≥ 12
Меняем знаки у ограничений с ≥, путём умножения на -1:
-4·x1 — 3·x2 — 2·x3 ≤ -33
— 3·x1 — 2·x2 — x3 ≤ -23
— x1 — x2 — 2·x3 ≤ -12
Для каждого ограничения с неравенством добавляем дополнительные переменные x4..x6.
Перепишем ограничения в каноническом виде:
— 4·x1 — 3·x2 — 2·x3 + x4 = -33
— 3·x1 — 2·x2 — x3 + x5 = -23
— x1 — x2 — 2·x3 + x6 = -12
Ищем начальное базисное решение:
Ограничение 1 содержит неравенство, базисной будет добавленная дополнительная переменная x4
Ограничение 2 содержит неравенство, базисной будет добавленная дополнительная переменная x5
Ограничение 3 содержит неравенство, базисной будет добавленная дополнительная переменная x6
Начальная симплекс-таблица
| C | 20 | 20 | 10 | 0 | 0 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x4 | -4 | -3 | -2 | 1 | 0 | 0 | -33 |
| x5 | -3 | -2 | -1 | 0 | 1 | 0 | -23 |
| x6 | -1 | -1 | -2 | 0 | 0 | 1 | -12 |
В столбце b присутствуют отрицательные значения.
Максимальное по модулю |b|max = |-33| находится в первой строке.
Максимальный по модулю элемент в первой строке = -4 находится в первом столбце.
В качестве базисной переменной x4 берём x1.
Делим первую строку на -4. Из второй и третьей строк вычитаем первую, умноженную на соответствующий элемент в первом столбце.
Обновлённая таблица:
| C | 20 | 20 | 10 | 0 | 0 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x1 | 1 |
3 4 |
1 2 |
—
1 4 |
0 | 0 |
33 4 |
| x5 | 0 |
1 4 |
1 2 |
—
3 4 |
1 | 0 |
7 4 |
| x6 | 0 | —
1 4 |
—
3 2 |
—
1 4 |
0 | 1 | —
15 4 |
В столбце b присутствуют отрицательные значения.
Максимальное по модулю |b|max = |-
| находится в третьей строке.
Максимальный по модулю элемент в третьей строке = —
находится в третьем столбце.
В качестве базисной переменной x6 берём x3.
Делим третью строку на —
. Из первой и второй строк вычитаем третью, умноженную на соответствующий элемент в третьем столбце.
Обновлённая таблица:
| C | 20 | 20 | 10 | 0 | 0 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x1 | 1 |
2 3 |
0 | —
1 3 |
0 |
1 3 |
7 |
| x5 | 0 |
1 6 |
0 | —
5 6 |
1 |
1 3 |
1 2 |
| x3 | 0 |
1 6 |
1 |
1 6 |
0 | —
2 3 |
5 2 |
Расчёт дельт
Дельты — это параметры, на основании которых проверяется оптимальность текущего решения и улучшается функция. Они рассчитываются для каждой из переменных ограничений и записываются последней строкой таблицы.
Для расчёта дельт используется следующая формула: Δi = ce1·a1i + ce2·a2i + … + cem·ami — ci. Проще говоря, чтобы вычислить дельту по заданной i-ой переменной, нужно перемножить коэффициенты условий в i-ом столбце на коэффициенты целевой функции при соответствующих базисных переменных, сложить эти произведения и вычесть из полученной суммы коэффициент целевой функции столбца i.
Пример 5
Таблица:
| C | 3 | 0 | 2 | 0 | 0 | -6 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x2 | 2 | 1 | -3 | 0 | 0 | 6 | 18 |
| x4 | -3 | 0 | 2 | 1 | 0 | -2 | 24 |
| x5 |
1 5 |
0 |
3 5 |
0 | 1 | —
4 5 |
36 5 |
Вычисляем дельты: Δi = C2·a1i + C4·a2i + C5·a3i — Ci
Симплекс-таблица с дельтами
| C | 3 | 0 | 2 | 0 | 0 | -6 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x2 | 2 | 1 | -3 | 0 | 0 | 6 | 18 |
| x4 | -3 | 0 | 2 | 1 | 0 | -2 | 24 |
| x5 |
1 5 |
0 |
3 5 |
0 | 1 | —
4 5 |
36 5 |
| Δ | -3 | 0 | -2 | 0 | 0 | 6 | 0 |
Проверка плана на оптимальность
После того как дельты рассчитаны, необходимо проверить оптимальность текущего плана. Критерий оптимальности формулируется следующим образом:
При максимизации функции: текущее решение считается оптимальным, если в таблице отсутствуют отрицательные дельты.
При минимизации функции: текущее решение считается оптимальным, если в таблице отсутствуют положительные дельты.
Пример 6
9·x1 + 5·x2 + 4·x3 + 3·x4 + 2·x5 → max
x1 — 2·x2 + 2·x3 ≤ 6
x1 + 2·x2 + x3 + x4 = 24
2·x1 + x2 — 4·x3 + x5 = 30
Симплекс-таблица с дельтами
| C | 9 | 5 | 4 | 3 | 2 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x6 | 1 | -2 | 2 | 0 | 0 | 1 | 6 |
| x4 | 1 | 2 | 1 | 1 | 0 | 0 | 24 |
| x5 | 2 | 1 | -4 | 0 | 1 | 0 | 30 |
| Δ | -2 | 3 | -9 | 0 | 0 | 0 | 132 |
Критерий оптимальности: план оптимален, если в таблице отсутствуют отрицательные дельты.
План не оптимален, так как ищется максимум функции, а Δ1 = -2 отрицательна.
Если текущий план оптимален, то алгоритм завершает свою работу. Значениям переменных соответствуют значения столбца свободных коэффициентов b. Если свободной переменной нет в базисе, то её значение считается нулевым. Значение целевой функции, принимаемой на данном наборе, находится в строке с дельтами в том же столбце. Если какое-либо из значений столбца b отрицательно, то решения задачи не существует.
Переход к более оптимальному решению
Если текущий план оказался не оптимальным, то алгоритм ищет столбец с наименьшей (с наибольшей, если ищется минимум) дельтой. После чего вычисляются симплекс-отношения Q. Для этого значения свободных коэффициентов делятся на ненулевые коэффициенты из найденного столбца. Если результат деления получается отрицательным, то такие отношение игнорируются.
Среди найденных симплекс-отношений ищется строка, в которой находится симплекс-отношение с наименьшим значением. Если таких отношений нет, то алгоритм останавливает свою работу, так как целевая функция не ограничена и решения не существует.
Пример 7
Симплекс-таблица с дельтами
| C | 2 | 1 | -2 | 0 | 0 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x1 | 1 | -5 | 0 | -3 | 0 | -1 | 25 |
| x5 | 0 | -16 | 0 | -7 | 1 | -3 | 57 |
| x3 | 0 | -6 | 1 | -2 | 0 | -1 | 17 |
| Δ | 0 | 1 | 0 | -2 | 0 | 0 | 16 |
Проверяем план на оптимальность: план не оптимален, так как ищется минимум функции, а Δ2 = 1 положительна.
Определяем разрешающий столбец — столбец, в котором находится максимальная дельта: 2, Δ2: 1
Находим симплекс-отношения Q, путём деления коэффициентов b на соответствующие значения второго столбца
| C | 2 | 1 | -2 | 0 | 0 | 0 | 0 | |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b | Q |
|---|---|---|---|---|---|---|---|---|
| x1 | 1 | -5 | 0 | -3 | 0 | -1 | 25 | — |
| x5 | 0 | -16 | 0 | -7 | 1 | -3 | 57 | — |
| x3 | 0 | -6 | 1 | -2 | 0 | -1 | 17 | — |
| Δ | 0 | 1 | 0 | -2 | 0 | 0 | 16 |
Все значения второго столбца отрицательны. Функция не ограничена. Оптимальное решение отсутствует.
В противном случае строка с наименьшим отношением считается разрешающей и, аналогично избавлению от отрицательных свободных коэффициентов, делится на разрешающий элемент, расположенный в найденных столбце и строке, и из остальных строк вычитается найденная строка, разделённая на значения, стоящие в этом же столбце соответствующей строки. Переменная, стоящая в разрешающем столбце заменяет базисную переменную, находящуюся в найденной строке.
После этого вычисляются новые дельты и проверяется новый план. Так продолжается до тех пор пока не будет выполнен критерий оптимальности плана или не будет установлено, что решение не существует.
Пример 8
Симплекс-таблица с дельтами
| C | 9 | 5 | 4 | 3 | 2 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x6 | 1 | -2 | 2 | 0 | 0 | 1 | 6 |
| x4 | 1 | 2 | 1 | 1 | 0 | 0 | 24 |
| x5 | 2 | 1 | -4 | 0 | 1 | 0 | 30 |
| Δ | -2 | 3 | -9 | 0 | 0 | 0 | 132 |
Проверяем план на оптимальность: план не оптимален, так как Δ1 = -2 отрицательна.
Итерация 1
Определяем разрешающий столбец — столбец, в котором находится минимальная дельта: 3, Δ3: -9
Находим симплекс-отношения Q, путём деления коэффициентов b на соответствующие значения третьего столбца
В найденном столбце ищем строку с наименьшим значением Q: Qmin = 3, строка 1.
На пересечении найденных строки и столбца находится разрешающий элемент: 2
В качестве базисной переменной x6 берём x3.
| C | 9 | 5 | 4 | 3 | 2 | 0 | 0 | |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b | Q |
|---|---|---|---|---|---|---|---|---|
| x3 | 1 | -2 | 2 | 0 | 0 | 1 | 6 | 6 / 2 = 3 |
| x4 | 1 | 2 | 1 | 1 | 0 | 0 | 24 | 24 / 1 = 24 |
| x5 | 2 | 1 | -4 | 0 | 1 | 0 | 30 | — |
| Δ | -2 | 3 | -9 | 0 | 0 | 0 | 132 |
Делим первую строку на 2. Из второй и третьей строк вычитаем первую, умноженную на соответствующий элемент в третьем столбце.
Вычисляем новые дельты: Δi = C3·a1i + C4·a2i + C5·a3i — Ci
| C | 9 | 5 | 4 | 3 | 2 | 0 | 0 | |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b | Q |
|---|---|---|---|---|---|---|---|---|
| x3 |
1 2 |
-1 | 1 | 0 | 0 |
1 2 |
3 | 3 |
| x4 |
1 2 |
3 | 0 | 1 | 0 | —
1 2 |
21 | 24 |
| x5 | 4 | -3 | 0 | 0 | 1 | 2 | 42 | — |
| Δ |
5 2 |
-6 | 0 | 0 | 0 |
9 2 |
159 |
Текущий план X: [ 0, 0, 3, 21, 42, 0 ]
Целевая функция F: 9·0 + 5·0 + 4·3 + 3·21 + 2·42 + 0·0 = 159
Проверяем план на оптимальность: план не оптимален, так как Δ2 = -6 отрицательна.
Итерация 2
Определяем разрешающий столбец — столбец, в котором находится минимальная дельта: 2, Δ2: -6
Находим симплекс-отношения Q, путём деления коэффициентов b на соответствующие значения второго столбца
В найденном столбце ищем строку с наименьшим значением Q: Qmin = 7, строка 2.
На пересечении найденных строки и столбца находится разрешающий элемент: 3
В качестве базисной переменной x4 берём x2.
| C | 9 | 5 | 4 | 3 | 2 | 0 | 0 | |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b | Q |
|---|---|---|---|---|---|---|---|---|
| x3 |
1 2 |
-1 | 1 | 0 | 0 |
1 2 |
3 | — |
| x2 |
1 2 |
3 | 0 | 1 | 0 | —
1 2 |
21 | 21 / 3 = 7 |
| x5 | 4 | -3 | 0 | 0 | 1 | 2 | 42 | — |
| Δ |
5 2 |
-6 | 0 | 0 | 0 |
9 2 |
159 |
Делим вторую строку на 3. Из первой и третьей строк вычитаем вторую, умноженную на соответствующий элемент во втором столбце.
Вычисляем новые дельты: Δi = C3·a1i + C2·a2i + C5·a3i — Ci
| C | 9 | 5 | 4 | 3 | 2 | 0 | 0 | |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b | Q |
|---|---|---|---|---|---|---|---|---|
| x3 |
2 3 |
0 | 1 |
1 3 |
0 |
1 3 |
10 | — |
| x2 |
1 6 |
1 | 0 |
1 3 |
0 | —
1 6 |
7 | 7 |
| x5 |
9 2 |
0 | 0 | 1 | 1 |
3 2 |
63 | — |
| Δ |
7 2 |
0 | 0 | 2 | 0 |
7 2 |
201 |
Текущий план X: [ 0, 7, 10, 0, 63, 0 ]
Целевая функция F: 9·0 + 5·7 + 4·10 + 3·0 + 2·63 + 0·0 = 201
Проверяем план на оптимальность: отрицательные дельты отсутствуют, следовательно план оптимален.
Ответ: x1 = 0, x2 = 7, x3 = 10, x4 = 0, x5 = 63, F = 201
Метод искусственного базиса
Очень часто при решении задачи линейной оптимизации бывает довольно сложно выполнять алгебраические преобразования над коэффициентами ограничений для поиска начального базиса. Для упрощения вычислений существует альтернативный метод решения, называемый методом искусственного базиса. Его суть заключается в том, что вместо того, чтобы искать базис среди имеющихся основных и дополнительных переменных, ввести так называемые искусственные переменные, которые сформируют начальный базис. Возможно, звучит сложно и непонятно, но сейчас мы всё объясним.
Подготовительный этап
Аналогично базовому симплекс-методу для всех ограничений с неравентством вводятся дополнительные переменные, причём для ограничений с ≥ они берутся с коэффициентом -1, а для ограничений с ≤ с коэффициентом 1. Ограничения с равенством остаются без изменений. Если свободный коэффициент какого-либо из ограничений меньше нуля, то такое ограничение умножается на -1 (знак неравенства при этом меняется на противоположный). После этого приступают к поиску базиса.
Пример 9
3·x1 + 2·x2 + 3·x3 → min
-2·x1 — x2 — x3 ≥ -2
3·x1 + 8·x2 + 2·x3 ≥ 8
2·x1 + x3 = 1
Меняем знаки у ограничений с отрицательными свободными коэффициентами, путём умножения на -1:
2·x1 + x2 + x3 ≤ 2
3·x1 + 8·x2 + 2·x3 ≥ 8
2·x1 + x3 = 1
Для каждого ограничения с неравенством добавляем дополнительные переменные x4 и x5.
Ограничение 1 содержит неравенство, базисной будет добавленная дополнительная переменная x4
Ограничение 2 содержит неравенство с ≥. Базисная переменная для этого ограничения будет определена позднее.
Ограничение 3 содержит равенство. Базисная переменная для этого ограничения будет определена позднее.
Начальная симплекс-таблица
| C | 3 | 2 | 3 | 0 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | b |
|---|---|---|---|---|---|---|
| x4 | 2 | 1 | 1 | 1 | 0 | 2 |
| ?1 | 3 | 8 | 2 | 0 | -1 | 8 |
| ?2 | 2 | 0 | 1 | 0 | 0 | 1 |
Формирование начального базиса
Для того, чтобы сформировать начальный базис в первую очередь можно поискать столбец, у которого одно значение равно единице, а все значения остальные значения равны нулю, и сделать соответствующую переменную базисной для этой строки. Однако такое случается довольно редко, поэтому проще сразу перейти к следующему пункту. Для всех ограничений, не имеющих базисной переменной, добавляем искусственную переменную с коэффициентом 1. В целевую функцию добавляем эту же переменную с коэффициентов -M, если ищется максимум или с коэффициентом M, если ищется минимум. M всего лишь является очень большим числом.
Пример 10
x1 — x2 → min
2·x1 + x2 = 1
x1 — 3·x2 + x3 = 3
x1 + 11·x2 = 11
Ограничение 1 содержит равенство. Базисная переменная для этого ограничения будет определена позднее.
Столбец 3 является частью единичной матрицы. Переменная x3 входит в начальный базис
Ограничение 3 содержит равенство. Базисная переменная для этого ограничения будет определена позднее.
Начальная симплекс-таблица
| C | 1 | -1 | 0 | 0 |
| базис | x1 | x2 | x3 | b |
|---|---|---|---|---|
| ?1 | 2 | 1 | 0 | 1 |
| x3 | 1 | -3 | 1 | 3 |
| ?3 | 1 | 11 | 0 | 11 |
Для ограничения 1 добавляем искусственную переменную u1 и делаем её базисной.
Для ограничения 3 добавляем искусственную переменную u2 и делаем её базисной.
В целевую функцию добавляем искусственные пременные с коэффициентом M, где M — очень большое число.
Таблица с искусственными переменными
| C | 1 | -1 | 0 | M | M | 0 |
| базис | x1 | x2 | x3 | u1 | u2 | b |
|---|---|---|---|---|---|---|
| u1 | 2 | 1 | 0 | 1 | 0 | 1 |
| x3 | 1 | -3 | 1 | 0 | 0 | 3 |
| u2 | 1 | 11 | 0 | 0 | 1 | 11 |
Перепишем условие задачи с учётом добавленных искусственных переменных:
F = 1x1 -1x2 + Mu1 + Mu2 → min
2·x1 + x2 + u1 = 1
x1 — 3·x2 + x3 = 3
x1 + 11·x2 + u2 = 11
Расчёт дельт и проверка плана на оптимальность
После того, как начальный базис сформирован необходимо вычислить дельты. Дельты вычисляются полностью аналогично базовому методу: Δi = ce1·a1i + ce2·a2i + … + cem·ami — ci. Единственным отличием будет тот факт, что результат может содержать значения с M. Когда дельты будут получены необходимо проверить текущий опорный план на оптимальность (см. проверку плана на оптимальность в базовом симплекс-методе). Если план оптимален, то алгоритм завершает свою работу, иначе формирует более оптимальное решение и повторяет процесс.
Пример 11
Таблица с искусственными переменными
| C | 3 | 2 | 3 | 0 | 0 | 0 | M | M | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | u1 | u2 | b |
|---|---|---|---|---|---|---|---|---|---|
| x4 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 2 |
| u1 | 3 | 0 | 2 | 0 | -1 | 0 | 1 | 0 | 3 |
| u2 | 0 | 0 | 1 | 0 | 0 | -1 | 0 | 1 | 1 |
Вычисляем дельты: Δi = C4·a1i + C7·a2i + C8·a3i — Ci
Δ1 = C4·a11 + C7·a21 + C8·a31 — C1 = 0·2 + M·3 + M·0 — 3 = -3 + 3M
Δ2 = C4·a12 + C7·a22 + C8·a32 — C2 = 0·1 + M·0 + M·0 — 2 = -2
Δ3 = C4·a13 + C7·a23 + C8·a33 — C3 = 0·1 + M·2 + M·1 — 3 = -3 + 3M
Δ4 = C4·a14 + C7·a24 + C8·a34 — C4 = 0·1 + M·0 + M·0 — 0 = 0
Δ5 = C4·a15 + C7·a25 + C8·a35 — C5 = 0·0 + M·(-1) + M·0 — 0 = -M
Δ6 = C4·a16 + C7·a26 + C8·a36 — C6 = 0·0 + M·0 + M·(-1) — 0 = -M
Δ7 = C4·a17 + C7·a27 + C8·a37 — C7 = 0·0 + M·1 + M·0 — M = 0
Δ8 = C4·a18 + C7·a28 + C8·a38 — C8 = 0·0 + M·0 + M·1 — M = 0
Δb = C4·b1 + C7·b2 + C8·b3 — C9 = 0·2 + M·3 + M·1 — 0 = 4M
Симплекс-таблица с дельтами
| C | 3 | 2 | 3 | 0 | 0 | 0 | M | M | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | u1 | u2 | b |
|---|---|---|---|---|---|---|---|---|---|
| x4 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 2 |
| u1 | 3 | 0 | 2 | 0 | -1 | 0 | 1 | 0 | 3 |
| u2 | 0 | 0 | 1 | 0 | 0 | -1 | 0 | 1 | 1 |
| Δ | -3 + 3M | -2 | -3 + 3M | 0 | -M | -M | 0 | 0 | 4M |
Текущий план X: [ 0, 0, 0, 2, 0, 0, 3, 1 ]
Целевая функция F: 3·0 + 2·0 + 3·0 + 0·2 + 0·0 + 0·0 + M·3 + M·1 = 4M
Проверяем план на оптимальность: план не оптимален, так как Δ1 = -3 + 3M положительна.
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
ВВЕДЕНИЕ
В математике взаимосвязь элементов множества, определяемая правилом, при котором каждое значение зависит от другого бесконечного числа величин, называется функцией. Для определения её крайних значений применяется линейное программирование. Решить поставленную задачу можно несколькими способами. Один из них — симплекс-метод.
1 Понятие о симплексном методе
Под симплексным методом понимается последовательный переход от одного базисного нахождения системы решений к другому. Эта перестановка повторяется до тех пор, пока переменная величина цели не достигнет своего наибольшего или наименьшего значения. Такой подход является универсальным, его можно использовать для решения любой задачи последовательного программирования.
Метод был разработан в 1947 году математиком из США Бернардом Данцигом. Предложенный способ оказался весьма эффективным для решения разнообразных землеустроительных и других экономических задач, связанных с оптимизацией использования ограниченных ресурсов. То есть он позволяет оценить и откорректировать параметры системы, а также получить качественные аналитические результаты. Универсальность данного метода проявляется в том, что он позволяет решать задачи различной размерности, в которых технико-экономические коэффициенты (αij) при переменных (Хij) выражены в разных единицах измерения.
В процессе решения задачи на каждой итерации осуществляется переход из одной вершины ОДР в смежную, связанную с не худшим значением целевой функции. Для этого используется процедура метода главных элементов. Количество итераций, необходимых для получения оптимального решения, находится в пределах от m до 2m, где m-количество ограничений в задаче.
2 Двухфазный симплекс-метод
Если в условии задачи линейного программирования не все ограничения представлены неравенствами типа «≤», то далеко не всегда нулевой вектор будет допустимым решением. Однако каждая итерация симплекс-метода является переходом от одной вершины к другой, и если неизвестно ни одной вершины, алгоритм вообще не может быть начат.Такой метод можно использовать, когда свободные члены уравнений являются любыми числами.
Процесс нахождения исходной вершины не сильно отличается от однофазного симплекс-метода, однако может в итоге оказаться сложнее, чем дальнейшая оптимизация.
3 Алгоритм решения задач
Алгоритм решения задачи линейного программирования симплекс методом следующий:
1. При постановке задачи формулируется: оптимальные значения, каких неизвестных необходимо найти, при каких условиях (ограничениях) по видам и размерам ресурсов, какая функция цели и на что она ориентирована (на максимум или минимум).
Например, необходимо определить оптимальное сочетание объемов производства трех видов продукции (Х1, Х2, Х3) при имеющихся в хозяйстве трех видах ресурсов в размере в1=100, в2=40, в3=50 -это трудовые ресурсы с целью получения максимальной денежной выручки.
Экономико-математическая модель в симплексном методе составляется в следующей последовательности:
2. записывается уравнение функции цели, правая часть которого представляет собой сумму произведений искомых неизвестных (Х1, Х2, Х3) на соответствующие им по условиям задачи коэффициенты целевой функции:
Zmax =20Х1+10Х2+30Х3
3. условия задачи записываются в виде неравенств с ограничениями типа ≤. Каждое из неравенств выражает собой ограничения по одному из видов ресурсов, поэтому в левой части неравенства проставляют искомые переменные с коэффициентами, выражающими расход данного вида ресурса на единицу искомой переменной или, наоборот, выход данного вида ресурса с единицы соответствующей переменной. В правой части неравенства проставляется тип ограничения ≤ и величина соответствующего вида ресурса;
4. количество неравенств в системе ограничений обусловлено условиями задачи. При записи неравенств необходимо контролировать правильность их оформления: технико-экономические коэффициенты при переменных, состав переменных (в левой части неравенства), вид и размер ресурса (в правой части неравенства) должны строго соответствовать условиям задачи и характеру её постановки.
Таким образом, система ограничений выглядит следующим образом:
3Х1+5Х2+8Х3≤100
2,5Х1+3Х2+6Х3≤40
2Х1+4Х2+3Х3≤50
5. после записи основных условий задачи в виде системы ограничений обязательно формулируется условие не отрицательности переменных, так как алгоритм симплексного метода позволяет решать задачи только с положительными значениями переменных (Хj):
Х1≤0; Х2≤0; Х3≤0.
6. Представленная выше форма записи условий задачи в виде неравенств называется стандартной. Для заполнения первой симплексной таблицы (исходного плана) необходимо перейти от стандартной формы записи условий задачи к канонической, а от неё – к симплексной.
Каноническая форма записи условий задачи предусматривает преобразование неравенств (стандартной формы записи) в уравнения, для этого в левую часть каждого из неравенств вводят дополнительные переменные со следующими знаками: с плюсом, если неравенство типа « ≤ » и с минусом, если неравенство типа « ≥ ». Дополнительным переменным (Х4, Х5, Х6) поочередно присваиваются номера, продолжающие нумерацию основных переменных (Х1, Х2, Х3). В уравнение дополнительные переменные вводятся с коэффициентом 1, а в целевую функцию с нулевыми коэффициентами для исключения их влияния на результаты решения задачи.
Преобразуем приведенную выше систему неравенств в систему уравнений:
3Х1+5Х2+8Х3+Х4≤100
2,5Х1+3Х2+6Х3+Х5≤40
2Х1+4Х2+3Х3+Х6≤50
7. Для дальнейшего преобразования канонической формы записи в симплексную система уравнений решается относительно дополнительных переменных:
Х4=100-(3Х1+5Х2+8Х3)
Х5=40-(2,5Х1+3Х2+6Х3)
Х6=50-(2Х1+4Х2+3Х3)
8. Исходя из симплексной формы записи условий задачи, становится ясен экономический смысл дополнительных переменных. На начальном этапе решения задачи принимается условие, что основные переменные равны нулю, а значения дополнительных переменных, исходя из симплексной формы записи, будут равны величинам ресурсов. В нашем примере: при Х1=0, Х2=0, Х3=0 будем иметь Х4=100, Х5=40, Х6=50.
В экономическом отношении это означает, что пока не реализовано ни одно из мероприятий, намечаемых по условиям задачи, ресурсы остаются неиспользованными. Исходя из данной установки, создается исходный базис, на основе которого начинается поиск оптимального решения задачи из числа допустимых её решений.
9. Если при решении отыскивается ответ с максимумом или минимумом линейной формы и все неосновные переменные получаются только положительными, то задача считается выполненной.
10. Если найденный максимум (минимум) линейной формы в функции имеет одну или несколько неосновных переменных с отрицательными коэффициентами, необходимо перейти к новому базисному решению.
11. Из переменных, входящих в форму с отрицательными или положительными коэффициентами, выбирается наибольшая (по модулю) и переводится в основные.
12. Другими словами, указывается оптимальное опорное решение, способ перехода от одного нахождения ответа к другому, варианты улучшения расчётов. После нахождения первоначального решения с «единичным базисом» вычисляется оценка разложения векторов по базису и заполняется симплексная таблица 1.
Таблица 1 –Первая симплексная таблица
|
Номера строк (ограниче-ний), i |
Номера переменных, вошедших в базис, Xn+i |
Коэффициенты целевой функции при базисной переменной, Сi |
Свободные члены (ресурсы),вi |
Коэффициенты целевой функции, Сj |
Сумма по строке |
Отношение |
|||||
|
20 |
10 |
30 |
0 |
0 |
0 |
||||||
|
Коэффи-циенты при небазисных переменных |
Коэффициенты при базисных переменных |
||||||||||
|
Х1 |
Х2 |
Х3 |
Х4 |
Х5 |
Х6 |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
1 |
Х4 |
0 |
100 |
3 |
5 |
8 |
1 |
0 |
0 |
117 |
12,5 |
|
2 |
Х5 |
0 |
40 |
25 |
3 |
6 |
0 |
1 |
0 |
52,5 |
6,67 |
|
3 |
Х6 |
0 |
50 |
2 |
4 |
3 |
0 |
0 |
1 |
60 |
16,67 |
|
m+1 |
Zj-Cj |
0 |
-20 |
-10 |
-30 |
0 |
0 |
0 |
-60 |
Столбцы 5-7 – это столбцы основных переменных (соответственно, Х1, Х2, Х3). Из первого уравнения 3Х1+5Х2+8Х3+Х4=100 коэффициенты при основных переменных (Х1, Х2, Х3), соответственно 3,5 и 8 занесены в столбцы данных переменных по первой строке таблицы и так далее.
Столбцы 8-10 – это столбцы дополнительных переменных (Х4, Х5, Х6), в которых проставляются коэффициенты при данных переменных по каждому уравнению, в которое входит соответствующая переменная. Так, дополнительная переменная Х4 входит в первое уравнение с коэффициентом 1, поэтому данный коэффициент записываем. В остальных столбцах дополнительных переменных Х5 и Х6 по первой строке проставляем нули, т.к. данные дополнительные переменные не входят в первое уравнение.
Столбец 11 – в него записывается суммы, полученные путем сложения свободного члена (вj) и коэффициентов (аij) по соответствующей строке таблицы. Так, если сложить по первой строке таблицы свободный член и коэффициенты (100+3+5+8+1=117), то получим число 117. Аналогичным образом получаем значения для других.
Столбец 12 – в него записываются значения, полученные в результате построчного деления значений свободных членов (вj) на положительные коэффициенты ключевого (k-го) столбца.
Для выполнения таких расчетов необходимо предварительно выбрать ключевой столбец (k–й столбец). В качестве ключевого (k-го) выбирается столбец (из числа столбцов основных переменных Х1, Х2, Х3, по которому в индексной (m+n) строке таблицы стоит максимальное по абсолютной величине: отрицательное число при решении задачи на максимум и, наоборот, положительное число, при решении задачи на минимум. В данной задаче таким максимальным по абсолютной величине числом является -30 (т.к. Z→max).
Теперь можно выполнить расчеты для заполнения столбца 12. По первой строке указанное отношение получаем, разделив свободный член 100 (в1=100) на положительный коэффициент 8 (в1=8), стоящий по данной строке в ключевом столбце. Оно равно 12,5 ( ).
Столбец m+1 – это индексная строка симплексной таблицы. На ней записывается численное значение функции цели (Z). В первой симплексной таблице оно равно нулю (Z=0).
Все остальные элементы индексной (m+1) строки рассчитываются по формуле:
13. Анализ плана на оптимальность
Признаком оптимальности опорного плана является отсутствие в индексной (m+1) строке при решении задачи на минимум – положительных коэффициентов или нулей. Если это условие не выполняется, то план не оптимален и необходимо его улучшать.
Новую симплексную таблицу (улучшенный план) с новым базисным решением составляют в следующей последовательности:
Вместо базисной переменной, стоявшей в базисе (столбец 2) по ключевой l-строке предыдущей таблицы в новую таблицу записывают переменную Хj, столбец которой выбран в качестве ключевого. Этим самым в базис новой симплексной таблицы вводится новая базисная переменная, а прежняя – выводится из базиса;
— в столбец 3, рядом с новой переменной, введенной в базис, записывают её коэффициент целевой функции. Остальные базисные переменные и их коэффициенты целевой функции (столбцы 2 и 3) переписываются в новую таблицу из предыдущей без изменения;
— элементы ( ) для заполнения в новой таблице строки, стоящей на месте ключевой l-строки предыдущей таблицы, вычисляются как отношение соответствующего элемента (alj) ключевой l-строки на главный элемент (alk) предыдущей таблицы, т.е. по формуле:
— элементы остальных строк новой симплексной таблицы, за исключением строки, стоящей на месте бывшей ключевой l-строки, пересчитываются по одной из следующих формул:
, ( )
де , аij – однотипные коэффициенты, соответственно новой и предыдущей симплексной таблиц;
, аlj – коэффициенты строки, стоящей в новой таблице на месте бывшей ключевой l-строки и, соответственно, коэффициенты ключевой l-строки в предыдущей таблице;
aik – коэффициенты ключевого К-столбца предыдущей симплексной таблицы;
alk – главный (генеральный) элемент предыдущей симплексной таблицы, стоящий на пересечении ключевых l-строки и К-столбца.
Расчеты по указанным выше формулам выполняются для заполнения всех строк новой симплексной таблицы, включая индексную (m+1) строку, но исключая ключевую l-строку.
Таким образом получаем оптимальный план, представленный на таблице 3.
Таблица 2 — Вторая симплексная таблица
|
i |
Базис, Xn+i |
Сi |
вi |
20 |
10 |
30 |
0 |
0 |
0 |
Сумма по строке |
Контроль |
|
|
Х1 |
Х2 |
Х3 |
Х4 |
Х5 |
Х6 |
|||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
1 |
Х4 |
0 |
46,66 |
-0,333 |
1 |
0 |
1 |
-1,333 |
0 |
47,00 |
— |
47,00 |
|
2 |
Х3 |
30 |
6,667 |
0,417 |
0,5 |
1 |
0 |
0,167 |
0 |
8,751 |
15,86 |
8,751 |
|
3 |
Х6 |
0 |
30 |
0,750 |
2,5 |
0 |
0 |
-0,5 |
1 |
33,750 |
40 |
33,750 |
|
m+1 |
200 |
-7,5 |
5 |
0 |
0 |
5 |
0 |
202,500 |
— |
202,500 |
Таблица 3 — Третья симплексная таблица
|
i |
Базис, Xn+i |
Сi |
вi |
20 |
10 |
30 |
0 |
0 |
0 |
Сумма по строке |
Контроль |
|
|
Х1 |
Х2 |
Х3 |
Х4 |
Х5 |
Х6 |
|||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
1 |
Х4 |
0 |
51,990 |
0 |
1,399 |
0,799 |
1 |
-1,199 |
0 |
53,989 |
53,989 |
|
|
2 |
Х1 |
20 |
15,988 |
1 |
1,199 |
2,398 |
0 |
0,400 |
0 |
20,985 |
20,985 |
|
|
3 |
Х6 |
0 |
18,010 |
0 |
1,600 |
-1,799 |
0 |
-0,799 |
1 |
18,012 |
18,012 |
|
|
m+1 |
319,909 |
0 |
13,993 |
17,985 |
0 |
8,003 |
0 |
359,890 |
359,890 |
14. Контроль правильности задачи должен осуществляться на всех этапах её решения: от составления экономико-математической модели задачи до анализа оптимального её решения.
В порядке осуществления текущего контроля правильности решения задачи и исключения «зацикливания», в поиске оптимального её решения необходимо иметь в виду следующее:
— если в ключевом К — столбце все коэффициенты (aik) отрицательные, то решения задачи не существует;
— если в столбце свободных членов (ресурсов) имеются нули, то при последующем решении задачи может произойти зацикливание (вырождение). Для преодоления вырожденности плана нули заменяют на малые положительные числа, не оказывающие влияния на результаты решения задачи;
Если перечисленные условия контроля соблюдены, то это гарантирует получение оптимального решения задачи. Контроль оптимального плана осуществляется в процессе его анализа.
4 Модификация ограничений
Все ограничения задачи модифицируются согласно следующим правилам:
ограничения типа «≤» переводятся на равенства созданием дополнительной переменной с коэффициентом «+1». Эта модификация проводится и в однофазном симплекс-методе, дополнительные переменные в дальнейшем используются как исходный базис.
ограничения типа «≥» дополняются одной переменной с коэффициентом «−1». Поскольку такая переменная из-за отрицательного коэффициента не может быть использована в исходном базисе, необходимо создать ещё одну, вспомогательную, переменную. Вспомогательные переменные всегда создаются с коэффициентом «+1».
ограничения типа «=» дополняются одной вспомогательной переменной.
Соответственно, будет создано некоторое количество дополнительных и вспомогательных переменных. В исходный базис выбираются дополнительные переменные с коэффициентом «+1» и все вспомогательные.
ЗАКЛЮЧЕНИЕ
Симплекс-метод позволяет эффективно найти оптимальное решение, избегая простой перебор всех возможных угловых точек. Основной принцип метода: вычисления начинаются с какого-то «стартового» базисного решения, а затем ведется поиск решений, «улучшающих» значение целевой функции. Это возможно только в том случае, если возрастание какой-то переменной приведет к увеличению значения функционала.
СПИСОК ЛИТЕРАТУРЫ
Симплексный метод решения задач линейного программирования [Электронный ресурс]// Информационный ресурс studopedia – Режим доступа: https://studopedia.ru/22_110893_simpleksniy-metod-resheniya-zadach-lineynogo-programmirovaniya.html/, свободный — Загл. с экрана.
Метод симплекса [Электронный ресурс]// Информационный ресурс nauka – Режим доступа: https://nauka.club/matematika/metod-simpleksa.html/, свободный — Загл. с экрана.
Симплекс-метод [Электронный ресурс]// Информационный ресурс wikipedia – Режим доступа: https://ru.wikipedia.org/wiki/Симплекс-метод/, свободный — Загл. с экрана.
Подробный разбор симплекс-метода [Электронный ресурс]// Информационный ресурс habr – Режим доступа: https://habr.com/ru/post/474286/, свободный — Загл. с экрана.
Поскольку, как
было показано в п. 3.1 решение задачи
линейного программирования находится
в одной из крайних (угловых) точек ОДЗ,
важным вопросом является изучение не
системы неравенств (4), а соответствующей
системы уравнений AX
= B, решение
которой дает угловые точки ОДЗ.
Если уравнения
системы АX = B
линейно независимы, то система имеет
множество решений при n > m
и единственное решение при
n = m.
При решении задачи линейного
программирования симплекс-методом
всегда будет выполняться n > m,
поэтому для получения некоторого одного
решения, «лишние» n – m
переменных приравниваются нулю.
Если приравнять
к нулю n – m
произвольных переменных (например,
переменные xm+1,
xm+2,
…, xn)
и, решив систему, найти значения оставшихся
m
переменных (x1, x2, …, xm),
то такое решение называется базисным.
Если нулю приравнять
некоторые другие n – m
переменных – получим другое базисное
решение. Любое базисное решение, у
которого все переменные неотрицательные
называется допустимым
базисным решением.
Переменные, которые
были приравнены нулю, называются
небазисными.
Оставшиеся т
переменных,
значение которых получены из решения
системы, называются базисными.
Допустимое базисное
решение представляет собой угловую
вершину ОДЗ.
Решение задачи
симплекс-методом сводится к направленному
перебору смежных друг с другом угловых
точек, которые представляют собой
допустимые базисные решения.
Сформулируем в
общем виде алгоритм симплекс-метода:
1: Приведение задачи
к стандартной форме. Стандартной
формой
задачи
линейного программирования будем
называть задачу, у которой все ограничения
записаны как равенства и при этом правые
части ограничений неотрицательны.
2: Выделение
исходного базисного решения (по
возможности из стандартной формы). То
есть определение тех переменных n – m
переменных, которые приравниваются
нулю и нахождение значений оставшихся
базисных переменных.
3: Определение,
является ли полученное базисное решение
оптимальным, если да, то решение окончено,
иначе переходим к шагу 4.
4: Определение
переменной, которая войдет в базис и
переменной, которая из базиса выйдет
таким образом, чтобы новое решение было
лучше предыдущего. То есть, если текущее
базисное решение неоптимально, необходимо
определить, какую из базисных переменных
приравнять нулю, и какую из небазисных
переменных вместо нее включить в базис.
5: Использование
эквивалентных преобразований методом
Жордана-Гаусса для нахождения нового
допустимого базисного решения. Переход
к шагу 3.
Чтобы привести
задачу линейного программирования к
стандартной форме необходимо:
1. Убедиться, что
во всех ограничениях правые части bi
неотрицательны. Если есть отрицательные
правые части ограничений, такие
ограничения нужно умножить на –1 (при
этом учесть, что в ограничениях типа
или
знак ограничения изменится на
противоположный).
2. К левой части
ограничений типа
нужно прибавить новую, дополняющую
переменную S,
которая уравнивала бы левую и правую
часть и показывала бы насколько левая
часть ограничения меньше правой.
То есть ограничение
ai1x1
+ …+
ainxn
£
bi
в стандартном виде
будет выглядеть так:
ai1x1
+ …+
ainxn
+ Si
= bi.
3. Из левой части
ограничений типа
нужно вычесть новую, избыточную
переменную
e,
которая уравнивала бы левую и правую
часть и показывала бы насколько левая
часть ограничения больше правой.
То есть ограничение
ai1x1
+ …+
ainxn
bi
в стандартном виде
будет выглядеть так:
ai1x1
+ …+
ainxn
– ei
= bi.
Дополняющие
переменные S
и избыточные e
будем называть вспомогательными,
в то время, как переменные x
– основными.
Чтобы из стандартной
формы сразу выделить базисное решение,
необходимо в качестве базисных переменных
выбрать те m
переменных, каждая из которых встречается
только в одном из уравнений и включена
в него с коэффициентом, равным единице.
В качестве исходных
базисных переменных в задачах с
ограничениями
удобно брать переменные S1,
…, Sn.
Реализацию алгоритма
симплекс-метода проиллюстрируем на
следующем примере.
Пример 3.2.
Мебельная
фабрика может производить шкафы, столы,
стулья. При изготовлении мебели
используются древесина, труд рабочих
на столярном и отделочном участках.
Необходимое количество ресурсов для
изготовления шкафов, столов и стульев
приведено в таблице:
Таблица 3.1 –
Исходные данные к примеру 3.2
|
Ресурсы |
Шкаф |
Стол |
Стул |
|
Древесина |
8 м2 |
6 м2 |
1 м2 |
|
Отделочные работы |
4 часа |
2 часа |
1,5 часа |
|
Столярные |
2 часа |
1,5 часа |
0,5 часа |
В распоряжении
фабрики ежедневно имеется 48 м2
древесины, 20 часов времени на участке
отделки, 8 часов на столярном участке.
Известно также, что потребность в шкафах
и стульях неограниченна. Однако не более
5 столов может быть продано ежедневно.
Цены реализации продукции следующие:
шкаф – 60 у.е., стол – 30 у.е., стул – 20 у.е.
Мебельная фабрика
хотела бы использовать имеющиеся ресурсы
наилучшим образом, приносящим наивысший
доход.
Построим
математическую модель. Обозначим х1
– количество производимых шкафов, х2
– число столов, х3
– количество стульев.
Задача линейного
программирования примет вид:
1) Целевая функция
2) Система ограничений
3) Ограничения на
знак переменных
х1,
х2,
х3
0
.
Преобразуем модель
к стандартной форме:
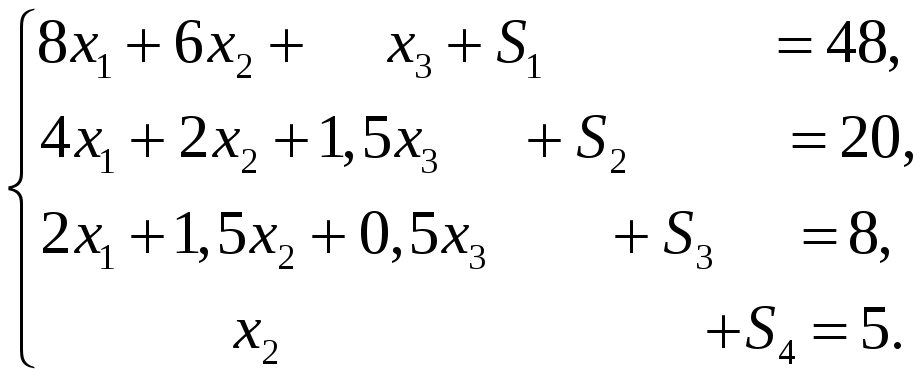
В качестве исходного
базиса, очевидно, удобно выбрать
переменные S1,
S2,
S3,
S4,
так как очевидно базисное решение:
S1
= 48, S2
= 20,
S3
= 8, S4
= 5.
Дальнейшие шаги
алгоритма симплекс-метода (шаг 3, 4, 5)
удобно представить в специальной
таблице, называемой симплекс-таблицей.
Построим первую
симплекс-таблицу. В первом столбце
укажем переменные, образующие базис,
во втором столбце (cj)
– коэффициенты целевой функции, при
переменных, входящих в базис. В третьем
столбце (bi)
– правые части ограничений. В остальных
столбцах (x1,
x2,
…, S4)
записываются коэффициенты целевой
функции и коэффициенты в ограничениях
при соответствующих переменных.
Последняя строка
симплекс-таблицы ()
особая. Она получается из целевой функции
следующим образом. В целевой функции
все переменные переносятся в левую
часть. Получается
.
Полученные коэффициенты и правая часть
целевой функции (0) записывается по
аналогии с коэффициентами ограничений:
в столбце bi
– правая часть целевой функции, которая
изначально равна нулю, в остальных
столбцах – обратные значения коэффициентов
целевой функции (–сj)
при соответствующих переменных.
Таким образом,
исходная симплекс-таблица имеет вид:
Таблица 3.2 –
Исходная симплекс-таблица к примеру
3.2
|
Базис |
cj |
|
х1 |
х2 |
х3 |
S1 |
S2 |
S3 |
S4 |
с.о. |
|
60 |
30 |
20 |
0 |
0 |
0 |
0 |
||||
|
0 |
48 |
8 |
6 |
1 |
1 |
0 |
0 |
0 |
48:8 = 6 |
|
0 |
20 |
4 |
2 |
3/2 |
0 |
1 |
0 |
0 |
20:4 = 5 |
|
0 |
8 |
2 |
3/2 |
1/2 |
0 |
0 |
1 |
0 |
8:2 = 4 |
|
0 |
5 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
– |
|
|
0 |
-60 |
-30 |
-20 |
0 |
0 |
0 |
0 |
max |
Заметим, что столбец
отражает не только правые части
ограничений, он также показывает значение
базисных переменных S1,
…, S4.
(Напомним, что значение небазисных
переменных х1,
х2,
х3
равно нулю.) Тот же столбец в строке
целевой функции
отражает значение целевой функции при
данном базисном решении. Ведь,
действительно, целевая функция Z
при х1 = х2 = х3 = 0,
тоже равна нулю.
Последняя строка
таблицы
называется строкой
целевой функции
или индексной
строкой.
Признаком
оптимальности в задаче на максимум
является наличие в индексной строке
всех неотрицательных
значений. В нашем примере индексная
строка содержит отрицательные элементы
(–60, –30, –20).
Следовательно,
текущее базисное решение неоптимально
и его нужно улучшать.
В случае если
решается задача на минимум, можно
использовать один из двух вариантов:
1) умножить целевую
функцию на –1 и решать задачу не на
минимум, а на максимум;
2) признаком
оптимальности в задаче на минимум
считать наличие в индексной строке
всех неположительных
значений. Так, если бы данная задача 3.2
ставила минимизацию целевой функции,
то текущее базисное решение было бы
оптимальным (в строке
не положительных значений).
Определив, что
текущее базисное решение неоптимально,
нужно выяснить какую из небазисных
переменных х1,
х2,
х3
нужно включить в базис. Коэффициент
–60 в индексной строке показывает,
что при введении в базис переменной x1
в базис со значением 1, целевая функция
улучшится на 60 единиц. При введении в
базис x2
со значением 1, ЦФ улучшится на 30 единиц.
При введении в базис x3
– на 20.
Наилучший прирост
целевой функции дает введение в базис
переменной x1.
Таким образом, при
решении задачи на максимум в базис
войдет та переменная, которая имеет
отрицательное значение в индексной
строке и из всех отрицательных значений,
оно наибольшее по модулю.
Рассуждая аналогично,
при решении задачи на минимум, используя
вариант 2), в базис войдет та переменная,
которая имеет положительное значение
в индексной строке и из всех положительных
значений, оно наибольшее.
Столбец с переменной,
которая собирается войти в базис
называется разрешающим
столбцом. В
нашей задаче разрешающим, является
столбец х1.
Выясним, какая
переменная выйдет из базиса и с каким
значением переменная х1
войдет в базис. Эти задачи взаимосвязанные.
Вывести из базиса нужно такую переменную,
чтобы став равной нулю, она не привела
к тому, что какая-то из остальных базисных
переменных станет отрицательной
(недопустимой). Нужно, чтобы приравняв
одну из базисных переменных нулю,
остальные базисные переменные, в том
числе и та, которая входит в базис,
оставались неотрицательными.
Поэтому для
определения того, какая переменная
покинет базис, необходимо рассчитать
отношения
,
где bi
– значения коэффициентов правых частей
ограничений в столбце
bi
симплекс-таблицы,
aij
– значения разрешающего столбца ( j):
48:8 = 6; 20:4 =5; 8:2 = 4.
Данные отношения
называются симплексными
отношениями.
Они записываются в последнем столбце
симплекс-таблицы (с.о.). Рассчитывать
имеет смысл только
неотрицательные
симплексные отношения. Отрицательное
симплекс-отношение обозначает, что ни
при каком допустимом значении входящей
в базис переменной нельзя обеспечить
непротиворечивое равенство в том
ограничении, в котором переменная
покидает базис.
Из полученных
неотрицательных симплексных отношений
выбираем наименьшее. В нашем случае
наименьшее симплексное отношение
получается в строке 3) S3,
следовательно, переменная S3
покинет базис, а данная строка
будет разрешающей
строкой.
Элемент, стоящий
на пересечении разрешающего столбца и
разрешающей строки также называется
разрешающим
элементом.
Вместо S3
в третью строку новой симплекс-таблицы
войдет х1
с коэффициентом cj
равным
60, т.к. 60 – коэффициент целевой функции
при x1.
Разрешающий столбец
,
который сейчас имеет вид
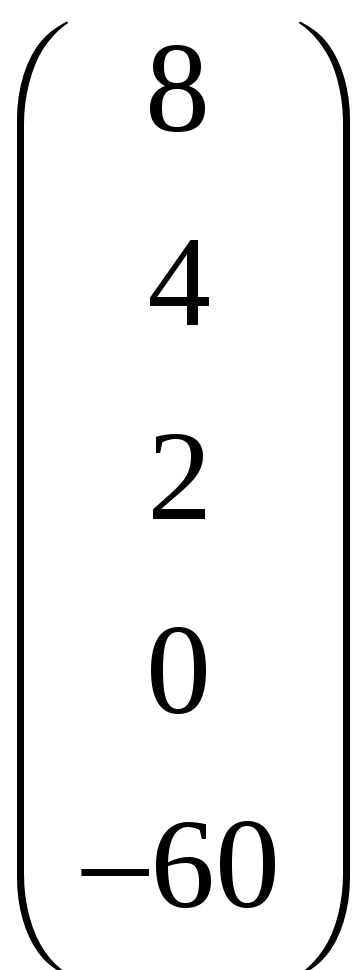
нужно преобразовать к виду
,
то есть к такому
же виду, какой имел столбец S3
в таблице 3.2.
Воспользуемся
методом Жордана-Гаусса.
На месте разрешающего
элемента нужно получить единицу.
Следовательно, всю разрешающую строку
(кроме столбца сj)
нужно разделить на разрешающий элемент.
Строку 3) х1
разделим на 2, она примет вид:
|
3) |
4 |
1 |
3/4 |
1/4 |
0 |
0 |
1/2 |
0 |
Строку 4) S4
переносим из первой симплекс-таблицы
во вторую без изменений, так как в столбце
х1
уже находится нулевой элемент.
Строку 1) S1
необходимо обновить таким образом,
чтобы в столбце х1
был коэффициент 0. Для этого из строки
S1
следует вычесть разрешающую строку х1,
умноженную на 8.
|
1) S1 8х1 S1-8х1 |
48 |
8 |
6 |
1 |
1 |
0 |
0 |
0 |
|
-32 |
-8 |
-6 |
-2 |
0 |
0 |
-4 |
0 |
|
|
16 |
0 |
0 |
-1 |
1 |
0 |
-4 |
0 |
Со строкой 2) S2
поступаем аналогично (из строки S2
следует вычесть 4 строки
):
|
2) S2 4х1 S2-4х1 |
20 |
4 |
2 |
3/4 |
0 |
1 |
0 |
0 |
|
-16 |
-4 |
-3 |
-1 |
0 |
0 |
-2 |
0 |
|
|
4 |
0 |
-1 |
1/2 |
0 |
1 |
-2 |
0 |
Для обновления
строки
к ней необходимо прибавить 60 строк
.
|
|
0 |
-60 |
-30 |
-20 |
0 |
0 |
0 |
0 |
|
240 |
60 |
45 |
15 |
0 |
0 |
30 |
0 |
|
|
240 |
0 |
15 |
-5 |
0 |
0 |
30 |
0 |
Заполним
вторую симплекс-таблицу.
Таблица
3.3 – Вторая
симплекс-таблица к примеру 3.2
|
Базис |
cj |
|
х1 |
х2 |
х3 |
S1 |
S2 |
S3 |
S4 |
с. о. |
|
60 |
30 |
20 |
0 |
0 |
0 |
0 |
||||
|
1) S1 |
0 |
16 |
0 |
0 |
-1 |
1 |
0 |
-4 |
0 |
– |
|
2) S2 |
0 |
4 |
0 |
-1 |
1/2 |
0 |
1 |
-2 |
0 |
8 |
|
3) х1 |
60 |
4 |
1 |
3/4 |
1/4 |
0 |
0 |
1/2 |
0 |
16 |
|
4) S4 |
0 |
5 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
– |
|
|
240 |
0 |
15 |
-5 |
0 |
0 |
30 |
0 |
max |
Из таблицы видно,
что полученное новое базисное решение
стало лучше предыдущего: выпуск 4 шкафов
(x1 = 4)
позволяет получить уже 240 у.е. дохода.
Однако, это решение не оптимальное. Это
видно из индексной строки таблицы:
требование оптимальности не выполнено,
так как имеется отрицательный элемент
(–5). Будем улучшать план. В качестве
разрешающего столбца теперь выбираем
столбец
,
так как он содержит отрицательный
элемент (–5). Разрешающую строку выберем,
как и ранее, используя симплексное
отношение (16 не делим на (-1), так как
отрицательные значения не рассматриваются):
4:
=
8; 4:
= 16.
Из полученных
симплексных отношений выбираем
наименьшее, следовательно, в качестве
разрешающей строки выбираем вторую
строку. Переменная х3
вытесняет
S2
из базиса. Вновь используем метод
Жордана-Гаусса, добиваемся того, чтобы
столбец х3
имел вид:
.
Заполним итоговую
симплекс-таблицу.
Таблица 3.4 –
Итоговая симплекс-таблица к примеру
3.2
|
Базис |
cj |
|
х1 |
х2 |
х3 |
S1 |
S2 |
S3 |
S4 |
|
60 |
30 |
20 |
0 |
0 |
0 |
0 |
|||
|
1) S1 |
0 |
24 |
0 |
-2 |
0 |
1 |
2 |
-8 |
0 |
|
2) х3 |
20 |
8 |
0 |
-2 |
1 |
0 |
2 |
-4 |
0 |
|
3) х1 |
60 |
2 |
1 |
5/4 |
0 |
0 |
-1/2 |
3/2 |
0 |
|
4) S4 |
0 |
5 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
|
|
280 |
0 |
5 |
0 |
0 |
10 |
10 |
0 |
В
строке целевой функции все коэффициенты
при переменных неотрицательны,
следовательно, мы нашли оптимальное из
допустимых решений. Базис образуют
переменные
,
то есть для получения максимального
дохода следует выпускать продукцию
и
,
так как переменная
не входит в базис (а значит равна нулю).
В столбце
имеем оптимальные значения базисных
переменных: x1 = 2,
x3 = 8.
Значения вспомогательных переменных
S1 = 24,
S4 = 5
можно интерпретировать следующим
образом: 24 м2
древесины осталось не использовано,
спрос на столы не удовлетворен на 5
единиц. Тот факт, что S2 = S3 = 0,
говорит о том, что все ресурсы по участку
отделки и столярному участку использованы
полностью.
Целевая функция
нашей
задачи имеет вид:
.
Для определения
ее максимального значения подставим в
нее значения переменных, образующих
оптимальное базисное решение:
Это же значение
видно в последней симплекс-таблице на
пересечении индексной строки и столбца
.
Таким образом,
наибольший доход 280 у.е. получается при
производстве 2 единиц товара
(шкафы) и 8 единиц товара
(стулья).
Проанализируем
полученное решение.
Каждая из
вспомогательных переменных S1, …, S4
соответствовала одному из ограничений
и показывала, насколько левая часть
ограничения (фактические затраты
ресурсов) меньше правой части (их запаса).
Таким образом, в тех ограничениях, где
левая часть равна правой (запас ресурсов
исчерпан полностью), соответствующая
вспомогательная переменная S
будет равна нулю. Вспомним, что такое
ограничение называется связующим и
отражает критический (дефицитный)
ресурс.
Запасы ресурсов
на участке отделки и столярном участке
использованы полностью S2
= S3
= 0. Древесина
же осталось неиспользованной (S1 = 24).
Если увеличить запас древесины (с 48 до,
например, 68), приведет ли это к улучшению
решения? Нет. Поскольку она и так осталась
лишняя увеличение правой части
несвязующего ограничения приведет к
тому, что увеличится значение
соответствующей вспомогательной
переменной (станет S1 = 44),
но оптимальный план не изменится.
Дефицитные же
ресурсы являются ценными в том смысле,
что их увеличение приведет к возможности
улучшения оптимального плана. Оценка
ценности данных ресурсов приведена в
строке целевой функции
:
при указанных переменных стоят
коэффициенты 10. Эти величины называются
теневыми
ценами и
отражают степень важности ресурса с
точки зрения его вклада в оптимальный
результат. Теневая цена показывает,
насколько изменится значение целевой
функции, если изменить правую часть
соответствующего ограничения на 1
единицу. Теневые цены рассчитывается
только для ресурсов, которые использованы
полностью, то есть для связующих
ограничений.
В строке целевой
функции
коэффициент 5 при свободной основной
переменной x2
носит название снижающей
оценки и
показывает, насколько ухудшится целевая
функция, если мы примем решение производить
хотя бы 1 стол. Снижающую оценку можно
интерпретировать и с другой стороны:
она показывает, насколько нужно увеличить
цену на столы, чтобы их производство
стало выгодно, и они вошли в базис.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #