Система уравнений как найти катеты

Тема 8.

Решение систем уравнений второй степени и решение задач с помощью таких систем.

Какие основные способы решения систем уравнений вы знаете? (методы сложения, подстановки, графический)

Каким способом можно решить систему, одно из уравнений которой – уравнение второй степени?

Такие системы всегда можно решить способом подстановки. Для этого поступают следующим образом:

1. Выражают из уравнения первой степени одну переменную через другую;
2. Подставляют полученное выражение в уравнение второй степени, в результате чего приходят к уравнению с одной переменной;
3. Решают получившееся уравнение с одной переменной;
4. Находят соответствующие значения второй переменной.

Рассмотрим пример:

Решим систему уравнений:

x2+y=14,y-x=8;

Выразим из первого уравнения переменную y и подставим во второе:

y=14-x2,14-x2-x=8;

Решим второе уравнение, относительно х:

x² + x — 6 = 0, корни которого равны (– 3) и 2.

Вернемся к системе:

x1=-3,y1=14—32;

x1=-3,y1=14—32;

x1=-3,y1=5;

x2=2,y2=10;

Рассмотрим еще один пример, решим систему

x2-y2=17,x-y=2;

Эту систему так же можно решить методом подстановки, выразив переменную x, но можно упростить первое уравнение.

Заметим, что левую часть первого уравнения можно разложить на множители по формуле разности квадратов, получим:

x-yx+y=17,x-y=2;

Из второго уравнения разность x — y = 2. Поэтому вместо первой скобки в первое уравнение подставим число 2, получим:

2x+y=17,x-y=2;

2x+y=17,x-y=2;

Разделим обе части первого уравнения на 2, получим:

x+y=8,5,x-y=2;

А эту систему давай решим методом сложения, сложим два уравнения, а затем из первого уравнения вычтем второе, получим:

2x=10,5,2y=6,5;

x=5,25,y=3,25.

А теперь решим несколько задач с помощью систем: уравнений второй системы:

Сумма двух чисел равна 12, а их произведение равно 35. Найдите эти числа.

Пусть число x – первое число, а y – второе число. Тогда получим:

x+y=12,x∙y=35;

Выразим из первого уравнения переменную х и подставим во второе, получим:

x=12-y,x∙y=35;

x=12-y,12-yy=35;

Решим уравнение:

12y — y² — 35 = 0

y² — 12y + 35 = 0

Получим корни 5 и 7.

Возвращаемся к нашей системе:

y1=55x=35

y2=7,7x=35;

y1=5×1=7

y2=7×2=5

Ответ: (7;5) и (5;7)

Рассмотрим еще одну задачу:

Площадь прямоугольного треугольника равен 24 см², а его гипотенуза равна 10 см. Каковы катеты треугольника?

Пусть a – длина одного катета, а b – длина второго катета.

Вспомним формулу площади прямоугольного треугольника и теорему Пифагора:

Итак, площадь равна половине произведения катетов.

А квадрат гипотенузы равен сумме квадратов катетов:

12ab=24a2+b2=100

Решим эту систему, первое уравнение домножим на 2, получим:

ab=48a2+b2=100

Выразим переменную а из первого уравнения и подставим во второе, получим:

a=48b48b2+b2=100

Решим второе уравнение системы:

2304b2+b2-100=0,

b4-100b2+2304=0, решим это биквадратное уравнение:

Пусть b² = t, тогда получим:

t² — 100t + 2304 = 0, отсюда

t₁ = 64, t₂ = 36

Возвращаемся к нашей замене, получим:

b1,2=±8,b3,4=±6, так как b – это длина катета, то она не может быть отрицательной, следовательно, b равно 6 или 8, тогда второй катет равен 8 или 6 соответственно.

Алгебра и геометрия не только коллеги, но и лучшие подруги и сестры.

Порой хочется сделать так, чтобы решение даже самых обычных систем уравнений предстало перед учениками в красивом и неожиданном виде. И даже пусть существуют универсальные рецепты решения для многих систем, никто не запрещает вносить романтику творческого поиска и вдохновения в каждое конкретное решение.

Рассмотрим только одну систему уравнений, но решим ее двумя различными способами.

Задача.

Найти значение выражения xy + yz, где x, y, z – положительные числа, удовлетворяющие системе уравнений

{x² + y² = 9,
{y² + z² = 16,
{y² = xz.

Решение.

Решим алгебраически предложенную систему.

Воспользуемся третьим равенством системы. Заменим в первом и во втором уравнениях y² на xz, получим:

{x² + xz = 9,
{xz + z² = 16,
{y² = xz.

Вынесем общие множители за скобки в уравнениях x² + xz = 9 и xz + z² = 16. Будем иметь:

{x(x + z) = 9,
{z(x + z) = 16,
{y² = xz.

Теперь можно разделить второе уравнение системы на первое. При этом выражение в скобках сократится. Первое уравнение системы перепишем в исходном виде.

{x² + xz = 9,
{z/x = 16/9,
{y² = xz.

Из второго уравнения системы можно выразить x через z. Получим, что 9z = 16x. Чтобы не работать с дробями, умножим первое уравнение системы на 9:

{9 ·x² + 9 · zx = 9 · 9,
{9z = 16x,
{y² = xz.

Заменим 9z на 16x в первом уравнении

{9x² + 16x²= 81,
{9z = 16x,
{y² = xz;

и решим его отдельно:

9x² + 16x²= 81;

25x² = 81;

x² = 81/25.

x = 9/5.

При извлечении квадратного корня получается два ответа  – с плюсом и с минусом, но нам подходит только корень 9/5, т.к. по условию задачи x, y, z – положительные числа.

Вернемся к системе уравнений и вычислим y и z.

{x = 9/5,
{z = 16/5,
{y² = 144/25.

После извлечения квадратного корня в последнем уравнении системы получаем, что

{x = 9/5,
{z = 16/5,
{y = 12/5.

Осталось найти значение выражения xy + yz. Имеем:

xy + yz = 9/5 · 12/5 + 16/5 · 12/5 = 300/25 = 12.

Ответ: 12.

Как видим, все достаточно просто. А теперь познакомимся с применением геометрического метода решения систем алгебраических уравнений.

Итак, условие задачи осталось неизменным. Найти значение выражения xy + yz, где x, y, z – положительные числа, удовлетворяющие системе уравнений

{x² + y² = 9,
{y² + z² = 16,
{y² =xz.

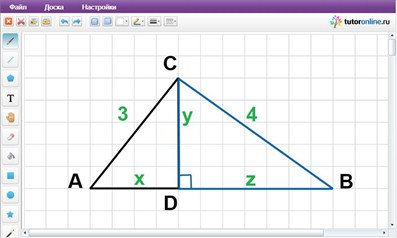
Запишем первое и второе уравнение системы в виде x² + y² = 3² и y² + z² = 4². Так как по условию задачи x > 0, y > 0 и z > 0, то по теореме, обратной теореме Пифагора, существует треугольник, назовем его ACD, с катетами, равными x и y, и гипотенузой, равной 3. Аналогично, существует треугольник, назовем его CDB, с катетами, равными y и z, и гипотенузой, равной 4. Изобразим эти треугольники на рисунке.

Сторона CD у треугольников ACD и CDB общая.

Вернемся к исходной системе. Сложив первые два уравнения, получим, что

 x² + 2y² + z² = 25.

Рассмотрим третье уравнение системы. Так как y² = xz, то уравнение x² + 2y² + z² = 25 можно переписать в виде x² + 2xz + z² = 25 или (x + z)² = 25. После того, как извлечем из левой и правой частей уравнения квадратный корень, получим уравнение x + z = 5.

Таким образом, в треугольнике ABC имеем, что сторона AC = 3, сторона CB = 4, а сторона AB = x + z = 5. Легко видеть, что по теореме, обратной теореме Пифагора, треугольник ABC является прямоугольным с гипотенузой AB = 5 (т.к. 3² + 4² = 5²).

Теперь рассмотрим выражение, значение которого необходимо найти по условию задачи и сделаем в нем некоторые преобразования:

 xy + yz = 2((xy)/2 + (yz)/2).

Воспользуемся формулой для нахождения площади прямоугольного треугольника: S = (ab)/2, где a и b – катеты прямоугольного треугольника. Значит выражения (xy)/2 и (yz)/2 – это площади треугольников ACD и CDB соответственно. Теперь перепишем исходное выражение следующим образом:

xy + yz = 2((xy)/2 + (yz)/2) = 2(S_ACD + S_CDB).

Так как сумма площадей треугольников  ACD и CDB есть не что иное, как площадь треугольника ABC, то можно сделать следующий вывод:

2(S_ACD + S_CDB) = 2 · S_ABC = 2 · (AC · CB) / 2 = AC · CB = 3 · 4 = 12.

Таким образом, имеем, что xy + yz = 12.

Ответ: 12.

На самом деле, абсолютно не важно, каким методом Вы будете решать систему уравнений. Ведь как сказал П.Д. Коэн, хорошая математика всегда красива.

 Остались вопросы? Не знаете, как решать системы уравнений?
Чтобы получить помощь репетитора – зарегистрируйтесь.

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Ответ:

Объяснение:

a, b — катеты.

с — гипотенуза.

Система уравнений:

a+b=17 ⇒ b=17-a

a²+b²=13²

1) a+b=17

(a+b)²=17²

a²+b²+2ab=17²

13²+2ab=17²

2ab=(17-13)(17+13)

ab=120/2

ab=60

a(17-a)=60

-a²+17a-60=0                                      ×(-1)

a²-17a+60=0 ⇒ D=289-240=49

a₁=(17-7)/2=5; b₁=17-5=12

a₂=(17+7)/2=12; b₂=17-12=5

Отсюда следует, что катеты прямоугольного треугольника равны:

a₁=5 см, b₁=12 см или a₂=12 см, b₂=5 см.

Ответ: 5 см и 12 см.

План урока:

Уравнения с двумя переменными

График уравнения с двумя переменными

Система уравнений с двумя переменными

Способ подстановки

Метод сложения

Разложение левой части уравнения на множители

Линейное неравенство с двумя переменными

Нелинейные неравенства с двумя переменными

Системы неравенств с двумя переменными

Уравнения с двумя переменными

Порою в ур-нии содержится не одна, а две переменных. Такие ур-ния мы уже изучали в 7 классе. Приведем несколько примеров уравнений с двумя переменными:

2х – 5у = 8

4t³– 6ht = h⁴

– 14z + 5v/z = 8

В абсолютном большинстве таких задач для обозначения переменных используют буквы х и у. Решение указывают в виде пары чисел, причем на первом месте пишут значение х, а на втором – значение у. Например, несложно убедиться, что пара чисел (– 1; 3) является решением ур-ния

х(х – у) = 4.

Для этого надо лишь вместо х подставить (– 1), а вместо у – число 3:

(– 1)(– 1 – 3) = 4

4 = 4

Получили верное равенство. Заметим, что пара (– 1; 3) является не единственным решением ур-ния. Например, пара (2; 0) также обращает ур-ние в верное рав-во:

2(2 – 0) = 4

4 = 4

У ур-ний с двумя неизвестными, как и у ур-ний с одной неизвестной, можно определить степень. Для этого надо представить их в таком виде, когда слева записан многочлен, а справа – ноль. Тогда степень ур-ния будет равна степени многочлена. Так как ур-ние содержит две переменных, то для обозначения такого многочлена используется запись Р(х; у).

Пример. Определите степень уравнения

х(х² + у) = х + 1

Решение. Раскроем скобки слева, а потом перенесем все слагаемые в одну сторону:

х(х² + у) = х + 1

х³ + ху = х + 1

х³ + ху – х – 1 = 0

В левой части стоит многочлен третьей степени (подробнее об определении степени полинома можно узнать из этого урока). Поэтому и степень ур-ния равна 3.

Ответ: 3

График уравнения с двумя переменными

Очень часто ур-ние с 2 переменными имеет бесконечное число решений. Их удобно изображать в виде графика, ведь каждой паре чисел (х₁; у₁) соответствует точка на координатной плоскости с координатами х₁ и у₁.

Проще всего строить график уравнения с двумя переменными в том случае, когда удается выразить переменную у через х. Например, пусть надо построить график ур-ния

6х + 3у = 9

Выразим неизвестную величину у через х, то есть попытаемся получить ф-цию у = у(х):

6х + 3у = 9

3у = 9 – 6х

у = 3 – 2х

Построим график ф-ции у = 3 – 2х. Он одновременно будет являться и графиком ур-ния 6х + 3у = 9:

Не всегда можно так преобразовать ур-ние, чтобы получилась ф-ция у = у(х). Действительно, по определению функции, каждому значению аргумента должно соответствовать только одно значение ф-ции. Однако рассмотрим пример ур-ния

х – у² = 0

Можно убедиться, что его обращают в верное рав-во пары чисел (1; 1) и (1; – 1):

1² – 1² = 0

1² – (– 1)² = 0

Получается, что одному значению х(х = 1) соответствует сразу 2 значения у (у = 1 и у = –1). Это значит, что графиком такого ур-ния не может являться ф-ция у = у(х)

В данном случае возможно выразить х через у. Перенесем слагаемое у² вправо:

х = у²

Получили «перевернутую ф-цию» х = х(у), где не у зависит от х, а х от у. Ф-ция является квадратичной, а потому ее графиком будет парабола:

Так как х и у в ф-ции поменялись местами, то ось параболы стала не вертикальной, а горизонтальной.

Встречаются случаи, когда из ур-ния невозможно получить ни ф-цию у(х), ни ф-цию х(у). Рассмотрим ур-ние

х² + у² = 25

Его решениями являются пары чисел (0; 5) и (0; – 5). То есть значению х = 0 соответствует два значения у (5 и – 5), поэтому не получиться записать ф-цию у(х). С другой стороны, решениями ур-ния являются также пары (5; 0) и (– 5; 0), то есть значению у = 0 также соответствует два значения х (– 5 и 5), поэтому и записать ф-цию х(у) не удастся. Вообще данное ур-ние является частным случаем ур-ния

х² + у² = R²

где R– некоторое постоянное число, или параметр. Оно называется уравнением окружности, потому что его графиком как раз и является окружность.

Докажем это утверждение. Пусть на координатной плоскости есть точка А с произвольными координатами (х; у):

Опустим из А перпендикуляр на ось Ох в точку В. Получили прямоугольный треугольник ОАВ. Его катет ОВ равен у, а катет АВ = х. По теореме Пифагора можно найти длину гипотенузы ОА, которая и является расстоянием от О до А:

ОА² = ОВ² + АВ² = х² + у²

Окружность радиусом R– это множество точек, удаленных от центра на расстояние R. То есть расстояние ОА равно R, то точка А лежит на окружности радиусом R c центром в О:

х² + у² = ОА² = R²

Таким образом, координаты любой точки, лежащей на расстоянии Rот центра, удовлетворяют ур-нию

х² + у² = R²

В частности, графиком ур-ния

х² + у² = 25

является окружность с радиусом 5 (так как 25 = 5²)

Система уравнений с двумя переменными

Рассмотрим задачу. Разность двух чисел равна единице, а сумма их квадратов составляет 25. Чему равны эти два числа?

В задаче неизвестны два числа. Поэтому обозначим их за неизвестные величины х и у. Первое условие задачи, «разность чисел равна 1», можно записать ур-нием:

х – у = 1

Второе условие записывается так:

х² + у² = 25

Нам надо найти такие х и у, которые удовлетворяют одновременно обоим условиям задачи. То есть необходимо решить систему уравнений с двумя переменными:

Напомним, что в 7 классе мы уже изучали сис-мы ур-ний, однако рассматривались только случаи, когда все они являлись линейными. В рассматриваемом случае второе ур-ние линейным НЕ является (потому что переменные величины стоят во второй степени).

Для каждого ур-ния построим отдельный график. Точки их пересечения и будут соответствовать решениям сис-мы. Ур-ниех² + у² = 25 задает окружность. Ур-ние х – у = 1 будет совпадать с графиком линейной ф-ции у = х – 1:

Графики пересеклись в двух точках: (4; 3) и (– 3; – 4). Подставив их в сис-му, можно убедиться, что именно эти пары чисел являются решениями этой сис-мы.

Конечно, графический метод решения сис-м не всегда точный. Однако он позволяет оценить количество корней и их примерное расположение. Также графики помогают при изучении сис-м, содержащих параметры.

Пример. Найдите с помощью графиков решение сис-мы ур-ний

Решение. Построим графики каждого ур-ния. График первого ур-ния представляет собой параболу, а второй график – это прямая у = 4 – х:

Видно, что графики пересеклись в двух точках: (– 1; 5) и (4; 0). Убедиться в точности построения можно, просто подставив эти значения в решаемую сис-му.

Пример. При каком а сис-ма ур-ний

имеет ровно 3 решения?

Решение. Преобразуем 2-ое ур-ние сис-мы:

у – а + х² = 0

у = – х² + а

График ур-ния х² + у² = 9 представляет собой окружность радиусом 3. График у = – х² + а является параболой с ветвями, смотрящими вниз. Покажем на плоскости различные варианты взаимного расположения этих графиков при различных значениях параметра а:

Видно, что 3 точки пересечения у параболы и окружности может быть только в случае, если вершина параболы касается окружности в точке (0; 3). Для этого парабола должна определяться ур-нием у = – х²+ 3. Это значит, что только при значении а = 3 сис-ма имеет 3 решения.

Ответ: 3

Метод подстановки

Конечно, решать сис-му ур-ний графическим способом не очень удобно, так как часто можно получить лишь приближенный ответ. При изучении систем линейных уравнений с двумя переменными мы познакомились с двумя универсальными способами их решения: методы подстановки и сложения. К сожалению, для нелинейных сис-м нет универсальных методов их решения. Однако тот же способ подстановки иногда может помочь.

Его суть заключается в том, что в одном ур-нии надо выразить одну переменную через другую. В результате получится ф-ция у(х) или х(у), и ее можно будет подставить во второе ур-ние и тем самым получить ур-ние с одной неизвестной. Иногда такое действие называют исключением переменной.

Пример. Найдите решение сис-мы уравнений методом подстановки:

Решение. Сразу видно, что во втором ур-нии можно выразить у через х:

у – х² + 6 = 0

у = х² – 6

Подставим выражение у = х² – 6 в первое ур-ние:

2х² + х – 3у – 16 = 0

2х² + х – 3(х² – 6) – 16 = 0

Получилось ур-ние, в котором уже нет у! Его достаточно легко решить, ведь оно сводится к квадратному ур-нию:

2х² + х – 3(х² – 6) – 16 = 0

2х² + х – 3х² + 18 – 16 = 0

– х² + х + 2 = 0

D = b²– 4ас = 1² – 4•(– 1)•2 = 1 + 8 = 9

х₁ = (– 1 – 3)/(– 2) = 2

х₂ = (– 1 + 3)/(– 2) = – 1

Получили два возможных значения х. Теперь выполним обратную подстановку:

у = х² – 6

у₁ = (– 1)² – 6 = – 5

у₂ = 2² – 6 = – 2

Итак, имеем две пары чисел, (– 1; – 5) и (2; – 2), которые являются решениями сис-мы ур-ний.

Ответ: (– 1; 5); (2; – 2)

Пример. При каких х и у справедлива сис-ма

Решение. Попробуем найти решение методом подстановки. Из второго ур-ния следует, что ни одна из переменных не равна нулю, ведь иначе бы произведение ху равнялось бы не 7, а нулю. Поэтому можно поделить второе ур-ние на х:

ху = 7

у = 7/х

У нас получилось выразить у через х. Подставим полученное выражение в первое ур-ние:

Заменим переменную х² на t:

t = x²

t + 49/t = 50

Умножим ур-ние на t. Так как х ≠ 0, то и t≠ 0,поэтому мы можем смело производить подобное умножение:

t² + 49 = 50t

t²– 50t + 49 = 0

Получили квадратное ур-ние. Можно честно решить его, однако мы поступим проще. По теореме Виета, произведение корней ур-ния должно равняться 49 (свободный член ур-ния), а в сумме они должны давать 50 (второй коэффициент ур-ния с противоположным знаком). Под эти условия подходят числа 1 и 49:

1 + 49 = 50

1•49 = 49

На всякий случай подставим их в квадратное ур-ние и убедимся, что они действительно являются его корнями:

1²– 50•1 + 49 = 1 – 50 + 49 = 0

49²– 50•49 + 49 = 2401 – 2450 + 49 = 0

Итак, имеем два корня: t₁ = 1 и t₂ = 49.

Теперь произведем обратную замену:

х² = t

х² = 1 или х² = 49

Имеем два квадратных ур-ния. Корнями первого являются числа

х₁= 1 и х₂ = – 1

У ур-ния х² = 49 корни – это числа

х₃ = – 7 и х₄ = 7

Получили четыре значения х. Для каждого из них можно вычислить соответствующее значение у по формуле у = 7/х:

при х = –1; у = 7/ – 1 = – 7

при х = 1; у = 7/1 = 7

при х = – 7; у = 7/– 7 = – 1

при х = 7; у = 7/7 = 1

В итоге имеем 4 пары решений: (– 1; – 7), (1; 7), (– 7; – 1) и (7; 1).

Ответ: (– 1; – 7), (1; 7), (– 7; – 1), (7; 1).

Метод сложения

Очевидно, что не всегда в ур-нии можно выразить одну переменную через другую. Такую ситуацию можно, например, наблюдать в сис-ме

Однако здесь в каждом ур-нии есть слагаемое 6у², взятое с разными знаками. За счет этого сис-му можно решить методом сложения, ведь при сложении левых частей ур-ний слагаемые 6у² и (– 6у²) сократятся, что позволит исключить переменную у из ур-ния. Для этого надо сложить по отдельности левые и правые части ур-ний и получить новое ур-ние:

(3х² – 6у² + 3х) + (– 2х² + 6у²) = –18 + 22

3х² – 6у² + 3х – 2х² + 6у² = 4

х² + 3х = 4

х² + 3х – 4 = 0

Получили ур-ние, не содержащее у. Его можно решить как обычное квадратное ур-ние:

D = b²– 4ас = 3² – 4•1•(– 4) = 9 + 16 = 25

х₁ = (– 3 – 5)/2 = – 4

х₂ = (– 3 + 5)/2 = 1

Нашли два значения х. Подставляя его второе ур-ние, получим

при х = – 4:

– 2•(– 4)² + 6у² = 22

6у² = 22 + 32

у² = 9

у₁ = 3 или у₂ = – 3

при х = 1:

– 2•1² + 6у² = 22

6у² = 22 + 2

у² = 4

у₃ = – 2 или у₄ = 2

Имеем 4 решения сис-мы (– 4; 3), (– 4; – 3), (1; – 2), (1; 2).

Мы рассмотрели простейший случай использования метода сложения уравнений, когда ур-ния сис-мы можно сложить сразу. Однако порою их надо сначала умножить на какие-то числа, и лишь потом складывать.

Пример. Укажите решение для сис-мы:

Решение. Сразу складывать эти ур-ния нет смысла, потому что при этом не исчезнет ни одна переменная. Напомним, что обе части любого ур-ния можно умножить на число, не равное нулю, и в результате получится равносильное ур-ние. Поэтому второе ур-ние умножим на (– 2):– 4х²+ 2у² = – 2

А вот теперь есть смысл сложить его с первым ур-нием, так как у них есть слагаемые 2у² с противоположными знаками:

(3х² – 2у²) + (– 4х² + 2у²) = 1 – 2

–х² = – 1

х² = 1

х = – 1 или х = 1

Полученные значения х будем подставлять в другое ур-ние, например, в 2х² – у² = 1 (на самом деле можно выбрать любое другое из ур-ний сис-мы).

При х = – 1:

2(– 1)² – у² = 1

у² = 1

у₁ = – 1 или у₂ = 1

Теперь подставим х = 1:

2•1² – у² = 1

у² = 1

у₃ = – 1 или у₄ = 1

В итоге получаем 4 решения: (– 1; – 1), (– 1; 1), (1; – 1) и (1; 1)

Ответ:(– 1; – 1), (– 1; 1), (1; – 1), (1; 1).

Порою метод сложения и метод подстановки следует использовать одновременно.

Пример. Решите систему методом сложения:

Решение: постараемся избавиться от слагаемых с буквенной частью ху. Для этого умножим второе ур-ние на (– 2):

– 2х – 2у – 2ху = 12

Сложим его с первым ур-нием:

(3х + у + 2ху) + (– 2х – 2у – 2ху) = – 6 + 12

х – у = 6

исключить переменную не удалось, однако мы получили линейное ур-ние. Выразим из него у:

у = х – 6

Теперь можно подставить это выражение, например, во второе ур-ние системы:

х + у + ху = – 6

х + (х – 6) + х(х – 6) = – 6

х² – 4х – 6 = – 6

х² – 4х = 0

х(х – 4) = 0

х = 0 или х – 4 = 0

х₁ = 0 или х₂ = 4

Подставим полученные результаты в выражение у = х – 6

у₁ = х₁ – 6 = 0 – 6 = – 6

у₂ = х₂ – 6 = 4 – 6 = – 2

Получили два решения: (0; – 6) и (4; – 2).

Ответ: (0; – 6) и (4; – 2).

Разложение левой части уравнения на множители

Если нельзя использовать ни метод подстановки, ни способ сложения, то могут помочь другие методы. Например, иногда в одном ур-нии справа можно оставить ноль, а слева – разложить многочлен на множители.

Пример. Решите систему:

Решение. В верхнем ур-нии можно выполнить следующие преобразования:

9х² – у² = 3х – у

(3х – у)(3х + у) = (3х – у)

(3х – у)(3х + у) – (3х – у) = 0

Можно заметить, что в левой части находится разность двух выражений, содержащих множитель (3х – у). Этот множитель можно вынести за скобки, при этом вместо второго выражения останется только единица, ведь его можно переписать как (3х – у)•1 (при умножении на единицу любое выр-ние остается неизменным):

(3х – у)(3х + у) – (3х – у)•1 = 0

(3х – у)(3х + у – 1) = 0

(а откуда -1?)

Вспомним, что произведение равно нулю, если один из его сомножителей нулевой. Поэтому

3х – у = 0 или 3х + у – 1 = 0

у = 3х или у = 1 – 3х

Получили два возможных варианта выражения для у. Будем подставлять их во второе ур-ние:

при у = 3х

х² + у = ху

х² + 3х = х•3х

– 2х² + 3х = 0

х(– 2х + 3) = 0

х = 0 или – 2х + 3 = 0

х₁ = 0 или х₂ = 1,5

Найдем значение у, учитывая, что у = 3х:

у₁ = 3х₁ = 3•0 = 0

у₂ = 3х₂ = 3•1,5 = 4,5

Имеем решения (0; 0) и (1,5; 4,5). Далее рассмотрим второй случай, когда у = 1 – 3х:

х² + у = ху

х² + (1 – 3х) = х(1 – 3х)

х² + 1 – 3х = х – 3х²

Перенося слагаемые влево, получаем квадратное ур-ние:

х² + 1 – 3х – х + 3х² = 0

4х² – 4х + 1 = 0

D = b²– 4ас = (– 4)² – 4•4•1 = 0

Получаем, что у квадратного ур-ния есть лишь один корень:

х₃ = – b/2а = 4/8 = 0,5

Найдем соответствующее ему значение у:

у₃ = 1 – 3х₃ = 1 – 3•0,5 = – 0,5

Получили третье решение: (0,5; – 0,5).

Ответ: (0; 0); (1,5; 4,5);(0,5; – 0,5).

Системы ур-ний часто используются при решении геометрических задач.

Пример. Площадь прямоугольного треугольника равна 150 см². Известно, что один из его катетов больше другого на 5 см. Каков периметр треугольника?

Решение. Традиционно катеты обозначают буквами а и b. Площадь прямоугольного треугольника равна половине произведения катетов:

S = 0,5•ab

Отсюда следует ур-ние:

0,5ab = 150

Будем считать, что катет а больше, чем b. Тогда из условия можно записать

а = 5 + b

Итак, получается система:

Очевидно, что систему можно решить подстановкой а = 5 + b

0,5ab = 150

0,5ab = 150

0,5(5 + b)b = 150

(5 + b)b = 300

b² + 5b – 300 = 0

Решая это квадратное ур-ние, легко получить два значения b: 20 и (– 15). По смыслу задачи длина катета должна измеряться положительным числом, а потому b = 20. Второй катет на 5 см меньше, то есть он равен 20 – 5 = 15 см. Длину гипотенузы с можно найти по теореме Пифагора:

с² = а² + b² = 20² + 15² = 625

c = 25

Периметр треугольника – это сумма его сторон, она равна 25 + 20 + 15 = 60 см.

Ответ: 60 см.

Линейное неравенство с двумя переменными

Изучение неравенств с двумя переменными начнем с простейших из них – линейных неравенств. Их можно получить из линейных ур-ний, поставив вместо знака «=» один из четырех знаков сравнения.

Приведем примеры линейных неравенств с двумя переменными:

5х + 7у – 2 > 0

– 18,4x + 45,325y + 54,36 < 0

– 67х – 12у + 4 ⩾ 0

Линейные ур-ния и линейные нер-ва тесно связаны друг с другом. Напомним, что графиком линейного ур-ния

ах + by + c = 0

является прямая. Эта прямая разбивает всю плоскость на две полуплоскости. Для всех точек одной их них выполняется нер-во

ах + by + c< 0

а для всех точек другой полуплоскости справедливо нер-во

ах + by + c> 0

Пример. Отметьте на координатной прямой все решения неравенства с двумя переменными

3х + 2у < 6

Решение. Заменим знак «<»на знак «=» и получим ур-ние 3х + 2у = 6. Преобразовав его, мы получим функцию у(х)

3х + 2у = 6

2у = 6 – 3х

у = 3 – 1,5х

Построим этот график:

Видно, что прямая разбила плоскость на две части. Но в какой из них выполняется нер-во 3х + 2у < 6? Для ответа на этот вопрос достаточно взять координаты любой точки из одной из полуплоскостей и подставить их в нер-во. Конечно, проще всего взять точку (0; 0), в ней нер-во справедливо:

3•0 + 2•0 < 6

0 < 6

Поэтому область, в которой находится начало координат, можно заштриховать. Тем самым мы покажем, что на ней выполняется данное в условии нер-во:

Обратите внимание, что саму прямую 3х + 2у = 6 мы нарисовали пунктиром. Тем самым мы показали, что точки плоскости, лежащие непосредственно на этой прямой, НЕ входят в решение нер-ва, ведь оно является строгим.

Пример. Покажите все решения нер-ва

– 2х + у + 4⩽ 0

Решение. Снова заменим знак сравнения в нер-ве на знак «=»:

– 2х + у + 4 = 0

у = 2х – 4

Получили график прямой. Сразу отметим, что в точке (0; 0) заданное нер-во НЕ выполняется:

– 2•0 + 0 + 4 ⩾ 0

а потому заштриховывать надо будет полуплоскость, к которой НЕ относится начало координат:

Здесь сама прямая – 2х + у + 4 = 0 отображена непрерывной линией. Тем самым показано, что ее точки входят в решение нер-ва, которое является нестрогим.

Нелинейные неравенства с двумя переменными

В случае с нелинейными нер-вами действует тот же принцип. Необходимо заменить знак сравнения на знак «=» и получить ур-ние, после чего построить график ур-ния. Он разобьет плоскость на несколько областей, в пределах которых исходное нер-во либо справедливо, либо нет.

Пример. Покажите множество решений нелинейного неравенства с двумя переменными

у – х² + 5 > 0

Решение. Рассмотрим ур-ние

у – х² + 5 = 0

Перенеся часть слагаемых вправо, можно получить функцию

у = х² – 5

Построим ее график. Он представляет собой параболу, которая разбивает плоскость на две области:

Для определения того, выполняется ли нер-во в той или иной области, достаточно рассмотреть по одной точке в каждой из областей. Начнем с внутренней области. К ней относится начало координат, точка (0; 0). Подставив х = 0 и у = 0 в нер-во, мы увидим, что оно выполняется:

0 – 0² + 5 > 0

5 > 0

Во второй области выполняется обратное нер-во у – х² + 5 < 0. В этом можно убедиться, взяв, например, точку (3; 0).

0 – 3² + 5< 0

– 4 < 0

В рассмотренном примере мы проверяли каждую из двух областей, хотя в случае линейных нер-в достаточно изучить лишь одну полуплоскость – в другой нер-во автоматически «меняло знак». Но, оказывается, что в случае с нелинейными нер-вами это правило может и не выполняться. Убедимся в этом на одном примере:

Пример. Отметьте на координатной плоскости множество решений нер-ва

х⁴ + 2х²у + у²> 0

Решение. Изучим ур-ние

х⁴ + 2х²у + у² = 0

В левой части стоит квадрат суммы слагаемых х² и у:

(х² + у)² = (х²)² + 2х²у + у² = х⁴ + 2х²у + у²

С учетом этого ур-ние можно переписать так:

(х² + у)² = 0

х² + у = 0

у = – х²

Построим график и определим, какое нер-во выполняется в полученных областях. В области I возьмем точку (0; – 1). При ее подстановке в исходное нер-во получаем:

0⁴ + 2•0²(– 1) + (– 1)²> 0

1 > 0

Однако и в области II выполняется то же самое нер-во. Это можно увидеть на примере точки (0; 1):

0⁴ + 2•0²•1 + 1²> 0

1 > 0

Получается, что решениями нер-ва являются точки обеих областей. То есть надо заштриховать всю координатную плоскость, кроме самой кривой у = – х² , которую мы покажем из-за этого штрихпунктирной линией:

Отдельно отметим, что возможны случаи, когда график ур-ния разбивает плоскость не на две, а на большее кол-во областей. В качестве примера можно привести нер-во

ху – 5> 0

Ему соответствует ур-ние ху – 5 = 0

Из него можно получить функцию у = 5/х, графиком которой является гипербола. Этот график образует 3 области. Будем действовать как и раньше – выберем из каждой области по одной точке и посмотрим, выполняется ли на нем нер-во ух – 5 > 0. Из области I возьмем точку (– 5; – 5):

ху – 5 = (– 5)•(– 5) – 5 = 25 – 5 > 0

Из II области выберем точку (5; 5):

ху – 5 = 5•5 – 5 = 20 > 0

Наконец, из III области возьмем точку (0; 0):

ху – 5 = 0•0 – 5 = 0 – 5 < 0

Системы неравенств с двумя переменными

Пусть надо решить систему неравенств с двумя переменными

Покажем графически решения для каждого отдельного нер-ва. Так как графиком ур-ния х² + у² = 9 является окружность радиусом 3, то решением первого нер-ва является круг:

Нер-во х – у > 0 является линейным. Его решением будет полуплоскость:

Теперь совместим два полученных решения. Решением системы нер-в будет пересечение заштрихованных областей. Ведь именно здесь оба нер-ва системы будут выполняться одновременно. Это пересечение представляет собой полукруг (он заштрихован квадратиками):

Пример. Постройте решение системы нер-в

Решение. Построим графики ур-ний х² – у = 2 и у² – х = 2. Первый из них будет являться параболой у = х² – 2. Второй же будет выглядеть, как парабола, повернутая на 90°. Это будет функция х = у² – 2:

В том, что мы выбрали правильную область на плоскости, можно убедиться, просто подставив одну из ее точек, в частности (0; 0), в систему:

Как составить систему уравнений

Уравнением называют аналитическую запись задачи о разыскании значений аргументов, при которых значения двух данных функций равны. Система – это совокупность уравнений, для которых требуется найти значения неизвестных, удовлетворяющих одновременно всем этим уравнениям. Так как успешное решение задачи невозможно без правильно составленной системы уравнений, необходимо знать основные принципы составления подобных систем.

Инструкция

Во-первых, определите неизвестные величины, которые требуется найти в данной задаче. Обозначьте их через переменные. Наиболее распространенные переменные, используемые при решении систем уравнений, это x, y и z. В отдельных задачах удобнее применять общепринятые обозначения, например, V для обозначения объема, или a для обозначения ускорения.

Пример. Пусть гипотенуза прямоугольного треугольника равна 5 м. Необходимо определить катеты, если известно, что после того, как один из них увеличить в 3 раза, а другой в 4, то сумма их длин составит 29 м. Для данной задачи необходимо обозначить длины катетов через переменные x и y.

Далее внимательно читайте условие задачи и связывайте неизвестные величины уравнениями. Иногда взаимосвязь между переменными будет очевидна. Например, в приведенном выше примере, катеты связывает следующее соотношение.Если «один из них увеличить в 3 раза» (3 * x), «а другой в 4» (4 * y), «то сумма их длин составит 29 м»: 3 * x + 4 * y = 29.

Другое уравнение для данной задачи менее очевидно. Оно кроется в условии задаче о том, что дан прямоугольный треугольник. Значит, можно применить теорему Пифагора. Т.е. x^2 + y^2 = 25. Итого получается два уравнения:
3 * x + 4 * y = 29 и x^2 + y^2 = 25.Для того чтобы система имела однозначное решение, количество уравнений должно быть равно количеству неизвестных. В приведенном примере имеется две переменных и два уравнения. Значит, система имеет одно конкретное решение: x = 3 м, y = 4 м.

При решении физических задач «неочевидные» уравнения могут заключаться в формулах, связывающих физические величины. Например, пусть в условии задачи необходимо найти скорости пешеходов Va и Vb. Известно, что пешеход A проходит расстояние S на 3 часа медленнее, чем пешеход B. Тогда можно составить уравнение, воспользовавшись формулой S = V * t, где S – это расстояние, V – скорость, t – время: S / Va = S / Vb + 3. Здесь S / Va — это время, за которое пройдет заданное расстояние пешеход A. S / Vb — время, за которое пройдет заданное расстояние пешеход B. По условию это время на 3 часа меньше.

Видео по теме

Обратите внимание

Все уравнения в системе должны поставлять дополнительную независимую от других уравнений информацию. Иначе система будет недоопределена и однозначного решения найти будет не возможно.

Полезный совет

После решения системы уравнений подставьте найденные значения в исходную систему и проверьте, что они удовлетворяют всем уравнениям.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?