Смежные углы как найти второй угол - Исправление недочетов и поиск решений вместе с Examum.ru

Смежные углы в геометрии

15 июня 2022

Два угла называются смежными, если у них общая вершина, общая сторона, а две других стороны образуют прямую.

В этом уроке:

Что такое смежные углы
Основное свойство смежных углов
Биссектрисы смежных углов
Тренировочные задачи

Это довольно простая, но очень важная тема.

1. Что такое смежные углы

Возьмём прямую $AB$ и отметим на ней точку $M$. Получим развёрнутый угол $AMB:$

Проведём из точки $M$ луч $MN$, не совпадающий с лучами $MA$ и $MB$.

Получим два новых угла: $angle AMN$ и $angle BMN$. Эти углы и называются смежными.

Определение. Два угла называются смежными, если у них одна общая сторона, а две других образуют прямую (или, что то же самое, являются дополнительными лучами).

Обратите внимание: чтобы углы стали смежными, им недостаточно просто иметь общую сторону. Вот эти углы — не смежные, хотя они и имеют общую сторону:

А вот дальше — смежные, хотя и расположены немного непривычно:

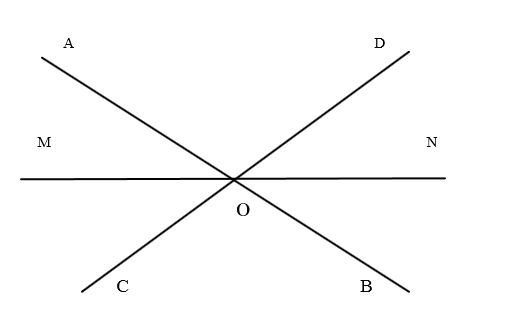
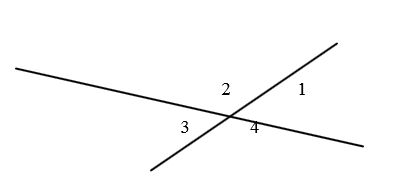
Часто смежные углы возникают в точке пересечения прямых. Например, при пересечении двух прямых

образуется четыре пары смежных углов: $angle ASM$ и $angle ASN$; $angle BSM$ и $angle MSN$; $angle ASN$ и $angle BSN$; наконец, $angle ASM$ и $angle BSM$.

2. Основное свойство внешних углов

У смежных углов есть замечательное свойство, которое будет преследовать нас на протяжении всей геометрии, до конца 11 класса.

Теорема. Сумма смежных углов равна 180°.

Доказательство. Рассмотрим смежные углы $AMN$ и $BMN$ с общей стороной $MN$:

Поскольку луч $MN$ делит угол $AMB$ на смежные углы $AMN$ и $BMN$, по основному свойству углов

[angle AMB=angle AMN+angle BMN]

Но угол $AMB$ — развёрнутый, поэтому

[angle AMN+angle BMN={180}^circ ]

Другими словами, если один угол равен $alpha $, то смежный с ним равен ${180}^circ -alpha $. Или если известно, что углы $alpha $ и $beta $ — смежные, то $alpha +beta ={180}^circ $.

Казалось бы, элементарные рассуждения, но их вполне достаточно, чтобы решать большой класс задач.

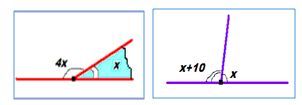
Задача 1. Найдите угол, смежный с углом $ABC$, если:

$angle ABC={36}^circ $.

$angle ABC={121}^circ $.

Решение

1) Обозначим смежный угол $DBC=x$. Он будет тупым:

Тогда $x=180-36=144$.

2) Обозначим смежный угол $DBC=x$. Он будет острым:

Тогда $x=180-121=59$.

Немного усложним задачу.

Задача 2. Найдите смежные углы, если:

один из них на 68° больше другого.

один из них в 5 раз больше другого.

их градусные меры относятся как 5 : 4.

Решение.

1) Пусть один из углов равен $x$. Тогда другой (очевидно, больший) будет равен $x+68$.

Поскольку углы смежные, их сумма равна 180 градусов:

[begin{align}2x+68&=180 \ 2x&=112 \ x&=56 end{align}]

Итак, один угол равен 56 градусов. Тогда другой равен $x+68=124$ градуса.

2) Пусть меньший угол равен $x$. Тогда смежный с ним равен $5x$.

Сумма смежных углов равна 180 градусов, поэтому

[begin{align}5x+x&=180 \ 6x&=180 \ x&=30 end{align}]

Мы нашли меньший угол — он равен 30 градусов. Тогда второй угол равен $5x=150$ градусов.

3) В задачах с отношениями величинам удобно обозначать их кратными некоторой переменной. Например, если углы относятся как 5 к 4, то пусть величина одного угла будет $5x$, а другого — $4x$.

Сумма смежных углов вновь равна 180 градусов:

[begin{align}5x+4x&=180 \ 9x&=180 \ x&=20 end{align}]

Поэтому сами углы равны $4x=80$ и $5x=100$ градусов.

3. Биссектрисы смежных углов

Вновь рассмотрим смежные углы $AMN$ и $BMN$:

Построим биссектрису $MC$ угла $AMN$ и биссектрису $MD$ угла $BMN$:

Если $angle AMC=x$ и $angle BMD=y$, то $angle AMN=2x$ и $angle BMN=2y$. Это смежные углы, поэтому

[begin{align}2x+2y&={180}^circ \ x+y&={90}^circ end{align}]

Получается, что биссектрисы смежных углов всегда пересекаются под углом 90°. Этот факт известен далеко не всем ученикам. Хотя он вполне может встретиться, например, на ЕГЭ.

Задача 3. Углы $ABC$ и $MBC$ смежные, $angle ABC={70}^circ $. Луч $BD$ принадлежит углу $ABC$, причём $angle ABD={40}^circ $. Найдите угол между биссектрисами углов $CBD$ и $MBC$.

Решение. Изобразим все углы на рисунке:

Видим, что углы $ABD$ и $MBD$ — смежные. Следовательно

[begin{align}angle MBD&={180}^circ -angle ABD= \ &={180}^circ -{40}^circ ={140}^circ end{align}]

Синим цветом отмечены биссектрисы углов $CBD$ и $MBC$. Обозначим величину углов переменными: $angle CBD=2x$, $angle MBD=2y$. Но $angle MBD=angle MBC+angle CBD$, поэтому

[begin{align}2x+2y&=140 \ x+y&=70 end{align}]

Это и есть искомый угол между биссектрисами. Он равен 70 градусов.

Задача 4. Дан треугольник $ABC$. Лучи $AM$ и $CN$ лежат на одной прямой со стороной $AB$ (см. рисунок). Известно, что $angle MAC+angle ABC={180}^circ $. Докажите, что $angle MAC=angle NBC$.

Пусть $angle ABC=x$. Тогда из условия следует, что $angle MAC={180}^circ -x$.

С другой стороны, углы $ABC$ и $NBC$ смежные, поэтому $angle NBC={180}^circ -x$.

Получается, что углы $MAC$ и $NBC$ равны одному и тому же выражению. Следовательно, $angle MAC=angle NBC$, что и требовалось доказать.

Смотрите также:

Что такое вертикальные углы
Перпендикулярные прямые — определение и свойства
Правила комбинаторики в задаче B6
Метод координат в пространстве
Четырехугольная пирамида: как найти координаты вершин
Задача B4 про три дороги — стандартная задача на движение

Источник

Главная
Справочники
Справочник по геометрии 7-9 класс
Начальные геометрические сведения
Смежные углы

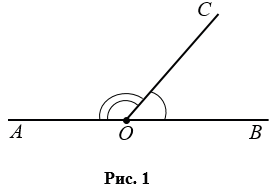
Смежные углы — это два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой.

На Рис.1 ОС — общая сторона, ОА и ОВ продолжают друг друга, значит АОС и СОВ — смежные.

Вместе смежные углы составляют развернутый угол, т.е. угол равный 180⁰. На Рис.1 АОВ = АОС + СОВ = 180⁰. Значит:

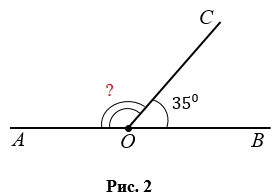
Зная один из смежных углов, всегда можно найти второй. На Рис.2 СОВ = 35⁰, тогда АОС = 180⁰ — СОВ = 180⁰— 35⁰ = 145⁰.

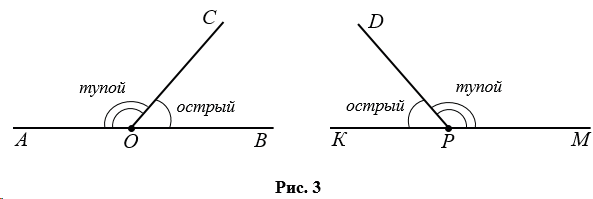
Если один из смежных углов острый, то второй будет тупой и наоборот (Рис.3).

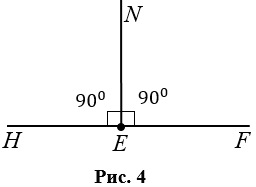
Если один из смежных углов прямой т.е. равен 90⁰, то второй также будет прямой (Рис.4).

Советуем посмотреть:

Точки, прямые, отрезки

Провешивание прямой на местности

Луч

Угол

Равенство геометрических фигур

Сравнение отрезков

Сравнение углов

Длина отрезка

Единицы измерения длины, расстояний

Градусная мера угла

Измерение углов на местности

Вертикальные углы

Перпендикулярные прямые

Построение прямых углов на местности

Начальные геометрические сведения

Правило встречается в следующих упражнениях:

7 класс

Задание 66,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 68,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 17,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 152,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 263,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 660,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 662,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 811,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 812,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 822,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Источник

Смежные углы. Полные уроки

Гипермаркет знаний>>Математика>>Математика 7 класс. Полные уроки>>Геометрия: Смежные углы. Полные уроки

Смежные углы.

Содержание

1 Что такое смежный угол
2 Теорема о смежных углах
3 Интересный факт
4 Геометрия вокруг нас
5 Решение задач
6 Математический диктант на повторение ранее выученного материала
7 Итог урока

Что такое смежный угол

Угол – это геометрическая фигура ( рис.1 ), образованная двумя лучами OA и OB ( стороны угла ), исходящими из одной точки O ( вершина угла ).

СМЕЖНЫЕ УГЛЫ — два угла, сумма которых равна 180°. Каждый из этих углов дополняет другой до развернутого угла.

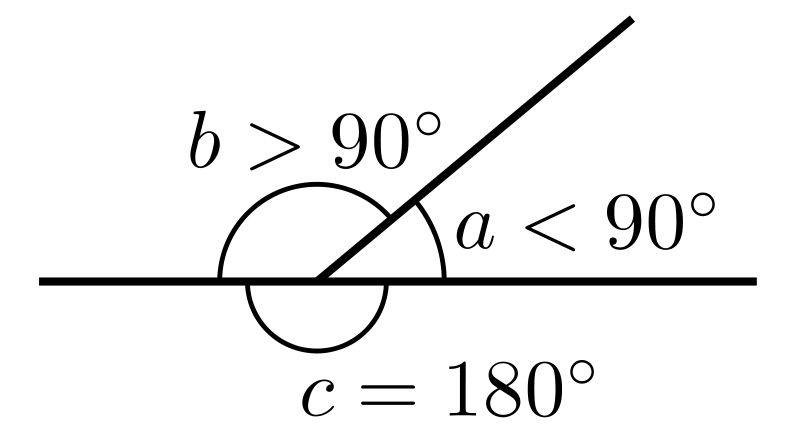
Смежные углы — (Agles adjacets) такие, которые имеют общую вершину и общую сторону. Преимущественно под этим именем подразумеваются такие углы, которых остальные две стороны лежат по противоположным направлениям одной прямой, проведенной через.

Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.

рис. 2

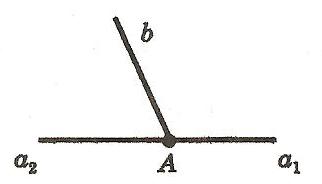
На рисунке 2 углы a1b и a2b смежные. У них общая сторона b, а стороны a1, a2 — дополнительные полупрямые.

рис. 3

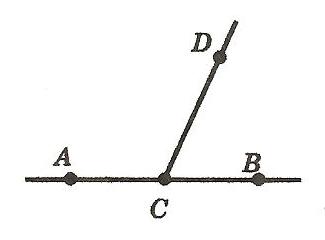
На рисунке 3 изображена прямая AB, точка C расположена между точками A и B. Точка D — точка не лежащая на прямой AB. Получается, что углы BCD и ACD смежные. У них общая сторона CD, а стороны CA и CB дополнительные полупрямые прямой AB, так как точки A, B разделены начальной точкой C.

Теорема о смежных углах

Теорема: сумма смежных углов равна 180°

Доказательство:
Углы a1b и a2b смежные (см. рис. 2) Луч b проходит между сторонами a1, и a2 развернутого угла. Следовательно, сумма углов a1b и a2b равна развернутому углу, то есть 180°. Теорема доказана.

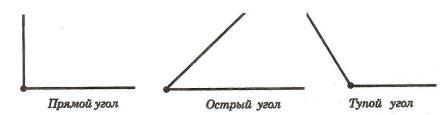
Угол, равный 90° называется прямым. Из теоремы о сумме смежных углов следует, что угол, смежный с прямым углом также прямой угол. Угол, меньший 90° называется острым, а угол больше 90° — тупым. Так как сумма смежных углов равна 180°, значит угол, смежный с острым углом — тупой угол. А угол смежный с тупым углом — острый угол.

Смежные углы — два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна 180°.

Определение 1. Углом называется часть плоскости, ограниченная двумя лучами с общим началом.

Определение 1.1. Углом называют фигуру, состоящую из точки — вершины угла — и двух различных полупрямых, исходящих из этой точки, — сторон угла.
Например, угол ВОС на рис1 Рассмотрим сначала две пересекающиеся прямые. При пересечении прямые образуют углы. Есть частные случаи:

Определение 2. Если стороны угла являются дополнительными полупрямыми одной прямой, то угол называется развернутым.

Определение 3. Прямой угол — это угол величиной в 90 градусов.

Определение 4. Угол, меньший 90 градусов, называется острым углом.

Определение 5. Угол, больший 90 градусов и меньший 180 градусов, называется тупым углом.
пересекающиеся прямые.

Определение 6. Два угла, одна сторона которых общая, а другие стороны лежат на одной прямой, называются смежными.

Определение 7. Углы, стороны которых продолжают друг друга, называются вертикальными углами.
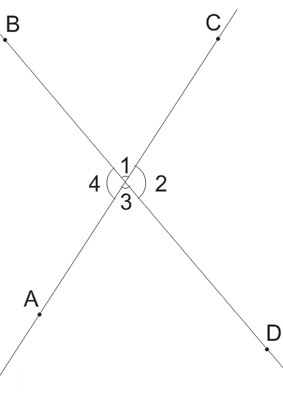
На рисунке 1:
смежные: 1 и 2; 2 и 3; 3 и 4; 4 и 1
вертикальные: 1 и 3; 2 и 4
Теорема 1. Сумма смежных углов равна 180 градусов.
Для доказательства рассмотрим на рис. 4 смежные углы АОВ и ВОС. Их суммой является развернутый угол АОС. Поэтому сумма данных смежных углов равна 180 градусов.

рис. 4

Интересный факт

Связь математики с музыкой

«Раздумывая об искусстве и науке, об их взаимных связях и противоречиях, я пришел к выводу, что математика и музыка находятся на крайних полюсах человеческого духа, что этими двумя антиподами ограничивается и определяется вся творческая духовная деятельность человека и, что между ними размещается все, что человечество создало в области науки и искусства.»
Г. Нейгауз
Казалось бы, искусство — весьма отвлеченная от математики область. Однако связь математики и музыки обусловлена как исторически, так и внутренне, несмотря на то, что математика — самая абстрактная из наук, а музыка — наиболее отвлеченный вид искусства.
Консонанс определяет приятное для слуха звучание струны
В основе этой музыкальной системы были два закона, которые носят имена двух великих ученых — Пифагора и Архита. Вот эти законы:
1. Две звучащие струны определяют консонанс, если их длины относятся как целые числа, образующие треугольное число 10=1+2+3+4, т.е. как 1:2, 2:3, 3:4. Причем, чем меньше число n в отношении n:(n+1) (n=1,2,3), тем созвучнее получающийся интервал.
2. Частота колебания w звучащей струны обратно пропорциональна ее длине l .
w = a : l ,
где а — коэффициент, характеризующий физические свойства струны.

Так же предложу вашему внимаю забавную пародию про спор двух математиков =)

Геометрия вокруг нас

Геометрия в нашей жизни имеет немаловажное значение. Ввиду того, что когда оглядеться вокруг, то не сложно будет заметить, что нас окружают различные геометрические фигуры. Мы с ними сталкиваемся повсюду: на улице, в классе, дома, в парке, в спортивном зале, в школьной столовой, в принципе везде, где бы мы с вами не находились.
Но темой сегодняшнего урока являются смежные угли. Поэтому давайте оглянемся вокруг и попытаемся в этом окружении найти углы. Если вы внимательно посмотрите в окно, то можете увидеть, что некоторые ветки дерева образуют смежные углы, а в перегородках на воротах можно заметить множество вертикальных углов.
Приведите свои примеры смежных углов, которые вы наблюдаете в окружающей обстановке.

Задание 1.

1. Вот на столе на книжной подставке стоит книга. Какой угол она образует?
2. А вот ученик работает за ноутбуком. Какой угол вы видите здесь?
3. Какой угол образует фото рамка на подставке?
4. Как вы думаете, возможно ли, чтобы два смежных угла были равными?

Задание 2.

Перед вами изображена геометрическая фигура. Что это за фигура, назовите ее? А теперь назовите все смежные углы, которые вы можете увидеть на этой геометрической фигуре.

Задание 3.

Перед вами изображение рисунка и картины. Рассмотрите их внимательно и скажите, какие виды улов вы видите на картине, а какие углы на рисунке.

Решение задач

 1) Даны два угла, относящиеся друг к другу как 1 : 2, а смежные с ними - как 7 : 5. Нужно найти эти углы.

 2) Известно, что один из смежных углов больше другого в 4 раза. Чему равны смежные углы?

 3) Необходимо найти смежные углы, при условии, что один из них на 10 градусов больше от второго.

Математический диктант на повторение ранее выученного материала

 1) Выполните рисунок: прямые a I b пересекаются в точке А. Отметьте меньший из образованных углов цифрой 1, а остальные углы – последовательно цифрами 2,3,4; дополняющие лучи прямой а - через а1 и а2, а прямой b - через b1 i b2.

 2) Пользуясь выполненным рисунком, впишите нужные значения и объяснения в места пропусков в тексте:

а) угол 1 и угол …. смежные, поскольку ...

б) угол 1 и угол …. вертикальные, поскольку ...

в) если угол 1 = 60°, то угол 2 = ..., потому что ...

г) если угол 1 = 60°, то угол 3 = ..., потому что ...

Решите задачи:

1. Может ли сумма 3-х углов, образованных при пересечении 2-х прямых, равняться 100°? 370°?
2. На рисунке найдите все пары смежных углов. А теперь вертикальных углов. Назовите эти углы.

3. Нужно найти угол, когда он втрое больше, чем смежный с ним.
4. Две прямые пересеклись между собой. В результате этого пересечения образовались четыре угла. Определите величину любого из них, при условии что:

а) сумма 2-х углов из четырех 84°;
б) разность 2-х углов из них равна 45°;
в) один угол в 4 раза меньше чем второй;
г) сумма трех из данных углов равна 290°.

Итог урока

1. назовите углы, которые образуются при пересечении 2-х прямых?
2. Назовите все возможные пары углов, находящихся на рисунке, и определите их вид.

Домашнее задание:

1. Найдите отношение градусных мер смежных углов, когда один из них на 54° больше второго.
2. Найдите углы, которые образуются при пересечении 2-х прямых, при условии, что один из углов равняется сумме 2-х других углов, смежных с ним.
3. Необходимо найти смежные углы, когда биссектриса одного из них образует со стороной второго угол, который больше чем второй угол на 60°.
4. Разница 2-х смежных углов равна трети от суммы этих двух углов. Определите величины 2-х смежных углов.
5. Разница и сумма 2-х смежных углов относятся как 1 : 5 соответственно. Найдите смежные углы.
6. Разница двух смежных составляет 25% от их суммы. Как относятся величины 2-х смежных углов? Определите величины 2-х смежных углов.

Вопросы:

Что такое угол?
Какие бывают типы углов?
Какая особенность смежных углов?

Предмети > Математика > Математика 7 класс

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов —
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других «взрослых» тем.

Разработка — Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email:

Источник

Как найти смежный угол

Плоским углом называют фигуру, образованную двумя лучами, исходящими из одной точки. Эта точка называется вершиной угла, а лучи — его сторонами. Если один из лучей продолжить за его начальную точку, то есть сделать прямой линией, то его продолжение образует со вторым лучом еще один угол — он называется смежным. Так как стороны угла равнозначны и продолжить можно любую из них, у каждого угла есть по два смежных.

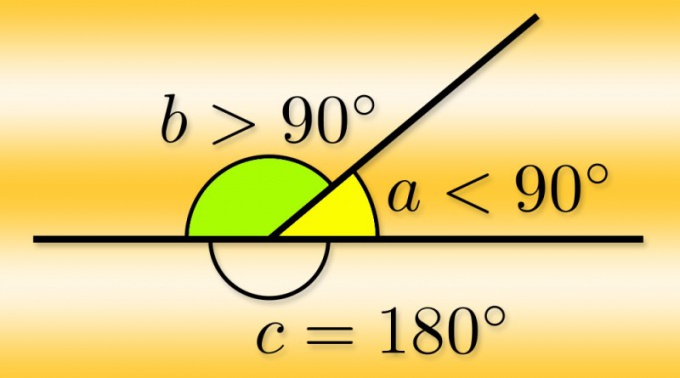
Инструкция

Если вам известна величина основного угла (α) в градусах, рассчитать градусную меру любого из пары смежных (α₁ и α₂) будет очень просто. Каждый из них дополняет основной угол до развернутого, то есть равного 180°, поэтому для их нахождения вычтите из этого числа известную величину основного угла α₁ = α₂ = 180°-α.

Величина исходного угла может быть приведена в радианах. Если и результат нужно получить в этих единицах, исходите из того, что развернутому углу соответствует количество радиан, равное числу Пи. Значит, формулу вычисления можно записать в таком виде: α₁ = α₂ = π-α.

Вместо градусной или радианной меры основного угла в условиях может быть дано соотношение величин основного и смежного углов. В этом случае составьте уравнение пропорции. Например, обозначьте через Y величину доли пропорции, относящуюся к основному углу, через X — относящуюся к смежному, а количество градусов, приходящееся на каждую единицу пропорции, обозначьте через k. Тогда общую формулу можно будет записать так: k*X+k*Y=180° или k*(X+Y)=180°. Выразите из нее общий множитель: k=180°/(X+Y). Затем рассчитайте величину смежного угла, умножив полученный коэффициент на долю этого угла в заданной пропорции: k*X = 180°/(X+Y)*X. Например, если это соотношение равно 5/13, величина смежного угла должна составлять 180°/(5+13)*13 = 10°*13 = 130°.

Если в исходных условиях ничего не сказано об основном угле, но дана величина вертикального угла, для вычисления смежных углов используйте формулы двух предыдущих шагов. Согласно определению вертикальный угол образуется двумя лучами, исходящими из той же точки, что и лучи основного угла, но направленными в строго противоположные стороны. Это значит, что градусная или радианная мера основного и вертикального угла равны, а значит, равны и величины смежных им углов.

Видео по теме

Источники:

как найти смежный угол в треугольнике если

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник