Загрузить PDF
Загрузить PDF
Периметр двумерной фигуры – это общая длина ее границы, равная сумме длин сторон фигуры.[1]
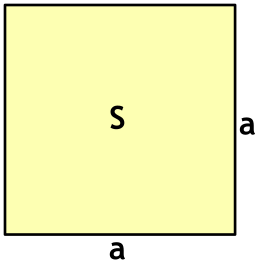
Квадрат – это фигура с четырьмя сторонами одинаковой длины, которые пересекаются под углом 90°.[2]
Так как в квадрате все стороны имеют одинаковую длину, то вычислить его периметр очень легко. Эта статья расскажет вам, как вычислить периметр квадрата по одной данной стороне, по данной площади и по данному радиусу окружности, описанной вокруг квадрата.
-
1
Формула для вычисления периметра квадрата: P = 4s, где s – длина стороны квадрата.
-
2
Определите длину одной стороны квадрата и умножьте ее на 4, чтобы найти периметр. Чтобы определить длину стороны, измерьте ее линейкой или посмотрите ее значение в учебнике (задаче). Вот некоторые примеры вычисления периметра:
- Если сторона квадрата равна 4, то P = 4 * 4 = 16.
- Если сторона квадрата равна 6, то P = 4 * 6 = 36.
Реклама
-
1
Формула для вычисления площади квадрата. Площадь любого прямоугольника (а квадрат – это частный случай прямоугольника) равна произведению его длины на его ширину.[3]
Поскольку длина и ширина квадрата равны, то его площадь вычисляется по формуле: A = s*s = s2, где s – длина стороны квадрата. -
2
Извлеките квадратный корень из значения площади, чтобы найти сторону квадрата. Для этого в большинстве случаев воспользуйтесь калькулятором (введите значение площади и нажмите клавишу «√»). Вы также можете вычислить квадратный корень вручную.
- Если площадь квадрата равна 20, то его сторона равна: s = √20 = 4,472.
- Если площадь квадрата равна 25, то s = √25 = 5.
-
3
Умножьте найденную сторону на 4, чтобы найти периметр. Вычисленное значение стороны подставьте в формулу для нахождения периметра: P = 4s. Вы найдете периметр квадрата.
- В нашем первом примере: P = 4 * 4,472 = 17,888.
- Периметр квадрата, площадь которого равна 25, а сторона равна 5, равен Р = 4 * 5 = 20.
Реклама
-
1
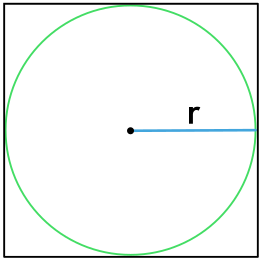
Вписанный квадрат – это квадрат, вершины которого лежат на окружности.[4]
-
2
Отношение между радиусом окружности и длиной стороны квадрата. Расстояние от центра описанной окружности до вершины вписанного в нее квадрата равно радиусу окружности. Чтобы найти сторону квадрата s, необходимо диагональю разделить квадрат на 2 прямоугольных треугольника. Каждый из этих треугольников будет иметь равные стороны a и b и общую гипотенузу с, равную удвоенному радиусу описанной окружности (2r).
-
3
Воспользуйтесь теоремой Пифагора, чтобы найти сторону квадрата. Теорема Пифагора гласит, что в любом прямоугольном треугольнике с катетами а и b и гипотенузой с: a2 + b2 = c2.[5]
Так как в нашем случае а = b (не забывайте, что мы рассматриваем квадрат!), и мы знаем, что с = 2r, то мы можем переписать и упростить это уравнение:- a2 + a2 = (2r)2«‘; теперь упростим это уравнение:
- 2a2 = 4(r)2; теперь разделим обе стороны уравнения на 2:
- (a2) = 2(r)2; теперь извлечем квадратный корень из обеих сторон уравнения:
- a = √(2r). Таким образом, s = √(2r).
-
4
Умножьте найденную сторону квадрата на 4, чтобы найти его периметр. В этом случае периметр квадрата: P = 4√(2r). Эту формулу можно переписать так: Р = 4√2 * 4√r = 5,657r, где r – радиус описанной окружности.[6]
-
5
Пример. Рассмотрим квадрат, вписанный в окружность радиусом 10. Это означает, что диагональ квадрата равна 2 * 10 = 20. Используя теорему Пифагора, мы получим: 2(a2) = 202, то есть 2a2 = 400. Теперь разделим обе стороны уравнения на 2 и получим: a2 = 200. Теперь извлечем квадратный корень из обеих сторон уравнения и получим: а = 14,142. Умножим это значение на 4 и вычислим периметр квадрата: P = 56,57.
- Обратите внимание, что вы могли бы получить тот же результат, просто умножив радиус (10) на 5,657: 10 * 5,567 = 56,57; но такой метод трудно запомнить, поэтому лучше пользоваться процессом вычисления, описанным выше.
Реклама
Похожие статьи
Об этой статье
Эту страницу просматривали 413 196 раз.
Была ли эта статья полезной?

{P = 4 cdot a}
Периметр квадрата рассчитывается довольно просто, но если вы забыли формулу или не имеете под рукой калькулятора, мы собрали для вас формулы для расчета периметра квадрата и онлайн калькулятор, который рассчитает периметр по длине стороны, диаметру, радиусам вписанной или описанной окружности, площади.
Содержание:
- калькулятор периметра квадрата
- формула периметра квадрата через длину стороны
- формула периметра квадрата через диагональ
- формула периметра квадрата через площадь
- формула периметра квадрата через радиус описанной окружности
- формула периметра квадрата через радиус вписанной окружности
- примеры задач
Квадрат — четырехугольник, у которого все стороны равны и все углы равны (прямые, 90 градусов). Квадрат так же называют правильным четырехугольником. Квадрат является частным случаем прямоугольника и ромба.
Кроме квадрата на сайте вы можете найти периметр ромба, прямоугольника, параллелограмма.
Формула периметра квадрата через длину стороны
{P = 4 cdot a}
a — сторона квадрата
Формула периметра квадрата через диагональ
{P = 2 sqrt{2} cdot d}
d — диагональ квадрата
Формула периметра квадрата через площадь
{P = 4sqrt{S}}
S — площадь квадрата
Формула периметра квадрата через радиус описанной окружности
{P = 4sqrt{2} cdot R}
R — радиус описанной около квадрата окружности
Формула периметра квадрата через радиус вписанной окружности
{P = 8r}
r — радиус вписанной в квадрат окружности
Примеры задач на нахождение периметра квадрата
Задача 1
Найти периметр квадрата, вписанного в окружность с R = 4√2.
Решение
Среди формул для решения этой задачи используем наиболее подходящую формулу №4. В условии сказано про квадрат, вписанный в окружность. Но при этом окружность будет описана около квадрата. Именно поэтому мы используем эту формулу. Подставим в нее известный из условия радиус вписанной окружности (в нашем случае он будет являться радиусом описанной окружности):
P = 4sqrt{2} cdot R = 4sqrt{2} cdot 4sqrt{2} = ({4sqrt{2}})^2 = {4^2 cdot ({sqrt{2}})^2} = 16 cdot 2 = 32 : см
Ответ: 32
Проверить полученный ответ можно с помощью калькулятора . Однако, радиус задан не просто числом, а выражением с квадратным корнем — 4√2. К счастью, наш калькулятор может анализировать математические выражения и производить с ними вычисления. Так как на клавиатуре компьютера нет знака квадратного корня, ввести значение радиуса необходимо в таком виде — 4*sqrt(2).
Задача 2
Найдите периметр квадрата сторона которого 13см.
Решение
Чтобы решить эту задачу используем первую формулу:
P = 4 cdot a = 4 cdot 13 = 52 : см
Ответ: 52 см
Проверить ответ поможет калькулятор .
Задача 3
Найдите периметр квадрата сторона которого 5см.
Решение
Для решения этой задачи также используем первую формулу:
P = 4 cdot a = 4 cdot 5 = 20 : см
Ответ: 20 см
Проверить ответ поможет калькулятор .
Задача 4
Найдите периметр квадрата с диагональю 2√2.
Решение
При решении этой задачи воспользуемся формулой №2:
P = 2 sqrt{2} cdot d = 2 sqrt{2} cdot 2 sqrt{2} = ({2 sqrt{2}})^2 = 2^2 cdot ({sqrt{2}})^2 = 4 cdot 2 = 8 : см
Ответ: 8 см
Проверить ответ к этой задаче можно с помощью калькулятора . Диагональ задана выражением с квадратным корнем, введем ее в виде, который сможет распознать наш калькулятор — 2 * sqrt(2).
Квадрат — это геометрическая фигура, правильный четырехугольник, у которого все углы и стороны равны.
Онлайн-калькулятор периметра квадрата
Противоположные стороны квадрата параллельны.
Другими словами, квадрат — это прямоугольник, у которого все стороны равны, или квадрат — это ромб, у которого все углы прямые. Квадрат имеет две диагонали, которые делятся точкой их пересечения пополам. Диагонали квадрата также делят его углы пополам и соединяют несмежные вершины.
Формула периметра квадрата
Для того чтобы найти периметр квадрата, нужно сложить длины всех его сторон.
P=a+a+a+a=4⋅aP=a+a+a+a=4cdot a
aa — длина стороны квадрата.
Разберем задачу на нахождение периметра квадрата.
Найти периметр квадрата со стороной 12 см.
Решение
a=12a=12
Воспользуемся формулой нахождения периметра квадрата и подставим вместо aa его численное значение:
P=4⋅a=4⋅12=48P=4cdot a=4cdot 12=48 см.
Ответ: 48 см.
Ищете, где заказать решение контрольной работы? Эксперты Студворк с радостью помогут вам!
Тест по теме «Периметр квадрата»
Download Article
Download Article
The perimeter of a two-dimensional shape is the total distance around the shape, or the sum of the length of its sides.[1]
By definition, a square is a four-sided shape with four straight sides of equal length, and four right (90°) angles.[2]
Since all four sides are the same length, this makes finding the perimeter of a square really easy! This article will first show you how to calculate the perimeter of a square if you know the length of one side. It will then show you how to find the perimeter of a square if you only know is its area, and finally, it will teach you to find the perimeter of a square that is inscribed in a circle with a known radius.
-
1
Recall the formula for the perimeter of a square. For a square of side length S, the perimeter is simply four times the side length: P=4s.[3]
-
2
Determine the length of one side, and multiply it by 4 to find the perimeter. Depending on the assignment, you may need to measure the side with a ruler, or look at other information on the page to determine the side length. Here are some examples of perimeter calculations:[4]
- If your square has a side length of 4, then P = 4 * 4, or 16.
- If your square has a side length of 6, its P = 4 * 6, or 24.
Advertisement
-
1
Know the formula for the area of a square. The area of any rectangle (remember, squares are special rectangles) is defined as its base times its height.[5]
Since the base and the height of a square are the same length, the area of a square with side length s is s*s, or A = s2. -
2
Find the square root of the area. The square root of the area will give you the length of one of the sides of the square. For most numbers, you will need to use a calculator to find the square root, by first typing in the value of the area, followed by the square root (√) key.[6]
You can also learn to Calculate a Square Root by Hand!- If the area of your square is 20, then the side length s =√20, or 4.472.
- If the area of the square is 25, then s = √25, or 5.
-
3
Multiply the side length by 4 to find the perimeter. Take the side length s you just calculated and plug it into the perimeter formula, P = 4s. The result will be the perimeter of your square!
- For the square with area 20 and side length 4.472, the perimeter P = 4 * 4.472, or 17.888.
- For the square with area 25 and side length 5, P = 4 * 5, or 20.
Advertisement
-
1
Understand what an inscribed square is. Inscribed shapes come up fairly often on standardized tests like the GMAT and GRE, so it is important to know what they are. A square inscribed in a circle is a square that is drawn inside of the circle, so that all four vertices (corners) lie on the edge of the circle.[7]
-
2
Recognize the relationship between the radius of the circle, and the side length of the square. The distance from the center of an inscribed square to each of its corners is equal to the radius of the circle. To find the length of s, we must first imagine cutting the square in half diagonally to form two right triangles. Each of these triangles will have equal sides a and b and hypotenuse c, which we know is equal to two times the radius of the circle, or 2r.[8]
-
3
Use the Pythagorean Theorem to find the side length of the square. The Pythagorean Theorem states that for any right triangle with sides a and b and hypotenuse c, a2 + b2 = c2. [9]
Since sides a and b are equal (remember, we are still dealing with a square!) and we know that c = 2r, we can write out the equation and simplify the equation to find the side length as follows:- a2 + a2 = (2r)2, now simplify the expressions:
- 2a2 = 4r2, now divide both sides by 2:
- a2 = 2r2, now take the square root of each side:
- a = √(2r2) = √2r. Our side length s for the inscribed square = √2r.
-
4
Multiply the side length of the square by four to find the perimeter. In this case, the perimeter of the square P = 4√2r. The perimeter of any square inscribed in a circle with radius r is defined as P = 5.657r!
-
5
Solve an example equation. Consider a square inscribed in a circle with radius 10. That means that the diagonal of this square = 2(10), or 20. Using the Pythagorean Theorem, we know that 2a2 = 202, so 2a2 = 400. Now divide both sides in half to find that a2 = 200. Then take the square root of each side to find that a = 14.142. Multiply this by 4, and you will find the perimeter of your square: P = 56.57.
- Notice that you could have found the same thing by simply multiplying the radius, 10, by 5.657. 10 * 5.567 = 56.57, but that might be hard to remember on a test, so it’s better to memorize the process we used to get there.
Advertisement
Calculator, Practice Problems, and Answers
Add New Question
-
Question
What is the perimeter of a garden that measures 16.3m x 16.7m?
66 m. The formula for perimeter of a rectangle is 2(l + b).
Hence the perimeter is = 2 x (16.3+16.7) = 2 x 33 = 66 m. -
Question
If I know two sides of a square, how do I calculate the other sides?
One of the fundamental properties of a square is that all sides are equal. This means that if you know just one of its side’s length, you also know all the lengths of the other 3 sides.
-
Question
The four sides of the garden, with fence, measure 10m, 8m, 4m, and 12m respectively. How long is the fence?
Add the sides together.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
The reason why is because a square has 4 sides.
Advertisement
Video
About This Article
Article SummaryX
To calculate the perimeter of a square, multiply the length of one of the sides by 4. If you don’t know the length of the square’s sides but you know the square’s area, start by finding the square root of the area, which is equal to the length of one side. Then, multiply the length of the side by 4 to find the perimeter. To learn how to calculate the perimeter of a square that’s inscribed in a circle, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 791,522 times.
Did this article help you?
В данной публикации мы рассмотрим, каким образом можно посчитать периметр квадрата и разберем примеры решения задач.
-
Формула вычисления периметра
- По длине стороны
- По длине диагонали
- Примеры задач
Формула вычисления периметра
По длине стороны
Периметр (P) квадрата равняется сумме длин его сторон.
P = a + a + a + a
Так как все стороны квадрата равны, формулу можно представить в виде произведения:
P = 4 ⋅ a
По длине диагонали
Периметр (P) квадрата равен произведению длины его диагонали на число 2√2:
P = d ⋅ 2√2
Данная формула следует из соотношения длин стороны (a) и диагонали (d) квадрата:
d = a√2.
Примеры задач
Задание 1
Найдите периметр квадрата, если его сторона равна 6 см.
Решение:
Используем формулу, в которой участвует значение стороны:
P = 6 см + 6 см + 6 см + 6 см = 4 ⋅ 6 см = 24 см.
Задание 2
Найдите периметр квадрата, диагональ которого равняется √2 см.
Решение 1:
С учетом известной нам величины воспользуемся второй формулой:
P = √2 см ⋅ 2√2 = 4 см.
Решение 2:
Выразим длину стороны через диагональ:
a = d / √2 = √2 см / √2 = 1 см.
Теперь, используя первую формулу, получаем:
P = 4 ⋅ 1 см = 4 см.