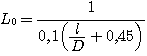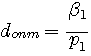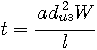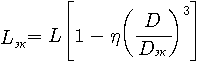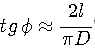Собственная ёмкость — это паразитный параметр катушки индуктивности. Паразитный, но не так, чтобы уж очень: не домашнее животное в виде
таракана, не нежданный гость в виде татарина, а так… мелкий, но важный аспект, требующий учёта и внимания.
Возникновение собственной ёмкости обусловлено наличием ёмкостей между отдельными витками катушки, между витками и сердечником, витками
и экраном, а также витками и близлежащими элементами конструкции. Все эти распределённые ёмкости суммируются и называются собственной
ёмкостью катушки CL.
Паразитная собственная ёмкость всегда подключена параллельно катушке и образует с её собственной индуктивностью параллельный колебательный
контур, резонансная частота которого является частотой собственного резонанса катушки.
Несмотря на кажущуюся простоту, точный расчёт этого параметра — это вовсе: не плёвое дело, не поиск халявы и не комариная плешь, по крайней
мере, практически все отечественные авторы справочной литературы, дружно повернулись спиной к суровой правде бытия, выдавая за истину
теорию, никак не подкреплённую экспериментом.
Для примера приведу выдержку из подобного умного справочника.
Совсем другое дело — буржуйские пытливые умы, преимущественно американской этнической национальности. Эти ребята копают и вглубь и
вширь похлеще азиатских хунвейбинов, восполняя нехватку теоретических обоснований многочисленными практическими экспериментами.
Вот как, к примеру, у них выглядит незамысловатая измерительная приблуда для определения собственной резонансной частоты катушки.
В результате всех этих раскопок из глубины на поверхность была извлечена совсем уж до неприличия простая формула определения собственной
ёмкости катушки:
CL(пф) ≈ 0,5×Dкат(см).
Казалось бы, вот оно — добро пожаловать «за грань добра и зла». Однако не всё так плохо — формула обеспечивает вполне приемлемую
точность вычислений и может быть использована для оценки собственных ёмкостей однослойных конструкций катушек с соотношением
длины намотки к диаметру:
0.5 < Lнам/Dкат < 2.
А как посчитать нам величину собственной ёмкости при другом форм-факторе катушки?
Найти всеобъемлющую формулу, позволяющую рассчитать этот параметр для любых вариаций (включая частотную зависимость) оказалось делом
нереальным — по крайней мере мне этого сделать не удалось. Поэтому самым простым и точным методом, позволяющим оценить собственную
ёмкость катушки, я посчитал интерполяцию графика экспериментальной зависимости, полученной англичанином R.G.Medhurst-ом, в лаборатории
компании General Electric.
По шкале X — отношение длины к диаметру катушки;
По шкале Y — коэффициент H, равный отношению собственной ёмкости к диаметру катушки;
Шкала зависимости — логарифмическая.
Формула значения собственной ёмкости катушки в данном случае выглядит следующим образом:
CL(пф) = H×Dкат(см).
Зависимость снята для однослойных бескаркасных катушек в диапазоне частот, находящихся ниже частоты собственного резонанса катушки.
В этом же источнике приведена и удобная таблица, отражающая изменение коэффициента H в зависимости от форм-фактора катушки.
И, как результат — формула, позволяющая с 2-3% точностью описать полученные экспериментальные зависимости:
H = 0,1126×L/D+0,08+0,27/√L/D.
Это то, что касается бескаркасных катушек. При наличии гладкого каркаса расчётная ёмкость изделия увеличится на величину
≈10×ε (%), где ε — относительная
диэлектрическая проницаемость материала каркаса. Для катушек, намотанных на каркасах с нарезкой для фиксации витков, коэффициент
увеличения ёмкости уже может составлять величину ≈20×ε (%).
И в завершении мероприятия просуммируем вышеизложенные идеи калькулятором.
ТАБЛИЦА РАСЧЁТА ЗНАЧЕНИЯ СОБСТВЕННОЙ ЁМКОСТИ БЕСКАРКАСНОЙ КАТУШКИ.
Будьте внимательны — в качестве значения межвиткового расстояния принято считать расстояние между центрами соседних витков,
а не зазор между ними, поэтому данное расстояние никак не может быть меньше величины диаметра провода.
|
Диаметр катушки (мм) |
|
|
Количество витков обмотки |
|
|
Диаметр обмоточного провода (мм) |
|
|
Расстояние между витками (мм) |
|
Длина намотки катушки (мм) |
|
Собственная ёмкость катушки (пФ) |
Значение собственной ёмкости многослойной катушки значительно больше и может достигать нескольких десятков пФ.
Здесь, помимо всего прочего, вступают в сложное взаимодействие и ёмкости между соседними витками, и ёмкости между слоями, и разные другие
факторы, значительно усложняющие структуру длинной линии, описывающей свойства моточного изделия.
Наверно по этой причине никто никому и не выносит мозг, все отдыхают на расслабоне. Формул — нет!
Или я чего-то пропустил в этой жизни…
Is there, I ask, can there be, a more interesting study than that of alternating currents
Никола Тесла
О собственной емкости однослойной катушки индуктивности
На высоких частотах катушку индуктивности корректнее представлять в виде длинной однопроводной линии передачи, свернутой в спираль. Как известно, такая линия представляет собой структуру с распределенными по ее длине индуктивностью и емкостью. Когда длина такой линии равна λ/4 (λ — длина электромагнитной волны в катушке), она находится в резонансном режиме и частота, соответствующая этой длине волны называется частотой собственного резонанса катушки. Катушки очень редко работают на частотах близких к собственному резонансу или выше его. Однако если это происходит, например в ВЧ дросселях, расчет такой катушки желательно вести в ВЧ электромагнитных симуляторах.

В процессе развития радиотехники неоднократно были предприняты попытки подобрать эмпирическую формулу для расчета собственной емкости. В разных справочниках можно найти разные формулы, от разных авторов, но чаще даже без указания источника. Какая же из этих формул более точная и правильная? Попробуем разобраться…
- Начнем с того, что впервые проблему собственной емкости катушки поднял J. C. Hubbard в 1917 году. S.Butterworth, известный всем новатор и дизайнер схем частотной фильтрации (вспомните фильтры Баттерворта) в 1926 году предложил свою формулу расчета, но она имела серьезные ограничения и не могла рассчитывать короткие катушки.(Что имеется ввиду под термином «короткие», читайте в статье, посвященной добротности)
- Примерно в тоже время был предложен способ определения собственной емкости катушки с помощью косвенного измерения. Измеряются две резонансные частоты контура с двумя разными внешними конденсаторами и затем по результатам измерений вычисляется как собственная емкость катушки, так и ее индуктивность. Вот онлайн калькулятор реализующий этот метод. Способ точный (но не абсолютно, далее станет понятно почему…). Однако он требует наличия измерительных приборов. Кроме того, так можно определить собственную емкость уже готовой катушки, а нам желательно оценить этот параметр еще на стадии разработки конструкции.
-
Формула, предложенная инженером A. J. Palermo в 1934 году в работе «Distributed Capacity of Single-Layer Coils»:
Cs = f * D
f = 2 π / arccosh (p / d)[1] - Сs — собственная емкость (пФ);
- D — диаметр катушки (см);
- p — шаг намотки (см);
- d — диаметр провода (см);
Довольно часто встречается в различных справочниках (например «Колебательный контур Скрипников 1970»), однако как показал дальнейший опыт формула не верна!
Палермо представлял катушку в виде электростатической структуры, в которой собственная емкость получалась как последовательная сумма емкостей между соседними витками. Логичный вывод — раздвигая витки мы уменьшаем эту суммарную емкость.
Несмотря на кажущуюся очевидность и наглядность, эта модель катушки неверна. Основное заблуждение заключается в том, что катушка представляется как структура связанная с магнитным полем. Такой подход ведет свою историю еще с изучения соленоидов с постоянным током. Помните пресловутые опилки, показывающие силовые линии? Распределение электрического поля вдоль провода катушки в этом случае пытаются рассматривать с таким же подходом — как электростатическое поле, независимое от магнитного. При этом забывается, что на высоких частотах вокруг катушки существует электромагнитное поле — единая сущность, в которой векторы электрического и магнитного полей всегда перпендикулярны, электрическая и магнитная компоненты этого поля не могут существовать независимо друг от друга.
Поскольку магнитные силовые линии идут в основном вдоль оси катушки, электрический вектор волны расположен почти перпендикулярно к оси, а компонента электрической составляющей поля, параллельная оси (между витками) практически не заметна, а как раз именно она соответствует межвитковой емкости, ведь как мы знаем — емкость характеризуется электрическим полем.
Да и почему катушка разбивается в этой модели на элементарные витки? Почему не на меньшие или большие части? Зачем городить огород, когда есть готовая теория цепей с распределенными параметрами. -
Формула G.Grandi, опубликована в работе «Stray Capacitances of Single-Layer Solenoid Air-Core Inductors — Grandi, Kazimierczuk, Massarini and Reggiani 1999»:
Cs = ε0 π2 D /
((N-1) ln{ ( p/d ) + √[ ( p/d )2 — 1 ] })[2] - N — число витков катушки;
- ε0 — диэлектрическая постоянная;
- D — диаметр катушки (см);
- p — шаг намотки (см);
- d — диаметр провода (см).
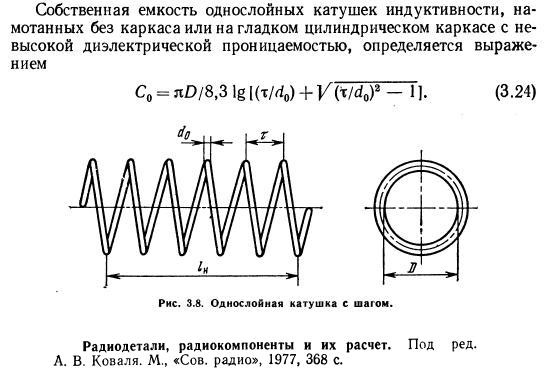
Это была попытка современной реанимации электростатической модели катушки, которая, как показано в случае с формулой Палермо, далека от действительной картины. Это — яркий пример, когда «бумажная» теория не проверяется экспериментом и тем не менее выдается за истину. Из формулы следует вывод: чем больше витков имеет катушка, т.е чем длиннее она — тем меньше паразитная емкость, что абсолютно противоречит практике. Также можно найти в справочниках, например «Радиодетали, радиокомпоненты и их расчет Коваль 1977».
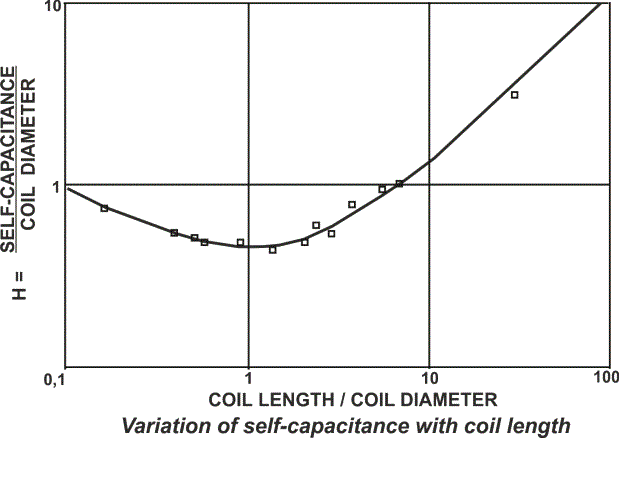
В 1947 году радиоинженер R.G.Medhurst — сотрудник исследовательской лаборатории компании «General Electric Co.Ltd.» опубликовал ряд работ, связанных с экспериментальными исследованиями катушек индуктивности. В результате тщательных измерений паразитной емкости большого количества катушек, Medhurst пришел к выводу, что собственная емкость катушки слабо зависит от шага намотки и модель Палермо не работает. В свою очередь Medhurst обнаружил зависимость емкости от форм-фактора катушки (отношения длины намотки к ее диаметру l/D). На основании своих измерений Medhurst предложил свою полу-эмпирическую формулу:
- D— диаметр катушки (см);
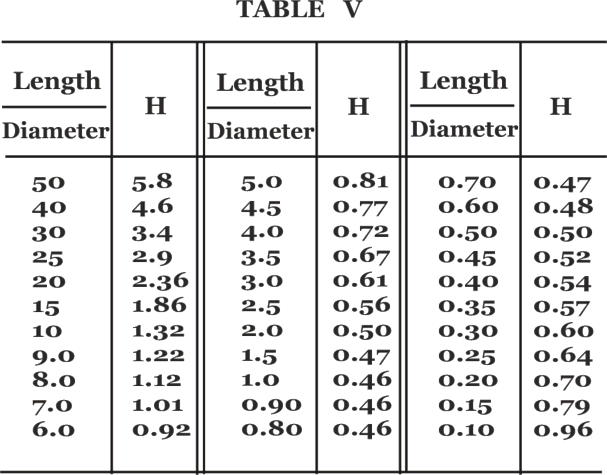
- H — коэффициент, характеризующий форм-фактор катушки, был представлен в виде таблицы:
| l/D | H | l/D | H | l/D | H |
|---|---|---|---|---|---|
| 50 | 5.8 | 5 | 0.81 | 0.7 | 0.47 |
| 40 | 4.6 | 4.5 | 0.77 | 0.6 | 0.48 |
| 30 | 3.4 | 4 | 0.72 | 0.5 | 0.50 |
| 25 | 2.9 | 3.5 | 0.67 | 0.45 | 0.52 |
| 20 | 2.36 | 3 | 0.61 | 0.4 | 0.54 |
| 15 | 1.86 | 2.5 | 0.56 | 0.35 | 0.57 |
| 10 | 1.32 | 2 | 0.50 | 0.3 | 0.60 |
| 9 | 1.22 | 1.5 | 0.47 | 0.25 | 0.64 |
| 8 | 1.12 | 1 | 0.46 | 0.2 | 0.70 |
| 7 | 1.01 | 0.9 | 0.46 | 0.15 | 0.79 |
| 6 | 0.92 | 0.8 | 0.46 | 0.1 | 0.96 |
Это просто данные реальных измерений. В последующем и самим Медхерстом и после него предлагались разные формулы, аппроксимирующие эти данные.Однако более известна самая простая формула для оценки собственной емкости катушек, которую предложил сам Медхерст:
- Cs — собственная емкость [пФ];
- D — диаметр катушки [см];
Формулу [4] вполне можно применять на практике для оценки собственной емкости большинства практических конструкций катушек на гладких полистироловых каркасах.
Или еще проще — собственная емкость однослойной катушки в пФ численно приблизительно равна радиусу намотки в см.
Только надо помнить, что это справедливо при 0.5 < l/D < 2, в противном случае надо брать коэффициент из таблицы. Как видим в формуле нет упоминаний о шаге намотки.
Измерения Медхерста неоднократно подтверждались в последующем, при этом использовались разные измерительные стенды и разные методы. К слову сказать Медхерст проводил измерения паразитной емкости катушки методом двух частот, о котором я упомянул выше. Однако он был в плену модели катушки, основанной на теории сосредоточенных элементов и не смог объяснить результаты своих лабораторных измерений.
В настоящее время сформировалось три подхода в понимании природы собственной емкости катушки:
- Теоретическая школа основанная на концепции электростатической межвитковой емкости. Для расчетов этой емкости используются формулы Палермо и Гранди. Как показано выше, эта школа ошибочна.
- Существует как бы компромиссный подход, в котором принимаются во внимание данные из таблицы Медхерста, однако наличие емкости между соседними витками не отрицается. Этот подход можно встретить в книге — «Детали контуров радиоаппаратуры, расчет и конструкция. В.А.Волгов 1954г.». Там используется такая формула:
Коэффициенты k и k1 приводятся в виде графиков. Анализ этих графиков показывает, что коэффициент k формулы Волгова соответствует коэффициенту f в формуле [1] Палермо, а коэффициент k1 пропорционален 2*H в формуле [3] Медхерста. Этот «симбиоз» призван подтвердить наличие емкости между витками. Но как показали эксперименты Медхерста, коэффициент k — ложный. Ниже приведен график из работы Медхерста. Кривая Палермо соответствует коэффициенту f в формуле [1] или k в формуле [5], а данные Медхерста — данные экспериментальных измерений.
Волгов делает отступление, говоря что упрощенно можно считать по формуле Cs≈0,5*D. Но какое может быть упрощение, если коэффициент k меняется в его формуле [5] в десятки раз при раздвигании витков! Это просто неявный отказ от коэффициента k и статической межвитковой емкости с ним связанной.
- Наиболее полной современной работой, посвященной паразитной собственной емкости катушки, является статья «The self-resonance and self-capacitance of solenoid coils Dr. David W Knight 2013» (G3YNH)
Приведу несколько цитат из этой работы:Существует даже школа мысли, которая говорит, что собственная емкость катушки обусловлена емкостью между соседними витками, и, хотя это отчасти верно для многослойных катушек, гипотеза оказывается безнадежно неверной моделью реактивного сопротивления однослойных катушек…
Решение, конечно, заключается в признании, что катушка — это линия передачи, с той лишь разницей, что решение вопроса в случае свернутой линии оказывается довольно сложным…
Тривиальные измерения подтверждают, что собственный резонанс катушки связан с общей длиной проводника. Поэтому странно, что собственная емкость однослойных катушек до сих пор обычно соотносится со статической емкостью которая предположительно существуют между соседними витками…
Дэвид Найт в своей работе усовершенствует довольно упрощенную эмпирическую формулу Медхерста. Ведь по сути, нам необходимо найти электрическую длину длинной линии, а она зависит от длины проводника, которым намотана катушка. А длина проводника, в свою очередь, зависит не только от диаметра и длины намотки, но также от шага намотки и числа витков. В программе Coil64 реализован расчет собственной емкости однослойной катушки, основанный на работе Девида Найта без учета влияния каркаса. Подразумевается, что катушка работает на частоте много ниже частоты собственного резонанса и является бескаркасной. Приближенно можно считать, что наличие каркаса увеличивает емкость по сравнению с расчетной на 15..30%, каркас с канавками под провод увеличивает емкость до 40%, пропитка и обволакивание катушки лаком или клеем увеличивает емкость до 50% и выше.

Понятие собственной емкости напрямую соотносится с частотой собственного резонанса катушки. Однако при рассмотрении физических процессов в однослойной катушке на частотах близких к частоте ее собственного резонанса необходимо отказаться от модели сосредоточенных элементов как несостоятельной и рассматривать катушку как линию передачи.
У обычной, «прямолинейной» линии передачи с малыми потерями, такие ее параметры, как погонная емкость и погонная индуктивность зависят исключительно от ее геометрии. В спиральной же линии, из-за влияния витков друг на друга, эти параметры являются кроме того еще и функцией частоты. Это обстоятельство приводит к таким важным последствиям:
- Резонансные частоты такой линии хотя и жестко связаны с общей длиной проводника, которым намотана катушка, однако не кратны друг другу.
- Собственная емкость катушки зависит от частоты на которой ее определяют. На низких частотах это одна величина, на частотах близких к собственному резонансу катушки — другая. Пренебречь влиянием частоты и вести речь о расчете собственной емкости катушки имеет смысл только тогда, когда катушка работает на частотах не превышающих 60-70% от частоты ее собственного резонанса. Справедливости ради надо отметить, что это относится и к расчету индуктивности! Ведь формулы расчета и того и другого основаны на предположении, что плотность тока во всех витках одинакова, что не имеет место при резонансе.
- На частотах много ниже частоты первого резонанса можно для упрощения пользоваться моделью катушки из сосредоточенных элементов. Однако стоит не забывать, что собственная емкость в таком случае — это не статическая межвитковая емкость, а интегральная погонная емкость длинной линии и зависит от длины и формы намотки проводника. Именно эту «низкочастотную» величину собственной емкости вы можете видеть в результатах расчета Coil64. Использовать ее для расчета собственного резонанса катушки нельзя по причине, о которой говорилось выше.
Каким же образом геометрия катушки влияет на ее собственную емкость? («низкочастотную»)
- Собственная емкость однослойной катушки при условии l/D ≈ 0,5…2 прямо пропорциональна ее диаметру.
- Оптимальной катушкой в плане паразитной емкости (емкость — минимальна), является катушка с l/D ≈ 1 при шаге намотки близком к удвоенному диаметру провода. При намотке виток к витку оптимальный форм-фактор катушки l/D ≈ 0,5.
- Как показано выше, увеличение шага между витками практически не оказывает влияния на величину собственной емкости. Изменяя шаг намотки, мы прежде всего меняем индуктивность катушки, а не ее собственную емкость. Это происходит от того, что соседние витки взаимодействуют друг с другом преимущественно через магнитное поле, а не через электрическое. Общая длина провода, которая определяет величину собственной емкости, при простом раздвигании витков не меняется.
Можно также отметить следующие моменты:
- Наличие диэлектрика рядом с проводом катушки, будь то изоляция провода, каркас, клей, компаунд, меняет параметры длинной линии (погонная емкость, волновое сопротивление, коэффициент укорочения), что эквивалентно изменению собственной емкости катушки. Наличие близлежащих деталей конструкции или экрана оказывает подобный эффект.
- Широко применявшийся ранее метод намотки дросселя с прогрессивным шагом, основанный на электростатической модели катушки, абсолютно бесполезен в плане уменьшения его собственной емкости. Об этой, не имеющей смысла технологии намотки ВЧ дросселей упоминается даже в Википедии в разделе «Конструкция», что говорит о преобладании электростатической модели катушки в массовом сознании радиолюбителей и специалистов в области радиотехники. Справедливости ради стоит отметить, что «прогрессивная» намотка имеет смысл только для уменьшения вероятности межвиткового пробоя дросселя, работающего в режиме с большим градиентом напряжения вдоль его длины.
- Шаг намотки слабо влияет на паразитную емкость катушки, но за счет эффекта близости является существенным фактором, влияющим на добротность, поэтому, например в случае контурных катушек, им пренебрегать нельзя. Часто встречается утверждение, что пресловутая межвитковая емкость обуславливает уменьшение добротности. Хочу акцентировать внимание, что эффект близости, уменьшающий добротность катушки, обусловлен взаимодействием ВЧ тока с магнитным полем от соседних витков и никак не связан с «межвитковой емкостью», которая характеризуется электрическим полем. Конечно же добротность катушки взаимосвязана с ее собственной емкостью, но никак не со статической емкостью между соседними витками.
- Все вышесказанное относится прежде всего к однослойным катушкам. У многослойных катушек статическая компонента собственной емкости (между слоями намотки) становится уже заметной.
У прочитавшего эту статью анонима возникает резонный вопрос. Если собственная емкость однослойной катушки — это не емкость между соседними витками, то тогда между чем и чем? В классической теории длинных линий, для линии из двух проводов мы можем ответить на подобный вопрос, потому что конфигурация электрических силовых линий переменного поля TEM-волны и электростатического поля в такой линии совпадают. В спиральной однослойной катушке распространяются поверхностные TE и TM волны, для которых такого совпадения не существует и поэтому сама постановка вопроса «где конденсатор?» бессмысленна. Никто ведь не ищет никаких виртуальных конденсаторов, например, в круглом волноводе или линии Зоммерфельда. Строго говоря, мы можем вести речь только о входном импедансе спиральной линии, который на низкой частоте (до первого резонанса) имеет только две составляющие — активную и индуктивную. Понятие о собственной емкости катушки появляется тогда, когда из этого импеданса мы вычтем индуктивное сопротивление, рассчитанное для идеальной катушки, у которой конфигурация магнитного поля совпадает с полем соленоида на нулевой частоте без учета волновых эффектов. Другими словами, отрицательную реактивность, возникающую при такой разности, можно считать ассоциированной не с физической емкостью, а просто математической коррекцией на волновые эффекты при расчете идеальной сосредоточенной индуктивности. Подробнее об этом по ссылке [3]. Мы называем эту отрицательную реактивность собственной емкостью в силу исторических причин, о которых шла речь выше, а также для удобства расчетов, но нужно понимать, что ей не соответствует никакая статическая емкость. Можно конечно поискать виртуальные «плавающие» конденсаторы в спиральном волноводе с помощью понятия поверхностного импеданса или привлекая к делу таких «сферических коней в вакууме», как емкость на бесконечно удаленную землю, но этот подход никак не приведет нас к пресловутой электростатической «межвитковой емкости». Ну это уже ахинея какая то! Если емкость — это не емкость, а математическая коррекция, то как же без нее происходит собственный резонанс в катушке? Скажет удивленный читатель. Да не нужна она для объяснения собственного резонанса однослойной катушки. Точно также, как не нужно искать никакую сосредоточенную емкость, чтобы объяснить объемный резонанс в полом волноводе. Более того, как мы уже отметили, если мы будем рассчитывать собственную резонансную частоту катушки по формуле Томсона, взяв за основу индуктивность и «собственную емкость» соленоида на рабочей частоте, мы получим неверный результат. Подробнее см. ссылку [4].
Литература по теме:
- Filters and an Oscillator Using a New Solenoid Model, Randy Rhea, Applied Microwave & Wireless, Nov 2000,p30-42.
- EM Wave Propagation on Helical Conductors, S Sensiper, Tech. Report No. 194, May 1951, MIT Research Lab. of Electronics.
Ссылки:
- Моделирование анодного дросселя как распределенной структуры — И.Гончаренко 2007-2012
- Паразитные резонансы в катушке П-контура — И.Гончаренко
- Высокочастотные катушки, винтовые резонаторы и увеличение напряжения из-за когерентных пространственных мод 2001г. (Оригинал статьи здесь)
- Собственный резонанс однослойной катушки индуктивности.
- Расчет параметров однослойной катушки индуктивности в электромагнитном симуляторе ANSYS HFSS;
Индуктивность является основным
параметром катушки индуктивности. Ее
величина (мкГн) определяется соотношением
|
L=L0W2 |
(2.28) |
где W —
число витков, D —
диаметр катушки в см, L0
— коэффициент, зависящий
от отношения длины катушки / к ее диаметру
О.
Для однослойных катушек
величина L0
определяется соотношением
|
|
(2.29) |
Оптимальными в этом случае
являются отношение
а диаметр катушки в пределах от 1 до 2
см. При расчете диаметр катушки D
принимается равным диаметру каркаса
D0
Для многослойных катушек
величина L0
зависит не только
от величины 1/D
, но и от отношения толщины намотки t к
диаметру катушки D. Она определяется по
графикам (рис.2.24). В этом случае внешний
диаметр катушки D=D0
+ 2t
При расчете катушки
индуктивности предварительно задаются
геометрическими размерами катушки и
определяют коэффициент L0,
а затем по заданной величине индуктивности
L
находят число витков:
|
|
(2.30) |
где I, —
в мкГн , D —
в см.
Для намотки катушки обычно
применяют провод оптимального диаметра,
который рассчитывается с помощью
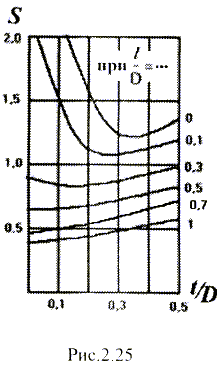
эмпирических формул и графиков. Для
этого по графику S=f(t/D;l/D)
(рис.2.25) находят вспомогательный
коэффициент S. Затем
рассчитывают коэффициент
|
|
(2.31) |
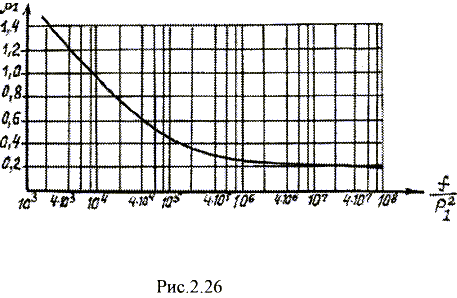
где f -в
мкГц , D — в см. Затем рассчитывают
коэффициент 1
где f
— частота в Гц. После чего по
графикуf(рис.
2.26) находят вспомогательный
коэффициент
и расчитывают оптимальный диаметр
провода (мм)
|
|
(2.32) |
Полученное значение
округляется до ближайшего стандартного
значения (табл.2.6) и выбирается марка
провода с диаметром dиз
После выбора оптимального
диаметра провода проверяют возможность
размещения обмотки в заданных размерах
l
и t.
Для однослойных катушек рассчитывают
шаг намотки
|
|
(2.33) |
Если dиз;
то обмотка размещается. В противном
случае задаются большей величиной
l и
повторяют расчет.
Для многослойных катушек рассчитывают
толщину обмотки
|
|
(2.34) |
где а —
коэффициент неплотности обмотки ( =
1,05…1,3), и находят фактическое значение
наружного диаметра катушки D=D0+2t.
Если эта величина
отличается от выбранной в начале расчета
более чем на 10%, то задаю тся новыми
значениями l и
t и расчет повторяют.
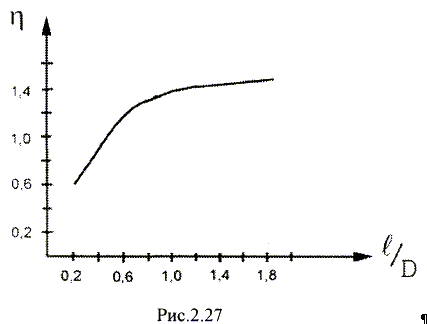
При помещении катушки в экран индуктивность
катушки уменьшается
|
|
(2.35) |
где
— коэффициент, зависящий
от отношения l/D
(рис.2.27),
D —
диаметр катушки,
Dэк-диаметр
экрана.
Индуктивность уменьшается
тем больше, чем меньше диаметр экрана.
В большинстве случаев Dэк/D
При
этом индуктивность уменьшается не более
чем на 20%.
Многослойные катушки обычно выполняют
с сердечниками броневого типа, при
использовании которых большая часть
силовых линий магнитного поля катушки
замыкается через сердечник, а меньшая-через
воздух, вследствие чего влияние экрана
на индуктивность катушки значительно
ослабляется.
Применение сердечников из
магнитных материалов позволяет уменьшить
число витков катушки индуктивности и
соответственно ее габариты. Основным
параметром сердечника является магнитная
проницаемость сПри
его наличии индуктивность катушки
становится равной
|
Lc |
(2.36) |
Поскольку в расчетные формулы входят
эмпирические коэффициенты, то индуктивность
изготовленной катушки отличается от
расчетной. Применение подстроечных
магнитных сердечников позволяет получить
требуемое значение индуктивности.
Собственная емкость является
паразитным параметром катушки
индуктивности, ограничивающим возможности
ее применения. Ее возникновение
обусловлено конструкцией катушки
индуктивности: емкость существует между
отдельными витками катушки, между
витками и сердечником, витками и экраном,
витками и другими элементами конструкции.
Все эти распределенные емкости можно
объединить в одну, называемую собственной
емкостью катушки CL
Наименьшей собственной емкостью обладают
однослойные катушки индуктивности
Приближенно она рассчитывается по
формуле (пФ)
|
СL |
(2.37) |
где D —
диаметр катушки в см. Обычно она не
превышает 1-2пФ.
Собственная емкость
многослойных катушек значительно
больше. При многослойной рядовой намотке
она достигает ЗОпФ; при намотке „внавал»
она несколько меньше. Существенное
уменьшение емкости многослойных катушек
достигается при использовании
универсальной обмотки, при выполнении
которой провод укладывается под некоторым
углом к образующей цилиндрического
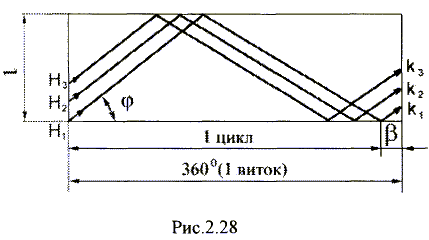
каркаса. Схема такой намотки показана
на рис.2.28. Как только провод доходит до
края катушки, направление укладки
меняется. Цикл универсальной обмотки
выбирается таким, что, совершив один
оборот вокруг каркаса, провод возвращается
к
положение, отличающееся от исходного
на угол.
Этот угол выбирается таким, чтобы каждый
последующий виток находился рядом с
предыдущим.
Очевидно, что
|
|
(2.38) |
Угол ,
под которым осуществляется укладка
провода, находится из соотношения
|
|
(2.39) |
где l-осевая
длина катушки,
D — диаметр витка.
Наименьшее значение угла
получается для витков, имеющих наименьший
диаметр, равный диаметру каркаса D0.
Обычно при использовании
универсальной обмотки длину катушки
принимают в пределах от 2 до 10мм. Количество
циклов намотки связано с рачетнным
числом витков W
соотношением
|
|
(2.40) |
Величина собственной емкости катушек
с универсальной обмоткой составляет
от 3 до 8пФ. Дополнительное снижение
емкости достигается серкцонированием
обмотки, как показано на рис.2.21,в.
Совместное действие индуктивности и
емкости можно учесть введением понятия
об эквивалентной индуктивности катушки,
определяемой из уравнения
откуда
|
|
(2.41) |
где
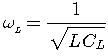
резонансная частота катушки индуктивности.
Если рабочая частота много
ниже собственной резонансной частоты
L,
то приближенно можно считать Lэ=L.
В процессе работы на катушку
действуют различные внешние
факторы:температура, влага и другие,
влияющие на ее индуктивность.Наиболее
существенным является влияние температуры,
которое оценивают температурным
коэффициентом
.
Температурная нестабильность индуктивности
обусловлена целым рядом факторов: при
нагреве увеличивается длина и диаметр
провода обмотки, увеличивается длина
и диаметр каркаса, в результате чего
изменяются шаг и диаметр витков; кроме
того при изменении температуры изменяются
диэлектрическая проницаемость материала
каркаса, что ведет к изменению собственной
емкости катушки.
Для повышения температурной
стабильности применяют каркасы из
материала с малым значением коэффициента
линейного расширения. Этим требованиям
в наибольшей степени удовлетворяет
керамика. Повышению температурной
стабильности катушек способствует
прочное сцепление обмотки с каркасом.
С этой целью обмотку выполняют методом
вжигания серебра в керамический каркас.
В этом случае изменение размеров
токопроводящего слоя определяется
только линейным расширением каркаса.
Такие катушки индуктивности имеют
TKL Стабильность
многослойных катушек существенно хуже,
так как в них невозможно избежать
изменения линейных размеров провода
обмотки. Многослойные катушки имеют
TKL
(50-100).10-6
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вс июн 19, 2016 12:52:58
Имеется в виду, что надо намотать соленоид, который бы вместил ( в виде тока)
Заряд конденсатора заданной емкости
Всем заранее спасибо
Вс июн 19, 2016 13:48:38
Coil: программа для расчета параметров и магнитного поля цилиндрического соленоида:
активное сопротивление, индуктивность, потребляемый ток, рассеиваемая мощность,
магнитная индукция в центре и в заданной точке пространства
к примеру..
зы
как там форум » MATRI-X» поживает?
Вс июн 19, 2016 14:29:25
Maykill,
спасибо, программу посмотрю
А кто такой матрикс?
Вс июн 19, 2016 14:44:02
ну значит тёзка ваш
обознатушки
Вс июн 19, 2016 15:02:18
Программу посмотрел.
Там не совсем то. Точнее совсем не то
Мне надо не емкость контура( т.е емкость кондера), а емкость соленоида
Вс июн 19, 2016 15:09:34
а ЁМКОСТЬ индуктивности существует?
Как параметр…?
Вс июн 19, 2016 15:23:18
Тоже стало интересно.
А как понимать фразу: «вместил заряд конденсатора заданной емкости»? Переживаете что не вся энергия войдет в катушку и часть останется в конденсаторе?
Вс июн 19, 2016 15:36:01
может он про ДЖОУЛИ?
тогда понятно
Вс июн 19, 2016 16:42:50
Не, ребята
Я про кулоны
А емкость имеет даже отрезок провода
Если слышали про бифиляр ( спец. намотка такая) так вот он отличается высокой электрической емкостью
В МЯУ перенес.
Бифилярная намотка(встречно намотанная катушка с последовательным соединением) используется тогда, когда по каким-то причинам надо создать катушку с минимальной, близкой к нулевой индуктивностью.
Бифилярная намотка часто используется в электротехнике как способ создания проволочного резистора с незначительной паразитной индуктивностью и т.д.
Все остальные свойства подобных катушек, как например создание ударных эфирных волн или получение пульсирующего повышенного давления эфира и прочее, осуждается только в соответствующем разделе, т.е. в МЯУ.
aen
Вс июн 19, 2016 16:51:22
мда…
оффсянка
http://vitanar.narod.ru/katuschki/katuschki.html
«Если бифилярные катушки намотать на концах ротора в форме свастики, то соединив их параллельно и подавая на них ток любой направленности и формы – синус, импульсы и т.д., можно между витками катушки получить пульсирующее повышенное давление эфира. И, значит, при определенных параметрах катушек и подаваемого тока можно заставить свастику вращаться вокруг оси, проходящей через центр свастики»
Вс июн 19, 2016 17:01:07
Если слышали про бифиляр ( спец. намотка такая) так вот он отличается высокой электрической емкостью
Бифиллярная намотка призвана избавить катушку от её индуктивности.
На ёмкость она вообще не влияет.
Вс июн 19, 2016 17:07:35
inimmid писал(а):Если слышали про бифиляр ( спец. намотка такая) так вот он отличается высокой электрической емкостью
Бифилярная намотка — это намотка катушки в два провода. Про энергетическую ёмкость — ни слова.
Вс июн 19, 2016 17:28:06
Может быть, чем считать, проще померить тестером в режиме «Измерение емкости», включив последовательно заведомо намного большей емкости конденсатор ?
Вс июн 19, 2016 17:29:21
inimmid писал(а):Не, ребята
Я про кулоны
А емкость имеет даже отрезок провода
Если слышали про бифиляр ( спец. намотка такая) так вот он отличается высокой электрической емкостью
Следующий Ваш логический шаг, любезный, логично же перенесет Вашу тему в МЯУ.
Патамушта ту ахинею, которую Вы тут начали нести, более нигде не прописывают.
Под емкостью уединенного проводника понимают его емкость относительно бесконечно удаленной проводящей сферы.
Абстракция такая.
Катушка в параллельном колебательном контуре имеет ту же самую разность потенциалов на своих выводах, что и присоединенный к ней конденсатор. В любой момент времени. В любой фазе колебательного процесса. То есть ЛЮБАЯ катушка, любой НЕНУЛЕВОЙ индуктивности с НЕНАСЫЩАЕМЫМ сердечником (например воздушным или деревянным) может «поместить в себя» всю энергию ранее заряженного конденсатора любой емкости. То есть в тот момент колебательного процесса, когда на конденсаторе будет НУЛЕВАЯ разность потенциалов (он будет не заряжен), в катушке будет наблюдаться максимальное значение тока. Активным сопротивлением катушки в этом нашем обсуждении пренебрегаем. Как и активным сопротивлением обкладок конденсатора и его утечкой.
То есть проблема «умещения заряда конденсатора в катушке» состоит лишь в выборе сечения намотанного на нее провода, чтобы она тупо не сгорела, а так же выбора сердечника, который не насытится при той напряженности магнитного поля, которую создал ток через эту катушку.
Последний раз редактировалось КРАМ Вс июн 19, 2016 17:42:00, всего редактировалось 1 раз.
Вс июн 19, 2016 17:37:11
если увязать сию катушку с предыдущей темой (схемой)….кое-что начинаю понимать
пока промолчу
Вс июн 19, 2016 17:46:53
Ежели в «той схеме» катушку намотать биффилярно, то ключ будет разряжать оба конденсатора ОДНОВРЕМЕННО и АПЕРИОДИЧНО (пренебрегаем сопротивлением катушки) с постоянной времени и начальным током определяемым сопротивлением резистора в «этой схеме». То есть если катушка — биффиляр, то ее можно заменить простым проводником.
Вс июн 19, 2016 18:19:38
КРАМ писал(а):Следующий Ваш логический шаг, любезный, логично же перенесет Вашу тему в МЯУ.
Патамушта ту ахинею, которую Вы тут начали нести, более нигде не прописывают.
Любезный КРАМ, что это вы так возбудились?. Вас это не красит.
А мне даже страшно становится вопросы задавать таким горячим парням
Однако,вы меня подтолкнули к методике решения той задачи, которую я сформулировал в названии темы.
Через магнитный поток
Еще раз спасибо.
Остальным спасибо также
Вс июн 19, 2016 18:21:59
Я не девушка, чтобы возбуждаться, любезный.
Я просто предупредил Вас о последствиях, если только они не есть Ваша цель.
Такшта не надо мне хамить.
Тем более, что я подробно ответил на Ваш вопрос.
А определение Вашего первого вопроса как ахинеи — это констатация факта, который Вы в общем то и признали.
ЗЫ. Рискну предположить, что о магнитном потоке у Вас примерно такое же представление, как и об электрической емкости катушки… Удачи…
Вт июн 21, 2016 22:27:11
Maykill писал(а):а ЁМКОСТЬ индуктивности существует?
Как параметр…?
Вообще то существует, как ни странно. Подразумевается межвитковая емкость. Иногда её и учитывают при расчетах. Например: выходной трансформатор лампового УНЧ.
А что Автор хочет, хрен его знает. Емкость то измерить не трудно: наливаешь пива…до краев…..
Ср июн 22, 2016 09:13:52
Да,Бригадир,
я тоже уже нашол
Паразитная емкость и собственный резонанс
Межвитковая паразитная емкость проводника в составе катушки индуктивности превращает катушку в сложную распределенную цепь. В первом приближении можно принять, что реальная катушка представляет эквивалентно собой идеальную индуктивность с параллельно присоединенным ей конденсатором паразитной емкости. В результате этого катушка индуктивности представляет собой колебательный контур с характерной частотой резонанса. Эта резонансная частота легко может быть измерена и называется собственной частотой резонанса катушки индуктивности. На частотах много ниже частоты собственного резонанса импеданс катушки индуктивный, при частотах вблизи резонанса в основном активный (на частоте резонанса чисто активный) и большой по модулю, на частотах много выше частоты собственного резонанса — ёмкостной. Обычно собственная частота указывается изготовителем в технических данных промышленных катушек индуктивности, либо в явном виде, либо косвенно — в виде рекомендованной максимальной рабочей частоты.
На частотах ниже собственного резонанса этот эффект проявляется в падении добротности с ростом частоты.
Для увеличения частоты собственного резонанса используют сложные схемы намотки катушек, разбиение одной обмотки на разнесённые секции.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





 Существует даже школа мысли, которая говорит, что собственная емкость катушки обусловлена емкостью между соседними витками, и, хотя это отчасти верно для многослойных катушек, гипотеза оказывается безнадежно неверной моделью реактивного сопротивления однослойных катушек…
Существует даже школа мысли, которая говорит, что собственная емкость катушки обусловлена емкостью между соседними витками, и, хотя это отчасти верно для многослойных катушек, гипотеза оказывается безнадежно неверной моделью реактивного сопротивления однослойных катушек…