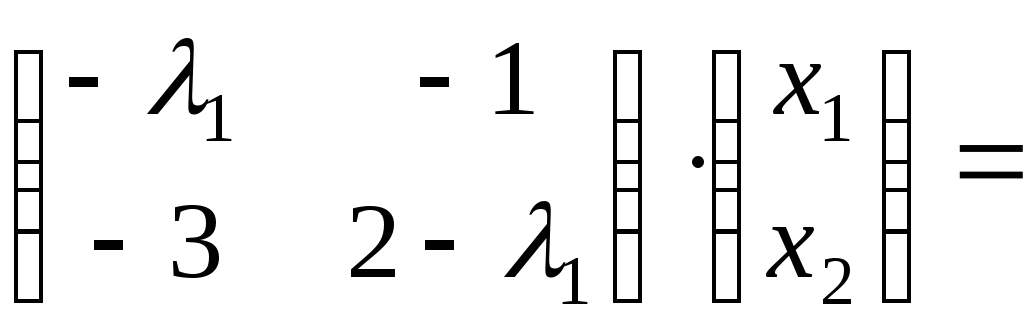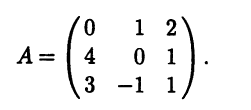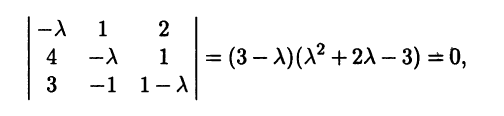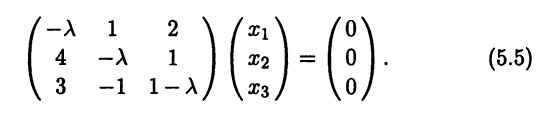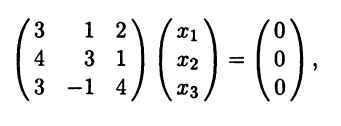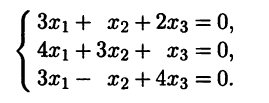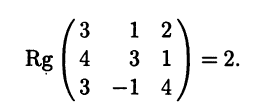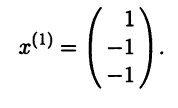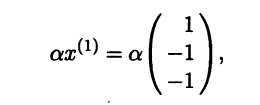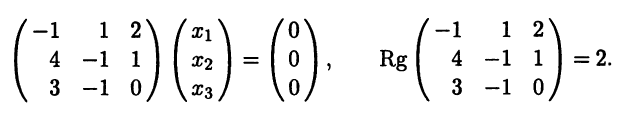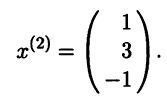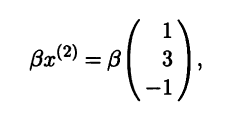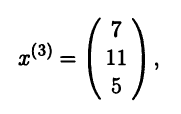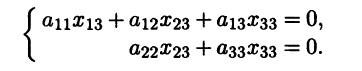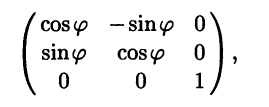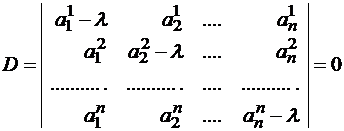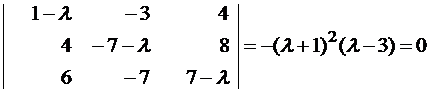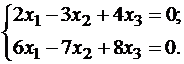Собственные значения линейного оператора как найти - Исправление недочетов и поиск решений вместе с Examum.ru

Собственные
векторы и собственные

значения
линейного оператора

Определение 1.
Собственным
вектором оператора

называют
ненулевой вектор
,
удовлетворяющий равенству:
=.

Определение 2.
Собственным
значением оператора

называют
число
,
для которого выполняется равенство:
=,
где

— ненулевой вектор.

(1)

(2)

Решив последнее
уравнение относительно
,
найдем собственные значения матрицы.
Уравнение (5.8) называют характеристическим
уравнением матрицы
.
Найдя корни характеристического
уравнения, последовательно подставляя
их в систему (1) и решая получаемые
системы, найдем собственные векторы
матрицы
,
каждый из которых соответствует
определенному собственному значению.

Рассмотрим несколько
примеров, в каждом из которых будем
выполнять последовательность действий
решения задачи об отыскании собственных
значений и собственных векторов матрицы.

Пример 1.

Найти собственные
значения и собственные векторы матрицы
.
Дать геометрическую интерпретацию
полученного решения.

Решение

Матрица имеет
размерность 22,
то есть является представлением
линейного оператора в пространстве
.
Собственный вектор матрицы будем искать
в виде:
.
Составим уравнение
для отыскания собственных векторов в
матричном виде:

3. Перепишем
матричное уравнение в виде системы
уравнений:

Однородная система
имеет ненулевые решения тогда и только
тогда, когда определитель ее главной
матрицы равен 0. Получаем характеристическое
уравнение системы и решаем его:

Собственные
значения матрицы
:

Найдем собственные
векторы для каждого собственного
значения:

;

Пусть
,
тогда собственное направление матрицы
,
соответствующее собственному значению
,
задается множеством векторов:

,
где
.

;

,
где
.

Пример
2. Найти собственные значения и
собственные векторы линейного оператора
, заданного в некотором базисе матрицей
А=.

Составим и решим
характеристическое уравнение
.

В нашей задаче
.

Тогда характеристическое
уравнение принимает вид:

,
или
,

— собственные
значения линейного оператора.

Найдем собственные
векторы, соответствующие собственному
значению
,
решая матричное уравнение:

х=0
или
,
т.е.

Полагая в последнем
равенстве
,
получим
.

Откуда собственные
векторы, соответствующие собственному
значению
,
имеют вид х¹=.

Найдем собственные
векторы, соответствующие собственному
значению
,
решая матричное уравнение:

х=0
или
,
т.е.

Полагая в последнем
равенстве
,
получим
.

Откуда собственные
векторы, соответствующие собственному
значению
,
имеют вид х²=.

Ответ. Собственному
значению
соответствуют собственные векторы
х¹=,
а собственному значению
собственные векторы

х²=.

Пример
3. Найти собственные значения и
собственные векторы линейного оператора
, заданного в некотором базисе матрицей
А=.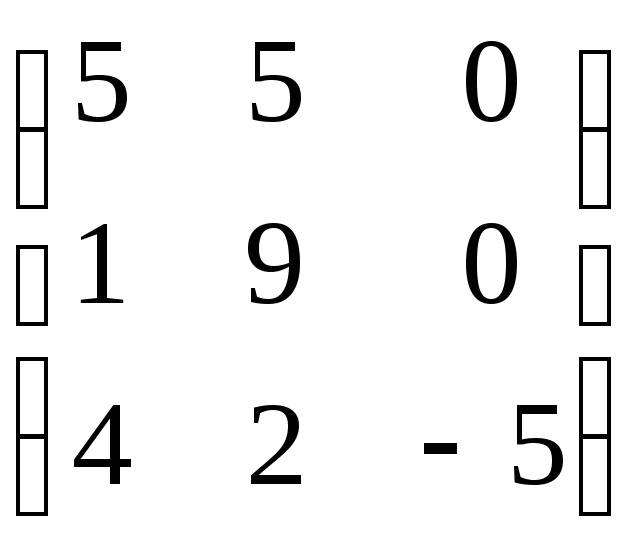

Найдем собственные
значения линейного оператора. Для этого
составим характеристическое уравнение
и найдем его корни:

,

— собственные значения линейного
оператора.

Найдем собственные
векторы, соответствующие собственному
значению
.
Исходя из соотношения
х=0
или в нашем случае

,
запишем систему:

Решая методом
Гаусса, получаем

Поскольку ранг
матрицы системы (r=2)
меньше количества неизвестных, то
система имеет бесконечное множество
решений. Записывая преобразованную
систему и решая ее, получим
,
.

Таким образом,
собственные векторы, соответствующие
собственному значению
,
имеют вид: Х¹=.

Найдем собственные
векторы, соответствующие собственному
значению
.
Исходя из соотношения
х=0
или в нашем случае

,
т.е.

Решая методом
Гаусса, получаем

откуда, система
принимает вид

Полагая
,
получим
.

Таким образом,
собственные векторы, соответствующие
собственному значению
,
имеют вид: Х²=.

Найдем собственные
векторы, соответствующие собственному
значению
.
Исходя из соотношения
х=0
или в нашем случае

,
т.е.

Решая методом
Гаусса, получаем

откуда, система
принимает вид

Полагая
,
получим
.

Таким
образом, собственные векторы,
соответствующие собственному значению
,
имеют вид: Х³=.

Соседние файлы в папке Математика

Источник

Характеристическое уравнение линейного оператора А: L → L, действующего в n-мерном линейном пространстве L, — это алгебраическое уравнение n-й степени с действительными коэффициентами. Среди его корней могут быть комплексные числа, но эти корни не относят к собственным значениям линейного оператора, так как, согласно определению, собственное значение линейного оператора — действительное число. Чтобы комплексные корни характеристического уравнения можно было рассматривать как собственные значения линейного оператора, в линейном пространстве должно быть определено умножение вектора на любые комплексные числа.

Как следует из доказательства теоремы 5.3, чтобы вычислить собственные значения линейного оператора А и найти его собственные векторы, нужно выполнить следующие операции:

— выбрать в линейном пространстве базис и сопоставить А матрицу А этого линейного оператора в выбранном базисе;

— составить характеристическое уравнение det (А — λЕ) = 0 и найти все его действительные корни λ_k, которые и будут собственными значениями линейного оператора;

— для каждого собственного значения λ_k найти фундаментальную систему решений
для однородной системы линейных алгебраических уравнений (СЛАУ) (А — λ_kЕ)х = 0. Столбцы фундаментальной системы решений представляют собой координаты векторов некоторого базиса в собственном подпространстве £(А, λ_k) линейного оператора А.

Любой собственный вектор с собственным значением λ_k принадлежит подпространству £(А,λ_k), и, следовательно, найденный базис в этом подпространстве позволяет представить любой собственный вектор с собственным значением λ_k.

Пример 5.4. Найдем собственные векторы и собственные значения линейного оператора А, имеющего в некотором базисе матрицу

В соответствии с описанной процедурой необходимо выполнить три действия. Первое действие можно опустить, так как оператор уже представлен своей матрицей в некотором базисе. Выполняем дальнейшие действия.

2) Находим собственные значения, решая характеристическое уравнение матрицы:

откуда λ₁ = -3, λ₂ = 1, λ₃ = 3.

3) Находим столбцы координат собственных векторов, ре-шая для каждого из трех собственных значений однородную СЛАУ

3а) Для λ = λ₁ = -3 система (5.5) имеет вид

или

Ранг матрицы этой системы равен 2:

Поэтому размерность линейного пространства решений систе-мы равна 3 — 2 = 1. Фундаментальная система решений содер-жит одно решение, например

Все множество собственных векторов линейного оператора с собственным значением λ₁ = -3 в координатной форме имеет вид

где α — произвольное ненулевое действительное число.

3б) При λ = λ₂ = 1 система (5.5) имеет вид

Как и в предыдущем случае, размерность линейного простран-ства решений равна 2 — 1 = 1 и фундаментальная система решений содержит одно решение. Выберем следующее:

Все множество собственных векторов с собственным значением λ = -1 в координатной форме имеет вид

где β — произвольное ненулевое действительное число.

3в) Для λ = λ₃ = 3 аналогично предыдущим двум случаям находим столбец координат одного из собственных векторов, например

который порождает собственное подпространство линейного оператора А, отвечающее собственному значению λ = 3.

Пример 5.5. Найдем собственные значения линейного оператора А, действующего в n-мерном линейном пространстве, матрица А которого в некотором базисе является верхней треугольной порядка n:

причем все ее диагональные элементы а_ii попарно различны, т.е. а_ii ≠ a_jj при i ≠ j.

Составляем характеристическое уравнение матрицы А:

det(А — λЕ) = (а₁₁ — λ)(а₂₂ — λ) … (а_nn — λ) = 0

(определитель верхней треугольной матрицы равен произведе-нию ее диагональных элементов). Находим все действительные корни этого уравнения:

λ_k = a_kk, k = 1,n

Как видим, линейный оператор А имеет n попарно различных собственных значений.

Отметим, что пересечение любых двух собственных подпространств линейного оператора содержит лишь нулевой вектор, так как собственный вектор не может отвечать двум различным собственным значениям. Поэтому собственные подпространства линейного оператора образуют прямую сумму, а размерность прямой суммы линейных подпространств, согласно следствию из теоремы 2.5, равна сумме их размерностей. Из этих соображений следует, что каждое из n собственных подпространств рассматриваемого линейного оператора является одномерным, так как их размерность не может быть меньше, но если бы одно из подпространств имело размерность больше единицы, то суммарная их размерность превышала бы размерность самого линейного пространства.

Итак, все собственные подпространства линейного операто-ра в нашем случае одномерны. Рассмотрим то из них, которое отвечает собственному значению λ_r = а_rr, где 1 ≤ r ≤ n. Соответствующий собственный вектор имеет столбец координат, который является ненулевым решением однородной СЛАУ

(А — a_rrЕ)х = 0. (5.6)

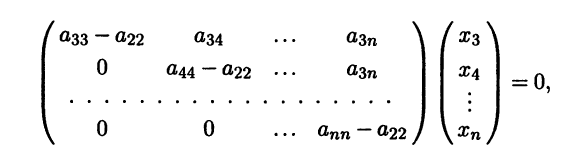
Достаточно очевидно, что ранг матрицы системы (5.6) равен n — 1, а базисный минор для этой матрицы получается вычер-киванием r-й строки и r-го столбца.

Наиболее просто решение системы (5.6) выглядит для r = 1. В этом случае собственным является вектор x₁ со столбцом координат (1 0 … 0)^T . При r = 2 все координаты собственного вектора, начиная с третьей, будут равны нулю, так как они удовлетворяют системе

получающейся выбрасыванием первых двух уравнений. Второе уравнение вытекает из всех последующих и может быть опуще-но, а первое уравнение определяет связь между первыми двумя координатами. Мы получаем, что собственному значению а₂₂ отвечает вектор x₂ со столбцом координат (-a₁₂ a₁₁ 0 … 0)^T . Собственному значению a₃₃ отвечает вектор x₃ со столбцом координат (x₁₃ x₂₃ x₃₃ 0 … 0)^T , у которого лишь первые три координаты отличны от нуля. Эти три координаты удовлетворяют однородной системе из двух уравнений

Эти рассуждения можно продолжить.

Пример 5.6. Преобразование поворота в V₃ на заданный острый угол вокруг некоторой оси — это линейный оператор. Его собственными векторами являются векторы, коллинеарные оси поворота. Например, если поворот выполняется вокруг оси Оz, то матрица оператора в базисе i, j, k будет иметь вид

а его собственными векторами будут векторы со столбцами координат вида λ(0 0 1)^T , λ ≠ 0.

Линейные операции над векторами
Базис. Cкалярное произведение
Векторное и смешанное произведения векторов
Декартова система координат. прямая на плоскости
Плоскость в пространстве
Прямая в пространстве
Кривые второго порядка — I
Кривые второго порядка — II
Поверхности второго порядка
Матрицы и операции с ними
Обратная матрица
Ранг матрицы
Системы линейных алгебраических уравнений
Свойства решений однородных и неоднородных СЛАУ

Источник

Линейные операторы

Собственные вектора и собственные значения линейного оператора

Определение

Самый простой линейный оператор — умножение вектора на число (lambda ). Этот оператор просто растягивает все вектора в (lambda ) раз. Его матричная форма в любом базисе — (diag(lambda ,lambda ,…,lambda )). Фиксируем для определенности базис ({e}) в векторном пространстве (mathit{L}) и рассмотрим линейный оператор с диагональной матричной формой в этом базисе, (alpha = diag(lambda _1,lambda _2,…,lambda _n)). Этот оператор, согласно определению матричной формы, растягивает (e_k) в (lambda _k) раз, т.е. (Ae_k=lambda _ke_k) для всех (k=1,2,…,n). С диагональными матрицами удобно работать, для них просто строится функциональное исчисление: для любой функции (f(x)) можно положить (f(diag(lambda _1,lambda _2,…,lambda _n))=diag(f(lambda _1),f(lambda _2),…,f(lambda _n))). Таким образом возникает естественный вопрос: пусть имеется линейный оператор (A), можно ли выбрать такой базис в векторном пространстве, чтобы матричная форма оператора (A) была диагональной в этом базисе? Этот вопрос приводит к определению собственных чисел и собственных векторов.

Определение.
Пусть для линейного оператора (A) существует ненулевой вектор (u) и число (lambda ) такие, что
[
Au=lambda cdot u. quad quad(59)
]
Тогда вектор (u) называют собственным вектором оператора (A), а число (lambda ) — соответствующим собственным числом оператора (A). Совокупность всех собственных чисел называют спектром линейного оператора (A).

Возникает естественная задача: найти для заданного линейного оператора его собственные числа и соответствующие собственные вектора. Эту задачу называют задачей о спектре линейного оператора.

Уравнение для собственных значений

Фиксируем для определенности базис в векторном пространстве, т.е. будем считать, что он раз и навсегда задан. Тогда, как обсуждалось выше, рассмотрение линейных операторов можно свести к рассмотрению матриц — матричных форм линейных операторов. Уравнение (59) перепишем в виде
[
(alpha -lambda E)u=0.
]
Здесь (E) — единичная матрица, а (alpha) — матричная форма нашего линейного оператора (A). Это соотношение можно трактовать как систему (n) линейных уравнений для (n) неизвестных — координат вектора (u). Причем это однородная система уравнений, и нам следует найти ее нетривиальное решение. Ранее было приведено условие существования такого решения — для этого необходимо и достаточно, чтобы ранг системы был меньше числа неизвестных. Отсюда следует уравнение для собственных чисел:
[
det(alpha -lambda E)=0. quad quad(60)
]

Определение. Уравнение (60) называется характеристическим уравнением для линейного оператора (A).

Опишем свойства этого уравнения и его решений. Если его выписывать в явном виде, получим уравнение вида
[
(-1)^nlambda ^n+…+det(A)=0. quad quad(61)
]
В левой части стоит полином по переменной (lambda ). Такие уравнения называются алгебраическими степени (n). Приведем необходимые сведения об этих уравнениях.

Справка об алгебраических уравнениях.

Основная теорема алгебры.
Уравнение (61) имеет решение на комплексной плоскости (mathbb{C}).

Следствие.
Уравнение (61) имеет на комплексной плоскости столько решений, какова его степень (решения учитываются с учетом кратности).

Пример.

Рассмотрим уравнение
[
lambda (lambda-1)^2(lambda+1)^3=0.
]
Это уравнение 6 степени. Оно имеет следующие решения: ( lambda =0), ( lambda =1), ( lambda =-1), причем кратность первого решения равна 1 (такие решения называют простыми корнями), кратность второго решения равна 2, кратность третьего решения равна 3. Решения, кратность которых выше 1, называют кратными . В нашем случае 1+2+3=6. Уравнения степени (n geq 5) невозможно решить с помощью радикалов (теорема Абеля-Руффини). Для уравнений степени (n=2,3,4) такие явные формулы существуют. Однако на практике уравнения высокой степени можно успешно решать с помощью компьютеров. Таким образом, в дальнейшем будем считать, что мы тем или иным способом построили решения уравнения (61).

Собственные вектора

Рассмотрим вопрос о построении собственного вектора, соответствующего известному собственному числу (lambda _k). Для этого обратимся к уравнению
[
(alpha -lambda_k E)u=0.
]
Это уравнение можно понимать как систему линейных уравнений для координат вектора (u) — собственного вектора, соответствующего собственному числу (lambda _k). При этом данная система имеет нетривиальное решение, так как ранг этой системы меньше числа неизвестных. Решая эту систему методом Гаусса, можно определить координаты вектора (u). Перебирая все значения (lambda _k), (k=1,2,…,n), находим соответствующие собственные вектора (u_k).

Пример. Найдем собственные значения и собственные вектора линейного преобразования, заданного в некотором базисе следующей матрицей:
[
A=left ( begin{array}{ccc}5 & -7 & 0 \-3 & 1 & 0 \12 & 6 & -3 end{array} right ).
]
Матрица (A-lambda E) имеет в данном случае вид:
[
A- lambda E=left ( begin{array}{ccc}5 -lambda & -7 & 0 \-3 & 1-lambda & 0 \12 & 6 & -3 -lambdaend{array} right ).
]
Вычисляем определитель (det(A-lambda E)) и выписываем уравнение на собственные значения:
[
det(A-lambda E)=-(lambda +3)(lambda ^2-6lambda -16)=0.
]
Отсюда находим 3 собственных значения: (lambda _1=-3, lambda _2=8, lambda _3=-2). Мы получили 3 собсвенных значения, все они имеют кратность 1, т.е. это
простые собственные числа. Вычислим соответствующие собственные вектора.

1. Рассмотрим (lambda _1=-3). Соответствующее уравнение для собственного вектора (u=(u_1,u_2,u_3)^T) имеет вид:
[
left( begin{array}{ccc}8 & -7 & 0 \-3 & 4 & 0 \12 & 6 & 0end{array} right) left( begin{array}{c}u_1 \ u_2 \ u_3 end{array} right)=0,
]
где справа стоит нулевой 3-вектор. Эта система уравнений для 3 неизвестных имеет следующее решение: (u=(0,0,1)^T).

2. Рассмотрим (lambda _2=8). Соответствующее уравнение для собственного вектора (u=(u_1,u_2,u_3)^T) имеет вид:
[
left ( begin{array}{ccc}-3 & -7 & 0 \-3 & -7 & 0 \12 & 6 & 5 end{array} right ) left( begin{array}{c}u_1 \ u_2 \ u_3 end{array} right)=0,
]
где справа стоит нулевой 3-вектор. Эта однородная система уравнений для неизвестных (u_1,u_2,u_3) имеет решение: (u=(7, -3, 0)^T).

3. Рассмотрим (lambda _3=-2). Соответствующее уравнение для собственного вектора (u=(u_1,u_2,u_3)^T) имеет вид:
[
left ( begin{array}{ccc}7 & -7 & 0 \-3 & 3 & 0 \12 & 6 & -1 end{array} right ) left( begin{array}{c}u_1 \ u_2 \ u_3 end{array} right)=0,
]
где справа стоит нулевой 3-вектор. Эта однородная система уравнений для неизвестных (u_1,u_2,u_3) имеет решение: (u=(1,1,0)^T).

Теорема.
Пусть все собственные числа линейного оператора (A) — простые. Тогда набор собственных векторов, соответствующих этим собственным числам, образует базис векторного пространства.

Из условий теоремы следует, что все собственные числа оператора (A) различны. Предположим, что набор собственных векторов линейно зависим, так что существуют константы (c_1,c_2,…,c_n), не все из которых нули, удовлетворяющие условию:
[
sum_{k=1}^nc_ku_k=0. quad quad(62)
]

Рассмотрим среди таких формул такую, которая включает минимальное число слагаемых, и подействуем на нее оператором (A). В силу его линейности получаем:
[
Aleft (sum_{k=1}^nc_ku_k right )=sum_{k=1}^nc_kAu_k=sum_{k=1}^nc_klambda _ku_k=0. quad quad(63)
]

Пусть, для определенности, (c_1 neq 0). Умножая (62) на (lambda _1) и вычитая из (63), получим соотношение вида (62), но содержащее на одно слагаемое меньше. Противоречие доказывает теорему.

Итак, в условиях теоремы появляется базис, связанный с данным линейным оператором — базис его собственных векторов. Рассмотрим матричную форму оператора в таком базисе. Как упоминалось выше, (k)-ый столбец этой матрицы — это разложение вектора (Au_k) по базису. Однако по определению (Au_k=lambda _ku_k), так что это разложение (то, что выписано в правой части) содержит только одно слагаемое и построенная матрица оказывается диагональной. В итоге получаем, что в условиях теоремы матричная форма оператора в базисе его собственных векторов равна (diag(lambda _1,lambda _2,…,lambda _n)). Поэтому если необходимо развивать функциональное исчисление для линейного оператора разумно работать в базисе его собственных векторов.

Если же среди собственных чисел линейного оператора есть кратные, описание ситуации становится сложнее и может включать так называемые жордановы клетки. Мы отошлем читателя к более продвинутым руководствам для изучения соответствующих ситуаций.

Найти собственные числа и собственные вектора линейного оператора, заданного в некотором базисе матрицей (A).

1.
[
A=left ( begin{array}{ccc}0 & 1 & 0 \-3 & 4 & 0 \-2 & 1 & 4 end{array} right ).
]

2.
[
A=left ( begin{array}{ccc}-3 & 2 & 0 \-2 & 1 & 0 \15 & -7 & 4 end{array} right ).
]

3.
[
A=left ( begin{array}{ccc}4 & 0 & 5 \ 7 & -2 & 9 \3 & 0 & 6 end{array} right ).
]

4.
[
A=left ( begin{array}{ccc}-1 & -2 & 12 \0 & 4 & 3 \0 & 5 & 6 end{array} right ).
]

Предыдущий раздел

Следующий раздел

Источник

Собственные векторы и значения линейного оператора (преобразования)

Пусть mathcal{A}colon Vto V — линейное преобразование n-мерного линейного пространства . Ненулевой вектор boldsymbol{s} линейного пространства , удовлетворяющий условию

mathcal{A}(boldsymbol{s})=lambdacdot boldsymbol{s},

(9.5)

называется собственным вектором линейного преобразования mathcal{A} . Число lambda в равенстве (9.5) называется собственным значением преобразования . Говорят, что собственный вектор соответствует (принадлежит) собственному значению lambda . Если пространство вещественное (комплексное), то собственное значение lambda — действительное (комплексное) число.

Множество всех собственных значений линейного преобразования называется его спектром.

Поясним геометрический смысл собственных векторов. Ненулевой вектор s является собственным для преобразования mathcal{A} , если его образ mathcal{A} (boldsymbol{s}) коллинеарен прообразу . Другими словами, если — собственный вектор, то преобразование имеет одномерное инвариантное подпространство operatorname{Lin}(boldsymbol{s}) . Справедливо и обратное утверждение.

В самом деле, пусть собственный вектор boldsymbol{s} соответствует некоторому собственному значению lambda . Любой вектор boldsymbol{v} из operatorname{Lin}(boldsymbol{s}) имеет вид boldsymbol{v}=alpha boldsymbol{s} , где alpha — любое число из заданного поля. Найдем образ этого вектора

mathcal{A}(boldsymbol{v})= mathcal{A}(alpha boldsymbol{s})= alphacdot mathcal{A}(boldsymbol{s})= alphacdot lambdacdot boldsymbol{s}in operatorname{Lin} (boldsymbol{s}).

Следовательно, mathcal{A}(boldsymbol{v})in operatorname{Lin}(boldsymbol{s}) для любого вектора boldsymbol{v}in operatorname{Lin}(boldsymbol{s}) , т.е. подпространство инвариантно относительно преобразования . Размерность подпространства operatorname{Lin} (boldsymbol{s}) равна единице, так как boldsymbol{s}ne boldsymbol{o} по определению.

Обратное утверждение доказывается, проводя рассуждения в обратном порядке.

Связь собственных векторов линейного преобразования (оператора) и его матрицы

Ранее рассматривались собственные векторы и собственные значения матрицы. Напомним, что собственным вектором квадратной матрицы n-го порядка называется ненулевой числовой столбец $s=begin{pmatrix}s_1&cdots&s_{n}end{pmatrix}^T$ , удовлетворяющий условию (7.13):

Acdot s=lambdacdot s.

(9.6)

Число lambda в (9.6) называется собственным значением матрицы . При этом считалось, что собственное значение lambda и числа s_i~(i=1,ldots,n) принадлежат полю комплексных чисел.

Эти понятия связаны с собственными векторами и собственными значениями линейного преобразования.

Теорема 9.3 о собственных векторах линейного преобразования и его матрицы. Пусть mathcal{A}colon Vto V — линейное преобразование n-мерного линейного пространства с базисом $boldsymbol{e}_1,ldots,boldsymbol{e}_n$ . Тогда собственное значение lambda и координатный столбец {s} собственного вектора boldsymbol{s} преобразования mathcal{A} являются собственным значением и собственным вектором матрицы этого преобразования, определенной относительно базиса $boldsymbol{e}_1,ldots, boldsymbol{e}_n$ , т.е.

mathcal{A}(boldsymbol{s})=lambdacdot boldsymbol{s}quad Rightarrowquad Acdot s=lambdacdot s, где $boldsymbol{s}=s_1 boldsymbol{e}_1+ldots+s_n boldsymbol{e}_n,~ s=begin{pmatrix}s_1&cdots& s_nend{pmatrix}^T.$

Обратное утверждение справедливо при дополнительных условиях: если столбец $s=begin{pmatrix} s_1&cdots&s_nend{pmatrix}^T$ и число lambda являются собственным вектором и собственным значением матрицы , причем числа s_1,ldots,s_n,lambda принадлежат тому же числовому полю, над которым определено линейное пространство , то вектор $boldsymbol{s}=s_1 boldsymbol{e}_1+ ldots+s_n boldsymbol{e}_n$ и число lambda являются собственным вектором и собственным значением линейного преобразования mathcal{A}colon Vto V с матрицей в базисе $boldsymbol{e}_1,ldots,boldsymbol{e}_n$ .

В самом деле, условие (9.5) в координатной форме имеет вид (9.6), что совпадает с определением (7.13) собственного вектора матрицы. Наоборот, из равенства (9.6) следует равенство (9.5) при условии, что векторы $boldsymbol{s}=s_1 boldsymbol{e}_1+ldots+s_n boldsymbol{e}_n$ и lambdacdot boldsymbol{s} определены, т.е. числа s_1,ldots,s_n, lambda принадлежат тому же числовому полю, над которым определено линейное пространство.

Напомним, что нахождение собственных значений матрицы сводится к решению ее характеристического уравнения Delta_A(lambda)=0 , где Delta_A(lambda)=det(A-lambda E) — характеристический многочлен матрицы . Для линейного преобразования введем аналогичные понятия.

Характеристическим многочленом линейного преобразования mathcal{A}colon Vto V n-мерного линейного пространства называется характеристический многочлен $Delta_{mathcal{A}}(lambda)=det(A-lambda E)$ матрицы этого преобразования, найденной относительно любого базиса пространства .

Уравнение $Delta_{mathcal{A}}(lambda)=0$ называется характеристическим уравнением линейного преобразования.

Преобразование mathcal{A}-lambdamathcal{E} называется характеристическим для линейного преобразования mathcal{A}colon Vto V .

Замечания 9.4

1. Характеристический многочлен линейного преобразования не зависит от базиса, в котором найдена матрица преобразования.

В самом деле, матрицы $mathop{A}limits_{(boldsymbol{e})}$ и $mathop{A}limits_{(boldsymbol{f})}$ линейного преобразования mathcal{A} в базисах $(boldsymbol{e})= (boldsymbol{e}_1,ldots, boldsymbol{e}_n)$ и $(boldsymbol{f})=(boldsymbol{f}_1,ldots,boldsymbol{f}_n)$ являются, согласно (9.4), подобными: $mathop{A}limits_{(boldsymbol{f})}=S^{-1}mathop{A}limits_{(boldsymbol{e})}S$ , где — матрица перехода от базиса к базису . Как показано ранее, характеристические многочлены подобных матриц совпадают (см. свойство 3). Поэтому для характеристического многочлена преобразования mathcal{A} можно использовать обозначение $Delta_{mathcal{A}}(lambda)$ , не указывая матрицу этого преобразования.

2. Из теоремы 9.3 следует, что любой комплексный (действительный, рациональный) корень характеристического уравнения является собственным значением линейного преобразования mathcal{A}colon Vto V линейного пространства , определенного над полем комплексных (действительных, рациональных) чисел.

3. Из теоремы 9.3 следует, что любое линейное преобразование комплексного линейного пространства имеет одномерное инвариантное подпространство, так как это преобразование имеет собственное значение (см. пункт 2), а следовательно, и собственные векторы. Таким подпространством является, например, линейная оболочка любого собственного вектора. У преобразования вещественного линейного пространства одномерных инвариантных подпространств может и не быть, если все корни характеристического уравнения комплексные (но не действительные).

Теорема 9.4 об инвариантных подпространствах линейного оператора вещественного пространства. У всякого линейного преобразования вещественного линейного пространства существует одномерное или двумерное инвариантное подпространство.

Действительно, составим матрицу линейного преобразования mathcal{A}colon Vto V n-мерного вещественного линейного пространства в произвольном базисе $boldsymbol{e}_1,ldots,boldsymbol{e}_n$ . Элементы этой матрицы — действительные числа. Следовательно, характеристический многочлен $Delta_{mathcal{A}}(lambda)=det(A-lambda E)$ — это многочлен степени с действительными коэффициентами. Согласно следствиям 3, 4 основной теоремы алгебры, такой многочлен может иметь действительные корни и пары комплексных сопряженных корней.

Если lambda=lambda_1 — действительный корень характеристического уравнения, то и соответствующий собственный вектор $s=begin{pmatrix}s_1&cdots&s_nend{pmatrix}^T$ матрицы также действительный. Поэтому он определяет собственный вектор $boldsymbol{s}=s_1 boldsymbol{e}_1+ldots+s_n boldsymbol{e}_n$ линейного преобразования (см. теорему 9.3). В этом случае существует одномерное инвариантное относительно mathcal{A} подпространство operatorname{Lin}(boldsymbol{s}) (см. геометрический смысл собственных векторов).

Если lambda=alphapmbeta i — пара комплексных сопряженных корней (betane0) , то собственный вектор sne o матрицы также с комплексными элементами: $s=begin{pmatrix}x_1+y_1i&cdots& x_n+y_n i end{pmatrix}^T$ . Его можно представить в виде s=x+yi , где x,,y — действительные столбцы. Равенство (9.6) при этом будет иметь вид

Acdot(x+yi)= (alpha+beta i)cdot(x+yi).

Выделяя действительную и мнимую части, получаем систему

$begin{cases}Ax=alpha x-beta y,\ Ay=beta x+alpha y.end{cases}$

(9.7)

Покажем, что столбцы {x} и {y} линейно независимы. Рассмотрим два случая. Если x=o , то из первого уравнения (9.7) следует, что y=o , так как betane0 . Тогда s=o , что противоречит условию sne o . Предположим, что xne o и столбцы и пропорциональны, т.е. существует такое действительное число gamma , что y=gamma x . Тогда из системы (9.7) получаем $begin{cases}Ax=(alpha-betagamma)x,\ gamma Ax=(beta-alphagamma)x. end{cases}$ Прибавляя ко второму уравнению первое, умноженное на (-gamma) , приходим к равенству [(beta+alphagamma)-gamma(alpha-betagamma)]x=o . Так как xne o , то выражение в квадратных скобках равно нулю, т.е. (beta+alphagamma)- gamma(alpha- betagamma)= beta(1+gamma^2)=0 . Поскольку betane0 , то gamma^2=-1 . Этого не может быть, так как gamma — действительное число. Получили противоречие. Таким образом, столбцы и линейно независимы.

Рассмотрим подпространство operatorname{Lin}(boldsymbol{x},boldsymbol{y}) , где $boldsymbol{x}= x_1 boldsymbol{e}_1+ldots+x_n boldsymbol{e}_n,~ boldsymbol{y}= y_1 boldsymbol{e}_1+ldots+ y_n boldsymbol{y}_n$ . Это подпространство двумерное, так как векторы линейно независимы (как показано выше, их координатные столбцы x,y линейно независимы). Из (9.7) следует, что $begin{cases}mathcal{A}(boldsymbol{x})=alpha boldsymbol{x}-beta boldsymbol{y},\ mathcal{A}(boldsymbol{y})=beta boldsymbol{x}+alpha boldsymbol{y},end{cases}$ т.е. образ любого вектора, принадлежащего operatorname{Lin}(boldsymbol{x},boldsymbol{y}) , также принадлежит . Следовательно, — двумерное подпространство, инвариантное относительно преобразования mathcal{A} , что и требовалось доказать.

Нахождение собственных векторов и значений линейного оператора (преобразования)

Для нахождения собственных векторов и собственных значений линейного преобразования mathcal{A}colon Vto V вещественного линейного пространства следует выполнить следующие действия.

1. Выбрать произвольный базис $boldsymbol{e}_1,ldots,boldsymbol{e}_n$ линейного пространства и найти в этом базисе матрицу преобразования mathcal{A} .

2. Составить характеристический многочлен преобразования $mathcal{A}colon, Delta_{mathcal{A}}(lambda)=det(A-lambda E)$ .

3. Найти все различные действительные корни lambda_1,ldots,lambda_k характеристического уравнения $Delta_{mathcal{A}}(lambda)=0$ . Комплексные (но не действительные) корни характеристического уравнения следует отбросить (см. пункт 2. замечаний 9.4).

4. Для корня lambda=lambda_1 найти фундаментальную систему $varphi_1, varphi_2,ldots,varphi_{n-r}$ решений однородной системы уравнений (A-lambda_1E)x=o , где $r=operatorname{rg}(A-lambda_1E)$ . Для этого можно использовать либо алгоритм решения однородной системы, либо один из способов нахождения фундаментальной матрицы.

5. Записать линейно независимые собственные векторы преобразования mathcal{A} , отвечающие собственному значению lambda_1:

$begin{matrix} boldsymbol{s}_1=varphi_{1,1}boldsymbol{e}_1+ ldots+ varphi_{n,1}boldsymbol{e}_n,\ boldsymbol{s}_2=varphi_{1,2}boldsymbol{e}_1+ ldots+ varphi_{n,2}boldsymbol{e}_n,\ vdots\ boldsymbol{s}_{n-r}=varphi_{1,n-r} boldsymbol{e}_1+ ldots+varphi_{n,n-r}boldsymbol{e}_n. end{matrix}$

Для нахождения совокупности всех собственных векторов, отвечающих собственному значению lambda_1 , образовать ненулевые линейные комбинации

$boldsymbol{s}= C_1 boldsymbol{s}_1+C_2 boldsymbol{s}_2+ldots+ C_{n-r}boldsymbol{s}_{n-r},$

где $C_1,C_2,ldots,C_{n-r}$ — произвольные постоянные, не равные нулю одновременно.

Повторить пункты 4, 5 для остальных собственных значений lambda_2,ldots,lambda_k линейного преобразования mathcal{A} .

Для нахождения собственных векторов линейного преобразования комплексного линейного пространства нужно в пункте 3 определить все корни характеристического уравнения и, не отбрасывая комплексные корни, выполнить для них пункты 4,5.

Примеры собственных векторов линейных операторов (преобразований)

1. Для нулевого преобразования mathcal{O}colon Vto V любой ненулевой вектор boldsymbol{s}in V является собственным, соответствующим нулевому собственному значению lambda=0 , так как mathcal{O}(boldsymbol{s})=0cdot boldsymbol{s}~ forall boldsymbol{s}in V .

2. Для тождественного преобразования mathcal{E}colon Vto V любой ненулевой вектор boldsymbol{s}in V является собственным, соответствующим единичному собственному значению lambda=1 , так как mathcal{E} (boldsymbol{s})=1cdot boldsymbol{s}~ forall boldsymbol{s}in V .

3. Для центральной симметрии $mathcal{Z}_{boldsymbol{o}}colon Vto V$ любой ненулевой вектор boldsymbol{s}in V является собственным, соответствующим собственному значению lambda=-1 , так как $mathcal{Z}_{boldsymbol{o}} (boldsymbol{s})=(-1)cdot boldsymbol{s}~ forall boldsymbol{s}in V$ .

4. Для гомотетии $mathcal{H}_{lambda}colon Vto V$ любой ненулевой вектор boldsymbol{s}in V является собственным, соответствующим собственному значению lambda (коэффициенту гомотетии), так как $mathcal{H}_{lambda} (boldsymbol{boldsymbol{s}})= lambdacdot boldsymbol{s}~ forall boldsymbol{s}in V$ .

5. Для поворота $mathcal{R}_{varphi}colon V_2to V_2$ плоскости (при varphinepi k,~ kinmathbb{Z} ) собственных векторов нет, так как при повороте на угол, не кратный , образ каждого ненулевого вектора неколлинеарен прообразу. Здесь рассматривается поворот вещественной плоскости, т.е. двумерного векторного пространства над полем действительных чисел.

6. Для оператора дифференцирования $mathcal{D}colon P_n(mathbb{R})to P_n(mathbb{R})$ любой ненулевой многочлен нулевой степени (не равный тождественно нулю) является собственным вектором, соответствующим нулевому собственному значению lambda=0 , так как mathcal{D}(s(x))=0cdot s(x) forall s(x)equiv text{const} . Любой многочлен ненулевой степени не является собственным вектором, так как многочлен не пропорционален своей производной: mathcal{D}(s(x))=s'(x)ne lambdacdot s(x) , поскольку они имеют разные степени.

7. Рассмотрим оператор $Pi_{L_1}colon Vto V$ проектирования на подпространство L_1 параллельно подпространству L_2 . Здесь V=L_1oplus L_2, $Pi_{L_1}(boldsymbol{v}_1+ boldsymbol{v}_2)=boldsymbol{v}_1$ для $boldsymbol{v}=boldsymbol{v}_1+boldsymbol{v}_2,$ $boldsymbol{v}_1in L_1,~ boldsymbol{v}_2in L_2$ . Для этого оператора любой ненулевой вектор $boldsymbol{v}_1in L_1$ является собственным, соответствующим собственному значению lambda=1 , так как $Pi_{L_1}(boldsymbol{v}_1)=1cdot boldsymbol{v}_1$ , а любой ненулевой вектор $boldsymbol{v}_2in L_2$ является собственным, соответствующим собственному значению lambda=0 , так как $Pi_{L_2}(boldsymbol{v}_2)=0cdot boldsymbol{v}_2$ . Другие векторы не являются собственными, так как равенство $Pi_{L_1}(boldsymbol{v}_1+boldsymbol{v}_2)= boldsymbol{v}_1= lambda(boldsymbol{v}_1+boldsymbol{v}_2)$ возможно либо при $boldsymbol{v}_1=boldsymbol{o}$ , либо при $boldsymbol{v}_2= boldsymbol{o}$ .

8. Рассмотрим оператор $mathcal{Z}_{L_1}colon Vto V$ отражения на подпространство L_1 параллельно подпространству L_2 . Здесь V=L_1oplus L_2 $mathcal{Z}_{L_1}(boldsymbol{v}_1+boldsymbol{v}_2)= boldsymbol{v}_1- boldsymbol{v}_2$ , для $boldsymbol{v}=boldsymbol{v}_1+boldsymbol{v}_2,$ $boldsymbol{v}_1in L_1,~ boldsymbol{v}_2in L_2$ . Для этого оператора любой ненулевой вектор $boldsymbol{v}_1in L_1$ является собственным, соответствующим собственному значению lambda=1 , так как $mathcal{Z}_{L_1} (boldsymbol{v}_1)= 1cdot boldsymbol{v}_1$ , а любой ненулевой вектор $boldsymbol{v}_2in L_2$ является собственным, соответствующим собственному значению lambda=-1 , так как $mathcal{Z}_{L_2} (boldsymbol{v}_2)= (-1)cdot boldsymbol{v}_2$ . Другие векторы не являются собственными, так как равенство $mathcal{Z}_{L_1}(boldsymbol{v}_1+boldsymbol{v}_2)= boldsymbol{v}_1- boldsymbol{v}_2= lambda(boldsymbol{}_1+ boldsymbol{v}_2)$ возможно либо при $boldsymbol{v}_1=boldsymbol{o}$ , либо при $boldsymbol{v}_2= boldsymbol{o}$ .

9. В пространстве V_3 радиус-векторов пространства, отложенных от фиксированной точки , рассмотрим поворот на угол varphinepi k,~ kinmathbb{Z} , вокруг оси ell , заданной радиус-вектором vec{ell} . Любой ненулевой вектор, коллинеарный вектору , является собственным, отвечающим собственному значению lambda=1 . Других собственных векторов у этого преобразования нет.

Пример 9.1. Найти собственные значения и собственные векторы оператора дифференцирования $mathcal{D}colon T_1to T_1$ , преобразующего пространство тригонометрических многочленов (частоты omega=1 ):

а) с действительными коэффициентами $T_1=T_1(mathbb{R})= operatorname{Lin} (sin{t},cos{t})$ ;

б) с комплексными коэффициентами $T_1=T_1(mathbb{C})= operatorname{Lin} (sin{t},cos{t})$ .

Решение. 1. Выберем стандартный базис $e_1(t)=sin{t},~ e_2(t)=cos{t}$ и составим в этом базисе матрицу оператора mathcal{D}:

$D=begin{pmatrix}0&-1\ 1&0 end{pmatrix}!.$

2. Составим характеристический многочлен преобразования $mathcal{D}colon, Delta_{mathcal{D}}(lambda)= begin{vmatrix}-lambda&-1\ 1&-lambdaend{vmatrix}= lambda^2+1.$ .

3. Характеристическое уравнение lambda^2+1=0 имеет комплексные сопряженные корни lambda_1=i,~ lambda_2=-i . Действительных корней нет, поэтому преобразование mathcal{D} вещественного пространства $T_1(mathbb{R})$ (случай (а)) не имеет собственных значений, а следовательно, и собственных векторов. Преобразование комплексного пространства $T_1(mathbb{C})$ (случай (б)) имеет комплексные собственные значения lambda_1,,lambda_2 .

4(1). Для корня lambda_1=i находим фундаментальную систему varphi_1 решений однородной системы уравнений (D-lambda_1 E)x=o:

$begin{pmatrix}-i&-1\ 1&-iend{pmatrix}!cdot! begin{pmatrix} x_1\x_2 end{pmatrix}= begin{pmatrix}0\0 end{pmatrix}!.$

Приведем матрицу системы к ступенчатому виду, умножая первое уравнение на {i} и вычитая его из второго уравнения:

$begin{pmatrix}-i&-1\ 1&-i end{pmatrix}sim begin{pmatrix}1&-i\ 1&-i end{pmatrix}sim begin{pmatrix}1&-i\ 0&0end{pmatrix}!.$

Выражаем базисную переменную x_1 через свободную: x_1=ix_2 . Полагая x_2=1 , получаем x_1=i , т.е. $varphi=begin{pmatrix}i&1 end{pmatrix}^T$ .

5(1). Записываем собственный вектор, отвечающий собственному значению $lambda_1= icolon, s_1(t)=icdotsin{t}+1cdotcos{t}$ . Совокупность всех собственных векторов, отвечающих собственному значению lambda_1=i , образуют ненулевые функции, пропорциональные s_1(t) .

4(2). Для корня lambda_2=-i аналогично находим фундаментальную систему (состоящую из одного вектора) $varphi_2=begin{pmatrix}-i&1 end{pmatrix}^T$ решений однородной системы уравнений (D-lambda_2E)x=o:

$begin{pmatrix}i&-1\ 1&i end{pmatrix}!cdot! begin{pmatrix} x_1\x_2 end{pmatrix}= begin{pmatrix}0\0 end{pmatrix}!.$

5(2). Записываем собственный вектор, отвечающий собственному значению $lambda_2=-icolon, s_2(t)=-icdotsin{t}+1cdotcos{t}$ . Совокупность всех собственных векторов, отвечающих собственному значению , образуют ненулевые функции, пропорциональные s_2(t) .

См. также Свойства собственных векторов линейных операторов (преобразований)

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Собственные числа и собственные векторы линейного оператора

Наиболее просто устроены матрицы диагонального вида . Возникает вопрос, нельзя ли найти базис, в котором матрица линейного оператора имела бы диагональный вид. Такой базис существует.

Пусть дано линейное пространство R_n и действующий в нем линейный оператор A; в этом случае оператор A переводит R_n в себя, то есть A:R_n
→ R_n.

Определение. Ненулевой вектор x называется собственным вектором оператора A, если оператор A переводит x в коллинеарный ему вектор, то есть A·x = λ·x. Число λ называется собственным значением или собственным числом оператора A, соответствующим собственному вектору x.

Отметим некоторые свойства собственных чисел и собственных векторов.

1. Любая линейная комбинация собственных векторов x₁, x₂, …, x_m оператора A, отвечающих одному и тому же собственному числу λ, является собственным вектором с тем же собственным числом.

2. Собственные векторы x₁, x₂, …, x_m оператора A с попарно различными собственными числами λ₁, λ₂, …, λ_m
линейно независимы.

3. Если собственные числа λ₁=λ₂= λ_m= λ, то собственному числу λ соответствует не более m линейно независимых собственных векторов.

Итак, если имеется n линейно независимых собственных векторов x₁, x₂, …, x_n, соответствующих различным собственным числам λ₁, λ₂, …, λ_n, то они линейно независимы, следовательно, их можно принять за базис пространства R_n. Найдем вид матрицы линейного оператора A в базисе из его собственных векторов, для чего подействуем оператором A на базисные векторы: 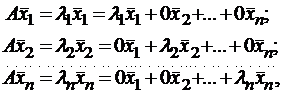тогда .

Таким образом, матрица линейного оператора A в базисе из его собственных векторов имеет диагональный вид, причем по диагонали стоят собственные числа оператора A.

Существует ли другой базис, в котором матрица имеет диагональный вид? Ответ на поставленный вопрос дает следующая теорема.

Теорема. Матрица линейного оператора A в базисе {ε_i} (i = 1..n) имеет диагональный вид тогда и только тогда, когда все векторы базиса — собственные векторы оператора A.

Правило отыскания собственных чисел и собственных векторов

Пусть дан вектор x=(x₁, x₂, …, x_n), где x₁, x₂, …, x_n — координаты вектора x относительно базиса {ε₁, ε₂, …, ε_n} и x — собственный вектор линейного оператора A, соответствующий собственному числу λ, то есть A·x=λ·x. Это соотношение можно записать в матричной форме

x·(A-λ·E). (*)

Уравнение (*) можно рассматривать как уравнение для отыскания x, причем x ≠ 0, то есть нас интересуют нетривиальные решения, поскольку собственный вектор не может быть нулевым. Известно, что нетривиальные решения однородной системы линейных уравнений существуют тогда и только тогда, когда det(A — λE) = 0. Таким образом, для того, чтобы λ было собственным числом оператора A необходимо и достаточно, чтобы det(A — λE) = 0.

Если уравнение (*) расписать подробно в координатной форме, то получим систему линейных однородных уравнений:

(1)

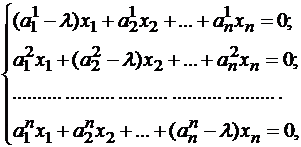
где — матрица линейного оператора.

Система (1) имеет ненулевое решение, если ее определитель D равен нулю

Получили уравнение для нахождения собственных чисел.

Это уравнение называется характеристическим уравнением, а его левая часть — характеристическим многочленом матрицы (оператора) A. Если характеристический многочлен не имеет вещественных корней, то матрица A не имеет собственных векторов и ее нельзя привести к диагональному виду.

Пусть λ₁, λ₂, …, λ_n — вещественные корни характеристического уравнения, причем среди них могут быть и кратные. Подставляя по очереди эти значения в систему (1), находим собственные векторы.

Пример №1. Линейный оператор A действует в R₃ по закону A·x=(x₁-3x₂+4x₃, 4x₁-7x₂+8x₃, 6x₁-7x₂+7x₃), где x₁, x₂, .., x_n — координаты вектора x в базисе e₁=(1,0,0), e₂=(0,1,0), e₃=(0,0,1). Найти собственные числа и собственные векторы этого оператора.

Решение. Строим матрицу этого оператора:

A·e₁=(1,4,6)

A·e₂=(-3,-7,-7)

A·e₃=(4,8,7)

.

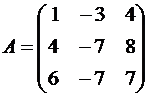
Составляем систему для определения координат собственных векторов:

(1-λ)x₁-3x₂+4x₃=0

x₁-(7+λ)x₂+8x₃=0

x₁-7x₂+(7-λ)x₃=0

Составляем характеристическое уравнение и решаем его:

λ_1,2 = -1, λ₃ = 3.

Подставляя λ = -1 в систему, имеем:

или

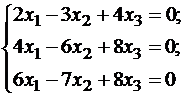
Так как 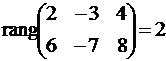, то зависимых переменных два, а свободное одно.

Пусть x₁ — свободное неизвестное, тогда 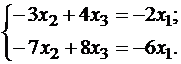Решаем эту систему любым способом и находим общее решение этой системы: Фундаментальная система решений состоит из одного решения, так как n — r = 3 — 2 = 1.

Множество собственных векторов, отвечающих собственному числу λ = -1, имеет вид: (x₁, 2x₁, x₁)=x₁(1,2,1), где x₁ — любое число, отличное от нуля. Выберем из этого множества один вектор, например, положив x₁ = 1: x₁=(1,2,1).

Рассуждая аналогично, находим собственный вектор, отвечающий собственному числу λ = 3: x₂=(1,2,2).

В пространстве R₃ базис состоит из трех линейно независимых векторов, мы же получили только два линейно независимых собственных вектора, из которых базис в R₃ составить нельзя. Следовательно, матрицу A линейного оператора привести к диагональному виду не можем.

Пример №2. Дана матрица .

1. Доказать, что вектор x=(1,8,-1) является собственным вектором матрицы A. Найти собственное число, соответствующее этому собственному вектору.

2. Найти базис, в котором матрица A имеет диагональный вид.

Решение находим с помощью калькулятора.

1. Если A·x=λ·x, то x — собственный вектор

Вектор (1, 8, -1) — собственный вектор. Собственное число λ = -1.

Диагональный вид матрица имеет в базисе, состоящем из собственных векторов. Один из них известен. Найдем остальные.

Собственные векторы ищем из системы:

(2-λ)x₁+3x₃=0;

10x₁-(3+λ)x₂-6x₃=0;

-x₁-(2+λ)x₃=0;

Характеристическое уравнение: ;

(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ² — 1) = 0

λ₁ = -3, λ₂ = 1, λ₃ = -1.

Найдем собственный вектор, отвечающий собственному числу λ = -3:

5x₁+3x₃=0;

10x₁-6x₃=0;

-x₁+x₃=0;

Ранг матрицы этой системы равен двум и равен числу неизвестных, поэтому эта система имеет только нулевое решение x₁ = x₃ = 0. x₂ здесь может быть любым, отличным от нуля, например, x₂ = 1. Таким образом, вектор (0,1,0) является собственным вектором, отвечающим λ = -3. Проверим:

Если λ = 1, то получаем систему

Ранг матрицы равен двум. Последнее уравнение вычеркиваем.

Пусть x₃ — свободное неизвестное. Тогда x₁ = -3x₃, 4x₂ = 10x₁ — 6x₃ = -30x₃ — 6x₃, x₂ = -9x₃.

Полагая x₃ = 1, имеем (-3,-9,1) — собственный вектор, отвечающий собственному числу λ = 1. Проверка:

Так как собственные числа действительные и различны, то векторы, им отвечающие, линейно независимы, поэтому их можно принять за базис в R₃. Таким образом, в базисе f₁=(1,8,-1), f₂=(0,1,0), f₃=(-3,-9,1) матрица A имеет вид:

.

Не всякую матрицу линейного оператора A:R_n→ R_n можно привести к диагональному виду, поскольку для некоторых линейных операторов линейно независимых собственных векторов может быть меньше n. Однако, если матрица симметрическая, то корню характеристического уравнения кратности m соответствует ровно m линейно независимых векторов.

Определение. Симметрической матрицей называется квадратная матрица, в которой элементы, симметричные относительно главной диагонали, равны, то есть в которой a_i^k=a_kⁱ.

Замечания.

Все собственные числа симметрической матрицы вещественны.
Собственные векторы симметрической матрицы, соответствующие попарно различным собственным числам, ортогональны.

В качестве одного из многочисленных приложений изученного аппарата, рассмотрим задачу об определении вида кривой второго порядка.

Перейти к онлайн решению своей задачи

Источник

Решение

Линейные операции над векторами

Базис. Cкалярное произведение

Векторное и смешанное произведения векторов

Декартова система координат. прямая на плоскости

Плоскость в пространстве

Прямая в пространстве

Кривые второго порядка — I

Кривые второго порядка — II

Поверхности второго порядка

Матрицы и операции с ними

Обратная матрица

Ранг матрицы

Системы линейных алгебраических уравнений

Свойства решений однородных и неоднородных СЛАУ

Линейные операторы

Собственные вектора и собственные значения линейного оператора

Собственные векторы и значения линейного оператора (преобразования)

Связь собственных векторов линейного преобразования (оператора) и его матрицы

Нахождение собственных векторов и значений линейного оператора (преобразования)

Примеры собственных векторов линейных операторов (преобразований)

Собственные числа и собственные векторы линейного оператора

Правило отыскания собственных чисел и собственных векторов