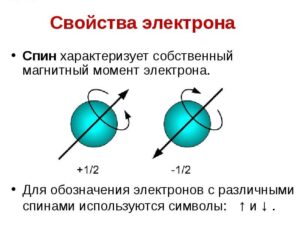
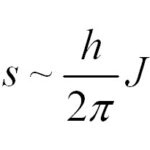Итак, полностью абстрагируемся и забываем любые классические определения. Ибо спин – это понятие, присущее исключительно квантовому миру. Попробуем разобраться в том, что это такое.
Больше полезной информации для учащихся – у нас в телеграм.
Спин и момент импульса
Спин (от английского spin – вращаться) – собственный момент импульса элементарной частицы.
Теперь вспомним, что такое момент импульса в классической механике.
Момент импульса – это физическая величина, характеризующая вращательное движение, точнее, количество вращательного движения.
В классической механике момент импульса определяется как векторное произведение импульса частицы на ее радиус вектор:
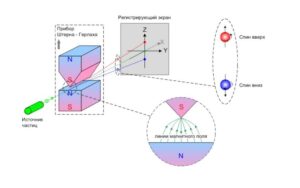
По аналогии с классической механикой спин характеризует вращение частиц. Их представляют в виде волчков, вращающихся вокруг оси. Если частица имеет заряд, то, вращаясь, она создает магнитный момент и явлеятся своего рода магнитом.
Однако данное вращение нельзя трактовать классически. Все частицы помимо спина обладают внешним или орбитальным моментом импульса, характеризующим вращение частицы относительно какой-то точки. Например, когда частица движется по круговой траектории (электрон вокруг ядра).
Спин же является собственным моментом импульса, то есть характеризует внутреннее вращательное состояние частицы вне зависимости от внешнего орбитального момента импульса. При этом спин не зависит от внешних перемещений частицы.
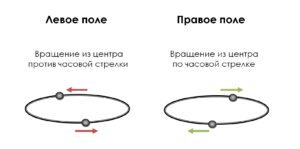
Представить, что же там вращается внутри частицы, невозможно. Однако факт остается фактом – для заряженных частиц с разнонаправленными спинами траектории движения в магнитном поле будут различны.
Спиновое квантовое число
Для характеристики спина в квантовой физике введено спиновое квантовое число.
Спиновое квантовое число – одно из квантовых чисел, присущих частицам. Часто спиновое квантовое число называют просто спином. Однако следует понимать, что спин частицы (в понимании собственного момента импульса) и спиновое квантовое число – это не одно и то же. Спиновое число обозначается буквой J и принимает ряд дискретных значений, а само значение спина пропорционально приведенной постоянной Планка:
Бозоны и фермионы
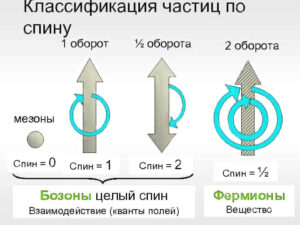
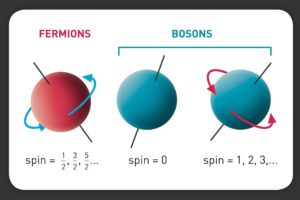
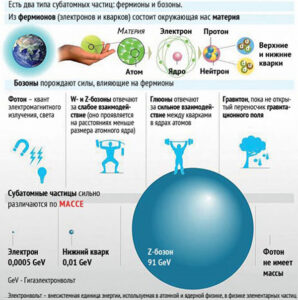
Разным частицам присущи разные спиновые числа. Так, главное отличие состоит в том, что одни обладают целым спином, а другие – полуцелым. Частицы обладающие целым спином называются бозонами, а полуцелым – фермионами.
Бозоны подчиняются статистике Бозе-Эйнштейна, а фермионы – Ферми-Дирака. В ансамбле частиц, состоящем из бозонов, любое их количество может находиться в одинаковом состоянии. С фермионами все наоборот – наличие двух тождественных фермионов в одной системе частиц невозможно.
Бозоны: фотон, глюон, бозон Хиггса. Подробнее о бозоне Хиггса — в отдельной статье.
Фермионы: электрон, лептон, кварк
Попробуем представить, чем отличаются частицы с разными спиновыми числами на примерах из макромира. Если спин объекта равен нулю, то его можно представить в виде точки. Со всех сторон, как ни вращай этот объект, он будет одинаков. При спине равном 1 поворот объекта на 360 градусов возвращает его в состояние, идентичное первоначальному состоянию.
Например, карандаш, заточенный с одной стороны. Спин равный 2 можно представить в виде карандаша, заточенного с двух сторон — при повороте такого карандаша на 180 градусов мы не заметим никаких изменений. А вот полуцелый спин равный 1/2 представляется объектом, для возвращения которого в первоначальное состояние нужно соверщить оборот в 720 градусов. Примером может служить точка, движущаяся по листу Мебиуса.
Итак, спин — квантовая характеристика элементарных частиц, которая служит для описания их внутреннего вращения, момент импульса частицы, не зависящий от ее внешних перемещений.
Надеемся, что вы осилите эту теорию быстро и сможете при случае применить знания на практике. Ну а если задачка по квантовой механике оказалось непосильно сложной или не можете не забывайте о студенческом сервисе, специалисты которого готовы прийти на выручку. Учитывая, что сам Ричард Фейнман сказал, что «в полной мере квантовую физику не понимает никто», обратиться за помощью к опытным специалистам – вполне естественно!
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Спин
Из
проекта Викизнание
Спин в квантовой механике обозначает собственный момент импульса
отдельных элементарных частиц и их связанных состояний в виде ядер и атомов. В отличие
от орбитального момента импульса, спин не связан с перемещением в пространстве
центра инерции частицы, и является её внутренней характеристикой. Поскольку
спин является вектором, он имеет направление в пространстве и отражает вращение
составных элементов частицы. У ядер и атомов спин определяется по правилам
квантовой механики как векторная сумма орбитальных и спиновых моментов импульса
составляющих частиц, с учётом квантования проекций моментов импульса. При
увеличении размеров системы и количества частиц в ней орбитальные моменты
импульса могут быть много больше, чем спиновые моменты импульса. Это приводит к
тому, что спин макросистемы в виде отдельного тела почти полностью зависит от
орбитального вращения элементов вещества тела вокруг некоторой оси.
В квантовой механике квантовые числа для спина не совпадают с квантовыми
числами для орбитального момента частиц, что приводит к неклассической
трактовке спина. Кроме этого, у спина и орбитального момента частиц возникает
различная связь с соответствующими магнитными дипольными моментами,
сопровождающими любое вращение заряженных частиц. В частности, в формуле для
спина и его магнитного момента гиромагнитное отношение не равно 1.
Концепция спина у электрона привлекается для объяснения многих явлений, таких
как расположение атомов в периодической системе химических элементов, тонкая
структура атомных спектров, эффект Зеемана, ферромагнетизм, а также для
обоснования принципа Паули. Недавно возникшая область исследований, называемая
«спинтроника», занимается манипуляциями спинов
зарядов в полупроводниковых устройствах. В ядерном магнитном резонансе
используется взаимодействие радиоволн со спинами ядер, позволяющее осуществлять
спектроскопию химических элементов и получать изображения внутренних органов в медицинской
практике. Для фотонов как частиц света спин связывается с поляризацией света.
Математическая теория спина была использована для построения теории изоспина элементарных частиц.
Оглавление
- 1 История
- 2 Спиновое квантовое число
- 2.1 Спин элементарных частиц
- 2.2 Спин составных частиц
- 2.3 Спин атомов и молекул
- 3 Связь между спином и
статистикой - 4 Спиновый магнитный момент
- 5 Ориентация спина
- 5.1 Квантовое число проекции
спина и мультиплетность - 5.2 Вектор спина
- 6 Математическая формулировка
спина в квантовой механике - 6.1 Оператор спина
- 6.2 Спин и принцип запрета
Паули - 6.3 Спин и вращения системы
координат - 6.4 Спин и лоренцевские преобразования
- 6.5 Матрицы Паули и
операторы спина - 6.6 Измерение спина вдоль
осей x, y, z - 6.7 Измерения спина вдоль
произвольной оси - 6.8 Совместимость измерений
спина - 7 Использование концепции
спина в науке и технике - 8 Обобщение спина
- 9 Сущность спина
- 9.1 Спин электрона
- 9.2 Характерный спин
- 9.3 Предельные соотношения
для нуклонов - 10 Ссылки
- 11 Справочная литература
- 12 Внешние ссылки
- 13 Смотри также
История
В 1922 г. был описан опыт Штерна — Герлаха,
который обнаружил пространственное квантование направления магнитных моментов у
атомов. Впоследствии, в 1927 г. это было интерпретировано как доказательство
существования спина у электронов. [1]
В 1924 г. Вольфганг Паули ввёл двухкомпонентную внутреннюю степень свободы
для описания эмиссионных спектров валентного электрона в щелочных металлах. Это
позволило ему сформулировать принцип Паули, согласно которому в некоторой системе
взаимодействующих частиц у каждого электрона должен быть свой собственный
неповторяющийся набор квантовых чисел (все электроны в каждый момент времени
находятся в разных состояниях). Поскольку физическая интерпретация спина у
электрона была неясна с самого начала (и это имеет место до сих пор), в 1925 г.
Ральф Крониг (ассистент известного физика Альфреда
Ланде) высказал предположение о спине как результате собственного вращения
электрона. Однако согласно Паули, в таком случае поверхность электрона должна
вращаться быстрее скорости света, что кажется невероятным. Тем не менее осенью 1925 г. Дж. Уленбек и С. Гаудсмит
постулировали, что электрон обладает спином
в
единицах постоянной
Дирака , и спиновым магнитным моментом, равным магнетону Бора. Это
предположение и было принято научным сообществом, поскольку удовлетворительно
объясняло известные факты.
В 1927 г. Паули модифицировал открытое ранее Шрёдингером и Гейзенбергом
уравнение Шрёдингера с целью учёта спиновой переменной, используя
спиновые операторы и матрицы Паули. Модифицированное таким образом
уравнение носит сейчас название уравнение Паули. При таком подходе у электрона
появляется новая спиновая часть волновой функции, которая описывается спинором
— «вектором» в некотором абстрактном спиновом пространстве.
В 1928 году Поль Дирак построил релятивистскую теорию спина на основе
четырёхкомпонентной величины, называемой биспинором.
Спиновое квантовое число
Спин элементарных частиц
В теории элементарных частиц обычно предполагается, что фотон, электрон и кварки не делятся на более мелкие
части и являются самыми «элементарными». Однако спин, который приписывается
этим частицам, слишком велик, чтобы его можно было объяснить вращением
составляющего вещества при известных оценках размеров частиц. Поэтому для этих
частиц спин полагается некоторым внутренним свойством, наподобие массы и
заряда, требующим особого, пока ещё не известного обоснования.
В квантовой механике спиновый момент импульса любой системы квантуется.
Амплитуда или длина вектора спинового момента в каждом состоянии равна:
где есть постоянная Дирака, а спиновое квантовое число s является положительным целым или полуцелым числом (0, 1/2, 1, 3/2, 2, …) и зависит от типа
частицы. В противоположность этому орбитальный момент импульса имеет только
целые квантовые числа.
Спин составных частиц
К составным частицам можно отнести атомные ядра, состоящие из нуклонов, а
также адроны, согласно кварковой концепции
состоящие из кварков. Спин составной частицы находится векторным суммированием
орбитальных и спиновых моментов импульса всех составляющих её частиц, с учётом
правил квантового сложения, и также квантуется, как любой момент импульса. В
квантовой механике каждая составная частица имеет некоторый минимально
возможный спин, не обязательно равный нулю (в этом состоянии моменты импульса
составляющих частиц частично компенсируют друг друга, уменьшая спин составной
частицы до минимума). Если же моменты импульса составляющих частиц
складываются, то это может приводить к состояниям, в которых составная частица
имеет значительный спин. Так, одним из наибольших спинов среди адронов обладает
барионный резонанс Δ(2950) со спином 15/2. Спин
ядер из-за их относительно больших размеров может превышать 20 .
В качестве других примеров можно привести Δ-барион
и какой-либо нуклон, протон или нейтрон. В кварковой
теории у Δ-бариона спины всех трёх кварков
складываются, давая спин 3/2. В нуклоне спины двух кварков противоположны и
вычитаются, и спин 1/2 нуклона равен спину третьего кварка. Картина однако усложняется тем, что в нуклонах кроме кварков
предполагаются глюоны как переносчики взаимодействия,
а также виртуальные частицы. Вследствие этого распределение момента импульса
между кварками и глюонами в адронах точно не
определено.
Спин атомов и молекул
Размеры атомов и молекул много больше размеров атомных ядер, так что спин
какого-либо атома определяется его электронной оболочкой. В заполненных атомных
оболочках количество электронов чётно и их суммарный момент импульса равен
нулю. Поэтому за спин атомов и молекул ответственны неспаренные
электроны, находящиеся обычно на внешней оболочке. Считается, что именно спин неспаренных электронов приводит к явлению парамагнетизма.
Ниже указаны спины некоторых элементарных и составных частиц.
|
спин |
общее название |
примеры |
|
0 |
скалярные частицы |
π-мезоны, K-мезоны, хиггсовский |
|
1/2 |
спинорные частицы |
электрон, кварки, протон, нейтрон, атомы и |
|
1 |
векторные частицы |
фотон, глюон, векторные мезоны, ортопозитроний |
|
3/2 |
спин-векторные |
Δ-изобары, гравитино |
|
2 |
тензорные частицы |
гравитон, тензорные мезоны |
Связь между спином и статистикой
В квантовой механике волновая функция системы из нескольких одинаковых
частиц может быть либо симметричной (неизменной) относительно перестановки
местами двух любых частиц, либо антисимметричной, что приводит к умножению
волновой функции на −1. В первом случае говорят, что частицы подчиняются
статистике Бозе – Эйнштейна, а сами частицы
называются бозонами. Во втором случае частицы называются фермионами и
подчиняются статистике Ферми – Дирака.
В 1940 г. Паули доказал теорему о связи спина со статистикой, которая
утверждает: «Частицы с целым спином (s = 0, 1,
2, …) являются бозонами, а частицы с полуцелым спином
(s = 1/2, 3/2, …) – фермионами». [2]
Это означает, что симметрия волновой функции относительно перестановки
одинаковых частиц определяется спиновыми квантовыми числами данных частиц.
Свойством частиц – бозонов является то, что в одном и том же квантовом
состоянии может находиться одновременно множество частиц. У фермионов каждая
частица в соответствии с принципом запрета Паули имеет квантовое состояние, не
совпадающее с состояниями других частиц.
Спиновый магнитный момент
Спин является частью полного механического момента импульса частицы, и если
последняя заряжена, то спину по формулам классической электродинамики можно
поставить в соответствие определённый магнитный дипольный момент. При этом
часто используется так называемое гиромагнитное отношение как отношение
магнитного момента к механическому моменту. Для частицы с массой m, зарядом q и спином S спиновый магнитный момент μ равен:
где безразмерная величина g называется g-фактором. Для чисто орбитального
(например, кругового) вращения элементов заряженного вещества частицы вокруг
оси g-фактор должен быть равен 1. У электрона g-фактор почти точно равен 2, что
существенно отличает спин от орбитального вращения. Отличие g-фактора электрона
от 2 в квантовой электродинамике обосновывается как следствие взаимодействия
заряда электрона с окружающим электромагнитным полем, включая самодействие поля
электрона. За счёт спинового магнитного момента частицы могут взаимодействовать
друг с другом и с внешними магнитными полями.
Как правило принимается, что нейтрино электрически
нейтральны, но при наличии некоторой ненулевой массы покоя у них не исключается
наличие магнитного момента.[3] [4] [5] Формула
для предполагаемого магнитного момента нейтрино имеет вид:
где есть масса-энергия
нейтрино в электронвольтах, –
магнетон Бора. Если исходить из оценок массы-энергии нейтрино, не превышающих
значение 1 eV, то из соображений ограниченности электромагнитной энергии по
сравнению с энергией покоя ожидается, что магнитный момент нейтрино не
превышает 10−14. [6]
Из имеющихся экспериментальных данных магнитный момент нейтрино не превышает
1,2 × 10–10 от величины магнитного момента электрона.
Наличие спина у составных частиц приводит к соответствующему спиновому
магнитному моменту. Многие нейтральные адроны, невзирая на равенство нулю у них
суммарного заряда, обладают магнитным моментом, причём направление магнитного
момента обычно противоположно спину. Это ясно указывает на их сложную
внутреннюю электромагнитную структуру. С точки зрения кварков, которым
приписываются различные заряды, магнитные моменты адронов приблизительно могут
быть получены как комбинации спиновых и орбитальных магнитных моментов
составляющих адроны кварков.
В веществе большинства тел магнитные моменты атомов направлены случайным
образом в различные стороны и взаимно вычитают друг друга, обращая суммарное
магнитное поле в нуль. В ферромагнитных материалах
ниже температуры Кюри возникает внутренняя магнитная упорядоченность за счёт
доменной структуры. В каждом домене магнитные моменты атомов выстраиваются
приблизительно параллельно, усиливая общее магнитное поле. В свою очередь
магнитные поля доменов суммируются векторно, приводя
к достаточно устойчивой намагниченности ферромагнетиков и превращая их в
магниты.
Магнитная упорядоченность возникает и под действием внешнего магнитного
поля. В парамагнитных материалах магнитные моменты атомов устанавливаются вдоль
приложенного магнитного поля, тогда как в диамагнитных веществах атомные
магнитные моменты направлены против поля и ослабляют его. Электронный
парамагнетизм есть следствие ориентации электронных магнитных моментов, которые
начинают прецессировать вдоль направления поля. Диамагнетизм вытекает из
действия закона электромагнитной индукции, согласно которому при изменении
магнитного потока в системе зарядов возникает электродвижущая сила.
Появляющееся по действием
этой силы движение зарядов приводит к магнитному полю, направленному
противоположно исходному магнитному полю (правило Ленца). Считается, что
существенная доля магнитных моментов атомов связана со спином электронов, хотя
вклады в магнитные эффекты делают и орбитальные магнитные моменты электронов.
Ориентация спина
Квантовое число проекции спина и мультиплетность
Поскольку спин является вектором момента импульса, он имеет и амплитуду и направление в пространстве. В квантовой механике
используется понятие о проекции момента импульса на некоторую выделенную ось
(обычно направление этой оси в пространстве задаётся внешним магнитным полем).
Пусть выделенное направление фиксируется осью z используемой системы отсчёта. Тогда возможные
проекции спина на эту ось имеют значения:
где s
есть спиновое квантовое число для частицы или системы частиц. Общее
число проекций спина sz равно 2s+1. В стандартной теории в
приближении спин-орбитальной связи число 2s+1 называется мультиплетностью спиновой системы.
В частности, для частиц со спином 1/2 получается
только два значения для проекции спина: sz
= +1/2 и sz = -1/2. Отсюда следует,
что для электрона в водородоподобном атоме мультиплетность равна 2, а спектры
таких атомов имеют дублетную природу. При наличии двух электронов, как это
происходит в гелии, суммарный спин обоих электронов равен 0 либо 1.
Соответственно, мультиплетность будет равна 1 для парагелия с одиночными
линиями в спектре, и равна 3 для ортогелия с триплетными линиями в спектре.
Вектор спина
В каждом квантовом состоянии можно ввести вектор спина ,
чьими компонентами являются ожидаемые значения проекций спина на оси системы
координат .
Этот вектор указывает «направление» спина, соответствующее в
классическом пределе оси вращения. В квантовомеханических
вычислениях вектор спина имеет особенность – его компоненты sx, sy и sz
не могут быть измерены одновременно из-за квантового принципа неопределённости Гейзенберга.
Однако для статистически больших наборов частиц при одинаковых начальных
квантовых состояниях, как это имеет место в опыте Штерна — Герлаха,
вектор спина и связанный с ним вектор магнитного момента имеют хорошо
определённое экспериментально направление – оно задаётся той ориентацией
детектора, при которой отмечается наибольшее
количество частиц из всего используемого набора.
Вследствие связи между спином и его магнитным моментом внешнее магнитное
поле будет приводить к прецессии спина вдоль магнитного поля. Этот эффект
аналогичен классическому гироскопическому эффекту – магнитное поле действует на
магнитный дипольный момент и создаёт крутящий момент, который прикладывается к
спиновому механическому моменту частицы и приводит к прецессии оси вращения и
спина частицы.
В квантовой механике спин описывается не просто вектором как классический
момент импульса, а с помощью математических объектов – спиноров. Поведение
векторов и спиноров при вращении координат различается. Например, каждое
вращение частицы со спином 1/2 на 360 градусов приводит частицу не в прежнее
состояние, а в состояние с противоположной квантовомеханической
фазой. Для частицы с нулевым спином её квантовое состояние при вращении не
меняется. Если же у частицы спин равен 2, то при вращении на 180 градусов она
получает прежнее квантовое состояние.
Математическая формулировка спина в квантовой механике
Оператор спина
Оператор спина подчиняется тем же соотношениям, что и оператор орбитального
момента импульса:
где εijk – символ Леви-Чивиты. Собственные векторы операторов S2
и Sz (выраженные через кет-векторы в общем S-базисе) равны:
где через m
обозначено квантовое число проекции спина на выделенную ось.
Операторы увеличения и уменьшения спина, действующие на данные собственные
векторы, дают соотношения:
,
где
В отличие от орбитального момента импульса, указанные собственные векторы (и
соответствующие матричные элементы) не выражаются через сферические гармоники и
не являются функциями углов θ и φ. Величины s и m могут быть полуцелыми числами.
В квантовой механике спин квантуется в единицах постоянной
Дирака , которая образуется путём деления постоянной Планка (постоянной
действия) на 2π. При этом функция состояния частицы зависит как от координат в виде радиус-вектора
, так и от
в виде дискретного набора
величин:
Здесь можно выделить бозоны (s = 0 или 1 или 2 или
…) и фермионы (s = 1/2 или 3/2 или 5/2 или …). В
процессах взаимодействия сохраняется общий момент импульса системы,
складывающийся из орбитального момента импульса и спина.
Спин и принцип запрета Паули
Для систем из N идентичных частиц действует принцип Паули, который
устанавливает, что перестановка между любыми двумя из N частиц может
привести к изменению волновой функции системы:
Для бозонов фактор ( − 1)2s
равен +1, а для фермионов равен –1. В квантовой механике все частицы
разделяются на бозоны и фермионы. В релятивистской квантовополевой
теории суперсимметрии допускаются частицы, имеющие и
бозонные и фермионные компоненты.
Электроны являются фермионами с величиной
s = 1/2; кванты света ( фотоны)
являются бозонами с величиной s = 1. Фотоны являются релятивистскими объектами и хорошо
вписываются в релятивистскую квантовую электродинамику. Однако полуцелые квантовые числа для спина фермионов отличаются от
целых квантовых чисел для орбитального момента и для бозонов, приводя к
затруднению при классическом объяснении спина.
Спин и вращения системы координат
Согласно квантовой механике проекция момента импульса на выделенную ось
квантуется, образуя ряд дискретный значений. В связи с этим наиболее подходящим
квантовомеханическим способом описания спина частицы
являются комплексные числа, соответствующие амплитудам вероятности
нахождения заданной величины проекции спина на выделенную ось. Например,
для частицы со спином 1/2 требуется два числа
, задающие амплитуды вероятности нахождения проекций
спина, равных и
, и
удовлетворяющие условию:
Поскольку эти числа зависят от выбора осей координат, при вращении осей они
должны преобразовываться соответствующим образом. Из линейности преобразований,
которые описываются матрицей вращения, результат последовательного вращения,
представляемого двумя матрицами A и B, должен быть равен с точностью до фазы
результату вращения, представляемого матрицей AB. Кроме этого, вращения
сохраняют квантовомеханическое произведение, задающее
матрицы преобразования:
С точки зрения математики, эти матрицы определяют унитарное проективное
представление группы вращения SO(3). Каждое такое представление соответствует
представлению покрывающей группы для SO(3), которым является SU(2). Имеется
одно n-мерное неприводимое представление SU(2) для каждого измерения, причём
это представление является n-мерным действительным для нечётных n и n-мерным комплексным для чётных n
(следовательно будет 2n действительное представление).
В частности, если у частиц спин 1/2, то при вращениях он трансформируется
согласно 2-мерному представлению, которое генерируется матрицами Паули:
где α, β, γ являются углами Эйлера.
При наличии у частиц более высоких спинов 1 и 3/2 они трансформируются аналогичным
образом с помощью многомерных представлений и соответствующих матриц вращения.
Спин и лоренцевские преобразования
При попытке использовать аналогичный указанному
выше подход для поведения спина при преобразованиях Лоренца возникает
препятствие. Оно связано с тем, что в отличие от группы преобразований вращения
SO(3), группа лоренцевских преобразований SO(3,1) не
является компактной и не имеет необходимого унитарного ограниченно-мерного
представления.
В случае частиц со спином 1/2 можно найти конструкцию, которая включает
ограниченно-мерное представление и скалярное произведение, соответствующее
этому представлению. Каждой частице можно приписать 4-компонентный спинор
Дирака ψ. Такие
спиноры преобразуются при преобразованиях Лоренца по следующему закону:
где γμ есть гамма-матрицы,
ωμν – антисимметричные 4×4 матрицы, параметризующие преобразование. При этом сохраняется
следующее скалярное произведение:
Матрицы Паули и операторы спина
Квантовомеханические операторы, связанные со
спиновыми наблюдаемыми величинами, имеют вид:
В особом случае спина 1/2 имеются три матрицы Паули σx, σy и σz:
Измерение спина вдоль осей x, y, z
Каждая из эрмитовых матриц Паули имеет два
собственных значения, +1 и -1. Соответствующими нормализованными волновыми
собственными векторами являются следующие:
Согласно постулатам квантовой механики, эксперимент, направленный на
измерение компонент электронного спина вдоль осей x, y или z может дать только
собственные значения спинового оператора (Sx, Sy, Sz) на эти оси, равные и
.
Квантовое состояние частицы с учётом спина может быть представлено
двухкомпонентным спинором:
Когда спин измеряется по отношению к заданной оси,
например оси x, вероятность, что измерение даст значение , равна
. Соответственно, вероятность того, что при измерении будет
получено значение , равна
. В ходе измерения спина спиновое состояние частицы в виде волновой
функции редуцируется так, что получается какое-либо собственное состояние.
В результате, если при измерении вдоль заданной оси получилось собственное
значение, то и последующие аналогичные измерения вдоль этой оси не изменят
результата (так как , и
т.д.).
Измерения спина вдоль произвольной оси
Оператор спина вдоль произвольной оси может быть получен с помощью спиновых
матриц Паули. Допустим u = (ux,uy,uz)
есть произвольный единичный вектор. Тогда оператор спина в этом направлении
определяется выражением . Оператор Su имеет собственные значения
,
как и обычные спиновые матрицы. Аналогичным способом находятся операторы спина
в произвольном направлении и для спинов более высокого порядка.
Нормализованный спинор для спина 1/2
в (ux,uy,uz) направлении (который справедлив для всех
случаев спиновых состояний, кроме состояния спин вниз, где получается 0/0),
имеет вид:
Этот спинор получается после диагонализации
σu–матрицы и определения
собственных состояний и собственных значений спина.
Совместимость измерений спина
Поскольку матрицы Паули не коммутируют между собой, измерения спина вдоль
осей системы отсчёта не совместны друг с другом. Это означает
например, что при известном спине вдоль оси
x
последующее измерение спина вдоль оси
y
изменяет значение спина, имевшееся вдоль оси x ранее. Это видно из свойств собственных
векторов (собственных состояний) матриц Паули:
Если при измерении спина частицы вдоль оси
x
получено значение ,
это значит, что волновая функция спинового состояния редуцировалась в
собственное состояние . Если затем измерять спин частицы вдоль
оси y,
спиновое состояние станет равным либо либо
, каждое с вероятностью
.
Допустим, было измерено значение .
Если теперь вернуться к измерению спина вдоль оси x, вероятность
получения значения или
будет равна
(эти вероятности равны
и
). Это
означает, что первоначальное значение спина вдоль оси x
изменилось за счёт проведённого измерения вдоль оси y,
так как вероятность получения значения спина
теперь равна только
.
Использование концепции спина в науке и технике
Понятие спина широко используется в ядерном магнитном резонансе в химической
спектроскопии, в электронном парамагнитном резонансе в химической и физической
спектроскопии, в магниторезонансных измерениях плотности протонных спинов с
целью сканирования внутренних органов в медицине, в технологиях современных
компьютерных жёстких дисков на основе гигантского магниторезистивного эффекта.
Спин рассматривается как возможный носитель двоичной информации в спиновых
транзисторах. Электроника, связанная с такими транзисторами, носит название спинтроника. [7]
Спин и принцип Паули оказываются необходимыми в квантовой механике для
объяснения ряда явлений и закономерностей, таких например, как периодическая
таблица Дмитрия Менделеева.
Обобщение спина
Введение спина означает применение новой физической идеи: постулирование
того, что существует пространство состояний, никак не связанных с перемещением
частицы в обычном пространстве. Обобщение этой идеи в ядерной физике привело к
понятию изотопического спина, который действует в особом изоспиновом
пространстве. В дальнейшем, при описании сильных
взаимодействий были введены внутреннее цветовое пространство и квантовое
число цвет, как более сложный аналог спина.
Сущность спина
Особенностью квантовой механики является то, что в ней реальные движения
частиц заменяются квантованными волновыми движениями, а результаты
экспериментов вычисляются в виде вероятностей тех или иных событий. Такой
подход принципиально не может объяснить природу спина, поскольку для этого требуются
субстанциональные модели частиц. Некоторые такие модели на основе теории бесконечной вложенности материи,
а также концепция динамического спина электрона были предложены Сергеем
Федосиным в 2009 г. [8] В теории бесконечной вложенности материи
спин ряда одинаковых объектов рассматривается как собственный характерный
момент импульса, которым в среднем обладают данные объекты. Если у элементарных
частиц характерный спин измеряется в единицах , то на
звёздном уровне материи вырожденные объекты типа
нейтронных звёзд имеют характерный момент импульса порядка Дж•с (смотри звёздная
постоянная Дирака). Различие спинов как характерных моментов импульса
приводит к различию соотношений
неопределённости на разных уровнях материи, например: [9]
для уровня элементарных
частиц,
для уровня звёзд.
Одним из следствий этого становится то, что приписывание частицам,
составляющим объект, того же самого значения спина, которым обладает данный
объект, оказывается не всегда правильным (такая ситуация предполагается для
трёх кварков внутри нуклона согласно квантовой хромодинамике
и особенно в преонных моделях элементарных частиц, где в результате
возникает «парадокс масс»).
Спин электрона
Расчёт баланса сил на поверхности электрона с учётом действия сильной гравитации и электрической
силы Кулона показывает, что электрон как самостоятельная частица не может иметь
какой-то определённый радиус – электрическая сила расталкивает частицы вещества
сильнее, чем сила гравитации. Стабилизация электрона в виде облака возможна в
атомах, где имеются дополнительные гравитационные и электрические силы
притяжения со стороны ядра, силы отталкивания от других электронов и
центростремительные силы при вращении вещества.
В субстанциональной модели спин
электрона носит не статическую, а динамическую природу. Он появляется за счёт
сложного движения электронного облака вокруг ядра в результате взаимодействия с
фотоном или другим электроном. Вещество электрона вращается вокруг центра
инерции облака, давая орбитальную компоненту момента импульса. Кроме этого
возникает общее вращение облака вокруг ядра атома, выражающееся во вращении
центра инерции облака относительно ядра и в появлении соответствующей
компоненты момента импульса. Эта компонента и является так называемым
динамическим спином электрона. Она ответственна за излучение электромагнитного
кванта при переходе электрона с верхнего уровня энергии на нижний, а также за
спиновый магнитный момент. В отсутствие динамического спина излучение из атома
стремится к нулю. Вследствие различия вращательных движений вещества,
ответственных за динамический спин и орбитальное вращение, возникает различие
значений g-факторов в формулах, связывающих спиновый и орбитальный моменты
импульса и соответствующие им магнитные моменты.
Согласно расчётам в основном состоянии атома, а также в s-состояниях
магнитный момент электрона в атоме связан не со спином (в этих состояниях
динамический спин равен нулю, центр электронного облака не вращается
относительно ядра), а с орбитальным вращением вещества электронного облака.
Динамический спин и соответствующий ему спиновый магнитный момент для
простейшего случая плоского движения вещества могут иметь два направления
относительно орбитального момента электрона. Это приводит к энергии
взаимодействия магнитного момента электрона и магнитного момента ядра,
вращающегося относительно центра инерции электронного облака. Данная энергия
приводит к расщеплению уровней энергии на дублеты в водородоподобном атоме, к
мультиплетности и к тонкой структуре атомных спектров. В субстанциональной
модели электрона даётся своё объяснение лэмбовскому
сдвигу уровней энергии, принципу Паули, магнитомеханическим явлениям с
электронами, связывающим намагничение образцов с их
вращением.
Характерный спин
В ряде случаев характерный спин элементарных частиц можно найти прямым
расчётом. В частности для некоторых адронов, исходя из аналогии строения их
вещества с нейтронными звёздами, используется соотношение между радиусом и массой
адрона: [10]
где и
– радиус и масса протона.
В следующей таблице приведены массы и радиусы протона, пиона и мюона,
необходимые для расчёта их спина. Радиус мюона находился с помощью теории подобия уровней материи, исходя из
радиуса белого карлика, соответствующего мюону.
|
Характеристики |
||||||
|
Частица |
Масса-энергия, |
Масса, 10–27 |
Радиус, 10–16 |
Энергия связи |
Характерный |
Квантовый спин |
|
Протон p+ |
938,272029 |
1,6726 |
8,7 |
938,272 |
5,34 |
ħ/2 |
|
Пион π+ |
139,567 |
0,249 |
16,4 |
11 |
0,54 |
0 |
|
Мюон μ+ |
105,658 |
0,188 |
10900 |
0,095 |
9,1 |
ħ/2 |
Массы частиц получаются путём деления массы-энергии, переведенной из МэВ в Дж,
на квадрат скорости света. Характерный момент импульса объекта находится по
формуле:
причём характерная скорость частиц вещества объекта связана с абсолютной
величиной полной энергии объекта в поле сильной гравитации: [9]
здесь для объектов типа нуклонов и нейтронных звёзд,
– постоянная сильной гравитации.
Для протона была также найдена формула ,
так что для характерного спина протона получается: , где
– скорость
света и характерная скорость частиц вещества протона, – постоянная Планка. Если применить
такой же подход для характерного спина мюона, получится следующее:
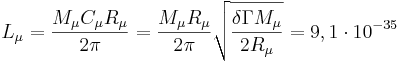
Характерный спин мюона превышает значение
квантового спина ħ/2 , принятого для фермионов и
лептонов. Для пиона при его радиусе согласно таблице спин получается
равным 0,05 ħ , то есть значительно меньше
минимального спина фермиона, равного ħ/2. Вследствие
этого квантовый спин пиона полагается равным нулю, а сам пион считается
бозоном. В квантовой статистике представление пиона в виде бозона существенно
отличает пион от протона, являющегося фермионом. Однако пион отличается от
протона лишь уменьшенной массой, так что общепринятое подразделение
элементарных частиц по значению спина на фермионы и бозоны не совсем корректно
в свете того, что бозонам и фермионам предписывается кардинальное различие в
поведении за счёт действия принципа Паули.
Предельные соотношения для нуклонов
Можно предположить, что протон имеет не только квантовомеханический
спин, равный , но
и предельный момент импульса собственного вращения как некоторый максимальный
спин. Тогда при предельном вращении возникает формула для магнитного момента
протона: [8]
Данная формула для нейтрона несколько изменяется, поскольку в отличие от
протона нейтрон в субстанциональной
модели имеет более сложную внутреннюю электромагнитную структуру с
неоднородным распределением электрического заряда.
Максимальный спин протона позволяет оценить его радиус путём сравнения
момента импульса поля сильной гравитации и спина. [11]
Ссылки
- B. Friedrich, D. Herschbach.
Stern
and Gerlach: How a Bad Cigar Helped Reorient
Atomic Physics. Physics Today, 2003, Vol. 56, issue 12, page 53. - W. Pauli «The Connection Between Spin and Statistics», Phys. Rev. 58, 716-722 (1940), pdf.
- W.J. Marciano, A.I. Sanda.
Exotic decays of the muon and heavy leptons in gauge theories. Physics Letters, 1977, Vol. B67, issue 3, page 303–305. - B.W. Lee, R.E. Shrock.
Natural suppression of symmetry violation in gauge theories: Muon- and
electron-lepton-number nonconservation. Physical Review, 1977, Vol. D16, issue 5, page 1444–1473. - K. Fujikawa, R.
E. Shrock. Magnetic Moment of a Massive Neutrino
and Neutrino-Spin Rotation. Physical Review Letters, 1980, Vol. 45, issue 12, page 963–966. - N.F. Bell et al. How Magnetic is
the Dirac Neutrino? Physical Review Letters, 2005, Vol. 95, issue 15, page
151802. arXiv hep-ph/0504134.
- Spintronics. Feature Article в Scientific American, June 2002.
- Федосин С.Г. Физические теории и бесконечная
вложенность материи. Пермь, 2009, 844 стр., Табл. 21, Ил.41, Библ. 289
назв. ISBN 978-5-9901951-1-0. - Федосин С. Г. Физика и философия подобия от преонов
до метагалактик, Пермь: Стиль-МГ, 1999, ISBN 5-8131-0012-1, 544 стр.,
Табл.66, Ил.93, Библ. 377 назв. - Комментарии к книге: Федосин
С.Г. Физические теории и бесконечная вложенность материи. Пермь, 2009, 844
стр., Табл. 21, Ил.41, Библ. 289 назв. ISBN 978-5-9901951-1-0. - Федосин С.Г. Современные проблемы физики. В
поисках новых принципов, М: Эдиториал УРСС,
2002, ISBN 5-8360-0435-8, 192 стр., Ил.26, Библ. 50 назв.
Справочная литература
- «Физическая
энциклопедия» под ред. Прохорова А.М. -М.: Научное издательство
«Большая российская энциклопедия».-1994 г. ISBN 5-85270-087-8.
Внешние ссылки
- Bigs animation The spin.
- Goudsmit on the discovery of electron spin.
- Nature
magazine Milestones in the field of ‘spin’ since 1896.
См. также
- Субстанциональная модель электрона
- Субстанциональная модель нейтрона
- Субстанциональная модель протона
- Принцип неопределённости Гейзенберга
- Модель кварковых квазичастиц
- Гравитационная модель сильного
взаимодействия
This article is about spin in quantum mechanics. For rotation in classical mechanics, see Angular momentum.
Spin is an intrinsic form of angular momentum carried by elementary particles, and thus by composite particles such as hadrons, atomic nuclei, and atoms.[1][2] Spin should not be simply understood as in the «rotating internal mass» sense. There is another type of angular momentum that more closely resembles rotation in classical mechanics, called orbital angular momentum. The orbital angular momentum operator appears when there is periodic structure to its wave function as the angle varies.[3][4] For photons, spin is the quantum-mechanical counterpart of the polarization of light; for electrons, the spin has no classical counterpart.[citation needed]
The existence of electron spin angular momentum is inferred from experiments, such as the Stern–Gerlach experiment, in which silver atoms were observed to possess two possible discrete angular momenta despite having no orbital angular momentum.[5] The existence of the electron spin can also be inferred theoretically from the spin–statistics theorem and from the Pauli exclusion principle—and vice versa, given the particular spin of the electron, one may derive the Pauli exclusion principle.
Spin is described mathematically as a vector for some particles such as photons, and as spinors and bispinors for other particles such as electrons. Spinors and bispinors behave similarly to vectors: they have definite magnitudes and change under rotations; however, they use an unconventional «direction». All elementary particles of a given kind have the same magnitude of spin angular momentum, though its direction may change. These are indicated by assigning the particle a spin quantum number.[2]
The SI unit of spin is the same as classical angular momentum (i.e., N·m·s, J·s, or kg·m2·s−1). In practice, spin is usually given as a dimensionless spin quantum number by dividing the spin angular momentum by the reduced Planck constant ħ, which has the same dimensions as angular momentum. Often, the «spin quantum number» is simply called «spin».
Quantum number[edit]
As the name suggests, spin was originally conceived as the rotation of a particle around some axis. While the question of whether elementary particles actually rotate is ambiguous (as they appear point-like), this picture is correct insofar as spin obeys the same mathematical laws as quantized angular momenta do; in particular, spin implies that the particle’s phase changes with angle. On the other hand, spin has some peculiar properties that distinguish it from orbital angular momenta:
- Spin quantum numbers may take half-integer values.
- Although the direction of its spin can be changed, an elementary particle cannot be made to spin faster or slower.
- The spin of a charged particle is associated with a magnetic dipole moment with a g-factor differing from 1. This could occur classically only if the internal charge of the particle were distributed differently from its mass.
The conventional definition of the spin quantum number is s = n/2, where n can be any non-negative integer. Hence the allowed values of s are 0, 1/2, 1, 3/2, 2, etc. The value of s for an elementary particle depends only on the type of particle and cannot be altered in any known way (in contrast to the spin direction described below). The spin angular momentum S of any physical system is quantized. The allowed values of S are
where h is the Planck constant, and 
Fermions and bosons[edit]
Those particles with half-integer spins, such as 1/2, 3/2, 5/2, are known as fermions, while those particles with integer spins, such as 0, 1, 2, are known as bosons. The two families of particles obey different rules and broadly have different roles in the world around us. A key distinction between the two families is that fermions obey the Pauli exclusion principle: that is, there cannot be two identical fermions simultaneously having the same quantum numbers (meaning, roughly, having the same position, velocity and spin direction). Fermions obey the rules of Fermi–Dirac statistics. In contrast, bosons obey the rules of Bose–Einstein statistics and have no such restriction, so they may «bunch together» in identical states. Also, composite particles can have spins different from their component particles. For example, a helium-4 atom in the ground state has spin 0 and behaves like a boson, even though the quarks and electrons which make it up are all fermions.
This has some profound consequences:
- Quarks and leptons (including electrons and neutrinos), which make up what is classically known as matter, are all fermions with spin 1/2. The common idea that «matter takes up space» actually comes from the Pauli exclusion principle acting on these particles to prevent the fermions from being in the same quantum state. Further compaction would require electrons to occupy the same energy states, and therefore a kind of pressure (sometimes known as degeneracy pressure of electrons) acts to resist the fermions being overly close. Elementary fermions with other spins (3/2, 5/2, etc.) are not known to exist.
- Elementary particles which are thought of as carrying forces are all bosons with spin 1. They include the photon, which carries the electromagnetic force, the gluon (strong force), and the W and Z bosons (weak force). The ability of bosons to occupy the same quantum state is used in the laser, which aligns many photons having the same quantum number (the same direction and frequency), superfluid liquid helium resulting from helium-4 atoms being bosons, and superconductivity, where pairs of electrons (which individually are fermions) act as single composite bosons. Elementary bosons with other spins (0, 2, 3, etc.) were not historically known to exist, although they have received considerable theoretical treatment and are well established within their respective mainstream theories. In particular, theoreticians have proposed the graviton (predicted to exist by some quantum gravity theories) with spin 2, and the Higgs boson (explaining electroweak symmetry breaking) with spin 0. Since 2013, the Higgs boson with spin 0 has been considered proven to exist.[6] It is the first scalar elementary particle (spin 0) known to exist in nature.
- Atomic nuclei have nuclear spin which may be either half-integer or integer, so that the nuclei may be either fermions or bosons.
Spin–statistics theorem[edit]
The spin–statistics theorem splits particles into two groups: bosons and fermions, where bosons obey Bose–Einstein statistics, and fermions obey Fermi–Dirac statistics (and therefore the Pauli exclusion principle). Specifically, the theory states that particles with an integer spin are bosons, while all other particles have half-integer spins and are fermions. As an example, electrons have half-integer spin and are fermions that obey the Pauli exclusion principle, while photons have integer spin and do not. The theorem relies on both quantum mechanics and the theory of special relativity, and this connection between spin and statistics has been called «one of the most important applications of the special relativity theory».[7]
Relation to classical rotation[edit]
Since elementary particles are point-like, self-rotation is not well-defined for them. However, spin implies that the phase of the particle depends on the angle as 
Photon spin is the quantum-mechanical description of light polarization, where spin +1 and spin −1 represent two opposite directions of circular polarization. Thus, light of a defined circular polarization consists of photons with the same spin, either all +1 or all −1. Spin represents polarization for other vector bosons as well.
For fermions, the picture is less clear. Angular velocity is equal by Ehrenfest theorem to the derivative of the Hamiltonian to its conjugate momentum, which is the total angular momentum operator J = L + S. Therefore, if the Hamiltonian H is dependent upon the spin S, dH/dS is non-zero, and the spin causes angular velocity, and hence actual rotation, i.e. a change in the phase-angle relation over time. However, whether this holds for free electron is ambiguous, since for an electron, S2 is constant, and therefore it is a matter of interpretation whether the Hamiltonian includes such a term. Nevertheless, spin appears in the Dirac equation, and thus the relativistic Hamiltonian of the electron, treated as a Dirac field, can be interpreted as including a dependence in the spin S.[8] Under this interpretation, free electrons also self-rotate, with the Zitterbewegung effect understood as this rotation.
Magnetic moments[edit]
Schematic diagram depicting the spin of the neutron as the black arrow and magnetic field lines associated with the neutron magnetic moment. The neutron has a negative magnetic moment. While the spin of the neutron is upward in this diagram, the magnetic field lines at the center of the dipole are downward.
Particles with spin can possess a magnetic dipole moment, just like a rotating electrically charged body in classical electrodynamics. These magnetic moments can be experimentally observed in several ways, e.g. by the deflection of particles by inhomogeneous magnetic fields in a Stern–Gerlach experiment, or by measuring the magnetic fields generated by the particles themselves.
The intrinsic magnetic moment μ of a spin-1/2 particle with charge q, mass m, and spin angular momentum S, is[9]
where the dimensionless quantity gs is called the spin g-factor. For exclusively orbital rotations it would be 1 (assuming that the mass and the charge occupy spheres of equal radius).
The electron, being a charged elementary particle, possesses a nonzero magnetic moment. One of the triumphs of the theory of quantum electrodynamics is its accurate prediction of the electron g-factor, which has been experimentally determined to have the value −2.00231930436256(35), with the digits in parentheses denoting measurement uncertainty in the last two digits at one standard deviation.[10] The value of 2 arises from the Dirac equation, a fundamental equation connecting the electron’s spin with its electromagnetic properties, and the correction of 0.002319304… arises from the electron’s interaction with the surrounding electromagnetic field, including its own field.[11]
Composite particles also possess magnetic moments associated with their spin. In particular, the neutron possesses a non-zero magnetic moment despite being electrically neutral. This fact was an early indication that the neutron is not an elementary particle. In fact, it is made up of quarks, which are electrically charged particles. The magnetic moment of the neutron comes from the spins of the individual quarks and their orbital motions.
Neutrinos are both elementary and electrically neutral. The minimally extended Standard Model that takes into account non-zero neutrino masses predicts neutrino magnetic moments of:[12][13][14]
where the μν are the neutrino magnetic moments, mν are the neutrino masses, and μB is the Bohr magneton. New physics above the electroweak scale could, however, lead to significantly higher neutrino magnetic moments. It can be shown in a model-independent way that neutrino magnetic moments larger than about 10−14 μB are «unnatural» because they would also lead to large radiative contributions to the neutrino mass. Since the neutrino masses are known to be at most about 1 eV, the large radiative corrections would then have to be «fine-tuned» to cancel each other, to a large degree, and leave the neutrino mass small.[15] The measurement of neutrino magnetic moments is an active area of research. Experimental results have put the neutrino magnetic moment at less than 1.2×10−10 times the electron’s magnetic moment.
On the other hand elementary particles with spin but without electric charge, such as a photon or a Z boson, do not have a magnetic moment.
Curie temperature and loss of alignment[edit]
In ordinary materials, the magnetic dipole moments of individual atoms produce magnetic fields that cancel one another, because each dipole points in a random direction, with the overall average being very near zero. Ferromagnetic materials below their Curie temperature, however, exhibit magnetic domains in which the atomic dipole moments spontaneously align locally, producing a macroscopic, non-zero magnetic field from the domain. These are the ordinary «magnets» with which we are all familiar.
In paramagnetic materials, the magnetic dipole moments of individual atoms will partially align with an externally applied magnetic field. In diamagnetic materials, on the other hand, the magnetic dipole moments of individual atoms align oppositely to any externally applied magnetic field, even if it requires energy to do so.
The study of the behavior of such «spin models» is a thriving area of research in condensed matter physics. For instance, the Ising model describes spins (dipoles) that have only two possible states, up and down, whereas in the Heisenberg model the spin vector is allowed to point in any direction. These models have many interesting properties, which have led to interesting results in the theory of phase transitions.
Direction[edit]
Spin projection quantum number and multiplicity[edit]
In classical mechanics, the angular momentum of a particle possesses not only a magnitude (how fast the body is rotating), but also a direction (either up or down on the axis of rotation of the particle). Quantum-mechanical spin also contains information about direction, but in a more subtle form. Quantum mechanics states that the component of angular momentum for a spin-s particle measured along any direction can only take on the values[16]
where Si is the spin component along the i-th axis (either x, y, or z), si is the spin projection quantum number along the i-th axis, and s is the principal spin quantum number (discussed in the previous section). Conventionally the direction chosen is the z axis:
where Sz is the spin component along the z axis, sz is the spin projection quantum number along the z axis.
One can see that there are 2s + 1 possible values of sz. The number «2s + 1» is the multiplicity of the spin system. For example, there are only two possible values for a spin-1/2 particle: sz = +1/2 and sz = −1/2. These correspond to quantum states in which the spin component is pointing in the +z or −z directions respectively, and are often referred to as «spin up» and «spin down». For a spin-3/2 particle, like a delta baryon, the possible values are +3/2, +1/2, −1/2, −3/2.
Vector[edit]
For a given quantum state, one could think of a spin vector 
![{textstyle langle Srangle =[langle S_{x}rangle ,langle S_{y}rangle ,langle S_{z}rangle ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a52cf750b43ecfaa01df6ca13a322d6561695f15)
As a qualitative concept, the spin vector is often handy because it is easy to picture classically. For instance, quantum-mechanical spin can exhibit phenomena analogous to classical gyroscopic effects. For example, one can exert a kind of «torque» on an electron by putting it in a magnetic field (the field acts upon the electron’s intrinsic magnetic dipole moment—see the following section). The result is that the spin vector undergoes precession, just like a classical gyroscope. This phenomenon is known as electron spin resonance (ESR). The equivalent behaviour of protons in atomic nuclei is used in nuclear magnetic resonance (NMR) spectroscopy and imaging.
Mathematically, quantum-mechanical spin states are described by vector-like objects known as spinors. There are subtle differences between the behavior of spinors and vectors under coordinate rotations. For example, rotating a spin-1/2 particle by 360° does not bring it back to the same quantum state, but to the state with the opposite quantum phase; this is detectable, in principle, with interference experiments. To return the particle to its exact original state, one needs a 720° rotation. (The Plate trick and Möbius strip give non-quantum analogies.) A spin-zero particle can only have a single quantum state, even after torque is applied. Rotating a spin-2 particle 180° can bring it back to the same quantum state, and a spin-4 particle should be rotated 90° to bring it back to the same quantum state. The spin-2 particle can be analogous to a straight stick that looks the same even after it is rotated 180°, and a spin-0 particle can be imagined as sphere, which looks the same after whatever angle it is turned through.
Mathematical formulation[edit]
Operator[edit]
Spin obeys commutation relations[17] analogous to those of the orbital angular momentum:
where εjkl is the Levi-Civita symbol. It follows (as with angular momentum) that the eigenvectors of 

The spin raising and lowering operators acting on these eigenvectors give
where 
But unlike orbital angular momentum, the eigenvectors are not spherical harmonics. They are not functions of θ and φ. There is also no reason to exclude half-integer values of s and ms.
All quantum-mechanical particles possess an intrinsic spin 




One distinguishes bosons (integer spin) and fermions (half-integer spin). The total angular momentum conserved in interaction processes is then the sum of the orbital angular momentum and the spin.
Pauli matrices[edit]
The quantum-mechanical operators associated with spin-1/2 observables are
where in Cartesian components
For the special case of spin-1/2 particles, σx, σy and σz are the three Pauli matrices:
Pauli exclusion principle[edit]
For systems of N identical particles this is related to the Pauli exclusion principle, which states that its wavefunction 
Thus, for bosons the prefactor (−1)2s will reduce to +1, for fermions to −1. In quantum mechanics all particles are either bosons or fermions. In some speculative relativistic quantum field theories «supersymmetric» particles also exist, where linear combinations of bosonic and fermionic components appear. In two dimensions, the prefactor (−1)2s can be replaced by any complex number of magnitude 1 such as in the anyon.
The above permutation postulate for N-particle state functions has most important consequences in daily life, e.g. the periodic table of the chemical elements.
Rotations[edit]
As described above, quantum mechanics states that components of angular momentum measured along any direction can only take a number of discrete values. The most convenient quantum-mechanical description of particle’s spin is therefore with a set of complex numbers corresponding to amplitudes of finding a given value of projection of its intrinsic angular momentum on a given axis. For instance, for a spin-1/2 particle, we would need two numbers a±1/2, giving amplitudes of finding it with projection of angular momentum equal to +ħ/2 and −ħ/2, satisfying the requirement
For a generic particle with spin s, we would need 2s + 1 such parameters. Since these numbers depend on the choice of the axis, they transform into each other non-trivially when this axis is rotated. It is clear that the transformation law must be linear, so we can represent it by associating a matrix with each rotation, and the product of two transformation matrices corresponding to rotations A and B must be equal (up to phase) to the matrix representing rotation AB. Further, rotations preserve the quantum-mechanical inner product, and so should our transformation matrices:
Mathematically speaking, these matrices furnish a unitary projective representation of the rotation group SO(3). Each such representation corresponds to a representation of the covering group of SO(3), which is SU(2).[18] There is one n-dimensional irreducible representation of SU(2) for each dimension, though this representation is n-dimensional real for odd n and n-dimensional complex for even n (hence of real dimension 2n). For a rotation by angle θ in the plane with normal vector 
where 
Proof
Working in the coordinate system where 
Using the spin operator commutation relations, we see that the commutators evaluate to i Sy for the odd terms in the series, and to Sx for all of the even terms. Thus:
as expected. Note that since we only relied on the spin operator commutation relations, this proof holds for any dimension (i.e., for any principal spin quantum number s).[19]
A generic rotation in 3-dimensional space can be built by compounding operators of this type using Euler angles:
An irreducible representation of this group of operators is furnished by the Wigner D-matrix:
where
is Wigner’s small d-matrix. Note that for γ = 2π and α = β = 0; i.e., a full rotation about the z axis, the Wigner D-matrix elements become
Recalling that a generic spin state can be written as a superposition of states with definite m, we see that if s is an integer, the values of m are all integers, and this matrix corresponds to the identity operator. However, if s is a half-integer, the values of m are also all half-integers, giving (−1)2m = −1 for all m, and hence upon rotation by 2π the state picks up a minus sign. This fact is a crucial element of the proof of the spin–statistics theorem.
Lorentz transformations[edit]
We could try the same approach to determine the behavior of spin under general Lorentz transformations, but we would immediately discover a major obstacle. Unlike SO(3), the group of Lorentz transformations SO(3,1) is non-compact and therefore does not have any faithful, unitary, finite-dimensional representations.
In case of spin-1/2 particles, it is possible to find a construction that includes both a finite-dimensional representation and a scalar product that is preserved by this representation. We associate a 4-component Dirac spinor ψ with each particle. These spinors transform under Lorentz transformations according to the law
where γν are gamma matrices, and ωμν is an antisymmetric 4 × 4 matrix parametrizing the transformation. It can be shown that the scalar product
is preserved. It is not, however, positive-definite, so the representation is not unitary.
Measurement of spin along the x, y, or z axes[edit]
Each of the (Hermitian) Pauli matrices of spin-1/2 particles has two eigenvalues, +1 and −1. The corresponding normalized eigenvectors are
(Because any eigenvector multiplied by a constant is still an eigenvector, there is ambiguity about the overall sign. In this article, the convention is chosen to make the first element imaginary and negative if there is a sign ambiguity. The present convention is used by software such as SymPy; while many physics textbooks, such as Sakurai and Griffiths, prefer to make it real and positive.)
By the postulates of quantum mechanics, an experiment designed to measure the electron spin on the x, y, or z axis can only yield an eigenvalue of the corresponding spin operator (Sx, Sy or Sz) on that axis, i.e. ħ/2 or –ħ/2. The quantum state of a particle (with respect to spin), can be represented by a two-component spinor:
When the spin of this particle is measured with respect to a given axis (in this example, the x axis), the probability that its spin will be measured as ħ/2 is just 


Measurement of spin along an arbitrary axis[edit]
The operator to measure spin along an arbitrary axis direction is easily obtained from the Pauli spin matrices. Let u = (ux, uy, uz) be an arbitrary unit vector. Then the operator for spin in this direction is simply
The operator Su has eigenvalues of ±ħ/2, just like the usual spin matrices. This method of finding the operator for spin in an arbitrary direction generalizes to higher spin states, one takes the dot product of the direction with a vector of the three operators for the three x-, y-, z-axis directions.
A normalized spinor for spin-1/2 in the (ux, uy, uz) direction (which works for all spin states except spin down, where it will give 0/0) is
The above spinor is obtained in the usual way by diagonalizing the σu matrix and finding the eigenstates corresponding to the eigenvalues. In quantum mechanics, vectors are termed «normalized» when multiplied by a normalizing factor, which results in the vector having a length of unity.
Compatibility of spin measurements[edit]
Since the Pauli matrices do not commute, measurements of spin along the different axes are incompatible. This means that if, for example, we know the spin along the x axis, and we then measure the spin along the y axis, we have invalidated our previous knowledge of the x axis spin. This can be seen from the property of the eigenvectors (i.e. eigenstates) of the Pauli matrices that
So when physicists measure the spin of a particle along the x axis as, for example, ħ/2, the particle’s spin state collapses into the eigenstate 




Higher spins[edit]
The spin-1/2 operator S = ħ/2σ forms the fundamental representation of SU(2). By taking Kronecker products of this representation with itself repeatedly, one may construct all higher irreducible representations. That is, the resulting spin operators for higher-spin systems in three spatial dimensions can be calculated for arbitrarily large s using this spin operator and ladder operators. For example, taking the Kronecker product of two spin-1/2 yields a four-dimensional representation, which is separable into a 3-dimensional spin-1 (triplet states) and a 1-dimensional spin-0 representation (singlet state).
The resulting irreducible representations yield the following spin matrices and eigenvalues in the z-basis:
- For spin 1 they are
- For spin 3/2 they are
- For spin 5/2 they are
- The generalization of these matrices for arbitrary spin s is
where indices
are integer numbers such that
Also useful in the quantum mechanics of multiparticle systems, the general Pauli group Gn is defined to consist of all n-fold tensor products of Pauli matrices.
The analog formula of Euler’s formula in terms of the Pauli matrices
for higher spins is tractable, but less simple.[20]
Parity[edit]
In tables of the spin quantum number s for nuclei or particles, the spin is often followed by a «+» or «−». This refers to the parity with «+» for even parity (wave function unchanged by spatial inversion) and «−» for odd parity (wave function negated by spatial inversion). For example, see the isotopes of bismuth, in which the list of isotopes includes the column nuclear spin and parity. For Bi-209, the only stable isotope, the entry 9/2– means that the nuclear spin is 9/2 and the parity is odd.
Applications[edit]
Spin has important theoretical implications and practical applications. Well-established direct applications of spin include:
- Nuclear magnetic resonance (NMR) spectroscopy in chemistry;
- Electron spin resonance (ESR or EPR) spectroscopy in chemistry and physics;
- Magnetic resonance imaging (MRI) in medicine, a type of applied NMR, which relies on proton spin density;
- Giant magnetoresistive (GMR) drive-head technology in modern hard disks.
Electron spin plays an important role in magnetism, with applications for instance in computer memories. The manipulation of nuclear spin by radio-frequency waves (nuclear magnetic resonance) is important in chemical spectroscopy and medical imaging.
Spin–orbit coupling leads to the fine structure of atomic spectra, which is used in atomic clocks and in the modern definition of the second. Precise measurements of the g-factor of the electron have played an important role in the development and verification of quantum electrodynamics. Photon spin is associated with the polarization of light (photon polarization).
An emerging application of spin is as a binary information carrier in spin transistors. The original concept, proposed in 1990, is known as Datta–Das spin transistor.[21] Electronics based on spin transistors are referred to as spintronics. The manipulation of spin in dilute magnetic semiconductor materials, such as metal-doped ZnO or TiO2 imparts a further degree of freedom and has the potential to facilitate the fabrication of more efficient electronics.[22]
There are many indirect applications and manifestations of spin and the associated Pauli exclusion principle, starting with the periodic table of chemistry.
History[edit]
Spin was first discovered in the context of the emission spectrum of alkali metals. In 1924, Wolfgang Pauli introduced what he called a «two-valuedness not describable classically»[23] associated with the electron in the outermost shell. This allowed him to formulate the Pauli exclusion principle, stating that no two electrons can have the same quantum state in the same quantum system.
The physical interpretation of Pauli’s «degree of freedom» was initially unknown. Ralph Kronig, one of Landé’s assistants, suggested in early 1925 that it was produced by the self-rotation of the electron. When Pauli heard about the idea, he criticized it severely, noting that the electron’s hypothetical surface would have to be moving faster than the speed of light in order for it to rotate quickly enough to produce the necessary angular momentum. This would violate the theory of relativity. Largely due to Pauli’s criticism, Kronig decided not to publish his idea.[24]
In the autumn of 1925, the same thought came to Dutch physicists George Uhlenbeck and Samuel Goudsmit at Leiden University. Under the advice of Paul Ehrenfest, they published their results.[25] It met a favorable response, especially after Llewellyn Thomas managed to resolve a factor-of-two discrepancy between experimental results and Uhlenbeck and Goudsmit’s calculations (and Kronig’s unpublished results). This discrepancy was due to the orientation of the electron’s tangent frame, in addition to its position.
Mathematically speaking, a fiber bundle description is needed. The tangent bundle effect is additive and relativistic; that is, it vanishes if c goes to infinity. It is one half of the value obtained without regard for the tangent-space orientation, but with opposite sign. Thus the combined effect differs from the latter by a factor two (Thomas precession, known to Ludwik Silberstein in 1914).
Despite his initial objections, Pauli formalized the theory of spin in 1927, using the modern theory of quantum mechanics invented by Schrödinger and Heisenberg. He pioneered the use of Pauli matrices as a representation of the spin operators and introduced a two-component spinor wave-function. Uhlenbeck and Goudsmit treated spin as arising from classical rotation, while Pauli emphasized, that spin is non-classical and intrinsic property.[26]
Pauli’s theory of spin was non-relativistic. However, in 1928, Paul Dirac published the Dirac equation, which described the relativistic electron. In the Dirac equation, a four-component spinor (known as a «Dirac spinor») was used for the electron wave-function. Relativistic spin explained gyromagnetic anomaly, which was (in retrospect) first observed by Samuel Jackson Barnett in 1914 (see Einstein–de Haas effect). In 1940, Pauli proved the spin–statistics theorem, which states that fermions have half-integer spin, and bosons have integer spin.
In retrospect, the first direct experimental evidence of the electron spin was the Stern–Gerlach experiment of 1922. However, the correct explanation of this experiment was only given in 1927.[27]
See also[edit]
- Chirality (physics)
- Dynamic nuclear polarization
- Helicity (particle physics)
- Holstein–Primakoff transformation
- Kramers’ theorem
- Pauli equation
- Pauli–Lubanski pseudovector
- Rarita–Schwinger equation
- Representation theory of SU(2)
- Spin angular momentum of light
- Spin engineering
- Spin-flip
- Spin isomers of hydrogen
- Spin–orbit interaction
- Spin tensor
- Spin wave
- Yrast
References[edit]
- ^ Merzbacher, Eugen (1998). Quantum Mechanics (3rd ed.). pp. 372–373. ISBN 9780471887027.
- ^ a b Griffiths, David (2005). Introduction to Quantum Mechanics (2nd ed.). pp. 183–184.
- ^ «Angular Momentum Operator Algebra», class notes by Michael Fowler.
- ^ A modern approach to quantum mechanics, by Townsend, p. 31, 80.
- ^ Eisberg, Robert; Resnick, Robert (1985). Quantum Physics of Atoms, Molecules, Solids, Nuclei, and Particles (2nd ed.). pp. 272–273. ISBN 9780471873730.
- ^ Information about Higgs Boson in CERN’s official website.
- ^ Pauli, Wolfgang (1940). «The Connection Between Spin and Statistics» (PDF). Phys. Rev. 58 (8): 716–722. Bibcode:1940PhRv…58..716P. doi:10.1103/PhysRev.58.716.
- ^ Peskin, M. E., & Schroeder, D. V. (1995). Quantum field theory, Ch. 3. The Advanced Book Program.
- ^ Physics of Atoms and Molecules, B. H. Bransden, C. J. Joachain, Longman, 1983, ISBN 0-582-44401-2.
- ^ «CODATA Value: electron g factor». The NIST Reference on Constants, Units, and Uncertainty. NIST. 2018. Retrieved 2019-06-04.
- ^ Feynman, R. P. (1985). «Electrons and their interactions». QED: The Strange Theory of Light and Matter. Princeton, New Jersey: Princeton University Press. p. 115. ISBN 978-0-691-08388-9.
After some years, it was discovered that this value [−1/2g] was not exactly 1, but slightly more – something like 1.00116. This correction was worked out for the first time in 1948 by Schwinger as j×j divided by 2π [sic] [where j is the square root of the fine-structure constant], and was due to an alternative way the electron can go from place to place: Instead of going directly from one point to another, the electron goes along for a while and suddenly emits a photon; then (horrors!) it absorbs its own photon.
- ^ Marciano, W. J.; Sanda, A. I. (1977). «Exotic decays of the muon and heavy leptons in gauge theories». Physics Letters. B67 (3): 303–305. Bibcode:1977PhLB…67..303M. doi:10.1016/0370-2693(77)90377-X.
- ^ Lee, B. W.; Shrock, R. E. (1977). «Natural suppression of symmetry violation in gauge theories: Muon- and electron-lepton-number nonconservation». Physical Review. D16 (5): 1444–1473. Bibcode:1977PhRvD..16.1444L. doi:10.1103/PhysRevD.16.1444. S2CID 1430757.
- ^ K. Fujikawa, R. E. Shrock (1980). «Magnetic Moment of a Massive Neutrino and Neutrino-Spin Rotation». Physical Review Letters. 45 (12): 963–966. Bibcode:1980PhRvL..45..963F. doi:10.1103/PhysRevLett.45.963.
{{cite journal}}: CS1 maint: uses authors parameter (link) - ^ Bell, N. F.; Cirigliano, V.; Ramsey-Musolf, M.; Vogel, P.; Wise, Mark; et al. (2005). «How Magnetic is the Dirac neutrino?». Physical Review Letters. 95 (15): 151802. arXiv:hep-ph/0504134. Bibcode:2005PhRvL..95o1802B. doi:10.1103/PhysRevLett.95.151802. PMID 16241715. S2CID 7832411.
- ^ Quanta: A handbook of concepts, P. W. Atkins, Oxford University Press, 1974, ISBN 0-19-855493-1.
- ^ Messiah, Albert (2014). «Angular Momentum in Quantum Mechanics». Quantum Mechanics. Mineola, NY: Dover Publications. p. 540. ISBN 978-1-306-51279-4. OCLC 874097814.
{{cite book}}: CS1 maint: date and year (link) - ^ B. C. Hall (2013). Quantum Theory for Mathematicians. Springer. pp. 354–358.
- ^ J. J. Sakurai, Modern Quantum Mechanics, p. 159.
- ^ Curtright, T. L.; Fairlie, D. B.; Zachos, C. K. (2014). «A compact formula for rotations as spin matrix polynomials». SIGMA. 10: 084. arXiv:1402.3541. Bibcode:2014SIGMA..10..084C. doi:10.3842/SIGMA.2014.084. S2CID 18776942.
- ^ Datta, S.; Das, B. (1990). «Electronic analog of the electrooptic modulator». Applied Physics Letters. 56 (7): 665–667. Bibcode:1990ApPhL..56..665D. doi:10.1063/1.102730.
- ^ Assadi, M. H. N.; Hanaor, D. A. H. (2013). «Theoretical study on copper’s energetics and magnetism in TiO2 polymorphs». Journal of Applied Physics. 113 (23): 233913–233913–5. arXiv:1304.1854. Bibcode:2013JAP…113w3913A. doi:10.1063/1.4811539. S2CID 94599250.
- ^ Wolfgang Pauli (December 13, 1946). «Exclusion Principle and Quantum Mechanics». Nobel Lecture. Nobel Prize.
- ^ Pais, Abraham (1991). Niels Bohr’s Times. Oxford: Clarendon Press. pp. 244. ISBN 978-0-19-852049-8.
- ^ Ehrenfest, P. (November 1925). «Ersetzung der Hypothese vom unmechanischen Zwang durch eine Forderung bezüglich des inneren Verhaltens jedes einzelnen Elektrons». Die Naturwissenschaften (in German). 13 (47): 953–954. doi:10.1007/bf01558878. ISSN 0028-1042. S2CID 32211960.
- ^ Ohanian, Hans C. (June 1986). «What is spin?». American Journal of Physics. 54 (6): 500–505. Bibcode:1986AmJPh..54..500O. doi:10.1119/1.14580. ISSN 0002-9505.
- ^ B. Friedrich, D. Herschbach (2003). «Stern and Gerlach: How a Bad Cigar Helped Reorient Atomic Physics». Physics Today. 56 (12): 53. Bibcode:2003PhT….56l..53F. doi:10.1063/1.1650229. S2CID 17572089.
{{cite journal}}: CS1 maint: uses authors parameter (link)
Further reading[edit]
- Cohen-Tannoudji, Claude; Diu, Bernard; Laloë, Franck (2006). Quantum Mechanics (2 volume set ed.). John Wiley & Sons. ISBN 978-0-471-56952-7.
- Condon, E. U.; Shortley, G. H. (1935). «Especially Chapter 3». The Theory of Atomic Spectra. Cambridge University Press. ISBN 978-0-521-09209-8.
- Hipple, J. A.; Sommer, H.; Thomas, H.A. (1949). «A precise method of determining the faraday by magnetic resonance». Physical Review. 76 (12): 1877–1878. Bibcode:1949PhRv…76.1877H. doi:10.1103/PhysRev.76.1877.2.
- Edmonds, A. R. (1957). Angular Momentum in Quantum Mechanics. Princeton University Press. ISBN 978-0-691-07912-7.
- Jackson, John David (1998). Classical Electrodynamics (3rd ed.). John Wiley & Sons. ISBN 978-0-471-30932-1.
- Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers (6th ed.). Brooks/Cole. ISBN 978-0-534-40842-8.
- Thompson, William J. (1994). Angular Momentum: An Illustrated Guide to Rotational Symmetries for Physical Systems. Wiley. ISBN 978-0-471-55264-2.
- Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics (5th ed.). W. H. Freeman. ISBN 978-0-7167-0809-4.
- Sin-Itiro Tomonaga, The Story of Spin, 1997
External links[edit]
Quotations related to Spin (particle physics) at Wikiquote
- Goudsmit on the discovery of electron spin.
- Nature: «Milestones in ‘spin’ since 1896.»
- ECE 495N Lecture 36: Spin Online lecture by S. Datta
Это продолжение разговора о неравенствах Белла. Начало здесь: Введение
Часть 1. Что такое спин?
Физические эксперименты всегда подразумевают измерение каких-либо величин. В экспериментах по схеме Белла мы «будем измерять» спин элементарных частиц, поэтому нам следует разобраться, что же это за штука такая.
В классической механике есть такая величина: момент импульса. Так же, как и просто импульс, момент импульса характеризует количество движения. Разница вот в чём: импульс характеризует поступательное движение тела в определённой системе отсчёта, а момент импульса — вращательное движение тела вокруг определённой оси вращения.
Вы знаете, конечно, что импульс определяется как произведение массы тела на его линейную скорость. А момент импульса определяется как произведение момента инерции тела на его угловую скорость, ту, которая измеряется в оборотах в секунду. Что такое момент инерции — я тут объяснять не буду, для нашей задачи это несущественно. Зато очень существенно вот что: момент импульса является величиной векторной, то есть, характеризуется не только абсолютным значением, но и направлением, которое всегда совпадает с направлением оси вращения. Тут вы можете спросить: но ведь у оси вращения два направления. Например, куда направлен вектор момента импульса вращающейся юлы-волчка, вверх или вниз? Отвечу: принято определять направление вектора момента импульса по «правилу буравчика». При вращении тела этот вектор направлен туда, куда вкручивался бы штопор, вращай мы его также. Так что, если юла раскручена по часовой стрелке, то считается, что вектор момента импульса направлен вниз. А если против часовой — тогда вверх.
Момент импульса, как и импульс, подчиняется закону сохранения. То есть, если вращающееся тело не взаимодействует ни с какими другими телами, его момент импульса остаётся неизменным, что бы там не происходило внутри самого тела. Даже если тело самопроизвольно развалится на несколько частей, то суммарный момент импульса всех осколков будет равен моменту импульса развалившегося тела. Причём, момент импульса не меняется не только по абсолютной величине, но и по направлению. Это можно наблюдать на примере той же юлы: пока она достаточно быстро крутится, её ось вращения направления не меняет. Повторяю: если тело ни с чем не взаимодействует, то его момент импульса сохраняется. Но если на тело воздействовать извне, то его момент импульса изменить можно, как по абсолютной величине (мы можем притормозить или раскрутить юлу), так и по направлению (если толкнуть вращающуюся юлу, её ось начнёт раскачиваться).
Спин элементарной частицы – это её момент импульса. Можно считать, что частица – это шарик, который вращается вокруг собственной оси, как, например, наша планета. Такое представление, вообще-то, довольно примитивно, но для нашей задачи сгодится. Надо только понимать, что спин, в отличие от классического момента импульса – величина квантовая, и поэтому обладает некоторыми специфическими особенностями, которые мы ниже рассмотрим.
Момент импульса тела может быть любым как по направлению, так и по абсолютной величине. Спин частицы по абсолютной величине изменяться не может: для каждого конкретного типа частиц значение спина — это «константа», так же как электрический заряд, например. С этим значением спина частица рождается, с ним же и умирает. А вот «направление» спина частицы изменить можно, например, подействовав на частицу магнитным полем. Стало быть, «измерять» мы будем именно направление спина.
Ну что же, перейдём к «практической» части. Нет, это ещё не «белловские» эксперименты, пока мы просто «поставим» несколько простых опытов, чтобы лучше понять свойства спина и поупражняться с его измерением.
Для измерения спина частиц используют устройство, которое называется «прибор Штерна-Герлаха», по фамилиям его изобретателей. Дальше мы будем называть это устройство сокращено: «ПШГ». Кратко рассмотрим принцип действия прибора.
Элементарная частица имеет электрический заряд и вращается, а значит, она представляет собой маленький магнит. Другими словами, если у частицы есть спин, значит, у неё есть и магнитные свойства, или, говоря более научно – магнитный момент (на всякий случай отмечу, что магнитным моментом обладают и частицы с нулевым зарядом, например, нейтроны, но механизм этого явления мы тут рассматривать не будем). Вот этот-то магнитный момент вращающейся частицы и использует ПШГ. Устройство ПШГ, а также прочее оборудование, необходимое для опытов, показаны на рисунке 1.1.
Собственно, сам ПШГ состоит из двух магнитов. Верхний и нижний магниты имеют различную форму, благодаря чему магнитное поле в промежутке между ними неравномерно. Также на рисунке изображены источник частиц, (надо же их откуда-то брать?) и экран, который регистрирует точку попадания частицы. Например, в качестве экрана может использоваться фотопластинка: попавшая в неё частица «засвечивает» точку попадания.
Для наших дальнейших опытов решающее значение будет иметь ориентация самого прибора, а также спинов частиц в
пространстве. Поэтому на рисунке показана система координат XYZ. Ориентацию ПШГ мы будем показывать толстой серой стрелкой. В данном случае прибор ориентирован вдоль положительного направления оси Z. Направление векторов спинов (для компактности будем говорить просто «направление спинов») частиц будем показывать тонкой черной стрелкой. На рисунке спин «красной» частицы направлен вверх, в направлении +Z, а спин «синей» частицы направлен вниз, в направлении –Z .
Итак, источник выпускает частицу в направлении оси X. Затем частица попадает в ПШГ и проходит через зазор между магнитами. Если частица не обладает спином, то магнитное поле на неё никак не влияет, она движется по прямой и попадает в центр экрана – его мы приняли за начало координат. Траектория такой частицы показана на рисунке зелёной линией. На самом деле мы тут будем «работать» только с частицами, обладающими ненулевым спином, так что зелёную траекторию я нарисовал чисто для того, чтобы обозначить центр экрана.
Если спин направлен вверх, то неравномерное магнитное поле в зазоре отклоняет частицу вверх (красная траектория). Если спин направлен вниз, то частица отклоняется вниз (синяя траектория). Таким образом, наблюдая на экране точку попадания частицы, мы определяем, как был направлен её спин – вверх или вниз.
Мы рассмотрели случаи, когда спин частицы направлен вдоль оси Z. То есть, направление спина совпадает с ориентацией прибора или строго противоположно ей. Но ведь спин частицы может быть ориентирован в пространстве как угодно. Возникает вопрос: а что же будет с частицей, если её спин и ориентация ПШГ не совпадают? Тут классическая физика и квантовая механика дают разные ответы.
Если рассматривать ситуацию чисто «классически», и представлять себе частицу как вращающийся заряженный шарик, то ответ будет такой: отклонение частицы пропорционально проекции её спина на направление ориентации прибора (в нашем случае это то же самое, что ось Z). То есть, максимальное отклонение точки попадания от центра экрана будет у тех частиц, у которых спин направлен параллельно оси Z (Рисунок 1.2-a, точка «Zmax»). Разумеется, если спин параллелен оси Z, но направлен в противоположную сторону, то частица попадёт в точку «–Zmax».
Если спин частицы направлен под углом к оси Z, частица должна попасть в точку где-то между -Zmax и Zmax (Рисунок 1.2-b). Если же спин частицы ориентирован перпендикулярно оси Z, например, вдоль оси Y? то частица вообще не должна отклоняться от центра (Рисунок 1.2-c).
Ось X на рисунке 1.2 и на следующих не показана, чтобы не загромождать. Можете считать, что она направлена от нас прямо вглубь рисунка. Места попадания частиц в регистрирующий экран показаны красной звёздочкой. Направление спина показано так, как мы условились раньше: тонкой чёрной стрелкой.
Квантовая механика предсказывает совершенно другой результат: все частицы будут отклоняться на максимально возможное расстояние и попадать только в одну из двух точек, причём, линия, походящая через эти две точки и центр экрана, будет параллельна ориентации прибора. В нашем случае, когда ПШГ ориентирован параллельно оси Z, это будут точки либо «Zmax», либо «–Zmax». В этом, собственно, и заключается «квантовость». Если в «классике» мы можем намерять любое отклонение, а значит и направление момента импульса, то в квантовой механике направление спина «квантуется»: есть только два возможных результата измерения.
Тут, чтобы вас не запутать на будущее, я должен оговорить вот что: на самом деле два результата измерения мы получим только на частицах с так называемым «полуцелым» спином. К таким частицам относятся, в частности, электроны, протоны, нейтроны и некоторые другие. Для прочих частиц возможны три результата, четыре, пять и так далее, но в любом случае число возможных результатов будет конечным. Чтобы не делать в дальнейшем таких оговорок, давайте определимся: мы будем в наших экспериментах работать только с протонами.
Итак, классическая физика и квантовая механика предсказывают разные результаты опытов с протонами. Ну что же, вооружившись банальностью «опыт – критерий истины» приступим к экспериментальной проверке.
Установка для опыта у нас уже есть, она показана на рисунке 1.1. Только там у нас был «источник частиц», теперь это будет источник конкретно протонов.
Предполагаем, что источник выпускает протоны со случайно ориентированным спином. Значит, если права классическая физика, то протоны должны попадать в экран со случайным отклонением по оси Z в диапазоне от «–Zmax» до «Zmax». Тогда, если мы выпустим достаточно много протонов, то картинка на экране должна будет выглядеть так, как показано на рисунке 1.3-a. То есть, будет сплошная полоса попаданий.
Ну а если права квантовая механика, то после серии «выстрелов» на экране будет картинка как на рисунке 1.3-b: только два варианта попаданий. Причём, попадания распределятся примерно пополам: половина вверх, половина вниз.
В реальности такой эксперимент даёт картинку в полном соответствии с предсказаниями квантовой механики, как на рисунке 1.3-b. Это один из тех экспериментов, о которых я говорил во введении: с точки зрения классической физики его результаты объяснить не удаётся, а квантовая механика объясняет их «на раз».
Сторонники классического подхода тут могут «уцепиться за соломинку»: мол, мы предположили, что спин протонов, испускаемых источником, ориентирован случайно, а вдруг это не так? Возможно, источник выпускает протоны, ориентированные только вертикально, вдоль оси Z. В таком случае «классический» расчёт даст такую же картину распределения попаданий, как и квантовый (рисунок 1.3-b).
Хорошо, мы это можем легко проверить. Повернём ПШГ на некоторый угол вокруг оси X и проделаем опять длинную серию «выстрелов». Если версия «классиков» верна, то мы увидим на экране картинку типа 1.4-a. Ну а если всё же правда на «квантовой» стороне, то картинка будет как 1.4-b.
Я пока не буду объяснять, почему классический (a) и квантовый (b) расчёты дадут при такой ориентации прибора именно эти картины распределения попаданий. Если вам непонятно, то предлагаю тут притормозить и разобраться самостоятельно. Вся необходимая для этого информация изложена выше и даже выделена жирным курсивом. Также вам помогут, надеюсь, дополнительные построения, нарисованные пунктирными линиями.
Разобрались? Отлично, тогда едем дальше. Проделав эксперимент с «повёрнутым» ПШГ (на рисунке 1.4 он повёрнут вокруг оси X на 60 градусов вправо), убеждаемся, что результаты опыта совпадают с квантовыми предсказаниями: половина (приблизительно) протонов попадает в точку A1, половина – в точку A2. Для верности можем провести эксперименты с разными углами поворота ПШГ и убедиться: результат всегда таков, как предсказывает квантовая механика. Заодно мы убедимся в том, что наше предположение о случайной ориентации спинов на входе прибора было правильным.
Итак, констатируем важный вывод, на который мы будем ссылаться в дальнейших рассуждениях:
Утверждение 1.1.
Вне зависимости от того, с каким направлением спина протон входит в измерительный прибор, мы получим только один из двух возможных результатов измерения: направление спина протона либо совпадает с ориентацией прибора, либо строго противоположно ему.
Для порядка отмечу, что в нашем случае измерительным прибором является устройство, включающее ПШГ и
регистрирующий экран. Однако, утверждение 1.1. верно и для любого другого устройства, измеряющего направление спина. Но мы будем и дальше пользоваться прибором Штерна-Герлаха. Только вот, в свете утверждения 1.1., регистрирующий экран нам больше не нужен. Поскольку из ПШГ все протоны выходят только по одной из двух возможных траекторий, мы можем вместо экрана поставить на каждой траектории детектор протонов. Теперь схема эксперимента, показанного на рисунке 1.1, будет выглядеть так, как на рисунке 1.5-a.
Детекторы обозначены как D+ (плюс – детектор) и D- (минус – детектор). В плюс – детектор будут попадать все протоны, направление спина которых совпадает с ориентацией прибора. В минус – детектор попадут все протоны с противоположной прибору ориентацией.
Разумеется, если мы теперь захотим покрутить ПШГ вокруг «линии выстрела», показанной на рисунке зелёным пунктиром, то мы должны будем соответствующим образом переместить и детекторы, иначе все «выстрелы» уйдут в «молоко». Чтобы не мучится с определением нового положения детекторов, мы можем просто объединить ПШГ и детекторы в единую конструкцию и вращать её всю целиком так, как нам требуется. Дальше при описании опытов я буду эту измерительную конструкцию изображать так, как показано на рисунке 1.5-b.
Пожалуй, на сегодня достаточно информации. Если что-то в рассказе непонятно, велкам, задавайте вопросы.
Продолжение тут.
Спин – это сложная для понимания и в высшей степени необычная величина в квантовой физике. Да и сам квантовый мир крайне причудлив. Поскольку в его царстве субатомные частицы действуют по правилам, далеким от привычных.
К примеру, квантовые частицы могут находиться в нескольких состояниях или в нескольких точках пространства одновременно. То есть существовать в тумане вероятностей. И им нет никакого дела до того, что мы этого не понимаем. Но сейчас не об этом. А о причудливом свойстве квантовых частиц, называемых в физике спином.
Содержание:
- Спин — что это за понятие в физике?
- Спин квантовой частицы — свойства
- Как понять направление вектора спина? Спин вращения
- Эксперимент Штерна-Герлаха
- Почему спин – это удивительная величина в квантовой физике?
- Спин и микролептоны
- Резюме
Хотя мы этого и не видим, и возможно даже никогда об этом не задумываемся, но всё что нас окружает, состоит из разнообразных частиц и находится в постоянном движении. Тот же телефон, которым вы пользуетесь, состоит из молекул, а те из атомов. И хотя «атом» в переводе с греческого означает «неделимый», он также состоит из еще более мелких частиц.
Соответственно, первичные, неразложимые частицы, из которых состоит вся материя, называются элементарными частицами. Или же квантовыми или фундаментальными частицами.
Спин — что это за понятие в физике?
Итак, спин — что это за понятие в физике, а точнее в квантовой механике, и чем он странен?
В переводе с английского спин (spin) – это вращение, вращаться. Если посмотреть определение, то спин — это собственный момент импульса элементарной частицы.
А вектор спина — это величина, характеризующая ориентацию спина в квантовой механике.
- Но суть в том, что спин никак не связан ни с движением, ни с перемещением, ни с вращением частицы. Хотя, если представить, что спин в чем-то он аналогичен вращению Земли, то это дает квантовой частице угловой момент и крошечное магнитное поле, называемое магнитным моментом.
С другой стороны, спин – это такая причудливая квантовая величина в физике, для которой невозможно представить и найти классического аналога.
Спиновый угловой момент или просто спин (для краткости) — это внутреннее свойство частицы. И им она обладает, если можно так сказать, по праву рождения. Так же как массой или зарядом. А все остальные свойства частицы уже зависят от того, что она делает.
И если попробовать по этому принципу разделить некоторые свойства квантовой частицы, то получим следующую таблицу:
Соответственно, спин частицы невозможно изменить, также как её заряд или массу. Это её неизменная квантовая характеристика.
Небольшое видео о том, что такое квантовый спин на английском языке. При желании всегда можно включить перевод в субтитрах.
- К тому же, в отличие от классического магнитного момента, спин квантуется. Другими словами, спин может принимать только одно из двух возможных значений.
Для определения спина в квантовой механике используют спиновое квантовое число. Спиновое число обозначается буквой J и принимает ряд дискретных значений. А само значение спина пропорционально постоянной Планка h
Кстати, одним из применений квантовой физики в жизни становятся квантовые компьютеры. И тогда спин электрона оказывается крайне важен. Ведь он является одной из физических реализаций квантовой системы с двумя состояниями.
Спин квантовой частицы – свойства
Понятие «спин» было предложено в 1925 году американскими физиками Джорджем Уленбеком и Абрахамом Гаудсмитом как объяснение существования спектральных линий. Вот как говорится об этом в книге «Квант. Эйнштейн, Бор и великий спор о природе реальности».
«В классической физике угловой момент, описывающий обычное вращение, может быть направлен в произвольном направлении. То, что предложил Уленбек было квантовым вращением — спином.
Свойства спина
- Спин — это двузначная величина. То есть спин может быть направлен “вверх” или “вниз”. Уленбек представлял себе эти два допустимые спиновые состояния как вращение электрона относительно вертикальной оси по или против часовой стрелки. При этом электрон продолжал вращаться по орбите вокруг ядра.
- При таком движении электрон генерирует собственное магнитное поле. Он ведет себя как стержневой электромагнит субатомных (очень малых) размеров.
- Магнитный момент электрона может быть ориентирован по внешнему магнитному полю либо против него.
- Понятно, что на любой разрешенной электронной орбите может находиться сразу два электрона. Но при условии, что у одного из них спин направлен “вверх”, а у другого “вниз”. Тогда этим двум направлениям спина соответствуют очень близкие, но не тождественно равные энергии. (Именно это и приводит к образованию в спектре щелочей дублета, то есть не одной, а двух очень близко расположенных друг к другу линий.)
- Уленбек и Гаудсмит показали, что спин электрона может равняться плюс или минус одной второй 1/2. Он удовлетворяет принципу запрета Паули.
И все же, впервые идею о существовании спина у электрона выдвинул 21-летний американец Ральф Крониг. Но не опубликовал это открытие из-за саркастической реакции Паули. “В будущем я буду доверять своим суждениям больше, чем чьим-либо еще”, — впоследствии жаловался он.
Позднее Джордж Уленбек открыто признал, что он и Гаудсмит вовсе не были первыми, кто предложил квантовать вращение электрона.
Даже годы спустя большинство физиков считало, что Гаудсмит и Уленбек должны были получить Нобелевскую премию.
В конце концов, спин электрона — одно из самых важных понятий физики XX века.
Но именно из-за инцидента с Паули и Кронигом Нобелевский комитет уклонился от присуждения награды Гаудсмиту и Уленбеку».
Наверное, именно таким двойным открытием реализовались в макромире квантовые свойства спина. Такая вот шутка от спина.
Как понять направление вектора спина? Спин вращения
Протоны, нейтроны, электроны, любые квантовые частицы из которых состоят ядра атомов, постоянно находятся в состоянии словно бы вращения. По аналогии с юлой или маленькими гироскопами. Вне зависимости от того, что вы делаете с ними, вы не можете замедлить или ускорить «вращение», то есть спин квантовой частицы. Вы можете только поменять их положение.
Спин вращения традиционно описывают словами «вверх» или «вниз», в зависимости от направления.
Так как же понять направление вектора спина субатомных частиц?
Есть несколько способов. Прежде всего, да и проще всего, спин вращения квантовой частицы можно определить так:
- Например, если представить себе наручные часы, лежащие на столе, то понятие вращения «вверх» будет соответствовать движению против часовой стрелки. А вращение «вниз» — по часовой стрелке.
- Кроме того, есть и другой удобный способ запомнить, что такое спин «вверх» и спин «вниз». Для этого смотрим на правую руку и сгибаем пальцы на руке в том направлении, в котором вращается квантовая частица. К примеру, протон или нейтрон. В результате, большой палец на правой руке будет направлен вдоль оси вращения. А его направление будет определять «направление» спина – «вверх» или «вниз».
Также, о правом и левом вращении можно прочитать в статье «Спасение и бич 21 века».
Эксперимент Штерна-Герлаха
«Эксперимент Штерна-Герлаха» впервые был проведен в 1922 году. Он дал первый намек на то, что квантовые частицы обладают неизвестным ранее видом магнетизма. Другими словами, исследователи обнаружили, что частицы обладают неким свойством, проявляющимся только в присутствии магнитного поля.
В ходе эксперимента физики Отто Штерн и Вальтер Герлах из Гамбургского университета в Германии запускали атомы серебра через магнитное поле. Затем они измеряли, где частицы приземляются на экране. И если обычный магнит может оказаться в любой точке, в зависимости от его силы и ориентации, то атомы появляются только в двух дискретных точках.
Экспериментаторы обнаружили, что в квантовой реальности электроны ведут себя так, словно они вращаются сами по себе очень быстро. При этом создаются крошечные магнитные поля вокруг электронов, независимые от тех, которые возникают при их орбитальном движении вокруг ядра.
Вскоре для описания этого процесса была использована терминология «спин» — видимое вращение субатомных частиц. Ведь они вели себя как миниатюрные магниты.
Следовательно, если вы пошлете электрон через магнитное поле и измерите его спин, то вы всегда получите только один из двух результатов.
Физики называют их «спин вверх” и “спин вниз”. И тогда “вверх” и «вниз» — это направления, определяемые магнитным полем.
Спины электронов всегда будут направлены вверх или вниз после измерения и никогда под некоторым углом между ними. Подробнее об этом в видео «Эксперимент Штерна-Герлаха. Спин электрона».
А если хочется углубиться в физику чуть больше, то в продолжении темы видео о том, как ведет себя спин в магнитном поле.
Почему спин – это удивительная величина в квантовой физике?
Итак, давайте обобщим.
- Во-первых, физики рассчитали, что для генерации подобного момента импульса, электрону надо было бы вращаться намного быстрее скорости света. А это не позволительно в нашей реальности.
Соответственно, получается что спин – это не вращение, а состояние самой частицы, которое вряд ли можно наглядно представить. Вращение в этом случае — это лишь ближайший аналог из макромира.
- Во-вторых, кажется, что электрон не имеет реального размера. Это безразмерная «точечная частица». И она не имеет наблюдаемой структуры вплоть до миллиардной доли миллиардного метра. А безразмерная точка не может никак вращаться. Каково это быть без структуры? И что тогда вращается вокруг оси?
- Далее, еще более странно то, что электрически нейтральные частицы, такие как нейтроны, также имеют спин. Как это возможно? Оказывается, они могут быть нейтральными, только если они состоят из более мелких частиц, которые не нейтральны. И тогда нейтроны все еще крошечные магниты.
А благодаря тому, что спин — это неотъемлемое свойство всех квантовых частиц, стало возможно классифицировать всю квантовую материю.
Точно так же, как мы легко объединяем вещи по видам и типам в соответствии с их общими характеристиками.
- Как и многие вещи в квантовом мире, спин квантован. А это означает, что спин частицы ограничен определенными точными значениями. Спин принято измерять в долях постоянной Планка, и минимальное возможное значение спина соответствует ½ постоянной Планка. Но, как правило, физики говорят просто ½, 1, 2 и так далее. То есть 0, 1/2, 1 или 3/2 могут быть. А, к примеру, 0,789 – уже нет.
Более того, эти допустимые значения делят каждую частицу во Вселенной на две категории, в зависимости от того, является ли ее спин целым числом (0, 1, 2), или дробным.
Ты либо бозон, либо фермион. Других вариантов нет.
Бозоны — это частицы в физике с целочисленными спинами. Например, фотон.
В то время как фермионы обладают полуцелыми спинами (электроны).
Спин и микролептоны
Таким образом, из-за того что вращение у спина квантовано, допускаются только определенные дискретные вращения у различных квантовых частиц. А это делает спин одним из самых сложных аспектов в квантовой физике и механике.
И хотя прошло уже почти 100 лет с момента открытия спина, но до сих пор нет однозначного понимания. Например, ученые ломают копья в вопросе «Из чего складывается спин протона?» А также склоняются к тому, что элементарные частицы, возможно, тоже составные.
Квантовый мир нехотя расстается со своими секретами. И все же уже открыто множество новых частиц. Одними из них были микролептоны.
Микролептоны легче электрона в миллионы и миллиарды раз.
Размер микролептонов – 10-24 м и меньше.
А вес от 1,3 *10-40 кг и меньше.
Таким образом, благодаря своему крайне малому размеру они способны проникают повсюду.
Как оказалось, именно они ответственны за связь между здоровьем, старением организма, водой и излучением электроприборов. Например, вот одно из последних исследований воздействия микроволновой печи на воду. Подробнее об этой связи можно узнать в статье «Как спин квантовой частицы влияет на здоровье?»
В тоже время, уже разработаны и активно используются защитные и восстанавливающие устройства.
Резюме
Надеюсь, статья помогла вам разобраться, что такое спин и почему это свойство такое сложное для понимания в квантовой физике. Да и не только в физике, но и в химии тоже.
Еще раз повторюсь, спин – это внутренняя характеристика электрона в квантовой физике, его собственный момент импульса, не связанный с вращением чего-либо или электрическим зарядом.
Здоровья и Добра!

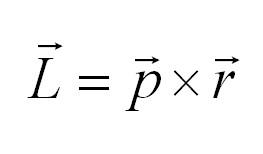
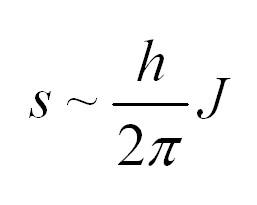
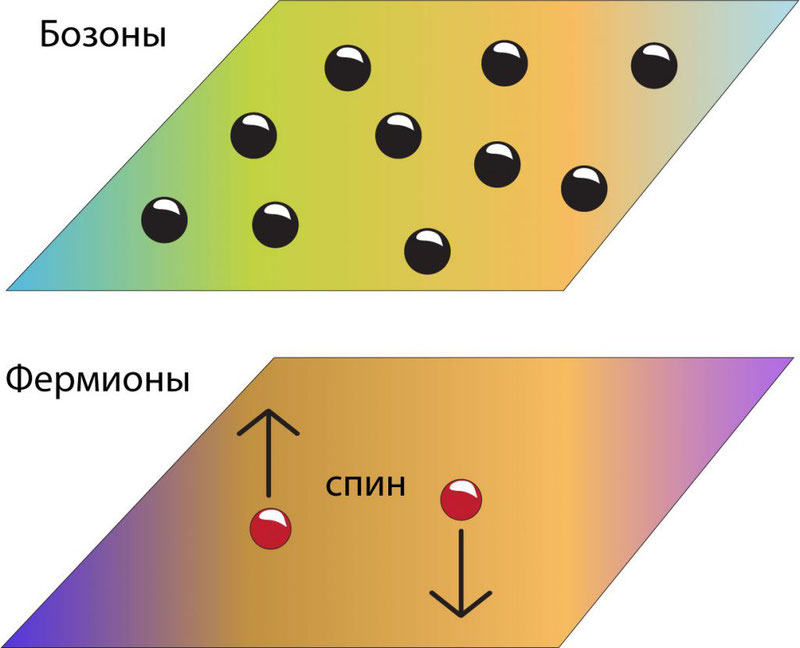

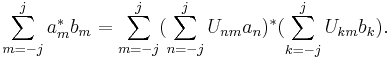
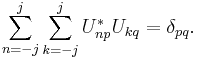
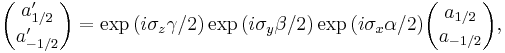
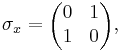
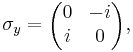
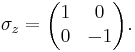
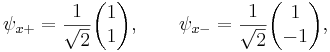
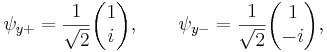
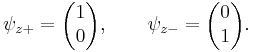
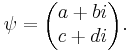
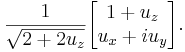







![{displaystyle left[{hat {S}}_{j},{hat {S}}_{k}right]=ihbar varepsilon _{jkl}{hat {S}}_{l},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/075f18d0a435c840e760e9a979522c36dc20c527)











![{displaystyle {begin{aligned}S_{x}rightarrow U^{dagger }S_{x}U&=e^{itheta S_{z}}S_{x}e^{-itheta S_{z}}\&=S_{x}+(itheta )left[S_{z},S_{x}right]+left({frac {1}{2!}}right)(itheta )^{2}left[S_{z},left[S_{z},S_{x}right]right]+left({frac {1}{3!}}right)(itheta )^{3}left[S_{z},left[S_{z},left[S_{z},S_{x}right]right]right]+ldots end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d466a19023cc990eea91797d4aa094ac96296ca7)
![{displaystyle {begin{aligned}U^{dagger }S_{x}U&=S_{x}left[1-{frac {theta ^{2}}{2!}}+ldots right]-S_{y}left[theta -{frac {theta ^{3}}{3!}}cdots right]\&=S_{x}cos theta -S_{y}sin theta ,end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fbfb9dc66203af13bfc41c46becffa25c88b7d8c)




![{displaystyle psi '=exp {left({tfrac {1}{8}}omega _{mu nu }[gamma _{mu },gamma _{nu }]right)}psi ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e11ff7900e4d19601a8520c61497413e2b47e9f)