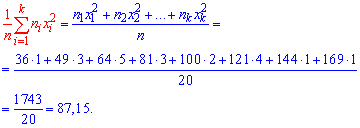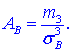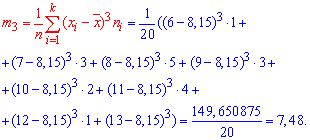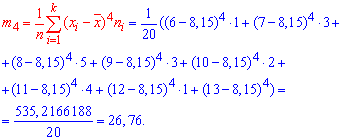Среднее эмпирическое как найти - Исправление недочетов и поиск решений вместе с Examum.ru

From Wikipedia, the free encyclopedia

The sample mean (or «empirical mean») and the sample covariance are statistics computed from a sample of data on one or more random variables.

The sample mean is the average value (or mean value) of a sample of numbers taken from a larger population of numbers, where «population» indicates not number of people but the entirety of relevant data, whether collected or not. A sample of 40 companies’ sales from the Fortune 500 might be used for convenience instead of looking at the population, all 500 companies’ sales. The sample mean is used as an estimator for the population mean, the average value in the entire population, where the estimate is more likely to be close to the population mean if the sample is large and representative. The reliability of the sample mean is estimated using the standard error, which in turn is calculated using the variance of the sample. If the sample is random, the standard error falls with the size of the sample and the sample mean’s distribution approaches the normal distribution as the sample size increases.

The term «sample mean» can also be used to refer to a vector of average values when the statistician is looking at the values of several variables in the sample, e.g. the sales, profits, and employees of a sample of Fortune 500 companies. In this case, there is not just a sample variance for each variable but a sample variance-covariance matrix (or simply covariance matrix) showing also the relationship between each pair of variables. This would be a 3×3 matrix when 3 variables are being considered. The sample covariance is useful in judging the reliability of the sample means as estimators and is also useful as an estimate of the population covariance matrix.

Due to their ease of calculation and other desirable characteristics, the sample mean and sample covariance are widely used in statistics to represent the location and dispersion of the distribution of values in the sample, and to estimate the values for the population.

Definition of the sample mean[edit]

The sample mean is the average of the values of a variable in a sample, which is the sum of those values divided by the number of values. Using mathematical notation, if a sample of N observations on variable X is taken from the population, the sample mean is:

${displaystyle {bar {X}}={frac {1}{N}}sum _{i=1}^{N}X_{i}.}$

Under this definition, if the sample (1, 4, 1) is taken from the population (1,1,3,4,0,2,1,0), then the sample mean is , as compared to the population mean of . Even if a sample is random, it is rarely perfectly representative, and other samples would have other sample means even if the samples were all from the same population. The sample (2, 1, 0), for example, would have a sample mean of 1.

If the statistician is interested in K variables rather than one, each observation having a value for each of those K variables, the overall sample mean consists of K sample means for individual variables. Let $x_{ij}$ be the i^th independently drawn observation (i=1,…,N) on the j^th random variable (j=1,…,K). These observations can be arranged into N
column vectors, each with K entries, with the K×1 column vector giving the i-th observations of all variables being denoted $mathbf {x} _{i}$ (i=1,…,N).

The sample mean vector is a column vector whose j-th element $bar{x}_{j}$ is the average value of the N observations of the j^th variable:

${displaystyle {bar {x}}_{j}={frac {1}{N}}sum _{i=1}^{N}x_{ij},quad j=1,ldots ,K.}$

Thus, the sample mean vector contains the average of the observations for each variable, and is written

${displaystyle mathbf {bar {x}} ={frac {1}{N}}sum _{i=1}^{N}mathbf {x} _{i}={begin{bmatrix}{bar {x}}_{1}\vdots \{bar {x}}_{j}\vdots \{bar {x}}_{K}end{bmatrix}}}$

Definition of sample covariance[edit]

The sample covariance matrix is a K-by-K matrix $textstyle mathbf{Q}=left[ q_{jk}right]$ with entries

$q_{jk}=frac{1}{N-1}sum_{i=1}^{N}left( x_{ij}-bar{x}_j right) left( x_{ik}-bar{x}_k right),$

where $q_{jk}$ is an estimate of the covariance between the j^th
variable and the k^th variable of the population underlying the data.
In terms of the observation vectors, the sample covariance is

${displaystyle mathbf {Q} ={1 over {N-1}}sum _{i=1}^{N}(mathbf {x} _{i}.-mathbf {bar {x}} )(mathbf {x} _{i}.-mathbf {bar {x}} )^{mathrm {T} },}$

Alternatively, arranging the observation vectors as the columns of a matrix, so that

$mathbf{F} = begin{bmatrix}mathbf{x}_1 & mathbf{x}_2 & dots & mathbf{x}_N end{bmatrix}$

which is a matrix of K rows and N columns.
Here, the sample covariance matrix can be computed as

$mathbf{Q} = frac{1}{N-1}( mathbf{F} - mathbf{bar{x}} ,mathbf{1}_N^mathrm{T} ) ( mathbf{F} - mathbf{bar{x}} ,mathbf{1}_N^mathrm{T} )^mathrm{T}$

where $mathbf{1}_N$ is an N by 1 vector of ones.
If the observations are arranged as rows instead of columns, so is now a 1×K row vector and $mathbf{M}=mathbf{F}^mathrm{T}$ is an N×K matrix whose column j is the vector of N observations on variable j, then applying transposes
in the appropriate places yields

$mathbf{Q} = frac{1}{N-1}( mathbf{M} - mathbf{1}_N mathbf{bar{x}} )^mathrm{T} ( mathbf{M} - mathbf{1}_N mathbf{bar{x}} ).$

Like covariance matrices for random vector, sample covariance matrices are positive semi-definite. To prove it, note that for any matrix the matrix ${displaystyle mathbf {A} ^{T}mathbf {A} }$ is positive semi-definite. Furthermore, a covariance matrix is positive definite if and only if the rank of the ${displaystyle mathbf {x} _{i}.-mathbf {bar {x}} }$ vectors is K.

Unbiasedness[edit]

The sample mean and the sample covariance matrix are unbiased estimates of the mean and the covariance matrix of the random vector , a row vector whose j^th element (j = 1, …, K) is one of the random variables.^[1] The sample covariance matrix has in the denominator rather than due to a variant of Bessel’s correction: In short, the sample covariance relies on the difference between each observation and the sample mean, but the sample mean is slightly correlated with each observation since it is defined in terms of all observations. If the population mean is known, the analogous unbiased estimate

$q_{jk}=frac{1}{N}sum_{i=1}^N left( x_{ij}-operatorname{E}(X_j)right) left( x_{ik}-operatorname{E}(X_k)right),$

using the population mean, has in the denominator. This is an example of why in probability and statistics it is essential to distinguish between random variables (upper case letters) and realizations of the random variables (lower case letters).

The maximum likelihood estimate of the covariance

$q_{jk}=frac{1}{N}sum_{i=1}^N left( x_{ij}-bar{x}_j right) left( x_{ik}-bar{x}_k right)$

for the Gaussian distribution case has N in the denominator as well. The ratio of 1/N to 1/(N − 1) approaches 1 for large N, so the maximum likelihood estimate approximately equals the unbiased estimate when the sample is large.

Distribution of the sample mean[edit]

For each random variable, the sample mean is a good estimator of the population mean, where a «good» estimator is defined as being efficient and unbiased. Of course the estimator will likely not be the true value of the population mean since different samples drawn from the same distribution will give different sample means and hence different estimates of the true mean. Thus the sample mean is a random variable, not a constant, and consequently has its own distribution. For a random sample of N observations on the j^th random variable, the sample mean’s distribution itself has mean equal to the population mean E(X_j) and variance equal to ${displaystyle sigma _{j}^{2}/N}$ , where is the population variance.

The arithmetic mean of a population, or population mean, is often denoted μ.^[2] The sample mean (the arithmetic mean of a sample of values drawn from the population) makes a good estimator of the population mean, as its expected value is equal to the population mean (that is, it is an unbiased estimator). The sample mean is a random variable, not a constant, since its calculated value will randomly differ depending on which members of the population are sampled, and consequently it will have its own distribution. For a random sample of n independent observations, the expected value of the sample mean is

{displaystyle operatorname {E} ({bar {x}})=mu }

and the variance of the sample mean is

${displaystyle operatorname {var} ({bar {x}})={frac {sigma ^{2}}{n}}.}$

If the samples are not independent, but correlated, then special care has to be taken in order to avoid the problem of pseudoreplication.

If the population is normally distributed, then the sample mean is normally distributed as follows:

${bar {x}}thicksim Nleft{mu ,{frac {sigma ^{2}}{n}}right}.$

If the population is not normally distributed, the sample mean is nonetheless approximately normally distributed if n is large and σ²/n < +∞. This is a consequence of the central limit theorem.

Weighted samples[edit]

In a weighted sample, each vector $textstyle {textbf {x}}_{i}$ (each set of single observations on each of the K random variables) is assigned a weight $textstyle w_{i}geq 0$ . Without loss of generality, assume that the weights are normalized:

$sum _{i=1}^{N}w_{i}=1.$

(If they are not, divide the weights by their sum).
Then the weighted mean vector is given by

$mathbf{bar{x}}=sum_{i=1}^N w_i mathbf{x}_i.$

and the elements $q_{jk}$ of the weighted covariance matrix are
^[3]

${displaystyle q_{jk}={frac {1}{1-sum _{i=1}^{N}w_{i}^{2}}}sum _{i=1}^{N}w_{i}left(x_{ij}-{bar {x}}_{j}right)left(x_{ik}-{bar {x}}_{k}right).}$

If all weights are the same, $textstyle w_{i}=1/N$ , the weighted mean and covariance reduce to the (biased) sample mean and covariance mentioned above.

Criticism[edit]

The sample mean and sample covariance are not robust statistics, meaning that they are sensitive to outliers. As robustness is often a desired trait, particularly in real-world applications, robust alternatives may prove desirable, notably quantile-based statistics such as the sample median for location,^[4] and interquartile range (IQR) for dispersion. Other alternatives include trimming and Winsorising, as in the trimmed mean and the Winsorized mean.

References[edit]

^ Richard Arnold Johnson; Dean W. Wichern (2007). Applied Multivariate Statistical Analysis. Pearson Prentice Hall. ISBN 978-0-13-187715-3. Retrieved 10 August 2012.
^ Underhill, L.G.; Bradfield d. (1998) Introstat, Juta and Company Ltd. ISBN 0-7021-3838-X p. 181
^ Mark Galassi, Jim Davies, James Theiler, Brian Gough, Gerard Jungman, Michael Booth, and Fabrice Rossi. GNU Scientific Library — Reference manual, Version 2.6, 2021.
Section Statistics: Weighted Samples
^ The World Question Center 2006: The Sample Mean, Bart Kosko

Источник

Сейчас Вы научитесь находить числовые характеристики статистического распределения выборки. Примеры подобраны на основании индивидуальных заданий по теории вероятностей, которые задавали студентам ЛНУ им. И. Франка. Ответы послужат для студентов математических дисциплин хорошей инструкцией на экзаменах и тестах. Подобные решения точно используют в обучении экономисты , поскольку именно им задавали все что приведено ниже. ВУЗы Киева, Одессы, Харькова и других городов Украины имеют подобную систему обучения поэтому много полезного для себя должен взять каждый студент. Задачи различной тематики связаны между собой линками в конце статьи, поэтому можете найти то, что Вам нужно.

Индивидуальное задание 1
Вариант 11

Задача 1. Построить статистическое распределение выборки, записать эмпирическую функцию распределения и вычислить такие числовые характеристики:

выборочное среднее;
выборочную дисперсию;;
подправленную дисперсию;
выборочное среднее квадратичное отклонение;
подправленное среднее квадратичное отклонение;
размах выборки;
медиану;
моду;
квантильное отклонение;
коэффициент вариации;
коэффициент асимметрии;
эксцесс для выборки:

Выборка задана рядом 11, 9, 8, 7, 8, 11, 10, 9, 12, 7, 6, 11, 8, 7, 10, 9, 11, 8, 13, 8.

Решение:
Запишем выборку в виде вариационного ряда (в порядке возрастания):
6; 7; 7; 7; 8; 8; 8; 8; 8; 9; 9; 9; 10; 10; 11; 11; 11; 11; 12; 13.
Далее записываем статистическое распределение выборки в виде дискретного статистического распределения частот:

Эмпирическую функцию распределения определим по формуле

Здесь n_x – количество элементов выборки которые меньше х. Используя таблицу и учитывая что объем выборки равен n = 20, запишем эмпирическую функцию распределения:

Далее вычислим числовые характеристики статистического распределения выборки.
Выборочное среднее вычисляем по формуле

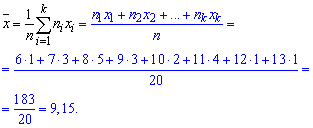
Выборочную дисперсию находим по формуле

Выборочное среднее, что фигурирует в формуле дисперсии в квадрате найдено выше. Остается все подставить в формулу

Подправленную дисперсию вычисляем согласно формулы

Выборочное среднее квадратичное отклонение вычисляем по формуле

Подправленное среднее квадратичное отклонение вычисляем как корень из подправленной дисперсии

Размах выборки вычисляем как разность между наибольшим и наименьшим значениями вариант, то есть:

Медиану находим по 2 формулам:
если число n — четное;
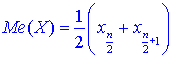
если число n — нечетное.
Здесь берем индексы в x_i согласно нумерации варианта в вариационном ряду.
В нашем случае n = 20, поэтому

Мода – это варианта которая в вариационном ряду случается чаще всего, то есть

Квантильное отклонение находят по формуле

где – первый квантиль, – третий квантиль.
Квантили получаем при разбивке вариационного ряда на 4 равные части.
Для заданного статистического распределения квантильное отклонения примет значение

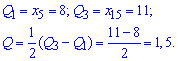
Коэффициент вариации равный процентному отношению подправленного среднего квадратичного к выборочному среднему

Коэффициент асимметрии находим по формуле

Здесь 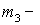центральный эмпирический момент 3-го порядка,

Подставляем в формулу коэффициента асимметрии

Эксцессом статистического распределения выборки называется число, которое вычисляют по формуле:

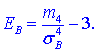
Здесь m₄ центральный эмпирический момент 4-го порядка. Находим момент

а далее эксцесс
Теперь Вы имеете все необходимые формулы чтобы найти числовые характеристики статистического распределения. Как найти моду, медиану и дисперсию должен знать каждый студент, который изучает теорию вероятностей.

Готовые решения по теории вероятностей

Следующая статья — Построение уравнения прямой регрессии Y на X

Источник

Вы́борочное
(эмпири́ческое) сре́днее —
это приближение теоретического среднего
распределения, основанное на выборке
из него.

Определение:
Пусть —выборка из распределения
вероятности,
определённая на некотором вероятностном
пространстве (Ω,F,P).
Тогда её выборочным средним
называется случайная
величина.

Свойства
выборочного среднего :

Пусть —выборочная
функция распределения данной
выборки. Тогда для любого
фиксированного ω функция является
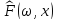
(неслучайной)функцией дискретного
распределения.
Тогда математическое
ожидание этого
распределения равно

Выборочное
среднее — несмещённая
оценка теоретического
среднего:

Выборочное
среднее — сильно
состоятельная оценка теоретического
среднего:

почти
наверное при .

Выборочное
среднее — асимптотически
нормальная оценка.
Пусть дисперсия случайных
величин 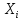конечна
и ненулевая, то есть

Тогда по
распределению при ,

где — нормальное
распределение со
средним 0 и
дисперсией .

Выборочное
среднее из нормальной выборки — эффективная
оценка её
среднего

20. Выборочная дисперсия, её свойства.

Выборочная
дисперсия в математической
статистике —
это оценка теоретической дисперсии
распределения на основе выборки.
Различают выборочную дисперсию и
несмещённую, или исправленную, выборочные
дисперсии.

Определения

Пусть —выборка из распределения
вероятности.
Тогда

Выборочная
дисперсия — это случайная
величина

где
символ обозначаетвыборочное
среднее.

Несмещённая
(исправленная) дисперсия — это случайная
величина

Замечание

Очевидно,

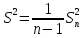
Свойства
выборочных дисперсий

Выборочная
дисперсия является
теоретической дисперсией выборочного
распределения.
Более точно, пусть 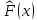—выборочная
функция распределения данной
выборки. Тогда для любого фиксированного ω
функция является
(неслучайной)функцией дискретного
распределения.
Дисперсия этого распределения равна .

Обе
выборочные дисперсии являются состоятельными
оценками теоретической
дисперсии. Если ,

И,

где обозначаетсходимость
по вероятности.

Выборочная
дисперсия является смещённой
оценкой теоретической
дисперсии, а исправленная выборочная
дисперсия несмещённой:

,И

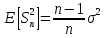
Выборочная
дисперсия нормального
распределения имеет распределение
хи-квадрат.
Пусть .
Тогда

21. Статистические оценки: несмещенные, эффективные, состоятельные

Состоятельной
называют такую точечную статистическую
оценку, которая при n стрем к бесконечн
стремится по вероятности к оцениваемому
параметру. В частности, если дисперсия
несмещенной оценки при n стр к беск
стремится к нулю, то такая оценка
оказывается и состоятельной.

Рассмотрим
оценку θ_n числового
параметра θ, определенную при n =
1, 2, … Оценка θ_nназывается состоятельной,
если она сходится по вероятности к
значению оцениваемого параметра θ при
безграничном возрастании объема
выборки. Выразим сказанное более
подробно. Статистика θ_n является
состоятельной оценкой параметра θ
тогда и только тогда, когда для любого
положительного числа ε справедливо
предельное соотношение

Пример
3. Из закона
больших чисел следует, что θ_n = является
состоятельной оценкой θ =М(Х) (в
приведенной выше теореме Чебышёва
предполагалось существование
дисперсии D(X); однако,
как доказал А.Я. Хинчин [6], достаточно
выполнения более слабого условия –
существования математического
ожидания М(Х)).

Пример
4. Все
указанные выше оценки параметров
нормального распределения являются
состоятельными.

Вообще,
все (за редчайшими исключениями) оценки
параметров, используемые в
вероятностно-статистических методах
принятия решений, являются состоятельными.

Пример
5. Так, согласно
теореме В.И. Гливенко, эмпирическая
функция распределенияF_n(x) является
состоятельной оценкой функции
распределения результатов наблюденийF(x)

Несмещенной
называют такую точечную статистическую
оценку Q*математическое
ожидание которой равно оцениваемому
параметру: M(Q*)=Q

Второе
важное свойство оценок – несмещенность.
Несмещенная оценка θ_n –
это оценка параметра θ, математическое
ожидание которой равно значению
оцениваемого параметра: М(θ_n)
= θ.

Пример
6. Из
приведенных выше результатов следует,
что иявляются
несмещенными оценками
параметровm и σ² нормального
распределения. Поскольку М()
= М(m**)
= m,
то выборочная медиана и
полусумма крайних членов вариационного
рядаm** —
также несмещенные оценки математического
ожидания mнормального
распределения. Однако

поэтому
оценки s² и
(σ²)**
не являются состоятельными оценками
дисперсии σ²нормального
распределения.

Оценки,
для которых соотношение М(θ_n)
= θ неверно, называются смещенными. При
этом разность между математическим
ожиданием оценки θ_n и
оцениваемым параметром θ, т.е. М(θ_n)
– θ, называется смещением оценки.

Пример
7. Для
оценки s²,
как следует из сказанного выше, смещение
равно

М(s²)
— σ² =
— σ²/n.

Смещение
оценки s² стремится
к 0 при n →
∞.

Оценка,
для которой смещение стремится к 0,
когда объем выборки стремится к
бесконечности, называется асимптотически
несмещенной.
В примере 7 показано, что оценка s² является
асимптотически несмещенной.

Практически
все оценки параметров, используемые в
вероятностно-статистических методах
принятия решений, являются либо
несмещенными, либо асимптотически
несмещенными. Для несмещенных оценок
показателем точности оценки служит
дисперсия – чем дисперсия меньше, тем
оценка лучше. Для смещенных оценок
показателем точности служит математическое
ожидание квадрата оценки М(θ_n –
θ)².
Как следует из основных свойств
математического ожидания и дисперсии,

(3)

т.е.
математическое ожидание квадрата
ошибки складывается из дисперсии оценки
и квадрата ее смещения.

Для
подавляющего большинства оценок
параметров, используемых в
вероятностно-статистических методах
принятия решений, дисперсия имеет
порядок 1/n,
а смещение – не более чем 1/n,
где n –
объем выборки. Для таких оценок при
больших n второе
слагаемое в правой части (3) пренебрежимо
мало по сравнению с первым, и для них
справедливо приближенное равенство

(4)

где с –
число, определяемое методом вычисления
оценок θ_n и
истинным значением оцениваемого
параметра θ.

Эффективной
называют такую точечную статистическую
оценку, которая при фиксированном n
имеет наименьшую дисперсию.

С
дисперсией оценки связано третье важное
свойство метода оценивания –эффективность.
Эффективная оценка – это несмещенная
оценка, имеющая наименьшую дисперсию
из всех возможных несмещенных оценок
данного параметра.

Доказано
[11], что иявляются
эффективными оценками
параметровm и σ²нормального
распределения. В то же время для
выборочной медианы справедливо
предельное соотношение

Другими
словами, эффективность выборочной
медианы, т.е. отношение дисперсии
эффективной оценки параметраm к
дисперсии несмещенной оценки этого
параметра при больших n близка к 0,637.
Именно из-за сравнительно низкой
эффективности выборочной медианы в
качестве оценки математического
ожидания нормального распределения
обычно используют выборочное среднее
арифметическое.

Понятие
эффективности вводится для несмещенных
оценок, для которых М(θ_n)
= θ для всех возможных значений параметра
θ. Если не требовать несмещенности, то
можно указать оценки, при некоторых θ
имеющие меньшую дисперсию и средний
квадрат ошибки, чем эффективные.

Пример
8. Рассмотрим
«оценку» математического ожидания m₁≡
0. Тогда D(m₁) =
0, т.е. всегда меньше дисперсии D()
эффективной оценки.
Математическое ожидание среднего
квадрата ошибкиd_n(m₁)
= m²,
т.е. при имеемd_n(m₁)
< d_n().
Ясно, однако, что статистикуm₁≡
0 бессмысленно рассматривать в качестве
оценки математического ожидания m.

Пример
9. Более
интересный пример рассмотрен американским
математиком Дж. Ходжесом:

Ясно,
что T_n –
состоятельная, асимптотически несмещенная
оценка математического ожидания m,
при этом, как нетрудно вычислить,

Последняя
формула показывает, что при m ≠
0 оценка T_n не
хуже (при
сравнении по среднему квадрату
ошибки d_n),
а при m =
0 – в четыре раза лучше.

Подавляющее
большинство оценок θ_n,
используемых в вероятностно-статистических
методах, являются асимптотически
нормальными, т.е. для них справедливы
предельные соотношения:

для
любого х,
где Ф(х) –
функция стандартного нормального
распределения с математическим ожиданием
0 и дисперсией 1. Это означает, что для
больших объемов выборок (практически
— несколько десятков или сотен наблюдений)
распределения оценок полностью
описываются их математическими
ожиданиями и дисперсиями, а качество
оценок – значениями средних квадратов
ошибок d_n(θ_n).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Definition of the sample mean[edit]

Definition of sample covariance[edit]

Unbiasedness[edit]

Distribution of the sample mean[edit]

Weighted samples[edit]

Criticism[edit]

See also[edit]

References[edit]

20. Выборочная дисперсия, её свойства.

21. Статистические оценки: несмещенные, эффективные, состоятельные