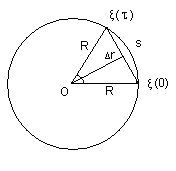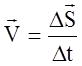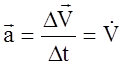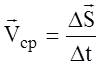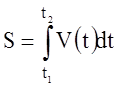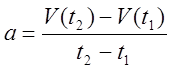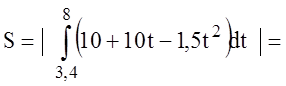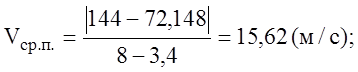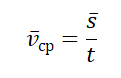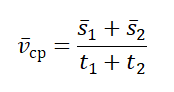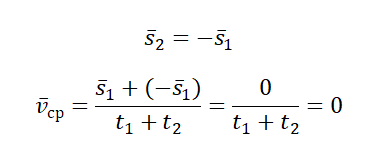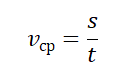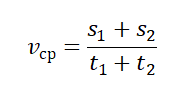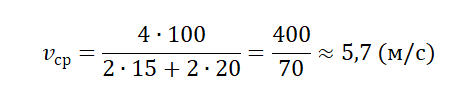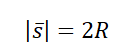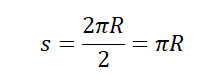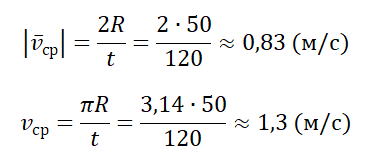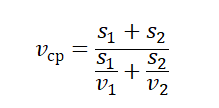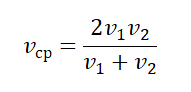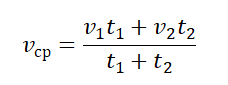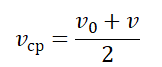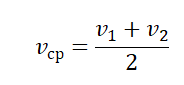Среднее путевое ускорение как найти

1. Средние угловая скорость и ускорение

Средний
вектор угловой скорости

‹
ω
› = Δφ
/Δ t,

где Δφ
− приращение
угла поворота за интервал времени Δ t
.

Средний
вектор углового ускорения

‹
β
› = Δω
/Δt
,

где Δω
−
приращение вектора угловой скорости
за интервал времени Δ/t.

Средняя
угловая скорость

‹
ω
› = Δ
φ
/Δt
,

Среднее
угловое ускорение;

‹
β
›
= Δω
/Δt.

1. Мгновенные угловая скорость и ускорение

Мгновенная
угловая скорость

ω
= dφ
/dt
;
ωz
= dφ
/ dt
,

где ωz
− проекция
угловой скорости на ось вращения.

Угловое
ускорение

‹ β
› = dω
/ dt
; βz
= dωz
/ dt
,

где βz
− проекция углового ускорения на ось
вращения.

Угловая
скорость и угловое ускорение являются
аксиальными вектора-

ми, их
направления совпадают с неподвижной в
пространстве осью враще-

ния.

Связь
между линейными и угловыми величинами:

S
= R φ
;
v
= ω R
; aτ
= βz R
; an
=
v² / R
= ω²
·
R ,

где R
− радиус
окружности, по которой движется точка;
S
− длина
дуги

окружности;
φ − угол
поворота, v
− линейная скорость; βz
− проекция
уг-

лового
ускорения на ось вращения; ω
− угловая
скорость; aτ
− тангенци-

альное
ускорение;
аn
− нормальное
ускорение.

При
постоянной угловой скорости ω
= 2π / T,
где Т − период(время од-

ного полного
оборота); v
− частота
вращения (число оборотов, совершаемых

движущейся
точкой в единицу времени) .
6

7. Кинематическое уравнение вращательного движения мате-

риальной
точки

t

φ
= ∫
ωz
dt
,

o

где φ
− угол
поворота; ωz
− проекция
угловой скорости на ось вращения. Ес-

ли угловое
ускорение β
= const,
то φ = φо
+ ωоt
+ βt²/
2 , где
ωо − началь-

ная угловая
скорость. Угловая скорость при таком
вращении

ω
= ωо + βt.

8.
Ускорение
в плоском криволинейном движении

a
= аn
+ aτ
, a
= √ an²
+ aτ
² ,
или

а = R
√ β
² +
ω²*²
,

где аτ
=
dv
/ dt
− скорость
изменения модуля скорости (см. рис. 1)

Сопоставление
уравнений поступательного и

вращательного
движений приведено в табл № 1.

Рис.
1
Таблица № 1

Поступательное движение	Вращательное движение
a = const	β = const
sx = x − xo = vox t + ax t² / 2	φz − φoz = ωoz t + β t² / 2
vx = vox + ax t	ωz = ωoz + βz t
2 axsx = vx² − vox²	2βz φz = ωz² − ωoz²

ВОПРОСЫ
И УПРАЖНЕНИЯ

1. Что изучает
механика как один из разделов физики?
Каково содержание:

а) классической
(ньютоновской); б) релятивистской; в)
квантовой механики?

2. Почему
приходится использовать модельные
представления
и абстрагиро-

ванные
понятия при изучении реальных физических
явлений и объектов?

Дайте
определения:

а)
материальной точки(частицы);

б)
системы материальных точек;

в)
абсолютно твердого тела.

3. Каково
содержание понятий пространства и
времени в классической и релятиви-

стской
механике? Что означает “однородность
пространства”, “однородность вре-

мени”,
“изотропность пространства”?

4. Какие
существуют способы описания движения
материальной точки? Дайте опре-

деления
системы отсчета, системы координат,
радиуса-вектора r
.

5. Покажите,
что задание кинематического закона
движения в координатной форме

х = х (t),
y
= (t)
, z
= z
(t)
эквивалентно заданию его в векторной
форме r
=r
(t),
где

х, у,z
– декартовы координаты положения
материальной точки,
r
– её радиус
–

вектор.
Каковы преимущества векторного описания
движения? 7

6. Дайте
определение кинематических величин:
а)перемещения r
; б) скорости
v
;

в) ускорения
a.
В каких единицах измеряются эти величины?
Как ориентирова-

ны векторы
скорости и ускорения относительно
траектории и друг друга?

7. Что называется
тангенциальным и нормальным ускорением?
Отчего зависит угол

между
векторами скорости v
и полного ускорения a
движущейся материальной

точки?

8. Какие векторы
называются аксиальными? Дайте определение
: а) угла поворота ;

б)угловой
скорости; в)углового ускорения относительно
неподвижной в простран-

стве оси
вращения. В каких единицах измеряются
эти величины?

9. Частица
движется по закону r
= ( vo
t
− g
t²
/ 2 ) k
, где vo
и g
− известные пос-

тоянные;
k
− орт
координатной оси z.
Найдите скорость v
частицы и
её уско-

рение a
, а также их
проекции vz
=d
z
/ d
t
и аz
= d
vz
/ d
t
как функции времени.

10.Ускорение
движущейся частицы a
= A
i
, где А –
известная постоянная; i
– орт

координатной
оси x.
В момент времени t
= 0 x
= xo
и vx
= vo
, где xo
и vo
— изве-

стные
постоянные(начальные условия). Найдите
проекцию скорости vx
= d
x
/ d
t

и координату
х как функцию времени.

ПРИМЕРЫ
РЕШЕНИЯ ЗАДАЧ

Пример
1.
С башни в горизонтальном направлении
брошено тело с

начальной
скоростью vо
= 10 м/с. Пренебрегая сопротивлением
воздуха, опре-

делить для
момента времени t
= 2 с после начала движения:1) скорость
тела v;

2) радиус
кривизны R
его траектории.

Д а н
о: vо
= 10 м/с, t
= 2 с.

О п р
е д е л и т ь: 1) v;
2) R.

Р е ш
е н и е. Тело участвует в двух взаимно
перпендикулярных движе-

ниях:
равномерном прямолинейном движении
вдоль оси Ох
( со скоростью vо)

и свободном
падении вдоль оси Оy
(со скоростью
vy
= gt)
(рис. 2). Следова-

тельно,
скорость тела в точке A

v
= √ vо²
+ g²t²

Из рисунка
видно, что нормальное ускорение тела

an
= g cos α = gvо
/ √ vо²
+ g²t² .

С другой
стороны, an
= v²/R,
откуда

R
= v²/an = (vо²
+ g²t²)³/² /gvо.

Рис.
2 Вычисляя, получаем:

1) v=
22 м/с; 2) R
= 109 м.

Пример
2.Кинематическое
уравнение движения материальной точки
по пря-

мой ( ось x
) имеет вид х
= A
+ Bt
+ Ct³,
где A
= 4 м, B
= 2 м /с, C
= −0,5 м/с².

для момента
времени t1
= 2 c
определить : 1) координату x1
точки, 2) мгновен-

ную скорость
v1,
3) мгновенное ускорение a1.

Д а н
о: A
= 4 м, B
= 2 м/с, С =
−0,5 м/с², t1
= 2 с.

О п р
е д е л и т ь: 1) x1;
2) v1;
3) a1.

Р е ш
е н и е. 1. Координату точки, для которой
известно кинематическое 8

уравнение
движения, найдем, подставив в уравнение
движения вместо t
задан-

ное значение
времени t1
:

x1
= A
+ Bt1
+ Ct³1.

Подставим
в это выражение значения A,
B,
C,
t1
и произведем вычисления:

x1
= ( 4 + 2 · 2 − 0,5 · 2³ ) м = 4 м.

1. Мгновенную скорость
   в произвольный момент времени найдем,
   про-

дифференцировав
координату
x
по времени:
v
= dx/d
t
= B
+ 3Ct².
Тогда в

данный момент
времени t1
мгновенная скорость

v1
= B
+ 3Ct²1.

Подставим
сюда значения B,
C,
t1
и произведём вычисления:

v1
= −4 м/с.

Знак минус
указывает на то, что в момент времени
t1
= 2 c
точка движется в

отрицательном
направлении координатной оси.

3. Мгновенное
ускорение в произвольный момент времени
найдем, взяв

вторую
производную от координаты x
по времени:
a
= d²x/dt²
= dv/dt
= 6Сt.

мгновенное
ускорение в заданный момент времени
t1
равно

a1
= 6Ct1.

Подставим
значения C,
t1
и произведем вычисления:

a1
= (−6 · 0.5 · 2) м/с = −6 м/с² .

Знак минус
указывает на то, что направление вектора
ускорения совпадает

с отрицательным
направлением координатной оси, причем
в условиях данной

задачи это
имеет место для любого момента времени.

Пример
3.
Кинематическое уравнение движения
материальной точки по

прямой(ось
x
) имеет вид x(t)
= A
+ Bt
+ Сt²,
где A
= 5 м, B
= 4 м/с, C
=−1 м/с².

1. Построить график
   зависимости координаты x
   и пути s
   от времени.

2. Определить среднюю
   скорость ‹ vx
   › за интервал времени от t1
   = 1 c
   до

t2
= 6 c.
3. Найти среднюю путевую скорость ‹ v
› за тот же интервал времени.

Р е ш е н и е.
1. Для построения графика зависимости
координаты точки

от времени найдем
характерные значения координаты –
начальное и макси-

мальное и моменты
времени, соответствующие указанным
координатам и ко-

ординате, равной
нулю.

Начальная
координата соответствует моменту t
= 0. Её значение равно

xo
= x(0)
= A
= 5 м.

Максимальное
значение координата достигнет в тот
момент, когда точка

начинает двигаться
обратно (скорость меняет знак). Этот
момент времени

найдем, приравняв
нулю первую производную от координаты
по времени:

v
= dx/dt
= B
+ 2Ct
= 0, откуда

t
= −B/2C
= 2 c.

9

Максимальная
координата

xmax
= x(2)
= 9 м.

Момент времени
t,
когда координата x
= 0, найдем
из выражения

x
= A
+ Bt
+ Ct²
= 0.

Решим полученное
квадратное уравнение относительно t
:

t
= (
−B
± √ B²
−4AC
) / 2C
.

Подставим значения
A,
B,
C
и произведём вычисления:

t
= (2 ± 3) c.

Таким
образом, получаем два значения времени:
t′=

=
5 c
и t»
= −1 c.
Второе значение времени отбра-

сываем,
так как оно не удовлетворяет условию
за-

дачи
( t≥
0 ).

График
зависимости координаты точки от вре-

мени
представляет собой кривую второго
порядка.

для
его построения необходимо иметь пять
точек,

так
как уравнение кривой второго порядка
содер-

жит
пять коэффициентов. Поэтому кроме трех
вы-

численных
ранее характерных значений координа-

ты
найдем ещё два значения координаты,
соответ-

ствующие
моментам t1
= 1 c
и t2
= 6 c:

x1
= A
+ Bt1
+ Ct²1
= 8 м,
x2
= A
+ Bt2
+ Ct²2
= −7 м.

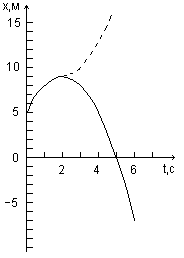
Рис. 3

Полученные
данные представим виде таблицы:

Время, с	to = 0	t1 = 1	tв = 2	t′ = 5	t2 = 6
Координата, м	xо = A = 5	x1 = 8	xmax = 9	x = 0	x2 = −7

Используя данные
таблицы, чертим график зависимости
координаты

от времени
( рис. 3).

График пути
построим, исходя из следующих соображений:
1) путь и

координата до
момента изменения знака скорости
совпадают; 2) начиная

с момента возврата
( tв
) точки она движется в обратном направлении
и,

следовательно,
координата её убывает, а путь продолжает
возрастать по

тому же закону, по
которому убывает координата.

Следовательно,
график пути до момента времени tв
= 2 с совпадает с

10

графиком координаты,
а начиная с этого момента является
зеркальным

отображением
графика координаты.

2. Средняя
скорость ‹ vx
› за интервал времени t2
− t1
определяется

выражением

‹ vx
› = (x2
− x1)
/ (t2
− t1).

Подставим значения
x1,
x2,
t1,
t2
из таблицы и произведем вычисления

‹ vx
› = ( −7 −8 ) / (6 −1) м = − 3 м/c.

3. Среднюю
путевую скорость ‹ v
› находим из выражения

‹ v
› = s
/ ( t2
− t1
),

где s
− путь,
пройденный точкой за интервал времени
t2
− t1.
Из графика

на рис. 3 видно, что
этот путь складывается из двух отрезков
пути: s1
=

= xmax
− x1,
который точка прошла за интервал времени
tв
− t1,
и s2
=

=
xmax
+ | x2
|, который она прошла за интервал
t2
− tв.
Таким образом,

путь

s
= s1
+s2
= ( xmax
− x1
) + ( xmax
+ | x2
| ) = 2 xmax
+ | x2
| − x1.

Подставим
в это выражение значения x1,
| x2
|, xmax
и произведем вычис-

ления

‹ s
› = ( 2 · 9 + 7 − 8 ) м = 17 м.

Тогда искомая
средняя путевая скорость

‹ v
›= 17 / ( 6 − 1 ) м/c
= 3.4 м /c
.

Заметим,
что средняя путевая скорость всегда
положительна.

Пример
4.
Автомобиль движется по закруглению
шоссе, имеющему ра-

диус кривизны
R
= 50 м. Уравнение движения автомобиля ξ
(t)
= A+
Bt+
Ct²,

где ξ
означает криволинейую координату,
отсчитанную по дуге окружности,

A
= 10 м, B
= 10 м/c,
C
=−0,5 м /c².
Найти : 1) скорость v
автомобиля, его

его
тангенциальное aτ,
нормальное an,
и полное a
ускорения в момент вре-

мени t
= 5 c;
2) длину пути s
и модуль
перемещения | Δr
| автомобиля
за

интервал
времени τ
= 10 c,
отсчитанный с момента начала движения.

Р е ш е н
и е. 1. Зная уравнение движения, найдем
скорость, взяв первую

производную
от координаты по времени: v
= dξ
/ dt
= B
+ 2Ct.
Подставим в

это выражение
значения B,
C,
t
и произведем
вычисления:

v
= 5 м /c.

Тангенциальное
ускорение найдем, взяв первую производную
от скорости

по времени:
aτ
= d
v
/dt
= 2 C.
Подставив значение C,
получим

aτ
= − 1 м/c².

11

Нормальное
ускорение определяется по формуле an
= v²/R.
Подставим сюда

найденное
значение скорости и заданнон значение
радиуса кривизны траекто-

рии и
произведем вычисления:

an
= 0,5 м/c².

Полное
ускорение, как видно из рис.1, является
геометрической суммой

ускорений
aτ
и an:
a
= aτ
+ an.
Модуль ускорения a
= √ a²τ
+ a²n
. Подста-

вив в это
выражение найденные значения
aτ
и an,
получим

a
= 1.12
м/c².

1. Чтобы определить
   путь s,
   пройденный автомобилем, заметим, что
   в слу-

чае движения в
одном направлении (как это имеет место
в условиях данной за-

дачи ) длина пути
s
равна изменению криволинейной
координаты ξ
, т.е.

s
= ξ
(
τ
) − ξ ( 0 ), или
s
= A + Bτ + Cτ² −
A = B + C
τ²
.

Подставим
в полученное выражение значения B,
C,
τ и
произведем вычисле-

ния:

s
= 50 м.

Модуль
перемещения, как это видно из рис.4, равен

|Δr|
= 2 R
sin
( α
/2 ),

где
α − угол между радиусами-векторами,
определя-

ющими
начальное ξ (0) и конечное ξ (τ)
положения

автомашины
на траектории. Этот угол (в радианах)
на-

ходим как
отношение длины пути к радиусу кривизны
R

траектории,
т.е. α = s
/ R.
Таким образом,

Рис.4
|Δr|
= 2 R
sin
(s
/ R).

Подставим
сюда значения R,
s
и произведем вычисления:

|Δr|
= 47.5 м.

Пример
5. Диск
радиусом R
= 5 см вращается вокруг неподвижной

оси так, что
зависимость угловой скорости от времени
задается уравнением

ω
= 2At
+
5Bt²*²
( A =
2 рад
/
c²,
B
= 1
рад
/ c²
c³
). Определить
для точек на

ободе диска
к концу первой секунды после начала
движения: 1) полное уско-

рение; 2)
число оборотов N,
сделанных диском.

Д а н о:
R
= 5 см = 0.05 м,
ω =2At
+ 5Bt²*,²
A
= 2 рад / c²
; B
= 1 рад /c²c³,

t
= 1 c.

О п р е д
е л и т ь: 1) a;
2) N.

Р е ш е н
и е. Полное ускорение
a
= √ aτ²
+an²
, где тангенциальная состав-

12

ляющая
ускорения aτ
= βR
( β
= dω
/ dt
− угловое
ускорение ), а нормальная

составляющая
ускорения an
= ω²R.

По условию
задачи, ω =
2At
+ 5Bt²*²;
следовательно,

aτ
= βR = R dω /dt = R ( 2A
+ 5B
t³
),

an
= ω²R
= R
( 2At
+ 5Bt²*²)²,

откуда
полное ускорение

a
= R √ (2At
+ 20Bt³)²
+ (2At
+
5Bt²*²)²*².

Угол
поворота диска φ
= 2π N
( N
− число
оборотов), но угловая ско-

рость ω
= dφ
/ dt
; следовательно,

t
t

φ
=
∫ ωdt
=
∫ (2At
+
5Bt²*²)dt
= At²+
Bt²t³.

о
o

Тогда
число оборотов, сделанных диском,

N
= φ
/ (2π)
= ( At²
+ Bt²*³
) / 2π
.

Вычисляя,
получим: 1) a
= 4.22 м/c²ж;
2) N
= 0.477.

Пример
6.
Маховик, вращавшийся с постоянной
частотой no
= 10 c־¹,

при торможении
начал вращаться равнозамедленно. Когда
торможение пре-

кратилось,
вращение маховика снова стало равномерным,
но уже с частотой

n
= 6 c־¹.
Определить угловое ускорение β
маховика
и продолжительность

t
торможения, если за время движения
маховик сделал
N
оборотов.

Р е ш е н
и е. Угловое ускорение маховика связано
с начальной ωо
и ко-

нечной ω
угловыми
скоростями
соотношением
ω²
− ωo²
= 2βφ,
откуда

откуда β
= ( ω²
− ωo²
) / (2φ).
Но так как φ
= 2π N,
ω
= 2 π N,
то

β
= ( ω²
− ωo²
) / 2φ
= π
( n²
− no²
) / N
.

Подставив
значения π, n,
no,
N
и вычислив,
получим

β
= 3.14 ( 6² − 10² ) / 50 рад / с² = −4.02 рад / c².

Знак минус
указывает на то, что маховик вращается
замедленно.

Определим
продолжительность торможения, используя
формулу,связыва-

ющую угол
поворота φ
со средней угловой скоростью
‹ ω
› вращения и

и временем
t:
φ
= ‹ ω
› t.
По условиям задачи, угловая скорость
линейно

зависит от
времени и поэтому можно написать ‹ ω
› = ( ωo
+ ω ) / 2 ,
тогда

φ
= ( ωo
+ ω
) t
/
2 = π ( no
+ n
) t
,

откуда

t
= φ
/ π (
no
+ n
) = 2 N
/ (no
+ n
).

13

Подставив
числовые значения и произведя вычисления,
получим

t
= 2 · 50 / ( 10
+ 6 ) = 6.25 с.

ЗАДАЧИ
ГРУППЫ А

1.(В.1.23)
Зависимость пройденного телом пути s
от времени t
да-

ется
уравнением s =А — Вt
+ Ct²,
где А = 6 м, В = 3 м/с и С = 2 м/c².
Найти

среднюю
скорость <v>
и ускорение a
тела для интервала времени 1 ≤ t
≤ 4.

Построить
график зависимости пути s,
скорости v
и ускорения a
от време-

ни t
для интервала 0 ≤ t
≤ 5 c
через 1 с.

Ответ:
<v>
= 7 м/c;
a
= 4 м/c²
.

2.(В.1.26)
С башни
высотой h
= 25,0 м горизонтально брошен камень

со скоростью
vx
= 15 м/c.
Какое время t
камень будет в движении? На ка-

ком расстоянии
l
от основания башни он упадет на землю?
С какой скоро-

стью v
он упадет на землю? Какой угол φ составит
траектория камня с го-

ризонтом в
точке его падения на землю?

Ответ
: t
= 2,3 c;
l
= 34 м; φ = 56°.

3.(В.1.31)
Камень
брошен горизонтально со скоростью vx
= 10,00 м/с.

Найти радиус
кривизны R
траектории камня через время t
= 3.00 с пос-

ле начала
движения.

Ответ
: R
= 305 м.

4.(В.1.32)
Мяч брошен
соскоростью vо
= 10.00 м/с под углом
α = 40º

к горизонту.
На какую высоту h
поднимется мяч? На каком расстоянии l

от места
бросания он упадет на землю? Какое время
t
он будет в движе-

нии?

Ответ
: h
= 2.1 м; l
= 10.0 м; t
= 1.3 с.

5.(В.1.34)
Тело
брошено со скоростью vо
под углом к горизонту. Вре-

мя полета
t
= 2.2 c.
На какую высоту h
поднимется тело ?

Ответ:
h
= 5.9 м.

6.(В.1.36)
Тело брошено со скоростью vо
= 14.7 м/с под углом α = 30º

к горизонту.
Найти нормальное a
n
и
тангенциальное a
τ
ускорения
тела

через время
t
= 1.25 с после начала движения.

Ответ:
a
n
= 9.2 м/c²;
a
τ
= 3.5 м/с².

7.(В.1.37)
Тело
брошено со скоростью vо
= 10.0 м/с под углом α = 45º

к горизонту.
Найти радиус кривизны R
траектории движения тела через

время t
= 1.00 с после начала движения.

Ответ:
R
= 6.3 м.

8.(В.1.39)
С башни
высотой hо
= 25.0 м брошен камень со скоростью

vo
= 15 м/с под углом α = 30º к горизонту. Какое
время t
камень будет в дви-

жении? На
каком расстоянии l
от основания башни он упадет на землю?
С ка-

14

кой скоростью
v
он упадет на землю? Какой угол φ
составит траектория дви-

женияния с
горизонтом в точке его падения на землю?

Ответ:
t
= 3.16 с; l
= 41.1 м ; φ
= 61º.

9.(В.1.50)
Вал вращается с частотой n
=180 об/мин. С некоторого момен-

та вал начал
вращаться равнозамедленно с угловым
ускорением β = 3 рад/с².

Через какое
время t
вал остановится? Найти число оборотов
N
вала до оста-

новки.

Ответ:
t
= 6.3 с ; N
= 9.4 об.

10.(В.1.53)
Точка
движется по окружности радиусом R
= 10.0 см с посто-

янным
тангенциальным ускорением a
τ.
Найти нормальное ускорение a
n
точ-

ки через
время t
= 20.0 с после начала движения, если
известно, что к концу

пятого
оборота после начала движения линейная
скорость точки v
= 10.0

см /c.

Ответ:
a
n
= v
v³
t²/16π²N²R³
= 0.010 м/с².

11.(В.1.55)
Колесо радиусом R
= 10 см вращается с угловым ускорением

β = 3.14 рад/с²
. Найти для точек на ободе колеса к концу
первой секунды пос=

ле начала
движения: а) угловую скорость ω ; б)
линейную скорость v
; в) тан-

генциальное
ускорение aτ
; г) нормальное ускорение n
; д) полное ускорение a;

е) угол φ,
составляемый вектором полного ускорения
с радиусом колеса.

Ответ:
ω
= 3.14 рад/с ; v
= 0.314 м/с ; aτ
= 0.314 м/с² ; a
n
= 0.986 м/с²;

a
= 1.03 м/с² ; φ
= 17º46′ .

12.(1.59)
Колесо
вращается с угловым ускоренрем β = 2.00
рад/с². Че-

рез время
t
= 0.500 c
после начала движения полное ускорение
колеса а = 13.6

см/с². Найти
радиус R
колеса.

Ответ:
R = a/β√ (1 + β²t²* ² ) = 6.1 см.

13.(В.1.61)
Колесо
радиусом R
= 5.00 см вращается так, что зависимость

угла поворота
радиуса колеса от времени дается
уравнением φ = A
+ Bt
+ Ct²
+

+ Dt³,
где D
= 1.000 рад/с³. Для точек, лежащих на ободе
колеса, найти прира-

щение модуля
тангенциального ускорения Δaτ
за единицу времени.

Ответ:
Δaτ
= 0.3 м/с².

14.(В.1.64)
Во сколько
раз нормальное ускорение an
точки, лежащей на

ободе
вращающегося колеса, больше ее
тангенциального ускорения aτ
для того

момента,
когда вектор полного ускорения точки
составляет угол φ = 30° с век-

тором её
линейной скорости?

Ответ:
an
/aτ
= tg
φ
= 0.58.

ЗАДАЧИ
ГРУППЫ Б

1.(
Ч.1.4) Первую
половину пути тело двигалось со скоростью
v1
= 2 м /c,

вторую −
со скоростью v2
= 8 м /c.
Определить среднюю путевую скорость ‹
v
›.

15

Ответ:
‹ v
› = 2v1·v2
/ ( v1
+ v2
) = 3,2 м/c
.

2.(
Ч.1.5) Тело
прошло первую половину пути за время
t1
= 2 c,
вторую-за

время t2
= 8 м /c.
Определить среднюю путевую скорость ‹
v
› тела, если дли-

на пути s
= 20 м.

Ответ:
‹ v
› = s
/ ( t1
+ t2
) = 2 м /c.

3.(И.1.6.)
Корабль
движется по экватору на восток со
скоростью vo
=30

км /ч. С
юго-востока под углом φ = 60º к экватору
дует ветер со скоростью v
=

= 15 км / ч.
Найти скорость v’
ветра относительно корабля и угол φ’
между эква-

тором и
направлением ветра в системе отсчета,
связанной с кораблем.

Ответ:
v’
= √ ( vo²
+ v²
+ 2 vo
v
cos
φ
) ≈ 40 км / ч, φ’ = 19º.

4.(Ч.1.26)
Материальная
точка движется в плоскости согласно
уравнению

r
(t)
= A
t³
i
+ B
t²
j.
Написать зависимости : 1) v
(t),
2) a
(t).

Ответ
: 1) v
(t) = 3A t²i
+
2B t j
; 2)
a
(t)
= 6 At i
+ 2B
j.

5.(Ч.1.33)
Движение
точки по окружности радиусом R
= 4 м задано уравне-

нием ξ =
А + В t
+ C
t²
, где ξ − криволинейная координата,
отсчитанная по

дуге
окружности, А = 10 м, В = − 2 м /c,
C
= 1 м/c².
Найти тангенциальное аτ,

нормальное
аn
и полное а ускорения точки в момент
времени t
= 2c.

Ответ
: 2 м /c²
; 1 м /c²
; 2.24 м /c²
.

6.(Ч.1.36)
Движение
точки по кривой задано уравнениями х
= А1 t³
и у =А2t,

где А1 = 1 м
/c³,
А2 = 2 м/c.
Найти уравнение траектории точки, её
скорость v
и

полное
ускорение а в момент времени t
= 0.8 c.

Ответ
: у³
− 8х ; 2.77 м /c
; 4.8 м/c².

7.(Ч.1.59)
Диск
вращается с угловым ускорением β = −
2 рад /c².
Сколько

оборотов N
сделает диск при изменении частоты
вращения от n1
= 240 мин ־¹

до n
= 90 мин ־¹
? Найти время
Δ t,
в течение которого это произойдет.

Ответ
: N
= π
( n2²
− n1²
) / β
= 21.6; Δ t
= 2 π ( n2
− n1
) / β = 7.85 c.

8.
На вал радиусом R
= 10 см намотана нить, к концу которой
призана гиря.

двигаясь
равноускоренно, гиря за t
= 20 с от начала движения опустилась на
h
=

= 2 м. Найти
угловую скорость и угловое ускорение
вала для этого момента вре-

мени.

Ответ
: ω
= 2 h
/(Rt)
= 2 рад /c;
β = 2h
/(Rt
²) = 0.1 рад /c.

9.(Ч.1.49)
Тело
брошено под углом φ = 30º к горизонту.
Найти тангенци-

альное аτ
и нормальное аn
ускорения в начальный момент времени
движения.

Ответ
: 4.9 м /c²
; 8.49 м /c²
.

10.
Тело брошено со скоростью vo
= 20 м /c
под углом φ = 30º к горизонту.

пренебрегая
сопротивлением воздуха, найти скорость
v
тела, а также его нор-

мальное аn
и тангенциальное аτ ускорения через
t
= 1.5 c
после начала движе-

ния. На какое
расстояние х переместится за это время
тело по горизонтали и на

какой высоте
у оно окажется?

Ответ
: v
= 17.9 м /c;
a
n
= 9.72 м /c²;
aτ
= 2.67 м /c²
; x
= 26 м; y
= 4м.

16

11.(C.1.15)
Частица
движется равномерно по часовой стрелке
по окруж-

Ности радиуса
R
, делая за время τ один оборот. Окружность
лежит в коор-

динатной
плоскости х,у,
причем центр
окружности совпадает с началом коор-

динат. В
момент t
= 0 частица находится в точке с координатами
х =
0, у =
R.

Найти среднее
значение скорости точки за промежуток
времени: а) от 0 до

τ /4, б) от
0 до τ /2, в) от 0 до 3τ /4, г) от 0 до τ,
д) от τ /4 до 3 τ /4.

Ответ:
a)‹v
› = (4 /τ) R ( i
−
j
),
б)‹
v ›
= − (4 /τ) R j,
в)‹
v
›=−(4/3)R(i
+ j),

г)
‹ v
› = 0, д) ‹ v
› = −( 4/τ)R
i.

12.(C.1.29)
Точка
движется вдоль оси х
, причем
координата х
изменя-

ется по
закону х
= A
cos
(2π
/T)
t.
Найти : a)
выражения для проекций на ось

х
скорости v
и ускорения а
точки, б)
путь s1,
пройденный точкой за про-

межуток
времени от t
=0 до t
= T/8,
в) путь s2,
пройденный точкой за проме-

жуток времени
от t
= T/8
до t
= T/4,
г) путь s
, пройденный точкой за проме-

жуток от 0
до t
= T.

Ответ
: а) vx
= − ( 2π
/ T)
A
sin
( 2π
/T)
t,
ax
=−( 2π
/T)²
A
cos
( 2π
/T)
t,

б)
s1
= 0.293A,
в) s2
= 0,707 A,
s
= 4A
.

ЗАДАЧИ
ГРУППЫ С

1.(И.1.13)
Точка А
движется равномерно со скоростью v
так, что

Вектор
v
все время
“ нацелен “ на точку В, которая в
свою очередь дви-

жется
прямолинейно и равномерно со скоростью
u
< v.
В начальный момент

v
перпендикулярен
u
и расстояние
между точками равно
l.
Через сколько

времени τ
точки
встретятся?

Ответ:
τ
= v
l
/ ( v²
— u²
).

2.(И.1.20)
Радиус-вектор частицы меяется со
временем по закону r
=

= b
t(
1- α
t
), где b
− постоянный вектор, α − положительная
постоянная. Най-

ти: a)
скорость v
и ускорение
а частицы
в зависимости от времени;

б) промежуток
времени Δ
t,
по истечении которого частица вернется
в ис-

ходную точку,
а также путь s,
который она пройдет при этом.

Ответ
:
a) v
=
b
(1
– 2 α
t),
a
=
− 2 αb
= const; Δt
=
1/α , s
=
b/2α.

3.(И.1.21)
В момент t
= 0 частица вышла из начала координат
в поло-

жительном
направлении оси
х. Её
скорость меняется со временем по закону

v
= vo
( 1 – t/τ
), где vo
− начальная скорость, модуль которой
vo
= 10,0 cм/c,

τ
= 5.0 c.
Найти: а) координату х
частицы в моменты времени 6,0, 10 и 20 с;

б) моменты
времени, когда частица будет находться
на расстоянии 10.0 см от

начала
координат.

Ответ
: a)
x
= vo
t
( 1 – t
/2τ);
0.24, 0 и −2.0 м; б) 1.1, 9 и 11 с.

4.(И.1.24)
Радиус-вектор
точки А относительно начала координат
меня-

ется со
временем t
по закону r
= α
t
i
+
β t²
j
, где α и
β −
постоянные,

i
и j
− орты осей х
и у.
Найти: a)
уравнение траектории точки у
( х );

изобразить
её график; б) зависимости от времени
скорости v,
ускорения а

и модулей
этих величин; в) зависимость от времени
угла φ между вектора-

ми а
и v.

17

Ответ:
а) y
= x²
β
/ α²;

б)
v
= α
i
+ 2β
t
j
, a
= 2 β
j
, v
= √ α²
+ 4β²t²
, α
= 2β
;

в)
tg
φ
= α
/2β
t.

5.(Т.1.25)
Нормальное
ускорение точки, движущейся по окружности
ради-

усом R
= 4 м, задается уравнением аn
= A
+ В
t
+ C
t²
( A
= 1 м /c²,
B
= 6 м/c³,

C
= 9 м /c²*².
Определить: 1) тангенциальное ускорение
аτ точки;
2) путь s,

пройденный
точкой за время t1
= 5 c
с после начала движения; 3) полное уско-

рение а
для момента
времени t2
= 1 c.

Ответ:
aτ
= 6 м /c²;
s
= 85 м; a
= 6.32 м /с².

6.(Т.1.28)
Точка
движется в плоскости ху
из положения
с координатами

х = у =
0
со скоростью v
= a
i
+ bx
j
, где а и
b
− постоянные;
i,
j
− орты

осей х
и у
. Определить:
1) уравнение траектории точки у
(х) ; 2) форму

траектории.

Ответ:
1) у
= bx²
/ 2a
; 2) парабола.

7.(И.1.10)
Два тела бросили одновременно из одной
точки: одно − верти-

кально вверх,
другое − под углом φ = 60º к горизонту.
Начальная скорость

каждого тела
vo
= 25 м /c.
Пренебрегая сопротивлением воздуха,
найти рассто-

яние l
между
телами через t
=1.7 c.

Ответ:
l
= vo
t
√ 2(1 – sin
φ
) = 22 м.

8.(С.1.32)
Небольшое тело (материальная точка)
брошено из точки О под

углом α
к горизонту
с начальной скоростью vo
( рис. 5). Пренебрегая сопро-

тивлением воздуха,
найти:

а) время полета
τ,

б) дальность
полета l,

в) наибольшую
высоту поднятия тела h,

г) уравнение
траектории тела в координатах

х’,
у’,

д) значения
| dv
/dt
| и d
| v
| /dt
в вершине

траектории,

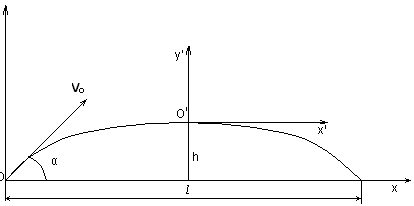
Рис.5
е) радиус кривизны R
траектории в точках

О и О’.

Точки
бросания и падения считать лежащими на
одном уровне.

Ответ:
a)
τ
= 2 vosin
α
/ g
, б) l
= vo²
sin
2α
/ g
, в) h
= vo²
sin²α
/ 2g,

г)
у’ = − g
x‘
²/ 2 vo²
cos²
α
, д) | dv
/dt
| = g,
d
| v|
/dt
= 0, е) Ro
= vo²
/ g
cos
α
,

R
o’
= vo²
cos²α
/g
.

9.(И.1.46)
Твердое тело вращается вокруг неподвижной
оси по закону

φ
= a
t
− b
t³,

где a
= 6.0 рад /с
, b
= 2.0 рад/c.
Найти: средние значения угловой скорости

и углового
ускорения за промежуток времени от t
= 0 до
остановки; б) угловое

ускорение
в момент остановки.

Ответ:
a)
‹ ω
› = 2a
/3 = 4 рад /c
, ‹ β
› = √ 3 ab
= 6 рад /c²;

Б)
β = 2
√ 3 аb
= 12 рад /c².

18

10.(И.1.47)
Твердое тело начинает вращаться вокруг
неподвижной оси с

угловым
ускорением β
= αt,
где α = 2.0
* 10־²
рад /c³.
Через сколько времени

после начала
вращения вектор полного ускорения
произвольной точки тела бу-

дет составлять
угол φ = 60º
с её вектором скорости ?

Ответ:
τ
= ³√ (4/α)
tgφ
= 7 c.

11.(И.1.35)
Частица движется в плоскости ху
со скоростью
v
= αi
+βxj,

где
i
и
j
− орты осей
х и
у
, α и
β −
постоянные. В начальный момент

частица
находилась в точке х
= у = 0.

Найти:

а)
уравнение траектории частицы у(
х
);

б) радиус
кривизны R
траектории в зависимости от х.

Ответ:
а) х
= (β
/2α)
x²,
б) R
= v²/
an
= v²/√
a²
− aτ²
= ( α / β)[1
+ (xβ/α)²]³/².

12.(И.1.37)
Точка движется по окружности со
скоростью v
= αt,
где α
=

= 0.50 м/c².
Найти её полное ускорение а
в момент, когда она пройдет n
=0.10

длины
окружности после начала движения.

Ответ:
a
= α
√ 1 + (4π
n)²
= 0.8 м/c².

13.(И.1.41)
Точка движется по плоскости так, что
её тангенциальное ус-

корение аτ
= α , а
нормальное ускорение аn
=βt²*²,
где α и β −
положитель-

ные постоянные,
t
− время. В
момент t
= 0 точка
покоилась. Найти зависи-

мости от
пройденного пути s
радиуса
кривизны R
траектории токи и её

полного
ускорения а.

Ответ:
R
= α³
/2βs
, a
= α
√ 1 + (4βs²/α³)²
.

14.(И.1.44)
Колесо вращается вокруг неподвижной
оси так, что угол φ

его поворота
зависит от времени как φ
= βt²,
где β = 0.20
рад /c².
Найти

полное
ускорение а
точки А
на ободе колеса в момент времени t
= 2.5 с,

если скорость
точки А в этот момент v
= 0.65 м/c.

Ответ:

a
= (v/
t)
√ 1 + 4β²t²*²
= 0.7 м/c².

15.(И.1.49)
Твердое тело вращается вокруг
неподвижной оси так, что

его угловая
скорость зависит от угла φ
по закону
ω = ωо −
а φ, где ωо
и а

− положительные
постоянные. В момент времени t
= 0 угол φ
=0. Найти

зависимости
от времени:

a)
угла поворота; б) угловой скорости.

—
at
—at

Ответ:
a) φ
= (1
— e ) ωo/a;
ω
=
ωo
e .

Занятие
2. Динамика
прямолинейного и криволинейного

движения
материальной точки

СОДЕРЖАНИЕ
ТЕОРИИ

1. Дифференциальное
   уравнение движения материальной точки.

2. Потенциальные и
   диссипативные силы в механике.

3. Динамика кругового
   движения материальной точки.

4. Закон изменения
   и сохранения импульса материальной
   точки.

19

ОСНОВНЫЕ
ФОРМУЛЫ ДЛЯ РЕШЕНИЯ ЗАДАЧ

Была ли эта статья полезной?

Министерство образования

Российской Федерации

Санкт-Петербургский
государственный горный институт им. Г.В. Плеханова

(технический университет)

Кафедра общей и технической физики.

Расчетно-графическая работа

 

По дисциплине  ________

	Кинематика движения материальной точки по прямой

 

Тема:

Автор: студент гр. ЭГР-02    ____________________                            
/_Башурова  А.С. /

                                                              
^{(подпись)                                                        (Ф.И.О.)}

ОЦЕНКА:     _____________

Дата: ___________________

ПРОВЕРИЛ: _________________                                       /Смирнова
Н. Н./

                       
                                                                     ^{(подпись)}

Санкт-Петербург

2003

Вариант № 3.

Задание.

Кинематическое
уравнение движения материальной точки по прямой (ось х) имеет вид: , а 
 t₁=3,4 c;  t₂=8 с;

                 Найти:

1)  Путь, пройденный
за интервал времени от t₁ до t₂; 

2) 
Среднюю
путевую скорость V_ср за тот же интервал времени;

3) 
Среднее
путевое ускорение.

4) 
Координату
материальной точки в момент времени tи t.

Построить графики
зависимостей  х(t) и а(t).

Краткие
теоретические сведения:

ü 
Система
отсчета –  это совокупность неподвижных друг относительно друга тел, по отношению
к которым рассматривается движение, и отсчитывающие время часы.

ü 
Координата  — это
совокупность чисел или независимых переменных, которые определяют положение
точки в пространстве.

ü 
Материальная
точка – это тело, размерами, которых можно пренебречь по сравнению с
расстоянием  до других тел. 

ü 
Траектория – линия, которую
описывает материальная точка при своем движении.

ü 
Если
точка двигаясь по траектории переместилась из точки 1 в точку 2, то это
расстояние называется длиной пройденного частицей пути или просто пройденным
частицей путем.

ü 
Перемещение – отрезок прямой,
проведенный из начального положения частицы в конечное.

ü 
Скорость – векторная
величина, которая характеризует не только быстроту движения частицы по
траектории, но и направление, в котором движется частица в каждый момент
времени.

                                            

ü 
Ускорение – векторная
физическая величина, характеризующая быстроту изменения скорости и равная
первой производной скорости по времени.

ü 
Средней
скоростью материальной точки в промежутке времени называется вектор, равный
отношению пройденного пути за этот промежуток времени к его продолжительности .

Основные
расчетные формулы:

            При равноускоренном
прямолинейном движении координата материальной точки по оси х имеет вид:

                   
;

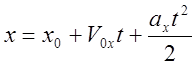
            Производная координаты
по времени есть модуль скорости:

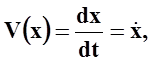
 где — первая производная координаты по времени

            Пусть
в момент времени тело находилось в точке с
координатой , а в более поздний момент — в точке с координатой . Разность — дает промежуток  времени , в течении которого двигалось тело;
абсолютное значение разности — равно
пройденному телом пути , поэтому модуль  средней 
путевой скорости:

                  
 ;

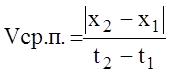
Модуль пути,
пройденный частицей за промежуток времени от до равен определенному интегралу от функции V(t), показывающий
как изменяется модуль скорости с течением времени:

         

            Принимая во внимание
то, что ускорение характеризует изменение скорости частицы  со временем, то
среднее значение модуля ускорения:

                     

Расчеты:

1) Путь, пройденный за интервал времени от t₁ до t₂:

      V(t) =;

м

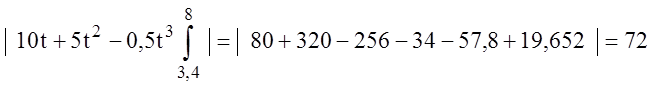
2)   Координату материальной точки в
момент времени tи t

      x(t)=10                                                                                                                                       
                                                                                                                                                                                                                             

    

3) Среднюю путевую скорость V_ср за тот же интервал времени:

        =10+10×3,4-1,5 =
26,66(м/с);

        =  = -6 =6 (м/с);

Знак минус
показывает, что тело движется в сторону противоположную направлению оси. В
формулу подставляем по модулю.

4)    Среднее путевое ускорение

       — движение
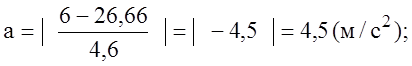
равнозамедленное.

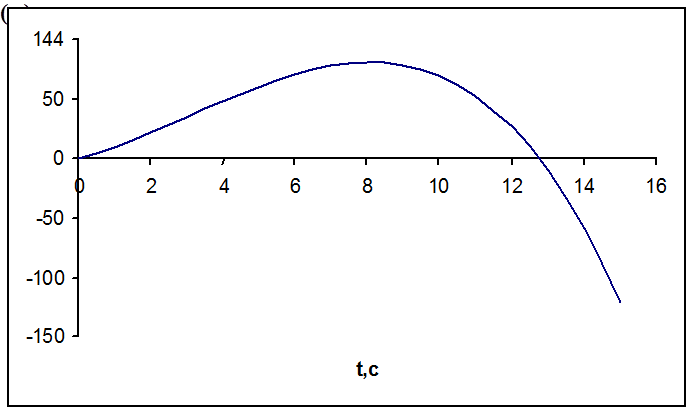
                                           Графики.

График зависимости
x(t):                                       
x(t) =10t+5

x	t
0	0
8	144
4	88
13	-123,5

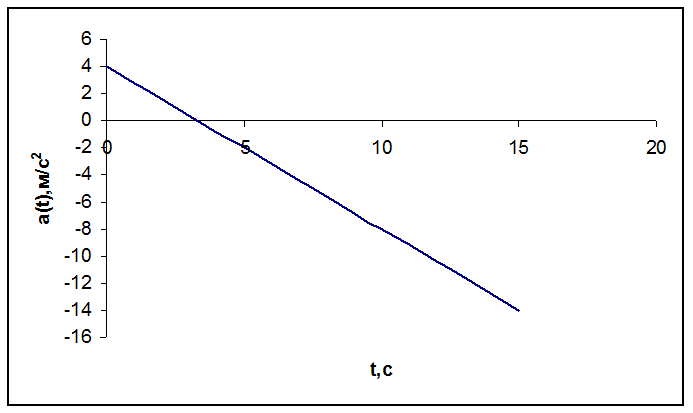
График
зависимости a(t):                                      

Окончательный
ответ:

1)

2)

3)  a =  м/с².

Вывод.

При заданном уравнении материальная
точка движется равнозамедленно, при чем, судя по знакам скоростей,  она
двигалась при времени по направлению оси, а при времени
 против оси. В работе найдены средняя
путевая скорость и координаты точки в заданные моменты времени.

Вектор скорости и ускорения материальной точки и их модули. Пример решения задач.

В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.

Траектория движения материальной точки через радиус-вектор

Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора – вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.

Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами – единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):

Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? “Наверное какой-то жуткий”, подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:

Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:

В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.

Вектор скорости материальной точки

Всем известно, что скорость материальной точки – это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.

Пример нахождения вектора скорости

Имеем закон перемещения материальной точки:

Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:

Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.

Как найти вектор ускорения материальной точки

Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:

Модуль вектора скорости точки

Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора – это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:

Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.

Модуль вектора ускорения

Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:

Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.

Еще примеры решений задачи нахождения вектора скорости и ускорения

А вот тут вы можете найти примеры решения и других задач по физике на тему “механика твердых тел”. А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.

Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.

Неравномерное движение и средняя скорость

теория по физике 🧲 кинематика

Неравномерное движение — движение с переменной скоростью, которая может менять как направление, так и модуль.

Неравномерное движение можно охарактеризовать средней скоростью. Различают среднюю векторную и среднюю скалярную скорости.

Средняя векторная скорость

Средняя векторная скорость — это скорость, равная отношению перемещения тела ко времени, в течение которого это перемещение было совершено.

v _ср — средняя векторная скорость, s — перемещение тела, совершенное за время t

Направление вектора средней скорости всегда совпадает с направлением вектора перемещения.

Чтобы вычислить среднюю векторную скорость, нужно поделить сумму всех перемещений на сумму всех временных промежутков, в течение которых эти перемещения были совершены:

Пример №1. Миша пробежал стометровку за 16 секунд. Через 1 минуту он вернулся на старт. Найти среднюю векторную скорость мальчика.

Миша совершил одинаковые по модулю, но разные по направлению перемещения. При сложении этих векторов получается 0. Поэтому средняя векторная скорость также равна нулю:

Средняя скалярная скорость

Средняя скалярная (путевая) скорость — это скорость, равная отношению пути, пройденного телом, ко времени, в течение которого этот путь был пройден.

v_ср — средняя путевая скорость, s — путь, пройденный телом за время t

Чтобы вычислить среднюю путевую скорость, нужно поделить сумму всех путей на сумму всех временных промежутков, в течение которых эти пути были преодолены:

Пример №2. Мальчик пробежал по периметру квадратного поля сто стороной 100 м. На первые две стороны мальчик потратил по 15 секунд, а на последние две — по 20 секунд. Найти среднюю путевую скорость мальчика.

У квадрата 4 стороны, поэтому путь мальчика составляют 4 дистанции по 100 м каждая. Поэтому средняя путевая скорость равна:

Средняя скалярная скорость всегда больше или равна модулю средней векторной скорости:

• v_ср= v _ср, если путь равен модулю перемещения. Так бывает в случае равномерного прямолинейного движения.
• v_ср>v _ср, если путь больше модуля перемещения. Так бывает в случае неравномерного прямолинейного или любого криволинейного движения.

Пример №3. Рыболов остановился на берегу круглого пруда и увидел на противоположном берегу удобное для рыбалки место. Он к нему шел в течение 2 минут. Вычислите среднюю путевую и среднюю векторную скорости рыболова после того, как он придет на новое место, если радиус пруда равен 50 м.

Две противоположные точки окружности соединяются отрезком, проходящим через его центр — диаметром. Поэтому модуль вектора перемещения равен двум радиусам пруда:

Чтобы дойти до диаметрально противоположной точки окружности, нужно пройти путь, равный половине окружности:

Переведя 2 минуты в СИ, получим 120 с. Модуль средней векторно скорости равен:

• Если известны скорости на первой и второй половине пути (s₁=s₂), средняя скорость равна:

• Если известно время прохождения отдельных участков пути и скорости движения на этих участках, средняя скорость равна:

• Если тело движется прямолинейно и равноускорено, его средняя скорость равна половине суммы начальной и конечной скорости:

• Если известны скорости тела за равные промежутки времени, его средняя скорость равна:

Пример №4. Первые полчаса автомобиль двигался со скоростью 90 км/ч, а потом 1 час он двигался со скоростью 60 км/ч. Найти среднюю скорость автомобиля.

Нам известны скорости на каждом из участков пути и время, в течение которого каждый из этих участков был преодолен. Поэтому:

Модуль вектора средней скорости по окружности

§ 17. Переменное движение. Средняя скорость. Средний модуль скорости

1. Переменное движение.

Определение 1. Движение называется переменным , если за любые равные промежутки времени точка совершает различные перемещения.

Перемещение — вектор. Он может изменяться по модулю и направлению. При переменном движении за любые равные промежутки времени перемещения могут отличаться либо модулями, либо направлениями, либо и модулями и направлениями.

2. Средняя скорость.

Определение 2а. Средней скоростью переменного движения называется отношение перемещения ко времени, за которое это перемещение произошло.

Запишем формулу скорости равномерного движения и средней скорости переменного движения.

Если посмотреть на правые части этих равенств, заметим, что они одинаковы. В этом заключается смысл средней скорости.

Определение 2б. Под средней скоростью переменного движения понимают скорость некоторого воображаемого равномерного прямолинейного движения, у которого перемещение и время одинаковы с переменным движением.

Согласно рисунку, представленному выше, это понимать надо так. Если бы точка двигалась не переменно по криволинейной траектории, а равномерно и прямолинейно прямо по вектору перемещения , то она за время попала бы в точку A из точки , если бы скорость этого воображаемого равномерного движения была бы одинаковой со средней скоростью переменного движения.

Модуль вектора средней скорости, или модуль средней скорости :

.

3. Средний модуль скорости.

На практике при составлении расписания движения поездов, автобусов используют ещё одно понятие средней скорости, которое называют средним модулем скорости, то есть средним по времени модулем всех скоростей, которые имела точка на различных участках траектории.

Определение 3а. Средним модулем скорости переменного движения называется отношение пути S ко времени t, за которое этот путь пройден.

— средний модуль скорости

Не надо путать средний модуль скорости с модулем вектора средней скорости.

Например, если автобус вышел на маршрут в начале дня и к концу дня возвратился в гараж, то перемещение за всё время движения равно нулю . Поэтому равны нулю средняя скорость и её модуль:

, .

Но средний модуль скорости отличен от нуля, так как не равен нулю путь, пройденный автобусом:

.

Аналогично для бумеранга.

За время полёта бумеранга средняя скорость его движения и модуль средней скорости равны нулю, так как равно нулю перемещение бумеранга относительно точки А (см. рис.). Но так как путь, который проделал бумеранг, не равен нулю, то и средний модуль скорости движения бумеранга отличен от нуля.

Если посмотреть на правые части формул модуля скорости равномерного движения и среднего модуля скорости переменного движения, то увидим, что правые части равенств одинаковы.

В этом заключается смысл среднего модуля скорости.

Определение 3б. Средний модуль скорости переменного движения равен модулю скорости такого воображаемого равномерного прямолинейного движения, у которого путь и время одинаковы с переменным движением.

Никакую часть этого материала ни в каких целях, включая образовательные и научные, нельзя без письменного разрешения владельца авторских прав дублировать в сети Интернет и воспроизводить в какой бы то ни было форме и какими бы то ни было средствами, будь то электронные или механические, включая запись на магнитный или электронный носитель, вывод на печать, фотокопирование.