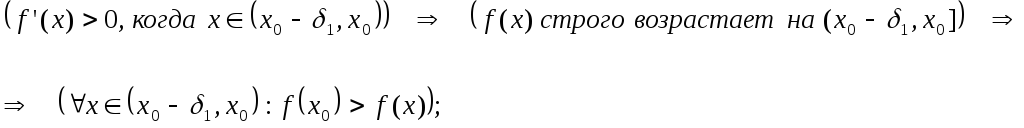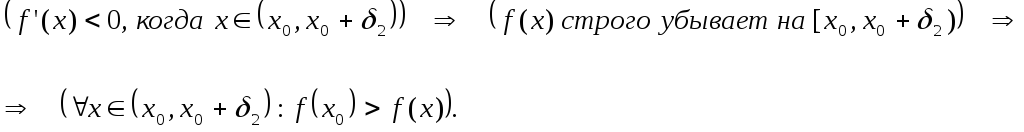Стационарные точки функции это как найти

1. Стационарные точки функции.
   Необходимое условие локального
   экстремума функции

2. Первое достаточное условие локального
   экстремума

3. Второе и третье достаточные условия
   локального экстремума

4. Наименьшее и наибольшее
   значения функции на сегменте

5. Выпуклые функции и точки перегиба

1. Стационарные точки функции. Необходимое условие локального экстремума функции

_{Определение 1.}
Пусть функция
определена на _{.
Точка
называется стационарной точкой функции
,
если
дифференцирована в точке
и .}

Теорема 1 (необходимое
условие локального экстремума функции).
Пусть функция
определена на
_{и имеет в точке
локальный экстремум. Тогда выполняется
одно из условий:}

1. функция
   _{не имеет в точке
   производной;}

2. функция
   _{имеет в точке
   производную и .}

_{Таким образом, для того,
чтобы найти точки, которые являются
подозрительными на экстремум, надо
найти стационарные точки функции и
точки, в которых производная функции
не существует, но которые принадлежат
области определения функции.}

_{Пример.
Пусть .
Найти для нее точки, которые являются
подозрительными на экстремум. Для
решения поставленной задачи, в первую
очередь, найдем область определения
функции: .
Найдем теперь производную функции:}

_.

_{Точки, в которых производная
не существует: .
Стационарные точки функции:}

_.

_{Поскольку и ,
и
принадлежат области определения функции,
то они обе будут подозрительными на
экстремум. Но для того, чтобы сделать
вывод, будет ли там действительно
экстремум, надо применять достаточные
условия экстремума.}

2. Первое достаточное условие локального экстремума

Теорема 1 (первое достаточное
условие локального экстремума).
Пусть функция
определена на
_{и дифференцирована на этом интервале
везде за исключением, возможно, точки
,
но в этой точке
функция является
непрерывной. Если
существуют такие правая и левая
полуокрестности точки ,
в каждой из которых
сохраняет определенный знак, то}

_{1) функция
имеет локальный экстремум в точке ,
если
принимает значения разных знаков в
соответствующих полуокрестностях;}

<sub>2) функция
не имеет локальный экстремум в точке
,
если справа и слева от точки

имеет одинаковый знак.</sub>

_{Доказательство.
1) Предположим, что в полуокрестности
производная ,
а в
.}

_{Таким образом в точке
функция
имеет локальный экстремум, а именно —
локальный максимум, что и нужно было
доказать.}

_{2) Предположим, что слева
и справа от точки
производная сохраняет свой знак,
например, .
Тогда на
и
функция
строго монотонно возрастает, то есть:}

_,

_.

_{Таким образом экстремума
в точке
функция
не имеет, что и нужно было доказать.}

_{Замечание 1.
Если производная
при прохождении через точку
меняет знак с «+» на «-», то в точке
функция
имеет локальный максимум, а если знак
меняется с «-» на «+», то локальный
минимум.}

_{Замечание 2.
Важным является условие непрерывности
функции
в точке .
Если это условие не выполняется, то
теорема 1 может не иметь места.}

_{Пример.
Рассматривается функция (рис.1):}

Эта функция определена на
<sub>и непрерывна везде, кроме точки ,
где она имеет устранимый разрыв. При
прохождении через точку

меняет знак с «-» на «+», но локального
минимума в этой точке функция не имеет,
а имеет локальный максимум по определению.
Действительно, около точки
можно построить такую окрестность, что
для всех аргументов из этой окрестности
значения функции будут меньше, чем
значение .
Теорема 1 не сработала потому, что в
точке
функция имела разрыв.</sub>

_{Замечание 3.
Первое достаточное условие локального
экстремума не может быть использовано,
когда производная функции
меняет свой знак в каждой левой и каждой
правой полуокрестности точки .}

_{Пример.
Рассматривается функция:}

_{Поскольку ,
то ,
а потому ,
но .
Таким образом:}

_,

_{т.е. в точке
функция
имеет локальный минимум по определению.
Посмотрим, сработает ли здесь первое
достаточное условие локального
экстремума.}

_{Для :}

_.

Для первого слагаемого правой
части полученной формулы имеем:

_,

_{а потому в малой окрестности
точки
знак производной определяется знаком
второго слагаемого, то есть:}

_,

<sub>а это означает, что в любой
окрестности точки

будет принимать как положительные, так
и отрицательные значения. Действительно,
рассмотрим произвольную окрестность
точки :
.
Когда</sub>

_,

_то

_{(рис.2), а
меняет свой знак здесь бесконечно много
раз. Таким образом, нельзя использовать
в приведенном примере первое достаточное
условие локального экстремума.}

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Значит, производная меняет знак только в точках (x=0) и (x=2).

В точке (x=0) она меняет знак с положительного на отрицательный, значит, это точка локального максимума со значением функции (f(0)=0).

В точке (x=2) она меняет знак с отрицательного на положительный, значит, это точка локального минимума со значением функции (f(2)=4).

From Wikipedia, the free encyclopedia

This article is about stationary points of a real-valued differentiable function of one real variable. For the broader term, see Critical point (mathematics).

Not to be confused with a fixed point where x = f(x).

In mathematics, particularly in calculus, a stationary point of a differentiable function of one variable is a point on the graph of the function where the function’s derivative is zero.^[1][2][3] Informally, it is a point where the function «stops» increasing or decreasing (hence the name).

For a differentiable function of several real variables, a stationary point is a point on the surface of the graph where all its partial derivatives are zero (equivalently, the gradient is zero).

Stationary points are easy to visualize on the graph of a function of one variable: they correspond to the points on the graph where the tangent is horizontal (i.e., parallel to the x-axis). For a function of two variables, they correspond to the points on the graph where the tangent plane is parallel to the xy plane.

Turning points[edit]

A turning point is a point at which the derivative changes sign.^[2] A turning point may be either a relative maximum or a relative minimum (also known as local minimum and maximum). If the function is differentiable, then a turning point is a stationary point; however not all stationary points are turning points. If the function is twice differentiable, the stationary points that are not turning points are horizontal inflection points. For example, the function has a stationary point at x = 0, which is also an inflection point, but is not a turning point.^[3]

Classification[edit]

Isolated stationary points of a real valued function are classified into four kinds, by the first derivative test:

• a local minimum (minimal turning point or relative minimum) is one where the derivative of the function changes from negative to positive;
• a local maximum (maximal turning point or relative maximum) is one where the derivative of the function changes from positive to negative;

• a rising point of inflection (or inflexion) is one where the derivative of the function is positive on both sides of the stationary point; such a point marks a change in concavity;
• a falling point of inflection (or inflexion) is one where the derivative of the function is negative on both sides of the stationary point; such a point marks a change in concavity.

The first two options are collectively known as «local extrema». Similarly a point that is either a global (or absolute) maximum or a global (or absolute) minimum is called a global (or absolute) extremum. The last two options—stationary points that are not local extremum—are known as saddle points.

By Fermat’s theorem, global extrema must occur (for a function) on the boundary or at stationary points.

Curve sketching[edit]

Determining the position and nature of stationary points aids in curve sketching of differentiable functions. Solving the equation f’(x) = 0 returns the x-coordinates of all stationary points; the y-coordinates are trivially the function values at those x-coordinates.
The specific nature of a stationary point at x can in some cases be determined by examining the second derivative f»(x):

• If f»(x) < 0, the stationary point at x is concave down; a maximal extremum.
• If f»(x) > 0, the stationary point at x is concave up; a minimal extremum.
• If f»(x) = 0, the nature of the stationary point must be determined by way of other means, often by noting a sign change around that point.

A more straightforward way of determining the nature of a stationary point is by examining the function values between the stationary points (if the function is defined and continuous between them).

A simple example of a point of inflection is the function f(x) = x³. There is a clear change of concavity about the point x = 0, and we can prove this by means of calculus. The second derivative of f is the everywhere-continuous 6x, and at x = 0, f′′ = 0, and the sign changes about this point. So x = 0 is a point of inflection.

More generally, the stationary points of a real valued function are those
points x₀ where the derivative in every direction equals zero, or equivalently, the gradient is zero.

Example[edit]

For the function f(x) = x⁴ we have f’(0) = 0 and f»(0) = 0. Even though f»(0) = 0, this point is not a point of inflection. The reason is that the sign of f’(x) changes from negative to positive.

For the function f(x) = sin(x) we have f’(0) ≠ 0 and f»(0) = 0. But this is not a stationary point, rather it is a point of inflection. This is because the concavity changes from concave downwards to concave upwards and the sign of f’(x) does not change; it stays positive.

For the function f(x) = x³ we have f’(0) = 0 and f»(0) = 0. This is both a stationary point and a point of inflection. This is because the concavity changes from concave downwards to concave upwards and the sign of f’(x) does not change; it stays positive.

See also[edit]

• Optimization (mathematics)
• Fermat’s theorem
• Derivative test
• Fixed point (mathematics)
• Saddle point

References[edit]

External links[edit]

• Inflection Points of Fourth Degree Polynomials — a surprising appearance of the golden ratio at cut-the-knot

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Математики и Data Science-специалисты должны хорошо разбираться в функциях. Предлагаем попрактиковаться в решении задач на обнаружение максимальных и минимальных значений у заданных функций.

Максимум

Задумываясь над тем, как найти максимальное значение функции, нужно четко понимать, с чем предстоит иметь дело. Для этого нужно запомнить такое определение:

Наибольшее значение функции y = f(x) на промежутке x – это max y = f(x₀). Оно будет при любом значении x€ X, x≠x₀ делает справедливым неравенство: f(x)≤f(x₀).

Максимальное значение (максимум) – это точка на функции, в которой значение функции больше, чем в соседних «отметках».

Минимум

Наименьшее значение функции находить так же легко, как и наибольшее. Но сначала нужно понимать, что это такое.

Значение функции на отрезке будет считаться минимумом, если оно меньше, чем в соседних «отметках». Здесь действует такое определение:

Наименьшее значение функции y=f(x) на промежутке x – это miny=f(x₀), которое при любом значении x€ X, x≠x₀ делает справедливым неравенство f(x)≥f(x₀).

Соответствующие определения являются достаточными и очевидными. Если говорить простыми словами, то максимум функции – это ее самое большое значение на заданном промежутке (участке) при абсциссе x₀, а минимум – самое маленькое.

Стационарные точки

При решении вопроса о том, как найти наибольшее или наименьшее значение функции, стоит обратить внимание на так называемые «стационарные точки». Это – значения аргумента функции, при которых ее производная будет равняться нулю.

Стационарная точка – это «отметка», в которой расположен экстремум дифференцируемой функции. А именно – локальный минимум или максимум. В одной из таких «отметок» записанное выражение будет достигать своих предельных параметров.

Здесь рекомендуется запомнить следующее:

1. Экстремум функции – это минимумы и максимумы.
2. Если определить производную в точках экстремумов, она будет равно 0.
3. Когда говорят «экстремумы», подразумевается значение функции. Если же речь идет об «отметках» экстремумов, рассматривать стоит x, в которых достигаются соответствующие пределы.

 Этого достаточно для того, чтобы разобраться, как найти наибольшее на заданном отрезке у выражения. Для реализации поставленной задачи вовсе не обязательно составлять график. Поэтому сначала воспользуемся записями формул и вычислений.

План действий

Пример – дана функция f(x) на отрезке [a, b]. Наибольшее и наименьшее значение такой непрерывной функции достигаются в определенных местах. Это – критические точки. Там, где производная записанного выражения будет равно нулю.

Для того, чтобы найти наибольшие значения уравнения, потребуется придерживаться следующего алгоритма:

1. Узнайте, какая перед вами функция. Для этого нужно проверить ее на непрерывность. В расчет обязательно берется заданный отрезок.
2. Если запись непрерывная – ищем производную.
3. После того, как найдем производную, приравниваем ее к нулю. Это поможет найти точки экстремумов. В результате получаются корни.
4. Образовавшиеся корни – это критические точки. Нужно выбрать те «параметры», что относятся к промежутку [a, b].
5. Вычислить значения функции на концах отрезка [a, b].
6. Определить значения имеющегося выражения в критических «отметках».

Теперь понятно, как найти наибольшие функции на заданном отрезке. После произведенных подсчетов остается выбрать из результатов M (максимум) и m (минимум).

На отрезке

Разобравшись в тем, как найти наибольшие «параметры» выражения «на бумаге», стоит рассмотреть соответствующий процесс на графиках. Определять максимумы/минимумы в данном случае будет проще.

Первый график указывает на выражение, у которого точка минимума и максимума находятся в стационарных точках на промежутке [-6;6]. Соответствующие «пределы» обозначены жирным.

Второй график указывает на изменение отрезка. Теперь он будет [1;6]. Минимальное значение останется прежним. А вот максимальное – изменится. Оно образуется в правой части в точке с абсциссой. Поиск минимального «параметра» окажется в критической точке.

Задумываясь, как найти наименьшие или «самые крупные» параметры выражения на графике, можно также рассмотреть третий рисунок. Здесь функция принадлежала промежутку [-3;2]. Чтобы найти наибольшее и наименьшее в таком случае, предстоит учитывать абсциссы. В них достигаются соответствующие пределы.

Открытый интервал

Если промежуток задан конкретным числом, определить экстремумы будет не так сложно. Иначе происходит, если интервал открыт.

Здесь:

1. Функция будет принимать максимум/минимум по значению в стационарных точках на открытом интервале от -6 до 6. Ответ – на 4 рисунке.
2. Если взять отрезок [1;6), минимум будет достигнут в стационарной точке. А вот максимум – неизвестен. Связано это с тем, что 6 не принадлежит к заданному интервалу. Если бы «шестерка» относилась к соответствующему промежутку, ответ на вопрос относительно определения максимума оказался понятным. Максимальный параметр был бы в точке с абсциссой 6.
3. На рисунке 6, задумываясь, как найти наименьшие «параметры», нужно обратить внимание на заданный интервал. Он равен (-3;2]. Минимум будет достигнут в правой границе. А вот максимум – не определен.

Найти значения на графиках обычно проще, чем «в чистых формулах». Соответствующие задания можно отыскать тут.

Бесконечность

Иногда значения функций нужно найти на бесконечном промежутке. Графически возможны такие ситуации:

На 7 рисунке функция достигает максимума в стационарной точке с абсциссой 1. Минимум окажется на границе интервала справа. На минус бесконечности значения приближаются к y=3 асимптотически.

Если взять интервал от 2-х до «плюс бесконечности», заданная функция не будет иметь ни максимумов, ни минимумов. Значения здесь стремятся к бесконечности. Связано это с тем, что x=2 является вертикальной асимптотой. Если абсцисса стремится к плюс бесконечности, значения будут асимптотически подходить к y=3. Соответствующий пример показан на рисунке 8.

Чтобы не приходилось долго разбираться с тем, как найти наименьшее у заданной функции, не путаться с тем, какие знаки производной использовать, а также легко строить графики, можно воспользоваться специальными онлайн калькуляторами. А еще – закончить тематические дистанционные онлайн курсы.