Стационарные точки функции как найти по графику - Исправление недочетов и поиск решений вместе с Examum.ru

Построение графиков функций

О чем эта статья:

11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие функции

Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
Графический способ — наглядно.
Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
Словесный способ.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида область определения выглядит так

х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Понятие графика функции

Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.

График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.

Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.

Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.

В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.

Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).

Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:

Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.

Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.

Исследование функции

Важные точки графика функции y = f(x):

стационарные и критические точки;
точки экстремума;
нули функции;
точки разрыва функции.

Стационарные точки — точки, в которых производная функции f(x) равна нулю.

Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.

Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.

Нули функции — это значения аргумента, при которых функция равна нулю.

Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.

Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:

Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.

Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.

Схема построения графика функции:

Найти область определения функции.
Найти область допустимых значений функции.
Проверить не является ли функция четной или нечетной.
Проверить не является ли функция периодической.
Найти нули функции.
Найти промежутки знакопостоянства функции, то есть промежутки, на которых она строго положительна или строго отрицательна.
Найти асимптоты графика функции.
Найти производную функции.
Найти критические точки в промежутках возрастания и убывания функции.
На основании проведенного исследования построить график функции.

У нас есть отличные курсы по математике для учеников с 1 по 11 классы!

Построение графика функции

Чтобы понять, как строить графики функций, потренируемся на примерах.

Задача 1. Построим график функции

Упростим формулу функции:

при х ≠ -1.

График функции — прямая y = x — 1 с выколотой точкой M (-1; -2).

Задача 2. Построим график функции

Выделим в формуле функции целую часть:

График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции

Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.

Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.

Вспомним, как параметры a, b и c определяют положение параболы.

Ветви вниз, следовательно, a 0.

Точка пересечения с осью Oy — c = 0.

Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.

Ветви вниз, следовательно, a 0.

Координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b

Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.

k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.

k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.

k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.

Задача 5. Построить график функции

Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.

Нули функции: 3, 2, 6.

Промежутки знакопостоянства функции определим с помощью метода интервалов.

Вертикальные асимптоты: x = 0, x = 4.

Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.

Вот так выглядит график:

Задача 6. Построить графики функций:

б)

г)

д)

Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.

а)

Преобразование в одно действие типа f(x) + a.

Сдвигаем график вверх на 1:

б)

Преобразование в одно действие типа f(x — a).

Сдвигаем график вправо на 1:

В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.

Сдвигаем график вправо на 1:

Сдвигаем график вверх на 2:

г)

Преобразование в одно действие типа

Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:

д)

Мы видим три преобразования вида f(ax), f (x + a), -f(x).

Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.

Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:

Стационарные критические и точки экстремума

Определения:

Экстремумом называют максимальное или минимальное значение функции на заданном множестве.

Точка экстремума – это точка, в которой достигается максимальное или минимальное значение функции.

Точка максимума – это точка, в которой достигается максимальное значение функции.

Точка минимума – это точка, в которой достигается минимальное значение функции.

На рисунке в окрестности точки х = 3 функция достигает максимального значения (то есть в окрестности именно этой точки нет точки выше). В окрестности х = 8 она опять же имеет максимальное значение (снова уточним: именно в этой окрестности нет точки выше). В этих точках возрастание сменяется убыванием. Они являются точками максимума:

В окрестности точки х = 5 достигается минимальное значение функции (то есть в окрестности х=5 точки ниже нет). В этой точке убывание сменяется возрастанием. Она является точкой минимума:

Точки максимума и минимума являются точками экстремума функции, а значения функции в этих точках – ее экстремумами.

Точка x_о является точкой максимума, если у нее существует окрестность, во всех точках которой f(x) меньше или равно f(x_о):

Упрощенная формулировка : если в точке x_о производная меняет знак с плюса на минус, то x_о является точкой максимума.

Точка х_о является точкой минимума, если у нее существует окрестность, во всех точках которой f(x) больше или равно f(x_о):

Упрощенная формулировка : если в точке x_о производная меняет знак с минуса на плюс, то x_о является точкой минимума.

Критические и стационарные точки функции:

Внутренние точки области определения функции, в которых функция непрерывна, но производная не существует, называют критическими точками.

Внутренние точки области определения функции, при которых производная функции равна нулю, называются стационарными точками.

Необходимое условие экстремума:

Если x_о – точка экстремума функции f (x), то в этой точке либо производная обращается в нуль (и это стационарная точка), либо производная не существует (критическая точка).

Достаточное условие экстремума:

Пусть x_о – критическая точка. Если производная f ′(x) при переходе слева направо через точку x_о меняет знак плюс на минус, то x_о – точка максимума:

Если производная f ′(x) при переходе слева направо через точку x_о меняет знак минус на плюс, то x_о – точка минимума:

Если при переходе через критическую точку производная не меняет знак, то в точке x_о экстремума нет.

На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].

Алгоритм исследования непрерывной функции y = f(x) на монотонность и экстремумы:

2) Найти стационарные (f ′(x) = 0) и критические (f ′(x) не существует) точки функции y = f(x).

3) Отметить стационарные и критические точки на числовой прямой и определить знаки производной на получившихся промежутках.

4) Сделать выводы о монотонности функции и ее точках экстремума.

Определение

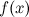
Точка называется точкой локального максимума функции , если существует такая окрестность этой точки, что для всех из этой окрестности выполняется неравенство: .

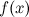
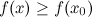
Точка называется точкой локального минимума функции , если существует такая окрестность этой точки, что для всех из этой окрестности .

Значение функции в точке максимума называется локальным максимумом, значение функции в точке минимума —локальным минимумом данной функции. Локальные максимум и минимум функции называются локальными экстремумами.

Точка называется точкой строгого локального максимума функции , если для всех из окрестности этой точки будет справедливо строгое неравенство .

Точка называется точкой строгого локального минимума функции , если для всех из окрестности этой точки будет справедливо строгое неравенство .

Наибольшее или наименьшее значение функции на промежутке называется глобальным экстремумом.

Замечание

Глобальный экстремум может достигаться либо в точках локального экстремума, либо на концах отрезка.

Необходимое условие экстремума

Теорема

(Необходимое условие экстремума)

Если функция имеет экстремум в точке , то ее производная либо равна нулю, либо не существует.

Точки, в которых производная равна нулю: , называются стационарными точками функции.

Точки, в которых выполняется необходимое условие экстремума для непрерывной функции, называются критическими точками этой функции. То есть критические точки — это либо стационарные точки (решения уравнения ), либо это точки, в которых производная не существует.

Замечание

Не в каждой своей критической точке функция обязательно имеет максимум или минимум.

Первое достаточное условие экстремума

Теорема

(Первое достаточное условие экстремума)

Пусть для функции выполнены следующие условия:

1. функция непрерывна в окрестности точки ;

2. или не существует;

3. производная при переходе через точку меняет свой знак.

Тогда в точке 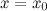функция имеет экстремум, причем это минимум, если при переходе через точку производная меняет свой знак с минуса на плюс; максимум, если при переходе через точку производная меняет свой знак с плюса на минус.

Если производная при переходе через точку не меняет знак, то экстремума в точке нет.

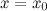
Таким образом, для того чтобы исследовать функцию на экстремум, необходимо:

1. найти производную ;

2. найти критические точки, то есть такие значения , в которых или не существует;

3. исследовать знак производной слева и справа от каждой критической точки;

4. найти значение функции в экстремальных точках.

Второе достаточное условие экстремума

Теорема

(Второе достаточное условие экстремума)

Пусть для функции выполнены следующие условия:

1. она непрерывна в окрестности точки ;

2. первая производная в точке ;

3. в точке .

Тогда в точке достигается экстремум, причем, если , то в точке функция имеет минимум; если , то в точке функция достигает максимум.

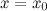
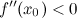
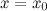
Выпуклость и точки перегиба. Основные понятия и определения. Достаточное условие выпуклости функции.

Определение. Кривая обращена выпуклостью вверх на интервале (а, b), если все ее точки лежат ниже любой ее касательной на этом интервале. Кривая, обращенная выпуклостью вверх, называется выпуклой, а кривая, обращенная выпуклостью вниз – называется вогнутой.

На рисунке показана иллюстрация приведенного выше определения.

Теорема 1. Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна, то кривая y = f(x) обращена выпуклостью вверх (выпукла).

Доказательство. Пусть х Î (a, b). Проведем касательную к кривой в этой точке.

Уравнение кривой: y = f(x);

Уравнение касательной:

Следует доказать, что .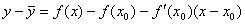

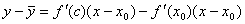
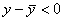
По теореме Лагранжа для f(x) – f(x ): , x x тогда x 0 и c – x > 0, и кроме того по условию

, следовательно, .

Пусть x 0 на интервале (a, b), то кривая y=f(x) вогнута на интервале (a, b).

Определение. Точка, отделяющая выпуклую часть кривой от вогнутой, называется точкой перегиба.

Очевидно, что в точке перегиба касательная пересекает кривую.

Теорема 2. Пусть кривая определяется уравнением y = f(x). Если вторая производная f¢¢(a) = 0 или f¢¢(a) не существует и при переходе через точку х = а f¢¢(x) меняет знак, то точка кривой с абсциссой х = а является точкой перегиба.

Доказательство. 1) Пусть f¢¢(x) 0 при x > a. Тогда при

x a кривая вогнута, т.е. точка х = а – точка перегиба.

2) Пусть f¢¢(x) > 0 при x b – выпуклостью вверх. Тогда x = b – точка перегиба.

Если f(x) имеет в данной точке x производную, то существует касательная к графику функции f(x) в точке M( x,f(x)) , причем угловой коэффициент этой касательной равен производной f'(x).

Устанавливая рекомендуемое программное обеспечение вы соглашаетесь
с лицензионным соглашением Яндекс.Браузера и настольного ПО Яндекса .

Описание презентации по отдельным слайдам:

10.03.17 Классная работа Критические точки и экстремумы функции

Найти значения х, при которых значение f(x) равно 0

x y O 1 1 4 7 9 12 15 19 По графику функции определите, на каких промежутках производная функции положительна, на каких — отрицательна? у = f ( x )

y = f ´(х) По графику производной функции определите, на каких промежутках функция возрастает, на каких убывает.

x y O x0 Точка максимума x0+ x0- x y(x0) y(x)

x O x0 Точка минимума y(x0) y Сформулируйте определение самостоятельно y(х) > y(x0) y(x) x

Точки максимума и минимума называются точками экстремума функции

Внутренние точки области определения функции, в которых ее производная равна нулю или не существует, называются критическими точками. Критические точки

Для того, чтобы точка была точкой экстремума функции необходимо, чтобы эта точка была критической точкой данной функции Но это условие не является достаточным

Необходимое и достаточное условие экстремума. Для того , чтобы точка х0 была точкой экстремума функции f(х): необходимо , чтобы х0 была критической точкой функции; достаточно, чтобы при переходе через критическую точку х0 производная меняла знак.

Алгоритм нахождения точек экстремума: Найти производную функции. Решить уравнение f ´(х)=0, и найти тем самым стационарные точки. Методом интервалов установить промежутки знакопостоянства производной. Если при переходе через точку х0: — производная не меняет знак, то х0 – точка перегиба; — производная меняет знак с «+» на «-», то х0 точка максимума; — производная меняет знак с «-» на «+», то х0 точка минимума.

Шкурина Анастасия ОлеговнаНаписать 1248 28.11.2018

Номер материала: ДБ-264040

28.11.2018 1371

28.11.2018 104

28.11.2018 566

28.11.2018 178

28.11.2018 2458

28.11.2018 93

28.11.2018 147

28.11.2018 190

Не нашли то что искали?

Вам будут интересны эти курсы:

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение редакции может не совпадать с точкой зрения авторов.

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако редакция сайта готова оказать всяческую поддержку в решении любых вопросов связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Экстремумы функции

Необходимое условие экстремума функции одной переменной

Достаточное условие экстремума функции одной переменной

Если в точке x * выполняется условие:

Пример №1 . Найти наибольшее и наименьшее значения функции: на отрезке [1; 3].
Решение.

Критическая точка одна x₁ = 2 (f’(x)=0). Эта точка принадлежит отрезку [1;3]. (Точка x=0 не является критической, так как 0∉[1;3]).
Вычисляем значения функции на концах отрезка и в критической точке.
f(1)=9, f(2)= 5 /₂, f(3)=3 8 /₈₁
Ответ: f_min= 5 /₂ при x=2; f_max=9 при x=1

Пример №2 . С помощью производных высших порядков найти экстремум функции y=x-2sin(x) .
Решение.
Находим производную функции: y’=1-2cos(x) . Найдем критические точки: 1-cos(x)=2, cos(x)=½, x=± π /₃+2πk, k∈Z. Находим y’’=2sin(x), вычисляем , значит x= π /₃+2πk, k∈Z – точки минимума функции; , значит x=- π /₃+2πk, k∈Z – точки максимума функции.

Пример №3 . Исследовать на экстремум фцнкцию в окрестностях точки x=0.
Решение. Здесь необходимо найти экстремумы функции. Если экстремум x=0 , то выяснить его тип (минимум или максимум). Если среди найденных точек нет x = 0, то вычислить значение функции f(x=0).
Следует обратить внимание, что когда производная с каждой стороны от данной точки не меняет своего знака, не исчерпываются возможные ситуации даже для дифференцируемых функций: может случиться, что для сколь угодно малой окрестности по одну из сторон от точки x₀ или по обе стороны производная меняет знак. В этих точках приходится применять другие методы для исследования функций на экстремум.

Пример №4 . Разбить число 49 на два слагаемых, произведение которых будет наибольшим.
Решение. Обозначим x — первое слагаемое. Тогда (49-x) — второе слагаемое.
Произведение будет максимальным: x·(49-x) → max
или
49x — x 2

источники:

http://planshet-info.ru/kompjutery/stacionarnye-kriticheskie-i-tochki-jekstremuma

http://math.semestr.ru/math/minmax.php

Источник

Как найти стационарные точки функции

Процесс исследования функции на наличие стационарных точек а также их нахождения является одним из важных элементов при построении графика функции. Найти стационарные точки функции можно, обладая определенным набором математических знаний.

Вам понадобится

— функция, которую необходимо исследовать на наличие стационарных точек;
— определение стационарных точек: стационарные точки функции — это точки (значения аргумента), в которых производная функции первого порядка обращается в нуль.

Инструкция

Используя таблицу производных и формулы дифференцирования функций, необходимо найти производную функции. Этот шаг является наиболее сложным и ответственным в ходе выполнения задачи. Если допустить ошибку на данном этапе, дальнейшие вычисления не будут иметь смысла.

Проверьте, зависит ли производная функции от аргумента. Если найденная производная не зависит от аргумента, то есть является числом (к примеру, f'(x) = 5), то в таком случае функция не имеет стационарных точек. Такое решение возможно, только если исследуемая функция является линейной функцией первого порядка (к примеру, f(x) = 5x+1). Если производная функции зависит от аргумента, то приступите к последнему этапу.

Составьте уравнение f'(x)= 0 и решите его. Уравнение может не иметь решений — в таком случае у функции стационарных точек не имеется. Если решения у уравнения есть, то именно эти найденные значения аргумента и будут являться стационарными точками функции. На данном этапе следует провести проверку решения уравнения методом подстановки аргумента.

Обратите внимание

При нахождении производной функции могут возникнуть трудности, если функция является сложной. В таком случае нужно использовать прием замены части функции промежуточным аргументом.

Полезный совет

Для выполнения данной задачи необходимо уделить особое внимание правилам дифференцирования.

Внимание и концентрация на задаче также помогут с ней справиться — перед выполнением задачи убедитесь в том, что вас ничто не будет отвлекать в процессе ее решения.
Знание стационарных точек функции значительно облегчает построение ее графика, так как именно в этих точках находится максимальное и минимальное значения функции.

Источники:

Производная функции — Википедия
Критическая точка (математика) — Википедия

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

найти экстремумы функции

f(x)=x2x−1

Производная этой функции —

f′(x)=xx−2(x−1)2

, значит, критические точки функции — это (x=0) и (x=2). Точка (x=1) не принадлежит области определения функции.

Они делят реальную числовую прямую на четыре интервала:

−∞;0∪0;1∪1;2∪2;+∞

. Знак первого интервала положительный (например,

f′

((-1)=0.75)). Второго — отрицательный, третьего — отрицательный, четвёртого — положительный.

−∞;0	0;1	1;2	2;+∞
(+)	(-)	(-)	(+)

Значит, производная меняет знак только в точках (x=0) и (x=2).

В точке (x=0) она меняет знак с положительного на отрицательный, значит, это точка локального максимума со значением функции (f(0)=0).

В точке (x=2) она меняет знак с отрицательного на положительный, значит, это точка локального минимума со значением функции (f(2)=4).

Источник

From Wikipedia, the free encyclopedia

This article is about stationary points of a real-valued differentiable function of one real variable. For the broader term, see Critical point (mathematics).

Not to be confused with a fixed point where x = f(x).

The stationary points are the red circles. In this graph, they are all relative maxima or relative minima. The blue squares are inflection points.

In mathematics, particularly in calculus, a stationary point of a differentiable function of one variable is a point on the graph of the function where the function’s derivative is zero.^[1]^[2]^[3] Informally, it is a point where the function «stops» increasing or decreasing (hence the name).

For a differentiable function of several real variables, a stationary point is a point on the surface of the graph where all its partial derivatives are zero (equivalently, the gradient is zero).

Stationary points are easy to visualize on the graph of a function of one variable: they correspond to the points on the graph where the tangent is horizontal (i.e., parallel to the x-axis). For a function of two variables, they correspond to the points on the graph where the tangent plane is parallel to the xy plane.

Turning points[edit]

A turning point is a point at which the derivative changes sign.^[2] A turning point may be either a relative maximum or a relative minimum (also known as local minimum and maximum). If the function is differentiable, then a turning point is a stationary point; however not all stationary points are turning points. If the function is twice differentiable, the stationary points that are not turning points are horizontal inflection points. For example, the function has a stationary point at x = 0, which is also an inflection point, but is not a turning point.^[3]

Classification[edit]

A graph in which local extrema and global extrema have been labeled.

Isolated stationary points of a $C^{1}$ real valued function are classified into four kinds, by the first derivative test:

a local minimum (minimal turning point or relative minimum) is one where the derivative of the function changes from negative to positive;
a local maximum (maximal turning point or relative maximum) is one where the derivative of the function changes from positive to negative;

Saddle points (stationary points that are neither local maxima nor minima: they are inflection points. The left is a «rising point of inflection» (derivative is positive on both sides of the red point); the right is a «falling point of inflection» (derivative is negative on both sides of the red point).

a rising point of inflection (or inflexion) is one where the derivative of the function is positive on both sides of the stationary point; such a point marks a change in concavity;
a falling point of inflection (or inflexion) is one where the derivative of the function is negative on both sides of the stationary point; such a point marks a change in concavity.

The first two options are collectively known as «local extrema». Similarly a point that is either a global (or absolute) maximum or a global (or absolute) minimum is called a global (or absolute) extremum. The last two options—stationary points that are not local extremum—are known as saddle points.

By Fermat’s theorem, global extrema must occur (for a $C^{1}$ function) on the boundary or at stationary points.

Curve sketching[edit]

Determining the position and nature of stationary points aids in curve sketching of differentiable functions. Solving the equation f’(x) = 0 returns the x-coordinates of all stationary points; the y-coordinates are trivially the function values at those x-coordinates.
The specific nature of a stationary point at x can in some cases be determined by examining the second derivative f»(x):

If f»(x) < 0, the stationary point at x is concave down; a maximal extremum.
If f»(x) > 0, the stationary point at x is concave up; a minimal extremum.
If f»(x) = 0, the nature of the stationary point must be determined by way of other means, often by noting a sign change around that point.

A more straightforward way of determining the nature of a stationary point is by examining the function values between the stationary points (if the function is defined and continuous between them).

A simple example of a point of inflection is the function f(x) = x³. There is a clear change of concavity about the point x = 0, and we can prove this by means of calculus. The second derivative of f is the everywhere-continuous 6x, and at x = 0, f′′ = 0, and the sign changes about this point. So x = 0 is a point of inflection.

More generally, the stationary points of a real valued function $fcolon mathbb{R}^{n} to mathbb{R}$ are those
points x₀ where the derivative in every direction equals zero, or equivalently, the gradient is zero.

Example[edit]

For the function f(x) = x⁴ we have f’(0) = 0 and f»(0) = 0. Even though f»(0) = 0, this point is not a point of inflection. The reason is that the sign of f’(x) changes from negative to positive.

For the function f(x) = sin(x) we have f’(0) ≠ 0 and f»(0) = 0. But this is not a stationary point, rather it is a point of inflection. This is because the concavity changes from concave downwards to concave upwards and the sign of f’(x) does not change; it stays positive.

For the function f(x) = x³ we have f’(0) = 0 and f»(0) = 0. This is both a stationary point and a point of inflection. This is because the concavity changes from concave downwards to concave upwards and the sign of f’(x) does not change; it stays positive.

References[edit]

^ Chiang, Alpha C. (1984). Fundamental Methods of Mathematical Economics (3rd ed.). New York: McGraw-Hill. p. 236. ISBN 0-07-010813-7.
^ ^a ^b Saddler, David; Shea, Julia; Ward, Derek (2011), «12 B Stationary Points and Turning Points», Cambridge 2 Unit Mathematics Year 11, Cambridge University Press, p. 318, ISBN 9781107679573
^ ^a ^b «Turning points and stationary points». TCS FREE high school mathematics ‘How-to Library’. Retrieved 30 October 2011.

External links[edit]

Inflection Points of Fourth Degree Polynomials — a surprising appearance of the golden ratio at cut-the-knot

Источник

Содержание:

Критические точки и экстремумы функции
Теорема Ферма (Необходимое условие существовании экстремумов)
Достаточное условие существования экстремума
Задача пример №117
Задача пример №118
Задача пример №119
Задача пример №120
Задача пример №121

Критические точки и экстремумы функции

В некоторых точках из области определения производная функции может быть равна нулю или вообще может не существовать. Такие точки из области определения называются критическими точками функции. Покажем критические точки на графике заданной функции.

1. Для значений равных угловой коэффициент касательной к графику равен 0. Т.e. . Эти точки являются критическими точками функции.

2. В точках функция не имеет производной. Эти тоже критические точки функции.

3. Для рассматриваемой нами функции критические точки делят ее область определения на чередующиеся интервалы возрастания и убывания. Точки — критические точки, которые не изменяют возрастание и убывание (или наоборот).

По графику видно, что в точках внутреннего экстремума производная функции равна нулю, а в точке производная не существует. Точки, в которых производная функции равна нулю, также называются стационарными точками.

Теорема Ферма (Необходимое условие существовании экстремумов)

Во внутренних точках экстремума производная либо равна нулю, либо не существует.

Примечание. Точка, в которой производная равна нулю, может и не быть точкой экстремума. Например, в точке производная функции равна нулю, но эта точка не является ни точкой максимума, ни точкой минимума.

На отрезке непрерывности функция может иметь несколько критических точек, точек максимума и минимума. Существование экстремума в точке зависит от значения функции в данной точке и в точках, близких к данной, т.е. имеет смысл локального (местного) значения. Поэтому иногда используют термин локальный максимум и локальный минимум.

Достаточное условие существования экстремума

Пусть функция непрерывна на промежутке и . Если является критической точкой, в окрестности которой функция дифференцируема, то, если в этой окрестности:

1 ) слева от точки положительна, а справа — отрицательна, то точка является точкой максимума.

2) слева от отрицательна, а справа — положительна, то точка является точкой минимума

3) с каждой стороны от точки имеет одинаковые знаки, то точка не является точкой экстремума.

Чтобы найти наибольшее (абсолютный максимум) или наименьшее (абсолютный минимум) значение функции, имеющей конечное число критических точек на отрезке, надо найти значение функции во всех критических точках и на концах отрезка, а затем из полученных значений выбрать наибольшее или наименьшее.

Соответствующие наибольшее и наименьшее значения функции на отрезке записываются как и .

Ниже представлены примеры определения максимума и минимума в соответствии со знаком производной первого порядка.

Задача пример №117

Для функции определите максимумы и минимумы и схематично изобразите график.

Решение:

Для решения задания сначала надо найти критические точки. Для данной функции этими точками являются точки (стационарные), в которых производная равна нулю.

1. Производная функции:

2. Критические точки функции:

3. Точки и разбивают область определения функции на три промежутка.

Проверим знак на интервалах, выбрав пробные точки:

для интервала

Интервал Пробные точки

Знак Возрастание и убывание

При имеем . (-1;3) — максимум

При имеем (1;-1) — минимум

4. Используя полученные для функции данные и найдя координаты нескольких дополнительных точек, построим график функции.

Задача пример №118

Найдите наибольшее и наименьшее значение функции на отрезке [-1;2].

Решение:

Сначала найдем критические точки. Так как , то критические точки можно найти из уравнения . Критическая точка не принадлежит данному отрезку [-1; 2], и поэтому мы ее не рассматриваем. Вычислим значение заданной функции в точке и на концах отрезка.

Из этих значений наименьшее — 4, наибольшее 12. Таким образом:

Задача пример №119

Найдите экстремумы функции .

Решение:

1. Производная функции:

2. Критические точки: ,

3. Интервалы, на которые критические точки делят область определения функции:

Проверим знак на интервалах, выбрав пробные точки.

Для промежутка возьмем

Для промежутка (0; 1,5) возьмем

Для промежутка возьмем

Интервал

Пробные точки

Знак Возрастание-убывание

Используя полученную для функции информацию и найдя значение функции еще в нескольких точках, можно построить график функции. При этом следует учитывать, что в точках с абсциссами и касательная к графику горизонтальна. Построение графика можно проверить при помощи графкалькулятора.

• Функция на промежутке возрастает.

• Точка критическая точка функции , но не является экстремумом.

• Функция на промежутке [0; 1,5] возрастает.

• Функция на промежутке убывает.

•

Задача пример №120

Найдите экстремумы функции

Решение:

1. Производная

2. Критические точки: для этого надо решить уравнение или найти точки, в которых производная не существует. В точке функция не имеет конечной производной. Однако точка принадлежит области определения. Значит, точка является критической точкой функции.

3. Промежутки, на которые критическая точка делит область определения функции: и

Определим знак , выбрав пробные точки для каждого промежутка:

Для возьмем Для возьмем

Интервал Пробные точки

Знак

Возрастание-убывание

• Функция на промежутке убывает.

• Функция на промежутке возрастает.

•

Задача пример №121

По графику функции производной схематично изобразите график самой функции.

Решение:

Производная в точке равна нулю, а при отрицательна, значит, на интервале функция убывающая. При производная положительна, а это говорит о том, что функция на промежутке возрастает. Точкой перехода от возрастания к убыванию функции является точка . Соответствующий график представлен на рисунке.