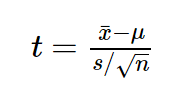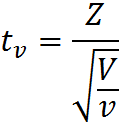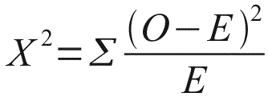Степень свободы это статистика как найти

О степенях свободы в статистике

В одном из предыдущих постов мы обсудили, пожалуй, центральное понятие в анализе данных и проверке гипотез — p-уровень значимости. Если мы не применяем байесовский подход, то именно значение p-value мы используем для принятия решения о том, достаточно ли у нас оснований отклонить нулевую гипотезу нашего исследования, т.е. гордо заявить миру, что у нас были получены статистически значимые различия.

Однако в большинстве статистических тестов, используемых для проверки гипотез, (например, t-тест, регрессионный анализ, дисперсионный анализ) рядом с p-value всегда соседствует такой показатель как число степеней свободы, он же degrees of freedom или просто сокращенно df, о нем мы сегодня и поговорим.

Степени свободы, о чем речь?

По моему мнению, понятие степеней свободы в статистике примечательно тем, что оно одновременно является и одним из самым важных в прикладной статистике (нам необходимо знать df для расчета p-value в озвученных тестах), но вместе с тем и одним из самых сложных для понимания определений для студентов-нематематиков, изучающих статистику.

Давайте рассмотрим пример небольшого статистического исследования, чтобы понять, зачем нам нужен показатель df, и в чем же с ним такая проблема. Допустим, мы решили проверить гипотезу о том, что средний рост жителей Санкт-Петербурга равняется 170 сантиметрам. Для этих целей мы набрали выборку из 16 человек и получили следующие результаты: средний рост по выборке оказался равен 173 при стандартном отклонении равном 4. Для проверки нашей гипотезы можно использовать одновыборочный t-критерий Стьюдента, позволяющий оценить, как сильно выборочное среднее отклонилось от предполагаемого среднего в генеральной совокупности в единицах стандартной ошибки:

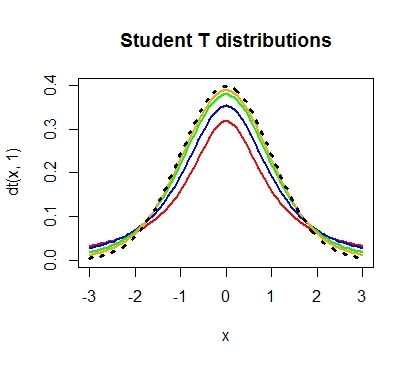
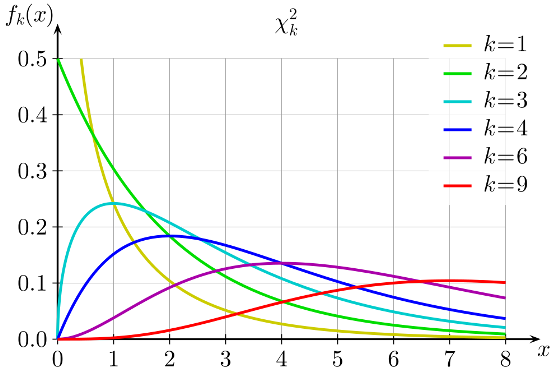
Проведем необходимые расчеты и получим, что значение t-критерия равняется 3, отлично, осталось рассчитать p-value и задача решена. Однако, ознакомившись с особенностями t-распределения мы выясним, что его форма различается в зависимости от числа степеней свобод, рассчитываемых по формуле n-1, где n — это число наблюдений в выборке:

Сама по себе формула для расчета df выглядит весьма дружелюбной, подставили число наблюдений, вычли единичку и ответ готов: осталось рассчитать значение p-value, которое в нашем случае равняется 0.004.

Но почему n минус один?

Когда я впервые в жизни на лекции по статистике столкнулся с этой процедурой, у меня как и у многих студентов возник законный вопрос: а почему мы вычитаем единицу? Почему мы не вычитаем двойку, например? И почему мы вообще должны что-то вычитать из числа наблюдений в нашей выборке?

В учебнике я прочитал следующее объяснение, которое еще не раз в дальнейшем встречал в качестве ответа на данный вопрос:

“Допустим мы знаем, чему равняется выборочное среднее, тогда нам необходимо знать только n-1 элементов выборки, чтобы безошибочно определить чему равняется оставшейся n элемент”. Звучит разумно, однако такое объяснение скорее описывает некоторый математический прием, чем объясняет зачем нам понадобилось его применять при расчете t-критерия. Следующее распространенное объяснение звучит следующим образом: число степеней свободы — это разность числа наблюдений и числа оцененных параметров. При использовании одновыборочного t-критерия мы оценили один параметр — среднее значение в генеральной совокупности, используя n элементов выборки, значит df = n-1.

Однако ни первое, ни второе объяснение так и не помогает понять, зачем же именно нам потребовалось вычитать число оцененных параметров из числа наблюдений?

Причем тут распределение Хи-квадрат Пирсона?

Давайте двинемся чуть дальше в поисках ответа. Сначала обратимся к определению t-распределения, очевидно, что все ответы скрыты именно в нем. Итак случайная величина:

имеет t-распределение с df = ν, при условии, что Z – случайная величина со стандартным нормальным распределением N(0; 1), V – случайная величина с распределением Хи-квадрат, с ν числом степеней свобод, случайные величины Z и V независимы. Это уже серьезный шаг вперед, оказывается, за число степеней свободы ответственна случайная величина с распределением Хи-квадрат в знаменателе нашей формулы.

Давайте тогда изучим определение распределения Хи-квадрат. Распределение Хи-квадрат с k степенями свободы — это распределение суммы квадратов k независимых стандартных нормальных случайных величин.

Кажется, мы уже совсем у цели, по крайней мере, теперь мы точно знаем, что такое число степеней свободы у распределения Хи-квадрат — это просто число независимых случайных величин с нормальным стандартным распределением, которые мы суммируем. Но все еще остается неясным, на каком этапе и зачем нам потребовалось вычитать единицу из этого значения?

Давайте рассмотрим небольшой пример, который наглядно иллюстрирует данную необходимость. Допустим, мы очень любим принимать важные жизненные решения, основываясь на результате подбрасывания монетки. Однако, последнее время, мы заподозрили нашу монетку в том, что у нее слишком часто выпадает орел. Чтобы попытаться отклонить гипотезу о том, что наша монетка на самом деле является честной, мы зафиксировали результаты 100 бросков и получили следующий результат: 60 раз выпал орел и только 40 раз выпала решка. Достаточно ли у нас оснований отклонить гипотезу о том, что монетка честная? В этом нам и поможет распределение Хи-квадрат Пирсона. Ведь если бы монетка была по настоящему честной, то ожидаемые, теоретические частоты выпадания орла и решки были бы одинаковыми, то есть 50 и 50. Легко рассчитать насколько сильно наблюдаемые частоты отклоняются от ожидаемых. Для этого рассчитаем расстояние Хи-квадрат Пирсона по, я думаю, знакомой большинству читателей формуле:

Где O — наблюдаемые, E — ожидаемые частоты.

Дело в том, что если верна нулевая гипотеза, то при многократном повторении нашего эксперимента распределение разности наблюдаемых и ожидаемых частот, деленная на корень из наблюдаемой частоты, может быть описано при помощи нормального стандартного распределения, а сумма квадратов k таких случайных нормальных величин это и будет по определению случайная величина, имеющая распределение Хи-квадрат.

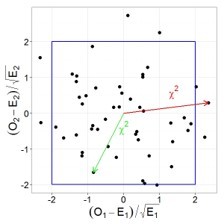
Давайте проиллюстрируем этот тезис графически, допустим у нас есть две случайные, независимые величины, имеющих стандартное нормальное распределение. Тогда их совместное распределение будет выглядеть следующим образом:

При этом квадрат расстояния от нуля до каждой точки это и будет случайная величина, имеющая распределение Хи-квадрат с двумя степенями свободы. Вспомнив теорему Пифагора, легко убедиться, что данное расстояние и есть сумма квадратов значений обеих величин.

Пришло время вычесть единичку!

Ну а теперь кульминация нашего повествования. Возвращаемся к нашей формуле расчета расстояния Хи-квадрат для проверки честности монетки, подставим имеющиеся данные в формулу и получим, что расстояние Хи-квадрат Пирсона равняется 4. Однако для определения p-value нам необходимо знать число степеней свободы, ведь форма распределения Хи-квадрат зависит от этого параметра, соответственно и критическое значение также будет различаться в зависимости от этого параметра.

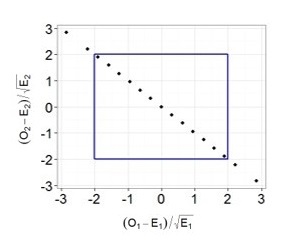
Теперь самое интересное. Предположим, что мы решили многократно повторять 100 бросков, и каждый раз мы записывали наблюдаемые частоты орлов и решек, рассчитывали требуемые показатели (разность наблюдаемых и ожидаемых частот, деленная на корень из ожидаемой частоты) и как и в предыдущем примере наносили их на график.

Легко заметить, что теперь все точки выстраиваются в одну линию. Все дело в том, что в случае с монеткой наши слагаемые не являются независимыми, зная общее число бросков и число решек, мы всегда можем точно определить выпавшее число орлов и наоборот, поэтому мы не можем сказать, что два наших слагаемых — это две независимые случайные величины. Также вы можете убедиться, что все точки действительно всегда будут лежать на одной прямой: если у нас выпало 30 орлов, значит решек было 70, если орлов 70, то решек 30 и т.д. Таким образом, несмотря на то, что в нашей формуле было два слагаемых, для расчета p-value мы будем использовать распределение Хи-квадрат с одной степенью свободы! Вот мы наконец-то добрались до момента, когда нам потребовалось вычесть единицу. Если бы мы проверяли гипотезу о том, что наша игральная кость с шестью гранями является честной, то мы бы использовали распределение Хи-квадрат с 5 степенями свободы. Ведь зная общее число бросков и наблюдаемые частоты выпадения любых пяти граней, мы всегда можем точно определить, чему равняется число выпадений шестой грани.

Все становится на свои места

Теперь, вооружившись этими знаниями, вернемся к t-тесту:

в знаменателе у нас находится стандартная ошибка, которая представляет собой выборочное стандартное отклонение, делённое на корень из объёма выборки. В расчет стандартного отклонения входит сумма квадратов отклонений наблюдаемых значений от их среднего значения — то есть сумма нескольких случайных положительных величин. А мы уже знаем, что сумма квадратов n случайных величин может быть описана при помощи распределения хи-квадрат. Однако, несмотря на то, что у нас n слагаемых, у данного распределения будет n-1 степень свободы, так как зная выборочное среднее и n-1 элементов выборки, мы всегда можем точно задать последний элемент (отсюда и берется это объяснение про среднее и n-1 элементов необходимых для однозначного определения n элемента)! Получается, в знаменателе t-статистики у нас спрятано распределение хи-квадрат c n-1 степенями свободы, которое используется для описания распределения выборочного стандартного отклонения! Таким образом, степени свободы в t-распределении на самом деле берутся из распределения хи-квадрат, которое спрятано в формуле t-статистики. Кстати, важно отметить, что все приведенные выше рассуждения справедливы, если исследуемый признак имеет нормальное распределение в генеральной совокупности (или размер выборки достаточно велик), и если бы у нас действительно стояла цель проверить гипотезу о среднем значении роста в популяции, возможно, было бы разумнее использовать непараметрический критерий.

Схожая логика расчета числа степеней свободы сохраняется и при работе с другими тестами, например, в регрессионном или дисперсионном анализе, все дело в случайных величинах с распределением Хи-квадрат, которые присутствуют в формулах для расчета соответствующих критериев.

Таким образом, чтобы правильно интерпретировать результаты статистических исследований и разбираться, откуда возникают все показатели, которые мы получаем при использовании даже такого простого критерия как одновыборочный t-тест, любому исследователю необходимо хорошо понимать, какие математические идеи лежат в основании статистических методов.

Онлайн курсы по статистике: объясняем сложные темы простым языком

Основываясь на опыте преподавания статистики в Институте биоинформатики , у нас возникла идея создать серию онлайн курсов, посвященных анализу данных, в которых в доступной для каждого форме будут объясняться наиболее важные темы, понимание которых необходимо для уверенного использования методов статистики при решении различного рода задача. В 2015 году мы запустили курс Основы статистики, на который к сегодняшнему дню записалось около 17 тысяч человек, три тысячи слушателей уже получили сертификат о его успешном завершении, а сам курс был награждён премией EdCrunch Awards и признан лучшим техническим курсом. В этом году на платформе stepik.org стартовало продолжение курса Основы статистики. Часть два, в котором мы продолжаем знакомство с основными методами статистики и разбираем наиболее сложные теоретические вопросы. Кстати, одной из главных тем курса является роль распределения Хи-квадрат Пирсона при проверке статистических гипотез. Так что если у вас все еще остались вопросы о том, зачем мы вычитаем единицу из общего числа наблюдений, ждем вас на курсе!

Стоит также отметить, что теоретические знания в области статистики будут определенно полезны не только тем, кто применяет статистику в академических целях, но и для тех, кто использует анализ данных в прикладных областях. Базовые знания в области статистики просто необходимы для освоения более сложных методов и подходов, которые используются в области машинного обучения и Data Mining. Таким образом, успешное прохождение наших курсов по введению в статистику — хороший старт в области анализа данных. Ну а если вы всерьез задумались о приобретении навыков работы с данными, думаем, вас может заинтересовать наша онлайн — программа по анализу данных, о которой мы подробнее писали здесь. Упомянутые курсы по статистике являются частью этой программы и позволят вам плавно погрузиться в мир статистики и машинного обучения. Однако пройти эти курсы без дедлайнов могут все желающие и вне контекста программы по анализу данных.

What Are Degrees of Freedom?

Degrees of freedom are the maximum number of logically independent values, which may vary in a data sample. Degrees of freedom are calculated by subtracting one from the number of items within the data sample.

Understanding Degrees of Freedom

Degrees of freedom are the number of independent variables that can be estimated in a statistical analysis and tell you how many items can be randomly selected before constraints must be put in place.

Within a data set, some initial numbers can be chosen at random. However, if the data set must add up to a specific sum or mean, for example, the number in the data set is constrained to evaluate the values of all other values in a data set, then meet the set requirement.

Examples of Degrees of Freedom

Example 1: Consider a data sample consisting of five positive integers. The values of the five integers must have an average of six. If four items within the data set are {3, 8, 5, and 4}, the fifth number must be 10. Because the first four numbers can be chosen at random, the degree of freedom is four.

Example 2: Consider a data sample consisting of five positive integers. The values could be any number with no known relationship between them. Because all five can be chosen at random with no limitations, the degree of freedom is four.

Example 3: Consider a data sample consisting of one integer. That integer must be odd. Because there are constraints on the single item within the data set, the degree of freedom is zero.

Degrees of Freedom Formula

The formula to determine degrees of freedom is:

D

f

=

N

−

1

where:

D

f

=

degrees of freedom

N

=

sample size

begin{aligned} &text{D}_text{f} = N — 1 \ &textbf{where:} \ &text{D}_text{f} = text{degrees of freedom} \ &N = text{sample size} \ end{aligned}

​Df​=N−1where:Df​=degrees of freedomN=sample size​

For example, imagine a task of selecting ten baseball players whose batting average must average to .250. The total number of players that will make up our data set is the sample size, so N = 10. In this example, 9 (10 — 1) baseball players can be randomly picked, with the 10th baseball player having a specific batting average to adhere to the .250 batting average constraint.

Applying Degrees of Freedom

In statistics, degrees of freedom define the shape of the t-distribution used in t-tests when calculating the p-value. Depending on the sample size, different degrees of freedom will display different t-distributions. Calculating degrees of freedom is critical when understanding the importance of a chi-square statistic and the validity of the null hypothesis.

Degrees of freedom also have conceptual applications outside of statistics. Consider a company deciding the purchase of raw materials for its manufacturing process. The company has two items within this data set: the amount of raw materials to acquire and the total cost of the raw materials.

The company freely decides one of the two items, but their choice will dictate the outcome of the other. Because it can only freely choose one of the two, it has one degree of freedom in this situation. If the company decides the amount of raw materials, it cannot decide the total amount spent. By setting the total amount to spend, the company may be limited in the amount of raw materials it can acquire.

Chi-Square Tests

There are two different kinds of chi-square tests: the test of independence, which asks a question of relationship, such as, «Is there a relationship between gender and SAT scores?»; and the goodness-of-fit test, which asks something like «If a coin is tossed 100 times, will it come up heads 50 times and tails 50 times?»

For these tests, degrees of freedom are utilized to determine if a null hypothesis can be rejected based on the total number of variables and samples within the experiment. For example, when considering students and course choice, a sample size of 30 or 40 students is likely not large enough to generate significant data. Getting the same or similar results from a study using a sample size of 400 or 500 students is more valid.

T-Test

To perform a t-test, you must calculate the value of t for the sample and compare it to a critical value. The critical value will vary, and you can determine the correct critical value by using a data set’s t distribution with the degrees of freedom.

Sets with lower degrees of freedom have a higher probability of extreme values, and higher degrees of freedom, such as a sample size of at least 30, will be much closer to a normal distribution curve. Smaller sample sizes will correspond with smaller degrees of freedom and result in fatter t-distribution tails.

In the examples above, many of the situations may be used as a 1-sample t-test. For instance, ‘Example 1,’ where five values are selected but must add up to a specific average, can be defined as a 1-sample t-test. This is because there is only one constraint being placed on the variable.

History of Degrees of Freedom

The earliest and most basic concept of degrees of freedom was noted in the early 1800s, intertwined in the works of mathematician and astronomer Carl Friedrich Gauss. The modern usage and understanding of the term were expounded upon first by William Sealy Gosset, an English statistician, in his article «The Probable Error of a Mean,» published in Biometrika in 1908 under a pen name to preserve his anonymity.

In his writings, Gosset did not specifically use the term «degrees of freedom.» He did explain the concept throughout developing what would eventually be known as «Student’s T-distribution.» The term was not popular until 1922. English biologist and statistician Ronald Fisher began using the term «degrees of freedom» when he published reports and data on his work developing chi-squares.

The Bottom Line

Some statistical analysis processes may call for an indication of the number of independent values that can vary within an analysis to meet constraint requirements. This indication is the degrees of freedom, the number of units in a sample size that can be chosen randomly before a specific value must be picked.

Число степеней
свободы это число свободно варьирующих
единиц в составе выборки. Так, если вся
выборка состоит из п
элементов
и характеризуется средней X,
то любой элемент этой совокупности
может быть получен как разность между
величи­ной n
• X
и суммой
всех остальных элементов, кроме самого
это­го элемента.

52

Пример. Рассмотрим
ряд 4.5: 2468 10. Мы помним, что сред­няя
этого ряда равна 6.
В этом ряду
5 чисел, следовательно N
= 5. Предположим,
что мы хотим получить последний элемент
ряда

— 10, зная все
предыдущие элементы и среднее этого
ряда. Тогда:

5-6-2-4-6-8= 10

Предположим, что
мы хотим получить первый элемент ряда

— 2, зная все
последующие элементы и среднее этого
ряда. Тогда:

5-6-4-6-8-10 = 2и т.д.

Следовательно,
один элемент выборки не имеет свободы
ва­риации и всегда может быть выражен
через другие элементы и среднее. Это
означает, что число степеней свободы у
выборочно­го ряда обозначаемое в
таких случаях символом k
будет
опреде­ляться как k
= п -1, где п
— общее
число элементов ряда (вы­борки).

При наличии не
одного, а нескольких ограничений свободы
вариации, число степеней свободы,
обозначаемое как v
(гречес-и.ш буква ню) будет равно v
= п — k,
где k
соответствует
числу ограничений свободы вариации.

В общем случае для
таблицы экспериментальных данных число
степеней свободы будет определяться
по следующей формуле:

v
= (с — 1)•(n—
1)
(4.8)

где с
— число
столбцов, а п
— число
строк (число испытуемых).

Следует подчеркнуть,
однако, что для ряда статистических
методов расчет числа степеней свободы
имеет свою специфику.

4.7. Понятие нормального распределения

Нормальное
распределение играет большую роль в
математи­ческой статистике, поскольку
многие статистические методы предполагают,
что, анализируемые с их помощью
эксперимен­тальные данные распределены
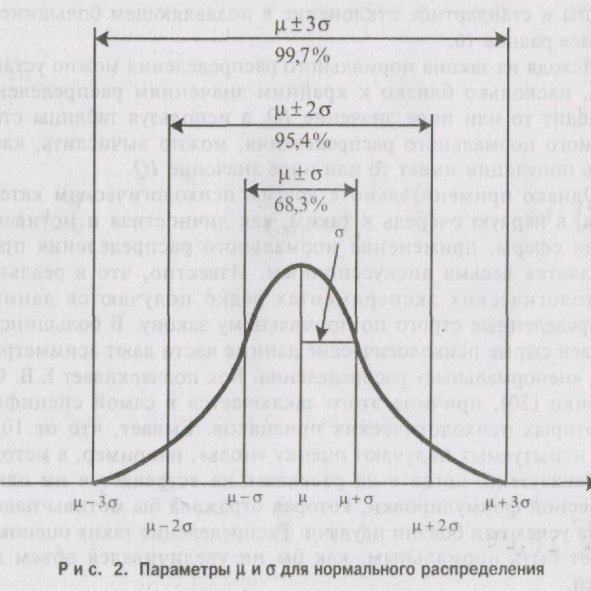
нормально. График нормального распределения
имеет вил колоколообразной кривой (см.
рис. 2).

53

Его важной
особенностью является то, что форма и
положение графика нормального
распределения определяется только
двумя параметрами: средней µ(мю) и
стандартным отклонением о (сиг­ма).
Если стандартное отклонение σ постоянно,
а величина сред­ней µ меняется, то
собственно форма нормальной кривой
оста­ется неизменной, а лишь ее график
смещается вправо (при уве­личении µ)
или влево (при уменьшении µ) по оси
абсцисс —ОХ.
При условии
постоянства средней ц изменение сигмы
влечет за собой изменение только ширины
кривой: при уменьшении сигмы кривая
делается более узкой, и поднимается при
этом вверх, а при увеличении сигмы кривая
расширяется, но опуска­ется вниз.
Однако во всех случаях нормальная кривая
оказывает­ся строго симметричной
относительно средней, сохраняя пра­вильную
колоколообразную форму.

54

Для нормального
распределения характерно также
совпаде­ние величин средней
арифметической, моды и медианы. Равен­ство
этих показателей указывает на нормальность
данного рас­пределения. Это распределение
обладает еще одной важной осо­бенностью:
чем больше величина признака отклоняется
от сред­него значения, тем меньше
будет частота встречаемости (веро­ятность)
этого признака в распределении.
«Нормальным» такое распределение было
названо потому, что оно наиболее часто
встречалось в естественно-научных
исследованиях и казалось «нормой»
распределения случайных величин.

В психологических
исследованиях нормальное распределение
используется в первую очередь при
разработке и применении те­стов
интеллекта и способностей. Так, отклонения
показателей интеллекта IQ
следуют
закону нормального распределения, имея
среднее значение равное 100 для любой
конкретной возрастной группы и стандартное
отклонение в подавляющем большинстве
случаев равное 16.

Исходя из закона
нормального распределения можно
устано­вить, насколько близко к крайним
значениям распределения подходит то
или иное значение IQ,
а используя
таблицы стан­дартного нормального
распределения, можно вычислить, какая
часть популяции имеет то или иное
значение IQ.

Однако применительно
к другим психологическим катего­риям,
в первую очередь к таким, как личностная
и мотиваци-онная сферы, применение
нормального распределения пред­ставляется
весьма дискуссионным. Известно, что в
реальных психологических экспериментах
редко получаются данные, распределенные
строго по нормальному закону. В большинстве
случаев сырые психологические данные
часто дают асимметрич­ные, «ненормальные»
распределения. Как подчеркивает Е.В.
Си­доренко (30), причина этого заключается
в самой специфике некоторых психологических
признаков. Бывает, что от 10 до 20% испытуемых
получают оценку «ноль», например, в
методи­ке Хекхаузена, когда в их
рассказах не встречается ни одной
словесной формулировки, которая отражала
бы мотивы надеж­ды на успех или боязни
неудачи. Распределение таких оценок не
может быть нормальным, как бы ни
увеличивался объем вы­борки.

55

Несмотря на это,
при обработке экспериментальных данных
всегда целесообразно проводить оценку
характера распределения (см. главу 8,
раздел 8.2). Эта оценка важна, потому что
в зависи­мости от характера распределения
решается вопрос о возможно­сти
применения того или иного статистического
метода. Как бу­дет понятно из дальнейшего
изложения, при нормальном рас­пределении
экспериментальных данных применяются
особые методы статистической обработки.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Многие задачи статистического вывода требуют от нас определения числа степеней свободы. Число степеней свободы выбирает одно распределение вероятностей из бесконечного множества. Этот шаг часто упускается из виду, но является важной деталью как при вычислении доверительных интервалов, так и при проверке гипотез.

Не существует единой общей формулы для количество степеней свободы. Однако существуют определенные формулы, используемые для каждого типа процедур в статистике вывода. Другими словами, настройка, в которой мы работаем, будет определять количество степеней свободы. Далее следует частичный список некоторых из наиболее распространенных процедур вывода, а также количество степеней свободы, используемых в каждой ситуации.

Standard Normal Распространение

Процедуры, включающие стандартное нормальное распределение, перечислены для полноты и прояснения некоторых заблуждений. Эти процедуры не требуют от нас определения числа степеней свободы. Причина этого в том, что существует единое стандартное нормальное распределение. Эти типы процедур включают в себя процедуры, включающие среднее значение генеральной совокупности, когда стандартное отклонение совокупности уже известно, а также процедуры, касающиеся пропорций совокупности.

Процедуры One Sample T

Иногда статистическая практика требует, чтобы мы использовали t-распределение Стьюдента. Для этих процедур, например тех, которые имеют дело со средним генеральным с неизвестным стандартным отклонением генеральной совокупности, количество степеней свободы на единицу меньше размера выборки. Таким образом, если размер выборки составляет n , тогда имеется n – 1 степень свободы.

T-процедуры с парными данными

Часто имеет смысл рассматривать данные как парные. Сопряжение обычно осуществляется из-за связи между первым и вторым значениями в нашей паре. Много раз мы делали пары до и после измерений. Наша выборка парных данных не является независимой; однако разница между каждой парой независима. Таким образом, если в выборке всего n пар точек данных (всего 2 n значений), то имеется n – 1 степень свободы.

T-процедуры для двух независимых групп

Для этих типов задач мы все еще используют t-распределение. На этот раз есть выборка из каждой нашей популяции. Хотя предпочтительно, чтобы эти две выборки были одного размера, это не обязательно для наших статистических процедур. Таким образом, у нас может быть два образца размером n₁ и n₂ . Есть два способа определить количество степеней свободы. Более точный метод – использовать формулу Уэлча, громоздкую в вычислительном отношении формулу, включающую размеры выборки и стандартные отклонения выборки.. Другой подход, называемый консервативным приближением, можно использовать для быстрой оценки степеней свободы. Это просто меньшее из двух чисел n₁ – 1 и n ₂ – 1.

Хи-квадрат для независимости

Одно из применений теста хи-квадрат – это проверить, есть ли два категориальные переменные, каждая из которых имеет несколько уровней, демонстрируют независимость. Информация об этих переменных записывается в двустороннюю таблицу с r строками и c столбцами. Число степеней свободы равно произведению ( r – 1) ( c – 1).

Степень соответствия по хи-квадрат

Оценка соответствия по хи-квадрат начинается с одной категориальной переменной с общим количеством уровней n . Мы проверяем гипотезу о том, что эта переменная соответствует заданной модели. Количество степеней свободы на единицу меньше количества уровней. Другими словами, существует n – 1 степеней свободы.

Однофакторный дисперсионный анализ

Однофакторный дисперсионный анализ (ANOVA) позволяет нам проводить сравнения между несколькими группами, устраняя необходимость в множественных попарных проверках гипотез. Поскольку тест требует, чтобы мы измерили как вариации между несколькими группами, так и вариации внутри каждой группы, мы получаем две степени свободы. F-статистика, которая используется для однофакторного дисперсионного анализа, представляет собой дробь. У числителя и знаменателя есть степени свободы. Пусть c будет количеством групп, а n – общим количеством значений данных. Число степеней свободы числителя на единицу меньше числа групп, или c – 1. Число степеней свободы знаменателя – это общее количество значений данных минус количество групп, или n – c.

Понятно видим, что мы должны быть очень осторожны, чтобы знать, с какой процедурой вывода мы работаем. Эти знания сообщат нам правильное количество используемых степеней свободы.