8. Геометрия в пространстве (стереометрия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Нахождение угла между прямыми
(blacktriangleright) Угол между прямыми – это такой угол (alpha), что (0leqslant alphaleqslant 90^circ).
(blacktriangleright) В пространстве существует 4 типа взаимного расположения прямых: совпадают, пересекаются, параллельны, скрещиваются.
(blacktriangleright) Скрещивающиеся прямые – это прямые, через которые нельзя провести одну плоскость.
Признак скрещивающихся прямых: если первая прямая пересекает плоскость, в которой лежит вторая прямая, в точке, не лежащей на второй прямой, то такие прямые скрещиваются.
(blacktriangleright) Порядок нахождения угла между скрещивающимися прямыми:
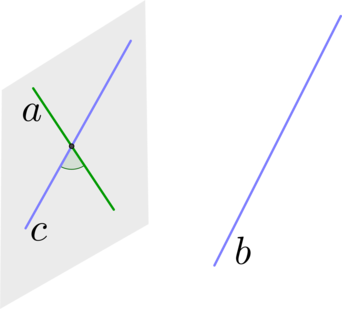
Шаг 1: через одну из двух прямых (a) провести плоскость, параллельную второй прямой (b) (напомним признак: прямая параллельна плоскости, если она параллельна какой-нибудь прямой из этой плоскости);
Шаг 2: в этой плоскости найти прямую (c), параллельную прямой (b);
Шаг 3: тогда угол между прямыми (a) и (b) будет равен углу между прямыми (a) и (c).
Задание
1
#934
Уровень задания: Равен ЕГЭ
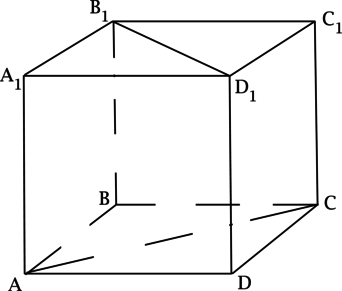
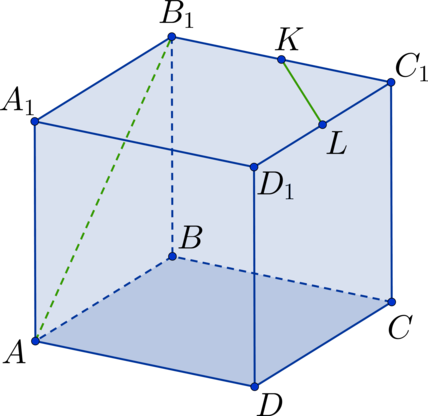
(ABCDA_1B_1C_1D_1) – куб. Найдите угол между прямыми, содержащими отрезки (AC) и (B_1D_1). Ответ дайте в градусах.
Прямая (BD) параллельна прямой (B_1D_1), тогда угол между (AC) и (B_1D_1) равен углу между (AC) и (BD), но (AC) и (BD) – диагонали квадрата, тогда они пересекаются под прямым углом, следовательно ответ (90^{circ}).
Ответ: 90
Задание
2
#2847
Уровень задания: Равен ЕГЭ
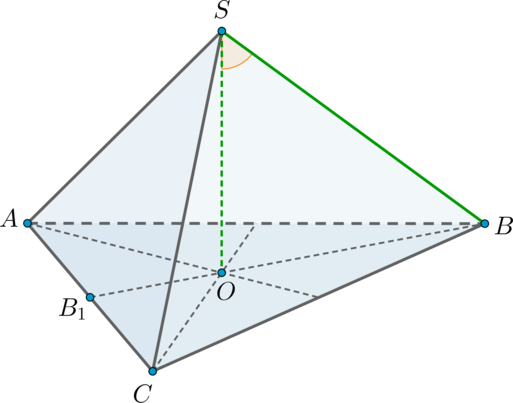
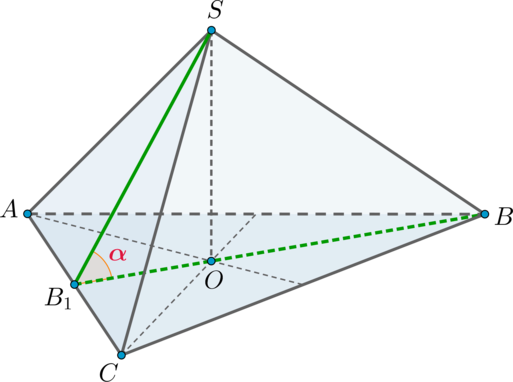
Дана правильная треугольная пирамида (SABC) с вершиной (S). Найдите угол между высотой пирамиды и ребром (SB), если высота пирамиды равна (2sqrt3), а сторона основания пирамиды равна (6). Ответ дайте в градусах.
Так как пирамида правильная, то в основании лежит правильный треугольник, следовательно, высота (SO) падает в точку пересечения медиан основания.
Пусть (BB_1) – медиана, а значит, и высота. По теореме Пифагора [BB_1=sqrt{BC^2-B_1C^2}=3sqrt3 quadRightarrowquad BO=dfrac23BB_1=2sqrt3,] так как медианы точкой пересечения делятся в отношении (2:1), считая от вершины.
Следовательно, прямоугольный (triangle SOB) является равнобедренным ((SO=BO=2sqrt3)), значит, острые углы равны по (45^circ).
Ответ: 45
Задание
3
#933
Уровень задания: Равен ЕГЭ
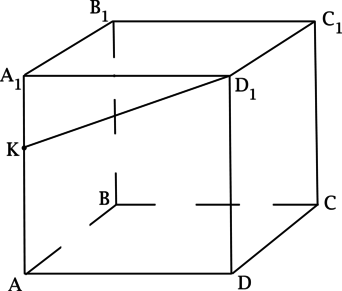
(ABCDA_1B_1C_1D_1) – куб. Точка (K) лежит на ребре (AA_1). Найдите угол между прямыми, содержащими отрезки (D_1K) и (AB). Ответ дайте в градусах.
Так как (ABCDA_1B_1C_1D_1) – куб, то (AB) перпендикулярен плоскости ((ADD_1)), тогда (AB) перпендикулярен любой прямой, лежащей в плоскости ((ADD_1)), следовательно, угол между прямыми, содержащими отрезки (D_1K) и (AB) равен (90^{circ}).
Ответ: 90
Задание
4
#2845
Уровень задания: Равен ЕГЭ
Дан правильный тетраэдр (SABC). Найдите квадрат тангенса угла между высотой грани (SAC), опущенной из вершины (S), и высотой грани (ABC), опущенной из вершины (B).
Пусть (SB_1) – высота грани (SAC). Так как тетраэдр правильный, то все его грани – равные правильные треугольники, то есть (SB_1) также является и медианой, значит, (AB_1=B_1C). Также у правильного тетраэдра высота из каждой вершины падает в точку пересечения медиан (биссектрис, высот) противоположной грани. Следовательно, если (SO) – высота, то (O) – точка пересечения медиан треугольника (ABC), а значит и высот, так как (triangle ABC) правильный. Следовательно, (BB_1) — медиана и высота.
Таким образом, необходимо найти (mathrm{tg}^2angle (SB_1,
BB_1)).
Пусть (a) – ребро тетраэдра. Тогда (BC=a, B_1C=0,5a), следовательно, по теореме Пифагора [BB_1=sqrt{BC^2-B_1C^2}=dfrac{sqrt3}2a] Так как (O) – точка пересечения медиан, а медианы точкой пересечения делятся в отношении (2:1), считая от вершины, то (OB_1=frac13BB_1=frac{sqrt3}6a).
Так как (triangle ABC=triangle SAC), то (SB_1=BB_1). Следовательно, из прямоугольного (triangle SB_1O): [cos
alpha=dfrac{OB_1}{SB_1}=dfrac13 quadRightarrowquad sin alpha
=sqrt{1-cos^2alpha}=dfrac{2sqrt2}3 quadRightarrowquad
mathrm{tg}^2alpha=(2sqrt2)^2=8.]
Ответ: 8
Задание
5
#1846
Уровень задания: Равен ЕГЭ
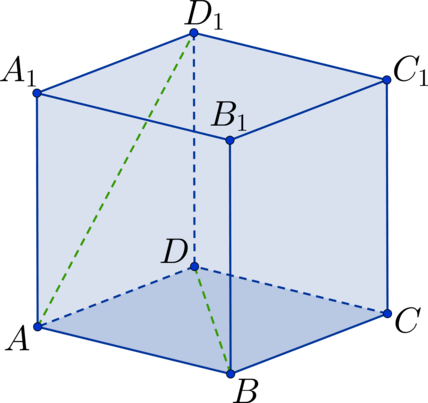
Дан куб (ABCDA_1B_1C_1D_1). Найдите угол между прямыми (AD_1) и (BD). Ответ дайте в градусах.
Заметим, что (BC_1 || AD_1), тогда рассмотрим треугольник (triangle BDC_1), в котором необходимо определить (angle DBC_1). Он состоит из диагоналей соответствующих квадратов. Так как квадраты между собой равны, то равны и диагонали (Rightarrow) (triangle BDC_1) – равносторонний треугольник (Rightarrow) (angle DBC_1 = 60^circ).
Ответ: 60
Задание
6
#1847
Уровень задания: Равен ЕГЭ
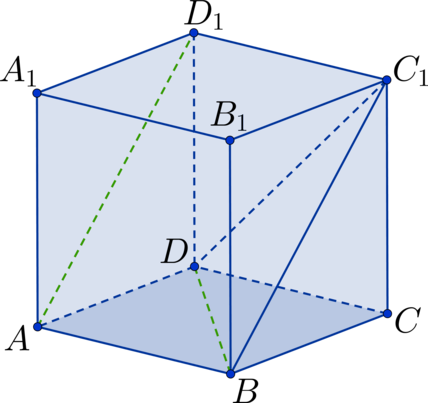
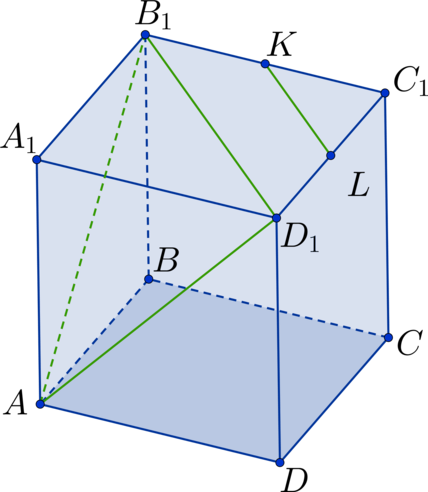
Дан куб (ABCDA_1B_1C_1D_1). Точка (K) – середина стороны (B_1C_1), а точка (L) – середина стороны (C_1D_1). Найдите угол между прямыми (AB_1) и (KL). Ответ дайте в градусах.
Проведем диагональ (B_1D_1) в квадрате (A_1B_1C_1D_1). Тогда (KL) – средняя линия в (triangle B_1C_1D_1) (Rightarrow) (KL || B_1D_1) (Rightarrow) (angle AB_1D_1) – искомый угол. Рассмотрим (triangle AB_1D_1). Он состоит из диагоналей соответствующих квадратов (Rightarrow) треугольник является равносторонним (Rightarrow) (angle AB_1D_1 = 60^circ).
Ответ: 60
Задание
7
#2846
Уровень задания: Сложнее ЕГЭ
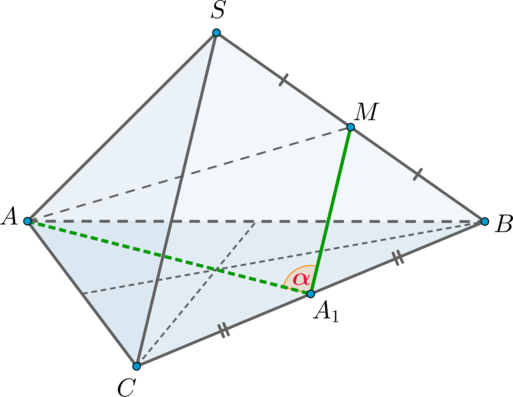
Дана правильная треугольная пирамида (SABC) с вершиной (S). Найдите косинус угла между высотой основания (AA_1) и ребром (SC), если сторона основания равна (sqrt3), а боковое ребро равно (2).
Так как пирамида правильная, то в основании лежит правильный треугольник, следовательно, (AA_1) также является и медианой.
Заметим, что прямые (AA_1) и (SC) скрещиваются. Проведем (A_1Mparallel SC), следовательно, (angle (AA_1, SC)=angle (AA_1,
A_1M)).
Так как (A_1Mparallel SC) и (A_1) – середина (BC), то (M) – середина (SB). Следовательно, (A_1M) – средняя линия и [A_1M=frac12SC=1.] По теореме Пифагора из (triangle ABA_1): [AA_1=sqrt{AB^2-A_1B^2}=dfrac32.] Медиану (AM) из (triangle SAB) можно найти по формуле медианы: [AM^2=dfrac{2AS^2+2AB^2-SB^2}4=dfrac52.] Следовательно, по теореме косинусов из (triangle AA_1M): [cos alpha=dfrac{AA_1^2+A_1M^2-AM^2}{2AA_1cdot A_1M}=dfrac14=0,25.]
Ответ: 0,25
Каждому школьнику, который готовится к ЕГЭ по математике, будет полезно повторить тему «Нахождение угла между прямыми». Как показывает статистика, при сдаче аттестационного испытания задачи по данному разделу стереометрии вызывают трудности у большого количества учащихся. При этом задания, требующие найти угол между прямыми, встречаются в ЕГЭ как базового, так и профильного уровня. Это значит, что уметь их решать должны все.
Основные моменты
В пространстве существует 4 типа взаимного расположения прямых. Они могут совпадать, пересекаться, быть параллельными или скрещивающимися. Угол между ними может быть острым или прямым.
Для нахождения угла между прямыми в ЕГЭ или, например, в решении задач по теореме о трех перпендикулярах, школьники Москвы и других городов могут использовать несколько способов решения задач по данному разделу стереометрии. Выполнить задание можно путем классических построений. Для этого стоит выучить основные аксиомы и теоремы стереометрии. Школьнику нужно уметь логически выстраивать рассуждение и создавать чертежи, для того чтобы привести задание к планиметрической задаче.
Также можно использовать векторно-координатный метод, применяя простые формулы, правила и алгоритмы. Главное в этом случае — правильно выполнить все вычисления. Отточить свои навыки решения задач по стереометрии и другим разделам школьного курса вам поможет образовательный проект «Школково».

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды
Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды
Как известно из курса планиметрии, две прямые в плоскости могут пересекаться (имеют общую точку) или быть параллельными (не имеют общую точку).
В пространстве мы можем найти множество примеров ситуаций, когда две прямые не пересекаются, но они и не параллельны.
Рис. (1). Дороги на земле и на эстакадах не пересекаются.
Скрещивающиеся прямые — это прямые, которые не лежат в одной плоскости и не имеют общих точек.
Теорема «Признак скрещивающихся прямых»
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).
Доказательство
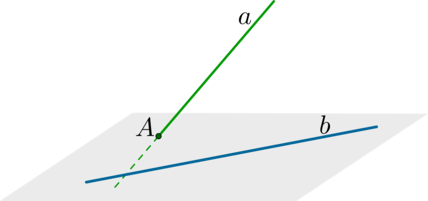
Рассмотрим прямую (AB), лежащую в плоскости, и прямую (CD), которая пересекает плоскoсть в точке (D), не лежащей на прямой (AB).
Рис. (2). Скрещивающиеся прямые.
1. Допустим, что прямые (AB) и (CD) всё-таки лежат в одной плоскости.
2. Значит, эта плоскость идёт через прямую (AB) и точку (D), то есть, она совпадает с плоскостью (α).
3. Это противоречит условиям теоремы, по которым прямая (CD) не находится в плоскости (α), а пересекает её.
Теорема доказана.
В пространстве прямые могут пересекаться, скрещиваться или быть параллельными. 
Рис. (3). Параллельные прямые.
Рис. (4). Пересекающиеся прямые.
Рис. (5). Скрещивающиеся прямые.
Теорема
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.
Доказательство
Рассмотрим скрещивающиеся прямые (AB) и (CD).
Рис. (6). Доказательство теоремы.
1. Через точку (D) можно провести прямую (DE), параллельную (AB).
2. Через пересекающиеся прямые (CD) и (DE) можно провести плоскость (α).
3. Так как прямая (AB) не лежит в этой плоскости и параллельна прямой (DE), то она параллельна плоскости.
4. Эта плоскость единственная, так как любая другая плоскость, проходящая через (CD), будет пересекаться с (DE) и (AB), которая ей параллельна.
Теорема доказана.
1. Если прямые параллельны, то угол между ними —
0°
.
2. Углом между двумя пересекающимися прямыми называют величину меньшего из углов, образованных этими прямыми. Если все углы равны, то эти прямые перпендикулярны (образуют угол
90°
).
3. Углом между двумя скрещивающимися прямыми называют угол между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.
Обрати внимание!
Провести соответственные прямые, параллельные данным скрещивающимся прямым, можно через любую точку. Иногда удобно выбрать эту точку на одной из данных скрещивающихся прямых и провести через эту точку прямую, параллельную другой из скрещивающихся прямых.
Пример:
Рис. (7). Куб.
Найти угол между
AB
и
B1D1
.
Выберем точку
B
на прямой
AB
и проведём через
B
прямую
BD
параллельно
B1D1
.
Рис. (8). Куб с дополнительными построениями.
Угол между
AB
и
BD
—
45°
, так как
ABCD
— квадрат.
Соотвeтственно, угол между
AB
и
B1D1
— тоже
45°
.
11
Авг 2013
Категория: Справочные материалы
Углы в пространстве
2013-08-11
2014-03-03
Угол между пересекающимися прямыми
Углом между пересекающимися прямыми, называется наименьший из углов, образованных при пересечении этих прямых (если при пересечении образовались четыре равных угла, то прямые перпендикулярны).
Угол между скрещивающимися прямыми
Углом между двумя скрещивающимися прямыми называется угол между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.
(Одну из прямых можно вполне и не переносить параллельно самой себе, а ограничиться только параллельным переносом одной из прямых до пересечения со второй).
Угол между прямой и плоскостью
Угол между прямой и плоскостью – угол между прямой и ее проекцией на плоскость
Угол между плоскостями
Угол между плоскостями равен углу между прямыми, по которым они пересекаются с любой плоскостью, перпендикулярной их линии пересечения.
Этот угол не зависит от выбора такой плоскости.
Угол между двумя параллельными плоскостями принимается равным нулю.
Автор: egeMax |
Нет комментариев
Определение угла между прямыми
Две прямые называются пересекающимися, если они имеют единственную общую точку. Эта точка называется точкой пересечения прямых. Прямые разбиваются точкой пересечения на лучи, которые образуют четыре неразвернутых угла, среди которых две пары вертикальных углов и четыре пары смежных углов. Если известен размер одного из углов, образованных пересекающимися прямыми, то легко определить размер остальных углов. Если один из углов прямой, то все остальные тоже прямые, а прямые перпендикулярны.
Определение Угол между прямыми — размер наименьшего из углов, образованных этими прямыми.
Угол между прямыми на плоскости
Угол между прямыми заданными уравнениями с угловым коэффициентом
Если две прямые заданы уравнениями с угловым коэффициентом
y = k1x + b1,
y = k2x + b2,
то угол между ними можно найти, используя формулу:
Если знаменатель равен нулю (1 + k1·k2 = 0), то прямые перпендикулярны.
Доказательство. Если прямые заданы уравнениями с угловыми коэффициентами, то легко найти углы между этими прямыми и осью OX
tg α = k1
tg β = k2
Соответственно легко найти угол между прямыми
γ = α — β
tg γ = tg (α — β) = tg α — tg β1 + tg α ·tg β = k1 — k21 + k1·k2
Угол между прямыми через направляющие векторы этих прямых
Если a — направляющий вектор первой прямой и b — направляющий вектор второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:
cos φ = |a · b||a| · |b|
Если уравнение прямой задано параметрически
x = l t + ay = m t + b
то вектор направляющей имеет вид {l; m}
Если уравнение прямой задано как
A x + B y + C = 0
то для вычисления направляющего вектора, можно взять две точки на прямой.
Например, если C ≠ 0, A ≠ 0, C ≠ 0 , при x = 0 => y = -CB значит точка на прямой имеет координаты K(0, -CB), при y = 0 => x = -CA значит точка на прямой имеет координаты M(-CA, 0). Вектор направляющей KM = {-CA; CB}.
Если дано каноническое уравнение прямой
x — x0 l = y — y0m
то вектор направляющей имеет вид {l; m}
Если задано уравнение прямой с угловым коэффициентом
y = kx + b
то для вычисления направляющего вектора, можно взять две точки на прямой, например, при x = 0 => y = b значит точка на прямой имеет координаты K(0, b), при x = 1 => y = k + b значит точка на прямой имеет координаты M(1, k + b). Вектор направляющей KM = {1; k}
Угол между прямыми через векторы нормалей этих прямых
Если a — вектор нормали первой прямой и b — вектор нормали второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:
cos φ = |a · b||a| · |b|
Если уравнение прямой задано как
A x + B y + C = 0
то вектор нормали имеет вид {A; B}
Если задано уравнение прямой с угловым коэффициентом
y = kx + b
то вектор нормали имеет вид {1; —k}
Угол между прямыми через направляющий вектор и вектор нормали этих прямых
Если a — направляющий вектор первой прямой и b — вектор нормали второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:
sin φ = |a · b||a| · |b|
Примеры задач на вычисления угла между прямыми на плоскости
Пример 1. Найти угол между прямыми y = 2x — 1 и y = -3x + 1.
Решение: Воспользуемся формулой для вычисления угла между прямыми заданными уравнениями с угловым коэффициентом:
tg γ =
k1 — k21 + k1·k2
=
2 — (-3)1 + 2·(-3)
=
5-5
= 1
Ответ. γ = 45°
Пример 2. Найти угол между прямыми y = 2x — 1 и x = 2t + 1y = t.
Решение: Воспользуемся формулой для вычисления угла между прямыми у которых известны направляющие векторы.
Для первой прямой направляющий вектор {1; 2}, для второй прямой направляющий вектор {2; 1}
cos φ =
|1 · 2 + 2 · 1|12 + 22 · 22 + 12
=
45 · 5
= 0.8
Ответ. φ ≈ 36.87°
Пример 3 Найти угол между прямыми 2x + 3y = 0 и
x — 23
=
y4
.
Решение: Для решения этой задачи можно найти направляющие векторы и вычислить угол через направляющие векторы или преобразовать уравнения в уравнения с угловым коэффициентом и вычислить угол через угловые коэффициенты.
Преобразуем имеющиеся уравнения в уравнения с угловым коэффициентом.
2x + 3y = 0 => y = -23x (k1 = -23)
x — 23 = y4 => y = 43x — 83 (k2 = 43)
tg γ =
k1 — k21 + k1·k2
=
-23 — 431 + (-23)·43
=
-631 — 89
= 18
Ответ. γ ≈ 86.82°
Угол между прямыми в пространстве
Если a — направляющий вектор первой прямой, а b — направляющий вектор второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:
cos φ = |a · b||a| · |b|
Если дано каноническое уравнение прямой
x — x0 l = y — y0m = z — z0n
то направляющий вектор имеет вид {l; m; n}
Если уравнение прямой задано параметрически
x = l t + ay = m t + bz = n t + c
то направляющий вектор имеет вид {l; m; n}
Пример 4. Найти угол между прямыми
x = 2t + 1y = tz = -t — 1
и
x = t + 2y = -2t + 1z = 1
.
Решение: Так как прямые заданы параметрически, то {2; 1; -1} — направляющий вектор первой прямой, {1; -2; 0} направляющий вектор второй прямой.
cos φ =
|2 · 1 + 1 · (-2) + (-1) · 0|22 + 12 + (-1)2 · 12 + (-2)2 + 02
=
06 · 5
= 0
Ответ. φ = 90°
Пример 5 Найти угол между прямыми
x — 23
=
y4
=
z — 35
и —
x — 22
= 1 — 3y =
3z — 52
.
Решение: Для решения этой задачи найдем направляющие векторы этих прямых.
Уравнение первой прямой задано в канонической форме, поэтому направляющий вектор {3; 4; 5}.
Преобразуем второе уравнение к каноническому вид.
—x — 22 = x — 2-2
1 — 3y = 1 + y-1/3 = y — 1/3-1/3
3z — 52 = z — 5/32/3
Получено уравнение второй прямой в канонической форме
x — 2-2 = y — 1/3-1/3 = z — 5/32/3
{-2; -13; 23} — направляющий вектор второй прямой.
cos φ =
3·(-2) + 4·(-13) + 5·2332 + 42 + 52 · (-2)2 + (-13)2 + (23)2
=
-6 — 43 + 1039 + 16 + 25 · 4 + 19 + 49
=
-450 · 41/9
=
12582
=
682205
Ответ. φ ≈ 74.63°
На этой странице вы узнаете
- Как мы сталкиваемся с двугранными углами, когда читаем книгу?
- Где в комнате можно найти перпендикулярные плоскости?
- Как с помощью линейки и листа воспроизвести в жизни теорему о трех перпендикулярах?
Стереометрия — это не просто раздел математики, который нужно долго и нудно учить. На самом деле стереометрия описывает всю нашу жизнь. Стало интересно? Давайте разбираться.
Углы между плоскостями
Мы точно знаем, что угол между стеной и полом равен 90°. Также, как и угол между стеной и потолком, или полом и любым предметом мебели.
Но чему равен угол между двумя открытыми страницами тетради? Или угол между стеной и полуоткрытой дверью? Угол между перилами и плоскостью пола? Все эти углы достаточно легко найти. И ответы на все эти вопросы нам дает именно стереометрия.
Начнем разбирать в углах между плоскостями с того, что введем понятие двугранного угла.
Двугранный угол — это часть пространства, заключенная между двумя полуплоскостями, имеющими общую границу.
Если мы откроем книгу не полностью и посмотрим на пространство между двумя страницами, это пространство и будет двугранным углом.

На рисунке:
АВ — общая прямая для плоскостей, ее называют ребром двугранного угла;
a, b — плоскости, которые образуют двугранный угол, они называются гранями двугранного угла.
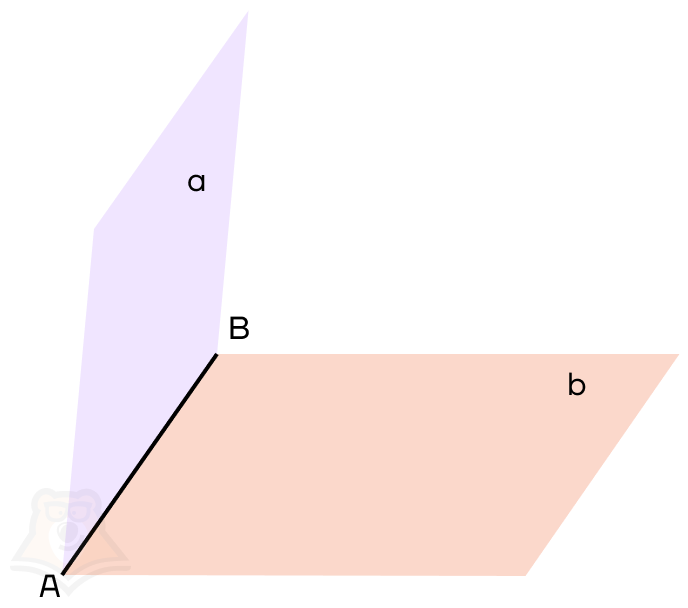
Если раскрыть книгу не полностью, то ее страницы будут образовывать двугранный угол, то есть часть пространства, заключенную между двумя страницами.
Заметим, что при пересечении двух плоскостей обычно образуется четыре двугранных угла. Нас интересует меньший из них.
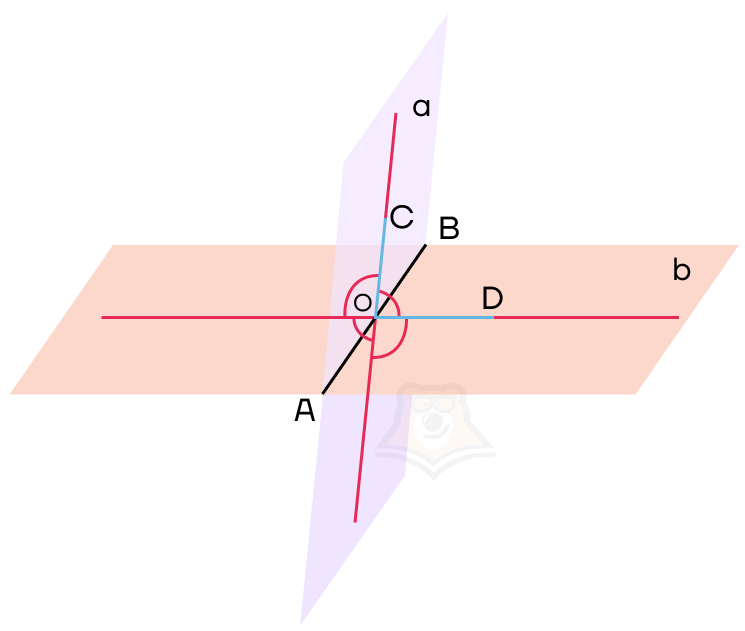
Настало время ввести понятие угла между двумя плоскостями. Но для этого нам нужно провести перпендикуляры к ребру двугранного угла в каждой плоскости. Важно, чтобы перпендикуляры пересекались в одной точке.
Проведенные перпендикуляры образовали четыре угла. Меньший из них и будет называться углом между плоскостями.
Угол между плоскостями — это угол между перпендикулярами, проведенными к линии пересечения плоскостей. Перпендикуляры должны лежать в данных плоскостях.
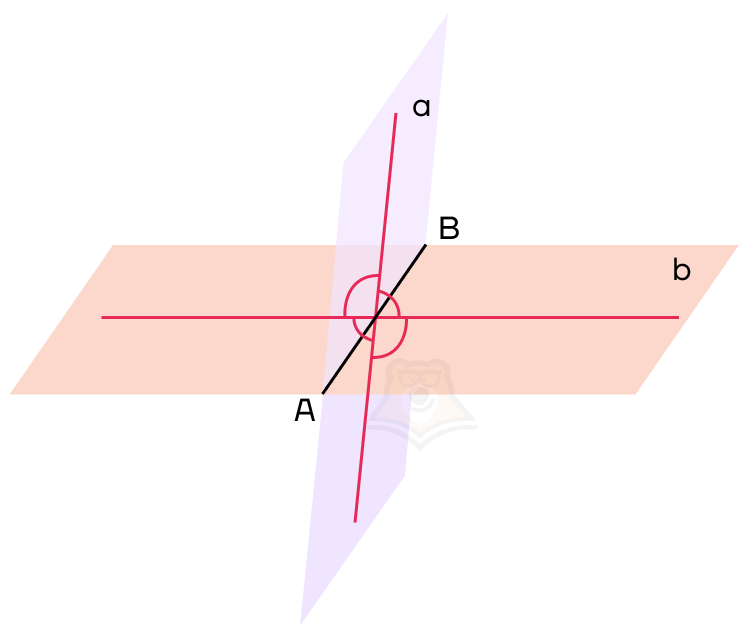
Обозначим нужный нам угол на рисунке как угол COD. Он и будет являться углом между данными плоскостями.
Угол COD также будет называться линейным углом двугранного угла.
Линейный угол двугранного угла показывает градусную меру двугранного угла. Поскольку двугранный угол — это часть пространства, то в этом пространстве можно провести множество линейных углов, которые будут равны между собой.
Как и обычные углы, углы между плоскостями бывают трех видов:
- Острые, то есть меньше 900
- Прямые, равные 900
- Тупые, которые больше 90и меньше 1800
Как уже было сказано выше, за угол между плоскостями всегда принимается острый угол, образованный этими плоскостями.
А что будет, если между плоскостями получится прямой угол?
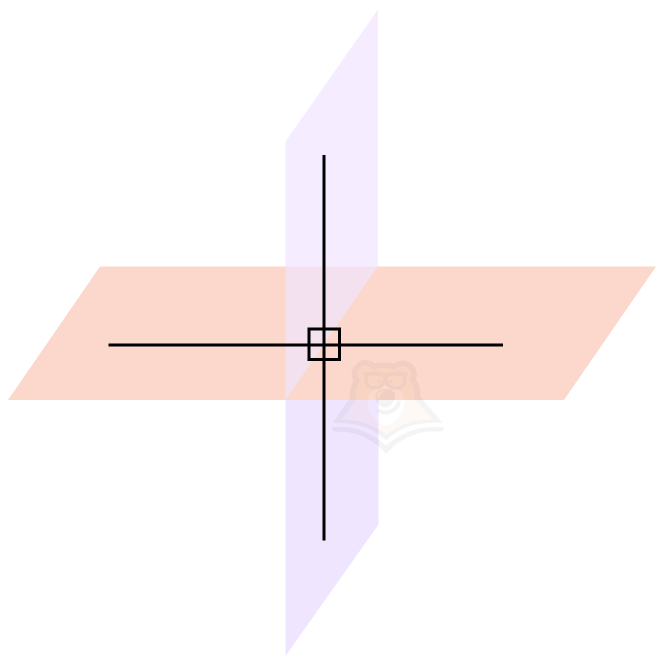
Такие плоскости называются перпендикулярными.
Достаточно посмотреть на стены и пол, или стены и потолок. А еще на углы потолка — в них будет три перпендикулярные плоскости.
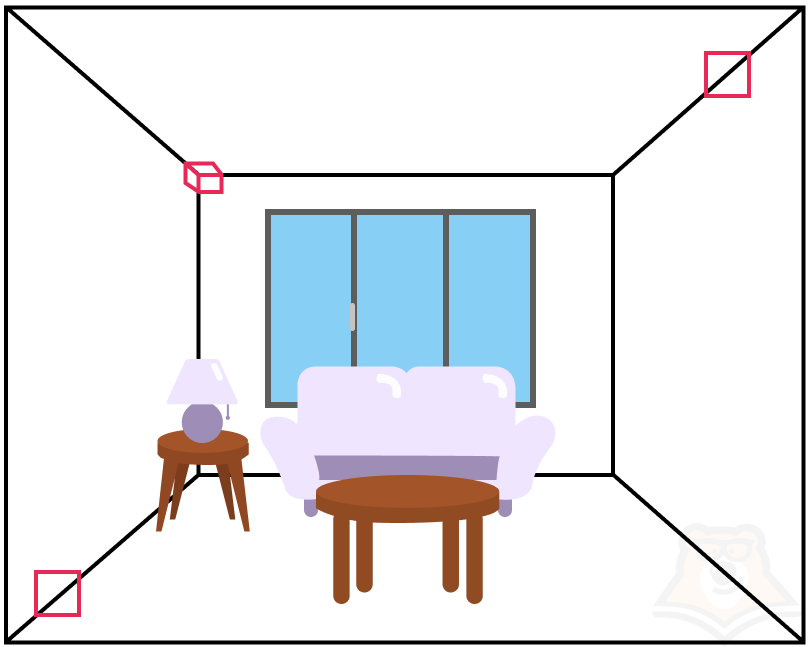
У перпендикулярных плоскостей есть одна очень интересная особенность: все углы, образованные ими, равны между собой и равняются 90° градусам.
Чтобы найти угол между плоскостями, необходимо следовать следующему алгоритму.
1 шаг. Найти линию пересечения плоскостей.
2 шаг. Достроить к этой линии перпендикуляр в каждой плоскости.
3 шаг. Найти острый угол между построенными перпендикулярами.
Углы между прямой и плоскостью
Если нарисовать две прямые на листе бумаги, мы с легкостью можем измерить угол между ними с помощью транспортира. А если провести прямую к плоскости, как точно измерить угол между ними?
И в этом вопросе к нам снова на помощь приходит стереометрия. Но для начала рассмотрим, что такое угол между прямой и плоскостью.
Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость.
Что такое проекция? Предположим, мы проткнем лист бумаги (плоскость) очень длинной иглой.
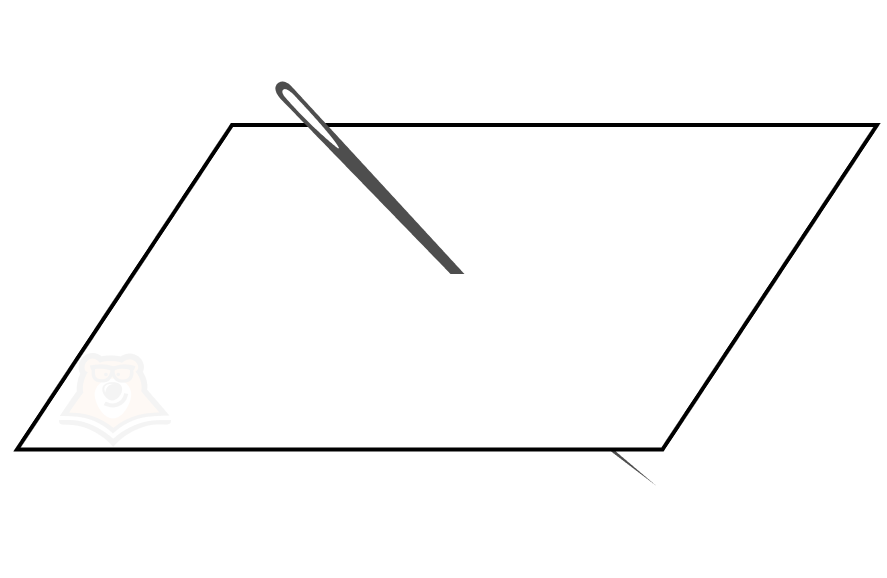
А теперь сделаем этот рисунок ближе к чертежу. Пусть плоскость а пересекает прямая а в точке О.
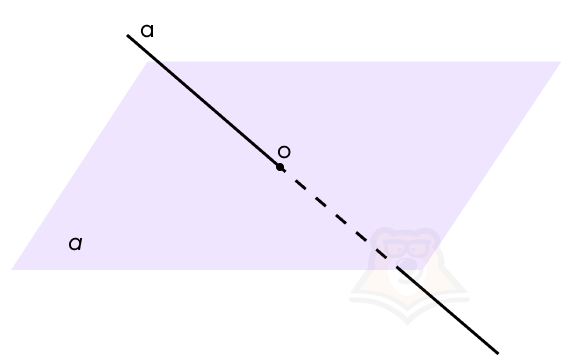
Начнем строить проекцию. Прежде чем разобраться, что такое проекция прямой на плоскость, найдем проекцию точки на плоскость.
Возьмем на нашей прямой а точку А и опустим из нее перпендикуляр к плоскости а. Точка, в которой перпендикуляр пересечет плоскость, будет называться проекцией точки на плоскость. На рисунке обозначим ее как А1.
Проекция точки на плоскость — это основание перпендикуляра, опущенного из этой точки на плоскость.
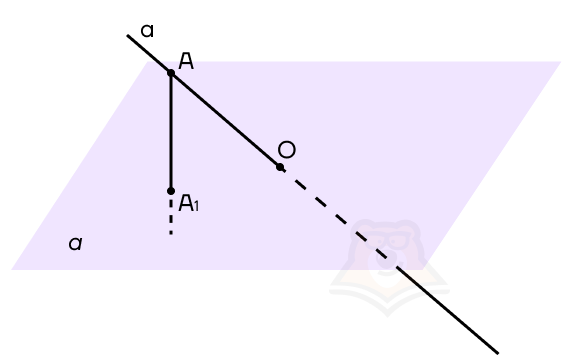
Теперь, если мы будем брать каждую точку на прямой и проектировать ее на плоскость а, то получим проекцию этой прямой на плоскость. Но поскольку на прямой бесконечное множество точек, достаточно соединить точки А1 и О, получаем, что А1О — проекция прямой а на плоскость а.
Заметим, что если мы проведем из любой точки прямой проекцию к плоскости, то попадем на прямую А1О.
Проекция прямой а на плоскость — это прямая а1, образованная проекциями всех точек прямой а на плоскость.
Таким образом можно построить проекции не только прямой, но и любой фигуры.
Мы построили угол из определения. Тогда углом между прямой а и плоскость а будет угол А1ОА.
В этом случае мы также берем острый угол, образованный прямой и плоскостью.
Шаг 1. Построить проекцию прямой на плоскость.
Шаг 2. Найти угол между прямой и построенной проекцией.
Если прямая параллельна плоскости угол будет равен 0.
Проекция прямой на плоскость будет этой же прямой, просто лежащей в плоскости.
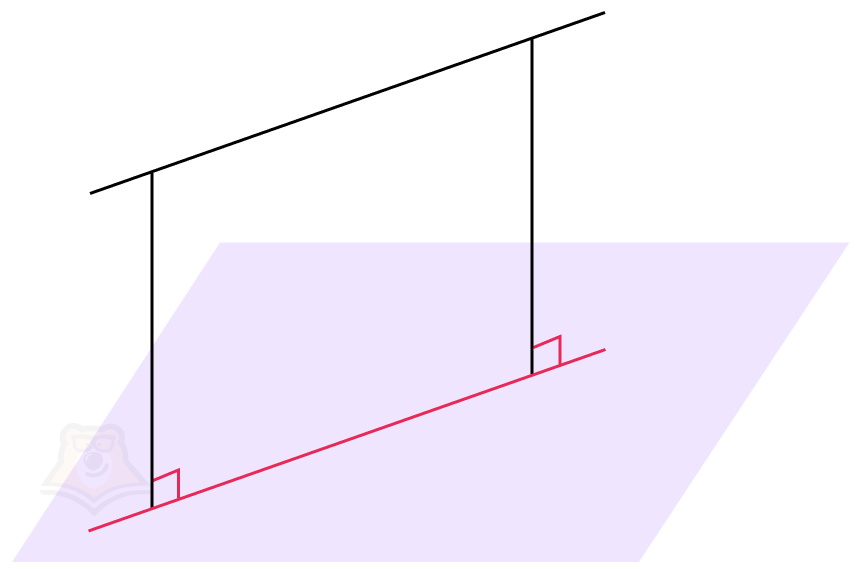
Когда прямая перпендикулярна плоскости, проекцией прямой на плоскость будет точка пересечения прямой и плоскости. Угол между прямой и плоскостью будет равен 90°.
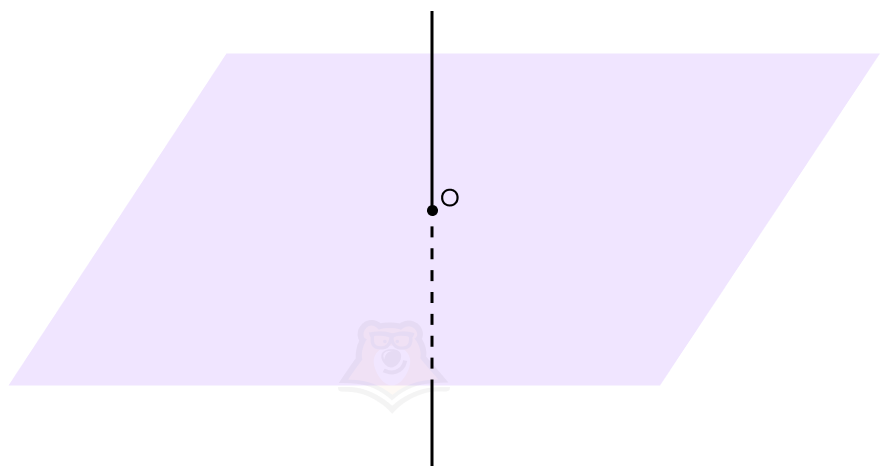
Чуть подробнее остановимся на случае, когда прямая перпендикулярна плоскости.
Прямая, перпендикулярная плоскости — прямая, которая перпендикулярна к каждой прямой, лежащей в этой плоскости.
А что делать, если прямая будет перпендикулярна только одной прямой из плоскости? По определению обязательно, чтобы она была перпендикулярна всем прямым из плоскости. Как тогда проверить перпендикулярность?
Для этого существует признак перпендикулярности прямой и плоскости:
- Если прямая перпендикулярна к двум пересекающимся прямым в этой плоскости, то она будет перпендикулярна этой плоскости.
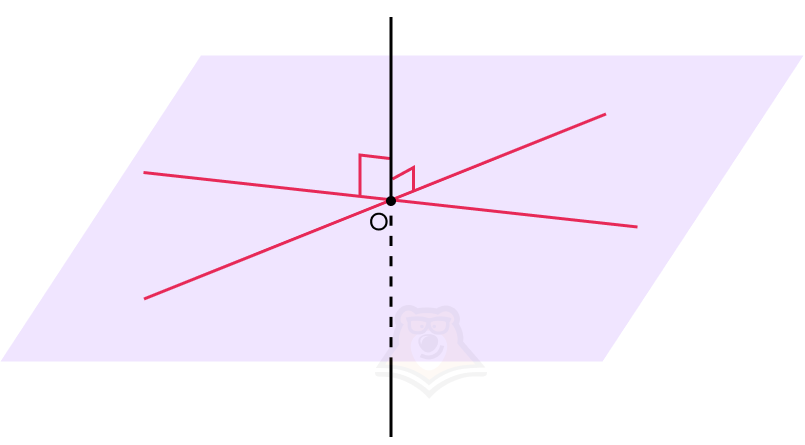
Следовательно, если необходимо в задаче доказать перпендикулярность прямой и плоскости, достаточно доказать, что прямая будет перпендикулярна всего двум пересекающимся прямым в этой плоскости, а не всему множеству прямых, лежащий в данной плоскости.
Рассмотрим несколько интересных свойств, связанных с прямой, перпендикулярной к плоскости.
Свойство 1. Через любую точку пространства можно провести единственную прямую, перпендикулярную плоскости.
Попробуйте подставить уголок к стене из любой точки. Получится ли у вас сделать так, что из одной и той же точки уголок встанет перпендикулярно стене несколько раз? Нет.
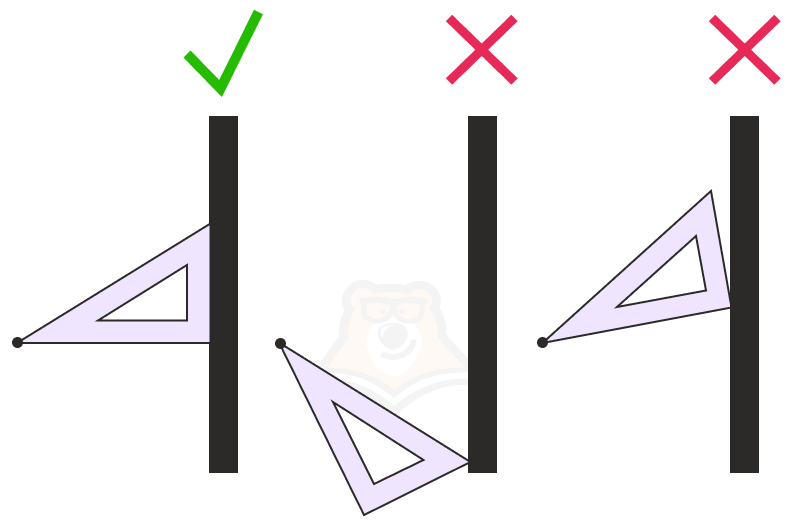
Свойство 2. Если две прямые перпендикулярны одной и той же плоскости, то такие прямые параллельны.
Здесь тоже просто все доказать. Достаточно построить в плоскости прямую, которая пересечет две данные прямые и посмотреть на рисунок “сбоку”. Заметим, что соответственные углы равны, а значит, прямые параллельны.
Подробнее про соответственные углы и параллельные прямые можно прочитать в статье “Основы планиметрии”.

Свойство 3. Если к одной прямой перпендикулярны две плоскости, то такие плоскости параллельны.
Тут такие же рассуждения, как и в предыдущем свойстве: достаточно построить прямые, принадлежащие плоскостям, и посмотреть на них “сбоку”.
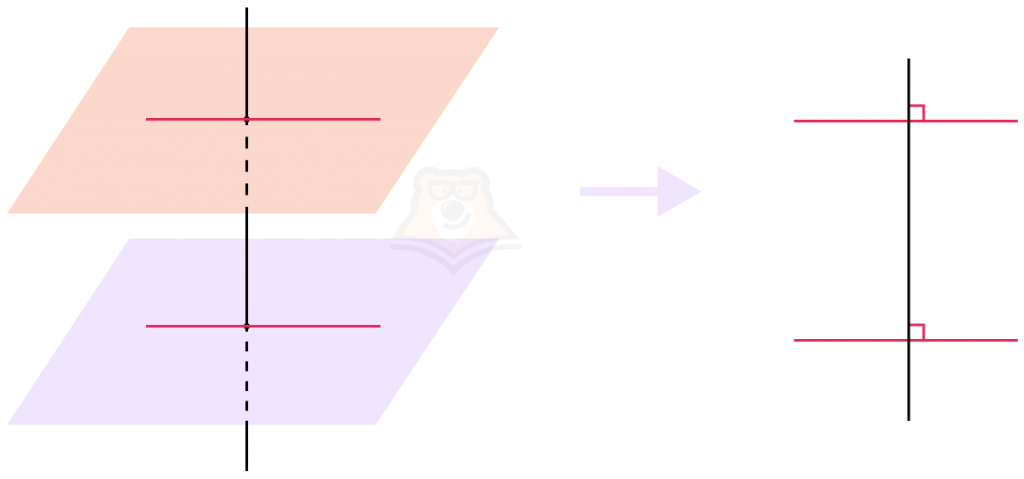
Свойство 4. Если через перпендикулярную к плоскости прямую проходит плоскость, то данные плоскости будут перпендикулярны.
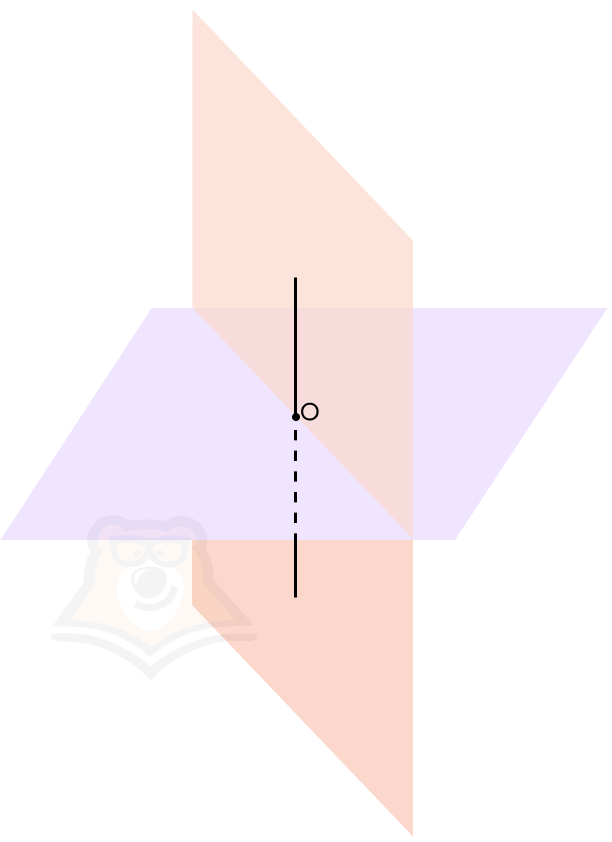
Это легко проверить, если найти любой двугранный угол между построенными плоскостями.
Теорема о трех перпендикулярах
Разберем еще одну очень интересную теорему, связанную с проекциями прямой на плоскость. А именно мы рассмотрим теорему о трех перпендикулярах.
Для начала попробуем понять ее на реальных предметах.
Как с помощью линейки и листа воспроизвести в жизни теорему о трех перпендикулярах?
Возьмем уголок и зафиксируем его строго вертикально на листе. Для удобства назовем уголок АВС, где С — прямой угол.
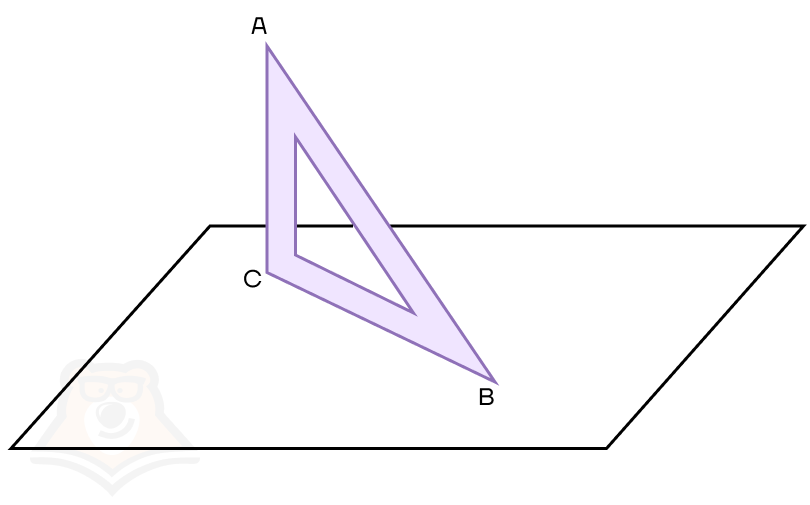
Сразу заметим, что прямая АС будет перпендикулярна плоскости листа (поскольку уголок стоит строго вертикально, а лист лежит строго горизонтально).
Дальше заметим, что прямые АС и ВС также перпендикулярны, поскольку в уголке угол С равен 90°.
Посмотрим чуть-чуть внимательнее и обратим внимание, что прямая ВС при этом будет проекцией на плоскость листа прямой АВ.
Немного достроим наш рисунок и через точку В проведем прямую, перпендикулярную ВС. Назовем эту прямую КМ.
Сразу отмечаем, что прямая КМ перпендикулярна ВС по построению, а также перпендикулярна прямой АС (поскольку АС — перпендикуляр к плоскости листа).
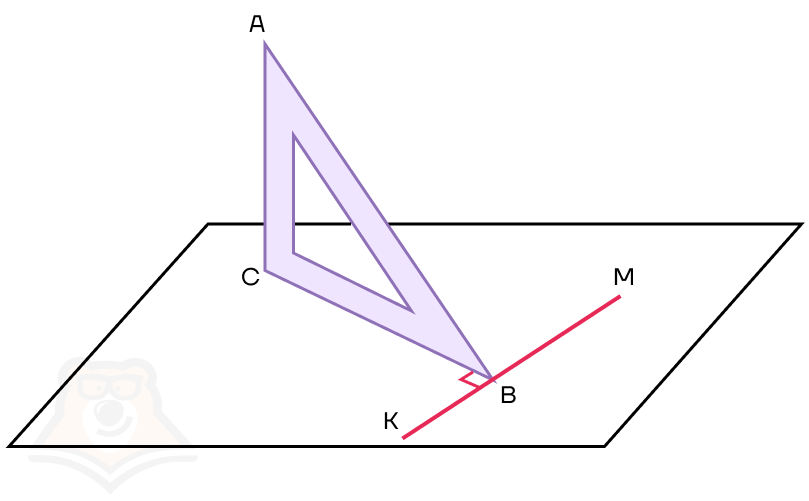
Можем ли мы что-то еще сказать про нашу ситуацию? Оказывается, прямая АВ также будет перпендикулярна прямой КМ.
Возникнет вопрос, почему?
1. Вспомним признак перпендикулярности прямой и плоскости: если прямая перпендикулярна к двум пересекающимся прямым в этой плоскости, то она будет перпендикулярна этой плоскости.
Теперь узнаем, как этот признак выполняется в данной ситуации.
2. Посмотрим на ситуацию немного под другим углом и в этот раз возьмем за плоскость не лист, а нашу линейку.
3. Тогда две пересекающиеся прямые в плоскости линейки будут перпендикулярны прямой КМ: BCKM по построению, а ACKM как прямая, перпендикулярная к плоскости листа, а значит, и перпендикулярная всем прямым в этой плоскости.
4. Получается, что прямая КМ перпендикулярна плоскости АВС, следовательно, перпендикулярна и всем прямым в этой плоскости, в том числе прямой АВ.
Таким образом, длинная сторона линейки будет наклонной прямой, основание — ее проекцией, а начерченная линия — перпендикуляром к проекции.
Мы рассмотрели теорему о трех перпендикулярах. Осталось ее только сформулировать математическим языком.
Теорема о трех перпендикулярах
Если наклонная прямая АВ к плоскости а перпендикулярна прямой КМ в этой плоскости, то и проекция прямой АВ на плоскость а перпендикулярна к прямой КМ.
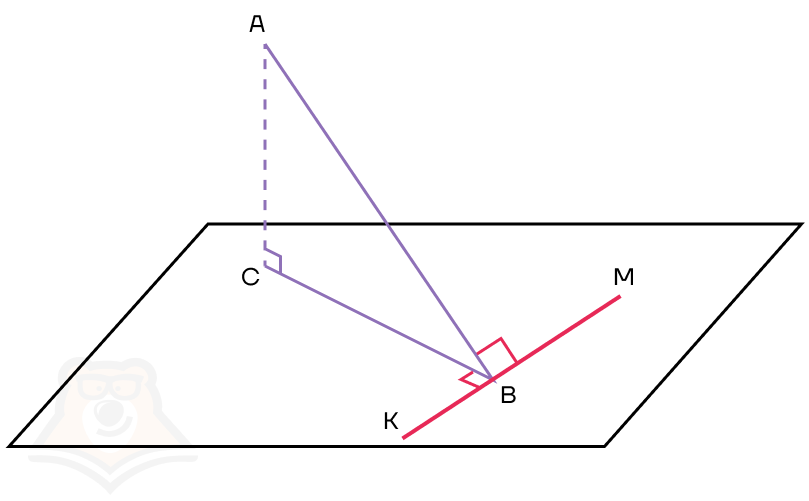
Для построения чертежа заменим линейку на несколько отрезков. Тогда АВ — наклонная, ВС — проекция, КМ — прямая в плоскости.
Для этого нужно взять лист бумаги и треугольную линейку. На листе бумаги построить произвольную прямую, а после поставить линейку строго вертикально так, чтобы основание линейки на листе было перпендикулярно начерченной прямой.
Таким образом, длинная сторона линейки будет наклонной прямой, основание — ее проекцией, а начерченная линия — перпендикуляром к проекции.
Вот и все, ничего сложного. А называется теорема так потому, что в построении действительно присутствуют три перпендикуляра, которые отлично видно на рисунке.
Теорему о трех перпендикулярах можно активно использовать для доказательства и решении задач.
Фактчек
- Двугранный угол — это часть пространства, заключенная между двумя полуплоскостями, имеющими общую границу. Градусной мерой двугранного угла будет линейный угол двугранного угла или, другими словами, угол между плоскостями.
- Угол между плоскостями — это угол между перпендикулярами, проведенными к линии пересечения плоскостей. Перпендикуляры должны лежать в данных плоскостях. За угол между плоскостями принимают острый угол, образованный этими плоскостями. Если угол между плоскостями равен 90°, то такие плоскости перпендикулярны.
- Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость. Чтобы найти угол между прямой и плоскостью, необходимо построить проекцию прямой на плоскость и найти угол между прямой и ее проекцией. Если прямая параллельна плоскости, то угол между ними будет равен 0°. Если прямая перпендикулярна плоскости, то угол между ними будет равен 90°.
- Прямая, перпендикулярная плоскости — прямая, которая перпендикулярна к каждой прямой, лежащей в этой плоскости. Чтобы доказать, что прямая перпендикулярна плоскости, достаточно доказать, что эта прямая перпендикулярна двум пересекающимся в плоскости прямым.
- Теорема о трех перпендикулярах гласит, что если наклонная прямая а к плоскости а перпендикулярна прямой b в этой плоскости, то и проекция прямой а на плоскость а перпендикулярна к прямой b.
Проверь себя
Задание 1.
Выберите верное утверждение.
- Градусной мерой двугранного угла будет линейный угол двугранного угла. При этом все линейные углы двугранного угла равны между собой;
- Градусной мерой двугранного угла будет линейный угол двугранного угла. При этом линейные углы двугранного угла не равны между собой;
- Грань двугранного угла — это общая прямая плоскостей, которые его образуют;
- Ребра двугранного угла — это плоскости, которые его образуют.
Задание 2.
Угол между плоскостями — это…
- Тупой угол между перпендикулярами, проведенными к линии пересечения плоскостей;
- Острый или прямой угол между перпендикулярами, проведенными к линии пересечения плоскостей;
- Тупой угол между двумя произвольными линиями, проведенными к линии пересечения плоскостей;
- Острый или прямой угол между двумя произвольными линиями, проведенными к линии пересечения плоскостей.
Задание 3.
Что такое проекция прямой на плоскость?
- Это любая прямая, проведенная из точки пересечения прямой и плоскости;
- Это перпендикуляр, опущенный из любой точки на плоскость;
- Это всегда точка пересечения прямой и плоскости;
- Это прямая, образованная проекциями всех точек прямой на плоскость.
Задание 4.
Какой будет проекция прямой, перпендикулярной к плоскости, на эту плоскость?
- Проекция будет равна этой прямой и параллельна ей;
- Проекция будет меньше прямой и образовывать с ней угол;
- Проекция будет точкой пересечения прямой и плоскости;
- Проекция будет больше прямой и образовывать с ней угол.
Задание 5.
Как доказать, что прямая перпендикулярна плоскости?
- Достаточно доказать, что прямая перпендикулярна одной любой прямой в плоскости;
- Достаточно доказать, что прямая перпендикулярна двум параллельным прямым в плоскости;
- Достаточно доказать, что угол между прямой и любой прямой в плоскости равен 90°;
- Достаточно доказать, что прямая перпендикулярна к двум пересекающимся прямым в этой плоскости.
Ответы: 1. — 1 2. — 2 3. — 4 4. — 3 5. — 4