-
Определение суммарной работы.
Суммарная
работа приведенного суммарного момента
сил вычисляется по формуле:
AΣ=
График работы сил
давления строится графическим
интегрированием графика суммарного
момента сил давления. Получившийся
график не касается оси абсцисс в конечной
своей точке – это результат действия
момента сил сопротивления. Отсюда
находят работу сил сопротивления и
величину момента сил сопротивления.
Опуская график работы сил давления так,
чтобы работа за цикл всех сил была равной
нулю, получают график суммарной работы.
2.5. Определение суммарного приведенного момента инерции.
Суммарный приведенный
момент инерции всего механизма равен
сумме приведенных моментов инерции
всех его звеньев. Суммарный приведенный
момент инерции второй группы звеньев
(ползунов 3,5 и шатунов 2,4) рассчитывается
по формуле:
Iпр
II=2(Iпр
3+
Iпр
2в+
Iпр
2п)
где Iпр
3 —
приведенный момент инерции цилиндра
3 и 5 при его поступательном движении;
Iпр
2п
-приведенный
момент инерции шатуна 2 и 4 при его
поступательном движении; Iпр
2в
— приведенный момент инерции шатуна 2 и
4 при его вращательном движении.
Приведенные моменты
инерции элементов при поступательном
движении рассчитываются по формулам:

V-скорость
поступательного движения звена [м/с];
-угловая скорость
кривошипа 1 [рад/с];
m -масса звеньев 3
и 2 соответственно [кг].
Приведенный момент
инерции шатуна 2 при его вращательном
движении рассчитывается по формуле:

где
1 и
2
-угловые
скорости кривошипа 1 и шатуна 2 [рад/с];
I2s
-момент
инерции шатуна 2 относительно оси,
проходящей через центр тяжести шатуна
[кгм2].
Числовые
данные для Iпр
II(φ)
; Iпр
3
(φ) ;
Iпр
2в(φ)
; Iпр
2,4п(φ)
приведены
в таблице 8:
Таблица 8.
Значения приведённых
моментов инерции.
|
град |
J3,5 |
J2,4п*40000 |
J2,4в*40000 |
J2,4*40000 |
JΣ*40000 |
|
0 |
0 |
9,4 |
5,2 |
14,5 |
29,1 |
|
30 |
2,5 |
10,8 |
4 |
14,7 |
32 |
|
60 |
10 |
14,2 |
1,4 |
15,6 |
41,2 |
|
90 |
18 |
17,1 |
0 |
17,1 |
52,2 |
|
120 |
17,7 |
16,2 |
1,4 |
17,6 |
52,9 |
|
150 |
7 |
11,9 |
4 |
15,9 |
38,8 |
|
180 |
0 |
9,4 |
5,2 |
14,6 |
29,2 |
Данные в таблице
приведены в размерности кг*м2.
Период получающихся
графиков 2π, внутри периода графики
симметричны относительно прямой φ=π.
2.6. Решение
уравнения движения модели.
Полная
кинетическая энергия представляет
собой сумму кинетической энергии второй
группы звеньев, включающей в себя ползун
и шатун, и первой группы звеньев,
включающей в себя кривошип.
T=TI+TII.
Причём графики
полной кинетической энергии и суммарной
работы будут повторять друг друга, но
отличаться на постоянную величину Тнач.
Чтобы найти значение
энергии первой группы звеньев, необходимо
вычислить
ТI=Т-ТII.
Энергия второй
группы звеньев находится в прямой
зависимости от суммарного приведённого
момента инерции, значит, что графики
этих величин совпадают, однако у них
разные единицы измерения и значения.
Соответственно, пересчитав масштаб, мы
получим график энергии второй группы
звеньев, т.е.:
µT=2µJ/ω1ср2,

мм/Дж, т.к.
ω1ср=2πn1хх,
ω1ср
=131,9 рад/с.
Далее находят
энергию первой группы звеньев. График
строят, вычитая из ординат Т ординаты
ТII.
График (приближённый)
угловой скорости 1(1**)
получают, осуществив переход от графика
ТI(1*),
т.е. определив масштаб угловой скорости
по формуле: μ ω=
μ АIпр
Iω1ср,

10,9 мм/радс-1.
Соседние файлы в папке 21 В(2)
- #
04.03.2014176.37 Кб60лист 2.3.dwg
- #
04.03.2014184.45 Кб47Лист 4.2.bak
- #
04.03.2014212.43 Кб55Лист 4.2.dwg
- #
04.03.2014184.38 Кб46лист3,2.bak
- #
04.03.2014184.38 Кб60лист3,2.dwg
- #
- #
- #
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,663 -
гуманитарные
33,654 -
юридические
17,917 -
школьный раздел
611,987 -
разное
16,906
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
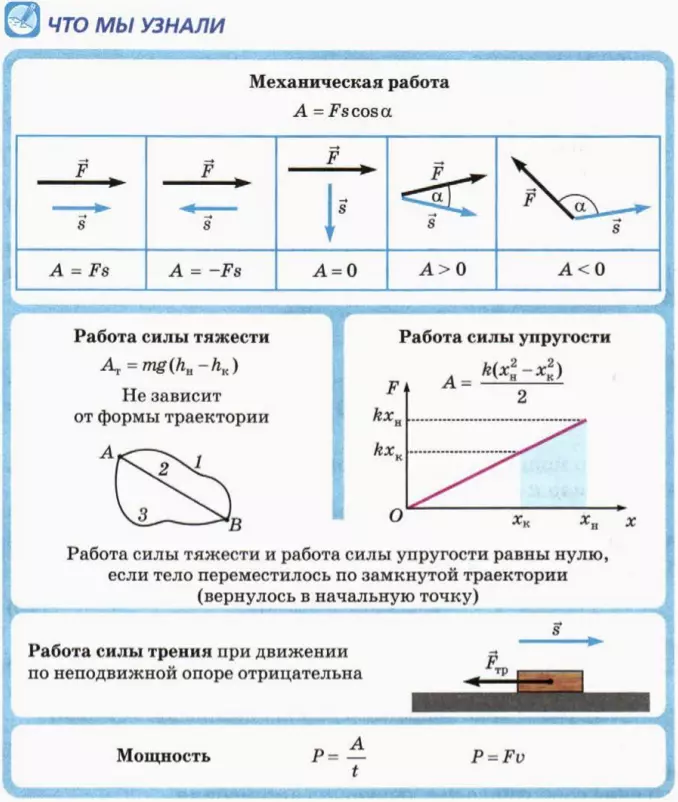
1. Определение работы
С механической работой (работой силы) вы уже знакомы из курса физики основной школы. Напомним приведенное там определение механической работы для следующих случаев.
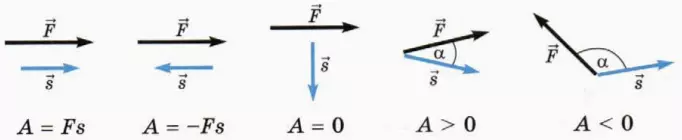
Если сила 
A = Fs (1)
В этом случае работа силы положительна.
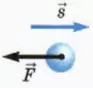
Если сила 
A = –Fs (2)
В этом случае работа силы отрицательна.
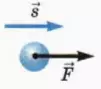
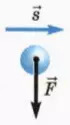
Если сила f_vec направлена перпендикулярно перемещению s_vec тела, то работа силы равна нулю:
A = 0 (3)
Работа – скалярная величина. Единицу работы называют джоуль (обозначают: Дж) в честь английского ученого Джеймса Джоуля, сыгравшего важную роль в открытии закона сохранения энергии. Из формулы (1) следует:
1 Дж = 1 Н * м.
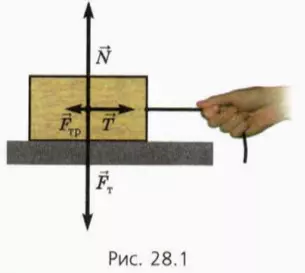
? 1. Брусок массой 0,5 кг переместили по столу на 2 м, прикладывая к нему силу упругости, равную 4 Н (рис. 28.1). Коэффициент трения между бруском и столом равен 0,2. Чему равна работа действующей на брусок:
а) силы тяжести m
б) силы нормальной реакции 
в) силы упругости 
г) силы трения скольжения 
Суммарную работу нескольких сил, действующих на тело, можно найти двумя способами:
1. Найти работу каждой силы и сложить эти работы с учетом знаков.
2. Найти равнодействующую всех приложенных к телу сил и вычислить работу равнодействующей.
Оба способа приводят к одному и тому же результату. Чтобы убедиться в этом, вернитесь к предыдущему заданию и ответьте на вопросы задания 2.
? 2. Чему равна:
а) сумма работ всех действующих на брусок сил?
б) равнодействующая всех действующих на брусок сил?
в) работа равнодействующей? В общем случае (когда сила f_vec направлена под произвольным углом к перемещению s_vec) определение работы силы таково.
Работа A постоянной силы 
A = Fs cos α (4)
? 3. Покажите, что из общего определения работы следуют к выводы, показанные на следующей схеме. Сформулируйте их словесно и запишите в тетрадь.
? 4. К находящемуся на столе бруску приложена сила, модуль которой 10 Н. Чему равен угол между этой силой и перемещением бруска, если при перемещении бруска по столу на 60 см эта сила совершила работу: а) 3 Дж; б) –3 Дж; в) –3 Дж; г) –6 Дж? Сделайте пояснительные чертежи.
2. Работа силы тяжести
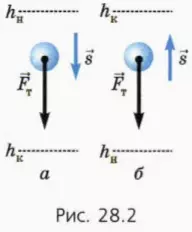
Пусть тело массой m движется вертикально от начальной высоты hн до конечной высоты hк.
Если тело движется вниз (hн > hк, рис. 28.2, а), направление перемещения совпадает с направлением силы тяжести, поэтому работа силы тяжести положительна. Если же тело движется вверх (hн < hк, рис. 28.2, б), то работа силы тяжести отрицательна.
В обоих случаях работа силы тяжести
A = mg(hн – hк). (5)
Найдем теперь работу силы тяжести при движении под углом к вертикали.
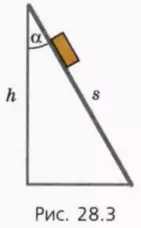
? 5. Небольшой брусок массой m соскользнул вдоль наклонной плоскости длиной s и высотой h (рис. 28.3). Наклонная плоскость составляет угол α с вертикалью.
а) Чему равен угол между направлением силы тяжести и направлением перемещения бруска? Сделайте пояснительный чертеж.
б) Выразите работу силы тяжести через m, g, s, α.
в) Выразите s через h и α.
г) Выразите работу силы тяжести через m, g, h.
д) Чему равна работа силы тяжести при движении бруска вдоль всей этой же плоскости вверх?
Выполнив это задание, вы убедились, что работа силы тяжести выражается формулой (5) и тогда, когда тело движется под углом к вертикали – как вниз, так и вверх.
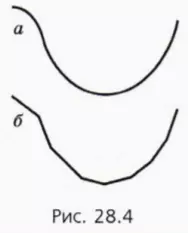
Но тогда формула (5) для работы силы тяжести справедлива при движении тела по любой траектории, потому что любую траекторию (рис. 28.4, а) можно представить как совокупность малых «наклонных плоскостей» (рис. 28.4, б).
Таким образом,
работа силы тяжести при движении но любой траектории выражается формулой
Aт = mg(hн – hк),
где hн – начальная высота тела, hк – его конечная высота.
Работа силы тяжести не зависит от формы траектории.
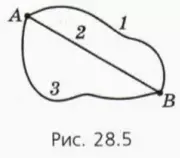
Например, работа силы тяжести при перемещении тела из точки A в точку B (рис. 28.5) по траектории 1, 2 или 3 одинакова. Отсюда, в частности, следует, что рибота силы тяжести при перемещении по замкнутой траектории (когда тело возвращается в исходную точку) равна нулю.
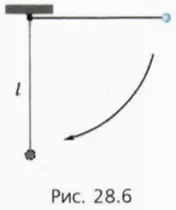
? 6. Шар массой m, висящий на нити длиной l, отклонили на 90º, держа нить натянутой, и отпустили без толчка.
а) Чему равна работа силы тяжести за время, в течение которого шар движется к положению равновесия (рис. 28.6)?
б) Чему равна работа силы упругости нити за то же время?
в) Чему равна работа равнодействующей сил, приложенных к шару, за то же время?
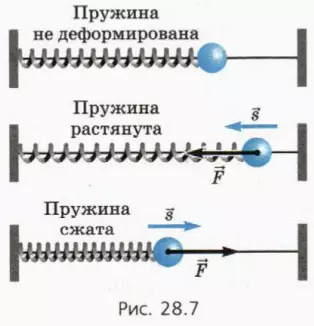
3. Работа силы упругости
Когда пружина возвращается в недеформированное состояние, сила упругости 
Найдем работу силы упругости 
Модуль этой силы связан с модулем деформации x соотношением (см. § 15)
F = kx. (6)
Работу такой силы можно найти графически.
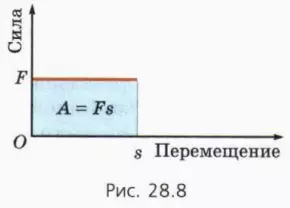
Заметим сначала, что работа постоянной силы численно равна площади прямоугольника под графиком зависимости силы от перемещения (рис. 28.8).
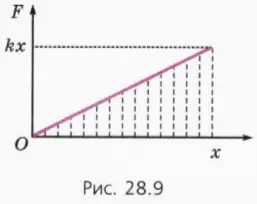
На рисунке 28.9 изображен график зависимости F(x) для силы упругости. Разобьем мысленно все перемещение тела на столь малые промежутки, чтобы на каждом из них силу можно было считать постоянной.
Тогда работа на каждом из этих промежутков численно равна площади фигуры под соответствующим участком графика. Вся же работа равна сумме работ на этих участках.
Следовательно, и в этом случае работа численно равна площади фигуры под графиком зависимости F(x).
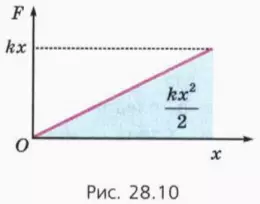
? 7. Используя рисунок 28.10, докажите, что
работа силы упругости при возвращении пружины в недеформированное состояние выражается формулой
A = (kx2)/2. (7)
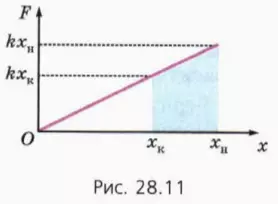
? 8. Используя график на рисунке 28.11, докажите, что при изменении деформации пружины от xн до xк работа силы упругости выражается формулой
Из формулы (8) мы видим, что работа силы упругости зависит только от начальной и конечной деформации пружины, Поэтому если тело сначала деформируют, а потом оно возвращается в начальное состояние, то работа силы упругости равна нулю. Напомним, что таким же свойством обладает и работа силы тяжести.
? 9. В начальный момент растяжение пружины жесткостью 400 Н/м равно 3 см. Пружину растянули еще на 2 см.
а) Чему равна конечная деформация пружины?
б) Чему равна работа силы упругости пружины?
? 10. В начальный момент пружина жесткостью 200 Н/м растянута на 2 см, а в конечный момент она сжата на 1 см. Чему равна работа силы упругости пружины?
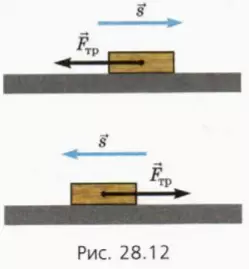
4. Работа силы трения
Пусть тело скользит по неподвижной опоре. Действующая на тело сила трения скольжения направлена всегда противоположно перемещению и, следовательно, работа силы трения скольжения отрицательно при любом направлении перемещения (рис. 28.12).
Поэтому если сдвинуть брусок вправо, а пегом на такое же расстояние влево, то, хотя он и вернется в начальное положение, суммарная работа силы трения скольжения не будет равна нулю. В этом состоит важнейшее отличие работы силы трения скольжения от работы силы тяжести и силы упругости. Напомним, что работа этих сил при перемещении тела по замкнутой траектории равна нулю.
? 11. Брусок массой 1 кг передвигали по столу так, что его траекторией оказался квадрат со стороной 50 см.
а) Вернулся ли брусок в начальную точку?
б) Чему равна суммарная работа действовавшей на брусок силы трения? Коэффициент трения между бруском и столом равен 0,3.
5. Мощность
Часто важна не только совершаемая работа, но и скорость совершения работы. Она характеризуется мощностью.
Мощностью P называют отношение совершенной работы A к промежутку времени t, за который эта работа совершена:
P = A/t. (9)
(Иногда мощность в механике обозначают буквой N, а в электродинамике – буквой P. Мы считаем более удобным одинаковое обозначение мощности.)
Единица мощности – ватт (обозначают: Вт), названная в честь английского изобретателя Джеймса Уатта. Из формулы (9) следует, что
1 Вт = 1 Дж/c.
? 12. Какую мощность развивает человек, равномерно поднимая ведро воды массой 10 кг на высоту 1 м в течение 2 с?
Часто мощность удобно выражать не через работу и время, а через силу и скорость.
Рассмотрим случай, когда сила направлена вдоль перемещения. Тогда работа силы A = Fs. Подставляя это выражение в формулу (9) для мощности, получаем:
P = (Fs)/t = F(s/t) = Fv. (10)
? 13. Автомобиль едет по горизонтальной дороге со скоростью 72 км/ч. При этом его двигатель развивает мощность 20 кВт. Чему равна сила сопротивления движению автомобиля?
Подсказка. Когда автомобиль движется по горизонтальной дороге с постоянной скоростью, сила тяги равна по модулю силе сопротивления движению автомобиля.
? 14. Сколько времени потребуется для равномерного подъема бетонного блока массой 4 т на высоту 30 м, если мощность двигателя подъемного крана 20 кВт, а КПД электродвигателя подъемного крана равен 75%?
Подсказка. КПД электродвигателя равен отношению работы по подъему груза к работе двигателя.
Дополнительные вопросы и задания
15. Мяч массой 200 г бросили с балкона высотой 10 и под углом 45º к горизонту. Достигнув в полете максимальной высоты 15 м, мяч упал на землю.
а) Чему равна работа силы тяжести при подъеме мяча?
б) Чему равна работа силы тяжести при спуске мяча?
в) Чему равна работа силы тяжести за все время полета мяча?
г) Есть ли в условии лишние данные?
16. Шар массой 0,5 кг подвешен к пружине жесткостью 250 Н/м и находится в равновесии. Шар поднимают так, чтобы пружина стала недеформированной, и отпускают без толчка.
а) На какую высоту подняли шар?
б) Чему равна работа силы тяжести за время, в течение которого шар движется к положению равновесия?
в) Чему равна работа силы упругости за время, в течение которого шар движется к положению равновесия?
г) Чему равна работа равнодействующей всех приложенных к шару сил за время, в течение которого шар движется к положению равновесия?
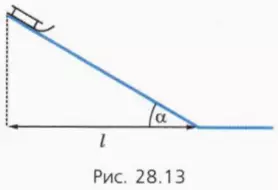
17. Санки массой 10 кг съезжают без начальной скорости со снежной горы с углом наклона α = 30º и проезжают некоторое расстояние по горизонтальной поверхности (рис. 28.13). Коэффициент трения между санками и снегом 0,1. Длина основания горы l = 15 м.
а) Чему равен модуль силы трения при движении санок по горизонтальной поверхности?
б) Чему равна работа силы трения при движении санок по горизонтальной поверхности на пути 20 м?
в) Чему равен модуль силы трения при движении санок по горе?
г) Чему равна работа силы трения при спуске санок?
д) Чему равна работа силы тяжести при спуске санок?
е) Чему равна работа равнодействующей сил, действующих на санки, при их спуске с горы?
18. Автомобиль массой 1 т движется со скоростью 50 км/ч. Двигатель развивает мощность 10 кВт. Расход бензина составляет 8 л на 100 км. Плотность бензина 750 кг/м3, а его удельная теплота сгорания 45 МДж/кг. Чему равен КПД двигателя? Есть ли в условии лишние данные?
Подсказка. КПД теплового двигателя равен отношению совершенной двигателем работы к количеству теплоты, которое выделилось при сгорании топлива.
| Работа | |
|---|---|
 |
|
| Размерность | L2MT−2 |
| Единицы измерения | |
| СИ | Дж |
| СГС | эрг |
| Примечания | |
| скалярная величина |
Механическая работа — это физическая величина — скалярная количественная мера действия силы (равнодействующей сил) на тело или сил на систему тел. Зависит от численной величины и направления силы (сил) и от перемещения тела (системы тел)[1].
Содержание
- 1 Используемые обозначения
- 2 Определение
- 2.1 Работа силы, приложенной к материальной точке
- 2.2 Работа сил, приложенных к системе материальных точек
- 3 Кинетическая энергия
- 4 Потенциальная энергия
- 5 Работа в термодинамике
- 6 Работа силы в теоретической механике
- 7 Размерность и единицы
- 8 См. также
- 9 Примечания
- 10 Литература
Используемые обозначения[править | править код]
Работа обычно обозначается буквой A (от нем. Arbeit — работа, труд) или буквой W (от англ. work — работа, труд).
Определение[править | править код]
Работа силы, приложенной к материальной точке[править | править код]
Суммарная работа по перемещению одной материальной точки, совершаемая несколькими силами, приложенными к этой точке, определяется как работа равнодействующей этих сил (их векторной суммой). Поэтому дальше будем говорить об одной силе, приложенной к материальной точке.
При прямолинейном движении материальной точки и постоянном значении приложенной к ней силы, работа (этой силы) равна произведению проекции вектора силы на направление движения и длины вектора перемещения, совершённого точкой:
Здесь точкой обозначено скалярное произведение, 

В общем случае, когда сила не постоянна, а движение не прямолинейно, работа вычисляется как криволинейный интеграл второго рода по траектории точки[2]:
(подразумевается суммирование по кривой, которая является пределом ломаной, составленной из последовательных перемещений 
Если существует зависимость силы от координат[3], интеграл определяется[4] следующим образом:
,
где 

- Следствие. Если направление приложенной силы ортогонально перемещению тела или перемещение равно нулю, то работа (этой силы) равна нулю.
Работа сил, приложенных к системе материальных точек[править | править код]
Работа сил по перемещению системы материальных точек определяется как сумма работ этих сил по перемещению каждой точки (работы, совершённые над каждой точкой системы, суммируются в работу этих сил над системой).
Даже если тело не является системой дискретных точек, его можно разбить (мысленно) на множество бесконечно малых элементов (кусочков), каждый из которых можно считать материальной точкой, и вычислить работу в соответствии с определением выше. В этом случае дискретная сумма заменяется на интеграл.
- Эти определения могут быть использованы как для вычисления работы конкретной силы или класса сил, так и для вычисления полной работы, совершаемой всеми силами, действующими на систему.
Кинетическая энергия[править | править код]
Кинетическая энергия вводится в механике в прямой связи с понятием работы.
Схема рассуждений такова: 1) попробуем записать работу, совершаемую всеми силами, действующими на материальную точку и, пользуясь вторым законом Ньютона (позволяющим выразить силу через ускорение), попытаемся выразить ответ только через кинематические величины, 2) убедившись, что это удалось, и что этот ответ зависит только от начального и конечного состояния движения, введём новую физическую величину, через которую эта работа будет просто выражаться (это и будет кинетическая энергия).
Если 
где 
Для сложных объектов, состоящих из множества частиц, кинетическая энергия тела равна сумме кинетических энергий частиц.
Потенциальная энергия[править | править код]
Сила называется потенциальной, если существует скалярная функция координат, известная как потенциальная энергия и обозначаемая 
Если все силы, действующие на частицу, консервативны, и 
 . .
|
Этот результат известен как закон сохранения механической энергии и утверждает, что полная механическая энергия в замкнутой системе, в которой действуют консервативные силы,
является постоянной во времени. Этот закон широко используется при решении задач классической механики.
Работа в термодинамике[править | править код]
В термодинамике работа, совершённая газом при расширении[6], рассчитывается как интеграл давления по объёму:

Работа, совершённая над газом, совпадает с этим выражением по абсолютной величине, но противоположна по знаку.
- Естественное обобщение этой формулы применимо не только к процессам, где давление есть однозначная функция объёма, но и к любому процессу (изображаемому любой кривой в плоскости PV), в частности, к циклическим процессам.
- В принципе, формула применима не только к газу, но и к чему угодно, способному оказывать давление (надо только чтобы давление в сосуде было всюду одинаковым, что неявно подразумевается в формуле).
Эта формула прямо связана с механической работой. Действительно, попробуем написать механическую работу при расширении сосуда, учитывая, что сила давления газа будет направлена перпендикулярно каждой элементарной площадке, равна произведению давления P на площадь dS площадки, и тогда работа, совершаемая газом для смещения h одной такой элементарной площадки будет
Видно, что это и есть произведение давления на приращение объёма вблизи данной элементарной площадкой. А просуммировав по всем dS, получим конечный результат, где будет уже полное приращение объёма, как и в главной формуле раздела.
Работа силы в теоретической механике[править | править код]
Рассмотрим несколько детальнее, чем это было сделано выше, построение определения энергии как риманова интеграла.
Пусть материальная точка 




Величина 






В соответствии с определением интеграла Римана, можем дать определение работе:
Предел, к которому стремится сумма 




Таким образом, если обозначить эту работу буквой 
,
следовательно,
(1).
Если положение точки на траектории её движения описывается с помощью какого-либо другого параметра 


Размерность и единицы[править | править код]
Единицей измерения работы в Международной системе единиц (СИ) является джоуль, в СГС — эрг
- 1 Дж = 1 кг·м²/с² = 1 Н·м
- 1 эрг = 1 г·см²/с² = 1 дин·см
- 1 эрг = 10−7 Дж
См. также[править | править код]
- Закон сохранения энергии
- Теорема о кинетической энергии системы
- Механические приложения криволинейных интегралов
Примечания[править | править код]
- ↑ Тарг С. М. Работа силы // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. — С. 193-194. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
- ↑ Это делается исходя из того, что можно разбить суммарное конечное перемещение на маленькие последовательные перемещения
, на каждом из которых сила будет почти постоянной, а значит можно будет воспользоваться определением для постоянной силы, введенным выше. Затем работы на всех этих перемещениях
суммируется, что и дает в результате интеграл.
- ↑ Как это очень часто бывает. Например, в случае кулоновского поля, растягивающейся пружины, силы тяготения планеты итд итд.
- ↑ По сути через предыдущий, поскольку здесь
; вектор же малого перемещения
совпадает с
.
- ↑ Тарг С. М. Кинетическая энергия // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2. — С. 360. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
- ↑ Работа, совершаемая газом при его сжатии, очевидно отрицательна, но вычисляется по той же формуле. Работа, совершаемая газом (или над газом) без его расширения или сжатия (например, в процессе перемешивания мешалкой), в принципе может быть выражена подобной формулой, но всё же не прямо этой, так как она требует обобщения: дело в том, что в формуле
давление подразумевается одинаковым по всему объему (что часто выполняется в термодинамике, поскольку речь там часто идет о процессах, близких к равновесным), что и приводит к наиболее простой формуле (в случае же вращающейся мешалки, например, давление будет разным на передней и задней стороне лопасти, что приведет к необходимому усложнению формулы, если мы захотим применить её к такому случаю; эти соображения относятся и ко всем другим неравновесным случаям, когда давление неодинаково в разных частях системы).
Литература[править | править код]
- История механики с древнейших времен до конца XVIII в. В 2 т. М.: Наука, 1972.
- Кирпичёв В. Л. Беседы о механике. М.-Л.: Гостехиздат, 1950.
- Льоцци М. История физики. М.: Мир, 1970.
- Мах Э. Принцип сохранения работы: История и корень его. СПб., 1909.
- Мах Э. Механика. Историко-критический очерк её развития. Ижевск: РХД, 2000.
- Тюлина И. А. История и методология механики. М.: Изд-во МГУ, 1979.
Работой силы FF, действующей на материальную точку, называют физическую величину, равную скалярному произведению вектора действующей силы на вектор перемещения точки drdr:
dA=(F⃗dr⃗)=Fdrcos(F⃗,dr⃗^)dA=(vec{F}dvec{r})=Fdrcos(widehat{vec{F},dvec{r}})
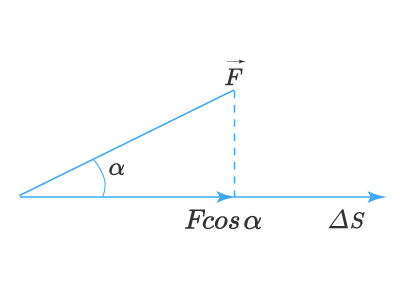
Иначе записывают dA=FcosαdsdA=Fcosalpha ds:
Выражают работу в СИ в джоулях. Джоуль – это работа силы в 1 Н на пути в 1 м условии, что направление действия силы и направление перемещения совпадают. В аналитическом виде
1 Дж = 1Н · 1м= 1 (кг·м2)/с2
Нулевая работа
Работа – скалярная величина. В зависимости от угла между направлениями действующей силы и перемещения она может быть положительной, отрицательной и равна нулю. Нулевой будет работа силы, которая перпендикулярна к направлению перемещения, в частности нулевой является работа центростремительных сил, работа силы тяжести во время движения тела в горизонтальной плоскости и др.
В основном, например, во время равномерного подъема тела, работа действующей силы сводится к преодолению силы тяжести. В случае равномерного движения тела на горизонтальной поверхности – к преодолению силы трения, в производственной сфере – к преодолению сопротивления почвы, сопротивления различных материалов при обработке и тому подобное. Поэтому под работой на практике понимают процесс преодоления сопротивления при перемещениях тел.
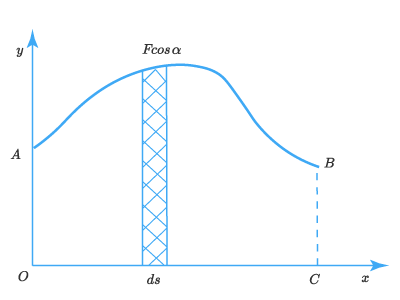
Работа переменной силы
Выше мы рассмотрели способ вычисления работы постоянной силы при прямолинейном перемещении тела. Работу переменной силы или произведение переменной проекции силы на направление перемещения, также определяют по формуле:
dA=(F⃗dr⃗)=Fdrcos(F⃗,dr⃗^)dA=(vec{F}dvec{r})=Fdrcos(widehat{vec{F},dvec{r}}),
которую можно применить только для бесконечно малого перемещения drdr.
Работу на всем пути найдем как сумму работ на всех элементарных перемещениях, на которые разделены путь. Эта операция сводится к вычислению интеграла:
A=∫SFcosαdsA=intlimits_{S}{Fcosalpha ds}
Наряду с аналитическим широко используют графический способ определения работы. Отложив по оси ОуОу проекцию действующей силы FcosаF cos а, а по оси ОхОх – пройденный телом путь ss, получим графическую зависимость между ними в виде кривой АВАВ:
Отсюда следует, что работа при элементарном перемещении
dA=FcosαdsdA=Fcos alpha ds:
равна площади заштрихованной полоски, а работа на всем пути – площади фигуры ОАВС. Например, если вычислить площадь фигуры с помощью индикатора.
Прибор, фиксирующий изменения любого параметра или объекта в форме, удобной для непосредственного восприятия человеком, то можно определить работу газа в цилиндре тепловой машины.
Работа силы тяжести
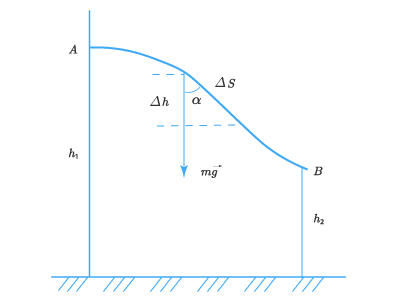
Рассмотрим важный пример работы силы тяжести при движении тела по некоторой кривой АВ:
Поделим весь путь на такие малые части, чтобы их можно было считать прямолинейными. Работа на одной из них:
ΔA=FΔscosα=mgΔscosα=mgΔhDelta A=FDelta scos alpha =mgDelta scos alpha =mgDelta h
Работу на всем пути найдем как сумму работ на отдельных его частях:
A=∑mgΔh=mg∑Δh=mg∑(h1−h2)A=sum{mgDelta h}=mgsum{Delta h}=mgsum{({{h}_{1}}-{{h}_{2}}})
Как видим, работа силы тяжести (или работа против силы тяжести) для тела, которое перемещается в поле тяготения, не зависит от формы траектории, а зависит только от разности высот его начальной и конечной точек приложения.
Если бы тело в поле притяжения описывало замкнутую траекторию, то суммарная работа силы тяжести равнялась бы нулю: положительная работа тела, возникающая в случае, когда оно опускается, компенсируется отрицательной работой тела, когда оно поднимается.
Силы, работа которых не зависит от траектории движения тела, а зависит только от начального и конечного его положений, называются потенциальными.
Таковы, например, силы всемирного тяготения, силы упругости, электростатические силы. Поля, в которых проявляется действие таких сил, называются потенциальными.
Система тел называется консервативной, если в ней внутренние силы взаимодействия потенциальные, а внешние силы, действующие на эти тела, –стационарные и потенциальные.

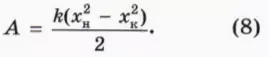











![W=int limits _{a}^{b}F[s(t)]s'(t)dt.](https://web.archive.org/web/20200114125534im_/https://wikimedia.org/api/rest_v1/media/math/render/svg/04cd7a765bbbbab38a11e8c286f1f1b24e069925)