{V= a cdot b cdot c}
Найти объем параллелепипеда довольно просто. Для этого необходимо знать длины трех его сторон или же две стороны (площадь основания) и высоту. Чтобы облегчить расчет объема параллелепипеда мы создали калькулятор для разных исходных данных. Просто введите известные значения и в режиме онлайн получите результат.
Параллелепипед — многогранник, состоящий из шести граней, причем все они являются параллелограммами.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани прямоугольники.
Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям.
Содержание:
- калькулятор объема параллелепипеда
- формула объема прямоугольного параллелепипеда через три стороны
- формула объема прямоугольного параллелепипеда через площадь основания и высоту
- формула объема наклонного параллелепипеда через длины сторон основания и высоту
- формула объема наклонного параллелепипеда через площадь основания и высоту
- примеры задач
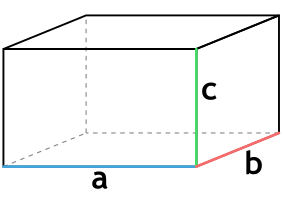
Формула объема прямоугольного параллелепипеда через три стороны
{V= a cdot b cdot c}
a — длина параллелепипеда
b — ширина параллелепипеда
c — высота параллелепипеда
Так как в основании параллелепипеда лежит прямоугольник, то в данной формуле ab — это площадь прямоугольника, который лежит в основании параллелепипеда. И тогда формулу можно сократить до {V= S h}
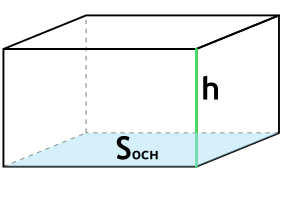
Формула объема прямоугольного параллелепипеда через площадь основания и высоту
{V= S_{осн} cdot h}
Sосн — площадь основания параллелепипеда
h — высота параллелепипеда
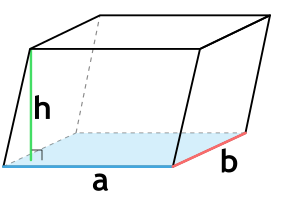
Формула объема наклонного параллелепипеда через длины сторон основания и высоту
{V= a cdot b cdot h}
a — длина основания параллелепипеда
b — ширина основания параллелепипеда
h — высота параллелепипеда
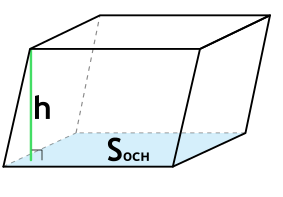
Формула объема наклонного параллелепипеда через площадь основания и высоту
{V= S_{осн} cdot h}
Sосн — площадь основания параллелепипеда
h — высота параллелепипеда
Примеры задач на нахождение объема параллелепипеда
Задача 1
Найдите объём прямоугольного параллелепипеда с измерениями 3см, 4см и 5см.
Решение
Для решения данной задачи нам подходит формула один. Подставим в нее значения длины, ширины и высоты прямоугольного параллелепипеда, произведем расчет и получим ответ.
V= a cdot b cdot c = 3 cdot 4 cdot 5 = 60 : см^3
Ответ: 60 см³
Проверим правильность ответа с помощью калькулятора .
Задача 2
Найдите объём наклонного параллелепипеда с площадью основания 12м² и высотой 3м.
Решение
Используем для решения четвертую формулу. Подставим в нее площадь основания и высоту.
V= S_{осн} cdot h = 12 cdot 3 = 36 : м^3
Ответ: 36 м³
Полученный ответ поможет проверить калькулятор .
|
Таблицы и формулы 2
|
В данной публикации мы рассмотрим, как можно найти объем параллелепипеда и разберем примеры решения задач для закрепления материала.
-
Формула вычисления объема параллелепипеда
- 1. Общая формула
- 2. Объем прямоугольного параллелепипеда
- Примеры задач
Формула вычисления объема параллелепипеда
1. Общая формула
Объем любого параллелепипеда равняется произведению площади его основания на высоту.
V = Sосн ⋅ h
- Sосн – площадь основания (ABCD или EFHG, равны между собой);
- h – высота.
Данная формула справедлива для всех видов геометрической фигуры:
- наклонной – боковые грани не перпендикулярны основаниям;
- прямой – все боковые грани (4 шт.) являются прямоугольниками;
- прямоугольной – все грани (боковые и основания) являются прямоугольниками;
- ромбоэдра – все грани являются равными ромбами;
- куба – все грани представляют собой равные квадраты.
2. Объем прямоугольного параллелепипеда
Объем фигуры равен произведению его длины на ширину на высоту.
V = a ⋅ b ⋅ c
Формула следует из следующих утверждений:
- Основанием фигуры является прямоугольник, площадь которого считается как произведение его длины (a) на ширину (b).
- Высота фигуры – это длина боковой грани (c).
Примеры задач
Задание 1
Найдите объем параллелепипеда, если известно, что площадь его основания равняется 20 см2, а высота – 7 см.
Решение:
Используем первую формулу, подставив в нее известные нам значения:
V = 20 см2 ⋅ 7 см = 140 см3.
Задание 2
Дан прямоугольный параллелепипед. Длина и ширина его основания равны 9 см и 5 см, соответственно, а высота составляет 6 см. Найдите объем фигуры.
Решение:
Воспользуемся формулой для данного типа фигуры:
V = 9 см ⋅ 5 см ⋅ 6 см = 270 см3.
Параллелепипед — это призма, основанием которой является параллелограмм.
Онлайн-калькулятор объема параллелепипеда
Как и у куба, у этого многогранного тела есть двенадцать ребер, шесть граней и восемь вершин. Вид параллелепипеда зависит от геометрической фигуры, лежащей в основании, и от угла, образованного им при пересечении с гранями.
Если его гранями являются прямоугольники, то он называется прямоугольным.
Если такие прямоугольники имеют отношение только к боковым граням, то он называется прямым.
Иногда бывают случаи, когда эти грани образуют не прямой угол с основанием. Тогда в данном случае параллелепипед является наклонным.
Если он состоит исключительно из равных ромбов, то он называется ромбоэдром.
Если все грани параллелепипеда являются одинаковыми квадратами, то получаем куб. Таким образом, куб — это частный случай параллелепипеда.
Формула объема прямоугольного параллелепипеда
Объемом такого параллелепипеда называется произведение всех его трех измерений: длины, ширины, высоты. Вычисляется он так:
V=a⋅b⋅cV=acdot bcdot c
a,b,ca, b, c — длина, ширина и высота прямоугольного параллелепипеда.
Рассмотрим несколько примеров.
Найти объем прямоугольного параллелепипеда, если известны его длина, равная 5 см.5text{ см.}, ширина, имеющая длину 10 см.10text{ см.} и высота длиной в 7 см.7text{ см.}
Решение
a=5a=5
b=10b=10
c=7c=7
Сразу подставляем в формулу численные значения:
V=a⋅b⋅c=5⋅10⋅7=350 см3V=acdot bcdot c=5cdot 10cdot 7=350text{ см}^3
Ответ
350 см3.350text{ см}^3.
Формула объема наклонного параллелепипеда
V=Sосн⋅hV=S_{text{осн}}cdot h
SоснS_{text{осн}} — площадь основания наклонного параллелепипеда;
hh — его высота.
Вычислить объем наклонного параллелепипеда, если в его основании лежит прямоугольник со сторонами в 4 см.4text{ см.} и 5 см.5text{ см.}, а высота его равна 10 см.10text{ см.}
Решение
a=4a=4
b=5b=5
h=10h=10
Находим площадь основания, то есть площадь прямоугольника:
Sосн=a⋅b=4⋅5=20S_{text{осн}}=acdot b=4cdot 5=20
Сам объем равен:
V=Sосн⋅h=20⋅10=200 см3V=S_{text{осн}}cdot h=20cdot 10=200text{ см}^3
Ответ
200 см3.200text{ см}^3.
Формула объема параллелепипеда через определитель
Альтернативным способом нахождения объема параллелепипеда является вычисление смешанного произведения векторов, на которых построен данный параллелепипед.
Пусть параллелепипед построен на векторах a⃗vec{a}, b⃗vec{b} и c⃗vec{c} с координатами:
a⃗=(ax,ay,az)vec{a}=(a_x, a_y, a_z)
b⃗=(bx,by,bz)vec{b}=(b_x, b_y, b_z)
c⃗=(cx,cy,cz)vec{c}=(c_x, c_y, c_z),
тогда объем соответствующего параллелепипеда это определитель, составленный из этих координат:
V=∣axayazbxbybzcxcycz∣V=begin{vmatrix}
a_x & a_y & a_z \
b_x & b_y & b_z \
c_x & c_y & c_z \
end{vmatrix}
Найти объем параллелепипеда через смешанное произведение векторов, координаты которых таковы: a⃗=(2,3,5)vec{a}=(2, 3, 5), b⃗=(1,4,4)vec{b}=(1, 4, 4), c⃗=(3,5,7)vec{c}=(3, 5, 7).
Решение
a⃗=(2,3,5)vec{a}=(2, 3, 5)
b⃗=(1,4,4)vec{b}=(1, 4, 4)
c⃗=(3,5,7)vec{c}=(3, 5, 7)
По формуле:
V=∣235144357∣=2⋅4⋅7+3⋅4⋅3+5⋅1⋅5−5⋅4⋅3−2⋅4⋅5−3⋅1⋅7=56+36+25−60−40−21=−4V=begin{vmatrix}
2 & 3 & 5 \
1 & 4 & 4 \
3 & 5 & 7 \
end{vmatrix}=2cdot4cdot7 + 3cdot4cdot3 + 5cdot1cdot5 — 5cdot4cdot3 — 2cdot4cdot5 — 3cdot1cdot7 = 56 + 36 + 25 — 60 — 40 — 21 = -4
Мы должны взять модуль этого числа, так как объем это неотрицательная величина:
V=4 см3V=4text{ см}^3
Ответ
4 см3.4text{ см}^3.
У вас не получается решить задачу по геометрии? Наши эксперты помогут вам!
Тест по теме «Объем параллелепипеда»
Как найти объем параллелепипеда
На данной странице калькулятор поможет рассчитать объем параллелепипеда онлайн. Для расчета задайте высоту, ширину и длину. Вычисления производятся в миллиметрах, сантиметрах, метрах. Результат выводится в кубических сантиметрах, литрах и кубических метров.
Прямоугольный параллелепипед – это многогранник, у которого все грани являются прямоугольниками.
Через стороны
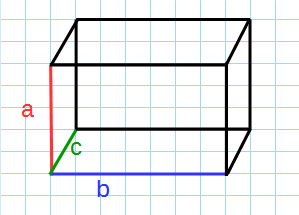
Формула объема параллелепипеда через его ребра:
a,b,c — ребра параллелепипеда.
Через стороны и высоту
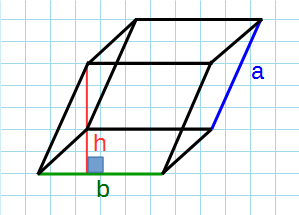
Формула объема параллелепипеда:
a,b — ребра параллелепипеда; h — высота параллелепипеда.