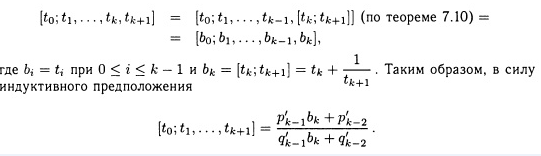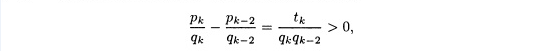Таблица подходящих дробей как составить

Вполне
очевидно, что [t₀,t₁,t₂,
…,
t_k],
для каждого к
представляет собой действительное
число. Запишем первые четыре подходящие
дроби и упростим их, выразив каждую как
отношение двух действительных чисел,
где как числитель, так и знаменатель
выражены через t_i.
Особый
интерес будут представлять чис­литель
и знаменатель каждой из подходящих
дробей.

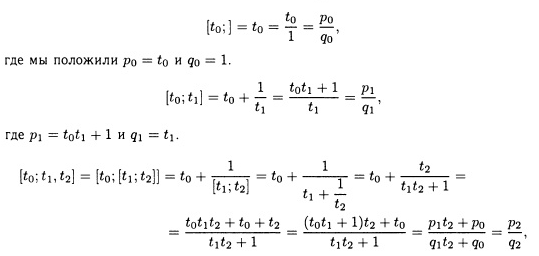
где
р₂
= p₁t₁
+
p₀
и q₂
= q₁t₂
+
q₀
Подобным образом вычисляем

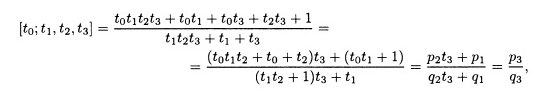
где
р₃
= p₂t₃
+
p₁
и q₃
= q₂t₃
+
q₁

в каждом случае число [t₀,t₁,t₂,…,t_k]
“переформировывается» из представления
цепной дробью без какого-либо «сокра­щения»
и образует отношение двух полиномов Р
и Q
в
переменных t₀,t₁,t₂,
…,
t_k
,
т.е.

Справедливым
является и то, что q₀,q₁,q₂
и q₃
положительны, поскольку получе­ны
путем умножения и сложения положительных
чисел. Рассмотренные примеры дают
основание сформулировать следующую
теорему.

ТЕОРЕМА
7.11. Пусть
n
— неотрицательное целое число и
t₀,t₁,t₂,…,t_n]
—
конечная
цепная дробь, которая рекурсивно
определяет конечные последователь­ности
p₀
,p₁
…
p_n
и q₀
,q₁
…
q_n
следующим образом:

ДОКАЗАТЕЛЬСТВО.
Не
представляет труда методом математической
индукции показать, что q_k
> 0 при 0 ≤ k
≤
n.
Эту часть теоремы предоставляем доказать
читателю. Выше было показано, что теорема
справедлива при к
= 0,1 и 2, т.е. [t₀]
= p₀
/q₀
[t₀,t₁]
= p₁
/q₁,
[t₀,t₁,t₂]
= p₂
/q₂

Предположим, что 2 ≤ k
< n,
и
для любой цепной дроби [b₀,b₁,b₂,
…,
b_k]
и любого j
0
≤ j
≤
k
справедливо утверждение о том, что
[b₀,b₁,b₂,
…,
b_j]
=
р_j‘/q_j‘.
где р_j‘
и q_j‘
определены способом, аналогичным
(а)-(с), но для цепной дроби [b₀,b₁,b₂,
…,
b_m]
Тогда

Поскольку
b_i
=
t_i
при
0
≤
i
≤
к
— 1, имеем, что для таких i
p_i
=
р_i‘
и q_i
= q’_i.
Подставляя
соответствующие выражения для b_k,
р_i‘
и q_i’,
получаем

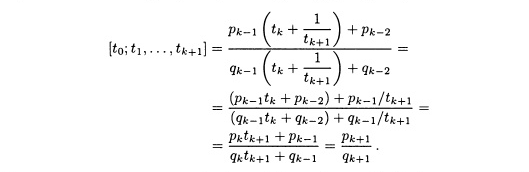
Следовательно,
по индукции, [t₀,t₁,t₂,…,t_k]=
p_k/q_k
при 0 ≤ k
≤ n.

Числа
p_k
и q_k
(теорема
7.11) определены вне зависимости от того,
что они могут быть использованы как
числитель и знаменатель выражения,
равного k-ой
подходящей дроби. Рекурсивное отношение,
заданное теоремой 7.11, обеспечива­ет
быстрый способ вычисления подходящих
дробей для заданной цепной дроби,
поскольку числитель р, и знаменатель
p_i
можно
вычислить одновременно и до­статочно
просто. Например, для х
= [-4; 2,5,2,1] =[t₀,t₁,t₂,t₃,t₄]
подходящие дроби можно вычислить
согласно приведенной ниже таблице:

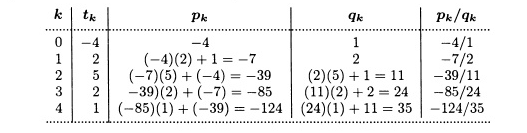
Так
что х
=
-124/35, т.е. числу, породившему цепную дробь
[—4; 2,5,2,1] (см. раздел 5.1).

Благодаря
рекурсивному способу задания цепных
дробей, имеется значи­тельное количество
соотношений, связывающих подходящие
дроби через числи­тели и знаменатели,
р_k
и q_k,
введенные
теоремой 7.11. Чтобы запись этих соотно­шений
сделать справедливой при k
= 0, зачастую удобно определять р_k
и q_k
при k
= -1, положив

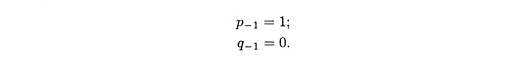
Таким
образом, р₁
= p₀t₁
+p_-1
=
t₀t₁
+ 1 и q₁
=
q_ot₁
+
q_-1
=
1• t₁
+0 = t₁,
как
в теореме 7.11.

ТЕОРЕМА
7.12. Если
t₀,t₁,t₂,…,t_n]
—
конечная цепная дробь, где t_i
— действи­тельные числа, p_k
и
q_k—
заданы теоремой 7.11, тогда

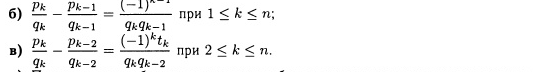
г) Подходящие
дроби четного порядка образуют
возрастающую последователь­ность,
т.е.

а
подходящие дроби нечетного порядка
образуют убывающую последова­тельность,
т.е.

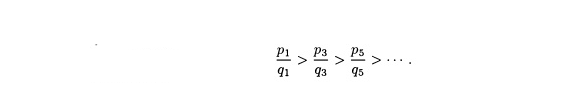
при
0 ≤
j
≤
[n/2]
и 0 ≤ i
≤
[(n
—
1)/2],
где
слева равенство имеет место, когда n

четное, а справа равенство имеет место,
когда п
нечетное.

д) Если
дробь [t₀;t₁,…,t_n]

— простая, то q_k
≥
k
при
0 ≤ k
≤ n.

е) Если
дробь [t₀;t₁,…,t_n]
—
простая, то q_k
<
q_k+1
при
1 ≤ k
≤ n-1
и q₀
≤
q₁

ДОКАЗАТЕЛЬСТВО,
а)
При k
=
1 p₁q₀
– p₀q₁
=
(t₁t₀
+ 1)(1) — t₀t₁
=
1 = (-1)^1-1
по теореме 7.11. Пусть 2 ≤ m
< n
и допустим, что формула в части (а)
справедлива при k
= m.
Показано,
что формула имеет место при k
=
т
+
1. Опять, используя теорему 7.11, имеем

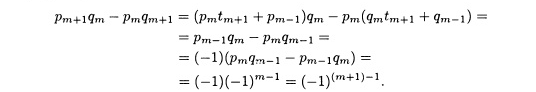
Таким
образом, формула в части (а) имеет место
при 1 ≤ k
≤ п.
Также
p₀q_-1
– q_op_-1
=t₀•0-
1•1
= -1 и формула справедлива при k
=
0.

б) Утверждение
теоремы следует из части (а), если в
соответствующем равенстве при k
≥
1 произвести деление на q_kq_k-1
.

в) Если
k
≥
2, то по теореме 7.11

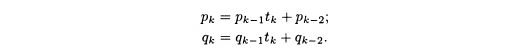
Умножение
первого из равенств на q_k-2,
а второго — на p_k-2
дает

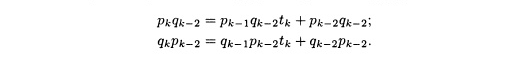
Вычитая
второе равенство из первого, получаем

Теперь,
учитывая утверждение в части (а), получаем

Разделив
на q_kq_k-2
>
0, получаем желаемый результат:

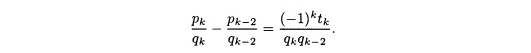
г) Если
2
≤ k
≤ n
и k—
четное, то k
— 2 тоже четное и k
—
2 ≥ 0. Поэтому (-1)^k
=
1 и из утверждения в части (в) вытекает,
что

поскольку
t_k
и
q_kq_k-2
положительные
при к
≥
1. Если 3≤
k<n
н k
—
нечетное, то k
—
2 также нечетное и k
— 2 ≥ 1. В этом случае (-l)^k
=
-1, так что из утверждения в части (в)
вытекает, что

так
как t_к
и q_kq_k-2положительны
при к
≥ 3.

Если
n
нечетное, то согласно (б)

так что [t₀,t₁,t₂,
…,
t_n]
=

P_n/q_n
больше, чем наибольшая подходящая дробь
четного порядка, P_n-1/q_n-1
Если п
четное, то

так что [t₀,t₁,t₂,
…,
t_n]
= P_n/q_n
меньше, чем P_n-1/q_n-1
наименьшая подходящая дробь нечетного
порядка, P_n-1/q_n-1

Доказательство
пунктов (д) и (е) оставляем за читателем.

Подходящие
дроби для х
= [-4; 2,5,2,1] вычислены ранее в данном разделе
и приведены в таблице. Подводя итог этим
результатам в контексте части (г),
находим, что

Непосредственным
вычислением определяем также, что

Значение
теоремы 7.12 состоит в том, что она точно
устанавливает, что последовательные и
взаимно исключающие подходящие дроби
могут отличать­ся не более, чем на
величину, обратно пропорциональную
“знаменателям» под­ходящих дробей,
а также, что подходящие дроби альтернативно
больше, чем [t₀,t₁,t₂,
…,
t_n].
И меньше, чем [t₀,t₁,t₂,
…,
t_n]

Практический
интерес представляют некоторые отношения
P_n/q_n
числите­лей и знаменателей подходящих
дробей. Эти отношения приведены в
следующей теореме, доказательство
которой предоставляется читателю.

ТЕОРЕМА
7.13. Для
конечной цепной дроби t₀,t₁,t₂,
…,
t_n]

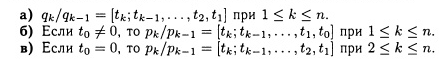
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Числа не управляют миром, но показывают, как управляется мир.

И. -В. Гете

Математика выявляет порядок, симметрию и определенность, а это – важнейшие виды прекрасного.

Аристотель

Математические знания в далеком прошлом применялись для решения повседневных задач, и именно практика в значительной степени руководила всем дальнейшим развитием математики. Так и цепные дроби получили свое развитие благодаря тому, что Х. Гюйгенс (1629 – 1695) при построении планетария в Париже хотел получить наилучшие приближения для отношений периодов обращения планет.

Действительные числа однозначно отображаются цепными дробями. Основное значение такого изображения заключается в том, что, зная цепную дробь, изображающую действительное число, можно определить это число с достаточной точностью.

Преимущество цепных дробей по сравнению с десятичными в том, что цепные дроби не связаны ни с какой системой счисления и в чистом виде воспроизводят свойства изображаемых ими чисел. Так, рациональность и иррациональность изображаемого числа находит выражение в конечности или бесконечности соответствующей ему цепной дроби. Кроме того, периодичность бесконечной цепной дроби указывает на то, что иррациональность – квадратичная.

Требование же практического характера, а именно находить приближенное значение изображаемого числа, цепные дроби удовлетворяют в высшей степени, намного лучше, чем десятичные дроби.

Недостатком цепных дробей является то, что для них никаких практически приемлемых правил арифметических действий не существует. Поэтому широкого применения они не получили.

Впервые увидев цепные дроби, хочется сказать: «Это красиво!» Затем встает вопрос: «Как это составляется и что означает?» И, наконец: «Для чего это нужно?»

«Красиво!», «Что это?», «Для чего это?». Ответы на эти вопросы и является целью данной работы. Итак, наша цель: исследовать такой математический объект как «Цепные дроби», показать, что цепные дроби имеют теоретическое и практическое значение. Цепные дроби в математике как бы в «тени». Но они достойны того, чтобы их изучать и применять на практике.

Для достижения цели ставятся следующие задачи:

1) Обработка теоретического материала (его отбор, а также последовательное и доступное изложение).

2) Поиск областей применения цепных дробей.

3) Составление практического материала в форме упражнений.

Понятие цепной дроби. Разложение действительных чисел в цепную дробь

Дробь можно записать в виде суммы целой части и правильной дроби:. Но , а дальше:. Значит,. Далее получим.

Продолжим этот процесс до тех пор, пока не придем к знаменателю. В результате мы представим обыкновенную дробь в виде:

Эйлер назвал дроби такого вида непрерывными. Приблизительно в то же время в Германии появился другой термин – цепная дробь. Так за этими дробями и сохранились оба названия. Ввиду громоздкости развернутой записи цепной дроби применяют компактную запись.

В качестве примера представим дробь в виде цепной дроби:.

Или в компактной форме: [1; 3, 2, 4 ].

Удобно получить разложение обыкновенной дроби с помощью алгоритма Евклида.

Мы познакомились с разложением в цепную дробь обыкновенной дроби, т. е. рационального числа. Любое рациональное число представимо в виде конечной цепной дроби. Конечность следует из алгоритма Евклида. Но в виде цепной дроби можно записать любое действительное число. Только конечными цепными дробями здесь не обойтись. Приведем разложение в непрерывную дробь числа.

и т. д. Видна закономерность.

Таким образом,

Т. е. в компактной форме = [1: 2, 2, 2, 2, 2].

Оказывается, квадратичные иррациональности (т. е. числа вида , где a, b, c — рациональные числа), и только они раскладываются в бесконечные периодические дроби. На этот факт впервые указал Эйлер, строгое его доказательство дал Лагранж.

Из утверждения Эйлера – Лагранжа вытекает, что иррациональные числа, не представимые в виде квадратичной иррациональности, изображаются бесконечными непериодическими цепными дробями. Интересное разложение нашел первый президент Лондонского Королевского общества лорд

У. Броункер (1620 – 1684):

Замечательные представления в виде непрерывных дробей имеют числа e и ln2:

Приведенные разложения поражают своей закономерностью и в какой-то мере объясняют исключительность этих чисел. Можно было бы дать их компактную запись. Для этого нужно представить полученные дроби в виде цепных с единицами в числителе, но тогда потеряется удивительная красота формул.

Подходящие дроби. Первое свойство цепных дробей

Если оборвать дробь на знаменателе , то останется дробь. Обращая ее в обыкновенную, получим. Это выражение называют k-й подходящей дробью для исходной цепной дроби.

Например, для нашей дроби имеем: нулевая подходящая дробь: , первая подходящая дробь: , вторая подходящая дробь: , третья подходящая дробь:. Она равна самому числу.

Для цепной дроби, представляющей число, имеем следующие подходящие дроби: нулевая подходящая дробь: , первая подходящая дробь: , вторая подходящая дробь: , третья подходящая дробь: и т. д.

Подходящие дроби удобно вычислять с помощью специальной таблицы. Для этого посмотрим, как вычисляются подходящие дроби:

и т. д. Вообще имеют место рекуррентные соотношения

Рk+1 = qk+1. Pk+Pk-1 и Qk+1= qk+1. Qk+Qk-1.

Эти вычисления удобно производить последующей схеме: q — q0 qk qk+1 P 1 P0 P1 P2 Pk-1 Pk Pk+1 Q 0 Q0 Q1 Q2 Qk-1 Qk Qk+1

В первой строке этой таблицы записаны недробные элементы, с которых мы начинали строить каждый «этаж», нашей многоэтажной дроби.

Во второй строке сначала записано число 1. Это ключевое число, и надо просто запомнить, что вторая строка начинается с числа 1. Далее записаны числители подходящих дробей.

В третьей строке сначала записано число 0. Это ключевое число, и надо просто запомнить, что третья строка всегда начинается с числа 0. Далее записаны знаменатели подходящих дробей.

Оказывается, что, зная лишь нулевую подходящую дробь, следуя нашим рекуррентным соотношениям, можно найти сколь угодно много числителей и знаменателей в подходящих дробях.

Для получения очередного числителя (знаменателя) необходимо взять элемент того же столбца из первой строки умножить на предыдущий числитель (знаменатель) и прибавить к произведению «предпредыдущий» числитель (знаменатель).

Составим таблицу подходящих дробей для цепной дроби, изображающей число.

— 1 2 2 2 2 2 2 1 1 3 7 17 41 99 239 0 1 2 5 12 29 70 169

При этом, если учесть, что , , , =1,41666, то можно увидеть, что чем дальше мы идем, тем лучшее приближение числа получаем.

Цепные дроби обладают следующим важным свойством: если действительное число x записать в виде непрерывной дроби, то подходящая дробь дает наилучшее приближение числа x среди всех дробей, знаменатели которых не превосходят. Т. е. чем больше k, тем k – подходящая дробь ближе к числу.

В связи с этим замечательным свойством рассмотрим применение цепных дробей в календаре, а также в «золотом сечении».

Календарь и подходящие дроби

Что такое год? Это время, за которое Земля совершает по своей орбите полный оборот вокруг Солнца. Астрономы подсчитали, что год составляет 365 суток 5 ч 48 мин 46 с или 365,242199 суток. Но пользоваться таким сложным числом очень неудобно. Хотелось бы, чтобы в году было целое число суток. Предположим, что продолжительность года равна 365 дням. Но тогда окончание каждого года приходилось бы всякий раз на новую точку на орбите, отстоящую от предыдущей на величину, которую Земля проходит примерно за 6ч.

Какой же из этого выход? Древнеримские жрецы, ведавшие исчислением времени, произвольно удлиняли некоторые года, чтобы согласовать календарные даты с сезонными явлениями природы. Впервые порядок в счете времени навел в I в. до нашей эры римский император Юлий Цезарь. Он постановил считать одни годы по 365 суток, а другие по 366 суток, чередуя их по правилу три года подряд коротких, четвертый – длинный. Гораздо позже, с введением христианского летоисчисления, високосным стали считать каждый год, порядковый номер которого делится на 4. Этот календарь в честь Юлия Цезаря называется юлианским. По нему продолжительность суток составляет 365 суток 6 ч, что больше истинной лишь на 11 мин 14 с. Однако и это решение оказалось неудовлетворительным. К XVI в. ошибка, накапливаясь, составила уже около 10 суток.

Следующую реформу календаря провел Григорий XIII – папа римский. Было решено: сдвинуть числа на 10 дней, оставить чередование простых и високосных лет, при этом, если порядковый номер года оканчивается двумя нулями, но число сотен не делится на 4, то этот год простой. В настоящее время расхождение между юлианским и новым, григорианским календарями составляет 13 дней, поскольку с тех пор накопилось еще три дня (в 1700, 1800 и 1900 гг. ). Продолжительность григорианского года составляет

365, 2425 суток, т. е. 365 суток 5 ч 49 мин 12 с, т. е. она больше истинной лишь на 26с. Полученная точность очень велика и вполне достаточна для практических нужд.

Интересная система календаря была предложена среднеазиатским математиком и поэтом Омаром Хайямом (ок. 1048-1122), по ней високосными годами должны были считаться 8 лет из каждых 33. Продолжительность года по О. Хайяму составляет 365 суток, его погрешность всего 19с в год.

В 1864 г. русский астроном И. Медлер предложил с XX столетия ввести в России следующую поправку к юлианскому календарю: через каждые 128 лет пропускать один високосный год из 32, которые выпадают на этот период. Этот календарь самый точный из всех перечисленных. Здесь погрешность сокращается всего до 1с. Однако календарь И. Медлера не был принят, видимо, из-за того, что период в 128 лет не является «круглым» числом.

Системы календаря оказываются связанными с записью астрономического года в виде цепной дроби:

Год продолжительностью 365 суток — это нулевая подходящая дробь этой цепной дроби, 365 — юлианский год – первая подходящая дробь, 365, 365 и 365 — вторая, третья и четвертая подходящие дроби. А именно:

Системой, соответствующей второй подходящей дроби: семь високосных лет из 29, никто не предложил воспользоваться, видимо, потому, что третья подходящая дробь не намного сложнее, а точность ее гораздо больше (вспомним, что это система О. Хайяма), а четвертой подходящей дроби соответствует система И. Медлера.

«Золотое сечение» и подходящие дроби

Термин «золотое сечение» впервые применил Леонардо да Винчи (1452-1519).

Суть задачи заключается в следующем:

Дан отрезок AB (для удобства рассуждений будем считать, что его длина равна единице). Найти на нем такую точку X, чтобы AX/ BX=BX/AB.

Говоря другими словами, необходимо разделить отрезок на две части так, чтобы меньшая часть относилась к большей, как большая часть ко всему отрезку.

Обозначим BX=x, тогда AX=1-x (так как AB приняли за 1) и по условию задачи

(1 — x): x = x:1.

Решая уравнение, получаем:.

Из двух значений корня возьмем , так как другое значение отрицательно.

Итак, x=.

Знаменитый александрийский математик Клавдий Птолемей (ок. 90 – ок. 160) предложил такое геометрическое решение этой задачи.

Пусть надо построить «золотое сечение» отрезка АВ. Посмотрим на рисунок.

A X B D C

С центром в точке В радиусом АВ проводим полуокружность АЕС. Разделим радиус ВС пополам, получим точку D. Проведем дугу окружности с центром в точке D радиусом DE до пересечения с АВ. Точка пересечения Х и есть искомая.

Действительно, если АВ = 1, ВD=1/2, то по теореме Пифагора DE=. Значит, и DX=, и, действительно, получаем, что ВХ==.

Таким образом, действительно, построение Птолемея ведет к цели.

Разложим в цепную дробь.

и т. д. Видна закономерность.

Следовательно, окончательно получаем

За исключением первого нуля полученная нами цепная дробь состоит из одних единиц! Запишем несколько подходящих дробей данной цепной дроби.

Нулевая подходящая дробь:.

Первая подходящая дробь:.

Вторая подходящая дробь:.

Третья подходящая дробь:.

Составим таблицу для числителей и знаменателей подходящих дробей нашей цепной дроби.

0 1 1 1 1 1 1 1 1 1 0 1 1 2 3 5 8 13 21 0 1 1 2 3 5 8 13 21 34 Особенность данной таблицы заключается в том, что, так как умножать надо на единицу, то фактически для получения следующего числителя достаточно сложить два предыдущих. То же самое получается и со знаменателями. Более того, в знаменателе повторяются те же числа, что и в числителе, только с «опозданием» на один шаг. Можно сказать, что те и другие образуются из такой последовательности чисел:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,

Но ведь это числа Фибоначчи!

Таким образом, данные подходящие дроби легко составить, помня, что в числителе и знаменателе стоят числа Фибоначчи, только в числителе они «опаздывают» на один шаг. И, следовательно, сколь угодно точно можно определить «золотое сечение».

Второе свойство цепных дробей

Вспомним, как вычисляются подходящие дроби.

и т. д. Имеют место рекуррентные соотношения

Рk+1 = qk+1. Pk+Pk-1 и Qk+1= qk+1. Qk+Qk-1.

Докажем следующее свойство цепных дробей: для любого k = 1,2,, n имеет место формула

Pk-1Qk – PkQk-1 = (-1)k.

Для этого воспользуемся методом математической индукции. В самом деле, для k=1 имеем

P0Q1 – P1Q0 = q0q1 – (q0q1 + 1) = -1 = (-1)1.

Предположим, что формула верна для номера k, и перейдем в левой части к номеру k+1. Используя рекуррентные соотношения, получим:

PkQk+1 – Pk+1Qk = Pk(qk+1Qk+Qk-1) – (qk+1Pk+Pk-1)Qk = -Pk-1Qk + PkQk-1 = (-1)k+1.

Таким образом, формула доказана для любого натурального k. Из нее, в частности, вытекает, что числа Pk и Qk взаимно просты.

Диофантовы уравнения вида ax+by=с

Используем отмеченное нами свойство цепных дробей для решения уравнения ax+by=c Коэффициенты a и b взаимно просты. Разложим в цепную дробь. При этом.

Поскольку обе дроби несократимы, то a = Pn, b = Qn. По свойству имеем bPn-1 – aQn-1 = (-1)n.

Умножив обе части этого равенства на (-1)nc, получим

(-1)n+1aQn-1c + (-1)nbPn-1c =c, откуда видно, что пара чисел x0 = (-1)n+1cQn-1, y0 = (-1)ncPn-1 представляет собой решение уравнения.

Общее решение запишется в виде: x = (-1)n+1c Qn -1 + bt, y = (-1)n c Pn –1 – at, где t принимает целые значения

Решим уравнение 17х + 13у = 5.

Поскольку , то n = 2, , откуда х0 = -5•3 = -15, у0 = 4•5 = 20 и общее решение имеет вид x = -15+13t, y = 20-17t.

Уравнение Пелля

Диофантово уравнение в натуральных числах вида x2 –ay2 =1 называется уравнением Пелля.

Как же отыскиваются решения уравнения Пелля в натуральных числах? Сначала надо найти наименьшее натуральное решение. Для небольших значений коэффициента а это можно сделать подбором, но при больших а подбор становится затруднительным, и здесь на выручку приходят цепные дроби. Используется разложение в цепную дробь числа. А далее по утверждению Лагранжа:

Пусть s – длина периода непрерывной дроби [q 0; q1, q2,] =. Если s четно, то находят подходящую дробь = [q 0;q1,,qs-1]. В этом случае наименьшее натуральное решение уравнения имеет вид x = Ps-1, y = Qs-1.

Если же s нечетно, то надо положить х = P2s-1, y = Q2s-1, где =

[q0; q1,,q2s-1]. Мы ограничимся нахождением наименьшего натурального решения.

Рассмотрим в качестве примера уравнение х2- 3у2 = 1. Разложение в непрерывную дробь нам известно (см. раздел Упражнения):

= [1; 1, 2, 1, 2,]

Здесь s = 2, и поэтому находим подходящую дробь , откуда х = 2, у = 1 – наименьшее решение уравнения в натуральных числах.

Упражнения

Разложение обыкновенных дробей в цепную дробь.

[0; 5, 1, 2, 1, 2]

[1; 1, 4]

[0; 1, 3, 5]

[0; 2, 5]

[0; 1, 1, 7, 3]

[4; 1, 5]

Разложение иррациональных чисел в цепную дробь.

[1; 2, 2, 2]

[1; 1, 2, 1, 2, 1, 2]

[2; 4, 4, 4, 4]

[2; 2, 4, 2, 4]

=[2; 1, 1, 1, 4, 1, 1, 1, 4]

[2; 1, 4, 1, 4, 1, 4 ]

[3; 6, 6, 6, 6]

[3; 3, 6, 3, 6, 3]

[3; 2, 6, 2, 6, 2, 6, 2]

[3; 1, 1, 1, 1, 6, 1, 1, 1, 1, 6]

Диофантовы уравнения вида ax + by = c.

При решении уравнений будем использовать следующий алгоритм.

1) Разлагаем в цепную дробь (с помощью алгоритма Евклида или с помощью соответствующих преобразований).

2) Из разложения =определяем значение n (т. е. длину цепной дроби).

3) Находим n-1 – подходящую дробь (в случае необходимости используем таблицу).

4) Применяем формулы:

Общее решение: x = (-1)n+1c Qn -1 + bt, y = (-1)n c Pn –1 – at.

Замечания.

1) Можно находить сначала частное решение: x0 = (-1)n+1cQn-1, y0= (-1)ncPn-1.

А затем общее решение: x = x0 + bt, y = y0 – at

2) Если уравнение имеет вид ax – by = c, то, очевидно, что x = (-1)n+1c Qn -1 + bt, y = (-1)n+1 c Pn –1 + at.

3) Если a > b и =, то = [0; q0, q1,,qn]

Задание 1. 15x + 13y = 1.

2) Длина цепной дроби n = 2.

3) P1 = 7, Q1 = 6.

4) x0 = (-1)6 = -6, y0 = 7.

Таким образом, общее решение x = -6 + 13t, y = 7 — 15t

Задание 2. 67x + 7y = 18.

2) Длина цепной дроби n = 3.

3) P2 = 19, Q2 = 2.

4) Общее решение x = 36 + 7t, y = -342 — 67t.

Задание 3. 5x + 7y = 12.

2) Длина цепной дроби n = 2.

3) P1 = 3, Q1 = 2.

4) x0 = (-1)212*3 = 36, y0 = (-1)12*2 = -24.

Таким образом, общее решение x = 36 — 7t, y = -24 + 5t.

Задание 4. 63х – 100у = 90.

1) = [0; 1; 1, 1, 2, 2, 1, 3],

2) Длина цепной дроби n=7.

3) Таблица подходящих дробей:

0 1 1 1 2 2 1 3 1 0 1 1 2 5 12 17 63 0 1 1 2 3 8 19 27 100 P6 = 17, Q6 = 27.

4) Общее решение х = 90· 27 + 100t, y = 90·17 + 63t.

Уравнения Пелля x2 — аy2 = 1.

При решении данных уравнений будем использовать следующий алгоритм.

1) Разлагаем в цепную дробь.

2) Записываем в компактной форме, находим длину периода этой дроби.

3) Если s четно, то находим подходящую дробь. В этом случае наименьшее натуральное решение уравнения имеет вид x = Ps-1, y = Qs-1.

Если же s нечетно, то находим подходящую дробь. В этом случае наименьшее натуральное решение имеет вид х = P2s-1, y = Q2s-1.

Задание 1. x2 — 6y2 = 1.

2) [2; 2, 4, 2, 4, 2, 4,], k=2, четное.

3) Наименьшее натуральное решение: x = Pk-1 = P1 = 5, y = Qk-1 = Q1 = 2.

Задание 2. x2 — 13y2 = 1.

2) [3; 1, 1, 1, 1, 6, 1, 1, 1, 1, 6], k = 5, нечетно.

3) Необходимо найти P2k-1 = P9, Q2k-1 = Q9.

Используем таблицу подходящих дробей.

3 1 1 1 1 6 1 1 1 1 1 3 4 7 11 18 119 137 256 393 649 0 1 1 2 3 5 33 38 71 109 180

Таким образом, наименьшее натуральное решение x = P9 = 649, y = Q9 = 180.

Задание 3. x2 — 12y2 = 1.

2) [3; 2, 6, 2, 6], k = 2, четно.

3) Наименьшее натуральное решение x = P1 = 7, y = Q1 = 2.

Задание 4. x2 — 11y2 = 1.

2) [3; 3, 6, 3, 6], k = 2.

3) Наименьшее натуральное решение x = P1 = 10, y = Q1 = 3.

Из истории цепных дробей

В процессе поиска наилучшего приближения значений квадратных корней итальянский математик Пиетро Антонио Катальди (1552- 1626) пришел в 1613г. к цепным дробям, с чего и началось их изучение. Правда, они встречались почти на 40 лет раньше в «Алгебре» другого итальянского математика – Рафаэля Бомбелли (ок. 1526- 1572). Но Катальди выделил цепные дроби в отдельный тип, выявил некоторые их свойства.

Современное обозначение непрерывных дробей предложил выдающийся нидерландский ученый Христиан Гюйгенс (1629- 1695). Гюйгенс был не только знаменитым физиком, он был и замечательным математиком, удивительным изобретателем и конструктором. К тому же он писал неплохие стихи.

К цепным дробям Гюйгенс вынужден был обратиться (1680) при построении планетария в Париже. Он хотел получить наилучшие приближения для отношений периодов обращения планет. Эти отношения и отношения чисел зубцов соответствующих связанных между собой шестерен планетария должны были совпадать. Но число зубцов шестерен по техническим причинам не могут быть очень большими. Необходимо было так их подобрать, чтобы полученные отношения как можно меньше отличались от истинных. Гюйгенс обратился к цепным дробям и с их помощью нашел решение стоящей перед ним задачи. При этом он детально изучил теорию цепных дробей.

Хотелось заглянуть всюду, где встречаются цепные дроби

Поиск областей применения цепных дробей привел к проблемам создания календаря. Оказывается, что цепная дробь, изображающая время, за которое Земля совершает полный оборот вокруг Солнца, может помочь в создании календаря, она дает различные системы, по которым может составляться календарь.

В ходе поиска приятно было встретиться с одной из интереснейших задач математики, с «золотым сечением». Разложив «золотое сечение» в цепную дробь, можно найти разные по точности его приближения, причем они оказываются связанными с числами Фибоначчи.

И, наконец, знаменитые диофантовы уравнения не обошлись без применения цепных дробей. Некоторые из них можно решать с помощью цепных дробей.

В ходе выполнения работы разложены в цепные дроби некоторые рациональные и, что более интересно, иррациональные числа, освоен новый прием решения некоторых диофантовых уравнений.

Попытка пройти по тропинкам, где встречалась цепная дробь, дала возможность над чем–то подумать, что–то новое узнать, применить свои силы к новому и увлекательному математическому объекту.

Были достигнуты следующие результаты:

1)Собран и скомпонован теоретический материал, составлены на основании изученных свойств алгоритмы решений приведенных в данной работе диофантовых уравнений. Сформулированы замечания, использующиеся при решении данных уравнений.

2)Найдены некоторые области применения цепных дробей.

3)Составлены и выполнены практические задания по разложению действительных чисел в цепные дроби, а также по решению диофантовых уравнений вида ax+by=c и уравнения Пелля.

Таким образом, несмотря на то, что цепные дроби широкого применения не получили, их существование в математике не бесполезно, А мне они показались еще и очень увлекательными.

XXVIII научно-практическая конференция

«Молодые умы – науке Красноярска»

«Цепные дроби и их приложения»

Исследовательская работа.

Автор работы:

Пирматова Алина Рустамбековна,

ученица 11 Г класса

МБОУ ЦО № 4

Научный руководитель:

Мустяца Елена Юрьевна,

учитель математики и информатики

I квалификационной категории

г. Красноярск-2015

ОГЛАВЛЕНИЕ

Введение	3
ГЛАВА I Теория цепных дробей	4
§1 Определение цепной дроби	5-7
§2 Вычисление подходящих дробей и их приложения	8
ГЛАВА II Ход и результаты исследования	13
§1 Решение уравнений в целых числах, различными методами	13-16
§2 Решение уравнений в целых числах, с помощью теории цепных дробей	16-20
Заключение	21
Литература	22

ВВЕДЕНИЕ

Обучаясь в выпускном классе по системе ускоренного обучения, передо мной возникла проблема выбора формы сдачи экзамена по математике. Для того чтобы успешно сдать экзамен на профильном уровне необходимо решать задания не только первой, но второй его части. Я обратилась к своему учителю математики со следующим вопросом: решение каких заданий поможет мне получить высокий балл?

Оказывается, в последних задачах ЕГЭ профильного уровня встречаются задания на решение уравнений и неравенств в целых числах. Решение такого задания поможет получить дополнительные баллы. Мне было предложено рассмотреть вопрос использования теории цепных дробей для решения заданий второй части экзамена.

Исходя из вышесказанного, тема нашей исследовательской работы «Цепные дроби и их приложения».

Цель нашей работы: исследование теории цепных дробей в качестве инструмента решение задач ЕГЭ профильного уровня.

Объектом исследования являются цепные дроби.

Предметом исследования – цепные дроби, как инструмент решения уравнений в целых числах.

Гипотеза исследования: если изучить теорию цепных дробей и их приложения, то можно научиться решать уравнения в целых числах (от учебных до олимпиадных).

Для достижения цели исследования и подтверждения выдвинутой гипотезы нами были сформулированы следующие задачи исследования:

1. Изучить теорию цепных дробей.

2. Проанализировать задания второй части ЕГЭ нескольких последних лет.

3. Соотнести возможные способы решения уравнений в целых числах с решением через использование теории цепных дробей.

База исследования: типовые задания последнего задания части единого государственного экзамена на профильном уровне – задачи на целые числа.

Глава I

Цепные дроби были введены в 1572 году итальянским математиком Бомбелли. Современное обозначение непрерывных дробей встречается у итальянского математика Катальди в 1613 году. Величайший математик XVIII века Леонардо Эйлер первый изложил теорию цепных дробей, поставил вопрос об их использовании для решения дифференциальных уравнений, применил их к разложению функций, представлению бесконечных произведений, дал важное их обобщение.

Многие важные результаты этой теории принадлежат французскому математику Лагранжу, который нашел метод приближенного решения с помощью цепных дробей дифференциальных уравнений.

В современной математике приближенное представление функций обычно разыскивается в виде многочленов от независимых переменных. В тех же случаях, когда нахождение таких многочленов затруднительно, обычно применяются различные численные методы.

При этом сравнительно редко пользуются приближениями, являющимися дробно — рациональными функциями от независимых переменных.

Между тем дробно — рациональные приближения иногда могут успешно заменять данную функцию в тех областях изменения аргумента, где разложение этой функции в степенной ряд расходится и где, следовательно, приближение в виде многочленов в большинстве случаев неприменимы.

Существуют методы, позволяющие получать сколь угодно много дробно — рациональных приближений данной функции и требующие сложных выкладок. Наиболее распространенным из таких методов является метод цепных дробей.

В последнее время вырос интерес к цепным дробям в связи с их большим теоретическим и практическим значениями.

Так например, цепные дроби являются одним из аппаратов приближения функций. Они обладают замечательным свойством малого накопления погрешности при их вычислении.

В настоящее время повышение интереса к теории цепных дробей объясняется еще и тем, что, несмотря на видимую громоздкость представления, процесс их вычислений является цикличным и легко поддаётся программированию при использовании ЭВМ.

§1. Определение цепной дроби.

Цепной дробью называется выражение вида:

Такое выражение называется правильной (конечной) цепной или правильной непрерывной дробью, при этом предполагается, что – целое число, а , …, — натуральные числа.

Где числа q₁, q₂, q₃, q₄, …, называются элементами цепной дроби.

Цепную дробь можно так же записать:

[q₁, q₂, q₃… q_n]

Что на много упрощает запись.

Алгоритм Евклида дает возможность найти представление (или разложение) любого рационального числа в виде цепной дроби. В качестве элементов цепной дроби получаются неполные частные последовательных делений в системе равенств (1), поэтому элементы цепной дроби называются также неполными частными. Кроме того, равенства системы (2) показывают, что процесс разложения в цепную дробь состоит в последовательном выделении целой части и перевертывании дробной части.

Последняя точка зрения является более общей по сравнению с первой, так как она применима к разложению в непрерывную дробь не только рационального, но и любого действительного числа.

Разложение рационального числа имеет, очевидно, конечное число элементов, так как алгоритм Евклида последовательного деления a на b является конечным.

Понятно, что каждая цепная дробь представляет определенное рациональное число, то есть равна определенному рациональному числу. Но возникает вопрос, не имеются ли различные представления одного и того же рационального числа цепной дробью? Оказывается, что не имеются, если потребовать, чтобы было .

Теорема. Существует одна и только одна конечная цепная дробь, равная данному рациональному числу, но при условии, что .

Доказательство: 1) Заметим, что при отказе от указанного условия единственность представления отпадает. В самом деле, при :

так что представление можно удлинить:

например, (2, 3, 1, 4, 2)=(2, 3, 1, 4, 1, 1).

2) Принимая условие , можно утверждать, что целая часть цепной дроби равна ее первому неполному частному . В самом деле:

1. если n=1, то

2. если n=2, то ; поэтому

3. если n2, то

=

,

где 1, т.к.

Поэтому и здесь . Докажем то, что рациональное число однозначно представляется цепной дробью , если .

Пусть с условием , . Тогда , так что . Повторным сравнением целых частей получаем , а, следовательно, и так далее. Если , то в продолжении указанного процесса получим также . Если же , например , то получим , что невозможно.

Теорема доказана.

Замечания:

1. В случае разложения правильной положительной дроби первый элемент , например, .

2. При разложении отрицательной дроби (отрицательный знак дроби всегда относится к числителю) первый элемент будет отрицательным, остальные положительными, так как целая часть отрицательной дроби является целым отрицательным числом, а ее дробная часть, как всегда, положительна.

Пример: , а так как , то .

1. Всякое целое число можно рассматривать как непрерывную дробь, состоящую из одного элемента.

Пример: 5=(5); .

Приведу несколько примеров разложения различных дробей и иррациональных корней в цепные дроби:

Пример 1. Разложим обыкновенную дробь 105/38 в цепную.

Включаем алгоритм Евклида.

105=38*2+29

38=29*1=9

29=9*3+2

9=2*4+1

2=1*2

Неполные частные (я их специально подчеркнул) нужно аккуратно расположить подряд на этажах цепной дроби перед знаками плюс, заменяя q. Получим:

Пример 2: Представим обыкновенную дробь 539/103 в цепную.

Так же при помощи алгоритма Евклида.

Решение:

539=103*5+24

103=24*4+7

24=7*3+3

7=3*2+1

3=1*3

Получим дробь:

Пример 3: Представим обыкновенную дробь 1578/685 в цепную.

Решение:

1578=685*2+208

685=208*3+61

208=61*3+25

61=25*2+11

25=11*2+3

11=3*3+2

3=2*1+1

2=1*2

Получим:

§2 Вычисление подходящих дробей.

В §1 я показал, как переводить обычные дроби и иррациональные числа в цепную дробь, но чаще необходимо решить обратную задачу и вычислить огромную многоэтажную дробь. Многие скажут, что это очень долго и проще не обращаться к цепным дробям.

На самом деле вычислять цепную дробь еще проще, чем переходить к ней, основную роль при этом играют дроби вида:

или

которые называются подходящими дробями данной непрерывной дроби или соответствующего ей числа .

Заметим, что ==. Считается, что подходящая дробь имеет порядок k.

Прежде чем приступить к вычислению подходящих дробей заметим, что переходит в , если в первой заменить выражением .

Имеем ,

,

, …,

при этом принимается, что , (это просто соглашение, не пугайтесь на ноль ни кто делить не собирается), , , , и так далее.

Закономерность, которую мы замечаем в построении формулы для (ее числителя и знаменателя ), сохраняется при переходе к и сохранится также при переходе от k к (k+1).

Поэтому, на основании принципа математической индукции, для любого k, где , имеем

;

причем

Получили две формулы, которыми и будем пользоваться для вычисления цепных дробей.

Вычислять дроби очень удобно, используя таблицу.

Пример 4

Вычислим разложенную ранее в Примере 1 дробь:

P_o=1 Q_o=0 P₁₌q₁ Q₁₌1

P₂₌1*2+1=3 Q₂₌1*1+0=1

P₃₌3*3+2=11 Q₃₌3*1+1=4

P₄₌4*11+3=47 Q₄₌4*4+1=17

P₅₌2*47+11=105 Q₅₌2*17+4=38

Отсюда видим, что ,

а — это и есть искомое число.

k	0	1	2	3	4	5
qk		2	1	3	4	2
Pk	1	2	3	11	47	105
Qk	0	1	1	4	17	38

Пример 5

Вычислим разложенную ранее в Примере 3 дробь:

Очень часто необходимо сначала перевести число в цепную дробь, а потом посчитать, такие примеры у меня представлены в приложении.

С помощью цепных дробей так же решать уравнения и задачи, которые необходимо решить в целых числах.

Пример 6 (уравнение):

142x+82y=6 /:2

Данное уравнение равносильно уравнению:

71x+41y=3

Разложим 71/41 в цепную дробь

71=41*1+30

41=30*1+11

30=11*2+8

11=8*1+3

8=3*2+2

3=2*1+1

2=1*2

Составим таблицу подходящих дробей:

k	0	1	2	3	4	5	6	7
qk		1	1	2	1	2	1	2
Pk	1	1	2	5	7	19	26	71
Qk	0	1	1	3	4	11	15	41

На основании свойства подходящих дробей

получим:

или

Умножив обе части на 3 находим:

т.е. х₀=-45, у₀=78 – частное решение данного уравнения.

Все решения могут быть найдены по формулам:

x=-45+41t y=78-71t

где t принимает любые целые значения.

Пример 7:

Решить уравнение в целых числах:

7k-20n=5

Разложим в цепную дробь:

Составим таблицу подходящих дробей

K	0	1	2	3	4
qk		0	2	1	6
Pk	1	0	1	1	7
Qk	0	1	2	3	20

По свойству подходящих дробей:

Отсюда:

Все решения могут быть найдены по формуле:

где t – все целые значения

Пример 8 (задача):

Транспортной организации, имеющей грузовые автомашины грузоподъемностью 3,5 и 4,5т, предложено перевезти 53т груза. Определим, сколько грузовых автомашин должен выделить диспетчер транспортной организации для перевозки указанного груза одним рейсом при условии полного использования грузоподъемности всех машин.

Решение:

Пусть х – число выделяемых машин грузоподъемностью 3,5т, у — число выделяемых машин грузоподъемностью 3,5т. Для получения ответа нужно решить уравнение

3,5х+4,5у=53

т.е.

35х+45у=530

в целых числах с учетом того, что

Уравнение (1) равносильно уравнению 7х+9у=106

Подсчитаем подходящие дроби.

K	0	1	2	3	4
qk		0	1	3	2
Pk	1	0	1	3	7
Qk	0	1	1	4	9

По свойству подходящих дробей

1) 2)

Решениями уравнения будут:

где t – любое целое число.

Теперь из всех решений выберем неотрицательные:

и

Пусть t=-47, значит Х=424+9(-47)=1 и Y=-318-7(-47)=11.

Ответ: х=1, у=11.

Глава II. Ход и результаты исследования

§1 Решение уравнений в целых числах , различными методами

Линейные уравнения в целых числах могут быть :

Метод прямого перебора

Использование неравенства

Использование отношение делимости

Выделение целой части

Метод остатков

Метод «спуска»

Метод последовательного уменьшения коэффициентов по модулю

Использование формул

Использование конечных цепных дробей

Пример№75

Решить в натуральных числах уравнения :

5х+8у=39

Метод: Использование неравенств

Решение: Для уменьшение перебора вариантов рассмотрим неравенства

{5x=39-8y≥0 {y≤4

{8y=39-5x≥0 {x≤7

Проведем перебор по неизвестной у:

Если у=1, то х=6,2 не является натуральным числом.

Если у=2, то х=4,6 не является натуральным числом.

Если у=3, то х=3.

Если у=4, то х=1,4 не является натуральным числом.

Ответ: (3;3)

Пример№76

Имеются контейнеры двух видов: по 130 кг и 160 кг. Сколько было контейнеров первого и сколько второго вида, если вместе они весят 3 тонны? Укажите все решения.

Метод: Использование отношения делимости

Решение: Обозначим количество контейнеров первого вида через х, второго – через у. Получаем уравнение 130х+160у=3000 или 13х+16у=300

Далее имеем

13х+13у+3у=13*23+1,

3у-1=13(23-х-у)

Отсюда следует, что разность 3у-1 делится на 13.

Если 3у-1=0, то у не является натуральным числом.

Если 3у-1=13, то у не является натуральным числом.

Если 3у-1=26, то у=9 и х=12.

Если 3у-1=39, то у не является натуральным числом.

Если 3у-1=52, то у не является натуральным числом.

Если 3у-1=65, то у=22, но 16*22=352300.

Ответ: 12 контейнеров по 130 кг и 9 по 160 кг.

Пример№77

У осьминога 8 ног, а у морских звезды 5. Сколько в аквариуме тех и других, если всего у них 39 ног?

Метод: Выделение целой части

Решение: Пусть х- количество осьминогов, у- количество морских звезд, тогда получаем уравнение 8х+5у=39

Выразим у из уравнения и выделим целую часть:

39-8х 3х-4

у= = 7-х .

5 5

Отсюда следует, что разность 3х-4 делиться на 5.

Если 3х-4=0, то х не является натуральным числом.

Если 3х-4=5, то х=3 и у=3.

Если 3х-4=10, то х не является натуральным числом.

Если 3х-4=15, то х не является натуральным числом.

Если 3х-4=20, то х=8, но 8*8=6439.

Ответ: 3 и 3.

Замечание: В двух последних примерах использовано отношение делимости, при этом уравнения приводились к разному виду. В этих примерах для уменьшения перебора вариантов можно было дополнительно использовать неравенства.

Пример№78

Решить в целых числах уравнение 3х-4у=1.

Метод: Остатков

Решение: Перепишем уравнение в виде 3х=4у+1. По сколько левая часть уравнения делится на3, то должна делится на 3 и правая часть. Рассмотрим три случая.

1.Если у=3m, где m € Ƶ, то 4у+1=12m+1 не делится на3.

2.Если у=3m+1, то 4у+1=4(3m+1)+1=12m+5 не делится на3.

3.Ели у=3m+2, то 4y+1=4(3m+2)+1=12m+9 делится на 3, поэтому 3х=12m+9, х=4m+3.

Ответ: х=4m+3, у=3m+2, где m € Ƶ

Пример №79

Решить в целых числах уравнение 5х-7у=3

Метод: «Спуска»

Решение: Выразим из уравнения то неизвестное, коэффициент при котором меньше по модулю:

7х+3 2у+3

х= = у+ .

5 5

Дробь 2у+3 должна быть равна целому числу.

5

Положим 2у+3 Z , где Z— целое число.

5

Тогда 2у+3=5z. Из последнего уравнения выразим то неизвестное, коэффициент при котором меньше по модулю, и проделаем аналогические преобразования:

5z-3 z+3

х= = у+ .

2 2

Дробь z+2 должна быть равна целому числу.

2

Обозначим z+2 = t, где t— целое число. Отсюда z=2t-3. Последовательно

2

возвращаемся к неизвестным х и у:

у=3(2t-3)-t=5t-9,

х=у+z=5t-9+2t-3=7t-12/

Ответ: х=7t-12, y=5t-9, где t € Ƶ.

Пример №80

Решить в целых числах уравнения 79у-23х=1

Метод: Последовательного уменьшения коэффициентов по модулю.

Решение: Проведем деление с остатком 79=23*3+10 и перепишем исходное уравнение в виде: 23х=79у-1=69у+10у-1,

23х-69у=10у-й.

Левая часть последнего уравнения делится нацело на 23 , поэтому и правая часть должна делиться на 23. Имеем 10у-1=23t, где t € Ƶ.

Для полученного нового уравнения повторим процедуру уменьшения коэффициента. 10y=23t+1=(2*10+3)t+1;

10y-20t=3t+1; 3t+1=10u, где u € Ƶ.

Выразим х и у через n. Так как u=3n+1, то

3t=10u-1=10(3n+1)-1=30n+9;

t=10n+3

10y=23t+1=23(10n+3)+1=230n+70;

y=23n+7.

23x=79y-1=79(23n+7)-1=79*23n+552;

x=79n+24.

Ответ: х=79n+24; y=23n+7, где n € Ƶ.

§2 Решение уравнений в целых числах, с помощью теории цепных дробей

Рассмотрим примеры из предыдущего параграфа, решив их с помощью теории цепных дробей.

Пример № 75

5x+8y=39

Составим цепную дробь

1) 5 0 + 1

8 1 + 1

1 + 1

1 + 1

2

2) 5=8*0+5

8=5*1+3

5=3*1+2

3=2*1+1 Составим таблицу подходящих дробей

K	0	1	2	3	4
qk		1	1	1	2
Pk	1	1	2	3	8
Qk	0	1	1	2	5

2=1*2

Из свойств подходящих дробей следует

3) 3*5-8*2= (-1)³

3*5-8*2= -1 /*(-1)

8*2+5*(-3)=1 /*39

8*78+5*(-117)=39

То есть частное решение имеет вид

x_o=78 y_o=-117

x=78+5t

y=-117-8t

Так как Х и У могут быть только положительные то

{78+5t≥0, {5t≥-78, t≥-15,6

{-117-8t≥0, {-8t≥117, t≤-14,625

Ответ: х=78-75=3

у=-117+120=3 где t € Ƶ

Пример №76

130x+16y=3000,

13x+16y=300,

Составим цепную дробь

1)13 0 + 1

16 1 + 1

4 + 1

1

2)13=16*0+13,

16=13*1+3, Составим таблицу подходящих дробей

K	0	1	2	3	4
qk		0	1	4	3
Pk	1	0	1	4	13
Qk	0	1	1	5	16

13=3*4+1,

3+1*3.

Из свойств подходящих дробей следует

3) 4*16-13*5= (-1)^4-1

4*16-13*5= -1 /* (-1)

13*5+16*(-4)=1 /*300

13*1500+16*(-1200)=300

То есть частное решение имеет вид

x_o=1500 y_o=-1200

x=1500+16t

y=-13t – 1200

Так как Х и У могут быть только положительные то

{1500+16t≥0, {16t≥-1500, {t≥-93,75, {x=1500+16*(-93), {x=1500-1488, {x=12,

{-13t-1200≥0, {-13t≥1200, {t≤-92(4/13), {y=-13*(-93)=1200, {y=1203-1200, {y=9.

Ответ: 12 и 9 где t € Ƶ

Пример №77

1) 8*х+5у=39, где х0 и у0

8 1

5 = + 1

1 + 1

1 +

2

2) 8=5*1+3

5=3*1+2

3=2*1+1

2=1*2

3)

K	0	1	2	3	4
qk		1	1	1	2
Pk	1	1	2	3	8
Qk	0	1	1	2	5

P2=q2* Р1+ Р0=1*1+1=2 Q2=q2* Q1+Q0=1*1+=1

P3=q3* Р2+ Р1=1*2+1=3 Q3=q3* Q2+Q1=1*1+1=2

P

4=q4* Р3+ Р2=2*3+2=8 Q4= q4* Q3+Q2=2*2+1=5

4) 3*5-8*2=(-1) ,

3*5-8*2= -1 /(-1)

8*2+5*(-3)=1 /*39,

8*78+5*(-117)=39

= XO=78 , УO= -117

5) Решение уравнения будет:

х=78+5t

y= -117-8t, где t c z

{78+5t0, {5t-78, t-15,6,

{-117-8t0, {-8t117, t

t= -15

x=78-75=3

y= -117+180=3 Ответ: 3 и 3

Пример №78

1)3х-4у=1

Составим цепную дробь

3 0 + 1

4 1 + 1

2+ 1

1

2) 3=4*0+3

4=3*1+1

3=1*2+1

1=1*1 Составим таблицу подходящих дробей

K	0	1	2	3	4
qk		0	1	2	1
Pk	1	0	1	2	3
Qk	0	1	1	3	4

Из свойств подходящих дробей следует

3) 2*4-3*3=(-1)³

2*4-3*3= -1 /*(-1)

3*3-4*2=1 /1

3*3-4*2=1

То есть частное решение имеет вид

x_o=3 y_o=2

Ответ: x=3+4t

у=2+3t где t € Ƶ

Пример №79

5x-7y=3

Составим цепную дробь

1) 5 = 0 + 1

7 1 + 1

2+ 1

2

2)5=7*0+5 Составим таблицу подходящих дробей

K	0	1	2	3	4
qk		0	1	2	2
Pk	1	0	1	2	5
Qk	0	1	1	3	7

7=5*1+2

5=2*2+1

2=1*2

Из свойств подходящих дробей следует

3) 2*7-5*3= (-1)³

2*7-5*3=-1 /*(-1)

5*3+2*(-7)= /*3

5*8-7*6=3

То есть частное решение имеет вид

x_o=9 y_o=6

Ответ: x=9+7t

y=6+5t где t € Ƶ

Пример №80

1)79у-23х=1

Составим цепную дробь

79 3 + 1

23 2 + 1

3 + 1

3

2)79=23*3+10

23=10*2+3

10=3*3+1

3=1*3

Составим таблицу подходящих дробей

К	0	1	2	3	4
qk		3	2	3	3
Pk	1	3	7	24	79
Qk	0	1	2	7	23

P₂₌q_2*P₁+P₀₌2*3+1=7 Q₂₌q_2*Q₁₊ Q₀₌2*1+0=2

P₃₌q_3*P₂₊P₁₌3*7+3=24 Q₃₌q_3*Q₂₊ Q₁₌3*2+1=7

P₄₌q_4*P₃+P₂₌3*24+2=79 Q₄₌q_4*Q₃₊ Q₂₌3*7+2=23

Из свойств подходящих дробей следует

3) 24*23-79*7= (-1)³

24*23-79*7= -1 /*(-1)

79*7+24*(-23)=1 /*1

79*7-23*24=1

То есть частное решение имеет вид

x₀₌7 y₀₌24

Ответ: х=7+23t

y=24+79t где t € Ƶ.

Заключение

В данной работе рассматривается очень интересное математическое понятие цепная дробь. Широкого практического применения они не получили, так как для них нет удобных правил выполнения арифметических действий, которые имеются для десятичных дробей. Но их преимуществом является в том, что их свойства не связаны ни с какой системой счисления. По этой причине цепные дроби эффективно используются в теоретических исследованиях. Изложение материала, которое представлено в данной работе, принципиально отличается от тех публикаций, с которыми работал автор, как по логике изложения, доступности, большому количеству практических задач и примеров, показывающих применение цепных дробей и оригинальность решения привычных задач.

Во второй главе, нашей исследовательской работы можно заметить насколько удобен оказался способ решения, линейных уравнений с двумя неизвестными. Для сравнения нами представлены решения этих задач различными методами, которые подразумевают, что учащийся должны обладать приличным «багажом знаний». Сравнивая рассмотренные методы с решениями через использование теории цепных дробей и свойств подходящих дробей, видно удобство и универсальность рассматриваемого способа решения.

Таким образом, цель нашего исследования достигнута частично, так как мы рассмотрели довольно узкий круг задач встречающихся в ЕГЭ по математики на профильном уровне. Однако, выдвинутая гипотеза полностью подтвердилась.

Литература

1. В.О. Бугаенко. Уравнения Пелля. – МЦНМО, 2002.

2. В.И. Арнольд. Цепные дроби. — МЦНМО, 2002.

3. Математическая энциклопедия, том V, М, «Советская энциклопедия», 85.

4. Ш.Х. Михелович. Теория чисел. М, «Высшая школа», 67.

5. А.А. Бухштаб. Теория чисел. М, «Просвещение», 96.

6. Г.Д. Балк. Математика после уроков. М, «Просвещение», 71.

7. А.А. Кочева. Задачник-практикум по алгебре и теории чисел. М, «Просвещение», 84.

8. Е.С. Ляпин, А.Е. Евсеев. Алгебра и теория чисел. М, «Просвещение», 74.

9. Л.Я. Куликов, А.И. Москаленко, А.А. Фомин. Сборник задач по алгебре и теории чисел. М, «Просвещение», 93.

10. И.М. Виноградов. Основы теории чисел. М, «Наука», 72.

11. Алгебра и теория чисел. Под редакцией Н.Я. Виленкина, М, «Просвещение»,

12. Математика ЕГЭ 2011 (типовые задания С6) . Задачи на целые числа (от учебных задач до олимпиадных) Корянов А.Г., и Прокофьев А.А.

-числители

-знаменатели