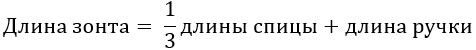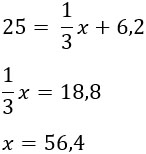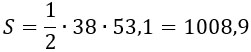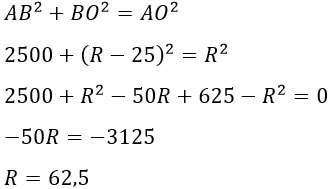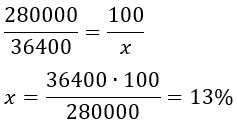Таня нашла площадь купола зонта как площадь - Исправление недочетов и поиск решений вместе с Examum.ru

Две подруги Оля и Таня задумались о том, как рассчитать площадь поверхности зонта.
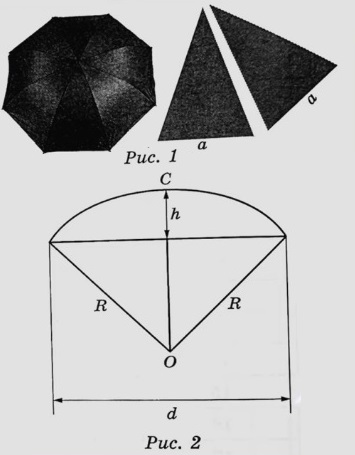
На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из двенадцати отдельных клиньев, натянутых на каркас из двенадцати спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.
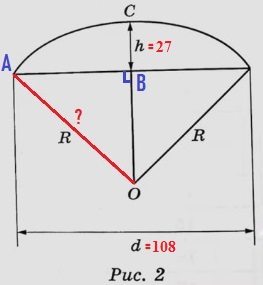
Оля и Таня сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 28 см. Высота купола зонта h (рис. 2) оказалась равна 27 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, – ровно 108 см.

Источник: ОГЭ Ященко 2023 (36 вар)

Задание 1

Длина зонта в сложенном виде равна 27 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,8 см.

Решение

Найдём треть длины спицы, отняв от длины всего зонта длину ручки:

27 см – 6,8 см = 20,2 см

Если это треть, то вся спица в 3 раза больше:

20,2·3 = 60,6 см

Ответ: 60,6.

Задание 2

«Поскольку зонт сшит из треугольников, – рассуждала Оля, – площадь его поверхности можно найти как сумму площадей треугольников». Вычислите площадь поверхности зонта методом Оли, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 59 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.

Решение

По первому условию зонт состоит из 12 треугольников с основанием а = 28 см и высотой h = 59 см.
Площадь одного такого треугольника:

S_{Delta}=frac{1}{2}ah=frac{1}{2}cdot 28cdot 59=14cdot 59=826

Найдём площадь поверхности зонта, методом Оли, округлив до ДЕСЯТКОВ:

S_{поверхности} = 12·S_Δ = 12·826 = 9912 ≈ 9910 см²

Ответ: 9910.

Задание 3

Таня предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ОС = R (рис. 2). Ответ дайте в сантиметрах.

Решение

Нам необходимо найти гипотенузу R в прямоугольном треугольнике АВО. АВ равно половине d:

AB = d/2 = 108/2 = 54

Т.к. по условию ОС = R, то:

ОВ = ОС – h = R – 27

По теореме Пифагора найдём ОА = R:

ОА² = АВ² + ОВ²
R² = 54² + (R – 27)²
R² = 2916 + R² – 54R + 729
R² – R² + 54R = 3645
54R = 3645
R = 3645/54 = 67,5

Ответ: 67,5.

Задание 4

Таня нашла площадь купола зонта как площадь поверхности сферического сегмента по формуле S = 2πRh‚ где R – радиус сферы, а h – высота сегмента. Рассчитайте площадь поверхности купола способом Тани. Число π округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.

Решение

S = 2πRh
π ≈ 3,14
R = 67,5
h = 27

Найдём площадь и округлим до целого:

S = 2πRh = 2·3,14·67,5·27 = 54·3,14·67,5 = 11445,3 ≈ 11445 см²

Ответ: 11445.

Задание 5

Рулон ткани имеет длину 20 м и ширину 90 см. На фабрике из этого рулона были вырезаны треугольные клинья для 15 зонтов, таких же, как зонт, который был у Оли и Тани. Каждый треугольник с учётом припуска на швы имеет площадь 850 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?

Решение:

Найдём площадь рулона ткани в см²:

S = 20м х 90см = 2000см х 90см = 180000 см²

Помня, что в одном зонте 12 треугольников найдём сколько ушло ткани на 15 зонтов:

S₁ = 15·12·850 = 153000 см²

Найдём сколько см² ткани рулона ушло в обрезки:

S₂ = S – S₁ = 180000 – 153000 = 27000 см²

Найдём сколько это процентов от начального рулона:

frac{27000}{180000}cdot 100%=frac{27}{180}cdot 100%=frac{3}{20}cdot 100%=frac{3 cdot 100}{20}%=frac{3 cdot 5}{1}%=15%

Ответ: 15.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 4.8 / 5. Количество оценок: 81

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник

Решение 2436. Длина зонта в сложенном виде равна 25 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,2 см.

Два друга Петя и Вася задумались о том, как рассчитать площадь поверхности зонта. На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.

Петя и Вася сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 38 см. Высота купола зонта h (рис. 2) оказалась равна 25 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно 100 см.

Задание 1. Длина зонта в сложенном виде равна 25 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,2 см.

Решение.

Треть спицы будет равна

25 – 6,2 = 18,8 см

следовательно, длина всей спицы:

18,8∙3 = 56,4 см

Ответ: 56,4

Задание 2. Поскольку зонт сшит из треугольников, рассуждал Петя, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Пети, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 53,1 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.

Решение.

Высота h = 53,1 см, проведенная к основанию a = 38 см, дает площадь каждого сегмента, равную:

Так как таких сегментов 8, то получаем полную площадь поверхности:

кв. см

Округляем до десятков, получаем 8070 кв. см.

Ответ: 8070

Задание 3. Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ОС = R (рис. 2). Ответ дайте в сантиметрах.

Решение.

Рассмотрим прямоугольный треугольник с катетами d/2 и R-h и гипотенузой R.

По теореме Пифагора можно записать равенство:

Решаем уравнение относительно R, имеем:

Ответ: 62,5

Задание 4. Вася нашёл площадь купола зонта как площадь поверхности сферического сегмента по формуле S = 2πRh , где R — радиус сферы, а h — высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число π округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.

Решение.

Подставим в формулу площади купола зонта числовые значения, получим:

Округляем до целого, имеем: 9813 см. кв.

Ответ: 9813

Задание 5. Рулон ткани имеет длину 35 м и ширину 80 см. На фабрике из этого рулона были вырезаны треугольные клинья для 29 зонтов, таких же, как зонт, который был у Пети и Васи. Каждый треугольник с учётом припуска на швы имеет площадь 1050 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?

Решение.

Вычислим площадь ткани в кв. см, получим:

S = 35∙100∙80 = 280 000 см. кв.

Площадь клиньев для 29 зонтов, равна:

29∙8∙1050 = 243 600 см. кв.

Площадь обрезков:

280 000 – 243 600 = 36 400 см. кв.

Что составляет:

Ответ: 13

Решение 4136. Длина зонта в сложенном виде равна 26 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,5 см.

Две подруги Ира и Юля задумались о том, как рассчитать площадь поверхности зонта. На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.

Ира и Юля сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 40 см. Высота купола зонта h (рис. 2) оказалась равна 26 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно 104 см.

Задание 1. Длина зонта в сложенном виде равна 26 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,5 см.

Решение.

Треть спицы будет равна

26 – 6,5 = 19,5 см

следовательно, длина всей спицы:

19,5∙3 = 58,5 см

Ответ: 58,5

Задание 2. Поскольку зонт сшит из треугольников, рассуждала Ира, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Иры, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 55 см. Ответ дайте в квадратных сантиметрах.

Решение.

Высота h = 55 см, проведенная к основанию a = 40 см, дает площадь каждого сегмента, равную:

Так как таких сегментов 8, то получаем полную площадь поверхности:

кв. см

Округляем до десятков, получаем 8800 кв. см.

Ответ: 8800

Задание 3. Юля предположила, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что OC = R (рис. 2). Ответ дайте в сантиметрах.

Решение.

Рассмотрим прямоугольный треугольник с катетами d/2 и R-h и гипотенузой R.

По теореме Пифагора можно записать равенство:

Решаем уравнение относительно R, имеем:

Ответ: 65

Задание 4. Юля нашла площадь купола зонта как площадь поверхности сферического сегмента по формуле S = 2πRh, где R — радиус сферы, а h — высота сегмента. Рассчитайте площадь поверхности купола способом Юли. Число π округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.

Решение.

Подставим в формулу площади купола зонта числовые значения, получим:

Округляем до целого, имеем: 10613 см. кв.

Ответ: 10613

Задание 5. Рулон ткани имеет длину 30 м и ширину 90 см. На фабрике из этого рулона были вырезаны треугольные клинья для 27 зонтов, таких же, как зонт, который был у Иры и Юли. Каждый треугольник с учётом припуска на швы имеет площадь 1150 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?

Решение.

Вычислим площадь ткани в кв. см, получим:

S = 30∙100∙90 = 270 000 см. кв.

Площадь клиньев для 27 зонтов, равна:

27∙8∙1150 = 248 400 см. кв.

Площадь обрезков:

270 000 – 248 400 = 21 600 см. кв.

Что составляет:

Ответ: 8

Решение 5236. Длина зонта в сложенном виде равна 28 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,2 см.

Два друга Дима и Юра задумались о том, как рассчитать площадь поверхности зонта. На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из двенадцати отдельных клиньев, натянутых на каркас из двенадцати спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.

Дима и Юра сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 30 см. Высота купола зонта h (рис. 2) оказалась равна 29 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно 116 см.

Задание 1. Длина зонта в сложенном виде равна 28 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,2 см.

Решение.

Треть спицы будет равна

28 – 6,2 = 21,8 см

следовательно, длина всей спицы:

21,8∙3 = 65,4 см

Ответ: 65,4

Задание 2. Поскольку зонт сшит из треугольников, рассуждал Дима, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Димы, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 63,7 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.

Решение.

Высота h = 63,7 см, проведенная к основанию a = 30 см, дает площадь каждого сегмента, равную:

Так как таких сегментов 12, то получаем полную площадь поверхности:

кв. см

Округляем до десятков, получаем 11470 кв. см.

Ответ: 11470

Задание 3. Юра предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ОС = R (рис. 2). Ответ дайте в сантиметрах.

Решение.

Рассмотрим прямоугольный треугольник с катетами d/2 и R-h и гипотенузой R.

По теореме Пифагора можно записать равенство:

Решаем уравнение относительно R, имеем:

Ответ: 72,5

Задание 4. Юра нашёл площадь купола зонта как площадь поверхности сферического сегмента по формуле S = 2πRh, где R — радиус сферы, a h — высота сегмента. Рассчитайте площадь поверхности купола способом Юры. Число π округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.

Решение.

Подставим в формулу площади купола зонта числовые значения, получим:

Округляем до целого, имеем: 13204 см. кв.

Ответ: 13204

Задание 5. Рулон ткани имеет длину 16 м и ширину 150 см. На фабрике из этого рулона были вырезаны треугольные клинья для 18 зонтов, таких же, как зонт, который был у Димы и Юры. Каждый треугольник с учётом припуска на швы имеет площадь 1000 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?

Решение.

Вычислим площадь ткани в кв. см, получим:

S = 16∙100∙150 = 240 000 см. кв.

Площадь клиньев для 18 зонтов, равна:

18∙12∙1000 = 216 000 см. кв.

Площадь обрезков:

240 000 – 216 000 = 24 000 см. кв.

Что составляет:

Ответ: 10

Решение 2536. Длина зонта в сложенном виде равна 27 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,8 см.

Две подруги Оля и Аня задумались о том, как рассчитать площадь поверхности зонта. На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из двенадцати отдельных клиньев, натянутых на каркас из двенадцати спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.

Оля и Аня сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 28 см. Высота купола зонта h (рис. 2) оказалась равна 27 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно 108 см.

Задание 1. Длина зонта в сложенном виде равна 27 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,8 см.

Решение.

Треть спицы будет равна

27 – 6,8 = 20,2 см

следовательно, длина всей спицы:

20,2∙3 = 60,6 см

Ответ: 60,6

Задание 2. Поскольку зонт сшит из треугольников, рассуждала Оля, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Оли, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 59 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.

Решение.

Высота h = 59 см, проведенная к основанию a = 28 см, дает площадь каждого сегмента, равную:

Так как таких сегментов 12, то получаем полную площадь поверхности:

кв. см

Округляем до десятков, получаем 9910 кв. см.

Ответ: 9910

Задание 3. Аня предположила, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что OC = R (рис. 2). Ответ дайте в сантиметрах.

Решение.

Рассмотрим прямоугольный треугольник с катетами d/2 и R-h и гипотенузой R.

По теореме Пифагора можно записать равенство:

Решаем уравнение относительно R, имеем:

Ответ: 67,5

Задание 4. Аня нашла площадь купола зонта как площадь поверхности сферического сегмента по формуле S = 2πRh, где R — радиус сферы, a h — высота сегмента. Рассчитайте площадь поверхности купола способом Ани. Число π округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.

Решение.

Подставим в формулу площади купола зонта числовые значения, получим:

Округляем до целого, имеем: 11445 см. кв.

Ответ: 11445

Задание 5. Рулон ткани имеет длину 20 м и ширину 90 см. На фабрике из этого рулона были вырезаны треугольные клинья для 15 зонтов, таких же, как зонт, который был у Оли и Ани. Каждый треугольник с учётом припуска на швы имеет площадь 850 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?

Решение.

Вычислим площадь ткани в кв. см, получим:

S = 20∙100∙90 = 180 000 см. кв.

Площадь клиньев для 15 зонтов, равна:

15∙12∙850 = 153 000 см. кв.

Площадь обрезков:

180 000 – 153 000 = 27 000 см. кв.

Что составляет:

Ответ: 15

Решение 5336. Длина зонта в сложенном виде равна 26,5 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,3 см.

Две подруги Катя и Таня задумались о том, как рассчитать площадь поверхности зонта. На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из десяти отдельных клиньев, натянутых на каркас из десяти спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.

Катя и Таня сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 34 см. Высота купола зонта h (рис. 2) оказалась равна 25 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно 110 см.

Задание 1. Длина зонта в сложенном виде равна 26,5 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,3 см.

Решение.

Треть спицы будет равна

26,5 – 6,3 = 20,2 см

следовательно, длина всей спицы:

20,2∙3 = 60,6 см

Ответ: 60,6

Задание 2. Поскольку зонт сшит из треугольников, рассуждала Катя, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Кати, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 58,2 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.

Решение.

Высота h = 58,2 см, проведенная к основанию a = 34 см, дает площадь каждого сегмента, равную:

Так как таких сегментов 10, то получаем полную площадь поверхности:

кв. см

Округляем до десятков, получаем 9890 кв. см.

Ответ: 9890

Задание 3. Таня предположила, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ОС = R (рис. 2). Ответ дайте в сантиметрах.

Решение.

Рассмотрим прямоугольный треугольник с катетами d/2 и R-h и гипотенузой R.

По теореме Пифагора можно записать равенство:

Решаем уравнение относительно R, имеем:

Ответ: 73

Задание 4. Таня нашла площадь купола зонта как площадь поверхности сферического сегмента по формуле S = 2πRh, где R — радиус сферы, a h — высота сегмента. Рассчитайте площадь поверхности купола способом Тани. Число π округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.

Решение.

Подставим в формулу площади купола зонта числовые значения, получим:

Округляем до целого, имеем: 11461 см. кв.

Ответ: 11461

Задание 5. Рулон ткани имеет длину 20 м и ширину 150 см. На фабрике из этого рулона были вырезаны треугольные клинья для 26 зонтов, таких же, как зонт, который был у Кати и Тани. Каждый треугольник с учётом припуска на швы имеет площадь 1050 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?

Решение.

Вычислим площадь ткани в кв. см, получим:

S = 20∙100∙150 = 300 000 см. кв.

Площадь клиньев для 26 зонтов, равна:

26∙10∙1050 = 273 000 см. кв.

Площадь обрезков:

300 000 – 273 000 = 27 000 см. кв.

Что составляет:

Ответ: 9

Источник

4 вариант Ященко И.В ОГЭ 2023 по математике с ответами и решением из нового сборника 36 тренировочных вариантов ОГЭ 2023 по математике 9 класс с полным видео разбором варианта, данный вариант вы можете скачать или решать онлайн.

4 вариант Ященко ОГЭ 2023 математика 9 класс с ответами

4вариант-ященко-огэ2023-математика

Полное видео решение заданий варианта

Задание 1-5. Две подруги Оля и Таня задумались о том, как рассчитать площадь поверхности зонта. На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из двенадцати отдельных клиньев, натянутых на каркас из двенадцати спиц (рис. 1).

Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт. Оля и Таня сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 28 см. Высота купола зонта h (рис. 2) оказалась равна 27 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, – ровно 108 см.

Задание 1. Длина зонта в сложенном виде равна 27 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,8 см.

Задание 2. Поскольку зонт сшит из треугольников, — рассуждала Оля, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхностей зонта методом Оли, если высота равнобедренного треугольника, проведённая к основанию, равно 59 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.

Задание 3. Таня предположила, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что OC = R (рис. 2). Ответ дайте в сантиметрах.

Задание 4. Таня нашла площадь купола зонта как площадь поверхности сферического сегмента по формуле S=2пRh, где R-радиус сферы, а h- высота сегмента. Рассчитайте площадь поверхности купола способом Тани. Число пи округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.

Задание 5. Рулон ткани имеет длину 20 м и ширину 90 см. На фабрике из этого рулона были вырезаны треугольные клинья для 15 зонтов, таких же, как зонт, который был у Оли и Тани. Каждый треугольник с учётом припуска на швы имеет площадь 850 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?

Задание 10. Оксана, Даня, Ваня, Артём и Рустам бросили жребий – кому начинать игру. Найдите вероятность того, что начинать игру должна будет девочка.

Задание 14. В кафе есть только квадратные столики, за каждый из которых могут сесть 4 человека. Если сдвинуть два квадратных столика, то получится стол, за который могут сесть 6 человек. На рисунке изображён случай, когда сдвинули 3 квадратных столика вдоль одной линии. В этом случае получился стол, за который могут сесть 8 человек. Сколько человек может сесть за стол, который получится, если сдвинуть 22 квадратных столиков вдоль одной линии?

Задание 15. Один из острых углов прямоугольного треугольника равен 23°. Найдите его другой острый угол. Ответ дайте в градусах.

Задание 16. Радиус окружности, вписанной в прямоугольную трапецию, равен 18. Найдите высоту этой трапеции.

Задание 17. Площадь параллелограмма равна 48, а две его стороны равны 8 и 16. Найдите его высоты. В ответе укажите меньшую высоту.

Задание 19. Какое из следующих утверждений верно?

1) Вписанный угол, опирающийся на диаметр окружности, прямой.
2) Если три угла одного треугольника равны соответственно трём углам другого треугольника, то такие треугольники равны.
3) Отношение площадей подобных треугольников равно коэффициенту подобия.

Задание 21. Свежие фрукты содержат 72% воды, а высушенные – 26%. Сколько сухих фруктов получится из 222 кг свежих фруктов?

Задание 23. Найдите боковою сторону АВ трапеции АВСD, если углы АВС и ВСD равны соответственно 60° и 150°, а СD = 33.

Задание 24. Биссектрисы углов С и D параллелограмма ABCD пересекаются в точке L, лежащей на стороне AB. Докажите, что L – середина AB.

Задание 25. Окружности радиусов 36 и 45 касаются внешним образом. Точки А и В лежат на первой окружности, точки С и D – на второй. При этом АС и ВD – общие касательные окружностей. Найдите расстояние между прямыми АВ и СD.

Ответы для 4 варианта

Вариант 3 Ященко ОГЭ 2023 математика 9 класс с ответами и решением
Вариант 2 Ященко ОГЭ 2023 математика 9 класс с ответами и решением

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Источник

1. Длина зонта в сложенном состоянии равна 25 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,2 см.

Представим условие задачи в виде формулы:

Обозначим длину спицы за х, подставим все величины в формулу и решим получившееся линейное уравнение:

Ответ: 56,4.

2. Поскольку зонт сшит из треугольников, рассуждал Петя, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Пети, если высота каждого равнобедренного треугольника, проведенная к основанию, равна 53,1 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.

Площадь треугольника равна половине произведения основания и высоты, проведенной к этому основанию.

Высота дана и равна 53,1. Основание, а оно же — расстояние между концами соседних спиц, тоже дано и равно 38.

Найдем площадь одного треугольника:

Не забываем, что зонт состоит из восьми таких треугольников, их общая площадь будет равна

1008,9 · 8 = 8071,2.

Осталось округлить это число до десятков. За десятки отвечает цифра 7; после нее стоит цифра 1, значит цифра 7 остается без изменений, а все числа после нее обращаются в 0. Таким образом, 8071,2 ≈ 8070.

Ответ: 8070.

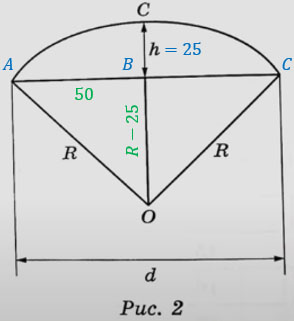
3. Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ОС=R (рис. 2). Ответ дайте в сантиметрах.

Из условия задачи нам известны h = 25 и d = AC = 100.

Зонт — это симметричная вещица, поэтому АВ = ВС = 50.

Если ОС = R и h = 25, то ОВ = R — 25.

Рассмотрим треугольник АВО. Очевидно, что он прямоугольный. Через теорему Пифагора найдем R:

Ответ: 62,5.

4. Вася нашел площадь купола зонта как площадь поверхности сферического сегмента по формуле S=2πRh, где R – радиус сферы, а h – высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число π округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.

R = 62,5 — из предыдущей задачи;

h = 25 — высота сегмента и высота купола равны между собой.

S = 2 · 3,14 · 62,5 · 25 = 9812,5 ≈ 9813.

Ответ: 9813.

5. Рулон ткани имеет длину 35 м и ширину 80 см. На фабрике из этого рулона были вырезаны треугольные клинья для 29 зонтов, таких же, как зонт, который был у Пети и Васи. Каждый треугольник с учетом припуска на швы имеет площадь 1050 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошла в обрезки?

Один зонт состоит из восьми треугольников, тогда 29 зонтов будут состоять из 232 треугольников.

Если на один треугольник требуется 1050 см² ткани, то на 232 треугольника нужно будет 1050 · 232 = 243 600 см².

Площадь ткани в рулоне равна 3500 · 80 = 280 000 см².

Площадь ткани, ушедшей в обрезки, равна 280 000 — 243 600 = 36 400 см².

Пусть 280 000 см² — 100%, а 36 400 — х%. Составим и решим пропорцию:

Ответ: 13.

А вы тоже находите проблему из ничего, как Вася и Петя?)

Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.

Источник

Задача «Зонтик»

Если присмотреться, то видно, что купол зонта состоит из двенадцати отдельных клиньев, натянутых на каркас из двенадцати спиц. Сферическая форма в раскрытом состоянии достигается за счет гибкости спиц и эластичности ткани, из которой изготовлен зонт.

Оля и Аня сумели измерить расстояние между концами соседних спиц а.
Оно оказалось равно 28 см.

Высота купола зонта h оказалась равна 27 см, а расстояние d
между концами спиц, образующих дугу окружности,
проходящей через вершину зонта, – равно 108 см.
h

Длина зонта в сложенном виде равна 27 см и складывается из длины
ручки и трети длины спицы (зонт в три сложения).
Найдите длину спицы, если длина ручки зонта равна 6,8 см.
Задача №1

Длина зонта в сложенном виде равна 27 см и складывается из длины
ручки и трети длины спицы (зонт в три сложения).
Найдите длину спицы, если длина ручки зонта равна 6,8 см.
Решение:
Задача №1
1) 27 см – 6,8 см = 20,2 см – третья часть спицы

Длина зонта в сложенном виде равна 27 см и складывается из длины
ручки и трети длины спицы (зонт в три сложения).
Найдите длину спицы, если длина ручки зонта равна 6,8 см.
Решение:
Ответ: 60,6 .
Задача №1
1) 27 см – 6,8 см = 20,2 см – третья часть спицы
2) 20,2 см · 3 = 60,6 см – длина спицы

Поскольку зонт сшит из треугольников, рассуждала Оля, то площадь его поверхности можно найти как сумму площадей треугольников. Высота каждого равнобедренного треугольника, проведенная к основанию, равна 59 см. Вычислите площадь поверхности зонта в квадратных сантиметрах с округлением до десятков.
Задача №2

Аня предположила, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ОС = R.
Ответ дайте в сантиметрах.
h
Задача №3

Аня предположила, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ОС = R.
Ответ дайте в сантиметрах.
h
Задача №3
Решение:

Аня предположила, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ОС = R.
Ответ дайте в сантиметрах.
h
Задача №3
Решение:
Ответ: 67,5.

Аня нашла площадь купола зонта по формуле S = 2πRh, где R – радиус сферы, h – высота сегмента. Рассчитайте площадь поверхности купола способом Ани. Число π округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.
h
Задача №4

Рулон ткани имеет длину 20 м и ширину 90 см. На фабрике из этого
рулона были вырезаны треугольные клинья для 15 зонтов, таких же,
как у Оли и Ани. Каждый треугольник имеет площадь 850 кв.см
с учетом припуска на швы. Оставшаяся ткань пошла в обрезки.
Сколько процентов ткани рулона пошло в обрезки?
h
Задача №5

Источник