Загрузить PDF
Загрузить PDF
Объем фигуры представляет собой занимаемое этой фигурой трехмерное пространство.[1]
Представьте себе объем как количество жидкости (или воздуха, или песка), которым можно заполнить данную фигуру. Объем измеряется в кубических единицах (мм3, см3, м3).[2]
Эта статья расскажет вам, как вычислять объем шести трехмерных фигур. Вы можете заметить, что многие формулы для вычисления объема схожи, что упрощает их запоминание.
-
1
Куб – это трехмерная фигура, которая имеет шесть одинаковых квадратных граней, то есть все ее стороны (ребра) равны.[3]
- Например, игральная кость – это куб.
-
2
Формула нахождения объема куба: V = s3, где V — объем, а s — длина ребра.
- Возведение в куб аналогично следующему умножению: s3 = s * s * s
-
3
Найдите длину стороны (ребра) куба. Она будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой). Так как ребра куба равны, измеряйте любое ребро.
- Если вы не уверены, что ваша фигура является кубом, измерьте каждую сторону, чтобы убедиться, что они равны. Если они не равны, перейдите к следующему разделу.
-
4
Подставьте длину ребра куба в формулу V = s3. Например, если ребро куба равно 5 см, напишите формулу следующим образом: V = 53 = 5 * 5 * 5 = 125 см3 – это объем куба.
-
5
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере ребро куба измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах. Если, например, сторона куба равна 3 см, то V = 33 = 27см3.
Реклама
-
1
Прямоугольный параллелепипед или прямоугольная призма – это трехмерная фигура с шестью гранями, каждая из которых является прямоугольником (вспомните коробку из под обуви). [4]
- Куб – это частный случай прямоугольного параллелепипеда, у которого все ребра равны.
-
2
Формула нахождения объема прямоугольного параллелепипеда или прямоугольной призмы: V = l*w*h, где V = объем, l = длина, w = ширина, h = высота.[5]
-
3
Длина прямоугольного параллелепипеда – это самое длинное ребро верхней или нижней грани, то есть грани, на которой стоит параллелепипед (нижняя грань) или параллельной ей грани (верхняя грань). Длина будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой).
- Пример: длина прямоугольного параллелепипеда равна 4 см, то есть l = 4 см.
- Не беспокойтесь о том, какие ребра выбрать в качестве длины, ширины и высоты. В любом случае в итоге вы получите правильный ответ (только измерьте три ребра, перпендикулярные друг другу).
-
4
Ширина прямоугольного параллелепипеда – это самое короткое ребро верхней или нижней грани, то есть грани, на которой стоит параллелепипед (нижняя грань) или параллельной ей грани (верхняя грань). Ширина будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой).
- Пример: ширина прямоугольного параллелепипеда равна 3 см, то есть w = 3 см.
- Если вы измеряете ребра параллелепипеда линейкой или рулеткой, не забудьте измерить их в одинаковых единицах измерения. Не измеряйте одно ребро в миллиметрах, а другое в сантиметрах.
-
5
Высота прямоугольного параллелепипеда – это расстояние между его нижней и верхней гранями. Высота будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой).
- Пример: высота прямоугольного параллелепипеда равна 6 см, то есть h = 6 см.
-
6
Подставьте найденные значения в формулу V = l*w*h.
- В нашем примере l = 4, w = 3 и h = 6. Поэтому V = 4*3*6 = 72.
-
7
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере ребра измерялись в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 72 см3.
- Если в прямоугольной призме l = 2 см, w = 4 см, h = 8 см, то V = 2*4*8 = 64 см3
Реклама
-
1
Цилиндр – это трехмерная фигура, ограниченная цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее.[6]
- Например, банка или батарейка АА имеют форму цилиндра.
-
2
Формула нахождения объема цилиндра: V = πr2h, где V — объем, h — высота, r – радиус основания и πr2 — площадь основания цилиндра.
- В некоторых задачах ответ требуется представить с пи, а в некоторых вместо пи подставить 3,14.
- Формула для нахождения объема цилиндра на самом деле очень похожа на формулу вычисления объема прямоугольной призмы, то есть вы перемножаете высоту и площадь основания. В прямоугольной призме площадь основания равна l*w, а в цилиндре она равна πr2.
-
3
Найдите радиус основания. Он, скорее всего, дан в задаче. Если дан диаметр, разделите его на 2, чтобы найти радиус (d = 2r).
-
4
Если радиус не дан, измерьте его. Для этого измерьте основание цилиндра при помощи линейки или рулетки. Измеряйте основание в его самой широкой части (то есть измерьте диаметр основания), а затем разделите полученное значение на 2, чтобы найти радиус.
- Другой вариант – измерьте длину окружности цилиндра (то есть измерьте обхват цилиндра) при помощи рулетки, а затем найдите радиус по формуле r = с/2π, где с – обхват (длина окружности) цилиндра (2π = 6,28).
- Например, если обхват цилиндра равен 8 см, то радиус будет равен 1,27 см.
- Если вам нужно точное измерение, вы можете использовать оба метода, чтобы убедиться, что значения радиуса совпадают (нахождение радиуса через длину окружности является более точным методом).
-
5
Вычислите площадь круглого основания. Для этого подставьте радиус в формулу πr2.
- Если радиус основания равен 4 см, то площадь основания равна π42.
- 42 = 4 * 4 = 16. 16*π = 16*3,14 = 50,24 см2
- Если дан диаметр основания, то помните, что d = 2r. Вам нужно разделить диаметр пополам, чтобы найти радиус.
-
6
Найдите высоту цилиндра. Это расстояние между двумя круглыми основаниями. Высота будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой).
-
7
Умножьте площадь основания на высоту цилиндра, чтобы найти его объем. Или же просто подставьте значения соответствующих величин в формулу V = πr2h. В нашем примере, когда радиус основания равен 4 см, а высота равна 10 см:
- V = π4210
- π42 = 50,24
- 50,24 * 10 = 502,4
- V = 502,4
-
8
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере все величины измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 502,4 см3.
Реклама
-
1
Пирамида – это трехмерная фигура, в основании которой лежит многоугольник, а грани являются треугольниками, имеющими общую вершину. [7]
Правильная пирамида – это трехмерная фигура, в основании которой лежит правильный многоугольник (с равными сторонами), а вершина проецируется в центр основания.[8]
- Обычно мы представляем пирамиду, имеющую квадратное основание, но в основании пирамиды может лежать многоугольник с 5, 6 или даже со 100 сторонами!
- Пирамида с круглым основанием называется конусом, который будет обсуждаться в следующем разделе.
-
2
Формула нахождения объема правильной пирамиды: V = 1/3bh, где b – площадь основания пирамиды, h – высота пирамиды (перпендикуляр, соединяющий основание и вершину пирамиды).
- Эта формула для вычисления объема пирамиды одинаково годна как для правильных пирамид (в которых вершина проецируется в центр основания), так и для наклонных (в которых вершина не проецируется в центр основания).
-
3
Вычислите площадь основания. Формула будет зависеть от фигуры, лежащей в основании пирамиды. В нашем примере в основании пирамиды лежит квадрат со стороной 6 см. Площадь квадрата равна s2, где s – сторона квадрата. Таким образом, в нашем примере площадь основания пирамиды равна 62 = 36 см2
- Площадь треугольника равна 1/2bh, где h – высота треугольника, b – сторона, к которой проведена высота.
- Площадь любого правильного многоугольника можно вычислить по формуле: А = 1/2ра, где А – площадь, р – периметр фигуры, а – апофема (отрезок, соединяющий центр фигуры с серединой любой стороны фигуры). Для получения дополнительной информации о нахождении площади многоугольников прочитайте эту статью.[9]
-
4
Найдите высоту пирамиды. Высота будет дана в задаче. В нашем примере высота пирамиды равна 10 см.
-
5
Умножьте площадь основания пирамиды на ее высоту, а затем разделите полученный результат на 3, чтобы найти объем пирамиды. Формула для вычисления объема пирамиды: V = 1/3bh. В нашем примере площадь основания равна 36, а высота равна 10, поэтому объем: 36*10*1/3 = 120.
- Если, например, дана пирамида с пятиугольным основанием площадью 26, а высота пирамиды равна 8, то объем пирамиды: 1/3*26*8 = 69,33.
-
6
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере все величины измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 120 см3.
Реклама
-
1
Конус – это трехмерная фигура, которая имеет круглое основание и одну вершину. Или конус – это особый случай пирамиды с круглым основанием.[10]
- Если вершина конуса находится непосредственно над центром круглого основания, то конус называется прямым; в противном случае конус называется наклонным. Но формула для вычисления объема конуса одинаковая для обоих типов конуса.
-
2
Формула для вычисления объема конуса: V = 1/3πr2h, где r – радиус круглого основания, h – высота конуса.
- b = πr2 – это площадь круглого основания конуса. Таким образом, формулу для вычисления объема конуса можно записать так: V = 1/3bh, что совпадает с формулой нахождения объема пирамиды!
-
3
Вычислите площадь круглого основания. Радиус должен быть дан в задаче. Если дан диаметр основания, то помните, что d = 2r. Вам нужно разделить диаметр пополам, чтобы найти радиус. Для вычисления площади круглого основания подставьте радиус в формулу πr2.
- Например, радиус круглого основания конуса равен 3 см. Тогда площадь этого основания равна π32.
- π32 = π(3*3) = 9π.
- = 28,27 см2
-
4
Найдите высоту конуса. Это перпендикуляр, опущенный из вершины к основанию пирамиды. В нашем примере высота конуса равна 5 см.
-
5
Перемножьте высоту конуса и площадь основания. В нашем примере площадь основания равна 28,27 см2, а высота равна 5 см, поэтому bh = 28,27 * 5 = 141,35.
-
6
Теперь умножьте полученный результат на 1/3 (или просто разделите его на 3), чтобы найти объем конуса. В описанном выше шаге вы нашли объем цилиндра, а объем конуса всегда в 3 раза меньше объема цилиндра.
- В нашем примере: 141,35 * 1/3 = 47,12 – это объем конуса.
- Или: 1/3π325 = 47,12
-
7
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере все величины измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 47,12 см3.
Реклама
-
1
Шар – это идеально круглая трехмерная фигура, каждая точка поверхности которой равноудалена от одной точки (центра шара). [11]
-
2
Формула для вычисления объема шара: V = 4/3πr3, где r – радиус шара.[12]
-
3
Найдите радиус шара. Радиус должен быть дан в задаче. Если дан диаметр шара, то помните, что d = 2r. Вам нужно разделить диаметр пополам, чтобы найти радиус. Например, радиус шара равен 3 см.
-
4
Если радиус не дан, вычислите его. Для этого измерьте длину окружности шара (например, теннисного мяча) в его самой широкой части при помощи веревки, нити или другого подобного предмета. Затем измерьте длину веревки, чтобы найти длину окружности. Разделите полученное значение на 2π (или на 6,28), чтобы вычислить радиус шара.
- Например, если вы измерили мяч и нашли, что длина его окружности равна 18 см, разделите это число на 6,28 и получите, что радиус мяча равен 2,87 см.
- Проделайте 3 измерения окружности шара, а затем усредните полученные значения (для этого сложите их и сумму разделите на 3), чтобы убедиться, что вы получили значение, близкое к истинному.
- Например, в результате трех измерений длины окружности вы получили следующие результаты: 18 см, 17,75 см, 18,2 см. Сложите эти значения: 18 + 17,5 + 18,2 = 53,95, а затем разделите их на 3: 53,95/3 = 17,98. Используйте это среднее значение в расчетах объема шара.
-
5
Возведите радиус в куб (r3). То есть r3 = r*r*r. В нашем примере r = 3, поэтому r3 = 3 * 3 * 3 = 27.
-
6
Теперь умножьте полученный результат на 4/3. Вы можете использовать калькулятор или выполнить умножение вручную, а затем упростить дробь. В нашем примере: 27*4/3 = 108/3 = 36.
-
7
Умножьте полученный результат на π (3,14), чтобы найти объем шара.
- В нашем примере: 36*3,14 = 113,09.
-
8
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере все величины измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 113,09 см3.
Реклама
Об этой статье
Эту страницу просматривали 74 719 раз.
Была ли эта статья полезной?
Download Article
Download Article
The volume of a shape is the measure of how much three-dimensional space that shape takes up.[1]
You can also think of the volume of a shape as how much water (or air, or sand, etc.) the shape could hold if it was filled completely. Common units of volume include cubic centimeters (cm3), cubic meters (m3), cubic inches (in3), and cubic feet (ft3).[2]
This article will teach you how to calculate the volume of six different three-dimensional shapes that are commonly found on math tests, including cubes, spheres, and cones. You might notice that a lot of the volume formulas share similarities that can make them easier to remember. See if you can spot them along the way!
-
1
Recognize a cube. A cube is a three-dimensional shape that has six identical square faces.[3]
In other words, it is a box shape with equal sides all around.- A 6-sided die is a good example of a cube you might find in your house. Sugar cubes, and children’s letter blocks are also usually cubes.
-
2
Learn the formula for the volume of a cube. Since all of the side lengths of a cube are the same, the formula for the volume of a cube is really easy. It is V = s3 where V stands for volume, and s is the length of the sides of the cube.[4]
- To find s3, simply multiply s by itself 3 times: s3 = s * s * s
Advertisement
-
3
Find the length of one side of the cube. Depending on your assignment, the cube will either be labeled with this information, or you may have to measure the side length with a ruler. Remember that since it is a cube, all of the side lengths should be equal so it doesn’t matter which one you measure.
- If you are not 100% sure that your shape is a cube, measure each of the sides to determine if they are equal. If they are not, you will need to use the method below for Calculating the Volume of a Rectangular Solid.
-
4
Plug the side length into the formula V = s3 and calculate. For example, if you find that the length of the sides of your cube is 5 inches, then you should write the formula out as follows: V = (5 in)3. 5 in * 5 in * 5 in = 125 in3, the volume of our cube!
- Make sure all of the lengths are in the same unit before multiplying them.[5]
- Make sure all of the lengths are in the same unit before multiplying them.[5]
-
5
Be sure to state your answer in cubic units.[6]
In the above example, the side length of our cube was measured in inches, so the volume was given in cubic inches. If the side length of the cube had been 3 centimeters, for example, the volume would be V = (3 cm)3, or V = 27cm3.
Advertisement
-
1
Recognize a rectangular solid. A rectangular solid, also known as a rectangular prism, is a three-dimensional shape with six sides that are all rectangles.[7]
In other words, a rectangular solid is simply a three-dimensional rectangle, or box shape.- A cube is really just a special rectangular solid in which the sides of all of the rectangles are equal.
-
2
Learn the formula for calculating the volume of a rectangular solid. The formula for the volume of a rectangular solid is Volume = length * width * height, or V = lwh.
-
3
Find the length of the rectangular solid. The length is the longest side of the rectangular solid that is parallel to the ground or surface it is resting on. The length may be given in a diagram, or you may need to measure it with a ruler or tape measure.
- Example: The length of this rectangular solid is 4 inches, so l = 4 in.
- Don’t worry too much about which side is the length, which is the width, etc. As long as you end up with three different measurements, the math will come out the same regardless of how your arrange the terms.
-
4
Find the width of the rectangular solid. The width of the rectangular solid is the measurement of the shorter side of the solid, parallel to the ground or surface the shape is resting on. Again, look for a label on the diagram indicating the width, or measure your shape with a ruler or tape measure.
- Example: The width of this rectangular solid is 3 inches, so w = 3 in.
- If you are measuring the rectangular solid with a ruler or tape measure, remember to take and record all measurements in the same units. Don’t measure one side in inches another in centimeters; all measurements must use the same unit!
-
5
Find the height of the rectangular solid. This height is the distance from the ground or surface the rectangular solid is resting on to the top of the rectangular solid. Locate the information in your diagram, or measure the height using a ruler or tape measure.
- Example: The height of this rectangular solid is 6 inches, so h = 6 in.
-
6
Plug the dimensions of the rectangular solid into the volume formula and calculate. Remember that V = lwh.
- In our example, l = 4, w = 3, and h = 6. Therefore, V = 4 * 3 * 6, or 72.
-
7
Be sure to express your answer in cubic units. Since our example rectangle was measured in inches, the volume should be written as 72 cubic inches, or 72 in3.
- If the measurements of our rectangular solid were: length = 2 cm, width = 4 cm, and height = 8 cm, the Volume would be 2 cm * 4 cm * 8 cm, or 64cm3.
Advertisement
-
1
Learn to identify a cylinder. A cylinder is a three-dimensional shape that has two identical flat ends that are circular in shape, and a single curved side that connects them.[8]
- A can is a good example of a cylinder, so is a AA or AAA battery.
-
2
Memorize the formula for the volume of a cylinder. To calculate the volume of a cylinder, you must know its height and the radius of the circular base (the distance from the center of the circle to its edge) at the top and bottom. The formula is V = πr2h, where V is the Volume, r is the radius of the circular base, h is the height, and π is the constant pi.
- In some geometry problems the answer will be given in terms of pi, but in most cases it is sufficient to round pi to 3.14. Check with your instructor to find out what she would prefer.
- The formula for finding the volume of a cylinder is actually very similar to that for a rectangular solid: you are simply multiplying the height of the shape by the surface area of its base. In a rectangular solid, that surface area is l * w, for the cylinder it is πr2, the area of a circle with radius r.
-
3
Find the radius of the base.[9]
If it is given in the diagram, simply use that number. If the diameter is given instead of the radius, you simply need to divide the value by 2 to get the radius (d = 2r). -
4
Measure the object if the radius is not given. Be aware that getting precise measurement of a circular solid can be a bit tricky. One option is to measure the base of the cylinder across the top with a ruler or tape measure. Do your best to measure the width of the cylinder at its widest part, and divide that measurement by 2 to find the radius.
- Another option is to measure the circumference of the cylinder (the distance around it) using a tape measure or a length of string that you can mark and then measure with a ruler. Then plug the measurement into the formula: C (circumference) = 2πr. Divide the circumference by 2π (6.28) and that will give you the radius.
- For example, if the circumference you measured was 8 inches, the radius would be 1.27in.
- If you need a really precise measurement, you might use both methods to make sure that your measurements are similar. If they are not, double check them. The circumference method will usually yield more accurate results.
-
5
Calculate the area of the circular base.[10]
Plug the radius of the base into the formula πr2. Then multiply the radius by itself one time, and then multiply the product by π. For example:- If the radius of the circle is equal to 4 inches, the area of the base will be A = π42.
- 42 = 4 * 4, or 16. 16 * π (3.14) = 50.24 in2
- If the diameter of the base is given instead of the radius, remember that d = 2r. You simply need to divide the diameter in half to find the radius.
-
6
Find the height of the cylinder.[11]
This is simply the distance between the two circular bases, or the distance from the surface the cylinder is resting on to its top. Find the label in your diagram that indicates the height of the cylinder, or measure the height with a ruler or tape measure. -
7
Multiply the area of the base times the height of the cylinder to find the volume.[12]
Or you can save a step and simply plug the values for the cylinder’s dimensions into the formula V = πr2h. For our example cylinder with radius 4 inches and height 10 inches:- V = π4210
- π42 = 50.24
- 50.24 * 10 = 502.4
- V = 502.4
-
8
Remember to state your answer in cubic units. Our example cylinder was measured in inches, so the volume must be expressed in cubic inches: V = 502.4in3. If our cylinder had been measured in centimeters, the volume would be expressed in cubic centimeters (cm3).
Advertisement
-
1
Understand what a regular pyramid is. A pyramid is a three-dimensional shape with a polygon for a base, and lateral faces that taper at an apex (the point of the pyramid).[13]
A regular pyramid is a pyramid in which the base of the pyramid is a regular polygon, meaning that all of the sides of the polygon are equal in length, and all of the angles are equal in measure.[14]
- We most commonly imagine a pyramid as having a square base, and sides that taper up to a single point, but the base of a pyramid can actually have 5, 6, or even 100 sides!
- A pyramid with a circular base is called a cone, which will be discussed in the next method.
-
2
Learn the formula for the volume of a regular pyramid. The formula for the volume of a regular pyramid is V = 1/3bh, where b is the area of the base of the pyramid (the polygon at the bottom) and h is the height of the pyramid, or the vertical distance from the base to the apex (point).
- The volume formula is the same for right pyramids, in which the apex is directly above the center of the base, and for oblique pyramids, in which the apex is not centered.
-
3
Calculate the area of the base. The formula for this will depend on the number of sides the base of the pyramid has. In the pyramid in our diagram, the base is a square with sides that are 6 inches in length. Remember that the formula for the area of a square is A = s2 where s is the length of the sides. So for this pyramid, the area of the base is (6 in) 2, or 36in2.
- The formula for the area of a triangle is: A = 1/2bh, where b is the base of the triangle and h is the height.
- It is possible to find the area of any regular polygon using the formula A = 1/2pa, where A is the area, p is the perimeter of the shape, and a is the apothem, or distance from the center of the shape to the midpoint of any of its sides. This is a pretty involved calculation that goes beyond the scope of this article, but check out Calculate the Area of a Polygon for some great instructions on how to use it. Or you can make your life easy and search for a Regular Polygon Calculator online.[15]
-
4
Find the height of the pyramid. In most cases, this will be indicated in the diagram. In our example, the height of the pyramid is 10 inches.
-
5
Multiply the area of the base of the pyramid by its height, and divide by 3 to find the volume. Remember that the formula for the volume is V = 1/3bh. In our example pyramid, that had a base with area 36 and height 10, the volume is: 36 * 10 * 1/3, or 120.
- If we had a different pyramid, with a pentagonal base with area 26, and height of 8, the volume would be: 1/3 * 26 * 8 = 69.33.
-
6
Remember to express your answer in cubic units. The measurements of our example pyramid were given in inches, so its volume must be expressed in cubic inches, 120in. If our pyramid had been measured in meters, the volume would be expressed in cubic meters (m3) instead.3
Advertisement
-
1
Learn the properties of a cone. A cone is a 3-dimesional solid that has a circular base and a single vertex (the point of the cone). Another way to think of this is that a cone is a special pyramid that has a circular base.[16]
- If the vertex of the cone is directly above the center of the circular base, the cone is called a «right cone». If it is not directly over the center, the cone is called an «oblique cone.» Fortunately, the formula for calculating the area of a cone is the same whether it is right or oblique.
-
2
Know the formula for calculating the volume of a cone. The formula is V = 1/3πr2h, where r is the radius of the circular base of the cone, h is the height of the cone, and π is the constant pi, which can be rounded to 3.14.
- The πr2 part of the formula refers to the area of the circular base of the cone. The formula for the volume of the cone is thus 1/3bh, just like the formula for the volume of a pyramid in the method above!
-
3
Calculate the area of the circular base of the cone. To do this, you need to know the radius of the base, which should be listed in your diagram. If you are instead given the diameter of the circular base, simply divide that number by 2, since the diameter is simply 2 times the radios (d = 2r). Then plug the radius into the formula A = πr2 to calculate the area.
- In the example in the diagram, the radius of the circular base of the cone is 3 inches. When we plug that into the formula we get: A = π32.
- 32 = 3 *3, or 0, so A = 9π.
- A = 28.27in2
-
4
Find the height of the cone. This is the vertical distance between the base of the cone, and its apex. In our example, the height of the cone is 5 inches.
-
5
Multiply the height of the cone by the area of the base. In our example, the area of the base is 28.27in2 and the height is 5in, so bh = 28.27 * 5 = 141.35.
-
6
Now multiply the result by 1/3 (or simply divide by 3) to find the volume of the cone. In the above step, we actually calculated the volume of the cylinder that would be formed if the walls of the cone extended straight up to another circle, instead of slanting in to a single point. Dividing by 3 gives us the volume of just the cone itself.
- In our example, 141.35 * 1/3 = 47.12, the volume of our cone.
- To restate it, 1/3π325 = 47.12
-
7
Remember to express your answer in cubic units. Our cone was measured in inches, so its volume must be expressed in cubic inches: 47.12in3.
Advertisement
-
1
Spot a sphere. A sphere is a perfectly round three-dimensional object, in which every point on the surface is an equal distance from the center. In other words, a sphere is a ball-shaped object.[17]
-
2
Learn the formula for the volume of a sphere. The formula for the volume of a sphere is V = 4/3πr3 (stated: «four-thirds times pi r-cubed») where r is the radius of the sphere, and π is the constant pi (3.14).[18]
-
3
Find the radius of the sphere. If the radius is given in the diagram, then finding r is simply a matter of locating it. If the diameter is given, you must divide this number by 2 to find the radius. For example, the radius of the sphere in the diagram is 3 inches.
-
4
Measure the sphere if the radius is not given. If you need to measure a spherical object (like a tennis ball) to find the radius, first find a piece of string large enough to wrap around the object. Then wrap the string around the object at its widest point and mark the points where the string overlaps itself. Then measure the string with a ruler to find the circumference. Divide that value by 2π, or 6.28, and that will give you the radius of the sphere.
- For example, if you measure a ball and find its circumference is 18 inches, divide that number by 6.28 and you will find that the radius is 2.87in.
- Measuring a spherical object can be a little tricky, so you might want to take 3 different measurements, and then average them together (add the three measurements together, then divide by 3) to make sure you have the most accurate value possible.
- For example, if your three circumference measurements were 18 inches, 17.75 inches, and 18.2 inches, you would add those three values together (18 + 17.5 + 18.2 = 53.95) and divide that value by 3 (53.95/3 = 17.98). Use this average value in your volume calculations.
-
5
Cube the radius to find r3. Cubing a number simply means multiplying the number by itself 3 times, so r3 = r * r * r. In our example, r = 3, so r3 = 3 * 3 * 3, or 27.
-
6
Now multiply your answer by 4/3. You can either use your calculator, or do the multiplication by hand and then simplify the fraction. In our example, multiplying 27 by 4/3 = 108/3, or 36.
-
7
Multiply the result by π to find the volume of the sphere. The last step in calculating the volume is simply to multiply the result so far by π. Rounding π to two digits is usually sufficient for most math problems (unless your teacher specified otherwise,) so multiply by 3.14 and you have your answer.
- In our example, 36 * 3.14 = 113.09.
-
8
Express your answer in cubic units. In our example, the measurement of the radius of the sphere was in inches, so our answer is actually V = 113.09 cubic inches (113.09 in3).
Advertisement
Worksheet and Practice Problems
Add New Question
-
Question
How do you find the volume of a box?
Grace Imson, MA
Math Instructor, City College of San Francisco
Grace Imson is a math teacher with over 40 years of teaching experience. Grace is currently a math instructor at the City College of San Francisco and was previously in the Math Department at Saint Louis University. She has taught math at the elementary, middle, high school, and college levels. She has an MA in Education, specializing in Administration and Supervision from Saint Louis University.
Math Instructor, City College of San Francisco
Expert Answer
Support wikiHow by
unlocking this expert answer.The volume of a box is equal to the product of the three dimensions of the box. You would multiply the length, the width, and the height of the box to find its volume. Make sure the dimensions have the same unit. Some tricky questions give different units for each dimension.
-
Question
How would you find the volume of a water tank?
Grace Imson, MA
Math Instructor, City College of San Francisco
Grace Imson is a math teacher with over 40 years of teaching experience. Grace is currently a math instructor at the City College of San Francisco and was previously in the Math Department at Saint Louis University. She has taught math at the elementary, middle, high school, and college levels. She has an MA in Education, specializing in Administration and Supervision from Saint Louis University.
Math Instructor, City College of San Francisco
Expert Answer
Support wikiHow by
unlocking this expert answer.Assuming the tank is a cylinder, you’ll need the radius or diameter of one of the circular bases as well as the height of the tank. Calculate the area of the circle using πr² (if you have the diameter, divide it in half to get the radius). Then, just multiply the area of the circular base by the height of the tank to find its volume.
-
Question
How do I calculate the volume of compound shapes?
If the compound shapes are made up of basic geometric solids, then you can try dissecting them into their simpler parts. Their volumes will be additive.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Things You’ll Need
- Writing utensil
- Paper
- Calculator (optional)
- Ruler (optional)
References
- ↑ https://www.nist.gov/pml/owm/si-units-volume
- ↑ http://www.mathsisfun.com/measure/us-standard-volume.html
- ↑ https://www.mathsisfun.com/definitions/cube.html
- ↑ Grace Imson, MA. Math Instructor, City College of San Francisco. Expert Interview. 1 November 2019.
- ↑ Grace Imson, MA. Math Instructor, City College of San Francisco. Expert Interview. 1 November 2019.
- ↑ Grace Imson, MA. Math Instructor, City College of San Francisco. Expert Interview. 1 November 2019.
- ↑ http://www.algebralab.org/lessons/lesson.aspx?file=Geometry_3Dprisms.xml
- ↑ https://www.mathsisfun.com/definitions/cylinder.html
- ↑ Grace Imson, MA. Math Instructor, City College of San Francisco. Expert Interview. 1 November 2019.
- ↑ Grace Imson, MA. Math Instructor, City College of San Francisco. Expert Interview. 1 November 2019.
- ↑ Grace Imson, MA. Math Instructor, City College of San Francisco. Expert Interview. 1 November 2019.
- ↑ Grace Imson, MA. Math Instructor, City College of San Francisco. Expert Interview. 1 November 2019.
- ↑ http://www.mathwords.com/p/pyramid.htm
- ↑ http://www.mathwords.com/r/regular_pyramid.htm
- ↑ http://www.calculatorsoup.com/calculators/geometry-plane/polygon.php
- ↑ http://www.mathopenref.com/cone.html
- ↑ https://www.mathsisfun.com/definitions/sphere.html
- ↑ https://www.splashlearn.com/math-vocabulary/geometry/volume
About This Article
Article SummaryX
To calculate volume with a cube, use the formula v = s^3, where s is the length of the sides of the cube. To calculate the volume of a cylinder, use the formula v = hπr^2, where r is the radius of the base, h is the height, and π is pi. If you’re trying to find the volume of a rectangular prism, use the formula v = lwh, where l is the length, w is the width, and h is the height. If you need to learn how to calculate the volume of a sphere or pyramid, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 1,417,412 times.
Reader Success Stories
-
«Thanks. I was doing science homework, and it said to find the volume of an object. I chose one shaped like a cake…» more
Did this article help you?
План урока:
Понятие объема
Свойства объема
Объем куба и прямоугольного параллелепипеда
Объем прямой призмы
Объем цилиндра
Понятие объема
Понятие объема появилось у человечества задолго до того, как геометрия оформилась как строгая наука. Многие вещества и товары, такие как зерно, рис и вода, необходимо хранить и транспортировать в различных упаковках (сосуды, бочки, ящики, контейнеры). При этом разные емкости могут вместить разное количество товаров. Например, пусть есть бочка, имеющая форму цилиндра, и контейнер, выглядящий как прямоугольный параллелепипед:
Предположим, что в бочку можно поместить 5 кг пшеницы, а в контейнер помещается уже 15 кг пшеницы, то есть в контейнер можно положить в 3 раза больше пшеницы, чем в бочку. Можно сказать, что вместимость контейнера втрое больше вместимости бочки. Однако измерять вместимость емкости с помощью массы пшеницы, помещаемой в него, неудобно, ведь в них можно класть и другие вещества. Мы можем положить в емкости что-нибудь более тяжелое, например сухой песок. Тогда в бочку может влезть уже 10 кг песка, а в контейнер – 30 кг. И снова получается, что вместимость контейнера втрое больше, хотя масса вещества увеличилась.
Именно для измерения вместимости и было введено понятие объема. Если в одну упаковку помещается вдвое больше товаров, чем во вторую упаковку, то и объем у нее будет вдвое больше. С древнейших времен замечено, что отношение объемов двух сосудов не зависит от того вещества, которое в них хранят. Например, если в один сосуд помещается в 5 раз больше риса, чем в другой сосуд, то в него также будет помещаться в 5 раз больше воды, в 5 раз больше песка, в 5 раз больше нефти и т. д. Таким образом, в практическом смысле объем – это количественная характеристика вместимости тех или иных упаковок.
В рамках стереометрии изучаются не реальные сосуды, а абстрактные тела. Каждое из них занимает определенную часть пространства, большую или меньшую. Объем используется для измерения этих частей пространства. Для обозначения объема используется латинская буква V.
Для измерения объема необходима единица измерения. Условно принимается, что куб, чьим ребром является единичный отрезок, имеет объем, равный единице. Такой куб именуется единичным. Заметим, что грани единичного куба – это единичные квадраты.
В случае, когда длина ребра куба является безразмерной величиной, то объем также будет безразмерной величиной. Если же указана единица измерения длины, то объем куба будет измеряться этой же единицей, к которой приписано слово «кубический». Например, если ребро куба равно 1 м, то объем куба будет равен 1 кубическому метру, или 1 м3. Объем куба с ребром 1 мм будет составлять 1 мм3 и т. д.

Свойства объема
Свойства объема во многом совпадают со свойствами площади. Ясно, что у равных тел будут одинаковы и объемы.
Второе свойство объема связано с тем, что он является аддитивной величиной. Это значит, что если тело можно разбить на несколько тел, то его объем будет равен сумме объемов этих тел.
Это свойство аддитивности объема уже позволяет решать некоторые стереометрические задачи.
Задание. Тело состоит из цилиндра объемом 12 см3 и конуса объемом 4 см3. Каков объем этого тела?
Решение. Здесь надо просто сложить объемы цилиндра и конуса, чтобы найти общий объем всей фигуры:
Ответ: 16 см3.
Задание. Найдите объем фигуры, показанной на рисунке:
Решение. Данную фигуру несложно разбить на три единичных куба:
Тогда объем тела будет равен сумме объемов трех единичных кубов, то есть трем:
Ответ: 3.
Задание. Вычислите объем фигуры, получающейся при рассечении куба плоскостью, проходящей через два его ребра.
Решение. Ясно, что такая секущая плоскость будет делить куб на две равные фигуры (иначе просто не удастся провести плоскость через два ребра):
Также понятно, что два получившихся многогранника равны друг другу. Обозначим объем каждого из них как V. Тогда в сумме их объем должен быть равен 1, ведь вместе эти фигуры образуют единичный куб. Это позволяет составить уравнение, из которого можно вычислить величину V:
Объем куба и прямоугольного параллелепипеда
Докажем важную вспомогательную теорему:
Действительно, пусть у двух параллелепипедов одинаковы основания. Тогда их можно совместить. Пусть общим основанием будет АВСD, а высотами параллелепипедов будут отрезки АР и АК, причем АР <АК. Объем меньшего параллелепипеда с высотой АР обозначим как VР, а большего – как VK:
Нам надо доказать, что объемы фигур пропорциональны их высотам:
Для начала рассмотрим случай, когда отношение высот является рациональным числом. Это означает, что существует некоторая дробь m/n, такая, что
где m и n – натуральные числа. Тогда разобьем отрезок АК как раз на n равных отрезков. В этом случае отрезок АР будет состоять в точности из m таких отрезков. Далее через концы отрезков проведем плоскости, параллельные основанию:
В результате мы получили n равных параллелепипедов («пластин»), которые все вместе образуют большой параллелепипед объемом VK. Поэтому объем одной такой пластины равен величине VK/n:
Итак, мы доказали теорему для случая, когда отношение высот является рациональным числом. Теперь перейдем к более сложному случаю, когда это отношение представляет собой иррациональное число. Здесь можно рассуждать от противного. Предположим, что теорема ошибочна, тогда для каких-нибудь двух параллелепипедов отношение их объемов будет равно не отношению их высот, а какому-то другому числу k:
Это значит, что k либо меньше, либо больше, чем отношение АР/АК. Рассмотрим случай, когда k< АР/АК (случай, когда k> АР/АК, рассматривается аналогичным образом). Тогда возьмем какое-нибудь рациональное число R, находящееся между числами k и АР/АК:
(Примечание. Здесь мы неявно используем утверждение, которое можно доказать в рамках алгебры – между любыми двумя различными действительными числами располагается хотя бы одно рациональное число).
Умножим это неравенство на длину АК:
Построим параллелепипеды с общим основанием АВСD и высотами АК и АР, а также с высотой АЕ = R•АК. Так как R•АК < АР, то точка Е будет лежать между А и Р:
Объем параллелепипеда с высотой АЕ обозначим как VЕ. Ясно, что
ведь число k не может быть одновременно и больше, и меньше R. Полученное противоречие означает, что исходное предположение об ошибочности теоремы неверно, и на самом деле она справедлива, ч. т. д.
Теперь с помощью доказанной теоремы можно вывести известную ещё из младших классов формулу для расчета объема прямоугольного параллелепипеда.Пусть измерения прямоугольного параллелепипеда являются числами а, b и c. Построим:
- единичный куб;
- параллелепипед с габаритами а, 1, 1 с объемом V1;
- параллелепипед с габаритами а, b, 1 с объемом V2;
- параллелепипед с габаритами а, b, c с объемом V.
Тогда можно последовательно вычислить их объемы. Объем первого параллелепипеда будет в а раз больше объема единичного куба, то есть он будет равен а. Объем второго параллелепипеда будет больше ещё в bраз, а третьего – ещё в с раз:
Соответственно, для расчета объема параллелепипеда используется формула
Иногда эту формулу формулируют несколько иначе: объем параллелепипеда – это произведение площади его основания на длину высоты, перпендикулярной этому основанию.
Задание. Три смежных ребра прямоугольного параллелепипеда имеют длины 9, 4 и 7 см. Каков объем параллелепипеда?
Решение. Здесь надо просто перемножить габариты параллелепипеда:
Ответ: 252 см3.
Куб можно рассматривать как прямоугольный параллелепипед с одинаковыми измерениями. Поэтому для вычисления его объема надо умножить ребро куба само на себя дважды, то есть возвести его в куб.
Задание. Вычислите объем куба с ребром 8 метров.
Решение. Просто возводим сторону ребро куба в третью степень:
Задание. Если ребро куба увеличить на 2 дм, то его объем вырастет на 98 дм3. Какова длина ребра этого куба?
Решение. Обозначим длину ребра буквой х. Тогда объем куба будет составлять х3 дм. Если ребро увеличить на 2 дм, то оно будет иметь длину х + 2 дм, и тогда объем куба будет равен уже (х + 2)3 дм. Условие задачи можно записать в виде уравнения:
Это квадратное уравнение имеет два корня, 3 и (– 5), что можно проверить с помощью теоремы Виета. Корень х = – 5 не имеет геометрического смысла, поэтому остается ответ х = 3.
Ответ: 3 дм.
Далее рассмотрим перевод единиц измерения объема. Например, как перевести 1 м3 в кубические сантиметры? Рассмотрим куб с ребром 1 м. Ясно, что его объем будет равен 1 м3. С другой стороны, можно сказать, что длина ребра этого куба составляет 100 см:
Тогда объем этого куба можно посчитать так:
Аналогично можно переводить и другие единицы измерения.
Объем прямой призмы
Рассмотрим сначала прямую призму, в чьем основании располагается прямоугольный треугольник. Ее можно достроить до прямоугольного параллелепипеда:
Ясно, что объем параллелепипеда будет вдвое больше объема исходной призмы, ведь он состоит из двух таких призм. Аналогично и площадь основания у параллелепипеда будет вдвое больше. Обозначим площадь основания призмы буквой S, а ее высоту как h, тогда площадь основания параллелепипеда будет 2S, а его объем составит 2S•h. Тогда объем призмы будет вдвое меньше, то есть он окажется равным S•h.
Далее рассмотрим прямую призму, в основании которой лежит уже произвольный треугольник. Проведем в этом треугольнике высоту, которая упадет на противоположную сторону (такую высоту всегда можно провести). Далее через эту высоту проведем плоскость, перпендикулярную основанию. В результате мы разделим призму на две прямых призмы, в основании каждой из которых будет лежать прямоугольный треугольник:
Пусть площади получившихся прямоугольных треугольников обозначены как S1и S2, а общая площадь основания исходной призмы – это S. Мы можем вычислить объемы этих призм:
Теперь, наконец, рассмотрим прямую призму, чье основание – произвольный многоугольник. Этот многоугольник можно разбить на несколько треугольников с площадями S1, S2, S3…, а призма соответственно будет разбита на несколько треугольных призм с объемами V1, V2, V3 и. т. д.
Объем каждой треугольный призмы мы можем рассчитать:
Задание. Все ребра правильной шестиугольной призмы одинаковы, их длина обозначена буквой а. Найдите объем такой призмы.
Решение. Сначала необходимо найти площадь основания призмы, то есть площадь правильного шестиугольника. Напомним формулы для правильных многоугольников, изученные ещё в девятом классе:
Для вычисления объема надо лишь умножить полученную площадь на высоту призмы, а она также равна а:
Задание. В кубе АВСDА1В1С1D1 через середины ребер СD и BC проведено сечение, параллельное ребру СС1. Это сечение отсекает от куба треугольную призму, чей объем равен 19. Найдите объем куба.
Решение. Ясно, что и куб, и треугольная призма будут прямыми призмами, причем у них одинаковая высота СС1. Тогда можно утверждать, что отношение их объемов равно отношению площадей их оснований:
Пусть сторона АВ имеет длину а. Тогда площадь квадрата АВСD будет составлять а2. Отрезки ЕС и FC будут вдвое короче АВ, то есть их длина составляет a/2. ∆EFC – прямоугольный, и его площадь может быть рассчитана как половина произведения его катетов:
Объем цилиндра
Цилиндр не получится разбить на несколько призм, поэтому для вычисления его объема используется другой метод. Впишем цилиндр в правильную n-угольную призму. Одновременно построим и другую правильную n-угольную призму, которая сама будет вписана в цилиндр. Объем вписанной призмы обозначим как Vв, а объем описанной призмы как Vо. Объем самого цилиндра – это Vц. При этом высоты всех трех фигур одинаковы:
Ясно, что объем вписанной призмы меньше объема цилиндра, а тот в свою очередь меньше объема описанной призмы:
Теперь будем неограниченно увеличивать число n. При этом площади Sв и Sо будут стремиться к площади основания цилиндра, равной величине πr2, где r– радиус основания цилиндра. Это возможно лишь в том случае, если справедливо равенство
Задание. Найдите объем цилиндра с высотой 5 см и радиусом 6 см.
Решение. Сначала находим площадь основания:
Задание. Известно, что высота цилиндра вдвое больше его радиуса, а объем цилиндра равен 54π. Найдите радиус цилиндра.
Решение. Обозначим радиус цилиндра буквой х. Тогда по условию высота будет вдвое больше, то есть она составит 2х. Вычислим объем цилиндра:
Ответ: 3.
Задание. Труба изготовлена из металла с плотностью 11,4 г/см3. Внутренний диаметр трубы равен 13 мм, а ее стенка имеет толщину 4 мм. Длина трубы – 25 метров. Какова ее масса?
Решение. Для расчета массы необходимо сперва вычислить объем трубы. Ясно, что если к объему трубы прибавить объем внутреннего отверстия, то в итоге получится объем большого цилиндра, чей диаметр равен наружному диаметру трубы:
Легко найти объем отверстия, ведь оно имеет форму цилиндра. Его радиус вдвое меньше диаметра, то есть он равен 13/2 = 6,5 мм. При расчете важно не забыть перевести высоту в миллиметры:
Сегодня мы узнали о такой характеристике тел, как объем. Если объем куба и прямоугольного параллелепипеда мы умели находить ещё в средней школе, то определять объем цилиндра и прямой призмы мы научились только сейчас. Однако все эти случаи по сути одинаковы – надо перемножить высоту фигуры и площадь ее основания. В будущем мы научимся вычислять объемы более сложных фигур – пирамиды, конуса, шара.
Как найти объем — Pronto Costo
 Как найти объем в кубических метрах
Как найти объем в кубических метрах
Кубические метры (м3) — это единица измерения объема, равная объему куба, стороны которого равны одному метру. Кубические метры являются предпочтительной единицей измерения при различных работах, например, при заливке бетона. Объем любого прямоугольного пространства длиной «L», шириной «W» и высотой «Н» вычисляется по формуле: Объем = L × W × H.
Вычисление объема трехмерных фигур
Измерьте все необходимые расстояния в метрах. Объем многих трехмерных фигур легко вычислить по соответствующим формулам. Однако все значения, подставляемые в формулы, должны измеряться в метрах. Таким образом, перед подстановкой значений в формулу убедитесь, что все они измеряются в метрах, или что вы конвертировали другие единицы измерения в метры.
1 мм = 0,001 м
1 см = 0,01 м
1 км = 1000 м
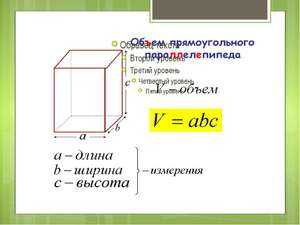
Для вычисления объема прямоугольных фигур (прямоугольный параллелепипед, куб) используйте формулу: объем = L × W × H (длину умножить на ширину умножить на высоту). Эту формулу можно рассматривать как произведение площади поверхности одной из граней фигуры на ребро, перпендикулярное этой грани.
Например, вычислим объем комнаты длиной 4 м, шириной 3 м и высотой 2,5 м. Для этого просто умножим длину на ширину и на высоту:
4 × 3 × 2,5
= 12 × 2,5
= 30. Объем этой комнаты равен 30 м3.
Куб – объемная фигура, у котрой все стороны равны. Таким образом, формулу для вычисления объема куба можно записать в виде: объем = L3 (или W3, или h4).
Например, вычислим объем колодца диаметром 1,5 м и глубиной 10 м. Разделите диаметр на 2, чтобы получить радиус: 1,5/2=0,75 м.
(3,14) × 0,752 × 10
= (3,14) × 0,5625 × 10
= 17,66. Объем колодца равен 17,66 м3.
Для вычисления объема шара используйте формулу: 4/3 х пи × R3. То есть вам нужно знать только радиус (R) шара.
Например, вычислим объем воздушного шара диаметром 10 м. Разделите диаметр на 2, чтобы получить радиус: 10/2=5 м.
4/3 х пи × (5)3
= 4/3 х (3,14) × 125
= 4,189 × 125
= 523,6. Объем воздушного шара равен 523,6 м3.
Для вычисления объема фигур в виде конуса используйте формулу: 1/3 х пи × R2 × H. Объем конуса равен 1/3 объема цилиндра, который имеет такую же высоту и радиус.
Например, вычислим объем конуса мороженного радиусом 3 см и высотой 15 см. Конвертируя в метры, получим: 0,03 м и 0,15 м соответственно.
1/3 х (3,14) × 0,032 × 0,15
= 1/3 х (3,14) × 0.0009 × 0,15
= 1/3 × 0.0004239
= 0,000141. Объем конуса мороженного равен 0,000141 м3.
pronto-costo.info
Калькулятор для расчета объёма груза. Как посчитать объём (м3)
Расчет
объема
Количество коробок
Рассчитать объём
Результат:
Объем одной
коробки(м3):
Общий
объем(м3):
Используйте полученный
результат для
оформления заявки
Количество труб
Рассчитать объём
Результат:
Объем одной трубы(м3):
Общий
объем(м3):
Используйте полученный
результат для
оформления заявки
У вас возник вопрос о доставке, а так же возникла необходимость знать, как вычислить объем груза, нужна наша помощь? Как вычислить объем груза мы знаем, на этой странице вы видите калькулятор, который точно выполнит расчеты.
А вообще, для какой цели рассчитывается объем?
Объем рассчитать необходимо для того, чтобы избежать недоразумений при погрузке груженых коробок в транспортное средство. Объем рассчитать при помощи современных технологий сегодня несложно, достаточно вашего нахождения тут.
Какие критерии мы используем для подсчета объема груза?
Во-первых, все знают – в процессе доставки важна каждая деталь, и немаловажно без ошибок посчитать объем груза в целом. Посчитать объем груза как уже говорилось поможет наш калькулятор объемов, он сделает это быстро и надежно!
Второе – калькулятор объемов, о его начини на нашем сайте, уже сказано выше, как видите, мы заботимся о наших клиентах. Калькулятор объемов, вот что может максимально облегчить работу с расчетами, и напрочь убить ваши сомнения.
Что мы вам даём?
Условия для умения объем груза рассчитать самостоятельно, т. е. это и формулы, пояснения к ним, и даже калькулятор. Объем груза рассчитать при таких возможностях можно за считанные минуты, главное не допустить никаких ошибок.
Что же еще необходимо?
Например…
Вы предприниматель, который занимается перевозками из Китая, и Вам постоянно необходим калькулятор расчета объема. Калькулятор расчета объемов вы быстро найдёте на страницах нашего сайта, и выполните свои расчеты сейчас же.
И все же.
В наше время предпринимательство держится на Китайском производстве товаров, а от куда возникла потребность рассчитать объем? Рассчитать объем необходимо для того что бы узнать общий объём груза, и далее выбрать вид транспорта.
Чем же является расчет объемов в доставке? И какую роль он играет?
Расчёт объема — это насколько, вы уже поняли очень важный этап в доставке, и доверять его надо в надёжные руки профессионалов. Расчёт объема груза надо делать тщательно, учитывая все размеры, и переведя их в метры кубические.
Но к сожалению, не все справляются с этими расчетами.
Еще в школьные времена мы изучали то как посчитать объем груза в м3, но к сожалению, всего этого не запомнишь. Как посчитать объем груза в м3 – бывают случаи когда этот вопрос встаёт на первое место, например во время доставки.
Для этого данная страница и существует!
Мы готовы объяснить, как посчитать объем м3, ведь это можно сделать самостоятельно или что бы проверить наши расчеты. Как посчитать объем м3, для этого необходимо перевести размеры в метры, затем перемножить, формула: Д*Ш*В.
Ведь эта страница для того и предназначена, чтобы помогать Вам в расчёте доставки.
Что бы выполнить расчет объема коробки, не надо стараться это делать самостоятельно, просто надо заполнить пустые поля. Расчет объема коробки автоматически выполнится нашим калькулятором, если вы сомневаетесь, проверьте сами.
Для этого мы и напомнили Вам формулу объемов.
Зачем вообще надо знать то, как рассчитать кубатуру?
Расчет объема груза в кубометрах необходим Вам для того, чтобы подать правильную заявку для его перевозки. Расчет объема груза в кубометрах, т. е. знание самого объема поможет определиться с тем какой вид доставки Вам подойдет.
А теперь перейдем к основному, поговорим о том, как совершать расчеты и для чего они необходимы.
Для начала разберемся…
А все ли помнят, что такое объем как посчитать его, формулу расчёта, конечно же большинство людей забыло, как и что это. Объем как посчитать его, пишется и объясняется в формулах, приведенных в статье, остается указать размеры.
Рассчитать объем груза не всегда просто, как кажется, всё это из-за того что, коробки могут быть разнообразной формы. Рассчитать объем груза прямоугольной коробки, пустяк, а вот остальных тяжеловато, необходимо знать формулы.
Для начала определим форму, для этого сначала узнаем, какие они существуют.
Какую форму может иметь коробка:
- Куб;
- Прямоугольника;
- Цилиндра;
- Усеченной пирамиды (очень редко).
Затем следуют измерения
Перед тем, как вычислить объем коробки измерим её, но запомните, чем точнее сделаны измерения, тем легче Вам. «Как вычислить объем коробки?» — что делать дальше: определить, какой она формы (куба или прямоугольника), размеры.
Что нам дает знание объёма?
Знание объёма коробки не позволит допустить недоразумений при погрузке товаров в любой вид транспорта, который может быть. От объёма коробки практически не чего не зависит, скорее наоборот все зависит от размеров самого товара.
А почему? Тут всё очевидно, прежде чем приобрести коробку, надо узнать размер груза, который Вы собираетесь перевозить через границу.
Ну вот Вы знаете размеры груза, теперь остаётся посчитать его объем (что бы приобрести коробу).
Итак, для того чтобы узнать, как рассчитать объем груза в м3 формула потребуется в первую же очередь. Как рассчитать объём груза в м3 формула поможет без сомнений в этом вопросе, вот так она выглядит V=a*b*h, всё очень просто.
Тем более она уже вам известна.
Хотим напомнить о том что…
Что бы Вам стало легче определить, какой вид транспорта выбрать для доставки, надо рассчитать объем груза в м3. Рассчитать объем груза в м3 очень просто, тут необходимо знать точные размеры, которые затем необходимо перемножить.
Единицы необходимо пе6реводить именно в м3, иначе не получится посчитать доставку.
А что делать, если форма коробки не прямоугольная, а округлая? Ведь это большая редкость, но все же бывает.
Можно объем посчитать коробки или ёмкости в основании которых лежит круг, и для этого так же существует формула. Объем посчитать коробки формой круга позволяет выражение V *r2*h, размеры прежде всего надо безошибочно измерить.
Калькулятор объемов
Предоставляем к вашему вниманию калькулятор: объем грузов в м3, с помощью него вы можете самостоятельно делать расчёты. Калькулятор объем грузов расположен на наем сайте специально для вашего удобства, и для быстроты расчетов.
Для чего нужен калькулятор расчета объема груза?
Мы с вами деловые люди и потерянное время порой несёт в себе большие минусы. Хотите получать грузы быстро и надёжно? И при этом в максимально короткие сроки узнавать цены на их перевозку и доставку?
Вот именно здесь, поможет калькулятор объёма груза!
Наш калькулятор объёмов позволяет вам рассчитать объём груза в м3, поэтому вопрос о объёме коробки больше не возникнет. Калькулятор объёмов простой и удобный в применении, он выдаст результаты как объёма коробки так и груза.
Итак, с помощью калькулятора объёма Вы решаете несколько вопросов:
Как вычислить объем груза (или коробки)? Не забывайте о количественной единице, которую вы берёте в расчёт.
Как посчитать объем коробки в м3? Калькулятор сразу считает в международной системной единице, никакого перевода не требуется.
Как рассчитать кубатуру коробки (груза)? Помните, что кубатура — это число кубических единиц в объёме данного тела.
Столкнулись с одним из них или возник подобный? Наша компания рада предложить для Вашего удобства объем в метрах кубических коробки посчитать, с помощью удобного калькулятора.
А напоследок, давайте вспомним математику!
Часто возникает вопрос: «как высчитать объем?», только вот объем чего: какой фигуры, какой формы, всё всегда по-разному. Как высчитать объем коробки и груза в целом – это интересует вас, ведь именно по этой причине Вы на сайте!
Какая проблема самая распространённая?
Многие путают то как вычислять объём плоских фигур и объемных, т. к., ошибаются в понятиях, точнее затрудняются с ответом. Как вычислять объём не надо знать, хватит того, что вы укажете размеры, главное не забывайте, что их 3.
Закончив все расчеты, остается еще одна задача.
После того, как рассчитать объем груза оказалось не проблемой, необходимо думать о том, какой вид доставки подобрать. Рассчитать объем груза для подборки транспорта Вам придётся точно, не допуская не каких ошибок и недочетов.
А какой Вам нужен транспорт?
Напомним, в доставке кроме того, как рассчитать кубатуру есть еще не менее важные вещи, например размещение товаров. Как рассчитать кубатуру вы знаете, поэтому всё остальное в ваших руках, теперь выбор транспорта зависит от вас.
dobroezzhev.ru
Как найти объем в физике 🚩 все величины в физике 🚩 Естественные науки
Вам понадобится
- калькулятор или компьютер, линейка, рулетка, мерная емкость
Инструкция
Чтобы найти массу , зная плотность, разделите объем тела или вещества на его плотность. То есть воспользуйтесь формулой: m = V / ρ, где:V – объем,
ρ – плотность,
V – объем.Перед расчетом массы приведите все единицы измерения в одну систему, например, в интернациональную систему измерения (СИ). Для этого, переведите объем в кубометры (м³), а плотность – в килограммы на кубометр (кг/м³). В этом случае значение массы получится в килограммах. Если плотность и объем заданы в одной системе единиц, то предварительный перевод в СИ производить необязательно. Масса тела или вещества в таком случае будет измеряться в той единице измерения массы, которая указана в числителе единицы измерения плотности (единицы измерения объема при расчете сократятся).
Так, например, если объем задан в литрах, а плотность в граммах на литр, то расчетная масса получится в граммах.
Если объем тела (вещества) неизвестен или не задан явно в условиях задачи, то попытайтесь его измерить, вычислить или узнать, используя косвенные (дополнительные) данные.
Если вещество сыпучее или жидкое, то оно, как правило, находится в емкости, которая обычно имеет стандартный объем. Так, например, объем бочки обычно равен 200 литров, объем ведра – 10 литров, объем стакана – 200 миллилитров (0,2 литра), объем столовой ложки – 20 мл, объем чайной – 5 мл. Об объеме трехлитровых и литровых банок нетрудно догадаться из их названия.
Если жидкость занимает не всю емкость или емкость нестандартная, то перелейте ее в другую тару, объем которой известен.
Если подходящей емкости нет, перелейте жидкость с помощью мерной кружки (банки, бутылки). В процессе вычерпывания жидкости просто посчитайте количество таких кружек и умножьте на объем мерной тары.
Если тело имеет простую форму, то вычислите его объем, используя соответствующие геометрические формулы. Так, например, если тело имеет форму прямоугольного параллелепипеда, то его объем будет равен произведению длин его ребер. То есть:Vпр.пар. = a*b*c, где:Vпр.пар. – объем прямоугольного параллелепипеда, а
a, b, c — значения его длины, ширины и высоты (толщины), соответственно.
Если тело имеет сложную геометрическую форму, то попробуйте (условно!) разбить его на несколько простых частей, найти объем каждой из них отдельно и затем сложить полученные значения.
Если тело невозможно разделить на более простые фигуры (например, статуэтку), то воспользуйтесь методикой Архимеда. Опустите тело в воду и измерьте объем вытесненной жидкости. Если тело не тонет, то «утопите» его с помощью тонкой палочки (проволоки).
Если объем вытесненной телом воды посчитать проблематично, то взвесьте вылившуюся воду, или найдите разность между начальной и оставшейся массой воды. При этом, количество килограммов воды будет равняться количеству литров, количество граммов – количеству миллилитров, а количество тонн – количеству кубометров.
www.kakprosto.ru
Как найти объем по химии 🚩 газ формула химия 🚩 Естественные науки
5 сентября 2011
Автор КакПросто!
Есть множество формул для нахождения объема. В первую очередь необходимо определить в каком агрегатном состоянии находится вещество, для которого мы ищем объем. Для объема газа подходят одни формулы, а для объема раствора совершенно другие.
Инструкция
Одна из формул объема раствора: V = m/p, где V – объем раствора(мл), m – масса(г), p – плотность(г/мл). Если требуется дополнительно найти массу, то это можно сделать, зная формулу и количество нужного вещества. С помощью формулы вещества мы найдем его молярную массу, сложив атомные массы всех элементов, входящих в его состав. Например, M(AgNO3) = 108+14+16*3 = 170 г/моль. Далее находим массу по формуле: m = n*M, где m – масса(г), n – количество вещества(моль), M – молярная масса вещества(г/моль). Подразумевается, что количество вещества дано в задаче. Следующая формула для нахождения объема раствора выводится из формулы молярной концентрации раствора: с = n/V, где c – молярная концентрация раствора(моль/л), n – количество вещества(моль), V – объем раствора(л). Выводим: V = n/c. Количество вещества можно дополнительно найти по формуле: n = m/M, где m – масса, M – молярная масса. Далее приведены формулы для нахождения объема газа. V = n*Vm, где V – объем газа(л), n – количество вещества(моль), Vm – молярный объем газа(л/моль). При нормальных условиях, т.е. давлении равным 101 325 Па и температуре 273 К молярный объем газа является величиной постоянной и равен 22,4 л/моль.
Для газовой системы существует формула: : q(x) = V(x)/V, где q(x)(фи) – объемная доля компонента, V(x) – объем компонента (л), V – объем системы (л). Из этой формулы можно вывести 2 другие: V(x) = q*V, а также V = V(x)/q.
Если в условии задачи присутствует уравнение реакции, решать задачу следует с помощью него. Из уравнения можно найти количество любого вещества, оно равно коэффициенту. Например, CuO + 2HCl = CuCl2 + h3O. Отсюда видим, что при взаимодействии 1 моля оксида меди и 2 моль соляной кислоты получилось 1 моль хлорида меди и 1 моль воды. Зная по условию задачи количество вещества всего одного компонента реакции, можно без труда найти количества всех веществ. Пусть, количество вещества оксида меди равно 0,3 моль, значит n(HCl) = 0,6 моль, n(CuCl2) = 0,3 моль, n(h3O) = 0,3 моль.
Обратите внимание
Не забывайте про единицы измерения!
Источники:
- «Сборник задач по химии», Г.П. Хомченко, И.Г. Хомченко, 2002.
- объем формула от массы
Масса любого вещества,молекулы равна сумме масс образующих ее атомов. Если при расчете использовать относительные атомные массы ,то получается относительная молекулярная масса вещества. Относительная молекулярная масса показывает во сколько раз абсолютная масса молекулы данного вещества больше 1/12 части абсолютной массы атома углерода. Обычно используют приблизительные значения относительных атомных и молекулярных масс. Эти величины безразмерны.
Инструкция
Подсчитайте в молекуле количество элементов.Например, молекула воды h3O состоит из двух атомов водорода и одного атома кислорода,а сульфат железа (III) Fe2(SO4)3 содержит два атома железа,три атома серы и двенадцать атомов кислорода. Подсчитайте,чему равна атомная масса каждого элемента в молекуле. Чтобы узнать относительную массу одного атома загляните в периодическую систему элементов.Порядковый номер и есть атомная масса. Также вы можете рассчитать ее по формуле Ar(элемента)=m(элемента)/1a.e.m. Для легкости расчетов используют приблизительные значения.
Ar(H)=1?2=2;Ar(O)=16?1=16Ar(Fe)=56?2=112;Ar(S)=32?3=96;Ar(O)=16?12=192
Сложите полученные результаты.Это и будет молекулярная масса вещества.
Mr(h3O)=2Ar(H)+Ar(O)=2+16=18
Mr(Fe2(SO4)3)=2Ar(Fe)+3Ar(S)+12Ar(O)=112+96+192=400
Кроме относительной молекулярной массы при расчетах чаще используют молярную массу. Ее единица измерения — г/моль. Она численно равна относительной молекулярной массе вещества.
M(h3O)=18 г/моль
M(Fe2(SO4)3=400 г/моль
Видео по теме
В химических реакциях принимают участие мельчайшие частицы (атомы, молекулы), и их число даже в небольшой порции вещества очень велико. Поэтому для упрощения расчетов была введена специальная единица измерения «количества вещества» — моль. 1 Моль содержит 6,02*1023 атомов или молекул. Как вычислить массу вещества?
Вам понадобится
- — вещество;
- — интернет;
- — таблица Менделеева.
Инструкция
Определите какой вид массы вам нужно рассчитать: обычную, молекулярную или молярную. Найдите формулу химического соединения, массу которого вам нужно вычислить. Если ее нет в задаче, запустите поиск по названию в интернете.
Подсчитайте количество химических элементов, входящих в молекулу интересующего вас вещества. Например, сульфат алюминия Al2(SO4)3 состоит из двух атомов алюминия, трех атомов серы и двенадцати атомов кислорода.
Откройте таблицу Менделеева. Атомная масса указана для каждого элемента под его буквенным обозначением, точные числа из таблицы при расчетах округляйте до ближайшего целого. Так, атомная масса алюминия = 27 (26,98154 по таблице), серы = 32 (32,06 в таблице), кислорода = 16 (15,9994). Запишите атомную массу каждого из элементов. Молекулярная масса равна сумме атомных масс всех элементов вещества, с учетом их количества в соединении.
Сложите атомные массы, умножая каждую из них на количество данного химического элемента в формуле, вы получите молекулярную массу вещества:
2Al +3S+12О = 2*27+3*32+12*16 = 342
Молекулярная масса не имеет единицы измерения.
Для определения обычной массы некоторого количества вещества нужно знать молярную массу (масса одного моля данного соединения, выражается она в граммах на моль, г/моль, и напрямую связана с молекулярной массой). Для этого к полученному значению молекулярной массы просто допишите «г/моль». То есть молярная масса сульфата алюминия составляет 342 г/моль.
Молярная и обычная массы взаимосвязаны формулой: m = ? * M , где m — обычная масса, выраженная в граммах, ? — количество вещества в молях, М — молярная масса в г/моль. Умножьте молярную массу на количество молей и получите массу вещества. Так, 1 моль сульфата алюминия весит 342 грамма, 2 моля — 684 грамм и т.д.
Если вам известно количество вещества в молях и его обычная масса, то молярную массу рассчитывайте по формуле M = m / ?.
Видео по теме
Источники:
- молярная масса алюминия
- Четыре бруска одинаковой массы изготовлены из алюминия
Часто бывает так, что в ходе химической реакции образуется малорастворимое вещество, выпадающее в осадок (к примеру, сульфат бария, фосфат кальция, хлорид серебра и т.д.). Предположим, химику поставлена задача: определить массу этого осадка. Каким образом можно это сделать?
Инструкция
Если вам неизвестны точные количества исходных веществ, то придется действовать опытным путем. То есть сначала отделите осадок от раствора (путем фильтрования или на обычной воронке, или с использованием воронки Бюхнера). После чего тщательно высушите его и взвесьте на аналитических весах. Так вы получите достаточно точный результат.
Ну а если вам известны точные количества веществ, вступавших в реакцию, то все будет гораздо проще. Например, изначально было 28,4 грамма сульфата натрия и 20,8 грамма хлорида бария. Сколько граммов осадка образовалось? Напишите правильное уравнение химической реакции: Na2SO4 + BaCl2 = BaSO4 + 2NaCl.В результате этой реакции образуется практически нерастворимое вещество – сульфат бария, мгновенно выпадающий в виде плотного белого осадка.
Вычислите, какое из веществ было взято в недостатке, а какое – в избытке. Для этого подсчитайте молярные массы исходных реагентов:46 + 32 + 64 = 142 г/моль – молярная масса сульфата натрия;
137 + 71 = 208 г/моль – молярная масса хлорида бария.То есть в реакцию вступали 0,2 моля сульфата натрия и 0,1 моля хлорида бария. Сульфат натрия был взят в избытке, следовательно, весь хлорид бария прореагировал.
Подсчитайте количество образовавшегося осадка. Для этого разделите молекулярную массу сульфата бария на молекулярную массу хлорида бария и результат умножьте на количество исходного вещества:20,8 * 233/208 = 23,3 грамма.
А если бы сульфат натрия был в недостатке? Предположим, в реакцию вступило бы не 28,4 грамма этой соли, а в 5 раз меньше – всего 5,68 грамма. И тут нет абсолютно ничего сложного. 5,68 грамма сульфата натрия составляют 0,04 моля. Следовательно, в реакцию с таким количеством этой соли могло вступить также всего 0,04 моля хлорида бария, то есть 0,04 х 208 = 8,32 грамма. Прореагировало только 8,32 грамма из исходных 20,8 граммов.
Умножив эту величину на соотношение молярных масс сульфата бария и хлорида бария, получите ответ: 8,32 * 233/208 = 9,32 грамма осадка.
Источники:
- как найти массу осадка в растворе
- Вычисление молярной массы эквивалента
Некоторые химические задачи требуют выполнения стандартных действий, поэтому их знание часто оказывается полезным. Алгоритм нахождения количества вещества достаточно прост, он может пригодиться для упрощения хода решения.
Инструкция
Определите для себя, что как теоретическое понятие представляет собой количество вещества. Это число показывает то количество структурных элементов, которые входят в данное вещество. При этом в качестве структурных частиц рассматриваются как атомы и молекула, так и протоны, электроны и т.д. Понимание позволит вам быстрее понять, что в данной задаче будет полезно вычислить количество вещества.
Запомните основную единицу выражения количества вещества – моль. 1 Моль – это такое количество вещества, которое содержит число частиц, равное количеству атомов в 12 грамма нуклида углерода. Это количество носит название постоянной Авогадро: для вычислений вам потребуется знать его примерное значение: 6,022*1023.
Познакомьтесь также с еще одним понятием, которое потребуется вам для вычисления количества вещества: это молярная масса, или масса одного моля отдельного атома элемента. Уже из определения заметно, что она измеряется в г/моль. Воспользуйтесь стандартной таблицей, которая содержит значения молярной массы для некоторых элементов.
Примените формулу для нахождения количества вещества: n = m/M, где n – искомая величина, m – его масса, а М – молярная масса. В задаче могут содержаться данные о молекулярной массе, представляющей собой массу одной молекулы, выраженной в атомной единице массы. В этом случае для нахождения молярной массы вам потребуется умножить это число на постоянную Авогадро.
Воспользуйтесь формулой для вычисления количества вещества для газообразных веществ, если в задаче предъявлены соответствующие условия. В этом случае вам необходимо оперировать не с массой, а с объемом исходного элемента, а вместо молярной массы используйте молярный объем газа при нормальных условиях (2,24 л/моль).
Масса вещества находится при помощи прибора, который называется весы. Можно также рассчитать массу тела, если известно количество вещества и его молярная масса или его плотность и объем. Количество чистого вещества можно находите по его массе или количеству молекул, которое в нем содержится.
Вам понадобится
- — весы;
- — таблица плотностей;
- — периодическая таблица элементов.
Инструкция
Чтобы найти массу тела положите его на весы и произведите измерения. В рычажных весах вес тела нужно будет уравновесить специальным противовесом, а в электронных просто положите тело на специальную платформу. Массу тела на рычажных весах типа медицинских определите по специальной шкале, а при равных плечах рычага (типа аптекарских), по массе противовеса.
Если взвесить вещество на весах не представляется возможным, рассчитайте его массу через плотность. Для этого найдите объем вещества. Измерьте его линейные размеры и произведите расчет. По специальной таблице найдите плотность этого вещества. Найдите его массу m, как произведение плотности ? на объем V (m=?•V). Например, если в комнате размером 6х8х3 метра находится воздух при температуре 20?С, то его массу найдите посчитав объем комнаты (газ занимает весь предоставленный ему объем) V=6•8•3=144 м?. После этого умножьте результат на плотность воздуха для этой температуры она равна 1,2 кг/м?, m=1,2•144=172,8 кг.
Для определения массы чистого вещества узнайте его химическую формулу. С помощью периодической таблицы элементов найдите его молярную массу. Для этого сложите массы всех элементов, входящих в формулу. Полученное число будет равно молярной массе вещества в граммах на моль. Для того чтобы найти массу m, умножьте молярную массу M на количество вещества ? (m=?•M). Массу получите в граммах.
Если же известна масса вещества, определите молярную массу по периодической таблице и найдите количество вещества. Для этого массу вещества в граммах m, поделите на его молярную массу M (?=m/M). Результат получите в молях. Например, если взято 108 грамм воды, то ее количество вещества будет ?=108/18= 6 моль, где 18 г/моль – молярная масса воды.
Если известно число молекул вещества, но найдите количество вещества, пользуясь числом Авогадро NA=6,022•10^23 1/моль (количество молекул вещества в 1 моле). Чтобы найти количество вещества поделите число молекул N на число Авогадро NA (? = N/ NA).
В ходе химической реакции могут образоваться самые разные вещества: газообразные, растворимые, малорастворимые. В последнем случае они выпадают в осадок. Часто возникает необходимость узнать, какова точная масса образовавшегося осадка. Каким образом это можно вычислить?
Вам понадобится
- — стеклянная воронка;
- — бумажный фильтр;
- — лабораторные весы.
Инструкция
Можете действовать опытным путем. То есть, проведите химическую реакцию, тщательно отделите образовавшийся осадок от фильтрата с помощью обычной стеклянной воронки и бумажного фильтра, например. Более полное отделение достигается с помощью вакуумной фильтрации (на воронке Бюхнера).
После этого осадок высушите – естественным путем или под вакуумом, и взвесьте с возможно большей точностью. Лучше всего, на чувствительных лабораторных весах. Вот так будет решена поставленная задача. К этому методу прибегают, когда неизвестны точные количества исходных веществ, вступивших в реакцию.
Если же вам известны эти количества, тогда задачу можно решить гораздо проще и быстрее. Предположим, необходимо вычислить, сколько хлористого серебра образовалось при взаимодействии 20 грамм хлористого натрия — поваренной соли — и 17 грамм азотнокислого серебра. Прежде всего, напишите уравнение реакции:NaCl + AgNO3 = NaNO3 + AgCl.
В ходе этой реакции образуется очень мало растворимое соединение – хлорид серебра, выпадающий в виде белого осадка.
Подсчитайте молярные массы исходных веществ. Для хлористого натрия она примерно составляет 58,5 г/моль, для азотнокислого серебра – 170 г/моль. То есть, изначально по условиям задачи вы имели 20/58,5 = 0,342 моля хлористого натрия и 17/170 = 0,1 моля азотнокислого серебра.
Таким образом, получается, что хлористый натрий изначально был взят в избытке, то есть, реакция по второму исходному веществу пройдет до конца (прореагируют все 0,1 моля азотнокислого серебра, «связав» те же 0,1 моля поваренной соли). Сколько же образуется хлористого серебра? Для ответа на этот вопрос, найдите молекулярную массу образовавшегося осадка: 108 + 35,5 = 143,5. Умножив изначальное количество азотнокислого серебра (17 грамм) на соотношение молекулярных масс продукта и исходного вещества, получите ответ: 17* 143,5/170 = 14,3 грамма. Вот такова будет точная масса осадка, образовавшегося в ходе реакции.
Полезный совет
Разумеется, полученный ответ не очень точный, поскольку вы использовали в расчетах округленные значения атомных масс элементов. Если требуется большая точность, необходимо учесть, что атомная масса серебра, к примеру, равна не 108, а 107,868. Соответственно, атомная масса хлора не 35,5, а 35, 453 и т.д.
Источники:
- вычислите массу осадка который образовался при взаимодействии
В задачах по химии школьного курса, как правило, требуется вычислить объем для газообразного продукта реакции. Вы можете это сделать, если известно количество молей любого участника химического взаимодействия. Или найдите это количество из других данных задачи.
Вам понадобится
- — ручка;
- — бумага для записей;
- — калькулятор;
- — таблица Менделеева.
Инструкция
Прежде всего, составьте уравнение реакции. Возьмите для примера реакцию горения аммиака в кислороде с образованием азота и воды. Вам необходимо найти объем выделившегося газа N2. 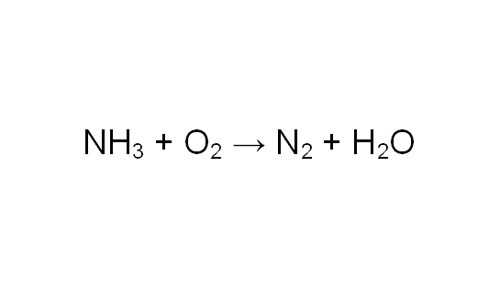
Например, известно, что масса полученной воды, m(h3O), 72 грамма. Рассчитайте молярную массу воды. Для этого найдите в таблице Менделеева значения атомных масс элементов, составляющих молекулу, и сложите их: М(h3O) = 2*1 + 16 = 18 г/моль. Вычислите количество молей образовавшейся воды: v(h3O) = m(h3O)/M(h3O) = 72/18 = 4 моля.
Определите, сколько молей азота получилось, составив пропорцию: 6 моль Н2О — 2 моля N2; 4 моля Н2О – х моль N2. Решите уравнение, найдя х: х = 2*4/6 = 1,33 моль.
Согласно закону Авогадро, один моль любого газа в нормальных условиях, т.е. при температуре 0о и давлении 101325 Па, занимает 22,4 литра. Рассчитайте объем выделившегося 1,33 моля азота: V(N2) = 22,4*1,33 = 29,8 литра.
Если вы знаете, что в реакцию вступило, к примеру, 18 литров кислорода, воспользуйтесь законом объемных отношений Гей-Люссака. Он определяет, что объемы газов, участвующих в реакции, относятся друг к другу, как простые целые числа. То есть из уравнения реакции следует, что из трех литров O2 получается два литра N2. Вы можете сделать вывод, что из 18 литров кислорода образуется 12 литров азота.
Источники:
- вычислите продукт реакции н2 s
www.kakprosto.ru
Как правильно с помощью формул найти объем прямоугольного параллелепипеда?
Прямоугольный параллелепипед, с точки зрения математики, является объемной фигурой с шестью гранями. Увидеть его можно, если посмотреть на прямоугольный бассейн, кирпич или спичечный коробок.
Эта фигура очень часто встречается в повседневной жизни, однако, нередко возникает необходимость узнать ее объем, что для многих представляет некоторые трудности. Например, какого объема необходим бак для воды на дачном участке, или каким размером делать бассейн.
Во многих других ситуациях возникает проблема, как найти объем параллелепипеда правильно.
Между тем вычислить это значение очень просто. Достаточно лишь знать ширину, длину и высоту предмета или объекта. И также необходимо знать формулу, с помощью которой и находят объем данной геометрической фигуры.
Основные особенности и формула для расчета
Для того чтобы найти объем параллелепипеда необходимо:
- определить длину, высоту и ширину объекта;
- и после этого перемножить данные значения друг на друга;
- получившиеся данные и будут объемом.
Это все предельно просто и не таит никаких подводных камней. Главное — это знать требуемые значения, без которых выполнить расчет будет невозможно.
При этом важно знать, что определить параметр можно в сантиметрах, кубометрах, дециметрах и некоторых других размерностях в зависимости от требований. Если говорить о Международной системе единиц (СИ), параметр рассчитывают в сантиметрах. Это оптимальный вариант. Но при желании всегда можно перевести значение в требуемые размерности.
Формула расчета в двух вариантах
Итак, для расчета по формуле нужно знать длину, ширину и высоту измеряемого предмета. Эти данные следует обозначить соответственно как А, B и C, а объем обычно представляют буквой V. Формула для определения объема прямоугольного параллелепипеда при этом будет выглядеть следующим образом: V = A x B x C.
Если определятся объем бассейна, то необходимо его длину, ширину и глубину перемножить. Для более простого восприятия давайте разберем правила расчета объема параллелепипеда на примере. Допустим, что его длина составляет 10 метров, ширина достигает 3 метров, а глубина — 1,5. В этом случае объем этого объекта определяется следующим образом: 10x3x1,5=45 кубометров, или 45 кубических метров.
Можно выделить и другую формулу, которая имеет некоторое отличие. Она представляет собой произведение площади основания на высоту. Формула выглядит следующим образом: V = S x h. Здесь h — высота параллелепипеда. S — площадь основания, которая представлена произведением двух сторон основания. Обычно их обозначают, как a и b: S = a x b.
При расчете можно пользоваться любой из двух приведенных формул. Обе являются верными и позволяют получить точные данные. Последний вариант удобен, когда уже известна площадь основания. Если же она неизвестна, проще перемножать сразу три линейных размера, исключая необходимость в лишней процедуре.
О чем еще следует знать для правильности расчета?
Для вычисления объема параллелепипеда необходимо понять, что это за фигура. Она представляет собой призму, основание которой — параллелограмм. Параллелепипед имеет 6 граней, каждый из которых является параллелограммом. При этом выделяют несколько видов фигур. Принцип расчета не имеет конкретных отличий, но сами фигуры внешне отличаются. Итак, можно выделить такие виды:
- Прямоугольный параллелепипед. Эта фигура представляет собой параллелепипед, который имеет все грани в виде прямоугольников.
- Прямым параллелепипедом является фигура, у которой 4 боковые грани — прямоугольники.
- Куб — это еще один вид параллелепипеда. Он представляет собой прямоугольный параллелепипед, все стороны которого равны между собой. Другими словами, все шесть граней такой фигуры, как куб — это равные квадраты.
И также важно помнить о том, что в процессе выполнения расчета у каждой составляющей формулы должна быть одна и та же размерность. Если опустить это простое правило, получить верный результат не удастся. Если вы выполняете расчеты просто на уроках математики, проблемой могут стать только неудовлетворительные оценки. А при проектировании и наличии ошибок в расчетах проблемы могут быть более серьезными.
Не стоит думать, что основные математические формулы по определению объемов геометрических фигур встречаются исключительно на уроках математики. В большинстве случаев они пригодятся и в последующей жизни. В частности, во время ремонтных или строительных работ, при проектировании и декорированию интерьера, а также в ряде других случаев. Именно тогда без правильной формулы обойтись не удастся.
Можно подвести итог: объем параллелепипеда равен произведению трех линейных размеров — длины, ширины, высоты. Параметр напрямую зависит от трех единиц измерения при любом вращении и повороте. Результат будет неизменным.
Видео
Видео поможет вам научиться находить объем прямоугольного параллелепипеда.
liveposts.ru
Как вычислить объем
Можно вычислить объем несколькими способами. Обычно для каждой из геометрических фигур существует несколько методов вычисления объема.
Рассмотрим основные способы нахождения объема основных правильных геометрических фигур.
- Объем прямоугольного параллелепипеда можно через его длину, высоту и ширину. Для этого их нужно перемножить:
- Объем цилиндра находят через радиус его основания и его высоту. Для этого нужно радиус возвести в квадрат и умножить на высоту и постоянное число Пи:
Известно, что радиус равен половине диаметра, поэтому данную формулу можно записать через диаметр:
- Объем пирамиды можно вычислить через площадь его основания и высоту пирамиды. Для этого нужно найти их произведение и разделить на три:
- Объем конуса находят через радиус основания и высоту. Для этого находят произведение квадрата радиуса на высоту и число Пи, а затем делят результат на три:
Или через диаметр:
- Объем сферы находят через ее радиус. Для этого радиус возводят в третью степень и умножают на число Пи и дробь 4/3:
Или через диаметр:
ru.solverbook.com
Как найти объем вещества?
Химия и физика всегда подразумевают вычисление различных величин, в том числе и объём вещества. Объем вещества можно рассчитать при помощи некоторых формул. Главное знать, в каком состоянии находится данное вещество. Агрегатных состояний, в которых могут пребывать частицы, существует четыре:
- газообразное;
- жидкое;
- твёрдое;
- плазменное.
Для вычисления объёма каждого из них есть своя конкретная формула. Для того чтобы найти объем, нужно иметь определённые данные. К ним относятся масса, молярная масса, а также для газов (идеальных) – газовая постоянная.
Процесс нахождения объема вещества
Давайте рассмотрим, как найти объём вещества, если оно находится, к примеру, в газообразном состоянии. Для подсчёта нужно выяснить условия задачи: что известно, какие параметры даются. Формула, по которой можно определить, каков объём данного газа, такова:
V = n*Vm
Необходимо молярное количество имеющегося вещества (именуемого n) умножить на молярный его объём (Vm). Так можно узнать объём (V). Когда газ находится в нормальных условиях — н. у., то его Vm – объём в молях составляет 22,4 л./моль. Если в условии сказано, сколько вещества в молях имеется (n), то нужно подставить данные в формулу и выяснить конечный результат.
Если условия не предусматривают указания данных о молярном количестве (n), его нужно выяснить. Есть формула, которая поможет сделать вычисление:
n = m/M
Нужно массу вещества (в граммах) разделить на его молярную массу. Теперь можно сделать вычисление и определить молярное количество. М – это константа, которую можно посмотреть в таблице Менделеева. Под каждым элементом есть число, которое обозначает его массу в молях.
Определение объема вещества в миллилитрах
Как определить объём вещества в миллилитрах? Что может быть указано в условиях задачи: масса (в граммах), консистенция в молях, количество данного вам вещества, а также его плотность. Существует такая формула, по которой можно подсчитать объём:
V = m/p
Масса в граммах должна быть разделена на плотность указанного вещества.
Если вам не известна масса, то её можно рассчитать так:
m = n*M
Молярное количество вещества нужно умножить на его молярную массу. Для того чтобы правильно подсчитать молярную массу (М), нужно знать формулу того вещества, которое даётся в условии задачи. Нужно сложить атомную массу каждого из элементов вещества. Также если нужно узнать плотность вещества, можно пользоваться такой обратной формулой:
q =m/V
Если вам известно молярное количество (n) и концентрация (с) вещества, можно также подсчитать объём. Формула будет выглядеть следующим образом:
V = n/c
Вам необходимо молярное количество данного в задаче вещества разделить на его молярную концентрацию. Отсюда можно вывести форму
elhow.ru
|
Один метр кубический является единицей объема. Чтобы найти объем какого-то предмета, имеющего КУБИЧЕСКУЮ форму (например, параллелепипед), нужно его длину (в метрах) умножить на ширину (тоже в метрах) и умножить на высоту (опять в метрах). Логично, не правда ли, что метр, умноженный сам на себя три раза превращается в метр кубический! Если требуется посчитать объем предмета НЕ КУБИЧЕСКОЙ формы (например, шар, призма, конус), то для вычисления их объема есть специальные формулы. Если они вам нужны, то советую посмотреть учебник по геометрии. автор вопроса выбрал этот ответ лучшим Ксарфакс 5 лет назад Думаю, всем понятно, что формула расчёта объёма в кубических метрах для каждой геометрической фигуры будет разной. Поэтому нужно произвести все необходимые измерения, а затем воспользоваться соответствующей формулой. Если фигура имеет неправильную формулу, то разбиваем её на несколько стандартных фигур, а затем складываем их объёмы между собой. Нужно помнить, что все измерения проводятся именно в метрах. Например, если высота объекта 70 см, то её нужно перевести в метры: 70 см = 0,7 м. Самый простейший пример — объём помещения Для того, чтобы посчитать объём, нужно воспользоваться формулой нахождения объёма прямоугольного параллелепипеда. V = abc. a — длина, b — ширина, c — высота. Таким образом, измеряем длину / ширину / высоту комнаты, а затем перемножаем эти значения между собой. Если вы знаете площадь, то посчитать объём ещё проще — достаточно измерить высоту и умножить это значение на данное значение. Например, длина комнаты = 6 м, ширина = 5 м, высота = 2,5 м. V = 6 * 5 * 2,5 = 75 м³. Nelli4ka 5 лет назад Для примера возьмем прямоугольник и параллелепипед. Прямоугольник лежит на плоскости, и мы можем найти либо его периметр (т.е. длину всех сторон данной фигуры), либо его площадь, которая будет выражаться, скажем, в сантиметрах или метрах квадратных. Параллелепипед — фигура трехмерного пространства, у нее есть помимо ширины и длины еще и высота. Когда значения высоты, длины и ширины умножаются друг на друга, находится объем трехмерной фигуры, которая уже будет выражаться не в квадратных, а в кубических сантиметрах, метрах и т.д., но для каждого некубического случая существует своя индивидуальная формула. Galina7v7 7 лет назад Если ваш вопрос трактовать так: «как посчитать объём 1 метра кубического , то V = 1м * 1 м = 1м = 1 м ^3 (1 метр кубический ) , и это единица измерения объёма в системе СИ. Если вас интересует тело в форме параллелепипеда ,где все соседние ребра перпендикулярны друг другу , то объём такого тела определяется путём произведения : длина *ширина * высота. ОБЪЁМ ТЕЛА = ДЛИНА (м) х ШИРИНА (м) х ВЫСОТА (м)Для того,чтобы получить объём в м^3 нужно все 3 параметра тоже выразить в метрах. Zolotynka 5 лет назад В метрах кубических можно высчитать объем предмета, который представляет собой форму куба. Для этого следует воспользоваться формулой: длина*ширина*высота. ** Данная формула имеет важное практическое значение. Рассмотрим на примере: Предположим, нам нужно рассчитать, расход бетона для того, чтобы сделать пол в сарае, размер которого: ширина 2.0 м, длина 2.0 м, а желаемая толщина бетона — 100 мм. Формула для расчета объема бетона в м3 будет выглядеть следующими образом: 2,0 × 2,0 × 0,1 = 0.4m3 Математика обязательный предмет в школьной программе, но знания уходят, забываются формулы, как проводить вычисления уже не каждый вспомнит, остается в голове то, что используется нами ежедневно, и на работе требуется все время, поэтому формула расчета кубического метра может придти в голову не сразу, и придется искать эту информацию, для тех, кому нужно — длину умножить на ширину и умножить на высоту. Kerbal Space Program 6 лет назад Крайне просто. Для этого достаточно брать длины и расстояния в метрах: будь то длина, высота и ширина или же радиус, при вычислении объема круга или цилиндра. Например, имеем: Параллелепипед длиной 1245 см, шириной 3 см и высотой 25 см. Эти длины переведем в метры и получим:
Считаем теперь объем: V=1,245*0,03*0,25=0,00933 метра кубических. moreljuba 5 лет назад Посчитать объём в метрах кубических вы вполне спокойно можете. Для это вам необходимо иметь представление о значениях для таких величин как высота, ширина (толщина) и длина. Переводите в метры и перемножаете эти три составляющие и получаете в результате объём в метрах кубических. FantomeRU 5 лет назад Чтобы вычислить объем необходимо умножить длину на ширину и на высоту. При этом, чтобы искомый результат был в кубических метрах, сначала нужно все стороны данного предмета выразить в метрах и только потом перемножать. vksvovko 6 лет назад Один из распространенных способов найти объем предмета неправильной формы — это налить воду в измерительный сосут и опустить туда предмет. далее смотрим сколько он вытеснил воды и легко подсчитываем объем в м3. EvgeniyAlekseevich 7 лет назад Высоту, выраженную в м3, умножить на длину и умножить на ширину. Знаете ответ? |






































































































































 Как найти объем в кубических метрах
Как найти объем в кубических метрах