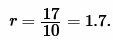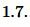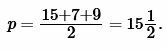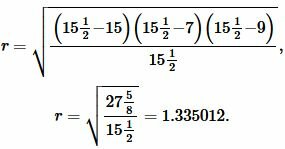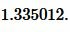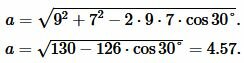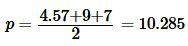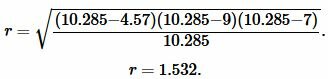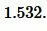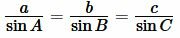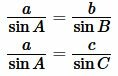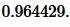Все формулы для радиуса вписанной окружности
Радиус вписанной окружности в треугольник
a , b , c — стороны треугольника
p — полупериметр, p=( a + b + c )/2
Формула радиуса вписанной окружности в треугольник ( r ):
Радиус вписанной окружности в равносторонний треугольник
a — сторона треугольника
r — радиус вписанной окружности
Формула для радиуса вписанной окружности в равносторонний треугольник ( r ):
Радиус вписанной окружности равнобедренный треугольник
1. Формулы радиуса вписанной окружности если известны: стороны и угол
a — равные стороны равнобедренного треугольника
b — сторона ( основание)
α — угол при основании
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через стороны ( r ) :
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) :
2. Формулы радиуса вписанной окружности если известны: сторона и высота
a — равные стороны равнобедренного треугольника
b — сторона ( основание)
h — высота
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) :
Треугольник вписанный в окружность
Определение
Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.
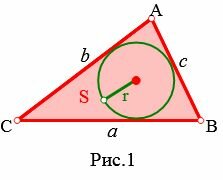
На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.
ВD = FC = AE — диаметры описанной около треугольника окружности.
O — центр вписанной в треугольник окружности.
Формулы
Радиус вписанной окружности в треугольник
r — радиус вписанной окружности.
- Радиус вписанной окружности в треугольник,
если известна площадь и все стороны:
Радиус вписанной окружности в треугольник,
если известны площадь и периметр:
Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:
Радиус описанной окружности около треугольника
R — радиус описанной окружности.
- Радиус описанной окружности около треугольника,
если известна одна из сторон и синус противолежащего стороне угла:
Радиус описанной окружности около треугольника,
если известны все стороны и площадь:
Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:
Площадь треугольника
S — площадь треугольника.
- Площадь треугольника вписанного в окружность,
если известен полупериметр и радиус вписанной окружности:
Площадь треугольника вписанного в окружность,
если известен полупериметр:
Площадь треугольника вписанного в окружность,
если известен высота и основание:
Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:
Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:
[ S = frac<1><2>ab cdot sin angle C ]
Периметр треугольника
P — периметр треугольника.
- Периметр треугольника вписанного в окружность,
если известны все стороны:
Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:
Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:
Сторона треугольника
a — сторона треугольника.
- Сторона треугольника вписанного в окружность,
если известны две стороны и косинус угла между ними:
Сторона треугольника вписанного в
окружность, если известна сторона и два угла:
Средняя линия треугольника
l — средняя линия треугольника.
- Средняя линия треугольника вписанного
в окружность, если известно основание:
Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:
Высота треугольника
h — высота треугольника.
- Высота треугольника вписанного в окружность,
если известна площадь и основание:
Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:
[ h = b cdot sin alpha ]
Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:
Свойства
- Центр вписанной в треугольник окружности
находится на пересечении биссектрис. - В треугольник, вписанный в окружность,
можно вписать окружность, причем только одну. - Для треугольника, вписанного в окружность,
справедлива Теорема Синусов, Теорема Косинусов
и Теорема Пифагора. - Центр описанной около треугольника окружности
находится на пересечении серединных перпендикуляров. - Все вершины треугольника, вписанного
в окружность, лежат на окружности. - Сумма всех углов треугольника — 180 градусов.
- Площадь треугольника вокруг которого описана окружность, и
треугольника, в который вписана окружность, можно найти по
формуле Герона.
Доказательство
Около любого треугольника, можно
описать окружность притом только одну.
окружность и треугольник,
которые изображены на рисунке 2.
окружность описана
около треугольника.
- Проведем серединные
перпендикуляры — HO, FO, EO. - O — точка пересечения серединных
перпендикуляров равноудалена от
всех вершин треугольника. - Центр окружности — точка пересечения
серединных перпендикуляров — около
треугольника описана окружность — O,
от центра окружности к вершинам можно
провести равные отрезки — радиусы — OB, OA, OC.
окружность описана около треугольника,
что и требовалось доказать.
Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.
Радиус вписанной в треугольник окружности онлайн
С помощю этого онлайн калькулятора можно найти радиус вписанной в треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
Открыть онлайн калькулятор
1. Радиус вписанной в треугольник окружности, если известна площадь и полупериметр треуольника
Пусть известна площадь S треугольника и полупериметр
| ( small p=frac<large a+b+c> <large 2 >) | (1) |
где a, b, c стороны треугольника (Рис.1).
Найдем радиус вписанной в треугольник окружности r.
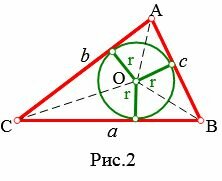
Из центра O вписанной в треугольник окружности проведем перпендикуляры к сторонам треугольника. Все эти перпендикуляры равны радиусу r вписанной в треугольник окружности (Рис.2).
Прямыми OA, OB, OC разделим треугольник ABC на три треугольника: AOC, COB, AOB. Найдем площадь треугольников AOC, COB, AOB:
| ( small S_=frac<large 1> <large 2>cdot r cdot b ,) ( small S_=frac<large 1> <large 2>cdot r cdot c, ) ( small S_=frac<large 1> <large 2>cdot r cdot a ) | (2) |
| ( small S=S_+S_+S_)( small =frac<large 1> <large 2>cdot r cdot b ) ( small +frac<large 1> <large 2>cdot r cdot c ) ( small +frac<large 1> <large 2>cdot r cdot a ) ( small =frac<large 1> <large 2>cdot r cdot ( a+b+c) ) | (3) |
| ( small S=r cdot p. ) | (4) |
Найдем радиус r вписанной в треугольник окружности из равенства (4):
| ( small r=frac<large S><large p>. ) | (5) |
Пример 1. Известны площадь ( small S=17 ) и полупериметр ( small p=10 ) треугольника. Найти радиус вписанной в треугольник окружности.
Решение. Для нахождения радиуса вписанной в треугольник окружности воспользуемся формулой (5).
Подставим значения ( small S=17 ) и ( small p=10 ) в (5):
Ответ:
2. Радиус вписанной в треугольник окружности, если известны все три стороны треугольника
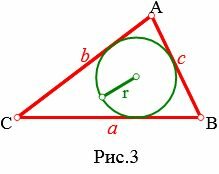
Пусть известны три стороны треугольника: a, b, c. Найдем радиус вписанной в треугольник окружности (Рис.3).
Площадь треугольника по трем сторонам вычисляется из формулы:
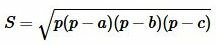 |
(6) |
где полупериметр p вычисляется из формулы (1).
Подставляя (6) в (5), получим формулу радиуса вписанной в треугольник окружности:
| ( small r=sqrt<frac<large (p-a)(p-b)(p-c)><large p>>, ) | (7) |
Пример 2. Известны стороны треугольника: ( small a=15 ,; b=7, ; c=9.) Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанный в треугольник найдем сначала полупериметр треугольника из формулы (1):
Подставим значения ( small a,; b, ; c, ; p ) в (7):
Ответ:
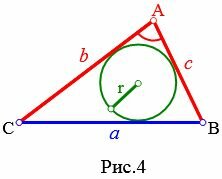
3. Радиус вписанной в треугольник окружности, если известны две стороны и угол между ними
Пусть известны стороны b и c треугольника и угол A между ними (Рис.4). Найдем формулу радиуса вписанной в треугольник окружности.
Из теоремы косинусов найдем сторону a треугольника:
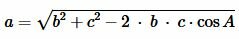 |
(8) |
Далее, для вычисления радиуса вписанной в треугольник окружности, воспользуемся формулой (7), где полупериметр p вычисляется из (1).
Пример 3. Известны стороны треугольника: ( small b=9 ,; c=7, ; ) и угол меджу ними A=30°. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанный в треугольник найдем сначала сторону a треугольника из формулы (8):
Далее найдем p из формулы (1):
Подставим значения ( small a,; b, ; c, ; p ) в (7):
Ответ:
4. Радиус вписанной в треугольник окружности, если известны сторона и прилежащие два угла
Пусть известны сторона a треугольника и прилежащие два угла B и C (Рис.5). Найдем радиус вписанной в треугольник окружности.
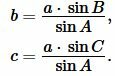 |
(9) |
Поскольку сумма углов треугольника равна 180°, то имеем ( small angle A=180°-(angle B+angle C). ) Из формул приведения тригонометрических функций имеем: ( small sin A=sin (180°-( B+ C)) ) ( small =sin (B+C). ) Тогда формулы (9) можно переписать так:
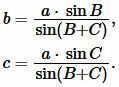 |
(10) |
Получая значения сторон b, c из (10) и значение p из (1), можно найди радиус вписанной в треугольник окружности из формулы (7). Таким образом, для нахождения радиуса вписанной в треугольник окружности через сторону и прилежащим двум углам применяется формула
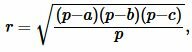 |
(11) |
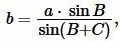 |
(12) |
 , , |
(13) |
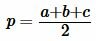 . . |
(14) |
Пример 4. Сторона треугольника равена: ( small a=7 ,) а прилежащие два угла равны соответственно ( small angle B=25°, ) ( small angle C=40°, ) Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (11). Найдем, сначала, стороны b и c из формул (12),(13). Подставим значения ( small a=7 ,) ( small angle B=25°, ) ( small angle C=40°, ) в (12) и (13):
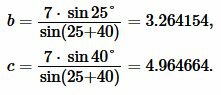
Далее найдем полупериметр p из формулы (14):
Подставляя значения a, b, c, p в (11), получим:
Ответ:
http://colibrus.ru/treugolnik-vpisannyy-v-okruzhnost/
http://matworld.ru/geometry/radius-vpisannoj-v-treugolnik-okruzhnosti.php
Окружность, описанная около треугольника
Окружность называют описанной около треугольника, если все вершины треугольника расположены на окружности.
Её центр равноудалён от всех вершин, то есть должен находиться в точке пересечения серединных перпендикуляров к сторонам треугольника.
Следовательно, около любого треугольника можно описать окружность, так как серединные перпендикуляры к сторонам пересекаются в одной точке.
Для остроугольного треугольника центр окружности находится в треугольнике.
Другая ситуация с прямоугольным и тупоугольным треугольниками.

Окружность, вписанная в треугольник
Окружность называют вписанной в треугольник, если все стороны треугольника касаются окружности.
Её центр равноудалён от всех сторон, то есть должен находиться в точке пересечения биссектрис треугольника.
Следовательно, в любой треугольник можно вписать окружность, так как биссектрисы треугольника пересекаются в одной точке.
Так как биссектрисы углов треугольника всегда пересекаются внутри треугольника, то для всех треугольников центр вписанной окружности находится в треугольниках.
Равносторонний треугольник
Обрати внимание!
У равностороннего треугольника совпадают биссектрисы, медианы и высоты, то есть, эти отрезки являются также серединными перпендикулярами. Это значит, что центры описанной и вписанной окружности совпадают.
Радиус описанной окружности
Радиус вписанной окружности
, где (h) — высота треугольника.
Если дана сторона треугольника (a), то
h=a32
.
Поэтому
r=a36
.
Прямоугольный треугольник
Радиус описанной окружности
, где (c) — гипотенуза.
Радиус вписанной окружности
, где (p) — полупериметр.
Произвольный треугольник
Радиус описанной окружности
, где
α
— угол, противолежащий стороне (a);
.
Радиус вписанной окружности
, где (p) — полупериметр.
Как найти радиус вписанной окружности треугольника
Содержание:
- Окружность, вписанная в треугольник — как найти радиус
-
Свойства вписанной в треугольник окружности
- Первое свойство
- Второе свойство
- Третье свойство
-
Формулы вычисления радиуса вписанной окружности
- Произвольный треугольник
- Прямоугольный треугольник
- Равнобедренный треугольник
- Равносторонний треугольник
- Как найти через высоту или стороны, примеры решения
Окружность, вписанная в треугольник — как найти радиус
Определение
Вписанной в треугольник окружностью называют такую окружность, которая занимает внутреннее пространство геометрической фигуры, соприкасаясь со всеми ее сторонами.
В таком случае грани треугольника представляют собой касательные к этой окружности. Сама геометрическая фигура с тремя углами считается описанной вокруг рассматриваемой окружности.
Свойства вписанной в треугольник окружности
Окружность, которую вписали в треугольник, обладает определенными свойствами. Основные из них можно записать таким образом:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- Центр окружности, которую вписали в треугольник, совпадает с точкой пересечения биссектрис этой геометрической фигуры.
- Во внутреннее пространство любого треугольника можно вписать лишь одну окружность.
- Формула радиуса окружности, который вписали во многоугольник с тремя углами, будет иметь такой вид:
В представленной формуле радиуса окружности использованы следующие величины:
- S – является площадью треугольника;
- р – представляет собой полупериметр геометрической фигуры;
- a, b, c – являются сторонами треугольника.
Перечисленные свойства необходимо доказать.
Первое свойство
Требуется доказать, что центр окружности, которую вписали в фигуру с тремя углами, совпадает с точкой пересечения биссектрис.
Доказательство построено в несколько этапов:
- Необходимо опустить из центральной точки окружности перпендикулярные прямые OL, OK и OM, которые опускаются на стороны треугольника АВС. Из вершин треугольника следует провести прямые, соединяющие их с центром фигуры OA, OC и OB.
- Далее можно рассмотреть пару треугольников AOM и AOK. Можно отметить, что они являются прямоугольными, так как OM и OK являются перпендикулярами к сторонам AC и AB. Гипотенуза OA является общей для пары этих фигур.
- Исходя из того, что касательная к окружности является перпендикуляром к радиусу, который проведен в точку касания, согласно свойству касательной к окружности, то катеты OМ и OК представляют собой радиусы окружности и, следовательно, равны.
- Согласно полученным утверждениям, можно сделать вывод о равенстве прямоугольных треугольников AOМ и AOК по гипотенузе и катету. Таким образом, углы OAМ и OAК тоже равны. Получается, что OA является биссектрисой угла BAC.
- Аналогично можно доказать, что OC является биссектрисой угла ACB, а OB – биссектрисой угла ABC.
- Таким образом, биссектрисы треугольника совпадают в одной точке, которая представляет собой центр вписанной окружности.
Данное свойство окружности доказано.
Второе свойство
Необходимо представить доказательства свойства окружности, согласно которому в любой треугольник можно вписать окружность, причем только одну.
Доказательство состоит из нескольких этапов:
- Окружность получится вписать в треугольник в том случае, когда существует точка, удаленная на равные расстояния от сторон геометрической фигуры.
- Можно построить пару биссектрис ОА и ОС. Из точки, в которой они пересекаются, необходимо опустить перпендикулярные прямые OK, OL и OM ко всем граням многоугольника с тремя углами ABC.
- Затем следует рассмотреть пару треугольников AOK и AOM.
- Эти фигуры обладают общей гипотенузой АО. Углы OAK и OAM равны, так как OA является биссектрисой угла KAM. Углы OKA и OMA прямые, то есть также равны, так как OK и OM являются перпендикулярами к сторонам AB и AC.
- Исходя из того, что две пары углов равны, можно сделать вывод о равенстве третьей пары AOM и AOK.
- Таким образом, получилось подтвердить равенство треугольников AOK и AOM по стороне AO и двум углам, которые к ней прилегают.
- Удалось определить равенство сторон ОМ и ОК, то есть они удалены на одинаковое расстояние от сторон геометрической фигуры АС и АВ.
- Аналогично можно доказать, что OM и OL равны, то есть равноудалены от граней AC и BC.
- Таким образом, точка равноудалена от сторон треугольника, что делает ее центром окружности, которая вписана в этот многоугольник.
- Аналогичным способом можно определить точку во внутреннем пространстве любой геометрической фигуры с тремя углами, которая будет удалена на равные расстояния от его сторон, и представляет собой центр окружности, вписанной в этот треугольник.
- Исходя из вышесказанного, можно сделать вывод о том, что в любой треугольник можно вписать окружность.
- Необходимо заметить, что центральная точка окружности совпадает с точкой, в которой пересекаются биссектрисы треугольника.
- Можно допустить ситуацию, при которой в геометрическую фигуру с тремя углами можно вписать две и более окружности.
- Необходимо провести три прямые из вершин геометрической фигуры к центральной точке окружности, вписанной в нее, и опустить перпендикулярные прямые к каждой грани треугольника. Таким образом, будет доказано, что рассматриваемая окружность лежит на пересечении биссектрис треугольника, согласно доказательству ее первого свойства.
- Получим совпадение центральной точки окружности и центра первой окружности, которая уже была вписана в этот треугольник, а ее радиус соответствует перпендикуляру, опущенному на сторону треугольника так же, как и в первом случае. Можно сделать вывод о совпадении этих окружностей.
- Аналогично любая другая окружность, вписанная в геометрическую фигуру с тремя углами, будет совпадать с первой окружностью.
- Таким образом, в треугольник получается вписать лишь одну окружность.
Свойство доказано.
Третье свойство
Требуется доказать, что радиус окружности, которую вписали в геометрическую фигуру с тремя углами, представляет собой отношение площади треугольника к полупериметру:
Кроме того, необходимо представить доказательства следующему равенству:
Доказательство:
- Следует рассмотреть произвольный треугольник АВС, стороны которого соответствуют a, b и c. Для расчета полупериметра данного треугольника целесообразно использовать формулу:
- Центральная точка окружности совпадает с точкой пересечения биссектрис геометрической фигуры с тремя углами. Прямые OA, OB и OC, которые соединяют O с вершинами треугольника АВС, разделяют геометрическую фигуру на три части: AOC, COB, BOA. Площадь треугольника ABC представляет собой сумму площадей этих трех частей.
- Исходя из того, что площадь какого-либо треугольника представляет собой половину произведения его основания на высоту, а высота треугольников AOC, COB, BOA рассчитывается, как радиус окружности r, то площади треугольников AOC, COB и BOA можно определить по формулам:
- Далее необходимо представить площадь S геометрической фигуры АВС, как сумму площадей нескольких треугольников:
- Следует отметить, что второй множитель является полупериметром геометрической фигуры с тремя углами АВС, что можно записать в виде равенства:
- Таким образом, доказано равенство радиуса вписанной окружности и отношения площади треугольника к полупериметру.
- Можно записать формулу Герона, смысл которой заключается в следующем: площадь треугольника (S) равняется квадратному корню из произведения его полупериметра (p) на разности полупериметра и каждой из его сторон (a, b, c)
- Далее следует преобразовать формулу для расчета радиуса:
Свойство окружности доказано.
Формулы вычисления радиуса вписанной окружности
Параметры окружности, которую вписали в геометрическую фигуру с тремя углами, можно рассчитать с помощью стандартных формул. Радиус окружности будет определен в зависимости от типа треугольника.
Произвольный треугольник
Определить радиус окружности, которая вписана в какой-либо треугольник, можно, как удвоенную площадь треугольника, поделенную на его периметр.
В данном случае, a, b, c являются сторонами геометрической фигуры с тремя углами, S – ее площадь.
Прямоугольный треугольник
Радиус окружности, которую вписали в треугольник с прямым углом, представляет собой дробь с числителем в виде суммы катетов за минусом гипотезы и знаменателем, равным числу 2.
В формуле a и b являются катетами, c – гипотенузой треугольника.
Равнобедренный треугольник
Радиус окружности, которая вписана в равнобедренный треугольник, определяют по формуле:
В этом случае a – боковые стороны, b – основание треугольника.
Равносторонний треугольник
Расчет радиуса окружности, которая вписана в правильный или равносторонний треугольник, выполняют по формуле:
где a – сторона геометрической фигуры с тремя углами.
Как найти через высоту или стороны, примеры решения
Задача 1
Имеется геометрическая фигура с тремя углами, стороны которой составляют 5, 7 и 10 см. Требуется определить радиус окружности, которая вписана в этот треугольник.
Решение
В первую очередь необходимо определить, какова площадь треугольника. Для этого можно воспользоваться формулой Герона:
Затем применим формулу для расчета радиуса круга:
Ответ: радиус окружности составляет примерно 1,48 см.
Задача 2
Необходимо рассчитать радиус окружности, которая вписана в равнобедренный треугольник. Боковые стороны геометрической фигуры составляют 16 см, а основание равно 7 см.
Решение
Следует использовать подходящую формулу для расчета радиуса, подставив в нее известные величины:
Ответ: радиус окружности примерно равен 2,8 см.
Содержание
- Определение
- Формулы
- Радиус вписанной окружности в треугольник
- Радиус описанной окружности около треугольника
- Площадь треугольника
- Периметр треугольника
- Сторона треугольника
- Средняя линия треугольника
- Высота треугольника
- Свойства
- Доказательство
Определение
Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.
На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.
ВD = FC = AE — не диаметры описанной около треугольника окружности.
O — центр вписанной в треугольник окружности.
Формулы
Радиус вписанной окружности в треугольник
r — радиус вписанной окружности.
- Радиус вписанной окружности в треугольник,
если известна площадь и все стороны:
[ r = frac{S}{(a+b+c)/2} ]
- Радиус вписанной окружности в треугольник,
если известны площадь и периметр:
[ r = frac{S}{frac{1}{2}P} ]
- Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:
[ r = sqrt{frac{(p-a)(p-b)(p-c)}{p}} ]
Радиус описанной окружности около треугольника
R — радиус описанной окружности.
- Радиус описанной окружности около треугольника,
если известна одна из сторон и синус противолежащего стороне угла:
[ R = frac{AC}{2 sin angle B} ]
- Радиус описанной окружности около треугольника,
если известны все стороны и площадь:
[ R = frac{abc}{4S} ]
- Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:[ R = frac{abc}{4sqrt{p(p-a)(p-b)(p-c)}} ]
Площадь треугольника
S — площадь треугольника.
- Площадь треугольника вписанного в окружность,
если известен полупериметр и радиус вписанной окружности:[ S = pr ]
- Площадь треугольника вписанного в окружность,
если известен полупериметр:[ S = sqrt{p(p-a)(p-b)(p-c)} ]
- Площадь треугольника вписанного в окружность,
если известен высота и основание:[ S = frac{1}2 ah ]
- Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:[ S = frac{a^2}{2cdot (sin(α)⋅sin(β)) : sin(180 — (α + β))} ]
- Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:[ S = frac{1}{2}ab cdot sin angle C ]
Периметр треугольника
P — периметр треугольника.
- Периметр треугольника вписанного в окружность,
если известны все стороны:
[ P = a + b + c ]
- Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:
[ P = frac{2S}{r} ]
- Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:[ P = sqrt{ b2 + с2 — 2 * b * с * cosα} + (b + с) ]
Сторона треугольника
a — сторона треугольника.
- Сторона треугольника вписанного в окружность,
если известны две стороны и косинус угла между ними:[ a = sqrt{b^2+c^2 -2bc cdot cos alpha} ]
- Сторона треугольника вписанного в
окружность, если известна сторона и два угла:
[ a = frac{b · sin alpha }{sin β} ]
Средняя линия треугольника
l — средняя линия треугольника.
- Средняя линия треугольника вписанного
в окружность, если известно основание:
[ l = frac{AB}{2} ]
- Средняя линия треугольника вписанного в окружность,
если известны две стороны, ни одна из них не является
основанием, и косинус угла между ними:
[ l = frac{sqrt{b^2+c^2-2bc cdot cos alpha}}{2} ]
Высота треугольника
h — высота треугольника.
- Высота треугольника вписанного в окружность,
если известна площадь и основание:[ h = frac{2S}{a} ]
- Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:[ h = b cdot sin alpha ]
- Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:[ h = frac{bc}{2R} ]
Свойства
- Центр вписанной в треугольник окружности
находится на пересечении биссектрис. - В треугольник, вписанный в окружность,
можно вписать окружность, причем только одну. - Для треугольника, вписанного в окружность,
справедлива Теорема Синусов, Теорема Косинусов
и Теорема Пифагора. - Центр описанной около треугольника окружности
находится на пересечении серединных перпендикуляров. - Все вершины треугольника, вписанного
в окружность, лежат на окружности. - Сумма всех углов треугольника — 180 градусов.
- Площадь треугольника вокруг которого описана окружность, и
треугольника, в который вписана окружность, можно найти по
формуле Герона.
Доказательство
Около любого треугольника, можно
описать окружность притом только одну.
Дано: окружность и треугольник,
которые изображены на рисунке 2.
Доказать: окружность описана
около треугольника.
Доказательство:
- Проведем серединные
перпендикуляры — HO, FO, EO. - O — точка пересечения серединных
перпендикуляров равноудалена от
всех вершин треугольника. - Центр окружности — точка пересечения
серединных перпендикуляров — около
треугольника описана окружность — O,
от центра окружности к вершинам можно
провести равные отрезки — радиусы — OB, OA, OC.
Следовательно: окружность описана около треугольника,
что и требовалось доказать.
Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.
Содержание
Треугольник и окружность
Вписанная окружность
В каждый треугольник можно вписать окружность, притом только одну.
Центр окружности, вписанной в треугольник — точка пересечения биссектрис треугольника.

Радиус вписанной в треугольник окружности равен отношению его площади к полупериметру [верно также для многоугольника]
$$ r = frac{S}{p}$$
Радиус вписанной в прямоугольный треугольник с катетами a, b и гипотенузой c окружности равен
$$r = frac{a+b-c}{2}$$
(для доказательства использовать формулу площади и теорему Пифагора)
Описанная окружность
Вписанный треугольник — треугольник, все вершины которого лежат на окружности. Тогда окружность называется описанной вокруг треугольника.
Около треугольника можно описать окружность, притом только одну.
Центр окружности, описанной вокруг треугольника — точка пересечения серединных перпендикуляров треугольника.
У остроугольного треугольника центр описанной окружности лежит внутри треугольника, у тупоугольного — вне треугольника, у прямоугольного — на середине гипотенузы.

Радиус описанной окружности:
$R = frac {abc}{4S}$
$ R = frac{a}{2sin alpha}$, где $alpha$ — угол, лежащий против стороны $a$
См. также Теорема синусов
Радиус описанной окружности по трем сторонам:
$R = frac{abc}{sqrt{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}} = frac{abc}{4sqrt{p(p-a)(p-b)(p-c)}}$
Связь радиусов
Формула Эйлера
$$R^2-2Rr=|OI|^2$$
где R — радиус описанной вокруг треугольника окружности, r — радиус вписанной в него окружности, O — центр описанной окружности, I — центр вписанной окружности.
Отношение радиусов
Треугольник имеет углы $alpha, beta, gamma$.
Найти отношение радиусов описанной и вписанной окружностей.
$$frac r R =cosalpha + cos beta + cos gamma -1$$
Предельная геометрическая интерпретация: если взять маленький кружок и описать около него очень тупоугольный треугольник, то радиус описанной окружности будет очень большим. Отношение будет стремиться к нулю с увеличением тупоугольности. Два косинуса будут стремиться к единичке, один к минус единичке, а всё выражение тоже к нулю.
$$frac{R}{r}=frac{R}{frac{2S}{a+b+c}}=frac{R(a+b+c)}{4R^2sinalphasinbetasingamma}=frac{sinalpha+sinbeta+singamma}{2sinalphasinbetasingamma}$$
См. также Формула Карно — Википедия
Пусть D — центр описанной окружности треугольника ABC. Тогда сумма расстояний от D до сторон треугольника ABC, взятых со знаком «-», когда высота из D на сторону целиком лежит вне треугольника, будет равна $R+r$, где r — радиус вписанной окружности, а R — описанной.
Учебники:
Радиус описанной окружности — Геометрия 9 класс Мерзляк, параграф 1 Решение треугольников