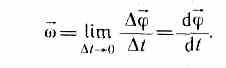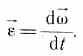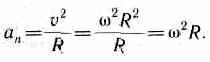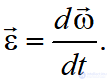Угловое ускорение как найти вектор

Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела в теории и на примерах решения задач.

Угловая скорость

Угловой скоростью называют скорость вращения тела, определяющуюся приращением угла поворота тела за некоторый промежуток (единицу) времени.

Обозначение угловой скорости: ω (омега).

Рассмотрим некоторое твердое тело, вращающееся относительно неподвижной оси.

С этим телом свяжем воображаемую плоскость П, которая совершает вращение вместе с заданным телом.

Вращательное движение определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения. Изменение этого угла с течением времени есть закон вращательного движения:

Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения Oz. Угол измеряется в радианах.

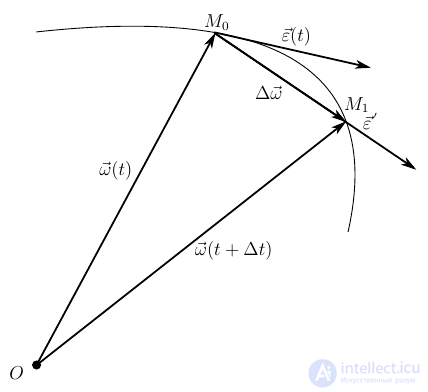
Быстрота изменения угла φ (перемещения плоскости П из положения П₁ в положение П₂) – это и есть угловая скорость:

Приняв вектор k как единичный орт положительного направления оси, получим:

Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.

Формулы угловой скорости

Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:

1. если известно количество оборотов n за единицу времени t:
   
2. если задан угол поворота φ за единицу времени:
   
3. если известна окружная скорость точки тела v и расстояние от оси вращения до этой точки r:
   

Размерности угловой скорости:

• Количество оборотов за единицу времени [об/мин], [c^-1].
• Угол поворота за единицу времени [рад/с].

Определение угловой скорости

Пример: Диск вращается относительно своего центра.
Известна скорость v некоторой точки A, расположенной на расстоянии r от центра вращения диска.

Определить величину и направление угловой скорости диска ω, если v = 5 м/с, r = 70 см.

Таким образом, угловая скорость диска составляет 7,14 оборотов в секунду. Направление угловой скорости можно определить по направлению скоростей её точек.

Вектор скорости точки A стремится повернуть диск относительно центра вращения против хода часовой стрелки, следовательно, направление угловой скорости вращения диска имеет такое же направление.

Другие примеры решения задач >

Угловое ускорение

Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:

Обозначение: ε (Эпсилон)

Единицы измерения углового ускорения: [рад/с²], [с^-2]

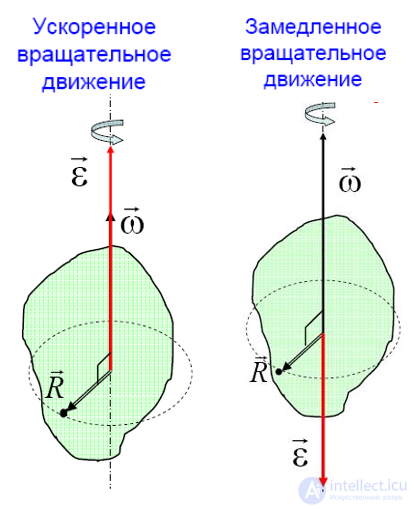
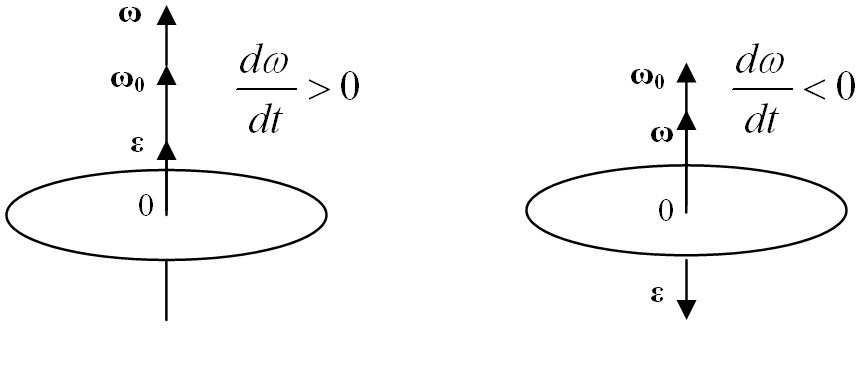
Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.

Другими словами, при положительном ускорении угловая скорость нарастает (вращение ускоряется), а при отрицательном — уменьшается (вращение замедляется).

Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:

Расчет углового ускорения

Пример: По заданному значению касательной составляющей полного ускорения a_τ точки B, расположенной на расстоянии r от центра вращения колеса.

Требуется определить величину и направление углового ускорения колеса ε, если a_τ = 10 м/с², r = 50 см.

Угловое ускорение колеса в заданный момент времени составляет 20 оборотов за секунду в квадрате. Направление углового ускорения определяется по направлению тангенциального ускорения точки.

Здесь, угловое ускорение направлено противоположно направлению угловой скорости вращения колеса. Это означает, что вращение колеса замедляется.

В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:

Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость

ω = 1,5 с^-1 = 9,42 рад/с.

Смотрите также:

• Примеры расчета угловой скорости и ускорения
• Скорости и ускорения точек вращающегося тела

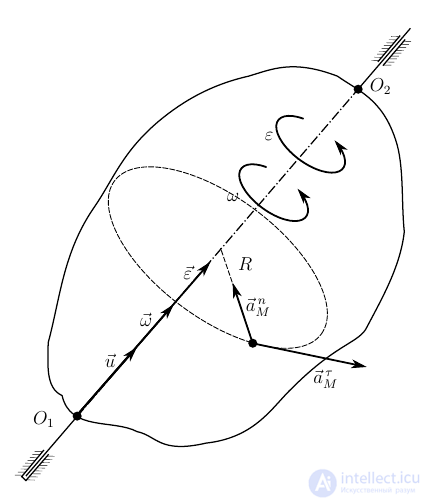
Рассмотрим
твердое тело, которое враща­ется
вокруг неподвижной оси. Тогда от­дельные
точки этого тела будут описывать
окружности разных радиусов, центры
ко­торых лежат на оси вращения. Пусть
не­которая точка движется по окружности
радиуса R
(рис.6).
Ее положение через промежуток времени
t
зададим
углом .
Элементарные (бесконечно малые) углы
поворота рассматривают как векторы.
Мо­дуль вектора d
равен
углу поворота, а его направление совпадает
с направле­нием поступательного
движения острия винта, головка которого
вращается в на­правлении движения
точки по окружности, т. е. подчиняется
правилу
правого, винта (рис.6).
Векторы, направления которых связываются
с направлением вращения, называются
псевдовекторами
или
акси­альными
векторами. Эти
векторы не имеют определенных точек
приложения: они мо­гут откладываться
из любой точки оси вращения.

Угловой
скоростью называется
вектор­ная величина, равная первой
производной угла поворота тела по
времени:

Вектор
«в направлен вдоль оси вращения по
правилу правого винта, т. е. так же, как
и вектор d
(рис. 7). Размерность угловой скорости
dim=T^-1,
a .
ее единица — радиан в секунду (рад/с).

Линейная скорость
точки (см. рис. 6)

В векторном виде
формулу для линейной скорости можно
написать как вектор­ное произведение:

При
этом модуль векторного произведе­ния,
по определению, равен

,
а
направление совпадает с
направлением
поступательного движения правого винта
при его вращении от 
к R.

Если
=const,
то
вращение равномер­ное и его можно
характеризовать перио­дом
вращения Т
—
временем, за которое точка совершает
один полный оборот, т. е. поворачивается
на угол 2.
Так как промежутку времени t=T
соответствует =2,
то =
2/Т,
откуда

Число
полных оборотов, совершаемых телом при
равномерном его движении по окружности,
в единицу времени называет­ся частотой
вращения:

Угловым
ускорением называется
век­торная величина, равная первой
производ­ной угловой скорости по
времени:

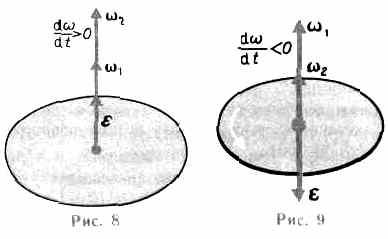
При вращении тела
вокруг неподвижной оси вектор углового
ускорения направлен вдоль оси вращения
в сторону вектора элементарного
приращения угловой ско­рости. При
ускоренном движении вектор

13

 сонаправлен
вектору 
(рис.8),
при замедленном.— противонаправлен
ему (рис. 9).

Тангенциальная
составляющая ускорения

Нормальная
составляющая ускорения

Таким
образом, связь между линейны­ми (длина
пути s,
пройденного
точкой по дуге окружности радиуса R,
линейная
ско­рость v,
тангенциальное
ускорение а_,
нор­мальное ускорение а_n)
и угловыми величи­нами (угол поворота
,
угловая скорость (о, угловое ускорение
)
выражается сле­дующими формулами:

В
случае равнопеременного движения точки
по окружности (=const)

где
₀
— начальная угловая скорость.

Контрольные
вопросы

• Что
называется материальной точкой? Почему
в механике вводят такую модель?

• Что
такое система отсчета?

• Что
такое вектор перемещения? Всегда ли
модуль вектора перемещения равен отрезку
пути,

пройденному точкой?

• Какое
движение называется поступательным?
вращательным?

• Дать
определения векторов средней скорости
и среднего ускорения, мгновенной
скорости

и мгновенного
ускорения. Каковы их направления?

• Что
характеризует тангенциальная
составляющая ускорения? нормальная
составляющая

ускорения? Каковы
их модули?

• Возможны
ли движения, при которых отсутствует
нормальное ускорение? тангенциальное

ускорение? Приведите
примеры.

• Что
называется угловой скоростью? угловым
ускорением? Как определяются их
направления?

• Какова
связь между линейными и угловыми
величинами?

Задачи

1.1.
Зависимость
пройденного телом пути от времени
задается уравнением s
= A+Вt+Сt²+Dt³
(С
= 0,1 м/с²,
D
= 0,03 м/с³).
Определить: 1) через какое время после
начала движения ускорение а тела будет
равно 2 м/с²;
2) среднее ускорение <а>
тела за этот промежуток времени. [ 1) 10
с; 2) 1,1 м/с²]

1.2.
Пренебрегая сопротивлением воздуха,
определить угол, под которым тело брошено
к гори­зонту, если максимальная высота
подъема тела равна 1/4 дальности его
полета. [45°]

1.3.
Колесо
радиуса R
=
0,1 м вращается так, что зависимость
угловой скорости от времени задается
уравнением 
= 2At+5Вt⁴
(A=2
рад/с²
и B=1
рад/с⁵).
Определить полное ускорение точек обода
колеса через t=1
с после начала вращения и число оборотов,
сделан­ных колесом за это время. [а =
8,5 м/с²;
N
= 0,48]

14

1.4.
Нормальное ускорение точки, движущейся
по окружности радиуса r=4
м,
задается уравнением а_n=А+-Bt+Ct²
(A=1
м/с²,
В=6
м/с³,
С=3
м/с⁴).
Определить: 1) тангенциальное ускорение
точки; 2) путь, пройденный точкой за время
t₁=5
с после начала движения; 3) полное
ускорение для момента времени t₂=1
с. [ 1) 6 м/с²;
2) 85 м; 3) 6,32 м/с²]

1.5.
Частота
вращения колеса при равнозамедленном
движении за t=1
мин
уменьшилась от 300 до 180 мин^-1.
Определить: 1) угловое ускорение колеса;
2) число полных оборотов, сделанных
колесом за это время. [1)
0,21 рад/с²;
2) 360]

1.6.
Диск
радиусом R=10
см вращается вокруг неподвижной оси
так, что зависимость угла поворота
радиуса диска от времени задается
уравнением =A+Bt+Ct²+Dt³
(B
= l рад/с,
С=1
рад/с²,
D=l
рад/с³).
Определить для точек на ободе колеса к
концу второй секунды после начала
движения: 1) тангенциальное ускорение
а_;
2) нормальное ускорение а_n;
3) полное ускорение а. [ 1) 0,14 м/с²;
2) 28,9 м/с²;
3) 28,9 м/с²]

Соседние файлы в папке Трофимова

• #
• #
• #
• #
• #
• #

Angular acceleration is the change in angular speed per unit of time. It can also be defined as the rate of change of angular acceleration. It is represented by the Greek letter alpha (α). The SI unit for the measurement of, Angular Acceleration is radians per second squared (rad/s²). In this article, we will learn about Angular Acceleration and its formula in detail.

What Is Angular Acceleration?

For an object in a circular motion, angular velocity varies with time and this change in angular velocity is called angular acceleration. It is a vector quantity that has both magnitude and direction and is also known as rotational acceleration. It can be interpreted as the time rate of change in the angular velocity. The image given below tells us about angular acceleration.

Angular Acceleration is usually expressed in radians per second whole square. Thus,

α = dω / dt

Angular acceleration is also known as rotational acceleration. Angular Acceleration is a pseudoscalar quantity. It is considered positive if the angular speed increases counterclockwise and is considered negative if the angular speed increases clockwise. 

Examples of Angular Acceleration include the motion of the wheel, fan, earth, etc.

Angular Acceleration Unit

The direction of the angular acceleration is always perpendicular to the plane of rotation. When the object rotates clockwise, then the angular acceleration points away from the observer, if the object rotates counterclockwise, then the vector of angular acceleration points toward the viewer.

SI unit of angular acceleration is (rad/s²) and is usually denoted by the alpha (α).  Its dimensional formula is given by [M⁰L¹ T^-2].

Angular Acceleration Formula

α = dω/dt

where,
α is the angular acceleration
ω is the angular velocity
t is the time taken by the object

If angular displacement θ is given then the angular acceleration is calculated as,

α = d²θ/dt²

Derivation

Suppose an object is doing circular motion with a linear velocity v, angular velocity ω on a circular path of radius r in time t.

Now, we know the angular acceleration of an object is the first derivative of its angular velocity with respect to time. So we get,

α = dω/dt   ……. (1)

Also we know that the angular velocity of an object is the first derivative of its radius with respect to time.

ω = dθ/dt   ……. (2)

Substituting (2) in (1) we get,

α = d(dθ/dt)/dt

α = d²θ/dt²

This derives the formula for angular acceleration.

How is Angular Acceleration Determined?

Angular acceleration is the rate at which the angular speed changes with respect to the time taken of a rotating object. Angular acceleration is a pseudovector quantity. that focuses on a path along with the turning pivot. Its unit is radians/s² and is calculated by the equation discussed below,

α = dω/dt

α = ω₂ – ω₁ / t₂ – t₁

where,
ω₂ is the final velocity
ω₁ is the initial velocity
t₁ is initial time
t₂ is finial time

What Causes Angular Acceleration?

If an object is pivoted at one endpoint and a force is applied on the other endpoint, then this applied force tends to rotate the object and is called torque. The torque applied on the body is directly proportional to the angular acceleration of the object, i.e. the more torque is applied the more the angular acceleration of the object.

This torque is the very reason that rotates a body. A body performing circular motion has an angular velocity if the angular velocity is constant then the object is in Uniform Circular Motion.

Also, Check

• Circular Velocity
• Dynamics of Circular Motion
• Motion in a Vertical Circle

Solved Examples on Angular Acceleration

Example 1: Calculate the angular acceleration of an object if its angular velocity changes at the rate of 50 rad/s for 5 seconds.

Solution:

dω = 50

dt = 5

Using the formula we have,

α = dω/dt
   = 50/5
   = 10 rad/s²

Example 2: Calculate the angular acceleration of an object if its angular velocity changes at the rate of 90 rad/s for 4 seconds.

Solution:

dω = 90

dt = 4

Using the formula we have,

α = dω/dt
   = 90/4
   = 22.5 rad/s²

Example 3: Calculate the angular velocity of an object if its angular acceleration is 30 rad/s² for 7 seconds.

Solution:

α = 30

dt = 7

Using the formula we have,

α = dω/dt

dω = α dt

dω = 30 (7)

dω = 210 rad/s

Example 4: Calculate the angular velocity of an object if its angular acceleration is 16 rad/s² for 3 seconds.

Solution:

α = 16

dt = 3

Using the formula we have,

α = dω/dt

dω = α dt

dω = 16 (3)

dω = 48 rad/s

Example 5: Calculate the time taken by an object if its angular velocity is 46 rad/s and acceleration is 23 rad/s².

Solution:

α = 23

dω = 46

Using the formula we have,

α = dω/dt

dt = dω/α

dt = 46/23

dt = 2 s

Example 6. Calculate the angular acceleration of an object if its angular displacement is 60 radians and its time is 12 seconds.

Solution:

dθ = 60 

dt = 12

Calculate the angular velocity of the object.

ω = dθ/dt 

ω = 60/12

ω = 5 rad/s

Using the formula we have,

α = dω/dt
   = 5/12
   = 0.416 rad/s²

Example 7: Calculate the angular acceleration of an object if its angular displacement is 45 radians and its time is 3 seconds.

Solution:

dθ = 45

dt = 3

Calculate the angular velocity of the object.

ω = dθ/dt

ω = 45/3

ω = 15 rad/s

Using the formula we have,

α = dω/dt
   = 15/3
   = 5 rad/s²

FAQs on Angular Acceleration

Question 1: What is angular acceleration?

Answer:

The rate of change of angular velocity is angular acceleration it is denoted by greek letter α.

Question 2: What are Angular Acceleration examples?

Answer:

Motion of rotating objects including tops, fans, Earth and others have angular acceleration.

Question 3: How is Angular acceleration measured?

Answer:

Acceleration is measured in radians per second squared (rad/s²), rad/s² is SI unit of angular acceleration.

Question 4: When is Angular acceleration zero?

Answer:

If angular velocity of a rotating objects never changes i.e. if the angular velocity is constant, then the angular acceleration is zero.

Question 5: What is the relationship between angular acceleration and angular velocity?

Answer:

Rate of change of angular velocity is angular acceleration, i.e. α = dω/dt

Question 6: When is Angular Acceleration negative?

Answer:

Angular acceleration is taken to be positive if the angular speed increases counterclockwise, and is taken to be negative if the angular speed increases clockwise.

Last Updated :
13 Mar, 2023

Like Article

Save Article

Сразу хочу сказать, что здесь никакой воды про угловое ускорение, и только нужная информация. Для того чтобы лучше понимать что такое
угловое ускорение , настоятельно рекомендую прочитать все из категории Физические основы механики.

угловое ускорение — псевдовекторная физическая величина, равная первой производной от псевдовектора угловой скорости по времени

Угловое ускорение — характеристика быстроты изменения угловой скорости

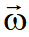
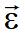
При неподвижной оси вращения и совпадают по направлению в случае ускоренного вращательного движения.

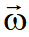
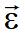
В случае замедленного вращательного движения и — противоположны

Угловое ускорение характеризует интенсивность изменения модуля и направления угловой скорости при движении твердого тела.

В случае неравномерного движения 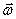не остается постоянной. Величина, характеризующая скорость изменения угловой скорости называется угловым ускорением и равна:

(2.5)

В случае вращения тела вокруг
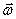
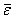
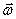
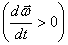
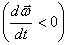
неподвижной оси изменение вектора обусловлено толькоизменением его численного значения. При этом вектор углового ускорения направлен вдоль оси вращения в ту же сторону, что и при ускоренном вращении и при замедленном в обратном направлении. ( рис 2.3 а),б) )

Как приходят к понятию углового ускорения: ускорение точки твердого тела при свободном движении

К понятию углового ускорения можно прийти, рассматривая вычисление ускорения точки твердого тела, совершающего свободное движение. Скорость точки тела при свободном движении, согласно формуле Эйлера, равна

где — скорость точки тела , принятой в качестве полюса; — псевдовектор угловой скорости тела; — вектор, выпущенный из полюса в точку, скорость которой вычисляется. Дифференцируя по времени данное выражение и используя формулу Ривальса , имеем

где — ускорение полюса ; — псевдовектор углового ускорения. Составляющая ускорения точки , вычисляемая через угловое ускорение называется вращательным ускорением точки вокруг полюса

Последнее слагаемое в полученной формуле, зависящее от угловой скорости, называют осестремительным ускорением ускорением точки вокруг полюса

Геометрический смысл псевдовектора углового ускорения[

Псевдовектор направлен по касательной к годографу угловой скорости . Об этом говорит сайт https://intellect.icu . Действительно, рассмотрим два значения вектора угловой скорости, в момент времени и в момент времени . Оценим изменение угловой скорости за рассматриваемый промежуток времени

Отнесем это изменение к тому промежутку времени, за которое оно произошло

Получившийся вектор называется вектором среднего углового ускорения. Он занимает положение секущей, пересекая годограф вектора угловой скорости в точках и . Перейдем к пределу при

Вектор среднего углового ускорения перейдет в вектор мгновенного углового ускорения и займет положение касательной в точке к годографу угловой скорости.

Выражение вектора углового ускорения через параметры конечного поворота

При рассмотрении вращения тела через параметры конечного поворота, вектор углового ускорения можно расписать формулой

где — орт, задающий направление оси поворота; — угол, на который совершается поворот вокруг оси .

Угловое ускорение при вращении тела вокруг неподвижной оси

При вращении тела вокруг неподвижной оси, проходящей через неподвижные точки тела и , производные орта оси вращения равны нулю

В этом случае вектор углового ускорения определяется тривиально через вторую производную угла поворота

или

где — алгебраическая величина углового ускорения. В этом случае псевдовектор углового ускорения, как и угловая скорость, направлен вдоль оси вращения тела. Если первая и вторая производные угла поворота имеют одинаковый знак

(),

то вектор углового ускорения и вектор угловой скорости совпадают по направлению (тело вращается ускоренно). В противном случае, при , векторы угловой скорости и углового ускорения направлены в противоположные стороны (тело вращается замедленно).

В курсе теоретической механики традиционным является подход, при котором понятие угловой скорости и углового ускорения вводится при рассмотрении вращения тела вокруг неподвижной оси. При этом в качестве закона движения рассматривается зависимость от времени угла поворота тела

В этом случае закон движения точки тела может быть выражен естественным способом, как длина дуги окружности, пройденная точкой при повороте тела от некоторого начального положения

где — расстояние от точки до оси вращения (радиус окружности, по которой движется точка). Дифференцируя последнее соотношение по времени получаем алгебраическую скорость точки

где — алгебраическая величина угловой скорости. Ускорение точки тела при вращении может быть представлено как геометрическая сумма тангенциального и нормального ускорения

причем тангенциальное ускорение получается как производная от алгебраической скорости точки

где — алгебраическая величина углового ускорения. Нормальное ускорение точки тела может быть вычислено по формулам

Выражение псевдовектора углового ускорения через тензор поворота тела

Если поворот твердого тела задан тензором ранга (линейным оператором), выраженным, например, через параметры конечного поворота

где — символ Кронекера; — тензор Леви-Чивиты, то, псевдовектор углового ускорения может быть вычислен по формуле

где — тензор обратного преобразования, равный

Вау!! 😲 Ты еще не читал? Это зря!

• кинематика вращательного движения , абсолютно твердое тело ,

• угол поворота твердого тела ,
• период обращения , частота обращения ,
• угловая скорость ,
• кинематика , вращение абсолютно твердого тела ,
• Крутящий момент
• Угловой момент

Статью про угловое ускорение я написал специально для тебя. Если ты хотел бы внести свой вклад в развии теории и практики,
ты можешь написать коммент или статью отправив на мою почту в разделе контакты.
Этим ты поможешь другим читателям, ведь ты хочешь это сделать? Надеюсь, что теперь ты понял что такое угловое ускорение
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Физические основы механики

Таким образом, числовое значение углового ускорения в данный момент времени равно первой производной от угловой скорости или второй производной от угла поворота по времени.

Размерность углового ускорения $1/T^2$ ($1/время^2$); в качестве единицы измерения обычно применяется $рад/с^2$ или, что то же, $1/с^2$ $(с^{-2})$.

Если модуль угловой скорости со временем возрастает, вращение тела называется ускоренным, а если убывает, замедленным. Легко видеть, что вращение будет ускоренным, когда величины $omega $ и $varepsilon $ имеют одинаковые знаки, и замедленным — когда знаки разные.

Рисунок 1. Вектор углового ускорения

Угловое ускорение тела можно представить в виде вектора $overrightarrow{varepsilon }=frac{doverrightarrow{omega }}{dt}$ , направленного вдоль оси вращения. Направление $overrightarrow{varepsilon }$ совпадает с направлением $overrightarrow{omega }$, когда тело вращается ускоренно (рис.1, а), и противоположно $overrightarrow{omega } $при замедленном вращении (рис.1, б).

Если угловое ускорение тела во все время движения остается постоянным (${mathbf varepsilon }$=const), то вращение называется равнопеременным. Найдем закон равнопеременного вращения, считая, что в начальный момент времени $t_0$ угол ${mathbf varphi }$ = ${mathbf varphi }$0, а угловая скорость ${mathbf omega }$ = ${mathbf omega }$0 (${mathbf omega }$0 — начальная угловая скорость).

Из формулы $varepsilon =frac{domega }{dt}=dot{omega }=ddot{varphi }$ имеем d$omega $ = $varepsilon $dt. Интегрируя левую часть в пределах от $omega_0$ до $omega $, а правую — в пределах от 0 до t, найдем:

$omega $ = $omega_0$ + $varepsilon $t, d$varphi $ = $omega $0dt + $varepsilon tdt$.

Вторично интегрируя, найдем отсюда закон равнопеременного вращения: ${mathbf varphi }={ {mathbf varphi }}_0 +{mathbf omega }t+frac{{mathbf varepsilon }t^2}{2}$

Если величины $omega $ и $varepsilon $ имеют одинаковые знаки, то вращение будет равноускоренным, а если разные — равнозамедленным.

Угловое ускорение связано с полным и тангенциальным. Для точки, неравномерно вращающейся по окружности радиуса R, $a_{tau }=varepsilon R$. Учитывая, что нормальное ускорение связано с угловой скоростью $a_n={omega }^2R$, для полного ускорения получаем: $a=sqrt{a^2_{tau }+a^2_n}=Rsqrt{{varepsilon }^2+{omega }^4}$. В случае равнопеременного движения $omega =varepsilon t$, $a_n={omega }^2R={varepsilon }^2t^2R$, $a=Rsqrt{{{varepsilon }^2+varepsilon }^4t^4}=Rvarepsilon sqrt{1+{varepsilon }^2t^4}$