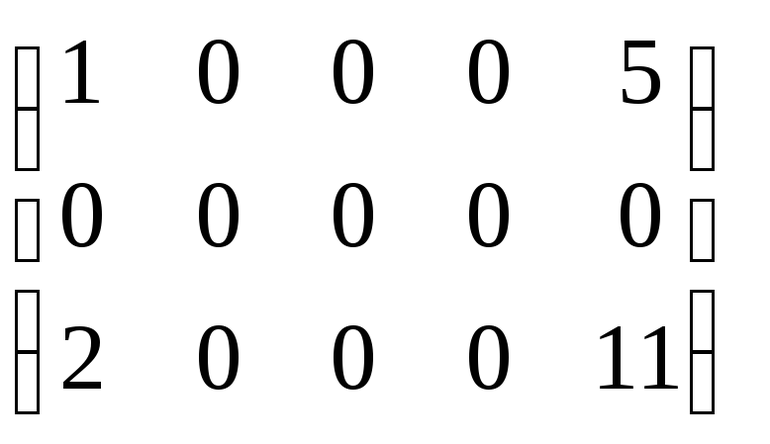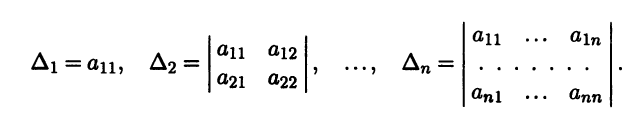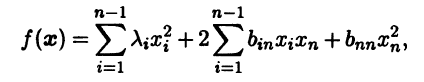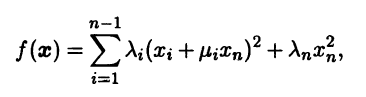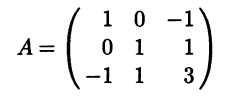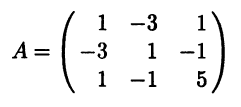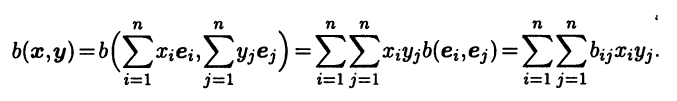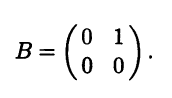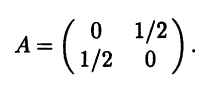Угловые миноры матрицы как найти

Решение

Коэффициенты
при квадратах переменных последовательно
выписываем по главной диагонали матрицы.
Коэффициенты при смешанных произведениях
делим пополам и выписываем на
соответствующих местах, симметричных
относительно главной диагонали:

.

3.3.2. Знакоопределенность квадратичной формы

Очевидно, всегда

Определение 2. Будем говорить, что
квадратичная формаположительна (отрицательна), если

Определение 3. Будем говорить, что
квадратичная форманеотрицательна (неположительна), если

Определение
4. Будем говорить, что квадратичная
формаквазиположительна (квазиотрицательна),
если она неотрицательна (неположительна),
но не является положительной
(отрицательной).

Иными словами, квадратичная форма
квазиположительна (квазиотрицательна),
еслии.

Определение 5. Будем говорить, что квадратичная форма нулевая, если.

Очевидно, у нулевой квадратичной формы
все коэффициенты равны нулю.

Нулевая квадратичная форма является
частным случаем неотрицательной,
неположительной, квазиположительной
и квазиотрицательной форм.

Определение 6.Будем говорить, что
квадратичная формазнакопеременна, если она принимает накак положительные, так и отрицательные
значения, т.е..

Иногда
употребляется терминология с использованием
слова «определена»: положительно
определена и т. д. и «полуопределена»
(вместо «квазиопределена»).

Для матриц
квадратичной формы используется
следующая терминология:

• положительно (отрицательно)
  определена – для положительной
  (отрицательной) квадратичной формы;

• положительно (отрицательно)
  квазиопределена – для квазиположительной
  (квазиотрицательной) квадратичной
  формы;

• неопределена – для
  знакопеременной квадратичной формы.

Классификация
видов знакоопределенности квадратичных
форм показано на рис.2

Рис. 2.

3.3.3. Угловые и главные миноры

Определение 7. Будем обозначать
через(или просто,
если понятно, о какой матрице идет речь)
угловой минор порядкаkматрицыА,
т.е. минор расположенный на пересеченииkпервых строк иkпервых
столбцов матрицыА.

Так, в матрице третьего порядка
— три угловых минора:

• первого
  порядка:
  ;

• второго
  порядка:
  ;

• третьего
  порядка:
  .

Определение 8.Будем обозначать
через(или без указания матрицы, если понятно,
о какой матрице идет речь) главный минор
порядкаkматрицыА, т.е. минор,
расположенный на пересеченииk строк иkстолбцов матрицыАс одинаковыми номерами.

Так, в матрице третьего порядка
– семь главных миноров:

• три –
  первого порядка:
  ;

• три –
  второго порядка:
  ;

• один –
  третьего порядка:
  .

3.3.4. Критерий Сильвестра Теорема (детерминантный критерий Сильвестра) Квадратичная форма

1. положительна
   тогда и только тогда, когда
   ;

2. отрицательна
   тогда и только тогда, когда
   ;

3. неотрицательна
   тогда и только тогда, когда
   ;

4. неположительна
   тогда и только тогда, когда
   ;

5. знакопеременна
   – в остальных случаях.

Из данной теоремы следует, что квадратичная
фора квазиположительнатогда и
только тогда, когда выполняется условие
3, но не выполняется условие 1 (т.е. все
главные миноры неотрицательны, но хотя
бы один из них равен нулю¹),
иквазиотрицательнатогда и только
тогда, когда выполняется условие 4, но
не выполняется условие 2.

Для установления
знакоопределенности квадратичной формы
может быть предложена следующая схема:

1. Составляется матрица
   квадратичной формы.

2. Определяются знаки ее
   угловых миноров.

3. Если знаки всех угловых
   миноров положительны, то квадратичная
   форма положительна; если некоторые из
   знаков заменяются нулями («мягкое»
   нарушение правила постоянства знаков)
   – нужно исследовать все главные миноры;
   если все они неотрицательны, то
   квадратичная форма квазиположительна
   (в обоих случаях – неотрицательна);

4. Если знаки угловых миноров
   чередуются, начиная с минуса, то
   квадратичная форма отрицательна; если
   некоторые из знаков заменяются нулями
   («мягкое» нарушение правила
   чередования знаков) – нужно исследовать
   все главные миноры; если все главные
   миноры порядка kимеют знак (-1)^k(или равны нулю), то квадратичная форма
   квазиотрицательна (в обоих случаях –
   неположительна);

5. Если ни первое (п.3), ни второе
   (п.4) правила знаков не соблюдаются
   («грубое» нарушение правила
   постоянства или чередования знаков:
   «+» заменяется на «-» или
   наоборот), то квадратичная форма
   знакопеременна.

Наглядно данное правило представлено
в следующей таблице:

Знакоопределенность квадратичной формы				………..
Положительная	+	+	+	……….	+
Отрицательная	–	+	–	……….	(–1)n
Неотрицательна	+ или 0	+ или 0	+ или 0	………..	+ или 0
Неположительна	– или 0	+ или 0	– или 0	………..	(–1)nили 0
Нулевая	0	0	0	………..	0

Замечания (следствия из теоремы):

1. Если все
   угловые миноры положительны, то и все
   главные миноры положительны;

2. Если знаки
   угловых миноров чередуются, начиная с
   «–», то
   и знаки всех главных миноров данного
   порядка совпадают со знаком соответствующего
   углового минора;

3. Если
   какой-нибудь угловой (главный) минор
   четного порядка (например, второго)
   отрицателен, то матрица неопределена
   (квадратичная форма знакопеременна);

4. Если знаки
   каких-нибудь угловых (главных) миноров
   нечетного порядка (например, первого
   и третьего) противоположны, то матрица
   неопределена (квадратичная форма
   знакопеременна);

5. Если
   какие-нибудь главные миноры одного
   порядка (например, первого) имеют
   противоположные знаки, то матрица
   неопределена (квадратичная форма
   знакопеременна).

Приведенная
выше схема – не догма. В каждом конкретном
случае следует искать наискорейший
путь к решению проблемы. Например, если
Вы видите, что на главной диагонали
матрицы стоят элементы различных знаков,
то сразу можно сделать вывод относительно
неопределенности данной матрицы (главные
миноры первого порядка имеют разные
знаки), т.е. знакопеременности
соответствующей квадратичной формы.

Пример

Соседние файлы в папке МОРы хсехелп

• #
• #
• #
• #
• #
• #

Общие сведения

При решении систем, состоящих из алгебраических и дифференциальных уравнений, для удобной их записи применяется таблица. Она содержит строки и столбцы, пересечение которых определяется элементами. Количество строк характеризуется числом уравнений, а столбцов — количеством неизвестных величин. После построения такой таблицы решение сводится к работе с ней. Совокупность элементов такой таблицы называют матрицей.

Над несколькими матрицами можно выполнять различные арифметические действия: преобразовывать, умножать, складывать. При этом допускается умножение строки на числа, отличные от нуля, сложение строк между собой и изменение их положения. Обозначают матрицу с помощью заглавной буквы латинского алфавита. Характеризуется она размерностью и может быть квадратной или прямолинейной.

При математической записи используют индексы. Первый из них обозначает строки, а второй — столбцы. На месте их пересечения находится элемент. То есть таблица вида m x n записывается как A = (aij)m, n, где: aij — элемент матрицы, располагающийся на пересечении и-той строки и йо-того столбца. Ранг же матрицы показывает наибольшее число линейно независимых столбцов или строк, при этом он не может превосходить размерность.

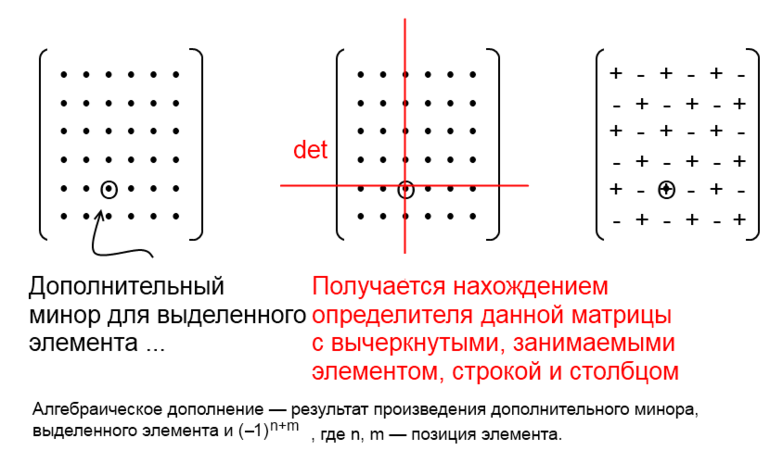
Важным параметром квадратной матрицы является определитель (детерминант). При его нахождении используется минор. Существует несколько его разновидностей:

• элемента;
• дополнительный;
• главный;
• базисный;
• окаймляющий.

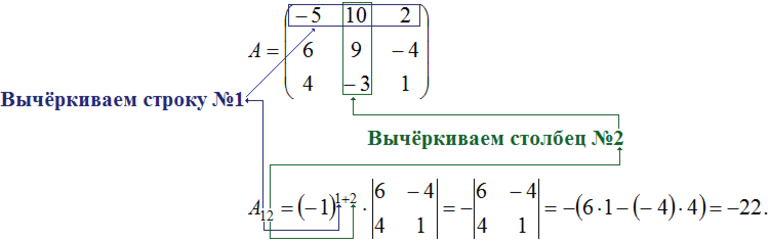
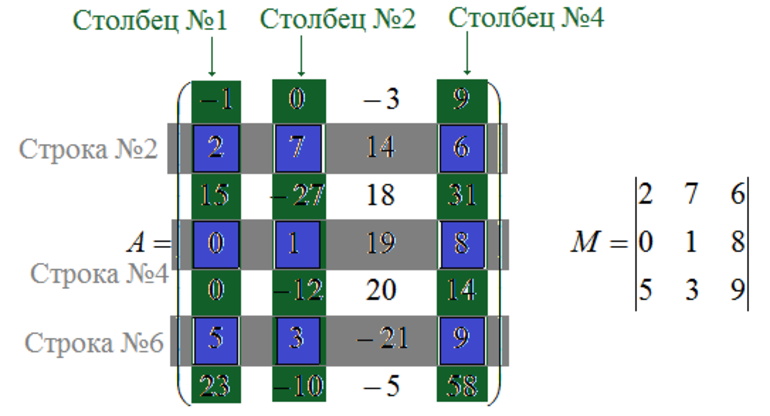
В общем случае под определением минора матрицы понимают определитель, находимый с помощью удаления строки и столбца определённого элемента. При рассмотрении алгебраических дополнений совместно с ними используют понятие угловой минор.

Для энного порядка под ним понимают определитель, полученный из набора элементов, находящихся вместе пересечения начальных эн строк и эн столбцов. Тут следует отметить, что алгебраическое дополнение применяется к элементу aij определителя и берётся со знаком (-1)^i+j.

Квадратная матрица

Минор принято разделять на элементный и матричный. Для лучшего понимания сначала следует разобрать минор квадратной матрицы. Рассматривать нужно её, так как минор — это определитель, а он бывает только у квадратной системы уравнений. Параметр элемента матрицы и определителя находят одинаково.

Вычисление минора обычно не вызывает трудностей. При этом стоит помнить простые правила определения детерминанта:

• для системы первого порядка определитель равен единственному элементу;
• в системах второго порядка детерминант находится из разницы произведений диагоналей в таблице;
• для вычисления определителя в матрицах высшего порядка используют рекурсивную формулу.

Пусть необходимо определить параметр элемента i, j. Для этого нужно посмотреть на записанную таблицу и выделить и-тую строчку и йо-тый столбец. На их пересечении будет стоять цифра, которая соответствует элементу aij. После вычёркивания элементов, расположенных от него по вертикали и горизонтали, оставшиеся в наборе и будут являться минором матрицы или определителя.

Например, пусть имеется определитель вида:

|2 5 7 8 9 |

|2 0 -2 21 13|

|2 -3 4 19 0|

|3 1 8 -2 1|

|4 6 5 -3 9 |

Нужно найти минор два три. На пересечении второй строчки и третьего столбца стоит цифра минус два. Убрав вторую соответствующую ей вертикаль и третью горизонталь, можно получить искомый минор M23:

|2 5 7 8 9 |

|2 -3 1 8 0 |

|3 1 -2 1|

|4 6 -3 9|

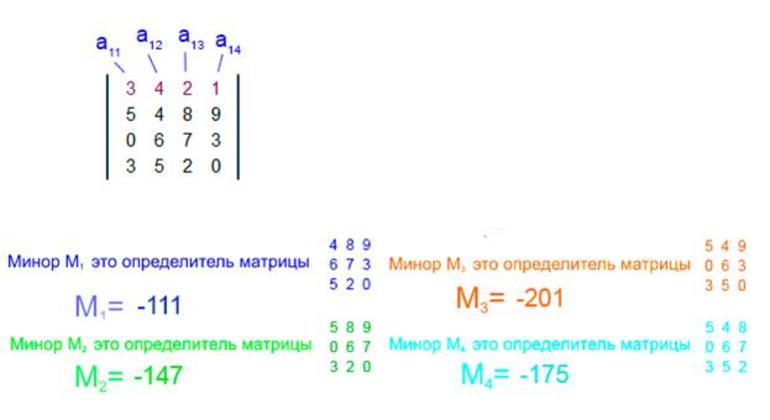
Теперь, чтобы найти минор единицы, нужно вычислить определитель полученной матрицы четвёртого порядка. Для этого удобно использовать теорему Лапласа для разложения по любой строке. Выбирать лучше ту, где стоят нули. После преобразования полученный ответ и будет минором. Аналогично выполняют действия и для определителя.

Алгебраическое дополнение элемента находится по формуле: Aij = (-1) i+j * Мij. Это выражение справедливо для любой квадратной матрицы. Для рассматриваемого примера такое дополнение будет равно следующему произведению: A23 = (-1)2+3 * M23 = — M23. Минор и алгебраическое дополнение имеют численные значения. Но при вычислении последнего необходимо учитывать, что сумма произведения определителя на дополнение к элементам будет равняться определителю, а сложение произведений двух элементов столбца или строки даст в ответе ноль.

Главный и базисный определитель

Минором высшего уровня описывают систему, состоящую из столбцов и строк, число которых превышает два. То есть минор восьмого порядка представляет собой определитель, состоящий из восьми столбцов и такого же числа строк. Тут следует отметить, что исходная матрица должна иметь больший порядок.

В таблице высшего порядка можно выделить несколько миноров. Например, в матрице восьмого уровня выделить пять столбцов и пять строк. Брать горизонтальные и вертикальные линии можно произвольно. В местах пересечения будут находиться значения, обозначающие элементы минора пятого порядка.

Записывают их соответственно, начиная с первой строки. После того как все члены выписаны, должен получиться новый определитель пятого порядка. Таких миноров указанного порядка может быть несколько.

В таблице чисел имеется главная диагональ. Начинается она с правого верхнего угла, то есть с элемента a11, и заканчивается на последнем правом элементе. В полученном миноре также можно выделить такую диагональ.

Если взять минор таким способом, что главная его диагональ будет состоять из элементов диагонали исходной таблицы, то такой минор называют главным. Иными словами, эта таблица, которая включает в себя элементы основной диагонали исходной матрицы. При этом необязательно, чтобы в главный минор матрицы были включены все главные элементы. Определитель же, находящийся из первых строк и столбцов, называется угловым минором матрицы.

Базисный определитель показывает, какой наибольший порядок может иметь полученный минор. Например, для системы данных, состоящей из семи строк и восьми столбцов, наибольший определитель может быть седьмого порядка. При этом базисным считается также последний определитель, который не равняется нулю. Если система уравнений имеет девятый порядок и при вычислениях выяснится, что система шестого уровня вырожденная, то предшествующий ему определитель также будет называться базисным. Значение базиса всегда будет наибольшим. Строки и столбцы, из которых состоит базис, называют также базисными. Их может быть несколько.

Когда из исходной таблицы выбран определитель не высшего порядка, то следующий за ним называется окаймляющим. Это значит, что необходимо добавить одну строку и столбец. Такого типа определителей может быть несколько, так как для того, чтобы их построить, можно добавить любую строку или столбец.

Решение задач

Для закрепления материала в школе и высших учебных заведениях учащимся предлагают выполнить расчёт несколько типовых заданий разной сложности. Умение их решать является доказательством понимания теории. Вот некоторые из них рекомендуемые для самостоятельного решения.

Найти в указанной матрице все определители второго уровня и алгебраические дополнения:

|5 7 3|

|8 5 6|

|6 8 10|

Для решения этой задачи нужно рассматривать первую и вторую строчки. Последовательно убирая строки и столбцы методом вычёркивания, можно получить шесть результатов:

1. M1,2 = |5 6| |8 5| = — 3;
2. ​ M1,3 = |5 3| |8 6| = — 6;
3. M2,3 = |6 3| |5 6| = — 3;
4. A1,2 = (-1)^1+2+1+2 * M1,2′ = 9;
5. A1,2 = (-1)^1+2+1+3 * M1,3′ = -8;
6. A1,2 = (-1) ^1+2+2+3 * M2,3′ = 7.

В следующей задаче рассматривается квадратная матрица три на три, в которой необходимо найти дополнительную характеристику:

(1 2 0)

(-2 0 3)

(3 4 -2)

По условию в таблице имеется девять позиций, для которых можно найти дополнительный элемент. При решении нужно последовательно их все перебрать, вычёркивая соответственные столбцы и строки:

1. M11 = |1 2 | |2 1| = -3;
2. M12 = |0 2| |3 1| = -6;
3. M13 = |0 1 | |3 2| = -3;
4. M21 = |2 -1| |3 1| = -1
5. M22 = |1 -1| |3 1| = 4;
6. M23 = |1 2| |3 2| = -4;
7. M31 = |2 -1| |1 2| = 5;
8. M32 = |1 -1 | |0 2| = -2;
9. M33 = |1 2| |0 1| = -1.

В следующем примере необходимо рассчитать первые три алгебраических дополнения. Пусть дана матрица A:

(1 2 -1)

(0 1 2)

(3 2 1)

Для нахождения первого параметра нужно вычеркнуть первый столбец и строку, при этом для определения знака использовать формулу: A = M (-1) ^j+i. В итоге получится определитель: A11 = |1 2| |2 1| = 1 — 4 = 3. Знак положительный, так как минус единица будет во второй степени. При этом можно отметить, что далее знак будет попросту чередоваться. Другие вычисления нужно делать аналогично: A12 = |0 2| |3 1| = (-6) * (-1) = 6; A13 = |0 1| |3 2| = -3.

Как видно из примеров, вычисления обычно не вызывают трудностей, но требуют внимательности и усидчивости. Особенно это касается нахождения обратной матрицы. Вычисляется она с помощью алгебраических дополнений, которые равны минорам, умноженным на минус единицу. Довольно часто знаки путают, и в итоге получается неправильный ответ. Поэтому в случае сложных систем есть резон использовать онлайн-калькуляторы.

Использование интернет-калькулятора

В интернете есть определённая группа сайтов, позволяющая выполнять различные математические вычисления в автоматическом режиме. На их страницах содержится специальный скрипт, выполняющий нахождение минора матрицы онлайн любой сложности. При этом от потребителя не требуется никаких особых знаний, он даже и вовсе может ничего не понимать в алгебраических вычислениях.

Всё, что ему необходимо будет сделать для получения ответа, — это ввести исходные данные в предложенную форму и нажать кнопку «Вычислить». Система автоматически определит нужный алгоритм и, используя свойства матрицы, выведет на экран ответ. При этом, кроме результата, пользователю будет предоставлена возможность ознакомиться с подробным решением.

По отзывам потребителей, из множества таких сервисов можно выделить пять следующих сайтов:

1. Allcalc — сервис с простым интерфейсом, но в то же время позволяющий выполнить любые действия с матрицей, включая нахождение миноров и алгебраических дополнений.
2. Onlinemschool — сайт, умеющий не только быстро выполнять вычисления, но и выводить пошаговое решение с комментариями.
3. MathSemestr — программное обеспечение калькулятора, понимает даже соотношения, взятые из таких популярных программ, как World и Excel.
4. Pikod — бесплатный сайт, предлагающий получить не только ответ, но и подробно расписанный ход решения.
5. Kontrolnaya-rabota — сервис позволяет выполнять любые преобразования матриц, при этом для сложных заданий существует режим «модульный конструктор».

Все указанные сайты доступны на русском языке, бесплатны, имеют простой и понятный интерфейс. На их страницах содержится справочная и теоретическая математическая информация. Кроме неё, для каждого раздела приводится типовой пример с объяснением. Использование онлайн-калькуляторов поможет сэкономить время и научит правильно выполнять действия по вычислению миноров.

Их использование будет полезным не только ученикам или студентам, желающим научиться самостоятельно решать задачи, но и инженерам, выполняющим сложные вычисления. Для специалистов они довольно востребованы, так как при самостоятельном решении небольшая ошибка по невнимательности приведёт к неправильному ответу, что исключено при расчёте в автоматическом режиме.

Квадратичные формы подразделяют на различные типы в зависимости от множества их значений.

Определение 8.3. Квадратичную форму f(x) = х^TАх, х = (х₁ … х_n)^T , будем называть:

— положительно (отрицательно) определенной, если для любого ненулевого столбца х выполняется неравенство f(x) > 0 (f(x) < 0);

— неотрицательно (неположительно) определенной, если f(x) ≥ 0 (f(x) ≤ 0) для любого столбца х, причем существует ненулевой столбец х, для которого f(x) = 0;

— знакопеременной (неопределенной), если существуют такие столбцы x и у, что f(x) > 0 и f(y) < 0.

Пример 8.6. Рассмотрим четыре квадратичные формы от трех переменных:

f₁(x₁,x₂,x₃) = x²₁ + x²₂ + x²₃,

f₂(x₁,x₂,x₃) = x²₁ + x²₂,

f₃(x₁,x₂,x₃) = x²₁ — x²₂ + x²₃,

f₃(x₁,x₂,x₃) = x₁x₂.

Квадратичная форма f₁ положительно определена, так как представляет собой сумму трех квадратов и потому принимает только положительные значения, если переменные одновременно не обращаются в нуль. Квадратичная форма f₂ неотрицательно определена: будучи суммой двух квадратов она не принимает отрицательных значений, но при х₁ = x₂ = 0 и х₃ ≠ 0 она принимает нулевые значения. Квадратичные формы f₃ и f₄ знакопеременны. Первая из них положительна при х = (1 0 0) и отрицательна при х = (0 1 0)^T . Вторая положительна при x = (1 1 0)^T и отрицательна при х = (1 -1 0)^T. Квадратичные формы f₂ и f₄ являются вырожденными, так как ранг каждой из них равен двум. #

Как следует из определения 8.3, тип квадратичной формы зависит только от множества значений, которые она принимает, но не зависит от переменных, в которых она записана. Поэтому, представив квадратичную форму в каноническом виде, сразу получаем следующие критерии для типа квадратичной формы в зависимости от множества собственных значений ее матрицы.

Хотя эта таблица дает удобную характеристику типам квадратичных форм, ее использование для определения типа конкретной квадратичной формы связано с вычислением соб-ственных значений матрицы. А это достаточно трудоемкая операция. На самом деле во многих случаях тип квадратичной формы можно определить, не вычисляя собственных значений ее матрицы. Метод состоит в вычислении и проверке знаков некоторых миноров матрицы квадратичной формы. Введем следующие обозначения.

Пусть матрица квадратичной формы f(x) = х^TАх имеет вид

где a_ij = a_ji, i,j = 1,n. Рассмотрим угловые миноры этой матрицы (которые также называют главными минорами):

Как видим, угловой минор порядка k расположен на пересечении первых k строк и первых k столбцов матрицы. Угловой минор максимального, n-го порядка представляет собой определитель матрицы.

Теорема 8.6 (критерий Сильвестра). Для того чтобы квадратичная форма от n переменных была положительно определена, необходимо и достаточно, чтобы выполнялись неравенства Δ₁ > 0, Δ₂ > 0, Δ₃ > 0, …, Δ_n > 0.

◄ Необходимость. Если квадратичная форма положительно определена, то в ее каноническом виде все коэффициенты должны быть положительны. Значит, и определитель матрицы квадратичной формы канонического вида положителен. Невырожденное преобразование квадратичной формы не меняет знака определителя, так как, согласно формуле преобразования (8.4), det(U^TAU) = (detU)²detА. Поэтому определитель матрицы исходной канонической формы тоже положителен, т.е. Δ_n > 0

Если квадратичная форма f(x₁, … ,х_n) от _n переменных положительно определена, то квадратичная форма f_k(x₁,… ,x_k) = f(x₁,…,x_k,0,…,0) от k переменных также положительно определена и, следовательно, определитель ее матрицы положителен. Но этот определитель совпадает с Δ_k, т.е. Δ_k > 0 при k = 1,n.

Достаточность. Используем метод математической индукции по количеству n переменных квадратичной формы. При n = 1 утверждение очевидно. Пусть утверждение верно для всех квадратичных форм от k переменных, k ≤ n — 1. Рассмотрим произвольную квадратичную форму f(x) с матрицей А = (a_ij) в базисе е = (e₁ … е_n), у которой все угловые миноры положительны. Квадратичная форма f_n-1(x₁,…,x_n-1) = f(x₁,… ,x_n-1,0) от n — 1 переменных определена на линейном подпространстве H_n-1= span{e₁,…,e_n-1} и имеет матрицу, совпадающую с матрицей минора Δ_n-1. Так как все угловые миноры для Δ_n-1, они же угловые миноры матрицы А, положительны, согласно предположению математической индукции квадратичная форма f_n-1 является положительно определенной. Заменой базиса (e₁ … e_n-1) подпространства H_n-1 новым базисом (f₁ … f_n-1) мы можем привести квадратичную форму f_n-1 к диагональному виду:

f_n-1(x) = λ₁x²₁ + … + λ_n-1x²_n-1, λ_i > 0, i = 1,n-1. (8.9)

В базисе (f₁ … f_n-1 e_n) квадратичная форма f(x) имеет вид

так как при х_n = 0 она совпадает с квадратичной формой f_n-1. Преобразуем последнее выражение для f(x), выделяя квадраты по переменным х₁, х_n-1:

где μ = b_in/λ_i, i = 1,n-1, λ_n = b_nn — λ₁μ²₁ — … — λ_n-1μ²_n-1 Выполнив линейную замену переменных х’_i = х_i + μ_ix_n, i = 1,n-1, х’_n = х_n с невырожденной матрицей, приходим к квадратичной форме канонического вида

f(x) = λ₁(x’₁)² + … + λ_n(x’_n)², (8.10)

в которой, согласно (8.9), коэффициенты λ₁, …, λ_n-1 положительны. У определителя матрицы квадратичной формы знак не зависит от выбора базиса. Поэтому в представлении (8.10) имеем λ₁… λ_n-1λ_n > 0, так как Дп > 0. Отсюда следует, что Ап > 0, так как все остальные коэффициенты А* положительны. Таким образом, в представлении (8.10) все коэффициенты положительны и квадратичная форма f(x) положительно определена. ►

Следствие 8.1. Для того чтобы квадратичная форма п переменных была отрицательно определена, необходимо и достаточно, чтобы выполнялись неравенства -Δ₁ > 0, Δ₂ > 0, -Δ₃ > 0, …, (-1)ⁿ Δ_n > 0 (знаки угловых миноров чередуются начиная с минуса).

◄ Если квадратичная форма f(x) отрицательно определена, то квадратичная форма -f(x) положительно определена, и наоборот. Матрицей квадратичной формы -f(x) является матрица -А, противоположная матрице А квадратичной формы f(x). Согласно критерию Сильвестра, для положительной определенности квадратичной формы -f(x) необходимо и достаточно, чтобы все угловые миноры Δ’_r, r = 1,n, матрицы -А были положительны. Но при умножении матрицы А на число — 1 все ее элементы умножаются на это число и поэтому Δ’_r = (-1)^r Δ_r, где Δ_r — угловой минор порядка r матрицы А. Таким образом, квадратичная форма -f(x) положительно определена тогда и только тогда, когда выполнены неравенства (-1)^r Δ_r > 0, r = 1,n, и это условие эквивалентно тому, что квадратичная форма f(x) отрицательно определена. ►

Следствие 8.2. Невырожденная квадратичная форма знакопеременна тогда и только тогда, когда для матрицы квадратичной формы выполнено хотя бы одно из условий:

— один из угловых миноров равен нулю;

— один из угловых миноров четного порядка отрицателен;

— два угловых минора нечетного порядка имеют разные знаки.

◄ Невырожденная квадратичная форма может быть либо положительно определенной, либо отрицательно определенной, либо знакопеременной — в зависимости от знаков коэффициентов в ее каноническом виде. Если имеется нулевой угловой минор или один из угловых миноров четного порядка отрицателен, то, согласно теореме 8.6 и следствию 8.1, эта квадратичная форма не является ни положительно, ни отрицательно определенной. То же можно утверждать и в случае, когда есть два угловых минора нечетного порядка с разными знаками. Значит, в этих случаях квадратичная форма знакопеременная. ►

Критерий Сильвестра и его следствия показывают, что тип квадратичной формы полностью определяется свойствами ее матрицы. Поэтому термины, введенные определением 8.3, можно перенести на симметрические матрицы. В частности, симметрическую матрицу А называют положительно (отрицательно) определенной и пишут А > 0 (А < 0), если положительно (отрицательно) определена соответствующая квадратичная форма. Согласно теореме 8.6 и ее следствиям, симметрическая матрица положительно определена, если все ее угловые миноры положительны. Симметрическая матрица отрицательно определена, если у ее угловых миноров знаки чередуются начиная со знака минус.

Следствие 8.3. Если симметрическая матрица положи-тельно определена, то все ее диагональные элементы положительны.

◄ Если А = (a_ij) — симметрическая положительно определенная матрица порядка n, то ее первый угловой минор положителен, т.е. а₁₁ = Δ₁ > 0. Воспользовавшись тем, что утверждение следствия верно для диагонального элемента а₁₁, докажем что и а_ii > 0 при i > 1. В квадратичной форме х^TАх, x = (x₁,…,x_n)^T сделаем замену переменных

х₁ = у_i, x_i = y₁, x_j = y_j при j ≠ 1,i.

В новых переменных матрица А’ = (а’_ij) квадратичной формы такова, что а_ii = а’₁₁ > 0. ►

Рассмотрим примеры на применение критерия Сильвестра.

Пример 8.7. Квадратичная форма х^TАх от трех переменных с матрицей

положительно определена, так как Δ₁ = Δ₂ = Δ₃ = 1 > 0.

Пример 8.8. Квадратичная форма х^TАх от трех переменных с матрицей

является знакопеременной, так как она невырождена (Δ₃ ≠ 0) и Δ₁ = 1 > 0, а Δ₂ = -8 < 0.

Пример 8.9. Квадратичная форма 2x₁x₂ от двух переменных является знакопеременной, так как она невырождена (Δ₂ = -1 ≠ 0), a Δ₁ = 0.

Пример 8.10. Квадратичная форма f(x₁, x₂, x₃, x₄) = 4х₁х₃ + 2x₂x₄ + х²₄ имеет угловые миноры Δ₁ = Δ₂ = Δ₃ = 0, Δ₄ = 4 и, согласно следствию 8.2, является знакопеременной. В этом можно убедиться, используя несложное преобразование вида квадратичной формы:

f(x₁,x₂,x₃,x₄) = (х₁ + x₃)² — х²₂ — (х₁ — x₃)² + (x₂ + x₄)².

Дополнение 8.1. Билинейные формы

Функцию b(х,у) от двух переменных, определенную в линейном пространстве L, называют билинейной формой, если эта функция линейна по каждому из своих аргументов, т.е. для любых действительных α и β и любых векторов x,y,z ∈ L выполняются равенства

b(αx + βy,z) = αab(x,z) + βb(y,z),

b(x,αy + βz) = αb(x,y) + βb{x,z).

Пример 8.11. Частным случаем билинейной формы является скалярное произведение. Действительно, аксиомы в) и г) скалярного умножения означают, что скалярное произведение как функция от двух переменных линейно по первому аргументу, а в силу аксиомы а) скалярное произведение линейно и по второму аргументу. #

Выберем в n-мерном линейном пространстве L некоторый базис е = (e₁ … е_n). Для билинейной формы b(х,у) обозначим b_ij = b(e_i,e_j), i,j = 1,n. Тогда для любых векторов х и у со столбцами координат х = (х₁ … x_n)^T и у = (у₁ … у_n)^T в базисе е

Используя квадратную матрицу В = (b_ij) порядка n, можем записать полученное представление в матричном виде:

b(х,у) = х^TВу. (8.11)

Матрицу В называют матрицей билинейной формы.

Тройное произведение, стоящее в правой части (8.11), нам уже встречалось (см., например, лемму на с. 185). Кстати, эта лемма показывает, что разным билинейным формам соответствуют разные матрицы. Таким образом, билинейная форма однозначно определяется своей матрицей в произвольно выбранном базисе. Кроме того, из леммы следует, что любая функция b, имеющая представление (8.11), является билинейной формой, и В является матрицей этой билинейной формы. Основываясь на этом, выясним, как изменяется матрица билинейной формы при изменении базиса.

Пусть билинейная форма b имеет в базисе b матрицу В_b, а в базисе е матрицу В_e. Обозначим через U матрицу перехода из базиса b в базис е. Тогда для любых двух векторов х, у со столбцами координат х_b, у_b в базисе b и х_e, у_e в базисе е имеем

b(x,y) = x^T_bA_by_b = (Ux_e)^TA_b(Uy_e) = x^T_e(U^TA_bU)y_e.

Сравнивая полученное представление с (8.11), делаем вывод, что матрица U^TA_bU является матрицей билинейной формы в базисе е, т.е.

А_e = U^TA_bU. (8.12)

Представление (8.11) билинейной формы в базисе похоже на запись (8.2) квадратичной формы в матричном виде. Кроме того, матрица билинейной формы преобразуется по тому же закону, что и матрица квадратичной формы (ср. (8.4) и (8.12)). Но матрица квадратичной формы симметрическая, в то время как матрица билинейной формы, вообще говоря, нет. Для того чтобы матрица билинейной формы b(x,у) в базисе е являлась симметрической, должны выполняться условия

b(e_i,e_j) = b(e_j,e_i), i,j = 1,n.

Если b(x,y) — билинейная форма, то функция b(х,х) в заданном базисе записывается в виде b(х, x) = х^TВх. Это матричное произведение представляет собой квадратичную форму от координат вектора х. Матрицей этой квадратичной формы является матрица А = 0,5(B + В^T). Матрицы билинейной и квадратичной форм совпадут, если матрица В билинейной формы симметрическая.

Пример 8.12. Функция b(x,y) = x₁y₁, заданная через координаты х = (x₁ x₂)^T и у = (y₁ y₂)^T векторов х и у в некотором базисе е двумерного линейного пространства, является билинейной формой с матрицей

Соответствующая ей квадратичная форма имеет вид f(x) = x₁x₂ и матрицу

Отметим, что квадратичная форма f(x) порождается так-же и билинейной формой b_s(x,y) = 0,5x₁y₂ + 0,5x₂y₁, имеющей матрицу А.

Определение 8.4. Билинейную форму b(х,у) называют симметрической (кососимметрической), если b(х,у) = = b(у,х) (b(х,у) = -b(у,х)) для любых векторов х и у.

Пример 8.13. Примером симметрической билинейной формы является скалярное произведение. По существу, определение 3.1 говорит, что скалярное произведение — это билинейная симметрическая форма, порождающая положительно определенную квадратичную форму (последнее — содержание аксиомы г) скалярного произведения). #

Если в билинейной форме b(х,у) поменять местами переменные, то получим новую билинейную форму b'(x,у) = b(у,x), матрица которой будет транспонированной к исходной. Действительно, если в некотором базисе b(х,у) = х^TBy, то в том же базисе

b'(х,у) = b(у,х) = у^TВх = (y^TBx)^T = х^TВ^Tу,

так как у^TВх — это число и транспонирование его не меняет.

Если билинейная форма b(у,х) симметрическая, то перестановка аргументов не меняет ее. В этом случае b'(x, у) = b(х, у) и В^T = В, т.е. матрица симметрической билинейной формы является симметрической. Верно и обратное утверждение: если матрица В билинейной форма b(у,х) симметрическая, то и сама билинейная форма симметрическая. Это следует из равенств

b(х,у) = х^TВу = (х^TВу)^T = у^TВ^Tх = у^TВх = b(у,х).

Итак, для симметричности билинейной формы необходима и достаточна симметричность ее матрицы. Отметим, что если билинейная форма имеет симметрическую матрицу в одном базисе, то ее матрица будет симметрической и в любом другом базисе. Случай косимметрической билинейной формы аналогичен. Для того чтобы билинейная форма была кососимметрической, необходимо и достаточно, чтобы ее матрица в каком-либо базисе была кососимметрической.

Теорема 8.7. Для любой квадратичной формы f(x) существует, и притом единственная, симметрическая билинейная форма В(х,у), для которой f(x) = В(х,х) для любого вектора х.

◄ Выберем произвольный базис е и запишем в нем матрицу А квадратичной формы f(x). Билинейная форма b(х,у) с симметрической матрицей А в этом же базисе является сим-метрической и порождает квадратичную форму f(x) с той же матрицей А. Разные симметрические билинейные формы порождают квадратичные формы с разными матрицами. Значит, нмкакой квадратичной форме не могут соответствовать две различные симметрические билинейные формы. ►

Замечание 8.2. По квадратичной форме соответствующая ей билинейная форма легко восстанавливается, при этом не нужно прибегать к записи функций в каком-либо базисе. Рассмотрим функцию

b(x,у) = 0,5(f(x + y) — f(x) — f(y)).

Это билинейная симметрическая форма, что следует из ее записи в произвольном базисе:

b(х, у) = 0,5 ((x + y)^T А(х + у) — х^TАх — у^TАу) = 0,5 (х^TАу + у^TАх) = 0,5(х^TАу + (у^TАх)^T) = 0,5 (х^TАу + х^TА^Tу)/2 = х^TАу,

где А — матрица квадратичной формы f(x) в этом же базисе. При этом

b( х,х) — х^TАх = f(x).

Вопросы и задачи

1. Найдите ранг квадратичных форм от трех переменных: а) х² + у² + 2xz; б) 2ху + 2xz + 2yz; в) (х + у)² — (х — у — z)²; г) (x — y — 2z)².
2. Приведите к каноническому виду методом Лагранжа следующие квадратичные формы от трех переменных:
   а) х² + 2у² + 2xz + 2yz; б) 2ху + 2xz + 2yz; в) х² — у² + 2z² + 2 ху + 2xz.
3. Приведите к каноническому виду при помощи ортогонального преобразования следующие квадратичные формы от двух переменных: а) х² + ху + у²; б) ху; в) 2х² + 3у² + 2ху.
4. Какой ранг может иметь положительно определенная квадратичная форма от n переменных?
5. Определите тип следующих квадратичных форм от двух переменных: а) х² — ху + у²; б) 2ху; в) х² + 4ху + 4у².
6. Квадратичная форма от двух переменных имеет вид ах² + bху + су², т.е. является квадратным трехчленом относительно любой из переменных. Как тип квадратичной формы связан с дискриминантом этого квадратного трехчлена?
7. Выясните, являются ли положительно определенными следующие квадратичные формы от трех переменных: а) х² + у² — z² + 2ху + 2xz + 2yz; б) ху + xz + yz; в) х² + у² + z² + 2ху; г) х² + у² + z² + ху + xz + yz.

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ

Заказать задачи по любым предметам можно здесь от 10 минут

Минор матрицы

Определение

Минор матрицы — это определитель $ n-1 $ порядка, составленный путём вычеркивания $ i $-ой строки и $ j $-го столбца из матрицы $ A $ порядка $ n $. Обозначается минор $ M_{ij} $

Формула минора матрицы выводится для каждого элемента этой матрицы отдельно. Пусть задана квадратная матрица $ A $ порядка $ n = 3 $:

$$ A = begin{pmatrix} a_{11}&a_{12}&a_{13} \ a_{21}&a_{22}&a_{23} \ a_{31}&a_{32}&a_{33} end{pmatrix} $$

По определению каждый минор $ M_{ij} $ равен определителю, получаемому при вычеркивании $ i $-ой строки и $ j $-ого столбца из матрицы $ A $.

$$ M_{11} = begin{vmatrix} a_{22}&a_{23} \ a_{32}&a_{33} end{vmatrix}; M_{12} = begin{vmatrix} a_{21}&a_{23} \ a_{31}&a_{33} end{vmatrix}; M_{13} = begin{vmatrix} a_{21}&a_{22} \ a_{31}&a_{32} end{vmatrix}; $$

$$ M_{21} = begin{vmatrix} a_{12}&a_{13} \ a_{32}&a_{33} end{vmatrix}; M_{22} = begin{vmatrix} a_{11}&a_{13} \ a_{31}&a_{33} end{vmatrix}; M_{33} = begin{vmatrix} a_{11}&a_{12} \ a_{21}&a_{22} end{vmatrix}; $$

$$ M_{31} = begin{vmatrix} a_{12}&a_{13} \ a_{22}&a_{23} end{vmatrix}; M_{32} = begin{vmatrix} a_{11}&a_{13} \ a_{21}&a_{23} end{vmatrix}; M_{33} = begin{vmatrix} a_{11}&a_{12} \ a_{21}&a_{22} end{vmatrix}; $$

Аналогично миноры находятся для любого порядка. В частности для матрицы второго порядка в определитель будет входить одно число.

Как найти?

Чтобы найти миноры матрицы $ M_{ij} $ нужно составить определители, полученные путем вычеркивания из матрицы $ A $ соответствующие строку и столбец.

Пример для матрицы второго порядка:

$$ M_{12} = begin{pmatrix} {a_{11}} & {a_{12}} \ a_{21}&{a_{22}} end{pmatrix} = a_{21} $$

Пример для матрицы третьего порядка:

$$ M_{12} = begin{pmatrix} {a_{11}}&{a_{12}}&{a_{13}} \ a_{21}&{a_{22}}&a_{23} \ a_{31}&{a_{32}}&a_{33} end{pmatrix} = begin{vmatrix} a_{21}&a_{23} \ a_{31}&a_{33} end{vmatrix} = a_{21}a_{33}-a_{23}a_{31} $$

Если полученный определитель:

1. Первого порядка, то записываем оставшееся число
2. Второго или третьего порядка, то вычисляем его по правилу треугольников
3. Четвертого и выше порядка, то выполняем разложение по строке (столбцу), либо методом Гаусса

Примеры решений

Пример 1

Определить миноры матрицы: $$ A = begin{pmatrix} 2&1 \ 0&5 end{pmatrix} $$

Решение

Вычеркиваем строку и столбец, которые соответствуют индексу при $M$: $$ M_{11} = begin{pmatrix} {2}&{1} \ {0}&5 end{pmatrix} = 5 $$ $$ M_{12} = begin{pmatrix} {2}&{1} \ 0&{5} end{pmatrix} = 0 $$ $$ M_{21} = begin{pmatrix} {2}&1 \ {0}&{5} end{pmatrix} = 1 $$ $$ M_{22} = begin{pmatrix} 2&{1} \ {0}&{5} end{pmatrix} = 2 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ M_{11} = 5; M_{12} = 0; M_{21} = 1; M_{22} = 2 $$

Пример 2

Найти миноры элементов на главной диагонали матрицы: $$ A = begin{pmatrix} 2&3&1 \ 1&-2&-3 \ 0&1&2 end{pmatrix} $$

Решение

Рассчитываем миноры: $$ M_{11} = begin{pmatrix} {2}&{3}&{1} \ {1}&-2&-3 \ {0}&1&2 end{pmatrix} = begin{vmatrix} -2&-3 \ 1&2 end{vmatrix} = -4+3 = -1 $$ $$ M_{22} = begin{pmatrix} 2&{3}&1 \ {1}&{-2}&{-3} \ 0&{1}&2 end{pmatrix} = begin{vmatrix} 2&1 \ 0&2 end{vmatrix} = 4-0 = 4 $$ $$ M_{33} = begin{pmatrix} 2&3&{1} \ 1&-2&{-3} \ {0}&{1}&{2} end{pmatrix} = begin{vmatrix} 2&3 \ 1&-2 end{vmatrix} = -4-3 = -7 $$

Ответ

$$ M_{11} = -1; M_{22} = 4; M_{33} = -7 $$