Как известно из курса планиметрии, две прямые в плоскости могут пересекаться (имеют общую точку) или быть параллельными (не имеют общую точку).
В пространстве мы можем найти множество примеров ситуаций, когда две прямые не пересекаются, но они и не параллельны.
Рис. (1). Дороги на земле и на эстакадах не пересекаются.
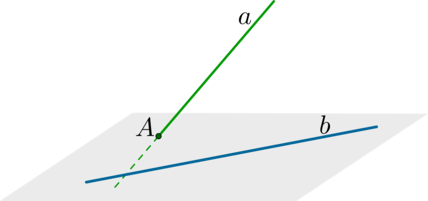
Скрещивающиеся прямые — это прямые, которые не лежат в одной плоскости и не имеют общих точек.
Теорема «Признак скрещивающихся прямых»
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).
Доказательство
Рассмотрим прямую (AB), лежащую в плоскости, и прямую (CD), которая пересекает плоскoсть в точке (D), не лежащей на прямой (AB).
Рис. (2). Скрещивающиеся прямые.
1. Допустим, что прямые (AB) и (CD) всё-таки лежат в одной плоскости.
2. Значит, эта плоскость идёт через прямую (AB) и точку (D), то есть, она совпадает с плоскостью (α).
3. Это противоречит условиям теоремы, по которым прямая (CD) не находится в плоскости (α), а пересекает её.
Теорема доказана.
В пространстве прямые могут пересекаться, скрещиваться или быть параллельными. 
Рис. (3). Параллельные прямые.
Рис. (4). Пересекающиеся прямые.
Рис. (5). Скрещивающиеся прямые.
Теорема
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.
Доказательство
Рассмотрим скрещивающиеся прямые (AB) и (CD).
Рис. (6). Доказательство теоремы.
1. Через точку (D) можно провести прямую (DE), параллельную (AB).
2. Через пересекающиеся прямые (CD) и (DE) можно провести плоскость (α).
3. Так как прямая (AB) не лежит в этой плоскости и параллельна прямой (DE), то она параллельна плоскости.
4. Эта плоскость единственная, так как любая другая плоскость, проходящая через (CD), будет пересекаться с (DE) и (AB), которая ей параллельна.
Теорема доказана.
1. Если прямые параллельны, то угол между ними —
0°
.
2. Углом между двумя пересекающимися прямыми называют величину меньшего из углов, образованных этими прямыми. Если все углы равны, то эти прямые перпендикулярны (образуют угол
90°
).
3. Углом между двумя скрещивающимися прямыми называют угол между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.
Обрати внимание!
Провести соответственные прямые, параллельные данным скрещивающимся прямым, можно через любую точку. Иногда удобно выбрать эту точку на одной из данных скрещивающихся прямых и провести через эту точку прямую, параллельную другой из скрещивающихся прямых.
Пример:
Рис. (7). Куб.
Найти угол между
AB
и
B1D1
.
Выберем точку
B
на прямой
AB
и проведём через
B
прямую
BD
параллельно
B1D1
.
Рис. (8). Куб с дополнительными построениями.
Угол между
AB
и
BD
—
45°
, так как
ABCD
— квадрат.
Соотвeтственно, угол между
AB
и
B1D1
— тоже
45°
.
Вопросы занятия:
· рассмотрим углы между пересекающимися и
скрещивающимися прямыми в пространстве.
Материал урока.
Напомню, что два луча
ОА и O1A1 в пространстве, не лежащие на одной прямой,
называются сонаправленными, если они параллельны и лежат в одной
полуплоскости с границей ОO1. Если
стороны двух углов соответственно сонаправленны, то такие углы равны.
Как вы уже знаете, любые
две пересекающиеся прямые лежат в одной плоскости и образуют четыре
неразвернутых угла. Если известен
один из этих углов, то можно найти и другие три угла.
Определение. Если пересекающиеся прямые образуют тупые и острые
углы, то углом между этими прямыми называется тот, который не
превосходит любой из трех остальных углов, т.е. наименьший из углов.
Если пересекающиеся
прямые образуют четыре равных угла, то угол между этими прямыми равен девяносто
градусов.
Пусть α – тот из углов,
который не превосходит любого из трех остальных углов. Тогда говорят, что угол
между пересекающимися прямыми равен α. Очевидно, что угол альфа между двумя пересекающимися
прямыми удовлетворяет условию: .
Теперь введем понятие угла
между скрещивающимися прямыми. Пусть нам даны две скрещивающиеся прямые а и
b. Возьмем произвольную точку М1 в
пространстве и проведем через нее прямые A1B1, параллельные прямым а и b
соответственно.
Тогда углом между
скрещивающимися прямыми а и b называется угол между построенными пересекающимися
прямыми A1B1. Т. е. если угол между прямыми A1B1 равен φ, то будем говорить, что угол между скрещивающимися
прямыми а и b равен φ.
Докажем, что угол
между скрещивающимися прямыми не зависит от выбора точки М1.
Возьмем любую другую
точку М2 и проведем через нее прямые a2 и b2,
параллельные прямым а и b соответственно. Пусть угол между прямыми a1 и b1 равен α1, а угол между прямыми a2 и b2 равен α2.
Если прямые a1, b1, a2, b2 лежат в
одной плоскости, то по свойству накрест лежащих углов при параллельных прямых
угол α1 равен
углу φ и равен углу α2.
Пусть теперь прямые a1 и b1,
пересекающиеся в точке М1, лежат в одной плоскости. А прямые a2 и b2,
пересекающиеся в точке М2 лежат в другой плоскости.
Так как прямая a1 параллельна прямой а и прямая a2 параллельна прямой а, то по признаку параллельности
прямых в пространстве прямые a1 и a2 также параллельны. Так как прямая b1 параллельна прямой b и прямая b2 параллельна прямой b, то по
признаку параллельности прямых в пространстве прямые b1 и b2 параллельны.
Отметим на прямых a1 и a2 точки A1 и A2 так, чтобы
отрезки М1А1 и М2А2 были равны. На
прямых b1 и b2 отметим точки B1 и B2 так,
чтобы отрезки M1B1и M2B2 были равны.
Угол A1M1B1 равен углу α1, угол A2M2B2 равен α2.
Тогда стороны угла A1M1B1 и угла A2M2B2 попарно сонаправлены. По теореме о равенстве углов с
сонаправленными сторонами получаем, что угол A1M1B1 равен углу A2M2B2. Т. е. имеем, что угол α1 равен углу α2.
Таким образом, величина
угла между скрещивающимися прямыми не зависит от выбора точки M1.
Замечание. Угол между параллельными прямыми в пространстве считается
равным 0º.
Рассмотрим пример. Пусть у нас есть треугольная пирамида DABC.
На ее ребре DB взята точка Т.
Тогда угол между
скрещивающимися прямыми BC и АТ равен углу между прямой АТ и прямой TF,
которая проходит через точку Т параллельно прямой BC в плоскости BDC.
Рассмотрим еще
пример. Пусть есть параллелепипед ABCDA1B1C1D1. И пусть точка О – точка пересечения диагоналей грани
A1B1C1D1, а точка F – точка пересечения диагоналей
грани AA1B1B.
Тогда угол между
скрещивающимися прямыми C1D и OF равен углу между прямыми OF и прямой OK,
проходящей через точку О и параллельной прямой C1D в плоскости C1DA1.
Задача. Дана правильная пирамида .
– средняя линия грани
. Найдите угол между
прямыми и
.
Решение.
Запишем ответ: 90º
Задача. Дан куб . Найдите угол между
прямыми и
.
Решение.
Ответ: 60º.
Подведем итоги
урока. На этом уроке мы рассмотрели
углы между пересекающимися и скрещивающимися прямыми. А также решили несколько
задач на нахождение скрещивающихся углов.
Описание презентации по отдельным слайдам:
-
1 слайд
Взаимное расположение прямых в пространстве.
Угол между прямыми. -
2 слайд
Цели урока:
Ввести формулировку и доказательство теоремы о равенстве углов с сонаправленными сторонами.
Научиться находить
угол между прямыми
в пространстве. -
3 слайд
Любая прямая а, лежащая в плоскости, разделяет плоскость на две части, называемые полуплоскостями.
а
а – граница
полуплоскостей.
А
В
С
Точки А и В лежат по одну
сторону от прямой а.
Точки А и С лежат по разные
стороны от прямой а.
? -
4 слайд
Углы с сонаправленными сторонами.
О
А
О1
А1
Лучи ОА и О1А1 не лежат на одной
прямой, параллельны, лежат в одной
полуплоскости с границей ОО1 →
сонаправленные
? -
5 слайд
Теорема об углах
с сонаправленными сторонами
Если стороны двух углов соответственно
сонаправлены, то такие углы равны.
О1
О
А1
В1
В
А -
6 слайд
Угол между скрещивающимися прямыми.
α
1800 — α
00 < α 900
1.
2.
Угол между
скрещивающимися
прямыми АВ и СD
определяется как угол
между пересекающимися
прямыми А1В1 и С1D1,
при этом А1В1|| АВ и С1D1|| CD.
А
В
D
С
А1
В1
С1
D1
α
М1 -
7 слайд
C1
C
A1
B1
D1
A
B
D
Дан куб АВСDА1В1С1D1.
Найдите угол между прямыми:
1.
ВС и СС1
2.
900
АС и ВС
450
3.
D1С1 и ВС
900
4.
А1В1 и АС
450 -
8 слайд
Задача №44.
Дано: ОВ || СD,
ОА и СD – скрещивающиеся.
Найти угол между ОА и СD, если:
О
В
C
D
A
а)
400
б)
450
в)
900 -
9 слайд
Дополнительная задача.
Треугольники АВС и АСD лежат
в разных плоскостях. РК – средняя
линия ∆АDC с основанием АС.
Определить взаимное расположение
прямых РК и АВ, найти угол между
ними, если
А
В
С
D
P
К
Ответ:
1) АВ и РК скрещивающиеся,
2) 600
Геометрия, 10 класс
Урок №5. Взаимное расположение прямых в пространстве
Перечень вопросов, рассматриваемых в теме
- признаки скрещивающихся прямых;
- определение углов с сонаправленными сторонами;
- доказательство теоремы о плоскости, проходящей через одну из скрещивающихся прямых;
- доказательство теоремы о равенстве углов с сонаправленными сторонами.
Глоссарий по теме
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.
Два отрезка называются параллельными, если они лежат на паралельных прямых.
Основная литература:
- Учебник Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. Геометрия 10-11 кл.– М.: Просвещение, 2014.
Дополнительная литература:
- Зив Б.Г. Дидактические материалы Геометрия 10 кл.– М.: Просвещение, 2014.
- Глазков Ю.А., Юдина И.И., Бутузов В.Ф. Рабочая тетрадь Геометрия 10 кл.-М.: Просвещение, 2013.
Открытый электронный ресурс:
- https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
Мы уже знаем, что прямы в пространстве могут располагаться параллельно или пересекаться. Существует еще один вид- скрещивающиеся прямые. С ним мы мимолетно познакомились на предыдущем уроке. А сегодня нам предстоит разобраться с этой темой более подробно.
Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости. (рис. 1)
Рисунок 1 – скрещивающиеся прямые
На прошлом уроке в качестве наглядного примера нами был приведен куб.
Сегодня предлагаем вам обратить внимание на окружающую вас обстановку и найти в ней скрещивающиеся прямые.
Примеры скрещивающихся прямых вокруг нас:
|
Одна дорога проходит по эстакаде, а другая под эстакадой |
|
|
Кабели моста |
|
|
Горизонтальные линии крыши и вертикальные линии стен |
|
Разберем и докажем теорему, которая выражает признак скрещивающихся прямых.
Теорема. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).
Доказательство.
Рассмотрим прямую AB лежащую в плоскости и прямую CD, которая пересекает плоскoсть в точке D, не лежащей на прямой AB (рис. 2).
- Допустим, что прямые AB и CD всё-таки лежат в одной плоскости.
2. Значит эта плоскость идёт через прямую AB и точку D, то есть она совпадает с плоскостью α.
3. Это противоречит условиям теоремы, что прямая CD не находится в плоскости α, а пересекает её.
Теорема доказана.
Рисунок 2 – скрещивающиеся прямые АВ и СD
Итак, возможны три случая расположения прямых в пространстве:
|
|
|
|
|
|
Разберем и докажем еще одну теорему о скрещивающихся прямых.
Теорема. Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.
Доказательство
Рассмотрим скрещивающиеся прямые AB и CD.(рис. 3)
1. Через точку D можно провести прямую DE параллельную AB.
2. Через пересекающиеся прямые CD и DE можно провести плоскость α
3. Так как прямая АB не лежит в этой плоскости и параллельна прямой DE, то она параллельна плоскости.
4. Эта плоскость единственная, так как любая другая плоскость, проходящая через CD, будет пересекаться с DE и AB, которая ей параллельна.
Теорема доказана.
Рисунок 3 – прямые АВ, СD, DЕ
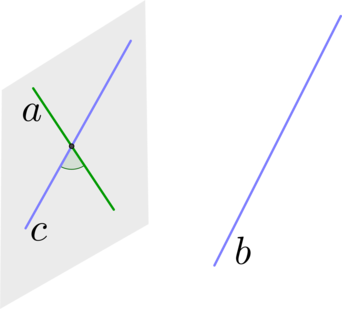
Любая прямая, например ОО1, рассекает плоскость на две полуплоскости. Если лучи ОА и О1А1 параллельны и лежат в одной полуплоскости, то они называются сонаправленными.
Лучи О1А1 и ОА не являются сонаправленными. Они параллельны, но не лежат в одной полуплоскости. (рис. 4)
Рисунок 4 – сонаправленные лучи
Теорема.Если стороны двух углов соответственно сонаправленны, то такие углы равны. (рис. 5)
Доказательство:
при доказательстве ограничимся случаем, когда углы лежат в разных плоскостях.
- Стороны углов сонаправлены, а, значит, параллельны. Проведем через них плоскости- как показано на чертеже.
Отметим на сторонах угла O произвольные точки A и B.
На соответствующих сторонах угла O1 отложим отрезки OA1 и O₁B₁ равные соответственно ОA и OB.
2. В плоскости рассмотрим четырехугольник OAA1O1.
Так как противолежащие стороны OA и O1A1 этого четырехугольника равны и параллельны по условию, то этот четырехугольник– параллелограмм и, следовательно, равны и параллельны стороны AA1 и OO1.
3. В плоскости, аналогично можно доказать, что OBB1O1 параллелограмм, поэтому равны и параллельны стороны ВВ1 и OO1.
4. Если две отрезка AA1 и BB1 равны параллельны третьему отрезку OO1, значит, они равны и параллельны, т. е. АА1||BB1 и AA1 = BB1.
По определению четырехугольник АВВ1А1 – параллелограмм и из этого получаем АВ=А1В1.
5.Из выше построенного и доказанного АВ=А1В1, ОA =O1A1 и OB =O1B1 следует, что треугольники AOB и A1 O1 B1. равны по трем сторонам, и поэтому О= О1.
Рисунок 5 – равные углы с сонаправленными сторонами
Любые две пересекающиеся прямые лежат в одной плоскости и образуют четыре неразвернутых угла. Если известен один из этих углов, то можно найти и другие три угла. Пусть а — тот из углов, который не превосходит любого из трех остальных углов. Тогда говорят, что угол между пересекающимися прямыми равен а. Очевидно, 0° < а ≤ 90°.
Введем теперь понятие угла между скрещивающимися прямыми(рис. 6, 7).Пусть АВ и СD- две скрещивающиеся прямые (рис. а.) Через произвольную точку М1 проведем прямые А1В1 и С1D1, соответственно параллельные прямым АВ и СВ (рис. б). Если угол между прямыми А1В1 и C1D1 равен φ, то будем говорить, что угол между скрещивающимися прямыми АВ и CD равен φ. Докажем, что угол между скрещивающимися прямыми не зависит от выбора точки М₁.
Действительно, возьмем любую другую точку М₂ и проведем через нее прямые А1В1 и С1D1, соответственно параллельные прямым АВ и СD (рис. б).
Так как А1В1||А1В1, C1D1|| С1D1, то стороны углов с вершинами М1 и М1 попарно сонаправлены (рис. б, такими углами являются ∟A1M1C1 и ∟A1M1C1, ∟A1M1D1 и ∟A1M1D1 и т.д.) Поэтому эти углы соответственно равны. Отсюда следует, что угол между прямыми А1В1 и С1D1 также равен φ. В качестве точки М, можно взять любую точку на одной из скрещивающихся прямых.
На рисунке в на прямой СD отмечена точка М и через нее проведена прямая А’В’, параллельная АВ. Угол между прямыми А’В’ и СD также равен φ.
Рисунок 6 – угол между скрещивающимися прямыми
Рисунок 7 – угол между скрещивающимися прямыми
Примеры и разбор решения заданий тренировочного модуля
Пример 1. Прямая с пересекает прямую а и не пересекает прямую b, параллельна прямой а. Докажите, что b и с- скрещивающиеся прямые .
Доказательство:
- a||b- через a и b проведем плоскость α (эта плоскость существует по определению параллельных прямых);
- пусть с пересекает а в точке М. a||b⇒ М ∉b.
- по теореме о признаке скрещивающихся прямых, с и b скрещиваются.
Пример 2. Выделите цветом верный ответ:
Дано: ОВ||CD
ОА и CD- скрещивающиеся
∟АОВ= 40°
Найти: угол между ОА и CD
- 50°
- 40°
- 140°
Решение:
- D ∈ A1D, A1D||AO
- угол между ОА и CD=∟A1DC
- ∟A1DC=∟AOB=40°.
Ответ: ∟A1DC=40°.
Правильный ответ:
- 50°
- 40°
- 140°
8. Геометрия в пространстве (стереометрия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Нахождение угла между прямыми
(blacktriangleright) Угол между прямыми – это такой угол (alpha), что (0leqslant alphaleqslant 90^circ).
(blacktriangleright) В пространстве существует 4 типа взаимного расположения прямых: совпадают, пересекаются, параллельны, скрещиваются.
(blacktriangleright) Скрещивающиеся прямые – это прямые, через которые нельзя провести одну плоскость.
Признак скрещивающихся прямых: если первая прямая пересекает плоскость, в которой лежит вторая прямая, в точке, не лежащей на второй прямой, то такие прямые скрещиваются.
(blacktriangleright) Порядок нахождения угла между скрещивающимися прямыми:
Шаг 1: через одну из двух прямых (a) провести плоскость, параллельную второй прямой (b) (напомним признак: прямая параллельна плоскости, если она параллельна какой-нибудь прямой из этой плоскости);
Шаг 2: в этой плоскости найти прямую (c), параллельную прямой (b);
Шаг 3: тогда угол между прямыми (a) и (b) будет равен углу между прямыми (a) и (c).
Задание
1
#934
Уровень задания: Равен ЕГЭ
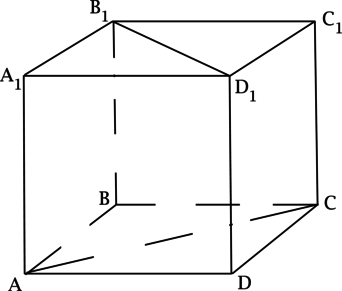
(ABCDA_1B_1C_1D_1) – куб. Найдите угол между прямыми, содержащими отрезки (AC) и (B_1D_1). Ответ дайте в градусах.
Прямая (BD) параллельна прямой (B_1D_1), тогда угол между (AC) и (B_1D_1) равен углу между (AC) и (BD), но (AC) и (BD) – диагонали квадрата, тогда они пересекаются под прямым углом, следовательно ответ (90^{circ}).
Ответ: 90
Задание
2
#2847
Уровень задания: Равен ЕГЭ
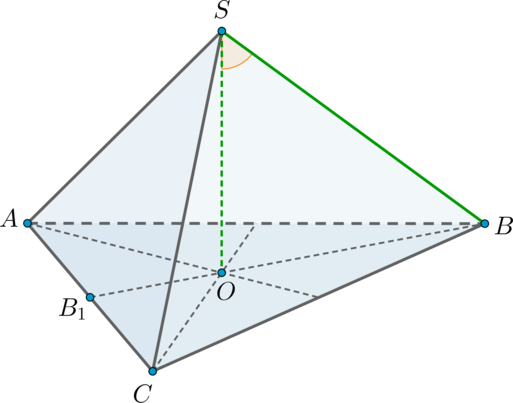
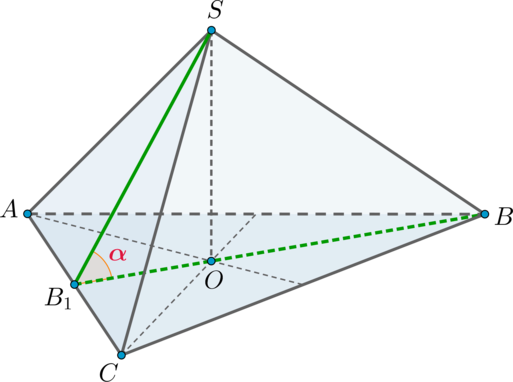
Дана правильная треугольная пирамида (SABC) с вершиной (S). Найдите угол между высотой пирамиды и ребром (SB), если высота пирамиды равна (2sqrt3), а сторона основания пирамиды равна (6). Ответ дайте в градусах.
Так как пирамида правильная, то в основании лежит правильный треугольник, следовательно, высота (SO) падает в точку пересечения медиан основания.
Пусть (BB_1) – медиана, а значит, и высота. По теореме Пифагора [BB_1=sqrt{BC^2-B_1C^2}=3sqrt3 quadRightarrowquad BO=dfrac23BB_1=2sqrt3,] так как медианы точкой пересечения делятся в отношении (2:1), считая от вершины.
Следовательно, прямоугольный (triangle SOB) является равнобедренным ((SO=BO=2sqrt3)), значит, острые углы равны по (45^circ).
Ответ: 45
Задание
3
#933
Уровень задания: Равен ЕГЭ
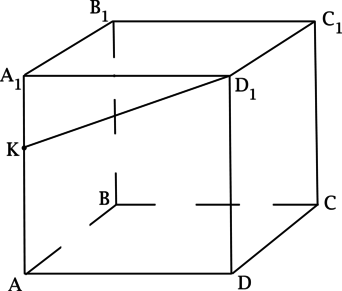
(ABCDA_1B_1C_1D_1) – куб. Точка (K) лежит на ребре (AA_1). Найдите угол между прямыми, содержащими отрезки (D_1K) и (AB). Ответ дайте в градусах.
Так как (ABCDA_1B_1C_1D_1) – куб, то (AB) перпендикулярен плоскости ((ADD_1)), тогда (AB) перпендикулярен любой прямой, лежащей в плоскости ((ADD_1)), следовательно, угол между прямыми, содержащими отрезки (D_1K) и (AB) равен (90^{circ}).
Ответ: 90
Задание
4
#2845
Уровень задания: Равен ЕГЭ
Дан правильный тетраэдр (SABC). Найдите квадрат тангенса угла между высотой грани (SAC), опущенной из вершины (S), и высотой грани (ABC), опущенной из вершины (B).
Пусть (SB_1) – высота грани (SAC). Так как тетраэдр правильный, то все его грани – равные правильные треугольники, то есть (SB_1) также является и медианой, значит, (AB_1=B_1C). Также у правильного тетраэдра высота из каждой вершины падает в точку пересечения медиан (биссектрис, высот) противоположной грани. Следовательно, если (SO) – высота, то (O) – точка пересечения медиан треугольника (ABC), а значит и высот, так как (triangle ABC) правильный. Следовательно, (BB_1) — медиана и высота.
Таким образом, необходимо найти (mathrm{tg}^2angle (SB_1,
BB_1)).
Пусть (a) – ребро тетраэдра. Тогда (BC=a, B_1C=0,5a), следовательно, по теореме Пифагора [BB_1=sqrt{BC^2-B_1C^2}=dfrac{sqrt3}2a] Так как (O) – точка пересечения медиан, а медианы точкой пересечения делятся в отношении (2:1), считая от вершины, то (OB_1=frac13BB_1=frac{sqrt3}6a).
Так как (triangle ABC=triangle SAC), то (SB_1=BB_1). Следовательно, из прямоугольного (triangle SB_1O): [cos
alpha=dfrac{OB_1}{SB_1}=dfrac13 quadRightarrowquad sin alpha
=sqrt{1-cos^2alpha}=dfrac{2sqrt2}3 quadRightarrowquad
mathrm{tg}^2alpha=(2sqrt2)^2=8.]
Ответ: 8
Задание
5
#1846
Уровень задания: Равен ЕГЭ
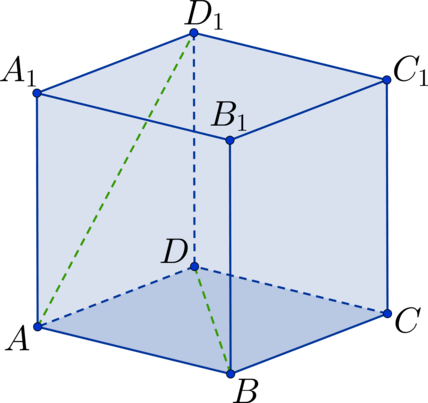
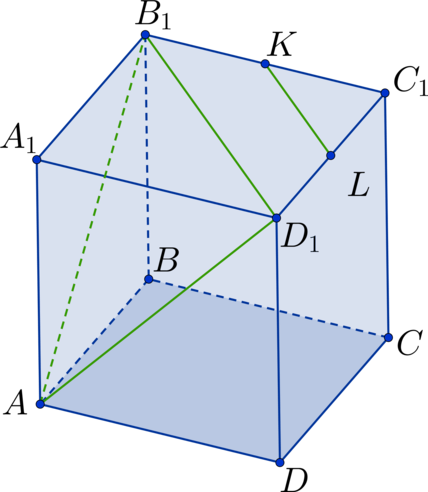
Дан куб (ABCDA_1B_1C_1D_1). Найдите угол между прямыми (AD_1) и (BD). Ответ дайте в градусах.
Заметим, что (BC_1 || AD_1), тогда рассмотрим треугольник (triangle BDC_1), в котором необходимо определить (angle DBC_1). Он состоит из диагоналей соответствующих квадратов. Так как квадраты между собой равны, то равны и диагонали (Rightarrow) (triangle BDC_1) – равносторонний треугольник (Rightarrow) (angle DBC_1 = 60^circ).
Ответ: 60
Задание
6
#1847
Уровень задания: Равен ЕГЭ
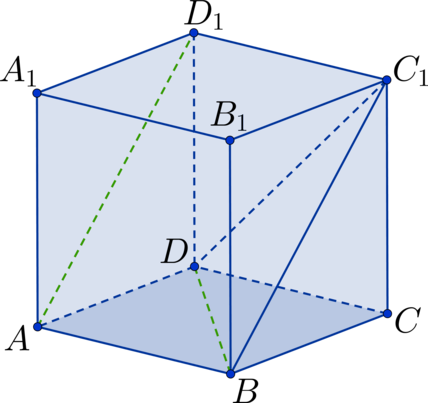
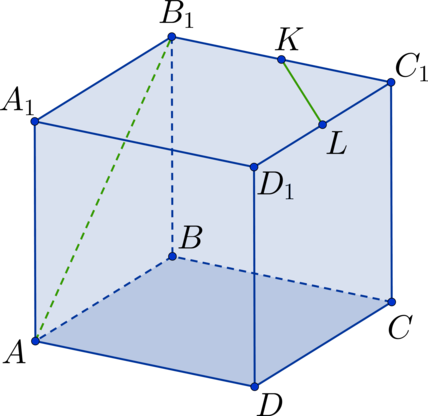
Дан куб (ABCDA_1B_1C_1D_1). Точка (K) – середина стороны (B_1C_1), а точка (L) – середина стороны (C_1D_1). Найдите угол между прямыми (AB_1) и (KL). Ответ дайте в градусах.
Проведем диагональ (B_1D_1) в квадрате (A_1B_1C_1D_1). Тогда (KL) – средняя линия в (triangle B_1C_1D_1) (Rightarrow) (KL || B_1D_1) (Rightarrow) (angle AB_1D_1) – искомый угол. Рассмотрим (triangle AB_1D_1). Он состоит из диагоналей соответствующих квадратов (Rightarrow) треугольник является равносторонним (Rightarrow) (angle AB_1D_1 = 60^circ).
Ответ: 60
Задание
7
#2846
Уровень задания: Сложнее ЕГЭ
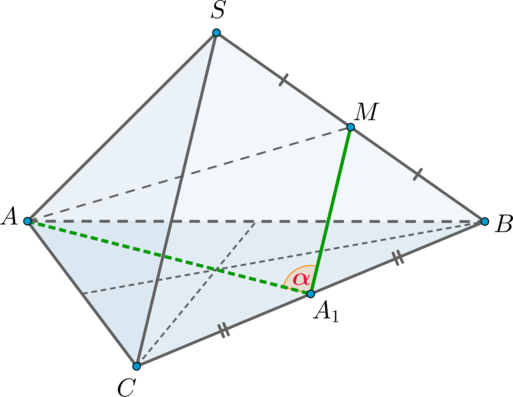
Дана правильная треугольная пирамида (SABC) с вершиной (S). Найдите косинус угла между высотой основания (AA_1) и ребром (SC), если сторона основания равна (sqrt3), а боковое ребро равно (2).
Так как пирамида правильная, то в основании лежит правильный треугольник, следовательно, (AA_1) также является и медианой.
Заметим, что прямые (AA_1) и (SC) скрещиваются. Проведем (A_1Mparallel SC), следовательно, (angle (AA_1, SC)=angle (AA_1,
A_1M)).
Так как (A_1Mparallel SC) и (A_1) – середина (BC), то (M) – середина (SB). Следовательно, (A_1M) – средняя линия и [A_1M=frac12SC=1.] По теореме Пифагора из (triangle ABA_1): [AA_1=sqrt{AB^2-A_1B^2}=dfrac32.] Медиану (AM) из (triangle SAB) можно найти по формуле медианы: [AM^2=dfrac{2AS^2+2AB^2-SB^2}4=dfrac52.] Следовательно, по теореме косинусов из (triangle AA_1M): [cos alpha=dfrac{AA_1^2+A_1M^2-AM^2}{2AA_1cdot A_1M}=dfrac14=0,25.]
Ответ: 0,25
Каждому школьнику, который готовится к ЕГЭ по математике, будет полезно повторить тему «Нахождение угла между прямыми». Как показывает статистика, при сдаче аттестационного испытания задачи по данному разделу стереометрии вызывают трудности у большого количества учащихся. При этом задания, требующие найти угол между прямыми, встречаются в ЕГЭ как базового, так и профильного уровня. Это значит, что уметь их решать должны все.
Основные моменты
В пространстве существует 4 типа взаимного расположения прямых. Они могут совпадать, пересекаться, быть параллельными или скрещивающимися. Угол между ними может быть острым или прямым.
Для нахождения угла между прямыми в ЕГЭ или, например, в решении задач по теореме о трех перпендикулярах, школьники Москвы и других городов могут использовать несколько способов решения задач по данному разделу стереометрии. Выполнить задание можно путем классических построений. Для этого стоит выучить основные аксиомы и теоремы стереометрии. Школьнику нужно уметь логически выстраивать рассуждение и создавать чертежи, для того чтобы привести задание к планиметрической задаче.
Также можно использовать векторно-координатный метод, применяя простые формулы, правила и алгоритмы. Главное в этом случае — правильно выполнить все вычисления. Отточить свои навыки решения задач по стереометрии и другим разделам школьного курса вам поможет образовательный проект «Школково».

УСТАЛ? Просто отдохни