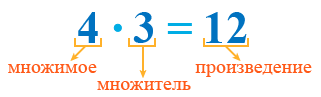Умножение натуральных чисел
- Множимое, множитель и произведение
- Проверка умножения
Умножение — это арифметическое действие, с помощью которого находят сумму одинаковых слагаемых.
Пример. Во дворе посадили 3 ряда ёлок, по 4 ёлки в каждом ряду. Сколько ёлок посадили во дворе?
Чтобы ответить на этот вопрос, надо найти сумму 3 слагаемых, каждое из которых равно 4.
4 + 4 + 4 = 12.
Складывая 3 раза по 4 ёлки, мы получим общее количество ёлок во всех трёх рядах.
Умножить – значит повторить одно число слагаемым столько раз, сколько в другом содержится единиц.
Для записи умножения используется знак х
(косой крест) или ·
(точка), который ставится между числами. Например:
4 х 3 или 4 · 3
Эта запись означает, что 4 надо умножить на 3. Справа от записи умножения ставится знак =
(равно), после которого записывается полученный результат:
4 · 3 = 12.
Умножение – это краткая запись сложения одинаковых слагаемых.
Пример. Умножить 6 на 5 — это значит найти сумму пяти слагаемых, каждое из которых равно шести:
6 + 6 + 6 + 6 + 6 = 30.
Сократим запись, заменив сложение на умножение:
6 · 5 = 30.
Оба выражения равны:
6 + 6 + 6 + 6 + 6 = 6 · 5 = 30,
но для краткости записей лучше всегда использовать умножение, когда число одинаковых слагаемых больше двух.
Множимое, множитель и произведение
Множимое — это число, которое умножают. Множитель — это число, на которое умножают. Например, в записи:
4 · 3,
4 — это множимое, 3 — множитель. Множимое является числом, которое выступает в качестве слагаемого. Множитель — это число, которое указывает количество одинаковых слагаемых.
Произведение — это число, которое получается в результате умножения. Например, в записи:
4 · 3 = 12,
12 — это произведение. При этом сама запись 4 · 3 тоже называется произведением.
Эту запись можно прочитать так: произведение четырёх и трёх равно двенадцати
, четыре умножить на три равно двенадцати
, по четыре взять три раза, получится двенадцать
.
Множимое и множитель иначе называются множителями или сомножителями.
Проверка умножения
Рассмотрим выражение:
4 · 3 = 12,
где 4 — это множимое, 3 — это множитель, а 12 — произведение. Чтобы узнать правильно ли было выполнено умножение, можно:
- Разделить произведение на множитель, если получится число, равное множимому, то умножение было выполнено верно:
12 : 3 = 4.
- Разделить произведение на множимое, если получится число, равное множителю, то умножение выполнено верно:
12 : 4 = 3.
Умножение двух чисел можно проверить делением, для этого произведение делят на один из сомножителей, если частное окажется равно другому сомножителю, то умножение выполнено верно.
- Главная
- Справочники
- Справочник по математике для начальной школы
- Умножение
В этом разделе познакомимся с умножением и узнаем, что сложение одинаковых слагаемых можно заменить умножением.
В математике существует знак для умножения — это точка посередине строки между числами, которые нужно перемножить.
Например, 6 + 6 + 6 + 6 = 24 можно записать по-другому: 6 • 4 = 24
Смысл действия умножения состоит в том, что при умножении находится сумма одинаковых слагаемых.
Первое число при умножении показывает, какое слагаемое повторяют несколько раз.
Второе число при умножении показывает, сколько раз повторяют это слагаемое.
Результат умножения показывает, какое число получается.
6 • 4 значит, что число 6 повторяют 4 раза: 6 + 6 + 6 + 6 = 24
6 — первый множитель
4 — второй множитель
24 — произведение
Числа при умножении
Первый множитель
Второй множитель
Результат умножения, или Произведение
Чтение числовых выражений
6 • 4 = 24
Этот пример можно прочитать по-разному.
- 6 умножить на 4 равняется 24.
- 6 увеличить в 4 раза – получится 24.
- Первый множитель – 6, второй множитель – 4, произведение – 24.
- Произведение 6 и 4 равно 24.
Умножение на 1
4 • 1 = 4, потому что это значит, что число 4 повторяют только 1 раз.
23 • 1 = 23, потому что это значит, что число 23 повторяют только 1 раз.
Умножение на 0
8 • 0 = 0, потому что это значит, что число 8 повторяют 0 раз.
26 • 0 = 0, потому что это значит, что число 26 повторяют 0 раз.
Умножение на 10
8 • 10 = 80, потому что число 8 повторяют 10 раз.
15 • 10 = 150, потому что число 15 повторяют 10 раз.
Связь деления и умножения
8 • 3 = 24, потому что 8 повторяют 3 раза.
24 : 3 = 8, потому что в 24 по 3 содержится 8 раз.
24 : 8 = 3, потому что в 24 по 8 содержится 3 раза.
В несколько раз больше
Решим задачу:
В магазине было 2 лисички, а котят в 4 раза больше. Сколько было котят?
Это значит, что котят было 4 раза по 2.
2 + 2 + 2 + 2 = 4 (к.)
Заменяем сложение умножением и получаем:
2 • 4 = 8 (к.)
Вывод: Если в задаче есть слова «в … раз больше», то задача решается умножением.
Во сколько раз больше? Во сколько раз меньше?
Например, решим задачу: В магазине было 8 котят и 2 лисички. Во сколько раз котят было больше, чем лисичек? Во сколько раз лисичек было меньше, чем котят?
Чтобы ответить на эти вопросы, нужно узнать, сколько раз по 2 содержится в 8?
8 : 2 = 4 (раза)
Значит, котят в 4 раза больше, чем лисичек, а лисичек в 4 раза меньше, чем котят.
Советуем посмотреть:
Табличное умножение
Внетабличное умножение
Умножение суммы на число
Умножение на однозначное число в столбик
Умножение на числа, оканчивающиеся нулями
Свойства умножения
Правило встречается в следующих упражнениях:
2 класс
Страница 64. Тест 1. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 66,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 72,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 78,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 60. Урок 24,
Петерсон, Учебник, часть 2
Страница 64. Урок 26,
Петерсон, Учебник, часть 2
Страница 76. Урок 31,
Петерсон, Учебник, часть 2
Страница 54. Урок 19,
Петерсон, Учебник, часть 3
Страница 90. Урок 35,
Петерсон, Учебник, часть 3
Страница 102. Повторение,
Петерсон, Учебник, часть 3
3 класс
Страница 76,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 85,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 99,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 45,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 72,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 44. Тест 2. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 55. Тест 2. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 20,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 25,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 25. Урок 11,
Петерсон, Учебник, часть 3
4 класс
Страница 11,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 40,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 93,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 10,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 13. Тест 1. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 15. Тест 2. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 12,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 15,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 82,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 95,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
5 класс
Номер 36,
Мерзляк, Полонский, Якир, Учебник
|
Название компонентов при умножении: 3 · 4 = 12 Как найти первый множитель? Чтобы Как найти второй множитель? Чтобы |
Название компонентов при умножении: 3 · 4 = 12 Как найти первый множитель? Чтобы Как найти второй множитель? Чтобы |
|
Название компонентов при умножении: 3 · 4 = 12 Как найти первый множитель? Чтобы Как найти второй множитель? Чтобы |
Название компонентов при умножении: 3 · 4 = 12 Как найти первый множитель? Чтобы Как найти второй множитель? Чтобы |
|
Название компонентов при умножении: 3 · 4 = 12 Как найти первый множитель? Чтобы Как найти второй множитель? Чтобы |
Название компонентов при умножении: 3 · 4 = 12 Как найти первый множитель? Чтобы Как найти второй множитель? Чтобы |
Целью этого материала будет объяснение важного математического действия, называемого умножением. Для начала попробуем дать вам общее представление о нем и помочь понять сам смысл процесса умножения. Затем мы разберемся с основными определениями и правилами записи, которые используются при умножении натуральных чисел. В последнем пункте мы остановимся на том, для решения каких задач нам пригодится умножение.
Общий смысл умножения
Ранее, разбирая действие сложения, мы говорили о нем как об объединении некоторых множеств. Умножение – тоже своего рода объединение множеств, только разница в том, что все множества будут одинаковы. Что это значит на практике?
Умножение связано с ростом, увеличением изначального количества чего-либо. Вспомним выражение «приумножать богатства» (т.е. приобрести больше богатства, чем было изначально), «приумножать добро» и т.д. Таким образом, умножение сводится к многократному увеличению исходного количества чего-либо.
Взяв за основу общее представление об умножении, выясним конкретный смысл этого понятия. Для этого разберем задачу. У нас есть два мастера, каждый из которых может сковать за день четыре меча. Цель – выяснить, сколько оба мастера изготовят за один день.
Есть два подхода к решению этой задачи. Мы можем определить нужное количество изделий, воспользовавшись методом сложения: 4+4=8. Сумма двух слагаемых и даст нам в итоге нужную цифру (для вычислений надо будет воспользоваться таблицей сложения).
А если нам нужно узнать общее количество изделий не для двух, а для 456 мастеров? Неужели придется складывать 456 одинаковых слагаемых? Ведь исходное число будет равно именно их сумме. Использовать метод сложения тем не менее можно (вспомним, как правильно складывать три натуральных числа и больше), однако подсчеты будут очень сложными и займут много времени. Удобнее применить для решения метод умножения: не складывать восьмерки 456 раз, а просто умножить 8 на 456. Сформулируем определение:
Умножить одно натуральное число на другое – значит совершить действие, в результате которого получится число, являющееся суммой одинаковых слагаемых. При этом значение первого числа будет соответствовать значению одного слагаемого, а второе будет указывать на количество этих слагаемых.
Решить задачу, приведенную ранее, мы можем, умножив числа 8 и 456. Это позволит нам получить точный результат намного быстрее, чем при подсчете методом сложения.
Отдельно отметим, что результат умножения натуральных чисел – это тоже натуральное число, равно как и сумма натуральных чисел дает нам в итоге другое натуральное число.
Основные понятия умножения
В этом пункте мы укажем основные термины, которые используют при описании умножения, и правила их записи.
Знак умножения обычно отображают на письме в виде точки «·», которая располагается между двумя умножаемыми числами. К примеру, 6·7 или 2·78 (два числа со знаком умножения вместе образуют числовое выражение). Иногда вместо точки пишут звездочку или знак «х».
Те числа, которые перемножают, называют множителями, а результат действия принято называть произведением натуральных чисел. Само числовое выражение из множителей и знака между ними также будем называть произведением.
При многоступенчатых подсчетах множители удобно нумеровать, т.е. указывать, что одно из чисел является первым множителем, другое – вторым и др.
Если нам нужно получить результат умножения некоторых чисел, то мы используем выражения «найти произведение», «вычислить произведение», «умножить одно число на другое».
Итог вычисления принято выражать на письме в виде верного равенства. Так, если мы умножаем 5 на 3 (как бы складываем три пятерки) и получаем 15, то записываем так: 5·3=15. С одной стороны от знака равенства у нас стоит числовое выражение, а с другой – результат подсчета. Прочитать запись можно как «пять умножить на три будет равно пятнадцати» или «произведение пяти и трех равно пятнадцати».
Таким образом, процесс нахождения произведения двух чисел схематично можно выразить так: множитель · множитель = произведение.
Типы задач, решаемых с помощью умножения
В этом пункте мы разберем примеры, когда умение умножать натуральные числа нам пригодится.
1. Нахождение количества элементов некоторого множества, которое получилось в результате объединения равных множеств. Например:
В коробку помещается 10 книг. Как найти, сколько книг поместится в 6 коробок?
Просто умножить 10 на 6.
Ответ: 60.
2. Нахождение итоговых значений каких-либо физических величин.
Период оборота Земли вокруг Солнца составляет один год, или в среднем 365 дней. Если Земля совершила 15 оборотов, то сколько прошло дней?
Результат легко вычислить с помощью умножения 365 на 15.
Ответ: 5475.
Еще один пример:
Гиря весит 1,5 кг. Сколько весит 50 таких одинаковых гирь?
Умножим 1,5·50.
Ответ: 75.
3. Если нужно найти, в какое количество раз одно множество больше, чем другое. Например:
В одном огороде посадили 3 яблони, а в другом в 5 раз больше. Для того чтобы вычислить, сколько яблонь посадили во втором огороде, мы должны умножить 3 на 5.
Ответ: 15.
Часто в таких задачах требуется вычислять возраст:
Внуку 15 лет, а дед старше в 4 раза. Как узнать, сколько лет деду?
Перемножим натуральные числа 15 и 4.
Ответ: 60.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Что такое умножение?
Умножение является арифметическим действием, в котором принимают участие два аргумента — множитель и сомножитель. В некоторых случаях первый аргумент принято называть множимым, а второй — множителем. Число, которое получается в результате умножения, называется произведением.
Впервые в истории умножение для натуральных чисел было определено, как многократное сложение. Чтобы умножить число а на число b, необходимо сложить b чисел a.
a × b= а + а + …+ а (b раз)
Позже умножение разделилось на рациональное, целое, вещественное, комплексное и некоторые другие виды чисел, согласно систематическому обобщению.
Сегодня в математике умножение имеет конкретный смысл, различные свойства и определения для разных математических объектов, а не только для определения чисел.
Умножение чисел между собой — это конкретная коммутативная операция, другими словами — это определенный порядок записи множителей-чисел, который никак не влияет на сам результат умножения.
Например, при умножении цифр 5 и 3 запись может выглядеть, как 3 × 5, так и 5 × 3 (произносится, как трижды пять и пятью три). В том и другом случае результатом вычисления будет являться число 15.
Давайте проверим эти действия через сложение:
5 + 5 + 5 = 15
3 + 3 + 3 + 3 = 15
Умножение матриц, векторов, кватернионов, множеств и т. д (т. е, нечисловых математических, физических и абстрактных величин) не всегда может являться коммутативной операцией. И здесь, при умножении физических величин будет важную роль играть их размерность.
В задачу общей алгебры, в частности теории колец и групп, всегда входит изучение общих свойств операции.
Что такое произведение в математике?
Произведением называется результат умножения. Умножаемые числа называются множителями и сомножителями. А под умножением подразумевается краткая запись суммы одинаковых слагаемых.
Например:
Когда мы видим значение 5 × 3, то имеется в виду, что нужно 5 сложить между собой три раза, другими словами, это обычная краткая запись для 5 + 5 + 5.
Запись произведения
Умножение может обозначаться крестиком «×», точкой «·» и звездочкой «*»:
5 × 3
5 * 3
5 · 3
Все обозначения одинаковы по своей сути и говорят об одном и том же действии.
Но иногда знак умножения в виде точки могут намеренно пропускать, если умножение идёт не на число, а на буквенную переменную и постоянную.
Например, вместо 5 × x обычно пишут 5х.
Если в действии есть несколько сомножителей, то вместо них можно поставить многоточие. Допустим, произведение целых чисел от 1 до 100 будет выглядеть таким образом:
1 × 2 × 3 × 4 ×…× 97 × 98 × 99 × 100
Что такое множимое?
В математических действиях множимое является первым числом или величиной, которое умножается на множитель.
Что такое множитель?
Множителем называется то число, которое показывает сколько раз следует повторять слагаемым какое-то другое число (множимое), чтобы получилось произведение.
Свойства умножения
В умножении существуют разные свойства: переместительное, сочетательное и распределительное.
По переместительному свойству: от перестановки разных множителей произведение остается неизменным.
Например: 5 × 2 = 10 и 2 × 5 = 10.
Соответственно, 5 × 2 = 2 × 5.
По сочетательному свойству: два соседних множителя можно заменить произведением.
Например: (3 × 2) × 5 = 3 × (2 × 5).
По распределительному свойству при умножении суммы на число можно умножать на него в отдельности каждое слагаемое, и потом складывать полученные результаты.
Например: (5 + 10) × 6 = 5 × 6 + 10 × 6 = 90.
Другие свойства
Чтобы умножить сумму на какое-то число, сначала необходимо выполнить сложение, а потом полученный результат умножить на число.
Например: (4 + 9) × 5 = 13 × 5 = 65.
Чтобы умножить число на произведение, нужно сначала сделать умножение в скобках, а затем умножить на полученный результат.
Например: 2 × (5 × 3) = 2 × 15 = 30.
Чтобы умножить число на сумму, сначала необходимо выполнить сложение, а потом умножить число на результат, который получился.
Например: 6 × (2 + 4) = 6 × 6 = 36.
Если при умножении хотя бы один множитель будет равным нулю, то и само произведение также будет равно нулю.
Например, для любых чисел a, b, c будет верным такое равенство: 0 × a × b × c = 0.
Таким образом, при умножении любого числа на 0, мы будем брать это число 0 раз, т. е, мы не будем брать его не разу, а значит, в результате ничего и не получится.
В случае, когда мы умножаем ноль на любое число, мы будем находить сумму нулей, но она, как известно, равна 0.
При умножении любого целого числа на единицу в результате всегда получится то же самое число. Другими словами, при умножении на единицу умножаемое число никогда не изменяется.
Например: а × 1 = а.
Если в произведении двух чисел один из сомножителей будет единицей, то произведение будет равным второму сомножителю:
a × 1 = 1 × a = a.
Так как при умножении любого числа на единицу это число берется только один раз, то в результате можно получить только это же число.
А если мы умножаем единицу на любое число, например, 1 × 9, то мы будем находить сумму девяти единиц, другими словами, то количество единиц, из которых и состоит данное число.
Поэтому сумма этих единиц будет равна данному числу:
1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 9.
Умножение многозначного числа на однозначное
Чтобы умножить многозначное на однозначное число, необходимо умножить это однозначное число на количество единиц в разряде многозначного числа, после чего все полученные результаты сложить.
Например, нам следует умножить: 985 × 4.
Мы будем складывать число 985 четыре раза: 985 + 985 + 985 + 985.
Нам нужно каждое из слагаемых 985 представить в виде суммы его разрядных слагаемых: 900 + 85 + 5.
Само выражение будет выглядеть следующим образом:
900 + 80 + 5 + 900 + 80 + 5 + 900 + 80 + 5 + 900 + 80 +5.