В данной публикации мы рассмотрим, как можно найти радиус вписанного в куб шара (сферы), если известна длина ребра куба или его диагональ.
Примечание: Напомним, что в любой куб можно вписать шар.
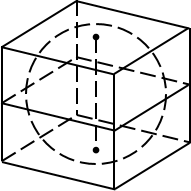
Для начала выполним чертеж.
- шар касается всех 6 граней куба (на рисунке показаны только 4 точки касания);
- центр шара – точка O, которая также является центром куба.
Радиус шара (R), вписанного в куб, равняется половине его ребра, т.е.:
R = a/2, где “a” – ребро куба (является стороной его грани).
Чтобы было понятнее, выполним сечение, параллельное одной из граней куба и проходящее через точки касания шара двух других параллельных друг другу граней. Это сечение, в том числе, проходит через середины соответствующих сторон.
Таким образом, мы получим квадрат со вписанной окружностью, радиус которой равняется половине его стороны, которая в свою очередь равна ребру куба.
Радиус вписанного шара через диагональ куба
Если известна длина диагонали куба (примем ее за “d”), радиус вписанного в него шара (R) можно вычислить так:
Радиус вписанной сферы куба представляет собой половину ребра куба, так как диаметр такой сферы точно совпадает с самим ребром. Поэтому чтобы найти ребро куба через радиус вписанной сферы, нужно умножить последний на два. (рис.2.2)
a=2r
Найти площадь стороны куба можно как площадь квадрата, стороной которого является ребро куба. Тогда, вместо того чтобы возводить во вторую степень ребро, нужно возвести удвоенный радиус вписанной в куб сферы. Площадь боковой поверхности куба и площадь полной поверхности куба будут равны четырем и шести таким площадям соответственно, так как они представлены эти количеством граней куба.
S=a^2=4r^2
S_(б.п.)=4S=16r^2
S_(п.п.)=6S=24r^2
Чтобы вычислить объем, необходимо возвести в куб ребро a или удвоенный радиус вписанной сферы. Таким образом, мы получим, что объем куба через радиус сферы, вписанной в него, равен кубу этого радиуса, умноженному на 8.
V=a^3=8r^3
Периметр куба, как сумма длин всех ребер по одной стороне, равен произведению длины одного ребра и двенадцать. Периметр, выраженный через радиус вписанной окружности, равен 24 таким радиусам.
P=12a=24r
Диагональ стороны куба, то есть диагональ квадрата, вычисляется как произведение ребра куба на корень из двух, в данном случае она будет выглядеть как произведение радиуса вписанной сферы на 2 корня из двух.
d=a√2=2√2 r
Чтобы найти диагональ куба через радиус вписанной сферы, воспользуемся готовой формулой для диагонали куба через ребро и подставим вместо него удвоенный радиус. (рис.2.1.)
D=a√3=2√3 r
Радиус окружности, описанной вокруг куба, равен половине диагонали, как видно из рисунка. Так как диагональ куба равна удвоенному произведению радиуса и корня из трех, то разделив это выражение на два, коэффициенты сократятся, и останется только радиус, умноженный на корень из трех. (рис.2.3.)
R=D/2=(2√3 r)/2=√3 r
22 января 2014
Это реальная задача из ЕГЭ по математике. Решается устно, если знать алгоритм. Тем не менее, мы подробно разберем все ключевые моменты решения этой задачи.
Задача B13. Найдите радиус сферы, вписанной в куб, ребра которого равны 42.

Самое веселое состоит в том, что искомый радиус уже присутствует на рисунке, т.е. для решения нужна обычная наблюдательность и хотя бы чуть-чуть трехмерного мышления. Тем не менее, «взгляд со стороны» на эту сферу дает нам больше уверенности в том, что мы ищем именно тот отрезок, который приведет нас к правильному ответу — радиусу.
Смотрите также:
- Сфера, описанная вокруг куба
- Случай четырехугольной пирамиды
- Сложение и вычитание дробей
- Комментарий к пробному ЕГЭ от 7 декабря
- Формулы приведения: ускоряем вычисления в тригонометрии
- Задача C1: показательные уравнения с ограничением
Как найти радиусы вписанной и описанной сфер для куба (гексаэдра)?
 Популярные ответы
Популярные ответы
- Когда буквы е, ё, ю, я обозначают два звука?
- Каким членом предложения может быть местоимение?
- Как правильно произносятся слова термин, шинель, темп?
- Как найти точки экстремума функции по графику производной?
- Как правильно: по средам (ударение на «а» или на «е»)?
- Какой официальный сайт Московского энергетического института (МЭИ)?
- На какие вопросы отвечает наречие?
- Где найти примеры сравнительных оборотов и других конструкций со словом «как»?
- Как в физике обозначается скорость движения?
- Где скачать задания по английскому языку олимпиады для школьников «Покори Воробьевы горы!»?
Куб, или гексаэдр (шестигранник) — правильный многогранник, каждая грань которого представляет собой квадрат.
- У куба 8 вершин, 12 ребер и 6 граней.
- В каждой вершине сходится 3 ребра.
- Каждая грань ограничена 4 ребрами.
У куба все грани — правильные четырехугольники (квадраты). Кубами можно замостить (покрыть без перекрытия) все пространство.
Угловые параметры куба:
- Угол между любыми двумя пересекающимися ребрами — 90°.
- Угол между непересекающимися ребрами — 0 или 90°.
- Угол наклона ребра к грани — 90°.
- Двугранный угол между двумя смежными гранями — 90°.
- Телесный угол при вершине — π/2 ≈ 1,5708 стерадиана.
Линейные параметры куба со стороной a:
- Площадь поверхности — 6·a2.
- Объём — a3.
- Высота — a.
- Большая диагональ — √3·a.
- Радиус вписаной сферы — a/2.
- Радиус описанной сферы — (√3/2)·a.
Ссылки:
- ru.wikipedia.org — Википедия: правильный многогранник;
- ru.wikipedia.org — Википедия: куб;
- ndspaces.narod.ru — свойства куба.
Дополнительно в базе данных Генона:
- Сколько существует правильных многогранников?
- Чему равна площадь поверхности куба?
- Что такое куб?
- Сколько вершин, ребер и граней у тетраэдра?
Последнее редактирование ответа: 25.03.2012
-
Оставить отзывОставить отзыв
Вы можете написать свои замечания к ответу, предложения об улучшении или просто поблагодарить автора. Комментарий, после проверки, увидят автор и редактор ответа. Будьте, пожалуйста, вежливыми. Спасибо!
Если Вы хотите получить уведомление об
исправлении ответа укажите свой e-mail:Неправильный формат адреса электронной почты
 Похожие вопросы
Похожие вопросы
В соответствии с пользовательским соглашением администрация не несет ответственности за содержание материалов, которые размещают пользователи. Для урегулирования спорных вопросов и претензий Вы можете связаться с администрацией сайта genon.ru.
Размещенные на сайте материалы могут содержать информацию, предназначенную для пользователей старше 18 лет, согласно Федерального закона №436-ФЗ от 29.12.2010 года «О защите детей от информации, причиняющей вред их здоровью и развитию». Обращение к пользователям 18+.
Ответ:5√3.
Объяснение:
Найдем радиус сферы вписанной в куб.
S сферы=4π*r².
4πr²=100π.
r²=100/4.
r=5.
Сторона куба.
5*2=10.
Диагональ основания куба. 10√2. ( пояснение √( 10²+10²)=10√2 ).
Найдем диагональ куба.
Катеты: 10; 10√2.
Диагональ 10√3.
Радиус сферы ,описанной около куба.
10√3/2.=5√3.